Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sun, 15 Oct 2017
Counting increasing sequences with Burnside's lemma
[ I started this article in March and then forgot about it. Ooops! ]
Back in February I posted an article about how there are exactly 715 nondecreasing sequences of 4 digits. I said that !!S(10, 4)!! was the set of such sequences and !!C(10, 4)!! was the number of such sequences, and in general $$C(d,n) = \binom{n+d-1}{d-1} = \binom{n+d-1}{n}$$ so in particular $$C(10,4) = \binom{13}{4} = 715.$$
I described more than one method of seeing this, but I didn't mention the method I had found first, which was to use the Cauchy-Frobenius-Redfeld-Pólya-Burnside counting lemma. I explained the lemma in detail some time ago, with beautiful illustrated examples, so I won't repeat the explanation here. The Burnside lemma is a kind of big hammer to use here, but I like big hammers. And the results of this application of the big hammer are pretty good, and justify it in the end.
To count the number of distinct sequences of 4 digits, where some sequences are considered “the same” we first identify a symmetry group whose orbits are the equivalence classes of sequences. Here the symmetry group is !!S_4!!, the group that permutes the elements of the sequence, because two sequences are considered “the same” if they have exactly the same digits but possibly in a different order, and the elements of !!S_4!! acting on the sequences are exactly what you want to permute the elements into some different order.
Then you tabulate how many of the 10,000 original sequences are left fixed by each element !!p!! of !!S_4!!, which is exactly the number of cycles of !!p!!. (I have also discussed cycle classes of permutations before.) If !!p!! contains !!n!! cycles, then !!p!! leaves exactly !!10^n!! of the !!10^4!! sequences fixed.
| Cycle class | Number of cycles | How many permutations? | Sequences left fixed |
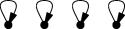 | 4 | 1 | 10,000 |
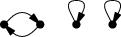 | 3 | 6 | 1,000 |
 
| 2 | 3 + 8 = 11 | 100 |

| 1 | 6 | 10 |
| 24 | 17,160 |
(Skip this paragraph if you already understand the table. The four rows above are an abbreviation of the full table, which has 24 rows, one for each of the 24 permutations of order 4. The “How many permutations?” column says how many times each row should be repeated. So for example the second row abbreviates 6 rows, one for each of the 6 permutations with three cycles, which each leave 1,000 sequences fixed, for a total of 6,000 in the second row, and the total for all 24 rows is 17,160. There are two different types of permutations that have two cycles, with 3 and 8 permutations respectively, and I have collapsed these into a single row.)
Then the magic happens: We average the number left fixed by each permutation and get !!\frac{17160}{24} = 715!! which we already know is the right answer.
Now suppose we knew how many permutations there were with each number of cycles. Let's write !!\def\st#1#2{\left[{#1\atop #2}\right]}\st nk!! for the number of permutations of !!n!! things that have exactly !!k!! cycles. For example, from the table above we see that $$\st 4 4 = 1,\quad \st 4 3 = 6,\quad \st 4 2 = 11,\quad \st 4 1 = 6.$$
Then applying Burnside's lemma we can conclude that $$C(d, n) = \frac1{n!}\sum_i \st ni d^i .\tag{$\spadesuit$}$$ So for example the table above computes !!C(10,4) = \frac1{24}\sum_i \st 4i 10^i = 715!!.
At some point in looking into this I noticed that $$\def\rp#1#2{#1^{\overline{#2}}}% \def\fp#1#2{#1^{\underline{#2}}}% C(d,n) = \frac1{n!}\rp dn$$ where !!\rp dn!! is the so-called “rising power” of !!d!!: $$\rp dn = d\cdot(d+1)(d+2)\cdots(d+n-1).$$ I don't think I had a proof of this; I just noticed that !!C(d, 1) = d!! and !!C(d, 2) = \frac12(d^2+d)!! (both obvious), and the Burnside's lemma analysis of the !!n=4!! case had just given me !!C(d, 4) = \frac1{24}(d^4 +6d^3 + 11d^2 + 6d)!!. Even if one doesn't immediately recognize this latter polynomial it looks like it ought to factor and then on factoring it one gets !!d(d+1)(d+2)(d+3)!!. So it's easy to conjecture !!C(d, n) = \frac1{n!}\rp dn!! and indeed, this is easy to prove from !!(\spadesuit)!!: The !!\st n k!! obey the recurrence $$\st{n+1}k = n \st nk + \st n{k-1}\tag{$\color{green}{\star}$}$$ (by an easy combinatorial argument1) and it's also easy to show that the coefficients of !!\rp nk!! obey the same recurrence.2
In general !!\rp nk = \fp{(n+k-1)}k!! so we have !!C(d, n) = \rp dn = \fp{(n+d-1)}n = \binom{n+d-1}d = \binom{n+d-1}{n-1}!! which ties the knot with the formula from the previous article. In particular, !!C(10,4) = \binom{13}9!!.
I have a bunch more to say about this but this article has already been in the oven long enough, so I'll cut the scroll here.
[1] The combinatorial argument that justifies !!(\color{green}{\star})!! is as follows: The Stirling number !!\st nk!! counts the number of permutations of order !!n!! with exactly !!k!! cycles. To get a permutation of order !!n+1!! with exactly !!k!! cycles, we can take one of the !!\st nk!! permutations of order !!n!! with !!k!! cycles and insert the new element into one of the existing cycles after any of the !!n!! elements. Or we can take one of the !!\st n{k-1}!! permutations with only !!k-1!! cycles and add the new element in its own cycle.)
[2] We want to show that the coefficients of !!\rp nk!! obey the same recurrence as !!(\color{green}{\star})!!. Let's say that the coefficient of the !!n^i!! term in !!\rp nk!! is !!c_i!!. We have $$\rp n{k+1} = \rp nk\cdot (n+k) = \rp nk \cdot n + \rp nk \cdot k $$ so the coefficient of the the !!n^i!! term on the left is !!c_{i-1} + kc_i!!.
[Other articles in category /math] permanent link


