Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 12 Jun 2007
How to calculate binomial coefficients
The binomial coefficient !!n\choose
k!! is usually defined as:
$${n\choose k} = {n!\over k!(n-k)!}$$
This is a fine definition, brief, closed-form, easy to prove theorems about. But these good qualities seduce people into using it for numerical calculations:
fact 0 = 1
fact (n+1) = (n+1) * fact n
choose n k = (fact n) `div` ((fact k)*(fact (n-k)))
(Is it considered bad form among Haskellites to use the
n+k patterns? The Haskell Report is decidedly
ambivalent about them.)
Anyway, this is a quite terrible way to calculate binomial
coefficients. Consider calculating !!100\choose 2!!, for example. The result
is only 4950, but to get there the computer has to calculate 100! and
98! and then divide these two 150-digit numbers. This requires the
use of bignums in languages that have bignums, and causes an
arithmetic overflow in languages that don't. A straightforward
implementation in C, for example, drops dead with an arithmetic
exception; using doubles instead, it claims that the value of 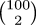 is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
Even in the best case, !!2n\choose n!!, the result is only on the order of 4n, but the algorithm has to divide a numerator of about 4nn2n by a denominator of about n2n to get it.
A much better way to calculate values of 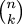 is to use the following recurrence:
is to use the following recurrence:
$${n+1\choose k+1} = {n+1\over k+1}{n\choose k}$$
This translates to code as follows:
choose n 0 = 1
choose 0 k = 0
choose (n+1) (k+1) = (choose n k) * (n+1) `div` (k+1)
This calculates !!8\choose 4!! as
!!{5\over1}{6\over2}{7\over3}{8\over4}
!!. None of the intermediate results are larger than the
final answer.An iterative version is also straightforward:
unsigned choose(unsigned n, unsigned k) {
unsigned r = 1;
unsigned d;
if (k > n) return 0;
for (d=1; d <= k; d++) {
r *= n--;
r /= d;
}
return r;
}
This is speedy, and it cannot cause an arithmetic overflow unless the
final result is too large to be represented.It's important to multiply by the numerator before dividing by the denominator, since if you do this, all the partial results are integers and you don't have to deal with fractions or floating-point numbers or anything like that. I think I may have mentioned before how much I despise floating-point numbers. They are best avoided.
I ran across this algorithm last year while I was reading the Lilavati, a treatise on arithmetic written about 850 years ago in India. The algorithm also appears in the article on "Algebra" from the first edition of the Encyclopaedia Britannica, published in 1768.
So this algorithm is simple, ancient, efficient, and convenient. And the problems with the other algorithm are obvious, or should be. Why isn't this better known?
[ Addendum 20070613: There is a followup article to this one. ]
[Other articles in category /math] permanent link


