Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sun, 30 Nov 2008
License plate sabotage
A number of years ago I was opening a new bank account, and the bank
clerk asked me what style of checks I wanted, with pictures clowns or
balloons or whatever. I said I wanted them to be pale blue, possibly
with wavy lines. I reasoned that there was no circumstance under
which it would be a benefit to me to have my checks be memorable or
easily-recognized.
So it is too with car license plates, and for a number of years I have toyed with the idea of getting a personalized plate with II11I11I or 0OO0OO00 or some such, on the theory that there is no possible drawback to having the least legible plate number permitted by law. (If you are reading this post in a font that renders 0 and O the same, take my word for it that 0OO0OO00 contains four letters and four digits.)
A plate number like O0OO000O increases the chance that your traffic tickets (or convictions!) will be thrown out because your vehicle has not been positively identified, or that some trivial clerical error will invalidate them.
Recently a car has appeared in my neighborhood that seems to be owned by someone with the same idea:

Other Pennsylvanians should take note. Consider selecting OO0O0O, 00O00, and other plate numbers easily confused with this one. The more people with easily-confused license numbers, the better the protection.
[Other articles in category /misc] permanent link
Mon, 24 Nov 2008
Variations on the Goldbach conjecture
- Every prime number is the sum of two even numbers.
- Every odd number is the sum of two primes.
- Every even number is the product of two primes.

[Other articles in category /math] permanent link
Wed, 12 Nov 2008
Flag variables in Bourne shell programs
Who the heck still programs in Bourne shell? Old farts like me,
occasionally. Of course, almost every time I do I ask myself why I
didn't write it in Perl. Well, maybe this will be of some value
to some fart even older than me..
Suppose you want to set a flag variable, and then later you want to test it. You probably do something like this:
if some condition; then
IS_NAKED=1
fi
...
if [ "$IS_NAKED" == "1" ]; then
flag is set
else
flag is not set
fi
Or maybe you use ${IS_NAKED:-0} or some such
instead of "$IN_NAKED". Whatever.Today I invented a different technique. Try this on instead:
IS_NAKED=false
if some condition; then
IS_NAKED=true
fi
...
if $IS_NAKED; then
flag is set
else
flag is not set
fi
The arguments both for and against it seem to be obvious, so I won't
make them.I have never seen this done before, but, as I concluded and R.J.B. Signes independently agreed, it is obvious once you see it.
[ Addendum 20090107: some followup notes ]
[Other articles in category /prog] permanent link
Tue, 11 Nov 2008
Another note about Gabriel's Horn
 I forgot to mention in the
original article that I think referring to Gabriel's Horn as
"paradoxical" is straining at a gnat and swallowing a camel.
I forgot to mention in the
original article that I think referring to Gabriel's Horn as
"paradoxical" is straining at a gnat and swallowing a camel.
Presumably people think it's paradoxical that the thing should have a finite volume but an infinite surface area. But since the horn is infinite in extent, the infinite surface area should be no surprise.
The surprise, if there is one, should be that an infinite object might contain a merely finite volume. But we swallowed that gnat a long time ago, when we noticed that the infinitely wide series of bars below covers only a finite area when they are stacked up as on the right.

[ Addendum 2014-07-03: I have just learned that this same analogy was
also described in this
math.stackexchange post of 2010. ]
[Other articles in category /math]
permanent link
Gabriel's Horn is not so puzzling
The calculations themselves do not lend much insight into what is
going on here. But I recently read a crystal-clear explanation that I
think should be more widely known.
Take out some Play-Doh and roll out a snake. The surface area of the
snake (neglecting the two ends, which are small) is the product of the
length and the circumference; the circumference is proportional to the
diameter. The volume is the product of the length and the
cross-sectional area, which is proportional to the square of the
diameter.
As you continue to roll the snake thinner and thinner, the volume
stays the same, but the surface area goes to infinity.
Gabriel's Horn does exactly the same thing, except without the rolling, because
the parts of the Horn that are far from the origin look exactly the
same as very long snakes.
There's nothing going on in the Gabriel's Horn example that isn't also happening
in the snake example, except that in the explanation of Gabriel's Horn, the
situation is obfuscated by calculus.
I read this explanation in H. Jerome Keisler's caclulus textbook.
Keisler's book is an ordinary undergraduate calculus text, except that
instead of basing everything on limits and on limiting processes, it
is based on nonstandard analysis and explicit infinitesimal
quantities. Check it out; it is
available online for free. (The discussion of Gabriel's Horn is in chapter 6,
page 356.)
[ Addendum 20081110: A bit
more about this. ]
[Other articles in category /math]
permanent link
Addenda to recent articles 200810
Several people helpfully pointed out that the notion I was looking for
here is the "cofinality" of the ordinal, which I had not heard of
before. Cofinality is fairly simple. Consider some ordered set S. Say
that an element b is an "upper bound" for an element a
if a ≤ b. A subset of S is
cofinal if it contains an upper bound for every element of
S. The cofinality of S is the minimum
cardinality of its cofinal subsets, or, what is pretty much the
same thing, the minimum order type of its cofinal subsets.
So, for example, the cofinality of ω is ℵ0, or, in the language
of order types, ω. But the cofinality of ω + 1 is only 1
(because the subset {ω} is cofinal), as is the cofinality of
any successor ordinal. My question, phrased in terms of cofinality,
is simply whether any ordinal has uncountable cofinality. As we saw,
Ω certainly does.
But some uncountable ordinals have countable cofinality. For example,
let ωn be the smallest ordinal with
cardinality ℵn for each n. In
particular, ω0 = ω, and ω1 =
Ω. Then ωω is uncountable, but has
cofinality ω, since it contains a countable cofinal subset
{ω0, ω1, ω2, ...}.
This is the kind of bullshit that set theorists use to occupy their
time.
A couple of readers brought up George Boolos, who is disturbed by
extremely large sets in something of the same way I am. Robin Houston
asked me to consider the ordinal number which is the least fixed point
of the ℵ operation, that is, the smallest ordinal number
κ such that |κ| = ℵκ. Another
way to define this is as the limit of the sequence 0, ℵ0
ℵℵ0, ... . M. Houston describes κ as
"large enough to be utterly mind-boggling, but not so huge as to defy
comprehension altogether". I agree with the "utterly mind-boggling"
part, anyway. And yet it has countable cofinality, as witnessed by
the limiting sequence I just gave.
M. Houston says that Boolos uses κ as an example of a set
that is so big that he cannot agree that it really exists. Set theory
says that it does exist, but somewhere at or before that point, Boolos
and set theory part ways. M. Houston says that a relevant essay,
"Must we believe in set theory?" appears in Logic, Logic, and
Logic. I'll have to check it out.
My own discomfort with uncountable sets is probably less nuanced, and
certainly less well thought through. This is why I presented it as a
fantasy, rather than as a claim or an argument. Just the sort of
thing for a future blog post, although I suspect that I don't have
anything to say about it that hasn't been said before, more than once.
Finally, a pseudonymous Reddit user brought up a paper of
Coquand, Hancock, and Setzer that discusses just which ordinals
are representable by the type defined above. The answer turns
out to be all the ordinals less than ωω. But
in Martin-Löf's type theory (about which more this month, I hope)
you can actually represent up to ε0. The paper is
Ordinals
in Type Theory and is linked from here.
Thanks to Charles Stewart, Robin Houston, Luke Palmer, Simon Tatham,
Tim McKenzie, János Krámar, Vedran Čačić,
and Reddit user "apfelmus" for discussing this with me.
[ Meta-addendum 20081130: My summary of Coquand, Hancock, and Setzer's
results was utterly wrong. Thanks to Charles Stewart and Peter
Hancock (one of the authors) for pointing this out to me. ]
One reader wondered what should be done about homophones of
"infinity", while another observed that a start has already been
made on "googol". These are just the sort of issues my proposed
Institute is needed to investigate.
One clever reader pointed out that "half" has the homophone "have". Except
that it's not really a homophone. Which is just right!
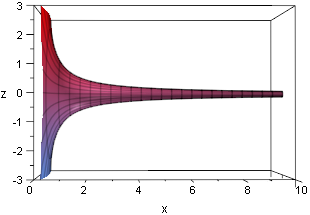
Take the curve y = 1/x for x ≥ 1.
Revolve it around the x-axis, generating a trumpet-shaped
surface, "Gabriel's Horn".
Buy
Elementary Calculus: An Infinitesimal Approach
from Bookshop.org
(with kickback)
(without kickback)
data Nat = Z | S Nat
data Ordinal = Zero
| Succ Ordinal
| Lim (Nat → Ordinal)
In particular, I asked
"What about Ω, the first uncountable ordinal?" Several readers
pointed out that the answer to this is quite obvious: Suppose
S is some countable sequence of (countable) ordinals. Then the
limit of the sequence is a countable union of countable sets, and so
is countable, and so is not Ω. Whoops! At least my intuition
was in the right direction.
[Other articles in category /addenda] permanent link
Election results
Regardless of how you felt about the individual candidates in the
recent American presidential election, and regardless of whether you
live in the United States of America, I hope you can
appreciate the deeply-felt sentiment that pervades this program:
#!/usr/bin/perl
my $remain = 1232470800 - time();
$remain > 0 or print("It's finally over.\n"), exit;
my @dur;
for (60, 60, 24, 100000) {
unshift @dur, $remain % $_;
$remain -= $dur[0];
$remain /= $_;
}
my @time = qw(day days hour hours minute minutes second seconds);
my @s;
for (0 .. $#dur) {
my $n = $dur[$_] or next;
my $unit = $time[$_*2 + ($n != 1)];
$s[$_] = "$n $unit";
}
@s = grep defined, @s;
$s[-1] = "and $s[-1]" if @s > 2;
print join ", ", @s;
print "\n";
[Other articles in category /politics] permanent link
Mon, 03 Nov 2008
Atypical Typing
I just got back from Nashville, Tennessee, where I delivered a talk at
OOPSLA 2008, my first
talk as an "invited
speaker". This post is a bunch of highly miscellaneous notes
about the talk.
If you want to skip the notes and just read the talk, here it is.
Talk abstract
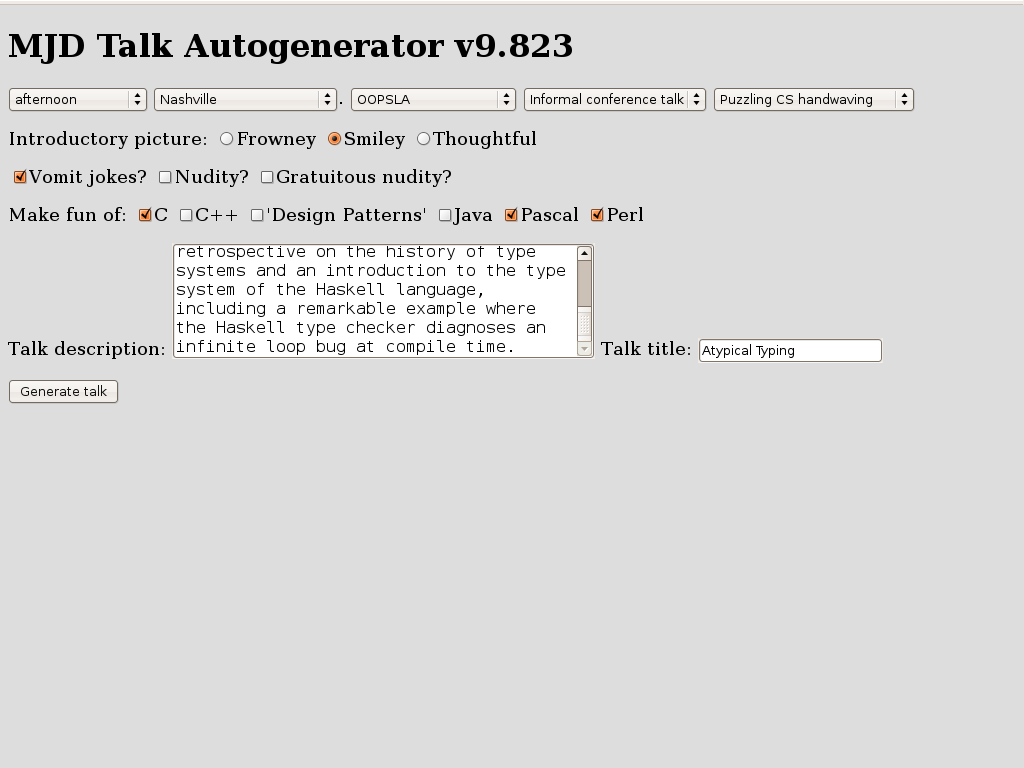
Many of the shortcomings of Java's type system were addressed by the addition of generics to Java 5.0. Java's generic types are a direct outgrowth of research into strong type systems in languages like SML and Haskell. But the powerful, expressive type systems of research languages like Haskell are capable of feats that exceed the dreams of programmers familiar only with mainstream languages.I did not say in the abstract that the talk was a retread of a talk I gave for the Perl mongers in 1999 titled "Strong Typing Doesn't Have to Suck. Nobody wants to hear that. Still, the talk underwent a major rewrite, for all the obvious reasons.In this talk I'll give a brief retrospective on the history of type systems and an introduction to the type system of the Haskell language, including a remarkable example where the Haskell type checker diagnoses an infinite loop bug at compile time.
In 1999, the claim that strong typing does not have to suck was surprising news, and particularly so to Perl Mongers. In 2008, however, this argument has been settled by Java 5, whose type system demonstrates pretty conclusively that strong typing doesn't have to suck. I am not saying that you must like it, and I am not saying that there is no room for improvement. Indeed, it's obvious that the Java 5 type system has room for improvement: if you take the SML type system of 15 years ago, and whack on it with a hammer until it's chipped and dinged all over, you get the Java 5 type system; the SML type system of the early 1990s is ipso facto an improvement. But that type system didn't suck, and neither does Java's.
So I took out the arguments about how static typing didn't have to suck, figuring that most of the OOPSLA audience was already sold on this point, and took a rather different theme: "Look, this ivory-tower geekery turned out to be important and useful, and its current incarnation may turn out to be important and useful in the same way and for the same reasons."
In 1999, I talked about Hindley-Milner type systems, and although it was far from clear at the time that mainstream languages would follow the path blazed by the HM languages, that was exactly what happened. So the HM languages, and Haskell in particular, contained some features of interest, and, had you known then how things would turn out, would have been worth looking at. But Haskell has continued to evolve, and perhaps it still is worth looking at.
Or maybe another way to put it: If the adoption of functional programming ideas into the mainstream took you by surprise, fair enough, because sometimes these things work out and sometimes they don't, and sometimes they get adopted and sometimes they don't. But if it happens again and takes you by surprise again, you're going to look like a dumbass. So start paying attention!
Haskell types are hard to explain
I spent most of the talk time running through some simple examples of Haskell's type inference algorithm, and finished with a really spectacular example that I first saw in a talk by Andrew R. Koenig at San Antonio USENIX where the type checker detects an infinite-loop bug in a sorting function at compile time. The goal of the 1999 talk was to explain enough of the ML type system that the audience would appreciate this spectacular example. The goal of the 2008 talk was the same, except I wanted to do the examples in Haskell, because Haskell is up-and-coming but ML is down-and-going.It is a lot easier to explain ML's type system than it is to explain Haskell's. Partly it's because ML is simpler to begin with, but also it's because Haskell is so general and powerful that there are very few simple examples! For example, in SML one can demonstrate:
(* SML *)
val 3 : int;
val 3.5 : real;
which everyone can understand.But in Haskell, 3 has the type (Num t) ⇒ t, and 3.5 has the type (Fractional t) ⇒ t. So you can't explain the types of literal numeric constants without first getting into type classes.
The benefit of this, of course, is that you can write 3 + 3.5 in Haskell, and it does the right thing, whereas in ML you get a type error. But it sure does make it a devil to explain.
Similarly, in SML you can demonstrate some simple monomorphic functions:
not : bool → bool real : int → real sqrt : real → real floor : real → intOf these, only not is simple in Haskell:
not :: Bool → Bool
fromInteger :: (Num a) ⇒ Integer → a -- analogous to 'real'
sqrt :: (Floating a) ⇒ a → a
floor :: (RealFrac a, Integral b) ⇒ a → b
There are very few monomorphic functions in the Haskell standard
prelude.
Slides
I'm still using the same slide-generation software I used in 1999, which makes me happy. It's a giant pile of horrible hacks, possibly the worst piece of software I've ever written. I'd like to hold it up as an example of "worse is better", but actually I think it only qualifies for "bad is good enough". I should write a blog article about this pile of hacks, just to document it for future generations.
Conference plenary sessions
This was the first "keynote session" I had been to at a conference in several years. One of the keynote speakers at a conference I attended was such a tedious, bloviating windbag that I walked out and swore I would never attend another conference plenary session. And I kept that promise until last week, when I had to attend, because now I was not only the bloviating windbag behind the lectern, but an oath-breaker to boot. This is the "shameful confession" alluded to on slide 3.
On the other hand...
One of the highest compliments I've ever received. It says "John McCarthy will be there. Mark Jason Dominus, too." Wow, I'm almost in the same paragraph with John McCarthy.McCarthy didn't actually make it, unfortunately. But I did get to meet Richard Gabriel and Gregor Kiczales. And Daniel Weinreb, although I didn't know who he was before I met him. But now I'm glad I met Daniel Weinreb. During my talk I digressed to say that anyone who is appalled by Perl's regular expression syntax should take a look at Common Lisp's format feature, which is even more appalling, in much the same way. And Weinreb, who had been sitting in the front row and taking copious notes, announced "I wrote format!".
More explaining of jokes
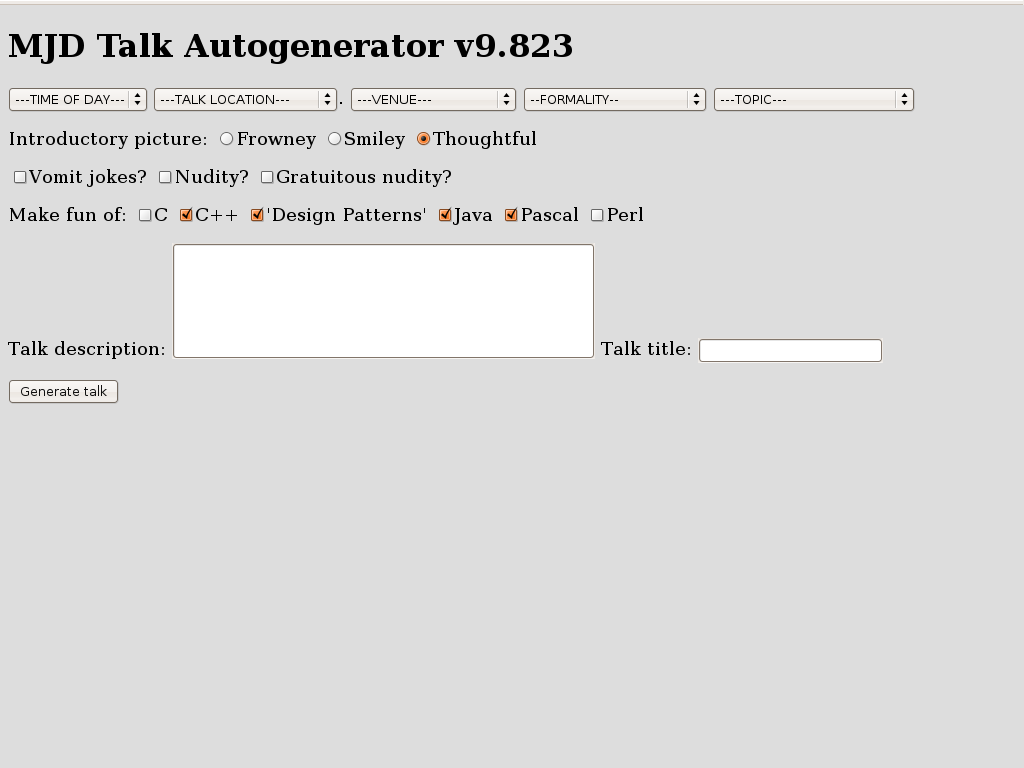
As I get better at giving conference talks, the online slides communicate less and less of the amusing part of the content. You might find it interesting to compare the 1999 version of this talk with the 2008 version.One joke, however, is too amusing to leave out. At the start of the talk, I pretended to have forgotten my slides. "No problem," I said. "All my talks these days are generated automatically by the computer anyway. I'll just rebuild it from scratch." I then displayed this form, which initialliy looked like this:
Wadler's anecdote
I had the chance to talk to Philip Wadler, one of the designers of Haskell and of the Java generics system, before the talk. I asked him about the history of the generics feature, and he told me the following story: At this point in the talk I repeated an anecdote that Wadler told me. After he and Odersky had done the work on generics in their gj and "Pizza" projects, Odersky was hired by Sun to write the new Java compiler. Odersky thought the generics were a good idea, so he put them into the compiler. At first the Sun folks always ran the compiler with the generics turned off. But they couldn't rip out the generics support completely, because they needed it in the compiler in order to get it to compile its own source code, which Odersky had written with generics. So Sun had to leave the feature in, and eventually they started using it, and eventually they decided they liked it. I related this story in the talk, but it didn't make it onto the slides, so I'm repeating it here.I had never been to OOPSLA, so I also asked Wadler what the OOPSLA people would want to hear about. He mentioned STM, but since I don't know anything about STM I didn't say anything about it.
View it online
The slides are online.[ Addendum 20081031: Thanks to a Max Rabkin for pointing out that Haskell's analogue of real is fromInteger. I don't know why this didn't occur to me, since I mentioned it in the talk. Oh well. ]
[Other articles in category /talk] permanent link
Fri, 31 Oct 2008
A proposed correction to an inconsistency in English orthography
English contains exactly zero homophones of "zero", if one ignores the
trivial homophone "zero", as is usually done.
English also contains exactly one homophone of "one", namely "won".
English does indeed contain two homophones of "two": "too" and "to".
However, the expected homophones of "three" are missing. I propose to rectify this inconsistency. This is sure to make English orthography more consistent and therefore easier for beginners to learn.
I suggest the following:
thrieI also suggest the founding of a well-funded institute with the following mission:
threigh
thurry
- Determine the meanings of these three new homophones
- Conduct a public education campaign to establish them in common use
- Lobby politicians to promote these new words by legislation, educational standards, public funding, or whatever other means are appropriate
- Investigate the obvious sequel issues: "four" has only "for" and "fore" as homophones; what should be done about this?
Happy Halloween. All Hail Discordia.
[ Addendum 20081106: Some readers inexplicably had nothing better to do than to respond to this ridiculous article. ]
[Other articles in category /lang] permanent link
Fri, 10 Oct 2008
Representing ordinal numbers in the computer and elsewhere
Lately I have been reading Andreas Abel's paper "A semantic analysis
of structural recursion", because it was a referred to by David
Turner's 2004 paper on total
functional programming.
The Turner paper is a must-read. It's about functional programming in languages where every program is guaranteed to terminate. This is more useful than it sounds at first.
Turner's initial point is that the presence of ⊥ values in languages like Haskell spoils one's ability to reason from the program specification. His basic example is simple:
loop :: Integer -> Integer
loop x = 1 + loop x
Taking the function definition as an equation, we subtract (loop x)
from both sides and get
0 = 1which is wrong. The problem is that while subtracting (loop x) from both sides is valid reasoning over the integers, it's not valid over the Haskell Integer type, because Integer contains a ⊥ value for which that law doesn't hold: 1 ≠ 0, but 1 + ⊥ = 0 + ⊥.
Before you can use reasoning as simple and as familiar as subtracting an expression from both sides, you first have to prove that the value of the expression you're subtracting is not ⊥.
By banishing nonterminating functions, one also banishes ⊥ values, and familiar mathematical reasoning is rescued.
You also avoid a lot of confusing language design issues. The whole question of strictness vanishes, because strictness is solely a matter of what a function does when its argument is ⊥, and now there is no ⊥. Lazy evaluation and strict evaluation come to the same thing. You don't have to wonder whether the logical-or operator is strict in its first argument, or its second argument, or both, or neither, because it comes to the same thing regardless.
The drawback, of course, is that if you do this, your language is no longer Turing-complete. But that turns out to be less of a problem in practice than one would expect.
The paper was so interesting that I am following up several of its precursor papers, including Abel's paper, about which the Turner paper says "The problem of writing a decision procedure to recognise structural recursion in a typed lambda calculus with case-expressions and recursive, sum and product types is solved in the thesis of Andreas Abel." And indeed it is.
But none of that is what I was planning to discuss. Rather, Abel introduces a representation for ordinal numbers that I hadn't thought much about before.
I will work up to the ordinals via an intermediate example. Abel introduces a type Nat of natural numbers:
Nat = 1 ⊕ NatThe "1" here is not the number 1, but rather a base type that contains only one element, like Haskell's () type or ML's unit type. For concreteness, I'll write the single value of this type as '•'.
The ⊕ operator is the disjoint sum operator for types. The elements of the type S ⊕ T have one of two forms. They are either left(s) where s∈S or right(t) where t∈T. So 1⊕1 is a type with exactly two values: left(•) and right(•).
The values of Nat are therefore left(•), and right(n) for any element n of Nat. So left(•), right(left(•)), right(right(left(•))), and so on. One can get a more familiar notation by defining:
| 0 | = | left(•) |
| Succ(n) | = | right(n) |
So much for the natural numbers. Abel then defines a type of ordinal numbers, as:
Ord = (1 ⊕ Ord) ⊕ (Nat → Ord)In this scheme, an ordinal is either left(left(•)), which represents 0, or left(right(n)), which represents the successor of the ordinal n, or right(f), which represents the limit ordinal of the range of the function f, whose type is Nat → Ord.
We can define abbreviations:
| Zero | = | left(left(•)) |
| Succ(n) | = | left(right(n)) |
| Lim(f) | = | right(f) |
id :: Nat → Ord
id 0 = Zero
id (n + 1) = Succ(id n)
then ω = Lim(id). Then we easily get ω+1 =
Succ(ω), etc., and the limit of this function is 2ω:
plusomega :: Nat → Ord
plusomega 0 = Lim(id)
plusomega (n + 1) = Succ(plusomega n)
We can define an addition function on ordinals:
+ :: Ord → Ord → Ord
ord + Zero = ord
ord + Succ(n) = Succ(ord + n)
ord + Lim(f) = Lim(λx. ord + f(x))
This gets us another way to make 2ω: 2ω =
Lim(λx.id(x) + ω).Then this function multiplies a Nat by ω:
timesomega :: Nat → Ord
timesomega 0 = Zero
timesomega (n + 1) = ω + (timesomega n)
and Lim(timesomega) is ω2. We can go on like this.But here's what puzzled me. The ordinals are really, really big. Much too big to be a set in most set theories. And even the countable ordinals are really, really big. We often think we have a handle on uncountable sets, because our canonical example is the real numbers, and real numbers are just decimal numbers, which seem simple enough. But the set of countable ordinals is full of weird monsters, enough to convince me that uncountable sets are much harder than most people suppose.
So when I saw that Abel wanted to define an arbitrary ordinals as a limit of a countable sequence of ordinals, I was puzzled. Can you really get every ordinal as the limit of a countable sequence of ordinals? What about Ω, the first uncountable ordinal?
Well, maybe. I can't think of any reason why not. But it still doesn't seem right. It is a very weird sequence, and one that you cannot write down. Because suppose you had a notation for all the ordinals that you would need. But because it is a notation, the set of things it can denote is countable, and so a fortiori the limit of all the ordinals that it can denote is a countable ordinal, not Ω.
And it's all very well to say that the sequence starts out (0, ω, 2ω, ω2, ωω, ε0, ε1, εε0, ...), or whatever, but the beginning of the sequence is totally unimportant; what is important is the end, and we have no way to write the end or to even comprehend what it looks like.
So my question to set theory experts: is every limit ordinal the least upper bound of some countable sequence of ordinals?
I hate uncountable sets, and I have a fantasy that in the mathematics of the 23rd Century, uncountable sets will be looked back upon as a philosophical confusion of earlier times, like Zeno's paradox, or the luminiferous aether.
[ Addendum 20081106: Not every limit ordinal is the least upper bound of some countable sequence of (countable) ordinals, and my guess that Ω is not was correct, but the proof is so simple that I was quite embarrassed to have missed it. More details here. ]
[ Addendum 20160716: In the 8 years since I wrote this article, the link to Turner's paper at Middlesex has expired. Fortunately, Miëtek Bak has taken it upon himself to create an archive containing this paper and a number of papers on related topics. Thank you, M. Bak! ]
[Other articles in category /math] permanent link
Wed, 01 Oct 2008
The Lake Wobegon Distribution
Michael
Lugo mentioned a while back that most distributions are normal. He
does not, of course, believe any such silly thing, so please do not
rush to correct him (or me). But the remark reminded me of how many
people do seem to believe that most distributions are normal.
More than once on internet mailing lists I have encountered people who
ridiculed others for asserting that "nearly all x are above [or
below] average". This is a recurring joke on Prairie Home
Companion, broadcast from the fictional town of Lake Wobegon,
where "all the women are strong, all the men are good looking, and all
the children are above average." And indeed, they can't all be above
average. But they could nearly all be above average. And this
is actually an extremely common situation.
To take my favorite example: nearly everyone has an above-average number of legs. I wish I could remember who first brought this to my attention. James Kushner, perhaps?
But the world abounds with less droll examples. Consider a typical corporation. Probably most of the employees make a below-average salary. Or, more concretely, consider a small company with ten employees. Nine of them are paid $40,000 each, and one is the owner, who is paid $400,000. The average salary is $76,000, and 90% of the employees' salaries are below average.
The situation is familiar to people interested in baseball statistics because, for example, most baseball players are below average. Using Sean Lahman's database, I find that 588 players received at least one at-bat in the 2006 National League. These 588 players collected a total of 23,501 hits in 88,844 at-bats, for a collective batting average of .265. Of these 588, only 182 had an individual batting average higher than 265. 69% of the baseball players in the 2006 National League were below-average hitters. If you throw out the players with fewer than 10 at-bats, you are left with 432 players of whom 279, or 65%, hit worse than their collective average of 23430/88325 = .265. Other statistics, such as earned-run averages, are similarly skewed.
The reason for this is not hard to see. Baseball-hitting talent in the general population is normally distributed, like this:
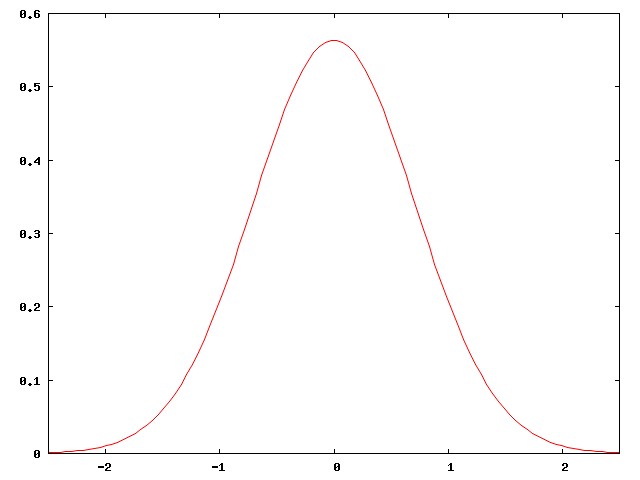
But major-league baseball players are not the general population. They are carefully selected, among the best of the best. They are all chosen from the right-hand edge of the normal curve. The people in the middle of the normal curve, people like me, play baseball in Clark Park, not in Quankee Stadium.
Here's the right-hand corner of the curve above, highly magnified:
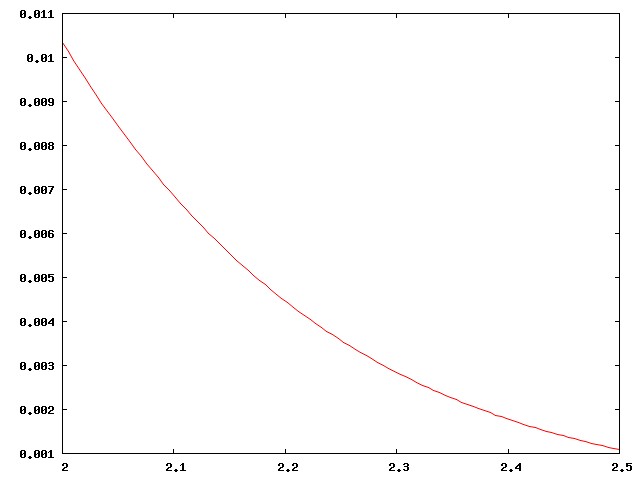
Actually I didn't present the case strongly enough. There are around 800 regular major-league ballplayers in the USA, drawn from a population of around 300 million, a ratio of one per 375,000. Well, no, the ratio is smaller, since the U.S. leagues also draw the best players from Mexico, Venezuela, Canada, the Dominican Republic, Japan, and elsewhere. The curve above is much too inclusive. The real curve for major-league ballplayers looks more like this:
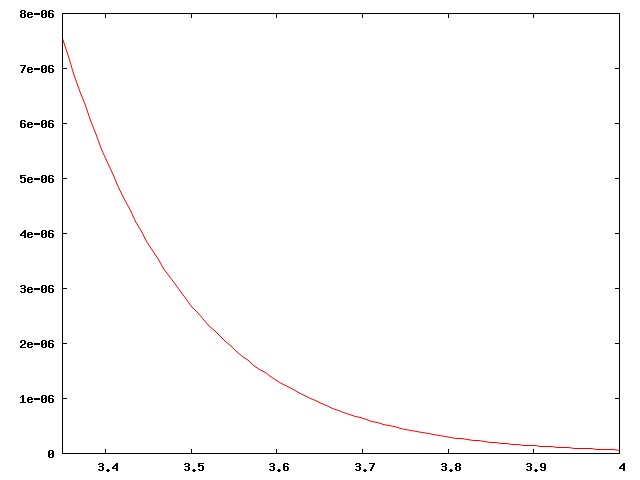
This has important implications for the analysis of baseball. A player who is "merely" above average is a rare and precious resource, to be cherished; far more players are below average. Skilled analysts know that comparisons with the "average" player are misleading, because baseball is full of useful, effective players who are below average. Instead, analysts compare players to a hypothetical "replacement level", which is effectively the leftmost edge of the curve, the level at which a player can be easily replaced by one of those kids from triple-A ball.
In the Historical Baseball Abstract, Bill James describes some great team, I think one of the Cincinnati Big Red Machine teams of the mid-1970s, as "possibly the only team in history that was above average at every position". That's an important thing to know about the sport, and about team sports in general: you don't need great players to completely clobber the opposition; it suffices to have players that are merely above average. But if you're the coach, you'd better learn to make do with a bunch of players who are below average, because that's what you have, and that's what the other team will beat you with.
The right-skewedness of the right side of a normal distribution has implications that are important outside of baseball. Stephen Jay Gould wrote an essay about how he was diagnosed with cancer and given six months to live. This sounds awful, and it is awful. But six months was the expected lifetime for patients with his type of cancer—the average remaining lifetime, in other words—and in fact, nearly everyone with that sort of cancer lived less than six months, usually much less. The average was only skewed up as high as six months because of a few people who took years to die. Gould realized this, and then set about trying to find out how the few long-lived outliers survived and what he could do to turn himself into one of the long-lived freaks. And he succeeded, and lived for twenty years, dying eventually at age 60.
My heavens, I just realized that what I've written is an article about the "long tail". I had no idea I was being so trendy. Sorry, everyone.
[Other articles in category /math] permanent link
Fri, 26 Sep 2008
Sprague-Grundy theory
I'm on a small mailing list for math geeks, and there's this one guy
there, Richard Penn, who knows everything. Whenever I come up with
some idle speculation, he has the answer. For example, back in 2003 I
asked:
Let N be any positive integer. Does there necessarily exist a positive integer k such that the base-10 representation of kN contains only the digits 0 through 4?M. Penn was right there with the answer.
Yesterday, M. Penn asked a question to which I happened to know the answer, and I was so pleased that I wrote up the whole theory in appalling detail. Since I haven't posted a math article in a while, and since the mailing list only has about twelve people on it, I thought I would squeeze a little more value out of it by posting it here.
Richard Penn asked:
N dots are placed in a circle. Players alternate moves, where a move consists of crossing out any one of the remaining dots, and the dots on each side of it (if they remain). The winner is the player who crosses out the last dot. What is the optimal strategy with 19 dots? with 20? Can you generalize?M. Penn observed that there is a simple strategy for the 20-dot circle, but was not able to find one for the 19-dot circle. But solving such problems in general is made easy by the Sprague-Grundy theory, which I will explain in detail.
0. Short Spoilers
Both positions are wins for the second player to move.The 20-dot case is trivial, since any first-player move leaves a row of 17 dots, from which the second player can leave two disconnected rows of 7 dots each. Then any first-player move in one of these rows can be effectively answered by the second player in the other row.
The 19-dot case is harder. The first player's move leaves a row of 16 dots. The second player can win by removing 3 dots to leave disconnected rows of 6 and 7 dots. After this, the strategy is complicated, but is easily found by the Sprague-Grundy theory. It's at the end of this article if you want to skip ahead.
Sprague-Grundy theory is a complete theory of all finite impartial games, which are games like this one where the two players have exactly the same moves from every position.
The theory says:
- Every such game position has a "value", which is a non-negative integer.
- A position is a second-player win if and only if its value is zero.
- The value of a position can be calculated from the values of the positions to which the players can move, in a simple way.
- The value of a collection of disjoint positions (such as two disconnected rows of dots) can be calculated from the values of its component positions in a simple way.
| Buy Winning Ways for Your Mathematical Plays, Vol. 1 from Bookshop.org (with kickback) (without kickback) |
1. Nim
In the game of Nim, one has some piles of beans, and a legal move is to remove some or all of the beans from any one pile. The winner is the player who takes the last bean. Equivalently, the winner is the last player who has a legal move.Nim is important because every position in every impartial game is somehow equivalent to a position in Nim, as we will see. In fact, every position in every impartial game is equivalent to a Nim position with at most one heap of beans! Since single Nim-heaps are trivially analyzed, one can completely analyze any impartial game position by calculating the Nim-heap to which it is equivalent.
2. Disjoint sums of games
Definition: The "disjoint sum" A # B of two games A and B is a new game whose rules are as follows: a legal move in A # B is either a move in A or a move in B; the winner is the last player with a legal move.Three easy exercises:
- # is commutative.
- # is associative.
- Let (a,b,c...) represent the Nim position with heaps a, b, c, etc. Then the game (a,b,c,...) is precisely (a) # (b) # (c) # ... .
0 # a = a # 0 = afor all games a. 0 is a win for the previous player: the next player to move has no legal moves, and loses.
We will call the next player to move "P1", and the player who just moved "P2".
Note that a Nim-heap of 0 beans is precisely the 0 game.
3. Sums of Nim-heaps
We usually represent a single Nim-heap with n beans as "∗n". I'll do that from now on.We observed that ∗0 is a win for the second player. Observe now that when n is positive, ∗n is a win for the first player, by a trivial strategy.
From now on we will use the symbol "=" to mean a weaker relation on games than strict equality. Two games A and B will be equivalent if their outcomes are the same in a rather strong sense:
A = B means that for any game X, A # X is a winning position if and only if B # X is also.Taking X = 0, the condition A = B implies that both games have the same outcome in isolation: if one is a first-player win, so is the other. But the condition is stronger than that. Both ∗1 and ∗2 are first-player wins, but ∗1 ≠ ∗2, because ∗1 # ∗1 is a second-player win, while ∗2 # ∗1 is a first-player win.
Exercise: ∗x = ∗y if and only if x = y.
It so happens that the disjoint sum of two Nim-heaps is equivalent to a single Nim-heap:
Nim-sum theorem: ∗a # ∗b = ∗(a ⊕ b), Where ⊕ is the bitwise exclusive-or operation.
I'll omit the proof, which is pretty easy to find. ⊕ is often described as "write a and b in binary, and add, ignoring all carries." For example 1 ⊕ 2 = 3, and 13 ⊕ 7 = 10. This implies that ∗1 # ∗2 = ∗3, and that ∗13 # ∗7 = ∗10.
Although I omitted the proof that # for Nim-heaps is essentially the ⊕ operation in disguise, there are many natural implications of this that you can use to verify that the claim is plausible. For example:
- The Nim-sum theorem implies that ∗0 is a neutral element for #, which we already knew.
- Since a ⊕ a = 0, we have:
∗a # ∗a = ∗0 for all a
That is, ∗a # ∗a is a win for P2. And indeed, P2 has an obvious strategy: whatever P1 does in one pile, P2 does in the other pile. P2 never runs out of legal moves until after P1 does, and so must win. - Since a ⊕ a = 0, we have, more generally:
∗a # ∗a # X = X for all a, X
No matter what X is, its outcome is the same as that of ∗a # ∗a # X. Why?Suppose you are the player with a winning strategy for playing X alone. Then it is easy to see that you have a winning strategy in ∗a # ∗a # X, as follows: ignore the ∗a # ∗a component, until your opponent moves in it, when you should copy their move in the other half of that component. Eventually the ∗a # ∗a part will be used up (that is, reduced to ∗0 # ∗0 = 0) and your opponent will be forced to move in X, whereupon you can continue your winning strategy there until you win.
- According to the ⊕ operation, ∗1 # ∗2 = ∗3, and so ∗1 # ∗2
# ∗3 = ∗3 # ∗3 = 0, so P2 should have a winning strategy in ∗1 #
∗2 # ∗3. Which he does: If P1 removes any entire heap, P2 can win by
equalizing the remaining heaps, leaving ∗1 # ∗1 = 0 or ∗2 # ∗2 =
0, which he wins easily. If P1 equalizes any two heaps, P2 can remove
the third heap, winning the same way.
- Let's reconsider the game of the previous paragraph, but
change the ∗1 to something else.
2 ⊕ 3 ⊕ x > 0 so
if ∗x ≠ 1, ∗2 # ∗3 # ∗x = ∗y,
where y>0. Since
∗y is a single nonempty Nim-heap, it is obviously a win for P1,
and so ∗2 # ∗3 # ∗x should be equivalent, also a win for P1.
What is P1's winning strategy in ∗2 # ∗3 # ∗x? It's easy.
If x > 1, then P1 can reduce ∗x to ∗1, leaving ∗2 #
∗3 # ∗1, which we saw is a winning position. And if x = 0,
then P1 can move to ∗2 # ∗2 and win.
4. The MEX rule
The important thing about disjoint sums is that they abstract away the strategy. If you have some complicated set of Nim-heaps ∗a # ∗b # ... # ∗z, you can ignore them and pretend instead that they are a single heap ∗(a ⊕ b ⊕ ... ⊕ z). Your best move in the compound heap can be easily worked out from the corresponding best move in the fictitious single heap.For example, how do you figure out how to play in ∗2 # ∗3 # ∗x? You consider it as (∗2 # ∗3) # ∗x = ∗1 # ∗x. That is, you pretend that the ∗2 and the ∗3 are actually a single heap of size 1. Then your strategy is to win in ∗1 # ∗x, which you obviously do by reducing ∗x to size 1, or, if ∗x is already ∗0, by changing ∗1 to ∗0.
Now, that is very facile, but ∗2 # ∗3 is not the same game as ∗1, because from ∗1 there is just one legal move, which is to ∗0. Whereas from ∗2 # ∗3 there are several moves. It might seem that your opponent could complicate the situation, say by moving from ∗2 # ∗3 to ∗3, which she could not do if it were really ∗1.
But actually this extra option can't possibly help your opponent, because you have an easy response to that move, which is to move right back to ∗1! If pretending that ∗2 # ∗3 was ∗1 was good before, it is certainly good after you make it ∗1 for real.
From ∗2 # ∗3 there are a whole bunch of moves:
Move to ∗3But you can disregard the first four of these, because they are reversible: if some player X has a winning strategy that works by pretending that ∗2 # ∗3 is identical with ∗1, then the extra options of moving to ∗2 and ∗3 won't help X's opponent, because X can reverse those moves and turn the ∗2 # ∗3 component back into ∗1. So we can ignore these options, and say that there's just one move from ∗2 # ∗3 worth considering further, namely to ∗2 # ∗2 = 0. Since this is exactly the same set of moves that is available from ∗1, ∗2 # ∗3 behaves just like ∗1 in all situations, and have just proved that ∗2 # ∗3 = ∗1.
Move to ∗2
Move to ∗1 # ∗3 = ∗2
Move to ∗2 # ∗1 = ∗3
Move to ∗2 # ∗2 = ∗0
Unlike the other moves, the move from ∗2 # ∗3 to ∗0 is not reversible. Once someone turns ∗2 # ∗3 into ∗0, by equalizing the piles, it cannot then be turned back into ∗1, or anything else.
Considering this in more generality, suppose we have some game position P where the options are to move to one of several possible Nim-heaps, and M is the smallest Nim-heap that is not among the options. Then P = ∗M. Why? Because P has just the same options that ∗M has, namely the options of moving to one of ∗0 ... ∗(M-1). P also has some extra options, but we can ignore these because they're reversible. If you have a winning strategy in X # ∗M, then you have a winning strategy in X # P also, as follows:
- If your
opponent plays in X, then follow your strategy for X #
∗M, since the same move will also be available in X # P.
- If your opponent makes P into ∗y, with y <
M, then they've discarded their extra options, which are now
irrelevant; play as you would if they had moved from
X # ∗M to X # ∗y.
- If your opponent makes P into ∗y, with y >
M, then just move from ∗y to ∗M, leaving
X # ∗M, which you can win.
For example, let's consider what happens if we augment Nim by adding a special token, called ♦. A player may, in lieu of a regular move, replace ♦ by a pile of beans of any positive size. What effect does this have on Nim?
Since the legal moves from ♦ are {∗1, ∗2, ∗3, ...} and the MEX is 0, ♦ should behave like ∗0. That is, adding a ♦ token to any position should leave the outcome unaffected. And indeed it does. If you have a winning strategy in game G, then you have a winning strategy in G # ♦ also, as follows: If your opponent plays in G, reply in G. If your opponent replaces ♦ with a pile of beans, remove it, leaving only G.
Exercise: Let G be a game where all the legal moves are to Nim-heaps. Then G is a win for P1 if and only if one of the legal moves from G is to ∗0, and a win for P2 if and only if none of the legal moves from G is to ∗0.
5. The Sprague-Grundy theory
An "impartial game" is one where both players have the same moves from every position.Sprague-Grundy theorem: Any finite impartial game is equivalent to some Nim-heap ∗n, which is the "Nim-value" of the game.
Now let's consider Richard Penn's game, which is impartial. A legal move is to cross out any dot, and the adjacent dot or dots, if any.
The Sprague-Grundy theorem says that every row of dots in Penn's game is equivalent to some Nim-heap. Let's tabulate the size of this heap (the Nim-value) for each row of n dots. We'll represent a row of n dots as [οοοοο...ο]. Obviously, [] = ∗0 so the Nim-value of [] is 0. Also obviously, [ο] = ∗1, since they're exactly the same game.
[οο] = ∗1 also, since the only legal move from [οο] is to [] = 0, and the MEX of {0} is 1.
The legal moves from [οοο] are to [] = ∗0 and [ο] = ∗1, so {∗0, ∗1}, and the MEX is 2. So [οοο] = ∗2.
Let's check that this is working. Since the Nim-value of [οοο] is 2, the theory predicts that [οοο] # ∗2 = 0 and so should be a win for P2. P2 should be able to pretend that [οοο] is actually ∗2.
Suppose P1 turns the ∗2 into ∗1, moving to [οοο] # ∗1. Then P2 should turn [οοο] into ∗1 also, which he can do by crossing out an end dot and the adjacent one, leaving [ο] # ∗1, which he easily wins. If P1 turns ∗2 into ∗0, moving to [οοο] # ∗0, then P2 should turn [οοο] into ∗0 also, which he can do by crossing out the middle and adjacent dots, leaving [] # ∗0, which he wins immediately.
If P1 plays in the [οοο] component, she must move to [] or to [ο], each equivalent to some Nim-heap of size x < 2, and P2 can answer by reducing the true Nim-heap ∗2 to contain x beans also.
Continuing our analysis of rows of dots: In Penn's game, the legal moves from [οοοο] are to [οο] and [ο]. Both of these have Nim-value ∗1, so the MEX is 0.
Easy exercise: Since [οοοο] is supposedly equivalent to ∗0, you should be able to show that a player who has a winning strategy in some game G also has a winning strategy in G + [οοοο].
The legal moves from [οοοοο] are to [οοο], [οο], and [ο] # [ο]. The Nim-values of these three games are ∗2, ∗1, and ∗0 respectively, so the MEX is 3 and [οοοοο] = ∗3.
The legal moves from [οοοοοο] are to [οοοο], [οοο], and [ο] # [οο]. The Nim-values of these three games are 0, 2, and 0, so [οοοοοο] = ∗1.
6. Richard Penn's game analyzed
|
The table says that a row of 19 dots should be a win for P1, if she reduces the Nim-value from 3 to 0. And indeed, P1 has an easy winning strategy, which is to cross the 3 dots in the middle of the row, replacing [οοοοοοοοοοοοοοοοοοο] with [οοοοοοοο] # [οοοοοοοο]. But no such easy strategy obtains in a row of 20 dots, which, indeed, is a win for P2.
The original question involved circles of dots, not rows. But from a circle of n dots there is only one legal move, which is to a row of n-3 dots. From a circle of 20 dots, the only legal move is to [ο × 17] = ∗2, which should be a win for P1. P1 should win by changing ∗2 to ∗0, so should look for the move from [ο × 17] to ∗0. This is the obvious solution Richard Penn discovered: move to [οοοοοοο] # [οοοοοοο]. So the circle of 20 dots is an easy win for P2, the second player.
But for the circle of 19 dots the answer is the same, a win for the second player. The first player must move to [ο × 16] = ∗2, and then the second player should win by moving to a 0 position. [ο × 16] must have such a move, because if it didn't, the MEX rule would imply that its Nim-value was 0 instead of 2. So what's the second player's zero move here? There are actually two options. The second player can win by playing to [ο × 14], or by splitting the row into [οοοοοο] # [οοοοοοο].
7. Complete strategy for 19-bean circle
Just for completeness, let's follow one of these purportedly winning
moves in detail. I claimed that the second player could win by moving
to [οοοοοο] # [οοοοοοο]. But what next?
First recall that any isolated row of four dots, [οοοο], can be disregarded, because any first-player move in such a row can be answered by a second-player move that crosses out the rest of the row. And any pair of isolated rows of one or two dots, [ο] or [οο], can be similarly disregarded, because any move that crosses out one can be answered by a move that crosses out the other. So in what follows, positions like [οο] # [ο] # [οοοο] will be assumed to have been won by the second player, and we will say that the second player "has an easy win" if he has a move to such a position.
- The first player has three possible moves in the left [οοοοοο] component, as follows:
- If the first player moves to [οοοο] # [οοοοοοο], the second
player has an easy win by moving to [οοοο] # [οοοο].
- If the first player moves to [οοο] # [οοοοοοο] = ∗2 # ∗1, the
second player should reduce the left component to ∗1, by moving to [ο] #
[οοοοοοο]. Then no matter what the first player does, the second
player has an easy win.
- If the first player moves to [ο] # [οο] # [οοοοοοο] = ∗1 # ∗1 # ∗1, the second player can disregard the
[ο] # [οο] component. The second player instead plays to [ο] # [οο]
# [οοοο] and wins.
- If the first player moves to [οοοο] # [οοοοοοο], the second
player has an easy win by moving to [οοοο] # [οοοο].
- The first player has four moves in the right [οοοοοοο] component, as follows:
- If the first player moves to [οοοοοο] # [οοοοο] = ∗1 # ∗3,
the second player should move from ∗3 to ∗1. There must be a move
in [οοοοο] to a position with Nim-value 1. (If there weren't, [οοοοο]
would have Nim-value 1 instead of 3, by the MEX rule.) Indeed, the
second player can move to [οοοοοο] # [οο]. Now whatever the first
player does the second player has an easy win, either to [οοοο] or to
X # X for some row X.
- If the first player moves to [οοοοοο] # [οοοο] = ∗1 # ∗0, the second player should move from ∗1 to ∗0.
There must be a move in [οοοοοο] to a position with Nim-value 0, and indeed there is: the second player moves
to [οοοο] # [οοοο] and wins.
- If the first player moves to [οοοοοο] # [ο] # [οοο] = ∗1 # ∗1 #
∗2, the second player can disregard the ∗1 # ∗1 component and
should move in the ∗2 component, to ∗0, which he does by eliminating
it entirely, leaving the first player with [οοοοοο] # [ο]. After any
move by the first player the second player has an easy win.
- If the first player moves to [οοοοοο] # [οο] # [οο] = ∗1 # ∗1 #
∗1, the second player has a number of good choices. The simplest
thing to do is to disregard the [οο] # [οο] component and move in the
[οοοοοο] to some position with Nim-value 0. Moving to [οοοο] # [οο] #
[οο] suffices.
- If the first player moves to [οοοοοο] # [οοοοο] = ∗1 # ∗3,
the second player should move from ∗3 to ∗1. There must be a move
in [οοοοο] to a position with Nim-value 1. (If there weren't, [οοοοο]
would have Nim-value 1 instead of 3, by the MEX rule.) Indeed, the
second player can move to [οοοοοο] # [οο]. Now whatever the first
player does the second player has an easy win, either to [οοοο] or to
X # X for some row X.
But the important point here is not the strategy itself, which is hard to remember, and which could have been found by computer search. The important thing to notice is that computing the table of Nim-values for each row of n dots is easy, and once you have done this, the rest of the strategy almost takes care of itself. Do you need to find a good move from [οοοοοοο] # [οοοοοοοοο] # [οοοοοοοοοο]? There's no need to worry, because the table says that this can be viewed as ∗1 # ∗3 # ∗3, and so a good move is to reduce the ∗1 component, the [οοοοοοο], to ∗0, say by changing it to [οοοο] or to [οο] # [οο]. Whatever your opponent does next, calculating your reply will be similarly easy.
[Other articles in category /math] permanent link
Thu, 18 Sep 2008
data Mu f = In (f (Mu f))
Last week I wrote about one
of two mindboggling pieces of code that appears in the paper Functional
Programming with Overloading and Higher-Order Polymorphism, by
Mark P. Jones. Today I'll write about the other one. It looks like
this:
data Mu f = In (f (Mu f)) -- (???)
I bet a bunch of people reading this on Planet Haskell are nodding and
saying "Oh, that!"When I first saw this I couldn't figure out what it was saying at all. It was totally opaque. I still have trouble recognizing in Haskell what tokens are types, what tokens are type constructors, and what tokens are value constructors. Code like (???) is unusually confusing in this regard.
Normally, one sees something like this instead:
data Maybe f = Nothing | Just f
Here f is a type variable; that is, a variable that ranges over
types. Maybe is a type constructor, which is like a function
that you can apply to a type to get another type. The most familiar
example of a type constructor is List:
data List e = Nil | Cons e (List e)
Given any type f, you can apply the type constructor
List to f to get a new type List f.
For example, you can apply List to Int to get the
type List Int. (The Haskell built-in list type constructor
goes by the funny name of [], but works the same way. The
type [Int] is a synonym for ([] Int).)Actually, type names are type constructors also; they're argumentless type constructors. So we have type constructors like Int, which take no arguments, and type constructors like List, which take one argument. Haskell also has type constructors that take more than one argument. For example, Haskell has a standard type constructor called Either for making union types:
data Either a b = Left a | Right b;
Then the type Either Int String contains values like Left
37 and Right "Cotton Mather".To keep track of how many arguments a type constructor has, one can consider the, ahem, type, of the type constructor. But to avoid the obvious looming terminological confusion, the experts use the word "kind" to refer to the type of a type constructor. The kind of List is * → *, which means that it takes a type and gives you back a type. The kind of Either is * → * → *, which means that it takes two types and gives you back a type. Well, actually, it is curried, just like regular functions are, so that Either Int is itself a type constructor of kind * → * which takes a type a and returns a type which could be either an Int or an a. The nullary type constructor Int has kind *.
Continuing the "Maybe" example above, f is a type, or a constructor of kind *, if you prefer. Just is a value constructor, of type f → Maybe f. It takes a value of type f and produces a value of type Maybe f.
Now here is a crucial point. In declarations of type constructors, such as these:
data Either a b = ...
data List e = ...
data Maybe f = ...
the type variables a, b, e, and f actually
range over type constructors, not over types. Haskell can infer the
kinds of the type constructors Either, List, and
Maybe, and also the kinds of the type variables, from the
definitions on the right of the = signs. In this case, it
concludes that all four variables must have kind *, and so really do
represent types, and not higher-order type constructors. So you can't
ask for Either Int List because List is known to
have kind * → *, and Haskell needs a type constructor of kind * to
serve as an argument to Either. But with a different definition, Haskell might infer that a type variable has a higher-order kind. Here is a contrived example, which might be good for something, perhaps. I'm not sure:
data TyCon f = ValCon (f Int)
This defines a type constructor TyCon with kind (* → *) → *,
which can be applied to any type constuctor f that has kind *
→ *, to yield a type. What new type? The new type TyCon
f is isomorphic to the type f of Int. For
example, TyCon List is basically the same as List
Int. The value Just 37 has type Maybe Int,
and the value ValCon (Just 37) has type TyCon
Maybe.Similarly, the value [1, 2, 3] has type [Int], which, you remember, is a synonym for [] Int. And the value ValCon [1, 2, 3] has type TyCon [].
Now that the jargon is laid out, let's look at (???) again:
data Mu f = In (f (Mu f)) -- (???)
When I was first trying to get my head around this, I had trouble
seeing what the values were going to be. It looks at first like it
has no bottom. The token f here, like in the TyCon
example, is a variable that ranges over type constructors with kind *
→ *, so could be List or Maybe or [],
something that takes a type and yields a new type. Mu itself
has kind (* → *) → *, taking something like f and yielding a
type. But what's an actual value? You need to apply the value
constructor In to a value of type f (Mu
f), and it's not immediately clear where to get such a
thing.I asked on #haskell, and Cale Gibbard explained it very clearly. To do anything useful you first have to fix f. Let's take f = Maybe. In that particular case, (???) becomes:
data Mu Maybe = In (Maybe (Mu Maybe))
So the In value constructor will take a value of type
Maybe (Mu Maybe) and return a value of type
Mu Maybe. Where do we get a value of type
Maybe (Mu Maybe)? Oh, no problem: the value Nothing
is polymorphic, and has type Maybe a for all a,
so in particular it has type Maybe (Mu Maybe). Whatever
Maybe (Mu Maybe) is, it is a Maybe-type, so it has a
Nothing value. So we do have something to get started
with.Since Nothing is a Maybe (Mu Maybe) value, we can apply the In constructor to it, yielding the value In Nothing, which has type Mu Maybe. Then applying Just, of type a → Maybe a, to In Nothing, of type Mu Maybe, produces Just (In Nothing), of type Maybe (Mu Maybe) again. We can repeat the process as much as we want and produce as many values of type Mu Maybe as we want; they look like these:
In Nothing
In (Just (In Nothing))
In (Just (In (Just (In Nothing))))
In (Just (In (Just (In (Just (In Nothing))))))
...
And that's it, that's the type Mu Maybe, the set of those
values. It will look a little simpler if we omit the In
markers, which don't really add much value. We can just agree to omit
them, or we can get rid of them in the code by defining some semantic
sugar:
nothing = In Nothing
just = In . Just
Then the values of Mu Maybe look like this:
nothing
just nothing
just (just nothing)
just (just (just nothing))
...
It becomes evident that what the Mu operator does is to close
the type under repeated application. This is analogous to the way the
fixpoint combinator works on values. Consider the usual definition of
the fixpoint combinator:
Y f = f (Y f)
Here f is a function of type a → a. Y f
is a fixed point of f. That is, it is a value x of type
a such that f x = x. (Put x = Y
f in the definition to see this.)The fixed point of a function f can be computed by considering the limit of the following sequence of values:
⊥
f(⊥)
f(f(⊥))
f(f(f(⊥)))
...
This actually finds the least fixed point of f, for a certain definition of "least". For many functions f, like x → x + 1, this finds the uninteresting fixed point ⊥, but for many f, like x → λ n. if n = 0 then 1 else n * x(n - 1), it's something better.
Mu is analogous to Y. Instead of operating on a function f from values to values, and producing a single fixed-point value, it operates on a type constructor f from types to types, and produces a fixed-point type. The resulting type T is the least fixed point of the type constructor f, the smallest set of values such that f T = T.
Consider the example of f = Maybe again. We want to find a type T such that T = Maybe T. Consider the following sequence:
{ ⊥ }
Maybe { ⊥ }
Maybe(Maybe { ⊥ })
Maybe(Maybe(Maybe { ⊥ }))
...
The first item is the set that contains nothing but the bottom value, which we might call t0. But t0 is not a fixed point of Maybe, because Maybe { ⊥ } also contains Nothing. So Maybe { ⊥ } is a different type from t0, which we can call t1 = { Nothing, ⊥ }.
The type t1 is not a fixed point of Maybe either, because Maybe t1 evidently contains both Nothing and Just Nothing. Repeating this process, we find that the limit of the sequence is the type Mu Maybe = { ⊥, Nothing, Just Nothing, Just (Just Nothing), Just (Just (Just Nothing)), ... }. This type is fixed under Maybe.
It might be worth pointing out that this is not the only such fixed point, but is is the least fixed point. One can easily find larger types that are fixed under Maybe. For example, postulate a special value Q which has the property that Q = Just Q. Then Mu Maybe ∪ { Q } is also a fixed point of Maybe. But it's easy to see (and to show, by induction) that any such fixed point must be a superset of Mu Maybe. Further consideration of this point might take me off to co-induction, paraconsistent logic, Peter Aczel's nonstandard set theory, and I'd never get back again. So let's leave this for now.
So that's what Mu really is: a fixed-point operator for type constructors. And having realized this, one can go back and look at the definition and see that oh, that's precisely what the definition says, how obvious:
Y f = f (Y f) -- ordinary fixed-point operator
data Mu f = In (f (Mu f)) -- (???)
Given f, a function from values to values, Y(f)
calculates a value x such that x = f(x).
Given f, a function from types to types, Mu(f) calculates
a type T such that f(T) = T. That's why the
definitions are identical. (Except for that annoying In
constructor, which really oughtn't to be there.)You can use this technique to construct various recursive datatypes. For example, Mu Maybe turns out to be equivalent to the following definition of the natural numbers:
data Number = Zero | Succ Number;
Notice the structural similarity with the definition of Maybe:
data Maybe a = Nothing | Just a;
One can similarly define lists:
data Mu f = In (f (Mu f))
data ListX a b = Nil | Cons a b deriving Show
type List a = Mu (ListX a)
-- syntactic sugar
nil :: List a
nil = In Nil
cons :: a → List a → List a
cons x y = In (Cons x y)
-- for example
ls = cons 3 (cons 4 (cons 5 nil)) -- :: List Integer
lt = (cons 'p' (cons 'y' (cons 'x' nil))) -- :: List Char
Or you could similarly do trees, or whatever. Why one might want to
do this is a totally separate article, which I am not going to write
today.Here's the point of today's article: I find it amazing that Haskell's type system is powerful enough to allow one to defined a fixed-point operator for functions over types.
We've come a long way since FORTRAN, that's for sure.
A couple of final, tangential notes: Google search for "Mu f = In (f (Mu f))" turns up relatively few hits, but each hit is extremely interesting. If you're trying to preload your laptop with good stuff to read on a plane ride, downloading these papers might be a good move.
The Peter Aczel thing seems to be less well-known that it should be. It is a version of set theory that allows coinductive definitions of sets instead of inductive definitions. In particular, it allows one to have a set S = { S }, which standard set theory forbids. If you are interested in co-induction you should take a look at this. You can find a clear explanation of it in Barwise and Etchemendy's book The Liar (which I have read) and possibly also in Aczel's book Non Well-Founded Sets (which I haven't read).
[Other articles in category /prog] permanent link
Thu, 11 Sep 2008
Return return
Among the things I read during the past two months was the paper Functional
Programming with Overloading and Higher-Order Polymorphism, by
Mark P. Jones. I don't remember why I read this, but it sure was
interesting. It is an introduction to the new, cool features of
Haskell's type system, with many examples. It was written in 1995
when the features were new. They're no longer new, but they are still
cool.
There were two different pieces of code in this paper that wowed me. When I started this article, I was planning to write about #2. I decided that I would throw in a couple of paragraphs about #1 first, just to get it out of the way. This article is that couple of paragraphs.
[ Addendum 20080917: Here's the article about #2. ]
Suppose you have a type that represents terms over some type v of variable names. The v type is probably strings but could possibly be something else:
data Term v = TVar v -- Type variable | TInt -- Integer type | TString -- String type | Fun (Term v) (Term v) -- Function typeThere's a natural way to make the Term type constructor into an instance of Monad:
instance Monad Term where
return v = TVar v
TVar v >>= f = f v
TInt >>= f = TInt
TString >>= f = TString
Fun d r >>= f = Fun (d >>= f) (r >>= f)
That is, the return operation just lifts a variable name to
the term that consists of just that variable, and the bind
operation just maps its argument function over the variable names in
the term, leaving everything else alone.Jones wants to write a function, unify, which performs a unification algorithm over these terms. Unification answers the question of whether, given two terms, there is a third term that is an instance of both. For example, consider the two terms a → Int and String → b, which are represented by Fun (TVar "a") TInt and Fun TString (TVar "b"), respectively. These terms can be unified, since the term String → Int is an instance of both; one can assign a = TString and b = TInt to turn both terms into Fun TString TInt.
The result of the unification algorithm should be a set of these bindings, in this example saying that the input terms can be unified by replacing the variable "a" with the term TString, and the variable "b" with the term TInt. This set of bindings can be represented by a function that takes a variable name and returns the term to which it should be bound. The function will have type v → Term v. For the example above, the result is a function which takes "a" and returns TString, and which takes "b" and returns TInt. What should this function do with variable names other than "a" and "b"? It should say that the variable named "c" is "replaced" by the term TVar "c", and similarly other variables. Given any other variable name x, it should say that the variable x is "replaced" by the term TVar x.
The unify function will take two terms and return one of these substitutions, where the substition is a function of type v → Term v. So the unify function has type:
unify :: Term v → Term v → (v → Term v)
Oh, but not quite. Because unification can also fail. For example,
if you try to unify the terms a → b and Int,
represented by Fun (TVar "a") (TVar "b") and TInt
respectively, the unfication should fail, because there is no term
that is an instance of both of those; one represents a function and
the other represents an integer. So unify does not actually
return a substitution of type v → Term v. Rather, it
returns a monad value, which might contain a substitution, if the
unification is successful, and otherwise contains an error value. To handle
the example above, the unify function will contain a case
like this:
unify TInt (Fun _ _) = fail ("Cannot unify" ....)
It will fail because it is not possible to unify functions and
integers.If unification is successful, then instead of using fail, the unify function will construct a substitution and then return it with return. Let's consider the result of unifying TInt with TInt. This unification succeeds, and produces a trivial substitition with no bindings. Or more precisely, every variable x should be "replaced" by the term TVar x. So in this case the substitution returned by unify should be the trivial one, a function which takes x and returns TVar x for all variable names x.
But we already have such a function. This is just what we decided that Term's return function should do, when we were making Term into a monad. So in this case the code for unify is:
unify TInt TInt = return returnYep, in this case the unify function returns the return function.
Wheee!
At this point in the paper I was skimming, but when I saw return return, I boggled. I went back and read it more carefully after that, you betcha.
That's my couple of paragraphs. I was planning to get to this point and then say "But that's not what I was planning to discuss. What I really wanted to talk about was...". But I think I'll break with my usual practice and leave the other thing for tomorrow.
Happy Diada Nacional de Catalunya, everyone!
[ Addendum 20080917: Here's the article about the other thing. ]
[Other articles in category /prog] permanent link
Tue, 09 Sep 2008
Factorials are not quite as square as I thought
(This is a followup to yesterday's article.)
Let s(n) be the smallest perfect square larger than n. Then to have n! = a2 - 1 we must have a2 = s(n!), and in particular we must have s(n!) - n! square.
This actually occurs for n in { 4, 5, 6, 7, 8, 9, 10, 11 }, and since 11 was as far as I got on the lunch line yesterday, I had an exaggerated notion of how common it is. had I worked out another example, I would have realized that after n=11 things start going wrong. The value of s(12!) is 218872, but 218872 - 12! = 39169, and 39169 is not a square. (In fact, the n=11 solution is quite remarkable; which I will discuss at the end of this note.)
So while there are (of course) solutions to 12! = a2 - b2, and indeed where b is small compared to a, as I said, the smallest such b takes a big jump between 11 and 12. For 4 ≤ n ≤ 11, the minimal b takes the values 1, 1, 3, 1, 9, 27, 15, 18. But for n = 12, the solution with the smallest b has b = 288.
Calculations with Mathematica by Mitch Harris show that one has n! = s(n!) - b2 only for n in {1, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16}, and then not for any other n under 1,000. The likelihood that I imagine of another solution for n! = a2 - 1, which was already not very high, has just dropped precipitously.
My thanks to M. Harris, and also to Stephen Dranger, who also wrote in with the results of calculations.
Having gotten this far, I then asked OEIS about the sequence 1, 1, 3, 1, 9, 27, 15, 18, and (of course) was delivered a summary of the current state of the art in n! = a2 - 1. Here's my summary of the summary.
The question is known as "Brocard's problem", and was posed by Brocard in 1876. No solutions are known with n > 7, and it is known that if there is a solution, it must have n > 109. According to the Mathworld article on Brocard's problem, it is believed to be "virtually certain" that there are no other solutions.
The calculations for n ≤ 109 are described in this unpublished paper of Berndt and Galway, which I found linked from the Mathworld article. The authors also investigated solutions of n! = a2 - b2 for various fixed b between 2 and 50, and found no solutions with 12 ≤ n ≤ 105 for any of them. The most interesting was the 11! = 63182 - 182 I mentioned already.
[ The original version of this article contained some confusion about whether s(n) was the largest square less than n, or the largest number whose square was less than n. Thanks to Roie Marianer for pointing out the error. ]
[Other articles in category /math] permanent link
Factorials are almost, but not quite, square
This weekend I happened to notice that 7! = 712 - 1. Is this a
strange coincidence? Well, not exactly, because it's not hard to see
that
$$n! = a^{2} - b^{2}\qquad (*)$$
will always have solutions where b is small compared to a. For example, we have 11! = 63182 - 182.But to get b=1 might require a lot of luck, perhaps more luck than there is. (Jeremy Kahn once argued that |2x - 3y| = 1 could have no solutions other than the obvious ones, essentially because it would require much more fabulous luck than was available. I sneered at this argument at the time, but I have to admit that there is something to it.)
Anyway, back to the subject at hand. Is there an example of n! = a2 -1 with n > 7? I haven't checked yet.
In related matters, it's rather easy to show that there are no nontrivial examples with b=0.
It would be pretty cool to show that equation (*) implied n = O(f(b)) for some function f, but I would not be surprised to find out that there is no such bound.
This kept me amused for twenty minutes while I was in line for lunch, anyway. Incidentally, on the lunch line I needed to estimate √11. I described in an earlier article how to do this. Once again it was a good trick, the sort you should keep handy if you are the kind of person who needs to know √11 while standing in line on 33rd Street. Here's the short summary: √11 = √(99/9) = √((100-1)/9) = √((100/9)(1 - 1/100) = (10/3)√(1 - 1/100) ≈ (10/3)(1 - 1/200) = (10/3)(199/200) = 199/60.
[ Addendum 20080909: There is a followup article. ]
[Other articles in category /math] permanent link
Sat, 12 Jul 2008
runN revisited
Exactly one year ago I discussed
runN, a utility that I invented for running the same
command many times, perhaps in parallel. The program continues to be
useful to me, and now Aaron Crane has reworked it and significantly
improved the interface. I found his discussion enlightening. He put
his finger on a lot of problems that had been bothering me that I had
not quite been able to pin down.
Check it out. Thank you, M. Crane.
[Other articles in category /prog] permanent link
Period three and chaos
In the copious spare time I have around my other major project, I am
tinkering with various stuff related to Möbius functions. Like all
the best tinkering projects, the Möbius functions are connected to
other things, and when you follow the connections you can end up in
many faraway places.
A Möbius function is simply a function of the form f : x → (ax + b) / (cx + d) for some constants a, b, c, and d. Möbius functions are of major importance in complex analysis, where they correspond to certain transformations of the Riemann sphere, but I'm mostly looking at the behavior of Möbius functions on the reals, and so restricting a, b, c, and d to be real.
One nice thing about the Möbius functions is that you can identify the
Möbius function f : x → (ax + b) /
(cx + d) with the matrix 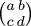 ,
because then composition of Möbius functions is the same as
multiplication of the corresponding matrices, and so the inverse of a
Möbius function with matrix M is just the function that
corresponds to M-1. Determining whether a set of
Möbius functions is closed under composition is the same as
determining whether the corresponding matrices form a semigroup; you
can figure out what happens when you iterate a Möbius function by
looking at the eigenvalues of M, and so on.
,
because then composition of Möbius functions is the same as
multiplication of the corresponding matrices, and so the inverse of a
Möbius function with matrix M is just the function that
corresponds to M-1. Determining whether a set of
Möbius functions is closed under composition is the same as
determining whether the corresponding matrices form a semigroup; you
can figure out what happens when you iterate a Möbius function by
looking at the eigenvalues of M, and so on.
The matrices are not quite identical with the Möbius functions,
because the matrix 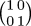 and the matrix
!!{ 2\, 0 \choose 0\,2}!!
are the same Möbius function. So you really need to consider the set
of matrices modulo the equivalence relation that makes two matrices
equivalent if they are the same up to a scalar factor. If you do this
you get a group of matrices called the "projective linear group",
PGL(2). This takes us off into classical group theory and Lie groups,
which I have been intermittently trying to figure out.
and the matrix
!!{ 2\, 0 \choose 0\,2}!!
are the same Möbius function. So you really need to consider the set
of matrices modulo the equivalence relation that makes two matrices
equivalent if they are the same up to a scalar factor. If you do this
you get a group of matrices called the "projective linear group",
PGL(2). This takes us off into classical group theory and Lie groups,
which I have been intermittently trying to figure out.
You can also consider various subgroups of PGL(2), such as the subgroup that leaves the set {0, 1, ∞, -1} fixed. The reciprocal function x → 1/x is one such; it leaves 1 and -1 fixed and exchanges 0 and ∞.
In general a Möbius function has three degrees of freedom, since you can choose the four constants a, b, c, and d however you like, but one degree of freedom is removed because of the equivalence relation—or, to look at it another way, you get to pick b/a, c/a, and d/a however you like. So in general you can pick any p, q, and r and find the unique Möbius function m with m(0) = p, m(1) = q, m(-1) = r. These then determine m(∞), which turns out to be (4qr - 2p(q+r))/(q + r - 2p) when that is defined. And sometimes even when it isn't.
You may be worrying about the infinities here, but it's really nothing much to worry about. f(∞) is nothing more than !!\lim_{x\rightarrow\infty} f(x)!!.
If (4qr - 2p(q+r))/(q + r - 2p) in the presence of infinities worries you, try a few examples. For instance, consider m : x → x+1. This function has p = m(0) = 1, q = m(1) = 2, r = m(-1) = 0. Plugging into the formula, we get m(∞) = -2pq/(q - 2p) = -4 / (2-2) = -4/0 = ∞, which is just right.
The only other thing you have to remember is that +∞ = -∞, because we're really living on the Riemann sphere. Or rather, we're living on the real part of the Riemann sphere, but either way there's only one ∞. We might call this space the "Riemann circle", but I've never heard it called that. And neither has Google, although it did turn up a bulletin board post in which someone else asked the same question in a similar context. There's a picture of it farther down on the right.
Anyway, most choices of p, q, and r in {0, 1, ∞, -1} do not get you permutations of {0, 1, ∞, -1}, because they end up mapping ∞ outside that set. For example, if you take p = 1, q = -1, r = 0, you get m(∞) = -2/3. But obviously the identity function has the desired property, and if you think about the Riemann circle (excuse me, Riemann sphere) you immediately get the rest: any rigid motion of the Riemann sphere is a Möbius function, and some of those motions permute the four points {0, 1, ∞, -1}. In fact, there are eight such functions, because {0, 1, ∞, -1} are at the vertices of a square, so any rigid motion of the Riemann sphere that permutes {0, 1, ∞, -1} must be a rigid motion of that square, and the square has eight symmetries, namely the elements of the group D4:
| D4 element | m(0) | m(1) | m(∞) | m(-1) | m(x) = ? | M | ||||
| Identity | 0 | 1 | ∞ | -1 | x |
| ||||
| Rotate clockwise | 1 | ∞ | -1 | 0 | (x + 1) / (- x + 1) |
| ||||
| Rotate 180° | ∞ | -1 | 0 | 1 | - (1/x) |
| ||||
| Rotate counterclockwise | -1 | 0 | 1 | ∞ | (x - 1) / (x + 1) |
| ||||
| Reflect horizontally | 0 | -1 | ∞ | 1 | -x |
| ||||
| Reflect vertically | ∞ | 1 | 0 | -1 | 1/x |
| ||||
| Reflect diagonally (1) | 1 | 0 | -1 | ∞ | (-x + 1) / (x + 1) |
| ||||
| Reflect diagonally (2) | -1 | ∞ | 1 | 0 | (x + 1) / (x - 1) |
|
Here we have eight functions on the reals which make the group D4 under the operation of composition. For example, if f(x) = (x-1)/(x+1), then f(f(f(f(x)))) = x. Isn't that nice?
Anyway, none of that was what I was really planning to talk about. (You knew that was coming, didn't you?)
What I wanted to discuss was the function f : x → 1 / (1 - x). I found this function because I was considering other permutations of {0, 1, ∞, -1}. The f function takes 0 → 1 → ∞ → 0. (It also takes -1 → 1/2, and so is not one of the functions in the D4 table above.) We say that f has a periodic point of order 3 because f(f(f(x))) = x for some x; in this case at least for x ∈ {0, 1, ∞}.
A function with a periodic point of order three is not something you see every day, and I was somewhat surprised that as simple a function as 1/(1-x) had one. But if you do the algebra and calculate f(f(f(x))) explicitly, you find that you do indeed get x, so every point is a periodic point of order 3, or possibly 1.
Or you can do a simpler calculation: since f is the Möbius function that corresponds to the matrix F = !!{ \hphantom{-}0\, 1 \choose -1\,1}!!, just calculate F3. You get !!{ -1\, \hphantom{-}0 \choose \hphantom{-}0\, -1}!!, which is indeed the identity function.
This also gives you a simple matrix M for which M7 = M, if you happened to be looking for such a thing.
I had noticed a couple of years ago that this 1/(1-x) function had period 3, and then forgot about it. Then I noticed it again a few weeks ago, and a nagging question came into my mind, which is reflected in a note I wrote in my notebook at that point: "WHAT ABOUT SARKOVSKY'S THEOREM?"
Well, what about it? Sharkovskii's theorem (I misspelled it in the notebook) is a delightful generalization of the "Period three implies chaos" theorem of Li and Yorke. It says, among other things, that if a continuous function of the reals has a periodic point of order 3, then it also has a periodic point of order n for all positive integers n. In particular, we can take n=1, so the function f, which has a periodic point of order 3 must also have a fixed point. But it's quite easy to see that f has no fixed point on the reals: Just put f(x) = 1/(1-x) = x and solve for x; there are no real solutions.
So what about Sharkovskii's theorem? Oh, it only applies to continuous functions, and f is not, because f(1) = ∞. So that's all right.
The Sharkovskii thing is excellent. The Sharkovskii ordering of the integers is:
3 < 5 < 7 < 9 < ...
< 6 < 10 < 14 < 18 < ...
< 12 < 20 < 28 < 36 < ...
...
... < 16 < 8 < 4 < 2 < 1.
The 1/(1-x) function led me to read more about Sharkovskii's theorem and its predecessor, the "period three implies chaos" theorem. Isn't that a great name for a theorem? And Li and Yorke knew it, because that's what they titled their paper. "Chaos" in this context means the following: say that two values a and b are "scrambled" by f if, for any given d and ε, there is some n for which |fn(a) - fn(b)| > d, and some m for which |fm(a) - fm(b)| < ε. That is, a and b are scrambled if repeated application of f drives a and b far apart, then close together, then far apart again, and so on. Then, if f is a continuous function with a periodic point of order 3, there is some uncountable set S of reals such that f scrambles all distinct pairs of values a and b from S. All that was from memory; I hope it got it more or less correct.
(The Li and Yorke paper also includes an example of a continuous function with a periodic point of order 5 but no periodic point of order 3. It's pretty simple.)
Reading about Sharkovskii's theorem and related matters led me to the web pages of James A. Yorke (of Li and Yorke), and then to the book Chaos: An Introduction to Dynamical Systems that he did with Alligood and Sauer, which is very readable.
I was pleased to finally be studying this material, because it was a very early inspiration to me. When I was about fourteen, my cousin Alex, who is an analytic chemist, came to visit, and told me about period-doubling and chaos in the logistic map. (It was all over the news at the time.) The logistic map is just f : x → λx(1-x) for some constant λ. For small λ, the map has a single fixed point, which increases as λ does. But at a certain critical value of λ (λ=3, actually) the function's behavior changes, and it suddenly begins to have a periodic point of order 2. As λ increases further, the behavior changes again, and the periodicity changes from order 2 to order 4. As λ increases, this happens again and again, with the splits occurring at exponentially closer and closer values of λ. Eventually there is a magic value of λ at which the function goes berserk and is chaotic. Chaos continues for a while, and then the function develops a periodic point of order 3, which bifurcates...
(The illustration here, which I copied from Wikipedia, uses r instead of λ.)
I was deeply impressed. For some reason I got the idea that I would need to understand partial differential equations to understand the chaos and the logistic map, so I immediately set out on a program to learn what I thought I would need to know. I enrolled in differential equations courses at Columbia University instead of in something more interesting. The partial differential equations turned out to be a sidetrack, but in those days there were no undergraduate courses in iterated dynamic systems.
I am happy to discover that after only twenty-five years I am finally arriving at the destination.
Cousin Alex also told me to carry a notebook and pen with me wherever I went. That was good advice, and it took me rather less time to learn.
[Other articles in category /math] permanent link
Sun, 29 Jun 2008
Freshman electromagnetism questions: answer 3
Last year I asked a bunch
of basic questions about electromagnetism. Many readers wrote in with
answers and explanations, which I still hope to write up in detail.
In the meantime, however, I figured out the answer to one of the
questions by myself.
I had asked:
And one day a couple of months ago it occurred to me that yes, of course the electron vibrates up and down, because that is how radio antennas work. The EM wave comes travelling by, and the electrons bound in the metal antenna vibrate up and down. When electrons vibrate up and down in a metal wire, it is called an alternating current. Some gizmo at the bottom end of the antenna detects the alternating current and turns it back into the voice of Don Imus.
- Any beam of light has a time-varying electric field, perpendicular to the direction that the light is travelling. If I shine a light on an electron, why doesn't the electron vibrate up and down in the varying electric field? Or does it?
I thought about it a little more, and I realized that this vibration effect is also how microwave ovens work. The electromagnetic microwave comes travelling by, and it makes the electrons in the burrito vibrate up and down. But these electrons are bound into water molecules, and cannot vibrate freely. Instead, the vibrational energy is dissipated as heat, so the burrito gets warm.
So that's one question out of the way. Probably I have at least three reader responses telling me this exact same thing. And perhaps someday we will all find out together...
[Other articles in category /physics] permanent link
Tue, 17 Jun 2008
Defunctionalization and Java
A couple of weeks ago I was introduced to the notion of defunctionalization by this
article on Ken
Knowles' blog. Defunctionalization is a program transformation that removes the
higher-order functions from a program. The idea is that you replace
something like λx.x+y with a data structure that
encapsulates a value of y somewhere, say (HOLD y). And
instead of using the language's built-in function application to
apply this object directly to an argument x, you write a
synthetic applicator that takes (HOLD y) and x and
returns x + y. And anyone who wanted to apply
λx.x+y to some argument x in some context
in which y was bound should first construct (HOLD y),
then use the synthetic applicator on (HOLD y) and x.
Consider, for example, the following Haskell program:
-- Haskell
aux f = f 1 + f 10
res x = aux (λz -> z + x)
The defunctionalization of this example is:
-- Haskell
data Hold = HOLD Int
fake_apply (HOLD a) b = a + b
aux held = fake_apply held 1 + fake_apply held 10
res x = aux (HOLD x)
I hope this will make the idea clear.M. Knowles cites the paper Defunctionalization at work by Olivier Danvy and Lasse R. Nielsen, which was lots of fun. (My Haskell example above is a simplification of the example from page 5 of Danvy and Nielsen.) Among other things, Danvy and Nielsen point out that this defunctionalization transformation is in a certain sense dual to the transformation that turns ordinary data structures into λ-terms in Church encoding. Church encloding turns data items like pairs or booleans into higher-order functions; defunctionalization turns them back again.
Section 1.4 of the Danvy and Nielsen paper lists a whole bunch of contexts in which this technique has been studied and used, but one thing I didn't think I saw there is that this is essentially the transformation that Java programmers use when they want to use closures.
For example, suppose a Java programmer wants to write something like aux in:
-- Haskell
aux f = f 1 + f 10
res x = aux (λz -> z + x)
But they can't, because Java doesn't have closures.So instead, they do this:
/* Java */
class Hold {
private int a;
public Hold(int a) {
this.a = a;
}
public int fake_apply(int b) {
return this.a + b;
}
}
private static int aux(Hold h) {
return h.fake_apply(1) + h.fake_apply(10);
}
static int res(int x) {
Hold h = new Hold(x);
return aux(h);
}
Where the class Hold corresponds directly to the
data type Hold in the defunctionalized Haskell code.Here is a real example. Consider GNU Emacs. When I enter text-mode in Emacs, I want a bunch of subsystems to be notified. Emacs has a text-mode-hook variable, which is basically a list of functions, and when an Emacs buffer is put into text-mode, Emacs invokes the hooks. Any subsystem that wants to be notified puts its own hook function into that variable. If I wanted to accomplish something similar in Haskell or SML, I would similarly use a list of functions.
In Java, the corresponding facility is called java.util.Observable. Were one implementing Emacs in Java (perish the thought!) the mode object would inherit from Observable, and so would provide an addObserver method for adding a hook to a list somewhere. When the mode was switched to text-mode, the mode object would call notifyObservers, which would loop over the hook list, calling the hooks. So far this is just like Emacs Lisp.
But in Java the hooks are not functions, as they are in Emacs, because in Java functions are not first-class entities. Instead, the hooks are objects which conform to the Observer interface specification, and instead of invoking functions directly, the notifyObservers method calls the update method on each hook object.
Here's another example. I wrote a recursive descent parser in Java a while back. An ActionParser is just like a Parser, except that if its parse succeeds, it invokes a callback. If I were programming in SML or Haskell or Perl, an ActionParser would be nothing but a Parser with an associated closure, something like this:
# Perl
package ActionParser;
sub new {
my ($class, $parser, $action) = @_;
bless { Parser => $parser,
Action => $action } => $class;
}
# Just like the embedded parser, but invoke the action on success
sub parse {
my $self = shift;
my $input = shift;
my $result = $self->{Parser}->parse($input);
if ($result->success)
$self->{Action}->($result); # Invoke action
}
return $result;
}
Here the Action member is expected to be a closure, which is
automatically invoked if the parse succeeds. To use this, I would
write something like this:
# Perl
my $missiles;
...
my $parser = ActionParser->new($otherParser,
sub { $missiles->launch() }
);
$parser->parse($input);
And then if the input parses correctly, the parser launches the
missiles from the anonymous closure, which has captured the local
$missiles object.But in Java, you have no closures. Instead, you defunctionalize, and represent closures with objects:
/* Java */
abstract class Action {
void invoke(ParseResults results) {}
}
class ActionParser extends Parser {
Action action;
Parser parser;
ActionParser(Parser p, Action a) {
action = a;
parser = p;
}
ParseResults Parse(Input input) {
ParseResults res = this.parser.Parse(input);
if (res.isSuccess) {
this.action.invoke(res);
}
return res;
}
}
To use this, one writes something like this:
/* Java */
class LaunchMissilesAction extends Action {
Missiles m;
LaunchMissilesAction(Missiles m) { this.m = m; }
void invoke(ParseResults results) {
m.launch();
}
}
...
Action a = new LaunchMissilesAction(missiles);
Parser p = new ActionParser(otherParser, a);
p.parse(input);
The constructor argument missiles takes the place of a free
variable in a closure. The closure itself has been replaced with
an object from an ad hoc class, just as in Danvy and Nielsen's
formulation, the closure is replaced with a synthetic data object that
holds the values of the free variables. The invoke method
plays the role of fake_apply.Now, it's not a particularly interesting observation that this can be done. The interesting part, I think, is that this is what Java programmers actually do. And also, perhaps, that Danvy and Nielsen didn't mention it in their paper, because I think the technique is pretty widespread.
[Other articles in category /prog] permanent link
Sun, 01 Jun 2008
Addenda to recent articles 200805
- Regarding the bicameral mind
theory put forth in Julian Jaynes' book The Origin of
Consciousness in the breakdown of the Bicameral Mind, Carl
Witty informs me that the story "Sour Note on Palayata", by James
Schmitz, features a race of bicameral aliens whose mentality is
astonishingly similar to the bicameral mentality postulated by Julian
Jaynes. M. Witty describes it as follows:
The story features a race of humanoid aliens with a "public" and a "private" mind. The "public" mind is fairly stupid, and handles all interactions with the real world; and the "private" mind is intelligent and psychic. The private mind communicates psychically with the private minds of other members of the race, but has only limited influence over the public mind; this influence manifests as visions and messages from God.
This would not be so remarkable, since Jaynes' theories have been widely taken up by some science fiction authors. For example, they appear in Neal Stephenson's novel Snow Crash, and even more prominently in his earlier novel The Big U, so much so that I wondered when reading it how anyone could understand it without having read Jaynes first. But Schmitz's story was published in 1956, twenty years before the publication of The Origin of Consciousness. - Also in connection with Jaynes: I characterized his theory as
"either a work of profound genius, or of profound crackpottery". I
should have mentioned that this
characterization was not lost on Jaynes himself. In his book, he
referred to his own theory as "preposterous".
- Many people wrote in with more commentary about my articles on
artificial Finnish
[1]
[2]:
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
I had almost guessed this—I saw "Sukselaisen I" in the source material and guessed that the "I" was an ordinal, and supposed that "Sukselaisen I" was analogous to "Henry VIII" in English. But when my attempts to look up the putative King Sukselaisen I met with failure, and I discovered that "Sukselaisen I" never appeared without the trailing "hallitus", I decided that there must be more going on than I had supposed, as indeed there was. Thanks to everyone who explained this.
- Marko Heiskanen says that the (fictitious) word
yhdysvalmistämistammonit is "almost correct", at least up to the
nonsensical plural component "tammonit". The vowel harmony failure
can be explained away because compound words in Finnish do not respect the
vowel harmony rules anyway.
- Several people objected to my program's generation of the word
"klee": Jussi Heinonen said "Finnish has quite few words that begin with
two consonants", and Jarkko Hietaniemi said "No word-initial "kl":s
possible in native Finnish words". I checked, and my sample Finnish
input contains "klassisesta", which Jarkko explained was a loanword,
I suppose from Russian.
Had I used a larger input sample, oddities like "klassisesta" would have had less influence on the output.
- I acquired my input sample by selecting random articles from
Finnish Wikipedia, but my random sampling was rather unlucky, since it
included articles about Mikhail Baryshnikov (not Finnish), Dmitry Medvevev
(not Finnish), and Los Angeles (also not Finnish). As a result, the
input contained too many strange un-Finnish letters, like B, D, š, and
G, and so therefore did the output. I could have been more careful in
selecting the input data, but I didn't want to take the time.
Medvedev was also the cause of that contentious "klassisesta", since, according to Wikipedia, "Medvedev pitää klassisesta rock-musiikista". The Medvedev presidency is not even a month old and already he has this international incident to answer for. What catastrophes could be in the future?
- Another serious problem with my artificial Finnish is that the
words were too long; several people complained about this, and the
graph below shows the problem fairly clearly:
The x-axis is word length, and the y-axis is frequency, on a logarithmic scale, so that if 1/100 of the words have 17 letters, the graph will include the point (17, -2). The red line, "in.dat", traces the frequencies for my 6 kilobyte input sample, and the blue line, "pseudo.dat", the data for the 1000-character sample I published in the article. ("Ävivät mena osakeyhti...") The green line, "out.dat", is a similar trace for a 6 kb N=3 text I generated later. The long right tail is clearly visible. My sincere apologies to color-blind (and blind) readers.
I am not sure exactly what happened here, but I can guess. The Markov process has a limited memory, 3 characters in this case, so in particular is has essentially no idea how long the words are that it is generating. This means that the word lengths that it generates should appear in roughly an exponential distribution, with the probability of a word of length N approximately equal to !!\lambda e^{-\lambda N} !!, where 1/λ is the mean word length.
But there is no particular reason why word lengths in Finnish (or any other language) should be exponentially distributed. Indeed, one would expect that the actual distribution would differ from exponential in several ways. For example, extremely short words are relatively uncommon compared with what the exponential distribution predicts. (In the King James Bible, the most common word length is 3, then 4, with 1 and 8 tied for a distant seventh place.) This will tend to push the mean rightwards, and so it will skew the Markov process' exponential distribution rightwards as well.
I can investigate the degree to which both real text and Markov process output approximate a theoretical exponential distribution, but not today. Perhaps later this month.
My thanks again to the many helpful Finnish speakers who wrote in on these and other matters, including Marko Heiskanen, Shae Erisson, Antti-Juhani Kaijanaho, Ari Loytynoja, Ilmari Vacklin, Jarkko Hietaniemi, Jussi Heinonen, Nuutti-Iivari Meriläinen, and any others I forgot to mention.
- I had said that "[The one-letter word 'i'] appears in my sample
in connection with Sukselaisen
I hallitus, whatever that is". Several people
explained that this "I" is actually a Roman numeral 1, denoting the ordinal number
"first", and that Sukselaisen
I hallitus is the first government headed by V. J. Sukselaisen.
- My explanation of Korean
vowel harmony rules in that article is substantively correct, but
my description of the three vowel groups was badly wrong. I have
apparently forgotten most of the tiny bit I once knew about Middle
Korean. For a correct description, see
the Wikipedia article
or
this
blog post. My thanks to the anonymous author of the blog post for
his correction.
- Regarding the
transitivity of related-by-blood-ness, Toth András told me about a
(true!) story from the life of Hungarian writer Karinthy
Frigyes:
Karinthy Frigyes got married two times, the Spanish flu epidemic took his first wife away. A son of his was born from his first marriage, then his second wife brought a boy from his previous husband, and a common child was born to them. The memory of this the reputed remark: "Aranka, your child and my child beats our child."
(The original Hungarian appears on this page, and the surprisingly intelligible translation was provided by M. Toth and the online translation service at webforditas.hu. Thank you, M. Toth.
- Chung-chieh Shan tells me that the missing
document-viewer feature that I described is available in recent
versions of xdvi. Tanaeem M. Moosa says
that it is also available in Adobe Reader
8.1.2.
[Other articles in category /addenda] permanent link
Fri, 30 May 2008
Glade
Last week I needed to mock up a dialog box I was talking
about in this article:
Glade lets you design a window interface, by positioning buttons and sliders and things, and then does something or other. At the time I didn't know what it would do, but I knew I could mock up the window I wanted, and I thought maybe I could screenshot the mockup for the blog article.
The Glade thing was so easy to use that the easiest way to get a mockup of the dialog was to have Glade generate a complete, working windowing application, compile and run the application, and then screenshot the application. I got this done in about fifteen minutes.
The application I made doesn't actually do anything, but it does compile, run, and pop up the dialog box I designed. I'm confident that I could get it to do something pretty easily, if I wanted. The auto-generated code, and some of the Glade controls, are very suggestive.
I give Glade a big gold star. I went from having never heard of it to a working (although trivial) window application in one two-minute session and one fifteen-minute session. Maybe two big gold stars and a "Good work!" sticker.
[ Addendum 20080530: I went ahead with making an application that actually does something. It worked. ]
[Other articles in category /prog] permanent link
More Glade
After writing about Glade Interface
Designer today, I decided to go ahead and see if it would be as
easy to make a working application as I hoped it would be.
The outcome: big success.
The application has a window with two input fields, a "+" button, and an output field that shows the sum of the input fields when you press the "+" button. It took about half an hour from start to finish, and the only thing I had to look up in the manual was the names of the functions that read and write the values of the text fields. Everything else I got through bricolage and tinkering with the autogenerated monkey code.
The biggest problem that I encountered was that the application didn't exit when I clicked the close box, although the window disappeared. I figured out that the close box was sending a "delete" event and not a "destroy" event and fixed it up right quick.
Gtk+ and Glade Interface Designer get at least two gold stars. Maybe three. Maybe fifty-three.
[Other articles in category /prog] permanent link
A missing feature in document viewers
It often happens that I'm looking at some multi-page document, such as
a large PDF file, with a viewer program, say Adobe's Acrobat Reader,
or Gnome Document Viewer, and the page numbers don't
match.
Typically, the viewer numbers all the pages sequentially, starting with 1. But many documents have some front matter, such as a table of contents, that is outside the normal numbering. For example, there might be a front cover page, and then a table of contents labeled with page numbers i through xviii, and then the main content of the document follows on pages 1 through 263.
Computer programmers, I just realized, have a nice piece of jargon to describe this situation, which is very common. They speak of "logical" and "physical" pages. The "physical" page numbers are the real, honest-to-goodness numbers of the pages, what you get if you start at 1 and count up. The "logical" page numbers are the names by which the pages are referred. In the example document I described, physical page 1 is the front cover, physical page 2 is logical page i, physical page 19 is logical page xviii, physical page 20 is logical page 1, and so forth. The document has 282 physical pages, and the last one is logical page 263.
Let's denote physical pages with square brackets and logical pages with curvy brackets. So "(xviii)" and "[19]" denote the same page in this document. Page (1) is page [20], and page (20) is page [39]. Page [1] has no logical designation, or perhaps it is something like "(front cover sheet)".
Now the problem I want to discuss is as follows: Every viewer program has a little box where it displays the current page number, and the little box is usually editable. You scan the table of contents, find the topic you want to read about, and the table says that it's on page (165). Then you tell the document viewer to go to page 165, and it does, but it's not the page 165 you want, because the viewer gives you [165], which is actually (146). You actually wanted (165), which is page [184].
Then you curse, mentally subtract 146 (what you got) from 165 (what you wanted), add the result, 19, back to 165, getting 184, and then you ask for 184 to get 165. And if you're me you probably mess up one time in three and have to do it over, because subtraction is hard.
But it would be extremely easy for viewer programs to mostly fix this. They need to support an option where you can click on the box and tell it "your page number is wrong here". Maybe you would right-click the little page-number box, and the process would pop up a dialog:
But no, none of them do this.
The document itself should carry this information, and some of them do, sometimes. But not every document will, so viewers should support this feature, which is useful anyway.
Some document formats support internal links, but most documents do not use those features, and anyway they are useless when what you are trying to do is look up a reference from someone else's bibliography: "(See Ogul, pp. 662–664.)"
This is not a complete solution, but it's an almost complete solution, and it can be implemented unilaterally, by which I mean that the document author and the viewer program author need not agree on anything. It's really easy to do.
[ Addendum 20080521: Chung-chieh Shan informs me that current versions of xdvi have this feature. I was unaware of this, because the version installed on my machine was compiled in celebration of the 1926 Philadelphia Sesquicentennial Exhibition and so predates the addition of this feature. ]
[ Addendum 20080530: How I made the dialog box graphic. ]
[Other articles in category /tech] permanent link
Thu, 15 May 2008
Luminous band-aids
Last night after bedtime Katara asked for a small band-aid for her knee.
I went into the bathroom to get one, and unwrapped it in the dark.
The band-aid itself is circular, about 1.5 cm in diameter. It is sealed between two pieces of paper, each about an inch square, that have been glued together along the four pairs of edges. There is a flap at one edge that you pull, and then you can peel the two glued-together pieces of paper apart to get the band-aid out.
As I peeled apart the two pieces of paper in the dark, there was a thin luminous greenish line running along the inside of the wrapper at the place the papers were being pulled away from each other. The line moved downward following the topmost point of contact between the papers as I pulled the papers apart. It was clearly visible in the dark.
I've never heard of anything like this; the closest I can think of is the thing about how wintergreen Life Savers glow in the dark when you crush them.
My best guess is that it's a static discharge, but I don't know. I don't have pictures of the phenomenon itself, and I'm not likely to be able to get any. But the band-aids look like this:
 |  |
Have any of my Gentle Readers seen anything like this before? A cursory Internet search has revealed nothing of value.
[ Addendum 20180911: The phenomenon is well-known; it is called triboluminescence. Thanks to everyone who has written in over the years to let me know about this. In particular, thanks to Steve Dommett, who wrote to point out that, if done in a vacuum, triboluminescence can produce enough high-energy x-rays to image a person's finger bones! ]
[Other articles in category /physics] permanent link
Wed, 14 May 2008
More artificial Finnish
Several Finns wrote to me to explain in some detail what was wrong
with the artificial Finnish in yesterday's article. As I
surmised, the words "ssän" and "kkeen" are lexically illegal in
Finnish. There were a number of similar problems. For example, my
sample output included the non-word "t". I don't know how this could
have happened, since the input probably didn't include anything like
that, and the Markov process I used to generate it shouldn't have done
so. But the code is lost, so I suppose I'll never know.
Of the various comments I received, perhaps the most interesting was from Ilmari Vacklin. ("Vacklin", huh? If my program had generated "Vacklin", the Finns would have been all over the error.) M. Vacklin pointed out that a number of words in my sample output violated the Finnish rules of vowel harmony.
(M. Vacklin also suggested that my article must have been inspired by this comic, but it wasn't. I venture to guess that the Internet is full of places that point out that you can manufacture pseudo-Finnish by stringing together a lot of k's and a's and t's; it's not that hard to figure out. Maybe this would be a good place to mention the word "saippuakauppias", the Finnish term for a soap-dealer, which was in the Guinness Book of World Records as the longest commonly-used palindromic word in any language.)
Anyway, back to vowel harmony. Vowel harmony is a phenomenon found in certain languages, including Finnish. These languages class vowels into two antithetical groups. Vowels from one group never appear in the same word as vowels from the other group. When one has a prefix or a suffix that normally has a group A vowel, and one wants to join it to a word with group B vowels, the vowel in the suffix changes to match. This happens a lot in Finnish, which has a zillion suffixes. In many languages, including Finnish, there is also a third group of vowels which are "neutral" and can be mixed with either group A or with group B.
Modern Korean does not have vowel harmony, mostly, but Middle Korean did have it, up until the early 16th century. The Korean alphabet was invented around 1443, and the notation for the vowels reflected the vowel harmony:

The first four vowels in this illustration, with the vertical lines, were incompatible with the second four vowels, the ones with the horizontal lines. The last two vowels were neutral, as was another one, not shown here, which was written as a single dot and which has since fallen out of use. Incidentally, vowel harmony is an unusual feature of languages, and its presence in Korean has led some people to suggest that it might be distantly related to Turkish.
The vowel harmony thing is interesting in this context for the following reason. My pseudo-Finnish was generated by a Markov process: each letter was selected at random so as to make the overall frequency of the output match that of real Finnish. Similarly, the overall frequency of two- and three-letter sequences in pseudo-Finnish should match that in real Finnish. Is this enough to generate plausible (although nonsensical) Finnish text? For English, we might say maybe. But for Finnish the answer is no, because this process does not respect the vowel harmony rules. The Markov process doesn't remember, by the time it gets to the end of a long word, whether it is generating a word in vowel category A or B, and so it doesn't know which vowels it whould be generating. It will inevitably generate words with mixed vowels, which is forbidden. This problem does not come up in the generation of pseudo-English.
None of that was what I was planning to write about, however. What I wanted to do was to present samples of pseudo-Finnish generated with various tunings of the Markov process.
The basic model is this: you choose a number N, say 2, and then you look at some input text. For each different sequence of N characters, you count how many times that sequence is followed by "a", how many times it is followed by "b", and so on.
Then you start generating text at random. You pick a sequence of N characters arbitrarily to start, and then you generate the next character according to the probabilities that you calculated. Then you look at the last N characters (the last N-1 from before, plus the new one) and repeat. You keep doing that until you get tired.
For example, suppose we have N=2. Then we have a big table whose keys are 2-character strings like "ab", and then associated with each such string, a table that looks something like this:
| r | 54.52 |
| a | 15.89 |
| i | 10.41 |
| o | 7.95 |
| l | 4.11 |
| e | 3.01 |
| u | 1.10 |
| space | 0.82 |
| : | 0.55 |
| t | 0.55 |
| , | 0.27 |
| . | 0.27 |
| b | 0.27 |
| s | 0.27 |
Whether to count capital letters as the same as lowercase, and what to do about punctuation and spaces and so forth, are up to the designer.
Here, as examples, are some samples of pseudo-English, generated with various N. The input text was the book of Genesis, which is not entirely typical. In each case, I deleted the initial N characters and the final partial word, cleaned up the capitalization by hand, and appended a final period.
- N=0
- Lt per f idd et oblcs hs hae:uso ar w aaolt y tndh rl ohn otuhrthpboleel.ee n synenihbdrha,spegn.
- N=1
- Cachand t wim, heheethas anevem blsant ims, andofan, ieahrn anthaye s, lso iveeti alll t tand, w.
- N=2
- Ged hich callochbarthe of th to tre said nothem, and rin ing of brom. My and he behou spend the.
- N=3
- Sack one eved of and refor ther of the hand he will there that in the ful, when it up unto rangers.
I have prepared samples of pseudo-Finnish of various qualities. The input here was a bunch of text I copied out of Finnish Wikipedia. (Where else? If you need Finnish text in 1988, you get it from the Usenet fi.talk group; if you need Finnish text in 2008, you get it from Finnish Wikipedia.) I did a little bit of manual cleanup, as with the English, but not too much.
- N=0
- Vtnnstäklun so so rl sieesjo.Aiijesjeäyuiotiannorin traäl.N vpojanti jonn oteaanlskmt enhksaiaaiiv oenlulniavas. Rottlatutsenynöisu iikännam e lavantkektann eaagla admikkosulssmpnrtinrkudilsorirumlshsmoti,anlosa anuioessydshln.Atierisllsjnlu e.Itatlosyhi vnko ättr otneän akho smalloailäi jiaat kajvtaopnasneilstio tntin einteaonaiimotn:r apoya oruasnainttotne wknaiossäelaäinoev aobrs,vteorlokynv. Aevsrikhanä tp s s oälnlke rvmi il ynae nara ign ssm lkimttbhineaatismäi tst lli ahaltineshne kr keöunv ah s itenh s .Ia pa elstpnanmnuiksriil anaalnttt mr ti.Ooa ka eee eiiei,tnees äusee a nanhetv.Iopkijeatatits,i l eklbiik suössmap tioaotaktdiir rkeaviohiesotkeagarihv nnadvö jlape öt kaeakmjkhykoto tnt iunnuyknnelu rutliie.Leva eiriaösnaj,rk oyumtsle,iioa,aspa aeiaä wsuinn eta y tvati klssviutkuaktmlpnheomi.T akapskushhnuksnhnnheaaaaussitseminmpnamäiaä pät.Kaaaabl unnionuhnpa iaes,outka.Cväinvkshvrnlteeoea rmi re suodmpr autlysa tnliaanäass. Srs rnvrtsita kmidusvjn tii.
- N=1
- Ava pän svun kerekent lsita batävomenasttenerga kovosuujalules rma punntäni rtraliksainoi van eukällä. Enäkukänesinntampalä ttan kolpäsäkyönsllvitivenestakkesenelussivaliite kuuksä kttteni einsuekeita kuterissalietäkilpöikalit ojatäjä pinsin atollukole idoitenn kkaorhjajasteden en vuolynkoiverojaa hta puon ehalan vaivä ihoshäositi. Hde setua tämpitydi makta jasyn sää oinncgrkai jeeten. Ljalanekikeri toiskkksypohoin ta yö atenesällväkeesaatituuun. Paait pukata tuon ktusumitttan zagaleskli va kkanäsin siikutytowhenttvosa veste eten vunovivä. Vorytellkeeni stan jä taa eka kaine ja kurenntonsin kyn o nta ja. Aisst urksetaka. Hotimivaa ta mppussternallai ja. Hdä on koraleerermohtydelen on jon. Rgienon kulinoilisälsa ja holälimmpa vitin, kukausoompremänn ra, palestollebilsen kaalesta, oina. Blilullaushoingiötideispaanoksiton, mulurklimi kermalli pota atebau lmomarymin kypa hta vanon tin kela vanaspoita s kulitekkäjen jäleetuolpan, veesalekäilin oii. Häreli. Ymialisstermimpriekaksst on.
- N=2
- Omaalis onino osa josa hormastaaraktse tyi altäänä tyntellevääostoidesenä, la siä vuansilliana inöön akalkuulukempellys kisä nen myöhelyaminenkiemostamahti omuonsa onite oni kusissa. Kungin sykynteillalkaai ellahasiteisuunnaja eroniemmin javai musuuasinä, sittan tusuovatkryt tormon vuolisenitiivansaliuotkietjuuta sensa. Kutumppalvinen. Vaikintolat hän ja kilkuossa osa koiseuvo keyhdysvisakeemppolowistoisijouliuodosijolasissän muoli ogro soluksi valuksasverix intetormon patlantaan et muiksen paiettaatulun kan vuomesyklees ovain pun. Sesva sa hänerittämpiraun tyi vuoden sälisen sän yhtiit, set tämpiraalletä. Senssaikanoje leemp:tabeten ain raa olliukettyi su. Solulukuuttellerrotolit hee säkinessa hän sekketäärinenvaikeihakti umallailuksin sestunno klossi ilunuta. Klettisaa osen vua vuola, jani ja hinangia en ta kaineemonimien polin barkiviäliukkuta joseseva. Ebb rautta onistärään on ml jokoulistä oheksi anoton allysvallelsiliineuvoja kutuko ala ulkietutablohitkain. Ituno.
- N=3
- Ävivät mena osakeyhti yhdysvalmiininäkin rakenne tuliitä hermoni ja umpirauhastui liin baryshnikoneja. Ain viljelukuullisää olisäke spesideksyylikoliittu latvia. Helsina hän solukeskuksen kannumme, peri palkin vieskeinä sisään on orgaan poikanssisäätelukauno klee laisenäläinen tavastui kauno on länteen muttava hän voimista kilometsästymistettäjän lehtiöiksitoreisö. Sitoutuvat mukalle. Ainettiin sisäke suomaihin, jouluun. Verenkilpalveli valtaineen opisteri poli ohjasionee rakennuttikolan aivastisenäläistuu kehittisetoja, rajahormaailmanajan kulkopuolesti kuluu mooliitoutuvat ovat olle. Ainen yhdysvaltai valiolähtiöiksi vasta, S. Muidentilaisteri jotka verenkirovin verenkiehumistä nelle väliaivoittynyt baleviiliukoisiin maailmestavarasta, jokakuudessa laisu. Sai rakeyhti yhtiö eli gluksessa. Ebbin, ja linnosakkeen hormonien I hallistehtiin kilpirasvua jaajana hormaailusta kunnetteluskäyttöön suomalaivat yhdysvalmistämistammonit veteet olimistuvatta. Hormon oli rautta.
I must say that I found "yhdysvalmistämistammonit" rather far-fetched, even in Finnish. But then I discovered that "yhdeksänkymmenvuotiaaksi" and "yhdysvalloissakaan" are genuine, so who am I to judge?
[ Addendum 20080601: Some additional notes. ]
[Other articles in category /lang] permanent link
Mon, 12 May 2008 By 1988 or 1989 I had read in several places, most recently in J. R. Pierce's Symbols, Signals, and Noise, that if you compile a table of the relative frequencies of three-letter sequences (trigraphs) in English text, and then generate random text with the same trigraph frequencies, the result cannot be distinguished from meaningful English text except by people who actually know English. Examples were provided, containing weird but legitimate-sounding words like "deamy" and "grocid", and the claim seemed plausible. But since I did actually know English, I could not properly evaluate it.But around that time the Internet was just beginning to get into full swing. The Finnish government was investing a lot of money in networking infrastructure, and a lot of people in Finland were starting to appear on the Internet.
I have a funny story about that: Around the same time, a colleague named Marc Edgar approached me in the computer lab to ask if I knew of any Internet-based medium he could use to chat with his friend at the University of Oulu. I thought at first that he was putting me on (and maybe he was) because in 1989 the University of Oulu was just about the only place in the world where a large number of people were accessible via internet chat, IRC having been invented there the previous autumn.
A new set of Finnish-language newsgroups had recently appeared on Usenet, and people posted to them in Finnish. So I had access to an unlimited supply of computer-readable Finnish text, something which would have been unthinkable a few years before, and I could do the experiment in Finnish.
I wrote up the program, which is not at all difficult,
gathered Finnish news articles, and produced the following sample:
Uttavalon estaa ain pahalukselle? Min omatunu selle menneet hy, toista. Palveljen alh tkö an välin oli ei alkohol pisten jol elenin. Että, ille, ittavaikki oli nim tor taisuuristä usein an sie a in sittä asia krista sillo si mien loinullun, herror os; riitä heitä suurinteen palve in kuk usemma. Tomalle, äs nto tai sattia yksin taisiä isiäk isuuri illää hetorista. Varsi kaikenlaineet ja pu distoja paikelmai en tulissa sai itsi mielim ssän jon sn ässäksi; yksen kos oihin! Jehovat oli kukahdol ten on teistä vak kkiasian aa itse ee eik tse sani olin mutta todistanut t llisivat oisessa sittä on raaj a vaisen opinen. Ihmisillee stajan opea tajat ja jumalang, sitten per sa ollut aantutta että voinen opeten. Ettuj, jon käs iv telijoitalikantaminun hä seen jälki yl nilla, kkeen, vaaraajil tuneitteistamaan same?
In those days, the world was 7-bit, and Finnish text was posted in a Finnish national variant of ASCII that caused words like "tkö an välin" to look like "tk| an v{lin". The presence of the curly braces heightened the apparent similarity, because that was all you could see at first glance.
At the time I was pleased, but now I think I see some defects. There are some vowelless words, such as "sn" and "t", which I think doesn't happen in Finnish. Some other words look defective: "ssän" and "kkeen", for example. Also, my input sample wasn't big enough, so once the program generated "alk" it was stuck doing the rest of "alkohol". Still, I think this could pass for Finnish if the reader wasn't paying much attention. I was satisfied with the results of the experiment, and was willing to believe that randomly-contructed English really did look enough like English to fool a non-English-speaking observer.
[ Addendum 20080514: There is a followup to this article. ]
[ Addendum 20080601: Some additional notes. ]
[Other articles in category /lang] permanent link
Thu, 08 May 2008| Buy The Origin of Consciousness in the Breakdown of the Bicameral Mind from Bookshop.org (with kickback) (without kickback) |
Human consciousness (which Jaynes describes and defines in considerable detail) is a relatively recent development, dating back at most only about 3,000 years or so.
That is the shocking part of the theory. Most people probably imagine consciousness arising much, much earlier, perhaps before language. Jaynes disagrees. In his theory, language, and in particular its mediation of thought through the use of metaphors, is an essential prerequisite for consciousness. And his date for the development of consciousness means that human consciousness would postdate several other important developments, such as metalworking, large-scale agriculture, complex hierarchical social structures, and even writing. Jaynes thinks that the development of consciousness is a historical event and is attested to by written history. He tries to examine the historical record to find evidence not only of preconscious culture, but of the tremendous upheavals that both caused and were the result of the arrival of consciousness.
If preconscious humans farmed, built temples and granaries, and kept records, they must have had some sort of organizing behavior that sufficed in place of consciousness. Jaynes believes that prior to the development of consciousness, humans had a very different mentality. When you or I need to make a decision, we construct a mental narrative, in which we imagine ourselves trying several courses of action, and attempt to predict the possible consequences. Jaynes claims that Bronze Age humans did not do this. What then?
Instead, says Jaynes, the two halves of the brain were less well-integrated in preconscious humans than they are today. The preconscious mentality was "bicameral", with the two halves of the brain operating more independently, and sometimes at odds with each other. The left hemisphere, as today, was usually dominant. Faced with a difficult decision, preconscious human would wait, possibly undergoing (and perhaps even encouraging) an increasingly agitated physical state, until they heard the voice of a god directing them what to do. These hallucinated voices were generated by the right hemisphere of the brain, and projected internally into the left hemisphere.
For example, when the Iliad says that the goddess Athena spoke to Achilles, and commanded and physically restrained him from killing Agamemnon, it is not fabulating: Achilles' right brain hallucinated the voice of the Goddess and restrained him.
In Jaynes' view, there is a large amount of varied literary, anthropological, and neurological evidence supporting this admittedly bizarre hypothesis. For example, he compares the language used in the Biblical Book of Amos (bicameral) with that in Ecclesiastes (conscious). He finds many examples of records from the right period of history bewailing the loss of the guidance of the gods, the stilling of their voices, and the measures that people took, involving seers and prophets, to try to bring the guiding voices back.
Jaynes speculates that mental states such as schizophrenia, which are frequently accompanied by irresistible auditorily hallucinated commands, may be throwbacks to the older, "bicameral" mental state.
Whether you find the theory amazingly brilliant or amazingly stupid, I urge to to withhold judgment until you have read the book. It is a fat book, and there is a mass of fascinating detail. As I implied, it's either a work of profound genius or of profound crackpottery, and I'm not sure which. (Yaakov Sloman tells me that the response to Wittgenstein's Tractatus Logico-Philosophicus was similarly ambivalent when it was new. I think the consensus is now on the genius side.) Either way, it is quite fascinating. There needs to be some theory to account for the historical development of consciousness, and as far as I know, this is the only one on offer.
Anyway, I did not mean to get into this in so much detail. The reason I brought this up is that because of my continuing interest in Jaynes' theory, and how it is viewed by later scholars, I am reading Muses, Madmen, and Prophets: Rethinking the History, Science, and Meaning of Auditory Hallucination by Daniel B. Smith. I am not very far into it yet, but Smith has many interesting things to say about auditory hallucinations, their relationship to obsessive-compulsive disorder, and other matters.
On page 37 Smith mentions a paper, which as he says, has a wonderful title: "Involuntary Masturbation as a Manifestation of Stroke-Related Alien Hand Syndrome". Isn't that just awesome? It gets you coming and going, like a one-two punch. First there's the involuntary masturbation, and while you're still reeling from that it follows up with "alien hand syndrome".
To save you the trouble of reading the paper, I will summarize. The patient is a 72-year-old male. He has lesions in his right frontal lobe. He is experiencing "alien hand syndrome", where his hand seems to be under someone else's control, grabbing objects, like the TV remote control, or grabbing pieces of chicken off his plate and feeding them to him, when what he wanted to do was feed himself with the fork in his right hand. "During his hospital stay, the patient expressed frustration and dismay when he realized that he was masturbating publicly and with his inability to voluntarily release his grasp of objects in the left hand."
Reaction time tests of his hands revealed that when the left hand was under his conscious control, it suffered from a reaction time delay, but when it was under the alien's control, it didn't.
Whee, freaky.
[Other articles in category /brain] permanent link
Thu, 01 May 2008
At that moment, the novice was enlightened...
Presented without further comment, a conversation I had yesterday on
IRC. I am yrlnry:
| --> You are now talking on #ubuntu | ||
| 23:37 | <yrlnry> | I upgraded to HH this afternoon. Since the upgrade, when I select a URL in gnome-terminal and then pick the "open this link" menu item, the link doesn't open in my browser. Instead, I get a dialog that says "Could not open the address "http://...": There was an error launching the default action command associated with this location." How can I fix this, or find out what the "error" was? |
| 23:38 | <lpkmgj> | yrlnry: this happeds in Windows |
| yrlnry: i get that in Windows 2 | ||
| 23:39 | <yrlnry> | lpkmgj: thanks! that fixed my problem! |
| <lpkmgj> | yrlnry: sarcasm? | |
| <yrlnry> | lpkmgj: No! | |
| <lpkmgj> | yrlnry: right .... | |
| 23:40 | <yrlnry> | lpkmgj: WHen you said that, I realized that the problem was that HH had installed Firefox 3, and that the terminal program wants to use the default browser, which is FF2, which is no longer present since the upgrade. |
| <yrlnry> | lpkmgj: so I told FF3 to make itself the default browser, and the problem went away. | |
| <lpkmgj> | yrlnry: oh, well glad i helped : ) | |
(I have changed the name of the other person.)
[Other articles in category /tech] permanent link
Wed, 23 Apr 2008
Recounting the rationals
I just read a really excellent math paper, Recounting
the rationals, by Calkin and Wilf.
Let b(n) be the number of ways of adding up powers of 2 to get n, with each power of 2 used no more than twice. So, for example, b(5) = 2, because there are 2 ways to get 5:
| 5 | = 4 + 1 |
| = 2 + 2 + 1 |
And b(10) = 5, because there are 5 ways to get 10:
| 10 | = 8 + 2 |
| = 8 + 1 + 1 | |
| = 4 + 4 + 2 | |
| = 4 + 4 + 1 + 1 | |
| = 4 + 2 + 2 + 1 + 1 |
The sequence of values of b(n) begins as follows:
1 1 2 1 3 2 3 1 4 3 5 2 5 3 4 1 5 4 7 3 8 5 7 2 7 5 8 3 7 4 5 ...Now consider the sequence b(n) / b(n+1). This is just what you get if you take two copies of the b(n) sequence and place one over the other, with the bottom one shifted left one place, like this:
1 1 2 1 3 2 3 1 4 3 5 2 5 3 4 1 5 4 7 3 8 5 7 2 7 5 8 3 7 4 5 ...
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1 2 1 3 2 3 1 4 3 5 2 5 3 4 1 5 4 7 3 8 5 7 2 7 5 8 3 7 4 5 ...
Reading each pair as a rational number, we get the sequence b(n) /
b(n+1), which is 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4,
4/3, 3/5, 5/2, ... .Here is the punchline: This sequence contains each positive rational number exactly once.
If you are just learning to read math papers, or you think you might like to learn to read them, the paper in which this is proved would be a good place to start. It is serious research mathematics, but elementary. It is very short. The result is very elegant. The proofs are straightforward. The techniques used are typical and widely applicable; there is no weird ad-hockery. The discussion in the paper is sure to inspire you to tinker around with it more on your own. All sorts of nice things turn up. The b(n) sequence satisfies a simple recurrence, the fractions organize themselves neatly into a tree structure, and everything is related to everything else. Check it out.
Thanks to Brent Yorgey for bringing this to my attention. I saw it in this old blog article, but then discovered he had written a six-part series about it. I also discovered that M. Yorgey independently came to the same conclusion that I did about the paper: it would be a good first paper to read.
[ Addendum 20080505: Brad Clow agrees that it was a good place to start. ]
[Other articles in category /math] permanent link
Fri, 18 Apr 2008
A few notes on "The Manticore"
Here are a few miscellaneous notes about The Manticore.
Early memories
Here is David Staunton's earliest memory, from chapter 2, section 1. (Page 87 in my Penguin paperback edition.)
Here is the earliest memory of Francis Cornish, the protagonist of Davies' novel What's Bred in the Bone (1985):Dr. Von Haller: What is the earliest recollection you can honestly vouch for?
Myself: Oh, that's easy. I was standing in my grandmother's garden, in warm sunlight, looking into a deep red peony. As I recall it, I wasn't much taller than the peony. It was a moment of very great—perhaps I shouldn't say happiness, because it was really an intense absorption. The whole world, the whole of life, and I myself, became a warm, rich, peony-red.
It was in a garden that Francis Cornish first became truly aware of himself as a creature observing a world apart from himself. He was almost three years old, and he was looking deep into a splendid red peony.That is the opening sentence of part two, page 63 in my Penguin Books copy.
The sideboard
This is from chapter 3 of The Manticore, David's diary entry of Dec. 20:
Inside, it is filled with ... gigantic pieces of furniture on which every surface has been carved within an inch of its life with fruits, flowers, birds, hares, and even, on one thing which seems to be an altar to greed but is more probably a sideboard, full-sized hounds; six of them with real bronze chains on their collars.The following quotation is from Davies' 1984 New York Times article "In a Welsh Border House, the Legacy of the Victorians", a reminiscence of the house his father lived in after his retirement in 1950:
Until my father had it dismantled and removed to a stable, the Great Hall was dominated by what I can only call an altar to gluttony against the south wall. It was a German sideboard of monumental proportions that the Naylors had acquired at the Great Exhibition of 1851. Every fruit, flower, meat, game, and edible was carved on it in life size, including four large hounds, chained to the understructure with wooden chains, so cunningly wrought that they could be moved, like real chains.This is reprinted in The Enthusiasms of Robertson Davies, Judith Skelton Grant, ed.
What do Canadians think of Saints?
Davies has said on a number of occasions that in Fifth Business he wanted to write about the nature of sainthood, and in particular how Canadians would respond if they found that they had a true saint among them. For example, in his talk "What May Canada Expect from Her Writers?" (reprinted in One Half of Robertson Davies, pp. 139–140) he says:
For many years the question occurred to me at intervals: What would Canada do with a saint, if such a strange creature were to appear within our borders? I thought Canada would reject the saint because Canada has no use for saints, because saints hold unusual opinions, and worst of all, saints do not pay. So in 1970 I wrote a book, called Fifth Business, in which that theme played a part.Fifth Business does indeed treat this theme extensively and subtly. In The Manticore he is somewhat less subtle. A perpetual criticism I have of Davies is that he is never content to trust the reader to understand him. He always gets worried later that the reader is not clever enough, and he always comes back to hammer in his point a little more obviously.
For example, Fifth Business ends with the question "Who killed Boy Staunton?" and a cryptic, oracular answer. But Davies was unable to resist the temptation to explain his answer for the benefit of people unable or unwilling to puzzle out their own answers, and the end of The Manticore includes a detailed explanation. I think there might be an even plainer explanation in World of Wonders, but I forget. I have a partly-finished essay in progress discussing this tendency in Davies' writing, but I don't know when it will be done; perhaps never.
What would Canada think of a saint? Fifth Business is one answer, a deep and brilliant one. But Davies was not content to leave it there. He put a very plain answer into The Manticore. This is again from David's diary entry of Dec. 20 (p. 280):
Eisengrim's mother had been a dominant figure in his own life. He spoke of her as "saintly," which puzzles me. Wouldn't Netty have mentioned someone like that?David's old nurse Netty did indeed mention Eisengrim's mother, although David didn't know that that was who was being mentioned. The mention appears in chapter 2, section 6, p. 160:
She had some awful piece of lore from Deptford to bring out. It seems there had been some woman there when she was a little girl who had always been "at it" and had eventually been discovered in a gravel pit, "at it" with a tramp; of course this woman had gone stark, staring mad and had to be kept in her house, tied up.If you want to know what Robertson Davies thinks that Canada would make of a saint, but you don't want to read and ponder Fifth Business to find out, there you have it in one sentence.
[ Addendum: The New York Times review of The Manticore is interesting for several reasons. The title is misspelled in the headline: "The Manitcore". The review was written by a then-unknown William Kennedy, who later became the author of Ironweed (which won the Pulitzer Prize) and other novels. Check it out. ]
[Other articles in category /book] permanent link
Thu, 17 Apr 2008
Is blood a transitive relation?
When you're first teaching high school students about the idea of a
relation, you give examples of the important properties of relations.
Relations can be some, none, or all of reflexive, symmetric,
antisymmetric, or transitive. You start with examples that everyone
is already familiar with, such as the identity relation, which is
reflexive, symmetric, and transitive, and the ≤ relation, which is
antisymmetric and transitive. Other good examples include familial
relations: "sister-in-law of" is symmetric on the set of women, but
not on the larger set of people; "ancestor of" is transitive but not
symmetric.
It might seem at first glance that "is related to" is transitive, but, at least under conventional definitions, it isn't, because my wife is not related to my cousins.
(I was once invited to speak at Haverford College, and, since I have no obvious qualifications in the topic on which I was speaking, I was asked how I had come to be there. I explained that it was because my wife's mother's younger brother's daughter's husband's older brother's wife was the chair of the mathematics department. Remember, it's not what you know, it's who you know.)
I think I had sometimes tried to turn "related to" into a transitive relation by restricting it to "is related to by blood". This rules out the example above of my wife being unrelated to my cousins, because my relationship with my wife is not one of blood. I don't quite remember using "related by blood" as an example of a transitive relation, but I think I might have, because I was quite surprised when I realized that it didn't work. I spent a lot of time that morning going over my counterexample in detail, writing it up in my head, as it were. I was waiting around in Trevose for the mechanic to finish examining my car, and had nothing better to do that morning. If I had had a blog then, I would probably have posted it. But it is a good thing that I didn't, because in spite of all my thought about it, I missed something important.
The example is as follows. A and B have a child, X. (You may suppose that they marry beforehand, and divorce afterward, if your morality requires it.) Similarly, C and D have a child, Z. Then B and C have a child Y. Y is now the half-sibling of both X and Z, and so is unquestionably a blood relative of both, but X and Z are entirely unrelated. They are not even step-siblings.
Well, this is all very well, but the reason I have filed it under oops/, and the reason it's a good thing I didn't post it on my (then nonexistent) blog is that this elaborate counterexample contains a much simpler one: X is the child and hence the blood relative of both A and B, who are not in general related to each other. C, D, Y, and Z are wholly unnecessary.
I wish I had some nice conclusion to draw here, but if there's something I could learn from it I can't think would it might be.
[Other articles in category /oops] permanent link
Fri, 28 Mar 2008
Suffering from "make install"
I am writing application X, which uses the nonstandard perl
modules DBI, DBD::SQLite, and Template.
These might not be available on the target system, so I got the idea
to include them in the distribution for X and have the build
process for X build and install the modules. X
already carries its own custom Perl modules in X/lib anyway,
so I can just install DBI and the others into X/lib
and everything will Just Work. Or so I thought.
After building DBI, for example, how do you get it to install itself into X/lib instead of the default system-wide location, which only the super-user has permission to modify?
There are at least five solutions to this common problem.
Uh-oh. If solution #1 had worked, people would not have needed to invent solution #2. If solution #2 had worked, people would not have needed to invent solution #3. Since there are five solutions, there is a good chance that none of them work.
You can, I am informed:
- Set PREFIX=X when building the Makefile
- Set INSTALLDIRS=vendor and VENDORPREFIX=X when
building the Makefile
- Or maybe instead of VENDORPREFIX you need to set INSTALLVENDORLIB or something
- Or maybe instead of setting them while building the Makefile you need to set them while running the make install target
- Set LIB=X/lib when building the Makefile
- Use PAR
- Use local::lib
Some of these items fail because they just plain fail. For example, the first thing everyone says is that you can just set PREFIX to X. No, because then the module Foo does not go into X/lib/Foo.pm. It goes into X/Foo/lib/perl5/site_perl/5.12.23/Foo.pm. Which means that if X does use lib 'X/lib'; it will not be able to find Foo.
 The manual (which goes by the marvelously
obvious and easily-typed name of ExtUtils::MakeMaker, by the
way) is of limited help. It recommends solving the problem by
travelling to Paterson, NJ, gouging your eyes out with your mom's
jewelry, and then driving over the Passaic River falls. Ha ha, just
kidding. That would be a big improvement on what it actually
suggests, for three reasons. First, it is clear and straightforward.
Second, it would feel better than the stuff it does suggest. And
third, it would actually solve your problem, although obliquely.
The manual (which goes by the marvelously
obvious and easily-typed name of ExtUtils::MakeMaker, by the
way) is of limited help. It recommends solving the problem by
travelling to Paterson, NJ, gouging your eyes out with your mom's
jewelry, and then driving over the Passaic River falls. Ha ha, just
kidding. That would be a big improvement on what it actually
suggests, for three reasons. First, it is clear and straightforward.
Second, it would feel better than the stuff it does suggest. And
third, it would actually solve your problem, although obliquely.
It turns out there is a simple solution that doesn't involve travelling to New Jersey. The first thing you have to do is give up entirely on trying to use make install to install the modules. It is completely broken for this application, because even if the destination could somehow be forced to be what you wanted—and, after all, why would you expect that make install would let you configure the destination directory in a simple fashion?—it would still install not only the contents of MODULE/lib, but also the contents of MODULE/bin, MODULE/man, MODULE/share, MODULE/pus, MODULE/dork, MODULE/felch, and MODULE/scrotum, some of which you probably didn't want.
So no. But the solution is actually simple. The normal module build process (as distinct from the install process) puts all this crap under MODULE/blib. The test suite is run against the blib installation. So the test programs have the same problem that X has. If they can find the stuff under blib, so can X, by replicating the layout under blib and then doing what the test suite does.
In fact, the modules are installed into the proper subdirectories of MODULE/blib/lib. So the simple solution is just to build the module and then, instead of trying to get the installer to put the right stuff in the right place, use cp -pr MODULE/blib/lib/* X/lib. Problem solved.
For modules with a shared library, you need to copy MODULE/blib/arch/auto/* into X/lib/auto also.
I remember suffering over this at least ten years ago, when a student in a class I was teaching asked me how to do it and I let ExtUtils::MakeMaker make a monkey of me. I was amazed to find myself suffering over it once again. I am relieved to have found the right answer.
This is one of those days when I am not happy with software. It sometimes surprises me how many of those days involve make.
Dennis Ritchie once said that "make is like Pascal. Everybody likes it, so they go in and change it." I never really thought about this before, but it now occurs to me that probably Ritchie meant that they like make in about the same way that they like bladder stones. Because Dennis Ritchie probably does not like Pascal, and actually nobody else likes Pascal either. They may say they do, and they may even think they do, but if you look a little closer it always turns out that the thing they like is not actually Pascal, but some language that more or less resembles Pascal. Unfortunately, the changes people make to make tend to make it bigger and wartier, and this improves make about as much as it would improve a bladder stone.
I would like to end this article on a positive note. If you haven't already, please read Recursive make Considered Harmful and be prepared to be blinded by the Glorious Truth therein.
[Other articles in category /prog] permanent link
Tue, 25 Mar 2008
The "z" command: output filtering
My last few articles
([1]
[2]
[p]
[p-2]) have been about
this z program. The first part of
this article is a summary of that discussion, which you can
skip if you remember it.
The idea of z is that you can do:
z grep pattern files...
and it does approximately the same as:
zgrep pattern files...
or you could do:
z sed script files...
and it would do the same as:
zsed script files...
if there were a zsed command, although there isn't.Much of the discussion has concerned a problem with the implementation, which is that the names of the original compressed files are not available to the command, due to the legerdemain z must perform in order to make the uncompressed data available to the command. The problem is especially apparent with wc:
% z wc *
411 2611 16988 ctime.blog
71 358 2351 /proc/self/fd/3
121 725 5053 /proc/self/fd/4
51 380 2381 files-talk.blog
48 145 885 find-uniq.pl
288 2159 12829 /proc/self/fd/5
95 665 4337 ssh-agent-revisted.blog
221 941 6733 struct-inode.blog
106 555 3976 sync-2.blog
115 793 4904 sync.blog
124 624 4208 /proc/self/fd/6
1651 9956 64645 total
Here /proc/self/fd/3 and the rest should have been names ending in .gz, such as env-2.blog.gz.
Another possible solution
At the time I wrote the first article, it occurred to me briefly that it would be possible to have z capture the output of the command and attempt to translate /proc/self/fd/3 back to env-2.blog.gz or whatever is appropriate, because although the subcommand does not know the original filenames, z itself does. The code would look something like this. Instead of ending by execing the command, as the original version of z did:exec $command, @ARGV; die "Couldn't run '$command': $!.\n";this revised version of z, which we might call zz, would end with the code to translate back to the original filenames:
open my($out), "-|", $command, @ARGV
or die "Couldn't run '$command': $!.\n";
while (<$out>) {
s{/proc/self/fd/(\d+)}{$old[$1]}g;
print;
}
Here @old is an array that translates from file descriptors
back to the original filename.At the time, I thought of doing this, and my immediate thought was "well, that is so obviously a terrible idea that it is not worth even mentioning", so I left it out. But since then at least five people have written to me to suggest it, so it appears that it is not obviously a terrible idea. I had to think a little deeper about why I thought it was a terrible idea.
Really the question is why I think this is a more terrible idea than the original z program was in the first place. Because one could say that z is garbling the output of its command, and the filtering code in zz is only un-garbling it. But I think this isn't the right way to look at it.
The output of the command has a certain format, a certain structure. We don't know ahead of time what that structure is, but it can be described for any particular command. For instance, the output of wc is always a sequence of lines where each line has four whitespace-separated fields, of which the first three are numerals and the last is a filename, and then a final total line at the end.
Similarly, the output of tar is a file in a complicated binary format, one which is documented somewhere and which is intelligible to other instances of the tar command that are trying to decode it.
The original behavior of z may alter the content of the command output to some extent, replacing some filenames with others. But it cannot disrupt the structure or the format of the file, ever. This is because the output of z tar is the output of tar, unmodified. The z program tampers with the arguments it gives to tar, but having done that it runs tar and lets tar do what it wants, and tar then must produce a tar-format output, possibly not the one it would have normally produced—the content might be a little different—but a properly-formatted one for sure. In particular, any program written to deal properly with the output of tar will still work with the output of z tar. The output might not have the same meaning, but we can say very particularly what the extent of the differences might be: if the output mentions filenames, then some of these might have changed from the true filenames to filenames of the form /proc/self/fd/37.
With zz, we cannot make any such guarantee. The output of zz tar zc foo.gz, for example, might be in proper .tar.gz format. But suppose the output of tar zc foo.gz creates compressed binary output that just happens to contain the byte sequence 2f70 726f 632f 7365 6c66 2f66 642f 33? (That is, "/proc/self/fd/3".) Then zz will silently replace these 15 bytes with the six bytes 666f 6f2e 677a.
What if the original sequence was understood as part of a sequence of 2-byte integers? The result is not even properly aligned. What if that initial 2f was a count? The resulting count (66) is much too long. The result would be utterly garbled and unintelligible to tar zx. What the tar command will do with a garbled input is not well-defined: it might dump core, or it might write out random garbage data, or overwrite essential files in the filesystem. We are into nasal demon territory. With the original z, we never get anywhere near the nasal demons.
I suppose the short summary here is that z treats its command as a black box, while zz pretends to understand what comes out of it. But zz's understanding is a false pretense. My experience says that programs should not screw around with things they don't understand, and this is why I instantly rejected the idea when I thought of it before.
One correspondent argued that the garbling is very unlikely, and proposed various techniques to make it even less likely, mostly by rewriting the input filenames to various long random strings. But I felt then that this was missing the point, and I still do. He says it is unlikely, but he doesn't know that it is unlikely, and indeed the unlikeliness depends on the format of the output of the command, which is precisely the unknown here. In my view, the difference between z and zz is that the changes that z makes are bounded, because you can describe them briefly, as I did above, and the changes that zz makes are unbounded, because there is no limit to what could happen as a result.
On the other hand, this correspondent made a good point that if the output of zz is not consumed by anything other than human eyeballs, there may be no real problem. And for some particular commands, such as wc, there is never any problem at all. So perhaps it's a good idea to add a command-line option to z to enable the zz behavior. I did this in my version, and I'm going to try it out and see how it goes.
Complete modified source code is available. (Diffs from previous version.)
[Other articles in category /Unix] permanent link
Sat, 22 Mar 2008
The "z" command: alternative implementations
In yesterday's article I discussed a
possibly-useful utility program named z, which has a flaw.
To jog your memory, here is a demonstration:
% z grep immediately *
ctime.blog:we want to update. It is immediately copied into a register, and
/proc/self/fd/3:All five people who wrote to me about this immediately said "oh, yes,
/proc/self/fd/5:program continues immediately, possibly posting its message. (It
struct-inode.blog:is a symbolic link, its inode is returned immediately; iname() would
sync.blog:and reports success back to the process immediately, even though the
For a detailed discussion, see the
previous article.Fixing this flaw seems difficult-to-impossible. As I said earlier, the trick is to fool the command into reading from a pipe when it thinks it is opening a file, and this is precisely what /proc/self/fd is for. But there is an older, even more widely-implemented Unix feature that does the same thing, namely the FIFO. So an alternative implementation creates one FIFO for each compressed file, with a gzip process writing to the FIFO, and tells the command to read from the FIFO. Since we have some limited control over the name of the FIFO, we can ameliorate the missing-filename problem to some extent. Say, for example, we create the FIFOs in /tmp/PID. Then the broken zgrep example above might look like this instead:
% z grep immediately *
ctime.blog:we want to update. It is immediately copied into a register, and
/tmp/7516/env-2.blog.gz:All five people who wrote to me about this immediately said "oh, yes,
/tmp/7516/qmail-throttle.blog.gz:program continues immediately, possibly posting its message. (It
struct-inode.blog:is a symbolic link, its inode is returned immediately; iname() would
sync.blog:and reports success back to the process immediately, even though the
The output is an improvement, but it is not completely solved, and the
cost is that the process and file management are much more
complicated. In fact, the cost is so high that you have to wonder if
it might not be simpler to replace z with a shell script that
copies the data to a temporary directory, uncompresses the files, and
runs the command on the uncompressed files, perhaps something along
these lines:
#!/bin/sh
DIR=/tmp/$$
mkdir $DIR
COMMAND=$1
shift
cp -p "$@" $DIR
cd $DIR
gzip -d *
$COMMAND *
This has problems too, but my point is that if you are willing to
accept a crappy, semi-working solution along the lines of the FIFO
one, simpler ones are at hand. You can compare the FIFO version
directly with the shell script, and I think the FIFO version loses.
The z implementation I have is a
solution in a different direction, and different tradeoffs, and so
might be preferable to it in a number of ways. But as I said, I don't know yet.
[ Addendum 20080325: Several people suggested a fix that I had considered so unwise that I didn't even mention it. But after receiving the suggestion repeatedly, I wrote an article about it. ]
[Other articles in category /Unix] permanent link
Fri, 21 Mar 2008
z-commands
The gzip distribution includes a command called zcat. Its
command-line arguments can include any number of filenames, compressed
or not, and it prints out the contents, uncompressing them on the fly
if necessary. Sometime later a zgrep command appeared, which
was similar but which also performed a grep search.
But for anything else, you either need to uncompress the files, or build a special tool. I have a utility that scans the web logs of blog.plover.com, and extracts a report about new referrers. The historical web logs are normally kept compressed, so I recently built in support for decompression. This is quite easy in Perl. Normally one scans a sequence of input files something like this:
while (<>) {
... do something with $_ ...
}
The <> operator implicitly scans all the lines in all the
files named in the command-line arguments, opening a new file each
time the previous one is exhausted. To decompress the files on the fly, one can preprocess the command-line arguments:
for (@ARGV) {
if (/\.gz$/) {
$_ = "gzip -dc $_ |";
}
}
while (<>) {
... do something with $_ ...
}
The for loop scans the command-line arguments, replacing each
one that has the form foo.gz with gzip -dc foo.gz |.
Perl's magic open semantics treat filenames specially if they end with
a pipe symbol: a pipe to a command is opened instead. Of course, anyone can
think of half a dozen ways in which this can go wrong. But Larry
Wall's skill in making such tradeoffs has been a large factor in Perl's
success. But it bothered me to have to make this kind of change in every program that wanted to handle compressed files. We have zcat and zgrep; where are zcut, zpr, zrev, zwc, zcol, zbc, zsed, zawk, and so on? Echh.
But after I got to thinking about it, I decided that I could write a single z utility that would do a lot of the same things. Instead of this:
zsed -e 's/:.*//' * | ...
where the * matches some files that have .gz
suffixes and some that haven't, one would write:
z sed -e 's/:.*//' * | ...
and it would Just Work. That's the idea, anyway.If sed were written in Perl, z would have an easy job. It could rely on Perl's magic open, and simply preprocess the arguments before running sed:
# hypothetical implementation of z
#
my $command = shift;
for (@ARGV) {
if (/\.gz$/) {
$_ = "gzip -dc $_ |";
}
}
exec $command, @ARGV;
die "Couldn't run command '$command': $!\n";
But sed is not written in Perl, and has no magic open. So I
have to play a trickier trick:
for my $file (@ARGV) {
if ($file =~ /\.gz$/) {
unless (open($fhs[@fhs], "-|", "gzip", "-cd", $file)) {
warn "Couldn't open file '$file': $!; skipping\n";
next;
}
my $fd = fileno $fhs[-1];
$_ = "/proc/self/fd/$fd";
}
}
# warn "running $command @ARGV\n";
exec $command, @ARGV;
die "Couldn't run command '$command': $!\n";
This is a stripped-down version to illustrate the idea. For various
reasons that I explained
yesterday, it does not actually work.
The
complete, working source code is here.The idea, as before, is that the program preprocesses the command-line arguments. But instead of replacing the arguments with pipe commands, which are not supported by open(2), the program sets up the pipes itself, and then directs the command to take its input from the pipes by specifying the appropriate items from /proc/self/fd.
The trick depends crucially on having /proc/self/fd, or /dev/fd, or something of the sort, because otherwise there's no way to trick the command into reading from a pipe when it thinks it is opening a file. (Actually there is at least one other way, involving FIFOs, which I plan to discuss tomorrow.) Most modern systems do have /proc/self/fd. That feature postdates my earliest involvement with Unix, so it isn't a ready part of my mental apparatus as perhaps it ought to be. But this utility seems to me like a sort of canonical application of /proc/self/fd, in the sense that, if you couldn't think what /proc/self/fd might be good for, then you could read this example and afterwards have a pretty clear idea.
The z utility has a number of flaws. Principally, the original filenames are gone. Here's a typical run with regular zgrep:
% zgrep immediately *
ctime.blog:we want to update. It is immediately copied into a register, and
env-2.blog.gz:All five people who wrote to me about this immediately said "oh, yes,
qmail-throttle.blog.gz:program continues immediately, possibly posting its message. (It
struct-inode.blog:is a symbolic link, its inode is returned immediately; iname() would
sync.blog:and reports success back to the process immediately, even though the
But here's the same thing with z:
% z grep immediately *
ctime.blog:we want to update. It is immediately copied into a register, and
/proc/self/fd/3:All five people who wrote to me about this immediately said "oh, yes,
/proc/self/fd/5:program continues immediately, possibly posting its message. (It
struct-inode.blog:is a symbolic link, its inode is returned immediately; iname() would
sync.blog:and reports success back to the process immediately, even though the
The problem is even more glaring in the case of commands like
wc:
% z wc *
411 2611 16988 ctime.blog
71 358 2351 /proc/self/fd/3
121 725 5053 /proc/self/fd/4
51 380 2381 files-talk.blog
48 145 885 find-uniq.pl
288 2159 12829 /proc/self/fd/5
95 665 4337 ssh-agent-revisted.blog
221 941 6733 struct-inode.blog
106 555 3976 sync-2.blog
115 793 4904 sync.blog
124 624 4208 /proc/self/fd/6
1651 9956 64645 total
So perhaps z will not turn out to be useful enough to be more than a curiosity. But I'm not sure yet.
This is article #300 on my blog. Thanks for reading.
[ Addendum 20080322: There is a followup to this article. ]
[ Addendum 20080325: Another followup. ]
[Other articles in category /Unix] permanent link
Closed file descriptors: the answer
This is the answer to yesterday's article about a
small program that had a mysterious error.
my $command = shift;
for my $file (@ARGV) {
if ($file =~ /\.gz$/) {
my $fh;
unless (open $fh, "<", $file) {
warn "Couldn't open $file: $!; skipping\n";
next;
}
my $fd = fileno $fh;
$file = "/proc/self/fd/$fd";
}
}
exec $command, @ARGV;
die "Couldn't run command '$command': $!\n";
When the loop exits, $fh is out of scope, and the
filehandle it contains is garbage-collected, closing the file."Duh."
Several people suggested that it was because open files are not preserved across an exec, or because the meaning of /proc/self would change after an exec, perhaps because the command was being run in a separate process; this is mistaken. There is only one process here. The exec call does not create a new process; it reuses the same one, and it does not affect open files, unless they have been flagged with FD_CLOEXEC.
Abhijit Menon-Sen ran a slightly different test than I did:
% z cat foo.gz bar.gz
cat: /proc/self/fd/3: No such file or directory
cat: /proc/self/fd/3: No such file or directory
As he said, this makes it completely obvious what is wrong, since
the two files are both represented by the same file descriptor.
[Other articles in category /prog/perl] permanent link
Thu, 20 Mar 2008
Closed file descriptors
I wasn't sure whether to file this on the /oops
section. It is a mistake, and I spent a lot longer chasing the bug
than I should have, because it's actually a simple bug. But it isn't
a really big conceptual screwup of the type I like to feature in the
/oops section.
It concerns a
program that I'll discuss in detail tomorrow. In the meantime, here's
a stripped-down summary, and a stripped-down version of the code:
my $command = shift;
for my $file (@ARGV) {
if ($file =~ /\.gz$/) {
my $fh;
unless (open $fh, "<", $file) {
warn "Couldn't open $file: $!; skipping\n";
next;
}
my $fd = fileno $fh;
$file = "/proc/self/fd/$fd";
}
}
exec $command, @ARGV;
die "Couldn't run command '$command': $!\n";
The idea here is that this program, called z, will preprocess
the arguments of some command, and then run the command
with the modified arguments. For some of the command-line arguments,
here the ones named *.gz, the original file will be replaced
by the output of some file descriptor. In the example above, the
descriptor is attached to the original file, which is pointless. But
once this part of the program was working, I planned to change the code
so that the descriptor would be
attached to a pipe instead.Having written something like this, I then ran a test, which failed:
% z cat foo.gz cat: /proc/self/fd/3: No such file or directory"Aha," I said instantly. "I know what is wrong. Perl set the close-on-exec flag on file descriptor 3."
You see, after a successful exec, the kernel will automatically close all file descriptors that have the close-on-exec flag set, before the exec'ed image starts running. Perl normally sets the close-on-exec flag on all open files except for standard input, standard output, and standard error. Actually it sets it on all open files whose file descriptor is greater than the value of $^F, but $^F defaults to 2.
So there is an easy fix for the problem: I just set $^F = 100000 at the top of the program. That is not the best solution, but it can be replaced with a better one once the program is working properly. Which I expected it would be:
% z cat foo.gz cat: /proc/self/fd/3: No such file or directoryHuh, something is still wrong.
Maybe I misspelled /proc/self/fd? No, it is there, and contains the special files that I expected to find.
Maybe $^F did not work the way I thought it did? I checked the manual, but it looked okay.
Nevertheless I put in use Fcntl and used the fcntl function to remove the close-on-exec flags explicitly. The code to do that looks something like this:
use Fcntl;
....
my $flags = fcntl($fh, F_GETFD, 0);
fcntl($fh, F_SETFD, $flags & ~FD_CLOEXEC);
And try it again:
% z cat foo.gz cat: /proc/self/fd/3: No such file or directoryHuh.
I then wasted a lot of time trying to figure out an easy way to tell if the file descriptor was actually open after the exec call. (The answer turns out to be something like this: perl -MPOSIX=fstat -le 'print "file descriptor 3 is ", fstat(3) ? "open" : "closed"'.) This told me whether the error from cat meant what I thought it meant. It did: descriptor 3 was indeed closed after the exec.
Now your job is to figure out what is wrong. It took me a shockingly long time. No need to email me about it; I have it working now. I expect that you will figure it out faster than I did, but I will also post the answer on the blog tomorrow. Sometime on Friday, 21 March 2008, this link will start working and will point to the answer.
[ Addendum 20080321: I posted the answer. ]
[Other articles in category /prog/perl] permanent link
Fri, 14 Mar 2008
Drawing lines
As part of this thing I sometimes do when I'm not writing in my
blog—what is it called?—oh, now I remember.
As part of my job I had to produce the following display:
If you wanted to hear more about phylogeny, Java programming, or tree algorithms, you are about to be disappointed. The subject of my article today is those fat black lines.
The first draft of the page did not have the fat black lines. It had some incredibly awful ASCII-art that was not even properly aligned. Really it was terrible; it would have been better to have left it out completely. I will not make you look at it.
I needed the lines, so I popped down the "graphics" menu on my computer and looked for something suitable. I tried the Gimp first. It seems that the Gimp has no tool for drawing straight lines. If someone wants to claim that it does, I will not dispute the claim. The Gimp has a huge and complex control panel covered with all sorts of gizmos, and maybe one of those gizmos draws a straight line. I did not find one. I gave up after a few minutes.
Next I tried Dia. It kept selecting the "move the line around on the page" tool when I thought I had selected the "draw another line" tool. The lines were not constrained to a grid by default, and there was no obvious way to tell it that I wanted to draw a diagram smaller than a whole page. I would have had to turn the thing into a bitmap and then crop the bitmap. "By Zeus's Beard," I cried, "does this have to be so difficult?" Except that the oath I actually uttered was somewhat coarser and less erudite than I have indicated. I won't repeat it, but it started with "fuck" and ended with "this".
Here's what I did instead. I wrote a program that would read an input like this:
>-v-<
'-+-`
and produce a jpeg file that looks like this:
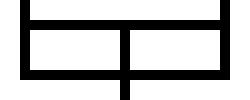
.---,
| >--,
'---` '-
Becomes this:
Now I know some of you are just itching to write to me and ask "why didn't you just use...?", so before you do that, let me remind you of two things. First, I had already wasted ten or fifteen minutes on "just use..." that didn't work. And second, this program only took twenty minutes to write.
The program depends on one key insight, which is that it is very, very easy to write a Perl program that generates a graphic output in "PBM" ("portable bitmap") format. Here is a typical PBM file:
P1
10 10
1111111111
1000000001
1000000001
1001111001
1001111001
1001111001
1001111001
1000000001
1000000001
1111111111
The P1 is a magic number that identifies the file format; it
is always the same. The 10 10 warns the processor that the
upcoming bitmap is 10 pixels wide and 10 pixels high. The following
characters are the bitmap data.
I'm not going to insult you by showing the 10×10 bitmap image
that this represents.PBM was invented about twenty years ago by Jef Poskanzer. It was intended to be an interchange format: say you want to convert images from format X to format Y, but you don't have a converter. You might, however, have a converter that turns X into PBM and then one that turns PBM into Y. Or if not, it might not be too hard to produce such converters. It is, in the words of the Extreme Programming guys, the Simplest Thing that Could Possibly Work.
There are also PGM (portable graymap) and PPM (portable pixmap) formats for grayscale and 24-bit color images as well. They are only fractionally more complicated.
Because these formats are so very, very simple, they have been widely adopted. For example, the JPEG reference implementation includes a sample cjpeg program, for converting an input to a JPEG file. The input it expects is a PGM or PPM file.
Writing a Perl program to generate a P?M file, and then feeding the output to pbmtoxbm or ppmtogif or cjpeg is a good trick, and I have used it many times. For example, I used this technique to generate a zillion little colored squares in this article about the Pólya-Burnside counting lemma. Sure, I could have drawn them one at a time by hand, and probably gone insane and run amuck with an axe immediately after, but the PPM technique was certainly much easier. It always wins big, and this time was no exception.
The program may be interesting as an example of this technique, and possibly also as a reminder of something else. The Perl community luminaries invest a lot of effort in demonstrating that not every Perl program looks like a garbage heap, that Perl can be as bland and aseptic as Java, that Perl is not necessarily the language that most closely resembles quick-drying shit in a tube, from which you can squirt out the contents into any shape you want and get your complete, finished artifact in only twenty minutes and only slightly smelly.
No, sorry, folks. Not everything we do is a brilliant, diamond-like jewel, polished to a luminous gloss with pages torn from one of Donald Knuth's books. This line-drawing program was squirted out of a tube, and a fine brown piece of engineering it is.
#!/usr/bin/perl
my ($S) = shift || 50;
$S here is "size". The default is to turn every character in
the input into a 50×50 pixel tile. Here's the previous example
with $S=10: 
my ($h, $w);
my $output = [];
while (<>) {
chomp;
$w ||= length();
$h++;
push @$output, convert($_);
}
The biggest defect in the program is right here: it assumes that each
line will have the same width $w. Lines all must be
space-padded to the same width. Fixing this is left as an easy
exercise, but it wasn't as easy as padding the inputs, so I didn't do it.The magic happens here:
open STDOUT, "| pnmscale 1 | cjpeg" or die $!;
print "P1\n", $w * $S, " ", $h * $S, "\n";
print $_, "\n" for @$output;
exit;
The output is run through cjpeg to convert the PBM data to
JPEG. For some reason cjpeg doesn't accept PBM data, only
PGM or PPM, however, so the output first goes through
pnmscale, which resizes a P?M input. Here the scale factor
is 1, which is a no-op, except that pnmscale happens to turn
a PBM input into a PGM output. This is what is known in the business
as a "trick". (There is a pbmtopgm program, but it does
something different.)If we wanted gif output, we could have used "| ppmtogif" instead. If we wanted output in Symbolics Lisp Machine format, we could have used "| pgmtolispm" instead. Ah, the glories of interchange formats.
I'm going to omit the details of convert, which just breaks each line into characters, calls convert_ch on each character, and assembles the results. (The complete source code is here if you want to see it anyway.) The business end of the program is convert_ch:
#
sub convert_ch {
my @rows;
my $ch = shift;
my $up = $ch =~ /[<|>^'`+]/i;
my $dn = $ch =~ /[<|>V.,+]/i;
my $lt = $ch =~ /[-<V^,`+]/i;
my $rt = $ch =~ /[->V^.'+]/i;
These last four variables record whether the tile has a line from its
center going up, down, left, or right respectively. For example,
"|" produces a tile with lines coming up and down from the
center, but not left or right. The /i in the regexes is
because I kept writing v instead of V in the
inputs.
my $top = int($S * 0.4);
my $mid = int($S * 0.2);
my $bot = int($S * 0.4);
The tile is divided into three bands, of the indicated widths. This
probably looks bad, or fails utterly, unless $S is a multiple
of 5. I haven't tried it. Do you think I care? Hint: I haven't tried
it.
my $v0 = "0" x $S;
my $v1 = "0" x $top . "1" x $mid . "0" x $bot;
push @rows, ($up ? $v1 : $v0) x $top;
This assembles the top portion of the tile, including the "up" line,
if there is one. Note that despite their names, $top also
determines the width of the left portion of the tile, and
$bot determines the width of the right portion. The letter
"v" here is for "vertical".Perhaps I should explain for the benefit of the readers of Planet Haskell (if any of them have read this far and not yet fainted with disgust) that "$a x $b" in Perl is like concat (replicate b a) in the better sorts of languages.
my $ls = $lt ? "1" : "0";
my $ms = ($lt || $rt || $up || $dn) ? "1" : "0";
my $rs = $rt ? "1" : "0";
push @rows, ($ls x $top . $ms x $mid . $rs x $bot) x $mid;
This assembles the middle section, including the "left" and "right"
lines.
push @rows, ($dn ? $v1 : $v0) x $bot;
This does the bottom section.
return @rows;
}
And we are done.
Nothing to it. Adding diagonal lines would be a fairly simple matter.Download the complete source code if you haven't seen enough yet.
There is no part of this program of which I am proud. Rather, I am proud of the thing as a whole. It did the job I needed, and it did it by 5 PM. Larry Wall once said that "a Perl script is correct if it's halfway readable and gets the job done before your boss fires you." Thank you, Larry.
No, that is not quite true. There is one line in this program that I'm proud of. I noticed after I finished that there is exactly one comment in this program, and it is blank. I don't know how that got in there, but I decided to leave it in. Who says program code can't be funny?
[Other articles in category /prog/perl] permanent link
Thu, 06 Mar 2008
Throttling qmail
This may well turn out to be another oops. Sometimes when I screw
around with the mail system, it's a big win, and sometimes it's a big
lose. I don't know yet how this will turn out.
Since I moved house, I have all sorts of internet-related problems that I didn't have before. I used to do business with a small ISP, and I ran my own web server, my own mail service, and so on. When something was wrong, or I needed them to do something, I called or emailed and they did it. Everything was fine.
Since moving, my ISP is Verizon. I have great respect for Verizon as a provider of telephone services. They have been doing it for over a hundred years, and they are good at it. Maybe in a hundred years they will be good at providing computer network services too. Maybe it will take less than a hundred years. But I'm not as young as I once was, and whenever that glorious day comes, I don't suppose I'll be around to see it.
One of the unexpected problems that arose when I switched ISPs was that Verizon helpfully blocks incoming access to port 80. I had moved my blog to outside hosting anyway, because the blog was consuming too much bandwidth, so I moved the other plover.com web services to the same place. There are still some things that don't work, but I'm dealing with them as I have time.
Another problem was that a lot of sites now rejected my SMTP connections. My address was in a different netblock. A Verizon DSL netblock. Remote SMTP servers assume that anybody who is dumb enough to sign up with Verizon is also too dumb to run their own MTA. So any mail coming from a DSL connection in Verizonland must be spam, probably generated by some Trojan software on some infected Windows box.
The solution here (short of getting rid of Verizon) is to relay the mail through Verizon's SMTP relay service. mail.plover.com sends to outgoing.verizon.net, and lets outgoing.verizon.net forward the mail to its final destination. Fine.
But but but.
If my machine sends more than X messages per Y time, outgoing.verizon.net will assume that mail.plover.com has been taken over by a Trojan spam generator, and cut off access. All outgoing mail will be rejected with a permanent failure.
So what happens if someone sends a message to one of the 500-subscriber email lists that I host here? mail.plover.com generates 500 outgoing messages, sends the first hundred or so through Verizon. Then Verizon cuts off my mail service. The mailing list detects 400 bounce messages, and unsubscribes 400 subscribers. If any mail comes in for another mailing list before Verizon lifts my ban, every outgoing message will bounce and every subscriber will be unsubscribed.
One solution is to get a better mail provider. Lorrie has an Earthlink account that comes with outbound mail relay service. But they do the same thing for the same reason. My Dreamhost subscription comes with an outbound mail relay service. But they do the same thing for the same reason. My Pobox.com account comes with an unlimited outbound mail relay service. But they require SASL authentication. If there's a SASL patch for qmail, I haven't been able to find it. I could implement it myself, I suppose, but I don't wanna.
So far there are at least five solutions that are on the "eh, maybe, if I have to" list:
- Get a non-suck ISP
- Find a better mail relay service
- Hack SASL into qmail and send mail through Pobox.com
- Do some skanky thing with serialmail
- Get rid of qmail in favor of postfix, which presumably supports SASL
It also occurred to me in the shower this morning that the old ISP might be willing to sell me mail relaying and nothing else, for a small fee. That might be worth pursuing. It's gotta be easier than turning qmail-remote into a SASL mail client.
The serialmail thing is worth a couple of sentences, because there's an autoresponder on the qmail-users mailing-list that replies with "Use serialmail. This is discussed in the archives." whenever someone says the word "throttle". The serialmail suite, also written by Daniel J. Bernstein, takes a maildir-format directory and posts every message in it to some remote server, one message at a time. Say you want to run qmail on your laptop. Then you arrange to have qmail deliver all its mail into a maildir, and then when your laptop is connected to the network, you run serialmail, and it delivers the mail from the maildir to your mail relay host. serialmail is good for some throttling problems. You can run serialmail under control of a daemon that will cut off its network connection after it has written a certain amount of data, for example. But there seems to be no easy way to do what I want with serialmail, because it always wants to deliver all the messages from the maildir, and I want it to deliver one message.
There have been some people on the qmail-users mailing-list asking for something close to what I want, and sometimes the answer was "qmail was designed to deliver mail as quickly and efficiently as possible, so it won't do what you want." This is a variation of "Our software doesn't do what you want, so I'll tell you that you shouldn't want to do it." That's another rant for another day. Anyway, I shouldn't badmouth qmail-users mailing-list, because the archives did get me what I wanted. It's only a stopgap solution, and it might turn out to be a big mistake, but so far it seems okay, and so at last I am coming to the point of this article.
I hacked qmail to support outbound message rate throttling. Following a suggestion of Richard Lyons from the qmail-users mailing-list, it was much easier to do than I had initially thought.
Here's how it works. Whenever qmail wants to try to deliver a message to a remote address, it runs a program called qmail-remote. qmail-remote is responsible for looking up the MX records for the host, contacting the right server, conducting the SMTP conversation, and returning a status code back to the main component. Rather than hacking directly on qmail-remote, I've replaced it with a wrapper. The real qmail-remote is now in qmail-remote-real. The qmail-remote program is now written in Perl. It maintains a log file recording the times at which the last few messages were sent. When it runs, it reads the log file, and a policy file that says how quickly it is allowed to send messages. If it is okay to send another message, the Perl program appends the current time to the log file and invokes the real qmail-remote. Otherwise, it sleeps for a while and checks again.
The program is not strictly correct. It has some race conditions. Suppose the policy limits qmail to sending 8 messages per minute. Suppose 7 messages have been sent in the last minute. Then six instances of qmail-remote might all run at once, decide that it is OK to send a message, and send one. Then 13 messages have been sent in the last minute, which exceeds the policy limit. So far this has not been much of a problem. It's happened twice in the last few hours that the system sent 9 messages in a minute instead of 8. If it worries me too much, I can tell qmail to run only one qmail-remote at a time, instead of 10. On a normal qmail system, qmail speeds up outbound delivery by running multiple qmail-remote processes concurrently. On my crippled system, speeding up outbound delivery is just what I'm trying to avoid. Running at most one qmail-remote at a time will cure all race conditions. If I were doing the project over, I think I'd take out all the file locking and such, and just run one qmail-remote. But I didn't think of it in time, and for now I think I'll live with the race conditions and see what happens.
So let's see? What else is interesting about this program? I made at least one error, and almost made at least one more.
The almost-error was this: The original design for the program was something like:
- do
- lock the history file, read it, and unlock it
- lock the history file, update it, and unlock it
- send the message
One way to fix this is to have the processes append to the history file, but never remove anything from it. That is clearly not a sustainable strategy. Someone must remove expired entries from the history file.
Another fix is to have the read and the update in the same critical section:
- lock the history file
- do
- read the history file
- update the history file and unlock it
- send the message
Cleaning the history file could be done by a separate process that periodically locks the file and rewrites it. But instead, I have the qmail-remote processes to it on the fly:
- do
- lock the history file, read it, and unlock it
- lock the history file, read it, update it, and unlock it
- send the message
Here's a mistake that I did make. This is the block of code that sleeps until it's time to send the message:
while (@last >= $msgs) {
my $oldest = $last[0];
my $age = time() - $oldest;
my $zzz = $time - $age + int(rand(3));
$zzz = 1 if $zzz < 1;
# Log("Sleeping for $zzz secs");
sleep $zzz;
shift @last while $last[0] < time() - $time;
load_policy();
}
The throttling
policy is expressed by two numbers, $msgs and $time,
and the program tries to send no more than $msgs messages per
$time seconds. The @last array contains a list of
Unix epoch timestamps of the times at which the messages of the last
$time seconds were sent.
So the loop condition checks to see if fewer than $msgs
messages were sent in the last $time seconds. If not, the
program continues immediately, possibly posting its message. (It
rereads the history file first, in case some other messages have been
posted while it was asleep.)
Otherwise the program will sleep for a while. The first three lines in the loop calculate how long to sleep for. It sleeps until the time the oldest message in the history will fall off the queue, possibly plus a second or two. Then the crucial line:
shift @last while $last[0] < time() - $time;
which discards the expired items from the history. Finally, the call
to load_policy() checks to see if the policy has changed, and
the loop repeats if necessary.The bug is in this crucial line. if @last becomes empty, this line turns into an infinite busy-loop. It should have been:
shift @last while @last && $last[0] < time() - $time;
Whoops. I noticed this this morning when my system's load was around
12, and eight or nine qmail-remote processes were collectively eating 100% of
the CPU. I would have noticed sooner, but outbound deliveries hadn't
come to a complete halt yet.Incidentally, there's another potential problem here arising from the concurrency. A process will complete the sleep loop in at most $time+3 seconds. But then it will go back and reread the history file, and it may have to repeat the loop. This could go on indefinitely if the system is busy. I can't think of a good way to fix this without getting rid of the concurrent qmail-remote processes.
Here's the code. I hereby place it in the public domain. It was written between 1 AM and 3 AM last night, so don't expect too much.
[Other articles in category /Unix] permanent link
Tue, 04 Mar 2008
"Boolean" or "boolean"?
In a recent article I wrote:
... a logical negation function ... takes a boolean argument and returns a boolean result.I worried for some time about whether to capitalize "boolean" here. But writing "Boolean" felt strange enough that I didn't actually try it to see how it looked on the page.
I looked at the the Big Dictionary, and all the citations were capitalized. But the most recent one was from 1964, so that was not much help.
Then I tried Google search for "boolean capitalized". The first hit was a helpful article by Eric Lippert. M. Lippert starts by pointing out that "Boolean" means "pertaining to George Boole", and so should be capitalized. That much I knew already.
But then he pointed out a countervailing consideration:
English writers do not usually capitalize the eponyms "shrapnel" (Henry Shrapnel, 1761-1842), "diesel" (Rudolf Diesel, 1858-1913), "saxophone" (Adolphe Sax, 1814-1894), "baud" (Emile Baudot, 1845-1903), "ampere" (Andre Ampere, 1775-1836), "chauvinist" (Nicolas Chauvin, 1790-?), "nicotine" (Jean Nicot, 1530-1600) or "teddy bear" (Theodore Roosevelt, 1858-1916).Isn't that a great paragraph? I just had to quote the whole thing.
Lippert concluded that the tendency is to capitalize an eponym when it is an adjective, but not when it is a noun. (Except when it isn't that way; consider "diesel engine". English is what it is.)
I went back to my example to see if that was why I resisted capitalizing "Boolean":
... takes a boolean argument and returns a boolean result.Hmm, no, that wasn't it. I was using "boolean" as an adjective in both places. Wasn't I?
Something seemed wrong. I tried changing the example:
... takes an integer argument and returns an integer result.Aha! Notice "integer", not "integral". "Integral" would have been acceptable also, but that isn't analogous to the expression I intended. I wasn't using "boolean" as an adjective to modify "argument" and "result". I was using it as a noun to denote a certain kind of data, as part of a noun phrase. So it is a noun, and that's why I didn't want to capitalize it.
I would have been happy to have written "takes a boolean and returns a boolean", and I think that's the controlling criterion.
Sorry, George.
[Other articles in category /lang] permanent link
Mon, 03 Mar 2008
Uniquely-decodable codes revisited
[ This is a followup to an earlier article. ]
Alan Morgan wrote to ask if there was a difference between uniquely-decodable (UD) codes for strings and for streams. That is, is there a code for which every finite string is UD, but for which some infinite sequence of symbols has multiple decodings.
I pondered this a bit, and after a little guessing came up with an example: { "a", "ab", "bb" } is UD, because it is a suffix code. But the stream "abbbbbbbbbb..." can be decoded in two ways.
After I found the example, I realized that I shouldn't have needed to guess, because I already knew that you sometimes have to see the last symbol of a string before you can know how to decode it, and in such a code, if there is no such symbol, the decoding must be ambiguous. The code above is UD, but to decode "abbbbbbbbbbbbbbb" you have to count the "b"s to figure out whether the first code word is "a" or "ab".
Let's say that a code is UD+ if it has the property that no two infinite sequences of code words have the same concatenation. Can we characterize the UD+ codes? Clearly, UD+ implies UD, and the example above shows that the converse is not true. A simple argument shows that all prefix codes are UD+. So the question now is, are there UD+ codes that are not prefix codes? I don't know.
[ Addendum 20080303: Gareth McCaughan points out that { "a", "ab" } is UD+ but not prefix. ]
[Other articles in category /CS] permanent link
Sun, 02 Mar 2008[ Note: You are cautioned that this article is in the oops section of my blog, and so you should understand it as a description of a mistake that I have made. ]
For more than a year now my day job has involved work on a large project written entirely in Java. I warned my employers that I didn't have any professional experience in Java, but they hired me anyway. So I had to learn Java. Really learn it, I mean. I hadn't looked at it closely since version 1.2 or so.
Java 1.5 has parametrized types, which they call "generics". These looked pretty good to me at first, and a big improvement on the cruddy 1975-style type system Java had had before. But then I made a shocking discovery: If General is a subtype of Soldier, then List<General> is not a subtype of List<Soldier>.
In particular, you cannot:
List<General> listOfGenerals = ...
List<Soldier> listOfSoldiers = listOfGenerals;
For a couple of weeks I went around muttering to myself about what
idiots the Java people must be. "Geez fuckin' Louise," I said. "The
Hindley-Milner languages have had this right for twenty years. How
hard would it have been for those Java idiots to pick up a damn book
or something?" I was, of course, completely wrong in all respects. The assignment above leads to problems that are obvious if you think about it a bit, and that should have been obvious to me, and would have been, except that I was so busy exulting in my superiority to the entire Java community that I didn't bother to think about it a bit.
You would like to be able to do this:
Soldier someSoldier = ...;
listOfSoldiers.add(someSoldier);
But if you do, you are setting up a type failure:
General someGeneral = listOfGenerals.getLast();
someGeneral.orderAttack(...);
Here listOfSoldiers and listOfGenerals refer to the
same underlying object, so we put a common soldier into that object
back on line 4, and then took it out again on line 5. But line 5 is
expecting it to be a General, and it is not. So we either have a type
failure right there, or else we have a General variable that holds a
a Soldier
object, and then on line 6 a mere private is
allowed to order an attack, causing a run-time type failure. If we're
lucky.The language designers must forbid one of these operations, and the best choice appears to be to forbid the assignment of the List<General> object to the List<Soldier> variable on line 2. The other choices seem clearly much worse.
The canonical Java generics tutorial has an example just like this one, to explain precisely this feature of Java generics. I would have known this, and I would have saved myself two weeks of grumbling, if I had picked up a damn book or something.
Furthermore, my premise was flawed. The H-M languages (SML, Haskell, Miranda, etc.) have not had this right for twenty years. It is easy to get right in the absence of references. But once you add references the problem becomes notoriously difficult, and SML, for example, has gone through several different strategies for dealing with it, as the years passed and more was gradually learned about the problem.
The naive approach for SML is simple. It says that if α is any type, then there is a type ref α, which is the type of a reference that refers to a storage cell that contains a value of type α. So for example ref int is the type of a reference to an int value. There are three functions for manipulating reference types:
ref : α → ref α
! : ref α → α
:= : (ref α * α) → unit
The ref function takes a value and produces a reference to
it, like & in C; if the original value had type α then
the result has type ref α. The ! function takes a reference
of type ref α and dereferences it, returning the value of type α that
it refers to, like * in C. And the := function,
usually written infix, takes a reference and a value, stores the value
into the place that the reference points to, replacing what was there
before, and returns nothing. So for example:
val a = "Kitty cat"; (* a : string *)
val r = ref a; (* r : ref string *)
r := "Puppy dog";
print !r;
This prints Puppy dog. But this next example fails, as you
would hope and expect:
val a = "Kitty cat";
val r = ref a;
r := 37; (* fails *)
because r has type ref string, but 37
has type int, and := requires that the type of
the value on the right match the type referred to by the reference on
the left. That is the obvious, naive approach. What goes wrong, though? The canonical example is:
fun id x = x (* id : α → α *)
val a = ref id; (* a : ref (α → α) *)
fun not true = false
| not false = true ; (* not: bool → bool *)
a := not;
(!a) 13
The key here is that a is a variable of type ref (α → α), that is,
a reference to a cell that can hold a function whose argument is any
type α and whose return value is the same type. Here it holds a
reference to id, which is the identity function.Then we define a logical negation function, not, which has type bool → bool, that is, it takes a boolean argument and returns a boolean result. Since this is a subtype of α → α, we can store this function in the cell referenced by a.
Then we dereference a, recovering the value it points to, which, since the assignment, is the not function. But since a has type ref (α → α), !a has type α → α, and so should be applicable to any value. So the application of !a to the int value 13 passes the type checker, and SML blithely applies the not function to 13.
I've already talked about SML way longer than I planned to, and I won't belabor you further with explanations of the various schemes that were hatched over the years to try to sort this out. Suffice it to say that the problem is still an open research area.
Java, of course, is all references from top to bottom, so this issue obtrudes. The Java people do not know the answer either.
The big error that I made here was to jump to the conclusion that the Java world must be populated with idiots who know nothing about type theory or Haskell or anything else that would have tipped them off to the error I thought they had committed. Probably most of them know nothing about that stuff, but there are a lot of them, and presumably some of them have a clue, and perhaps some of them even know a thing or two that I don't. I said a while back that people who want to become smarter should get in the habit of assuming that everything is more complex than they imagine. Here I assumed the opposite.
As P.J. Plauger once said in a similar circumstance, there is a name for people who are so stupid that they think everyone else is stupid instead.
Maybe I won't be that person next time.
[ Addendum 20201021: [Here's the original post by Plauger](https://groups.google.com/g/comp.std.c/c/aPENvL9wZFw/m/II24s61rOcoJ), in case I want to find it again, or someone else is interested. ]
[Other articles in category /oops] permanent link
Sat, 01 Mar 2008
More rational roots of polynomials
I have a big file of ideas for blog articles, and when I feel like
writing but I can't think of a topic, I look over the file. An item
from last April was relevant to yesterday's article about finding
rational roots of polynomials. It's a trick I saw in the first
edition (1768!) of the Encyclopædia Britannica.
Suppose you have a polynomial P(x) = xn + ...+ p = 0. If it has a rational root r, this must be an integer that divides p = P(0). So far so good.
But consider P(x-1). This is a different polynomial, and if r is a root of P(x), then r+1 is a root of P(x-1). So, just as r must divide P(0), r+1 must divide P(-1). And similarly, r-1 must divide P+1.
So we have an extension of the rational root theorem: instead of guessing that some factor r of P(0) is a root, and checking it to see, we first check to see if r+1 is a factor of P(-1), and if r-1 is a factor of P(1), and proceed with the full check only if these two auxiliary tests pass.
My notes conclude with:
Is this really less work than just trying all the divisors of P(0) directly?Let's find out.
As in the previous article, say P(x) = 3x2 + 6x - 45. The method only works for monic polynomials, so divide everything by 3. (It can be extended to work for non-monic polynomials, but the result is just that you have to divide everything by 3, so it comes to the same thing.) So we consider x2 + 2x - 15 instead. Say r is a rational root of P(x). Then:
| r-1 | divides | P(1) | = -12 |
| r | divides | P(0) | = -15 |
| r+1 | divides | P(-1) | = -16 |
So we need to find three consecutive integers that respectively divide 12, 15, and 16. The Britannica has no specific technique for this; it suggests doing it by eyeball. In this case, 2–3–4 jumps out pretty quickly, giving the root 3, and so does 6–5–4, which is the root -5. But the method also yields a false root: 4–3–2 suggests that -3 might be a root, and it is not.
Let's see how this goes for a harder example. I wrote a little Haskell program that generated the random polynomial x4 - 26x3 + 240 x2 - 918x + 1215.
| r-1 | divides | P(1) | = 512 | = 29 |
| r | divides | P(0) | = 1215 | = 35·5 |
| r+1 | divides | P(-1) | = 2400 | = 25·3·52 |
That required a fair amount of mental arithmetic, and I screwed up and got 502 instead of 512, which I only noticed because 502 is not composite enough; but had I been doing a non-contrived example, I would not have noticed the error. (Then again, I would have done the addition on paper instead of in my head.) Clearly this example was not hard enough because 2–3–4 and 4–5–6 are obviously solutions, and it will not always be this easy. I increased the range on my random number generator and tried again.
The next time, it came up with the very delightful polynomial x4 - 2735x3 + 2712101 x2 - 1144435245x + 170960860950, and I decided not going to go any farther with it. The table values are easy to calculate, but they will be on the order of 170960860950, and I did not really care to try to factor that.
I decided to try one more example, of intermediate difficulty. The program first gave me x4 - 25x3 + 107 x2 - 143x + 60, which is a lucky fluke, since it has a root at 1. The next example it produced had a root at 3. At that point I changed the program to generate polynomials that had integer roots between 10 and 20, and got x4 - 61x3 + 1364 x2 - 13220x + 46800.
| r-1 | divides | P(1) | = 34864 | = 22·33·17·19 |
| r | divides | P(0) | = 46800 | = 24·32·52·13 |
| r+1 | divides | P(-1) | = 61446 | = 2·3·72·11·19 |
This is just past my mental arithmetic ability; I got 34884 instead of 34864 in the first row, and balked at factoring 61446 in my head. But going ahead (having used the computer to finish the arithmetic), the 17 and 19 in the first and last rows are suggestive, and there is indeed a 17–18–19 to be found. Following up on the 19 in the first row suggests that we look for 19–20–21, which there is, and following up on the 11 in the last row, hoping for a 9–10–11, finds one of those too. All of these are roots, and I do have to admit that I don't know any better way of discovering that. So perhaps the method does have some value in some cases. But I had to work hard to find examples for which it made sense. I think it may be more reasonable with 18th-century technology than it is with 21st-century technology.
[Other articles in category /math] permanent link
Fri, 29 Feb 2008
Happy Leap Day! Persian edition
Roland Young has brought to my attention that the
Persian calendar uses a hybrid 7/29 and 8/33 system. I was going to
post this as an addendum to today's Leap Day article, but
it got too long.
If I understand the rules correctly, to determine if a Persian year is a leap year, one applies the following algorithm to the Persian year number y. (Note that the current Persian year is not 2008, but 1386. Persian year 1387 will begin on the vernal equinox.) I will write a % b to denote the remainder when a is divided by b. Then:
- Let a = (y + 2345) % 2820.
- If a is 2819, y is a leap year. Otherwise,
- Let b = a % 128.
- If b < 29, let c = b. Otherwise, let c = (b - 29) % 33.
- If c = 0, y is not a leap year. Otherwise,
- If c is a multiple of 4, y is a leap year. Otherwise,
- y is not a leap year.
This produces 683 leap years out of every 2820, which means that the average calendar year is 365.24219858 days.
How does this compare with the Dominus calendar? It is indeed more accurate, but I consider 683/2820 to be an unnecessarily precise representation of the vernal equinox year, especially inasmuch as the length of the year is changing. And the rule, as you see, is horrendous, requiring either a 2,820-entry lookup table or complicated logic.
Moreover, the Persian and Gregorian calendar are out of sync at present. Persian year 1387, which begins next month on the vernal equinox, is a leap year. But the intercalation will not take place until the last day of the year, around 21 March 2009. The two calendars will not sync up until the year 2092/1470, and then will be confounded only eight years later by the Gregorian 100-year exception. After that they will agree until 2124/1502. Clearly, even if it were advisable to switch to the Persian calendar, the time is not yet right.
I found this Frequently Asked Questions About Calendars page extremely helpful in preparing this article. The Wikipedia article was also useful. Thanks again to Roland Young for bringing this matter to my attention.
[Other articles in category /calendar] permanent link
Happy Leap Day!
I have an instructive followup to yesterday's article all ready to
go, analyzing a technique for finding rational roots of polynomials
that I found in the First Edition of the Encyclopædia
Britannica. A typically Universe-of-Discourse kind of
article. But I'm postponing it to next month so that I can bring you
this timely update.
Everyone knows that our calendar periodically contains an extra day, known to calendar buffs as an "intercalary day", to help make it line up with the seasons, and that this intercalary day is inserted at the end of February. But, depending on how you interpret it, this isn't so. The extra day is actually inserted between February 23 and February 24, and the rest of February has to move down to make room.
I will explain. In Rome, 23 February was a holiday called Terminalia, sacred to Terminus, the god of boundary markers. Under the calendars of the Roman Republic, used up until 46 BCE, an intercalary month, Mercedonius, was inserted into the calendar from time to time. In these years, February was cut down to 23 days (and good riddance; nobody likes February anyway) and Mercedonius was inserted at the end.
When Julius Caesar reformed the calendar in 46, he specified that there would be a single intercalary day every four years much as we have today. As in the old calendar, the intercalary day was inserted after Terminalia, although February was no longer truncated.
So the extra day is actually 24 February, not 29 February. Or not. Depends on how you look at it.
Scheduling intercalary days is an interesting matter. The essential problem is that the tropical year, which is the length of time from one vernal equinox to the next, is not an exact multiple of one day. Rather, it is about 365¼ days. So the vernal equinox moves relative to the calendar date unless you do something to fix it. If the tropical year were exactly 365¼ days long, then four tropical years would be exactly 1461 days long, and it would suffice to make four calendar years 1461 days long, to match. This can be accomplished by extending the 365-day calendar year with one intercalary day every four years. This is the Julian system.
Unfortunately, the tropical year is not exactly 365¼ days long. It is closer to 365.24219 days long. So how many intercalary days are needed?
It suffices to make 100,000 calendar years total exactly 36,524,219 days, which can be accomplished by adding a day to 24,219 years out of every 100,000. But this requires a table with 100,000 entries, which is too complicated.
We would like to find a system that requires a simpler table, but which is still reasonably accurate. The Julian system requires a table with 4 entries, but gives a calendar year that averages 365.25 days long, which is 0.00781 too many. Since this is about 1/128 day, the Julian calendar "gains a day" every 128 years or so, which means that the vernal equinox slips a day earlier every 128 years, and eventually the daffodils and crocuses are blooming in January.
Not everyone considers this a problem. The Islamic calendar is only 355 days long, and so "loses" 10 days per year, which means that after 18 years the Islamic new year has moved half a year relative to the seasons. The annual Islamic holy month of Ramadan coincided with July-August in 1980 and with January-February in 1997. The Muslims do intercalate, but they do it to keep the months in line with the phases of the moon.
Still, supposing that we do consider this a problem, we would like to find an intercalation scheme that is simple and accurate. This is exactly the problem of finding a simple rational approximation to 0.24219. If p/q is close to 0.24219, then one can introduce p intercalary days every q years, and q is the size of the table required. The Julian calendar takes p/q = 1/4 = 0.25, for an error around 1/128. The Gregorian calendar takes p/q = 97/400 = 0.2425, for an error of around 1/3226. Again, this means that the Gregorian calendar gains a day on the seasons every 3,226 years or so. Can we do better?
Any time the question is "find a simple rational approximation to a number" the answer is likely to involve continued fractions. 365.24219 is equal to:
$$ 365 + {1\over \displaystyle 4 + {\strut 1\over\displaystyle 7 + {\strut 1\over\displaystyle 1 + {\strut 1\over\displaystyle 3 + {\strut 1\over\displaystyle 24 + {\strut 1\over\displaystyle 6 + \cdots }}}}}}$$
which for obvious reasons, mathematicians abbreviate to [365; 4, 7, 1, 3, 24, 6, 2, 2]. This value is exact. (I had to truncate the display above because of a bug in my TeX formula tool: the full fraction goes off the edge of the A0-size page I use as a rendering area.)As I have mentioned before, the reason this horrendous expression is interesting is that if you truncate it at various points, the values you get are the "continuants", which are exactly the best possible rational approximations to the original number. For example, if we truncate it to [365], we get 365, which is the best possible integer approximation to 365.24219. If we truncate it to [365; 4], we get 365¼, which is the Julian calendar's approximation.
Truncating at the next place gives us [365; 4, 7], which is 365 + 1/(4 + 1/7) = 356 + 1/(29/7) = 365 + 7/29. In this calendar we would have 7 intercalary days out of 29, for a calendar year of 365.241379 days on average. This calendar loses one day every 1,234 years.
The next convergent is [365; 4, 7, 1] = 8/33, which requires 8 intercalary days every 33 years for an average calendar year of 0.242424 days. This schedule gains only one day in 4,269 years and so is actually more accurate than the Gregorian calendar currently in use, while requiring a table with only 33 entries instead of 400.
The real question, however, is not whether the table can be made smaller but whether the rule can be made simpler. The rule for the Gregorian calendar requires second-order corrections:
- If the year is a multiple of 400, it is a leap year; otherwise
- If the year is a multiple of 100, it is not a leap year; otherwise
- If the year is a multiple of 4, it is a leap year.
And one frequently sees computer programs that omit one or both of the exceptions in the rule.
The 8/33 calendar requires dividing by 33, which is its most serious problem. But it can be phrased like this:
- Divide the year by 33. If the result is 0, it is not a leap year. Otherwise,
- If the result is divisible by 4, it is a leap year.
Furthermore, the rule as I gave it above has another benefit: it matches the Gregorian calendar this year and will continue to do so for several years. This was more compelling when I first proposed this calendar back in 1998, because it would have made the transition to the new calendar quite smooth. It doesn't matter which calendar you use until 2016, which is a leap year in the Gregorian calendar but not in the 8/33 calendar as described above. I may as well mention that I have modestly named this calendar the Dominus calendar.
But time is running out for the smooth transition. If we want to get the benefits of the Dominus calendar we have to do it soon. Help spread the word!
[ Pre-publication addendum: Wikipedia informs me that it is not correct to use the tropical year, since this is not in fact the time between vernal equinoxes, owing to the effects of precession and nutation. Rather, one should use the so-called vernal equinox year, which is around 365.2422 days long. The continued fraction for 365.2422 is slightly different from that of 356.24219, but its first few convergents are the same, and all the rest of the analysis in the article holds the same for both years. ]
[ Addendum 20080229: The Persian calendar uses a hybrid 7/29 and 8/33 system. Read all about it. ]
[ Addendum 20240229: Alas, the clock has run out on my attempt to get the world to adopt the Dominus calendar. ]
[Other articles in category /calendar] permanent link
Thu, 28 Feb 2008
Algebra techniques that don't work, except when they do
In Problems
I Can't Fix in the Lecture Hall, Rudbeckia Hirta describes the
efforts of a student to
solve the equation 3x2 + 6x - 45 = 0.
She describes "the
usual incorrect strategy selected by students who can't do
algebra":
| 3x2 + 6x - 45 | = | 0 |
| 3x2 + 6x | = | 45 |
| x(3x + 6) | = | 45 |
She says "I stopped him before he factored out the x.".
I was a bit surprised by this, because the work so far seemed reasonable to me. I think the only mistake was not dividing the whole thing by 3 in the first step. But it is not too late to do that, and even without it, you can still make progress. x(3x + 6) = 45, so if there are any integer solutions, x must divide 45. So try x = ±1, ±3, ±5, ±9, ±15 in roughly that order. (The "look for the wallet under the lamppost" principle.) x = 3 solves the equation, and then you can get the other root, x=-5, by further application of the same method, or by dividing the original polynomial by x-3, or whatever.
If you get rid of the extra factor of 3 in the first place, the thing is even easier, because you have x(x + 2) = 15, so x = ±1, ±3, or ±5, and it is obviously solved by x=3 and x=-5.
Now obviously, this is not always going to work, but it works often enough that it would have been the first thing I would have tried. It is a lot quicker than calculating b2 - 4ac when c is as big as 45. If anyone hassles you about it, you can get them off your back by pointing out that it is an application of the so-called rational root theorem.
But probably the student did not have enough ingenuity or number sense to correctly carry off this technique (he didn't notice the 3), so that M. Hirta's advice to just use the damn quadratic formula already is probably good.
Still, I wonder if perhaps such students would benefit from exposure to this technique. I can guess M. Hirta's answer to this question: these students will not benefit from exposure to anything.
[ Addendum 20080228: Robert C. Helling points out that I could have factored the 45 in the first place, without any algebraic manipulations. Quite so; I completely botched my explanation of what I was doing. I meant to point out that once you have x(x+2) = 15 and the list [1, 3, 5, 15], the (3,5) pair jumps out at you instantly, since 3+2=5. I spent so much time talking about the unreduced polynomial x(3x+6) that I forgot to mention this effect, which is much less salient in the case of the unreduced polynomial. My apologies for any confusion caused by this omission. ]
[ Addendum 20080301: There is a followup to this article. ]
[Other articles in category /math] permanent link
Wed, 27 Feb 2008
Uniquely-decodable codes
Ricardo J.B. Signes asked me a few days ago if there was a way to decide
whether a given set S of strings had the property that any two
distinct sequences of strings from S have distinct
concatenations.
For example, consider S1 = { "ab", "abba", "b" }. This set does not have the specified property, because you can take the two sequences [ "ab", "b", "ab" ] and [ "abba", "b" ], and both concatenate to "abbab". But S2 = { "a", "ab", "abb" } does have this property.
Coding theory
In coding theory, the property has the awful name "unique decodability". The idea is that you have some input symbols, and each input symbol is represented with one output symbol, which is one of the strings from S. Then suppose you receive some message like "abbab". Can you figure out what the original input was? For S2, yes: it must have been ZY. But for S1, no: it could have been either YZ or XZX.In coding theory, the strings are called "code words" and the set of strings is a "code". So the question is how to tell whether a code is uniquely-decodable. One obvious way to take a non-uniquely-decodable code and turn it into a uniquely-decodable code is to append delimiters to the code words. Consider S1 again. If we delimit the code words, it becomes { "(ab)", "(abba)", "(b)" }, and the two problem sequences are now distinguishable, since "(ab)(b)(ab)" looks nothing like "(abba)(b)". It should be clear that one doesn't need to delimit both ends; the important part is that the words are separated, so one could use { "ab-", "abba-", "b-" } instead, and the problem sequences translate to "ab-b-ab-" and "abba-b-". So every non-uniquely-decodable code corresponds to a uniquely-decodable code in at least this trivial way, and often the uniquely-decodable property is not that important in practice because you can guarantee uniquely-decodableness so easily just by sticking delimiters on the code words.
But if you don't want to transmit the extra delimiters, you can save bandwidth by making your code uniquely-decodable even without delimiters. The delimiters are a special case of a more general principle, which is that a prefix code is always uniquely-decodable. A prefix code is one where no code word is a prefix of another. Or, formally, there are no code words x and y such that x = ys for some nonempty s. Adding the delimiters to a code turns it into a prefix code. But not all prefix codes have delimiters. { "a", "ba", "bba", "bbba" } is an example, as are { "aa", "ab", "ba", "bb" } and { "a", "baa", "bab", "bb" }.
The proof of this is pretty simple: you have some concatenation of code words, say T. You can decode it as follows: Find the unique code word c such that c is a prefix of T; that is, such that T = cU. There must be such a c, because T is a concatenation of code words. And c must be unique, because if there were c' and U' with both cU = T and c'U' = T, then cU = c'U', and whichever of c or c' is shorter must be a prefix of the one that is longer, and that can't happen because this is a prefix code. So c is the first code word in T, and we can pull it off and repeat the process for U, getting a unique sequence of code words, unless U is empty, in which case we are done.
There is a straightforward correspondence between prefix codes and trees; the code words can be arranged at the leaves of a tree, and then to decode some concatenation T you can scan its symbols one at a time, walking the tree, until you get to a leaf, which tells you which code word you just saw. This is the basis of Huffman coding.
Prefix codes include, as a special case, codes where all the words are the same length. For those codes, the tree is balanced, and has all branches the same length.
But uniquely-decodable codes need not be prefix codes. Most obviously, a suffix code is uniquely-decodable and may not be a prefix code. For example, {"a", "aab", "bab", "bb" } is uniquely-decodable but is not a prefix code, because "a" is a prefix of "aab". The proof of uniquely-decodableness is obvious: this is just the last prefix code example from before, with all the code words reversed. If there were two sequences of words with the same concatenation, then the reversed sequences of reversed words would also have the same concatenation, and this would show that the code of the previous paragraph was not uniquely-decodable. But that was a prefix code, and so must be uniquely-decodable.
But codes can be uniquely-decodable without being either prefix or suffix codes. For example, { "aabb", "abb", "bb", "bbba" } is uniquely-decodable but is neither a prefix nor a suffix code. Rik wanted a method for deciding.
I told Rik about the prefix code stuff, which at least provides a sufficient condition for uniquely-decodableness, and then started poking around to see what else I could learn. Ahem, I mean, researching. I suppose that a book on elementary coding theory would have a discussion of the problem, but I didn't have one at hand, and all I could find online concerned prefix codes, which are of more practical interest because of the handy tree method for speedy decoding.
But after tinkering with it for a couple of days (and also making an utterly wrong intermediate guess that it was undecidable, based on a surface resemblance to the Post correspondence problem) I did eventually figure out an algorithm, which I wrote up and released on CPAN, my first CPAN post in about a year and a half.
An example
The idea is pretty simple, and I think best illustrated by an example, as so many things are. We will consider { "ab", "abba", "b" } again. We want to find two sequences of code words whose concatenations are the same. So say we want pX1 = qY1, where p and q are code words and X1 and Y1 are some longer strings. This can only happen if p and q are different lengths and if one is a prefix of the other, since otherwise the two strings pX1 and qY1 don't begin with the same symbols. So we consider just the cases where p is a prefix of q, which means that in this example we want to find "ab"X1 = "abba"Y1, or, equivalently, X1 = "ba"Y1.Now X1 must begin with "ba", so we need to either find a code word that begins with "ba", or we need to find a code word that is a prefix of "ba". The only choice is "b", so we have X1 = "b"X2, and so X1 = "b"X2 = "ba"Y1, or equivalently, X2 = "a"Y1.
Now X2 must begin with "a", so we need to either find a code word that begins with "a", or we need to find a code word that is a prefix of "a". This occurs for "abba" and "ab". So we now have two situations to investigate: "ab"X3 = "a"Y1, and "abba"X4 = "a"Y1. Or, equivalently, "b"X3 = Y1, and "bba"X4 = Y1.
The first of these, "b"X3 = Y1 wins immediately, because "b" is a code word: we can take X3 to be empty, and Y1 to be "b", and we have what we want:
| "ab" X1 | = | "abba" Y1 |
| "ab" "b" X2 | = | "abba" Y1 |
| "ab" "b" "ab" X3 | = | "abba" Y1 |
| "ab" "b" "ab" | = | "abba" "b" |
where the last line of the table is exactly the solution we seek.
Following the other one, "bba"X4 = Y1, fails, and in a rather interesting way. Y1 must begin with two "b" words, so put "bb"Y2 = Y1, so "bba"X4 = "bb"Y2, then "a"X4 = Y2.
But this last equation is essentially the same as the X2 = "a"Y1 situation we were investigating earlier; we are just trying to make two strings that are the same except that one has an extra "a" on the front. So this investigation tells us that if we could find two strings with "a"X = Y, we could make longer strings "abba"Y = "b" "b" "a"X. This may be interesting, but it does not help us find what we really want.
The algorithm
Having seen an example, here's the description of the algorithm. We will tabulate solutions to Xs = Y, where X and Y are sequences of code words, for various strings s. If s is empty, we win.We start the tabulation by looking for pairs of keywords c1 and c2 with c1 a prefix of c2, because then we have c1s = c2 for some s. We maintain a queue of s-values to investigate. At one point in our example, we had X1 = "ba"Y1; here s is "ba".
If s begins with a code word, then s = cs', so we can put s' on the queue. This is what happened when we went from X1 = "ba"Y1 to "b"X2 = "ba"Y1 to X2 = "a"Y1. Here s was "ba" and s' was "a".
If s is a prefix of some code word, say ss' = c, then we can also put s' on the queue. This is what happened when we went from X2 = "a"Y1 to "abba"X4 = "a"Y1 to "bba"X4 = Y1. Here s was "a" and s' was "bba".
If we encounter some queue item that we have seen before, we can discard it; this will prevent us from going in circles. If the next queue item is the empty string, we have proved that the code is not uniquely-decodable. (Alternatively, we can stop just before queueing the empty string.) If the queue is empty, we have investigated all possibilities and the code is uniquely-decodable.
Pseudocode
Here's the summary:
- Initialization:
For each pair of code words c1 and
c2 with c1s =
c2, put s in the queue.
- Main loop: Repeat the following until termination
- If the queue is empty, terminate. The code is uniquely-decodable.
- Otherwise:
- Take an item s from the queue.
- For each code word c:
- If c = s, terminate. The code is not uniquely-decodable.
- If cs' = s, and s' has not been seen before, queue s'.
- If c = ss', and s' has not been seen before, queue s'.
To this we can add a little bookkeeping so that the algorithm emits the two ambiguous sequences when the code is not uniquely-decodable. The implementation I wrote uses a hash to track which strings s have appeared in the queue already. Associated with each string s in the hash are two sequences of code words, P and Q, such that Ps = Q. When s begins with a code word, so that s = cs', the program adds s' to the hash with the two sequences [P, c] and Q. When s is a prefix of a code word, so that ss' = c, the program adds s' to the hash with the two sequences Q and [P, c]; the order of the sequences is reversed in order to maintain the Ps = Q property, which has become Qs' = Pss' = Pc in this case.
Notes
As I said, I suspect this is covered in every elementary coding theory text, but I couldn't find it online, so perhaps this writeup will help someone in the future.After solving this problem I meditated a little on my role in the programming community. The kind of job I did for Rik here is a familiar one to me. When I was in college, I was the math guy who hung out in the computer lab with the hackers. Periodically one of them would come to me with some math problem: "Crash, I am writing a ray tracer. If I have a ray and a triangle in three dimensions, how can I figure out if the ray intersects the triangle?" And then I would go off and figure out how to do that and come back with the algorithm, perhaps write some code, or perhaps provide some instruction in matrix computations or whatever was needed. In physics class, I partnered with Jim Kasprzak, a physics major, and we did all the homework together. We would read the problem, which would be some physics thing I had no idea how to solve. But Jim understood physics, and could turn the problem from physics into some mathematics thing that he had no idea how to solve. Then I would do the mathematics, and Jim would turn my solution back into physics. I wish I could make a living doing this.
Puzzle: Is { "ab", "baab", "babb", "bbb", "bbba" } uniquely-decodable? If not, find a pair of sequences that concatenate to the same string.
Research question: What's the worst-case running time of the algorithm? The queue items are all strings that are strictly shorter than the longest code word, so if this has length n, then the main loop of the algorithm runs at most (an-1) / (a-1) times, where a is the number of symbols in the alphabet. But can this worst case really occur, or is the real worst case much faster? In practice the algorithm always seems to complete very quickly.
Project to do: Reimplement in Haskell. Compare with Perl implementation. Meditate on how they can suck in such completely different ways.
[ There is a brief followup to this article. ]
[ Addendum 20170318: Marius Buzea has brought to my attention that this is exactly the Sardinas-Patterson Algorithm. The Wikipedia article claims that the worst-case running time is !!O(nk)!! where !!k!! is the number of code words and !!n!! is their total length. ]
[Other articles in category /CS] permanent link
Thu, 21 Feb 2008
Crappiest literary theory this month
Someone on Wikipedia has been pushing the theory that the four bad
children in Charlie and the Chocolate Factory correspond
to the seven deadly sins.
[Other articles in category /book] permanent link
Mon, 18 Feb 2008
Cornaptious
Once I was visiting my grandparents while home from college. We were
in the dining room, and they were talking about a book they were
reading, in which the author had used a word they did not know:
cornaptious. I didn't know it either, and got up from the
table to look it up in their Webster's Second International
Dictionary. (My grandfather, who was for his whole life a both
cantankerous and a professional editor, loathed the permissive and
descriptivist Third International. The out-of-print Second
International Edition was a prized Christmas present that in those
days was hard to find.)
Webster's came up with nothing. Nothing but "corniculate", anyway, which didn't appear to be related. At that point we had exhausted our meager resources. That's what things were like in those days.
The episode stuck with me, though, and a few years later when I became the possessor of the First Edition of the Oxford English Dictionary, I tried there. No luck. Some time afterwards, I upgraded to the Second Edition. Still no luck.
Years went by, and one day I was reading The Lyre of Orpheus, by Robertson Davies. The unnamed Dean of the music school describes the brilliant doctoral student Hulda Schnakenburg:
"Oh, she's a foul-mouthed, cornaptious slut, but underneath she is all untouched wonderment.""Aha," I said. "So this is what they were reading that time."
More years went by, the oceans rose and receded, the continents shifted a bit, and the Internet crawled out of the sea. I returned to the problem of "cornaptious". I tried a Google book search. It found one use only, from The Lyre of Orpheus. The trail was still cold.
But wait! It also had a suggestion: "Did you mean: carnaptious", asked Google.
Ho! Fifty-six hits for "carnaptious", all from books about Scots and Irish. And the OED does list "carnaptious". "Sc. and Irish dial." it says. It means bad-tempered or quarrelsome. Had Davies spelled it correctly, we would have found it right away, because "carnaptious" does appear in Webster's Second.
So that's that then. A twenty-year-old spelling error cleared up by Google Books.
[ Addendum 20080228: The Dean's name is Wintersen. Geraint Powell, not the Dean, calls Hulda Schnakenburg a cornaptious slut. ]
[Other articles in category /lang] permanent link
Fri, 15 Feb 2008
Acta Quandalia
Several readers have emailed me to discuss my recent articles about
mathematical screwups, and a few have let drop casual comments that
suggest that they think that I invented Acta Quandalia as
a joke. I can assure you that no journal is better than Acta
Quandalia. Since it is difficult to obtain outside of
university libraries, however, I have scanned the cover of one of last
year's issues for you to see:
[Other articles in category /math] permanent link
Wed, 13 Feb 2008
The least interesting number
Berry's paradox goes like this: Some natural numbers, like 2, are
interesting. Some natural numbers, like 255610679 (I think), are not
interesting. Consider the set of uninteresting natural numbers. If
this set were nonempty, it would contain a smallest element s.
But then s, would have the interesting property of being the
smallest uninteresting number. This is a contradiction. So the
set of uninteresting natural numbers must be empty.
This reads like a joke, and it is tempting to dismiss it as a trite bit of foolishness. But it has rather interesting and deep connections to other related matters, such as the Grelling-Nelson paradox and Gödel's incompleteness theorem. I plan to write about that someday.
But today my purpose is only to argue that there are demonstrably uninteresting real numbers. I even have an example. Liouville's number L is uninteresting. It is defined as:
$$\sum_{i=1}^\infty {10}^{-i!} = 0.1100010000000000000001000\ldots$$
Why is this number of any concern? In 1844 Joseph Liouville showed that there was an upper bound on how closely an irrational algebraic number could be approximated by rationals. L can be approximated much more closely than that, and so must therefore be transcendental. This was the proof of the existence of transcendental numbers.The only noteworthy mathematical property possessed by L is its transcendentality. But this is certainly not enough to qualify it as interesting, since nearly all real numbers are transcendental.
Liouville's theorem shows how to construct many transcendental numbers, but the construction generates many similar numbers. For example, you can replace the 10 with a 2, or the n! with floor(en) or any other fast-growing function. It appears that any potentially interesting property possessed by Liouville's number is also possessed by uncountably many other numbers. Its uninterestingness is identical to that of other transcendental numbers constructed by Liouville's method. L was neither the first nor the simplest number so constructed, so Liouville's number is not even of historical interest.
The argument in Berry's paradox fails for the real numbers: since the real numbers are not well-ordered, the set of uninteresting real numbers need have no smallest element, and in fact (by Berry's argument) does not. Liouville's number is not the smallest number of its type, nor the largest, nor anything else of interest.
If someone were to come along and prove that Liouville's number was the most uninteresting real number, that would be rather interesting, but it has not happened, nor is it likely.
[Other articles in category /math] permanent link
Thu, 07 Feb 2008
Trivial theorems
Mathematical folklore contains a story about how Acta
Quandalia published a paper proving that all partially uniform
k-quandles had the Cosell property, and then a few months later
published another paper proving that no partially uniform
k-quandles had the Cosell property. And in fact, goes the
story, both theorems were quite true, which put a sudden end to the
investigation of partially uniform k-quandles.
Except of course it wasn't Acta Quandalia (which would never commit such a silly error) and it didn't concern k-quandles; it was some unspecified journal, and it concerned some property of some sort of topological space, and that was the end of the investigation of those topological spaces.
This would not qualify as a major screwup under my definition in the original article, since the theorems are true, but it certainly would have been rather embarrassing. Journals are not supposed to publish papers about the properties of the empty set.
Hmm, there's a thought. How about a Journal of the Properties of the Empty Set? The editors would never be at a loss for material. And the cover almost designs itself.
Handsome, isn't it? I See A Great Need!Ahem. Anyway, if the folklore in question is true, I suppose the mathematicians involved might have felt proud rather than ashamed, since they could now boast of having completely solved the problem of partially uniform k-quandles. But on the other hand, suppose you had been granted a doctorate on the strength of your thesis on the properties of objects from some class which was subsequently shown to be empty. Wouldn't you feel at least a bit like a fraud?
Is this story true? Are there any examples? Please help me, gentle readers.
[ Addendum 20210828: Mathematician [Carl Ludig Siegel once wrote in a letter](http://docmadhattan.fieldofscience.com/2019/12/carl-ludwig-siegel-number-thoery-pig.html) “I am afraid that mathematics will perish before the end of this century if the present trend for senseless abstraction — as I call it: theory of the empty set — cannot be blocked up.” ]
[Other articles in category /math] permanent link
Tue, 05 Feb 2008
Steganography in 1665: correction
(A correction to this.)
Phil Rodgers has pointed out that a "physique" is not an emetic, as I thought, but a laxative.
Are there any among you who doubt that Bruce Schneier can shoot sluggbullets out of his ass? Let the unbelievers beware!
[Other articles in category /IT] permanent link
Steganography in 1665
Today's entry in Samuel Pepys'
diary says:
He told us a very handsome passage of the King's sending him his message ... in a sluggbullet, being writ in cypher, and wrapped up in lead and swallowed. So the messenger come to my Lord and told him he had a message from the King, but it was yet in his belly; so they did give him some physique, and out it come.Sure, Bruce Schneier can mount chosen-ciphertext attacks without even choosing a ciphertext. But dare he swallow a "sluggbullet" and bring it up again to be read?
Silly me. Bruce Schneier can probably cough up a sluggbullet without swallowing one beforehand.
[ Addendum 20080205: A correction. ]
[Other articles in category /IT] permanent link
Major screwups in mathematics: example 1
Last month I asked for
examples of major screwups in mathematics. Specifically, I was
looking for cases in which some statement S was considered to
be proved, and later turned out to be false. I could not think of any
examples myself.
Readers suggested several examples, and I got lucky and turned up one on my own.
Some of the examples were rather obscure technical matters, where Professor Snorfus publishes in Acta Quandalia that all partially uniform k-quandles have the Cosell property, and this goes unchallenged for several years before one of the other three experts in partially uniform quandle theory notices that actually this is only true for Nemontovian k-quandles. I'm not going to report on matters that sounded like that to me, although I realize that I'm running the risk that all the examples that I do report will sound that way to most of the audience. But I'm going to give it a try.
General remarks
I would like to make some general remarks first, but I don't quite know yet what they are. Two readers independently suggested that I should read Proofs and Refutations by Imre Lakatos, and raised a number of interesting points that I'm sure I'd like to expand on, except that I haven't read the book. Both copies are checked out of the Penn library, which is a good sign, and the interlibrary loan copy I ordered won't be here for several days.Still, I can relate a partial secondhand understanding of the ideas, which seem worth repeating.
Sometime later, someone observed that Euler's theorem was false for polyhedra with holes in them. For example, consider the object shown at right. It has (F, E, V) = (9, 18, 9), giving F - E + V = 9 - 18 - 9 = 0.
Can we say that Euler was wrong? Not really. The question hinges on the definition of "polyhedron". Euler's theorem is proved for "polyhedra", but we can see from the example above that it only holds for "simply-connected polyhedra". If Euler proved his theorem at a time when "polyhedra" was implicitly meant "simply-connected", and the generally-understood definition changed out from under him, we can't hold that against Euler. In fact, the failure of Euler's theorem for the object above suggests that maybe we shouldn't consider it to be a polyhedron, that it is somehow rather different from a polyhedron in at least one important way. So the theorem drives the definition, instead of the other way around.
Okay, enough introductory remarks. My first example is unquestionably a genuine error, and from a first-class mathematician.
Mathematical background
Some terminology first. A "formula" is just that, for example something like this:
$$\displaylines{ ((\forall a.\lnot R(a,a)) \wedge\cr (\forall b\forall c.R(b,c)\to\lnot R(c,b))\wedge\cr (\forall d\forall e\forall f.(R(d,e)\wedge R(e,f)\to R(d,f))) \to\cr (\forall x\exists y.R(y,x)) }$$
It may contain a bunch of quantified variables (a, b, c, etc.), relations (like R), and logical connectives like ∧. A formula might also include functions and constants (which I didn't) or equality symbols (there are none here).One can ask whether the formula is true (or, in the jargon, "valid"), which means that it must hold regardless of how one chooses the set S from which the values of the variables will be drawn, and regardless of the meanings assigned to the relation symbols (and to the functions and constants, if there are any). The following formula, although not very interesting, is valid:
$$ \forall a\exists b.(P(a)\wedge P(b))\to P(a) $$
This is true regardless of the meaning we ascribe to P, and regardless of the set from which a and b are required to be drawn.The longer formula above, which requires that R be a linear order, and then that the linear order R have no minimal element, is not universally valid, but it is valid for some interpretations of R and some sets S from which a...f, x, and y may be drawn. Specifically, it is true if one takes S to be the set of integers and R(x, y) to mean x < y. Such formulas, which are true for some interpretations but not for all, are called "satisfiable". Obviously, valid formulas are satisfiable, because satisfiable formulas are true under some interpretations, but valid formulas are true under all interpretations.
Gödel famously showed that it is an undecidable problem to determine whether a given formula of arithmetic is satisfiable. That is, there is no method which, given any formula, is guaranteed to tell you correctly whether or not there is some interpretation in which the formula is true. But one can limit the form of the allowable formulas to make the problem easier. To take an extreme example, just to illustrate the point, consider the set of formulas of the form:
∃a∃b... ((a=0)∨(a=1))∧((b=0)∨(b=1))∧...∧R(a,b,...)
for some number of variables. Since the formula itself requires that a, b, etc. are each either 0 or 1, all one needs to do to decide whether the formula is satisfiable is to try every possible assignment of 0 and 1 to the n variables and see whether R(a,b,...) is true in any of the 2n resulting cases. If so, the formula is satisfiable, if not then not.
Kurt Gödel, 1933
One would like to prove decidability for a larger and more general class of formulas than the rather silly one I just described. How big can the class of formulas be and yet be decidable?It turns out that one need only consider formulas where all the quantifiers are at the front, because there is a simple method for moving quantifiers to the front of a formula from anywhere inside. So historically, attention has been focused on formulas in this form.
One fascinating result concerns the class of formulas called [∃*∀2∃*, all, (0)]. These are the formulas that begin with ∃a∃b...∃m∀n∀p∃q...∃z, with exactly two ∀ quantifiers, with no intervening ∃s. These formulas may contain arbitrary relations amongst the variables, but no functions or constants, and no equality symbol. [∃*∀2∃*, all, (0)] is decidable: there is a method which takes any formula in this form and decides whether it is satisfiable. But if you allow three ∀ quantifiers (or two with an ∃ in between) then the set of formulas is no longer decidable. Isn't that freaky?
The decidability of the class [∃*∀2∃*, all, (0)] was shown by none other than Gödel, in 1933. However, in the last sentence of his paper, Gödel added that the same was true even if the formulas were also permitted to include equality:
In conclusion, I would still like to remark that Theorem I can also be proved, by the same method, for formulas that contain the identity sign.
Oops
This was believed to be true for more than thirty years, and the result was used by other mathematicians to prove other results. But in the mid-1960s, Stål Aanderaa showed that Gödel's proof would not actually work if the formulas contained equality, and in 1983, Warren D. Goldfarb proved that Gödel had been mistaken, and the satisfiability of formulas in the larger class was not decidable.
Sources
Gödel's original 1933 paper is Zum Entscheidungsproblem des logischen Funktionenkalküls (On the decision problem for the functional calculus of logic) which can be found on pages 306–327 of volume I of his Collected Works. (Oxford University Press, 1986.) There is an introductory note by Goldfarb on pages 226–231, of which pages 229–231 address Gödel's error specifically.I originally heard the story from Val Tannen, and then found it recounted on page 188 of The Classical Decision Problem, by Egon Boerger, Erich Grädel, and Yuri Gurevich. But then blog reader Jeffrey Kegler found the Goldfarb note, of which the Boerger-Grädel-Gurevich account appears to be a summary.
Thanks very much to everyone who contributed, and especially to M. Kegler.
(I remind readers who have temporarily forgotten, that Acta Quandalia is the quarterly journal of the Royal Uzbek Academy of Semi-Integrable Quandle Theory. Professor Snorfus, you will no doubt recall, won the that august institution's prestigious Utkur Prize in 1974.)
[ Addendum 20080206: Another article in this series. ]
[ Addendum 20200206: A serious mistake by Henri Lebesgue. ]
[Other articles in category /math] permanent link
Fri, 01 Feb 2008
Addenda to recent articles 200801
Here are some notes on posts from the last
month that I couldn't find better places for.
- As a result of my research into the Harriet Tubman mural that was
demolished in 2002, I learned that it had been repainted last year
at 2950 Germantown Avenue.
- A number of readers, including some honest-to-God Italians, wrote
in with explanations of Boccaccio's term
milliantanove, which was variously translated as
"squillions" and "a thousand hundreds".
The "milli-" part suggests a thousand, as I guessed. And "-anta" is the suffix for multiples of ten, found in "quaranta" = "forty", akin to the "-nty" that survives in the word "twenty". And "nove" is "nine".
So if we wanted to essay a literal translation, we might try "thousanty-nine". Cormac Ó Cuilleanáin's choice of "squillions" looks quite apt.
- My article about clubbing
someone to death with a loaded Uzi neglected an essential
technical point. I repeatedly said that
for my $k (keys %h) { if ($k eq $j) { f($h{$k}) } }could be replaced with:
f($h{$j})But this is only true if $j actually appears in %h. An accurate translation is:
f($h{$j}) if exists $h{$j}I was, of course, aware of this. I left out discussion of this because I thought it would obscure my point to put it in, but I was wrong; the opposite was true.
I think my original point stands regardless, and I think that even programmers who are unaware of the existence of exists should feel a sense of unease when presented with (or after having written) the long version of the code.
An example of this error appeared on PerlMonks shortly after I wrote the article.
- Robin Houston provides another example of a
nonstandard adjective in mathematics: a quantum group is not
a group.
We then discussed the use of nonstandard adjectives in biology. I observed that there seemed to be a trend to eliminate them, as with "jellyfish" becoming "jelly" and "starfish" becoming "sea star". He pointed out that botanists use a hyphen to distinguish the standard from the nonstandard: a "white fir" is a fir, but a "Douglas-fir" is not a fir; an "Atlas cedar" is a cedar, but a "western redcedar" is not a cedar.
Several people wrote to discuss the use of "partial" versus "total", particularly when one or the other is implicit. Note that a total order is a special case of a partial order, which is itself a special case of an "order", but this usage is contrary to the way "partial" and "total" are used for functions: just "function" means a total function, not a partial function. And there are clear cases where "partial" is a standard adjective: partial fractions are fractions, partial derivatives are derivatives, and partial differential equations are differential equations.
- Steve Vinoski posted a very interesting solution to my
question about how to set Emacs file modes: he suggested
that I could define a replacement aput function.
- In my utterly useless review of Robert Graves' novel King
Jesus I said "But how many of you have read I,
Claudius and Suetonius? Hands? Anyone? Yeah, I didn't think
so." But then I got email from James Russell, who said he had indeed
read both, and that he knew just what I meant, and, as a
result, was going directly to the library to take out King
Jesus. And he read the article on Planet Haskell. Wow! I am
speechless with delight. Mr. Russell, I love you. From now on,
if anyone asks (as they sometimes do) who my target audience is, I
will say "It is James Russell."
- A number of people wrote in with examples of "theorems" that were
believed proved, and later turned out to be false. I am preparing a
longer article about this for next month. Here are some teasers:
- Cauchy
apparently "proved" that if a sum of continuous functions converges
pointwise, then the sum is also a continuous function, and this error
was widely believed for several years.
- I just learned of a major
screwup by none other than Kurt Gödel concerning the decidability
of a certain class of sentences of first-order arithmetic which went
undetected for thirty years.
- Robert Tarjan proved in the
1970s that the time complexity of a certain algorithm for the
union-find problem was slightly worse than linear. And several people
proved that this could not be improved upon. But Hantao Zhang has a paper
submitted to STOC
2008 which, if it survives peer review, shows that that the
analysis is wrong, and the algorithm is actually O(n).
[ Addendum 20160128: Zhang's claim was mistaken, and he retracted the paper. ]
- Finally, several people, including John Von Neumann, proved that the
axioms of arithmetic are consistent. But it was shown later that no
such proof is possible.
- Cauchy
apparently "proved" that if a sum of continuous functions converges
pointwise, then the sum is also a continuous function, and this error
was widely believed for several years.
- A number of people wrote in with explanations of "more than twenty states"; I
will try to follow up soon.
[Other articles in category /addenda] permanent link
Thu, 31 Jan 2008
Unnecessary imprecision
This
article contains the following sentence:
McCain has won all of the state's 57 delegates, and the last primary before voters in more than 20 states head to the polls next Tuesday.Why "more than 20 states"? Why not just say "23 states", which is shorter and conveys more information?
I'm not trying to pick on CTV here. A Google News search finds 42,000 instances of "more than 20", many of which could presumably be replaced with "26" or whatever. Well, I had originally written "most of which", but then I looked at some examples, and found that the situation is better than I thought it would be. Here are the first ten matches:
- Australian Stocks Complete Worst Month in More Than 20 Years
- It said the US air force committed more than 20 cases of aerial espionage by U-2 strategic espionage planes this month.
- Farmland prices have climbed more than 20% over the past year in many Midwestern states...
- "We have had record-breaking growth in our monthly shipments, as much as more than 20 percent improvements per month," said Christopher Larkins, President...
- More than 20 people, including a district officer, were injured when two bombs exploded outside a stadium in the town yesterday...
- By a vote of 14-7, the Senate Finance Committee last night voted to deliver $500 tax rebates to more than 20 million American senior citizens...
- 9 killed, more than 20 injured in bus accident
- While Tuesday's results may not lock up the nomination for either candidate, Democrats will have their say in more than 20 states...
- Facing the potential anointment of his rival, John McCain, Romney has less than a week to convince voters in more than 20 states that...
- More than 20 Aberdeen citizens qualified for elections as April ...
#2 may be legitimate, if the number of cases of aerial espionage is not known with certitude, or if the anonymous source really did say "more than 20". Similarly #4 is entirely off the hook since it is a quotation.
#3 may be legitimate if the price of farmland is uncertain and close to 20%. #5 is probably a loser. #7 is definitely a loser: it was the headline of an article that began "Nine people were killed and at least 22 injured when...". The headline could certainly have been "9 killed, 22 injured in bus accident".
#8 and #9 are losers, but they are the same example with which I began the article, so they don't count. #10 is a loser.
So I have, of eight examples (disregarding #8 and #9) three certain or near-certain failures (#5, #7, and #10), one certain non-failure (#4), and four cases to which I am willing to extend the benefit of the doubt. This is not as bad as I feared. I like when things turn out better than I thought they would.
But I really wonder what is going on with all these instances of "more than 20 states". Is it just sloppy writing? Or is there some benefit that I am failing to appreciate?
[Other articles in category /lang] permanent link
Ramanujan's congruences
Let p(n) be the number of partitions of the integer
n. For example, p(4) = 5 because there are 5 partitions
of the integer 4, namely {4, 3+1, 2+2, 2+1+1, 1+1+1+1}.
Ramanujan's congruences state that:
| p(5k+4) | =0 | (mod 5) |
| p(7k+5) | =0 | (mod 7) |
| p(11k+6) | =0 | (mod 11) |
Looking at this, anyone could conjecture that p(13k+7) = 0 (mod 13), but it isn't so; p(7) = 15 and p(20) = 48·13+3.
But there are other such congruences. For example, according to Partition Congruences and the Andrews-Garvan-Dyson Crank:
$$ p(17\cdot41^4k + 1122838) = 0 \pmod{17} $$
Isn't mathematics awesome?
[Other articles in category /math] permanent link
Tue, 29 Jan 2008
The Census Bureau's data file
Last week I posted an article about calculations
with data provided by the U.S. Census Bureau. I'm thinking about
writing that up in more detail, but today I learned something so
astonishing that I couldn't wait to mention it.
The data is available from the Census Bureau's web site. It is a CSV file. Most of the file contains actual data, like this:
20220,,"Dubuque, IA",Metropolitan Statistical Area,"92,384","91,603","91,223","90,635","89,571","89,216","89,265","89,156","89,143"Experienced data mungers will feel a sense of foreboding as they look at the commas in those numerals. Commas are for people, and if the data file is written for people, rather than for computers, then getting the computer to read it is going to require at least a little bit of suffering. Indeed, the rest of the data is rather dirty. There is a useless header:
table with row headers in column A and column headers in rows 3 through 4 (leading dots indicate sub-parts),,,,,,,,,,,,^M "Table 1. Annual Estimates of the Population of Metropolitan and Micropolitan Statistical Areas: April 1, 2000 to July 1, 2006",,,,,,,,,,,,^M CBSA Code,"Metro Division Code",Geographic area,"Legal/statistical area description",Population estimates,,,,,,,"April 1, 2000",^M ,,,,"July 1, 2006","July 1, 2005","July 1, 2004","July 1, 2003","July 1, 2002","July 1, 2001","July 1, 2000",Estimates base,Census^M ,,Metropolitan statistical areas,,,,,,,,,,^MAnd there is a similarly useless footer on the bottom of the file. Any program that wants to use this data has to trim off the header and the footer, or ignore them, or the user will have to trim them off manually.
(I've translated ASCII CR characters to ^M sequences so that you can see that although the lines of the file are CR-LF terminated, some of the items contain extra LFs for no particular reason.)
Well, all this is minor. My real complaint is that some of the state name abbreviations are garbled:
19740,,"Denver-Aurora, CO1",Metropolitan Statistical Area,"2,408,750","2,361,778","2,326,126","2,299,879","2,276,592","2,245,030","2,193,737","2,179,320","2,179,240"
Notice that it says CO1 rather than CO, short for
"Colorado". I was fortunate to notice this garbling. Since it
occurred on the line for Denver (among others) the result was that the
program was unable to locate the population of Denver, which is the
capital of Colorado, and a mandatory part of the program's output. So
it raised a warning. Then I went in and manually corrected the
CO1 to say CO. I also added a check to the program
to make sure that it recognized all the state abbreviations; I should
have had this in there in the first place.Then I sent email to an acquaintance who works for the Census Bureau (identity suppressed to protect the innocent), pointing out the errors so that they could be corrected.
My contact checked with the people who produced the data, and informed me that, according to them, CO1 was not an error. Rather, the 1 was a footnote mark, directing me to a footnote at the bottom of the file:
"1Broomfield, CO was formed from parts of Adams, Boulder, Jefferson, and Weld Counties, CO on November 15, 2001 and was coextensive with Broomfield city.",,,,,,,,,,,,^M "For purposes of presenting data for metropolitan and micropolitan statistical areas for Census 2000, Broomfield is treated as if it were a county at the time of the 2000 census.",,,,,,,,,,,,^MA footnote.

I would like to suggest the following as a basic principle of computerized data processing:
Data files should contain data.
Not metadata. Not explanations. Not little essays. And not footnotes. Just the data.There's a larger issue here about confusing content and presentation. But "Data files should contain data" is simpler and easier to remember.
I suspect that this file was exported from a spreadsheet program, probably Excel. Spreadsheet programs desperately want you to confuse content and presentation. This is why one should not use a spreadsheet as a database.
I now recall another occasion when I had to deal with data that was exported from a spreadsheet that was pretending to be a database. It was a database of products made by a large cosmetics company. A typical record looked like this:
"Soft-Pressed Powder Blusher","618J-05","Warm, natural-looking powder colour for all skins. Wide range of shades-subtle to vibrant. With applicator brush.","Cheeks","Nudes","Chestnut Blush","All","","19951201","Yes","","14.5",""The 618J-05 here is a product code. Bonus points if you see what's coming next.
"Water-Dissolve Cream Cleanser","6.61E+01","Creamy cleanser for drier, more sensitive skins. Dissolves even the most tenacious makeups.","Cleansers","","","","Sub I, I, II","19951201","Yes","1","14.5",""
That 6.61E+01 should have been 661E-01, but Excel
decided that it was a numeral, in scientific notation, and put it into
normal form.Back to the Census Bureau, which almost screwed me by putting a footnote on a state name. What if they had decided to put footnotes on the population figures? Then I would have been really screwed, because it would have been completely undetectable.
No, wait! It's all become clear. That's why they put the commas in the numerals!
[ Addendum 20080129: My Census Bureau contact tells me that the authors of the data file have seen the wisdom of my point of view, in spite of my unconstructive and unhelpful feedback (I said "Wow, that is an incredibly terrible idea") and are planning to address the issue in the next release of the data. Hooray for happy endings! ]
[ Addendum 20080129: My Census Bureau contact tells me that they do sometimes put footnotes on the data items, so don't laugh too hard at my remark about the commas. ]
[Other articles in category /misc] permanent link
Fri, 25 Jan 2008
Nonstandard adjectives in mathematics
Ranjit Bhatnagar once propounded the notion of a "nonstandard"
adjective. This is best explained by an example. "Red" is not usually
a nonstandard adjective, because a red boat is still a boat, a red hat
is still a hat, and a red flag is still a flag. But "fake" is
typically nonstandard, because a fake diamond is not a diamond, a fake
Gucci handbag is not a Gucci handbag.
The property is not really attached to the adjective itself. Red emeralds are not emeralds, so "red" is nonstandard when applied to emeralds. Fake expressions of sympathy are still expressions of sympathy, however insincere. "Toy" often goes both ways: a toy fire engine is not a fire engine, but a toy ball is a ball and a toy dog is a dog.
Adjectives in mathematics are rarely nonstandard. An Abelian group is a group, a second-countable topology is a topology, an odd integer is an integer, a partial derivative is a derivative, a well-founded order is an order, an open set is a set, and a limit ordinal is an ordinal.
When mathematicians want to express that a certain kind of entity is similar to some other kind of entity, but is not actually some other entity, they tend to use compound words. For example, a pseudometric is not (in general) a metric. The phrase "pseudo metric" would be misleading, because a "pseudo metric" sounds like some new kind of metric. But there is no such term.
But there is one glaring exception. A partial function is not (in general) a function. The containment is in the other direction: all functions are partial functions, but not all partial functions are functions. The terminology makes more sense if one imagines that "function" is shorthand for "total function", but that is not usually what people say.
If I were more quixotic, I would propose that partial functions be called "partialfunctions" instead. Or perhaps "pseudofunctions". Or one could go the other way and call them "normal relations", where "normal" can be replaced by whatever adjective you prefer—ejective relations, anyone?
I was about to write "any of these would be preferable to the current confusion", but actually I think it probably doesn't matter very much.
[ Addendum 20080201: Another example, and more discussion of "partial". ]
[ Addendum 20081205: A contravariant functor is not a functor. ]
[ Addendum 20090121: A hom-set is not a set. ]
[ Addendum 20110905: A skew field is not a field. The Wikipedia article about division rings observes that this use of "skew" is counter to the usual behavior of adjectives in mathematics. ]
[ Addendum 20120819: A snub cube is not a cube. Several people have informed me that a quantum group is not a group. ]
[ Addendum 20140708: nLab refers to the red herring principle, that “in mathematics, a ‘red herring’ need not, in general, be either red or a herring”. ]
[ Addendum 20160505: The gaussian integers contain the integers, not vice versa, so a gaussian integer is not in general an integer. ]
[ Addendum 20190503: Timon Salar Gutleb points out that affine spaces were at one time called “affine vector spaces” so that every vector space was an affine vector space, but not vice versa. ] [ Addendum 20221106: the standard term for this appears to be “privative adjective”. ]
[Other articles in category /math] permanent link
Thu, 24 Jan 2008
Emacs and alists
[ This article is a few weeks old now. I wrote it and forgot to publish it
at the time. ]
Yesterday I upgraded Emacs, and since it was an upgrade, something that had been working for me for fifteen years stopped working, because that's what "upgrade" means. My .emacs file contains:
(aput 'auto-mode-alist "\\.pl\\'" (function cperl-mode))
(aput 'auto-mode-alist "\\.t\\'" (function cperl-mode))
(aput 'auto-mode-alist "\\.cgi\\'" (function cperl-mode))
(aput 'auto-mode-alist "\\.pm\\'" (function cperl-mode))
(aput 'auto-mode-alist "\\.blog\\'" (function text-mode))
(aput 'auto-mode-alist "\\.sml\\'" (function sml-mode))
I should explain this, since I imagine that most readers of this blog
are like me in that they touch Emacs Lisp only once a year on Saint
Vibrissa's Day. An alist ("association list") is a common data
structure in Lisp programs. It is a list of pairs; the first element
of each pair is a key, and the second element is an associated value.
The pairs in the special auto-mode-alist variable have regexes
as their keys and functions as their values. Whenever Emacs opens a
new file, it scans this alist, until it finds a regex that matches the
name of the file. It then executes the associated function. Thus the
effect of the first line above is to have Emacs enable the
cperl-mode function on any file whose name ends in ".pl".
The aput function is for maintaining alists. It takes an alist, a key, and a value, scans the alist looking for a matching key, and then if it finds it, it amends the corresponding value. Otherwise, it appends a new association onto the front of the alist.
When I upgraded emacs, this broke. The aput function was moved into a separate package, which I now had to load with (require 'assoc).
I asked about this on IRC, and was told that the correct way to do this, if I did not want to (require 'assoc), was to use the following abomination:
(mapc (lambda (x) (when (eq 'perl-mode (cdr x)) (setcdr x 'cperl-mode)))
(append auto-mode-alist interpreter-mode-alist))
The effect of this is to scan over auto-mode-alist (and also
interpreter-mode-alist, a related variable) looking for any
association whose value was the perl-mode function, and
using setcdr to replace perl-mode with
cperl-mode.(This does not address the issue of what to do with .t files or .blog files, for which no association exists yet, presumably, but I did not ask about those specifically on IRC.)
I was totally boggled. Choosing the right editing mode for a file is a basic function of emacs. I could not believe that the best and simplest way to add or change associations was to use mapc lambda gobhorn oleo potatopudding quote potrzebie. I was assured that this was indeed the only correct method. Struck almost speechless, I managed to come up with "Bullshit."
Apparently the issue was that if auto-mode-alist already contains an association for ".pl", there is no guarantee that my new association will be found and preferred to the old one, unless I somehow remove the old one, or edit it to be the way I want.
This seemed very unlikely to me. You see, an alist is a list. This means that it is searched from head to tail, because this is the only way a list can be searched. So in particular, if you cons a second association to the front of the list, which has the same key as a later (older) association, the search will find the new one first, and the older one becomes inoperative. I asked if there was not a guarantee that the alist would be searched from front to back. I was told that there is not.
I looked in the manual, and reported that the assoc function, which is the getter that corresponds to aput, taking an alist and a key, and returning the corresponding value, is expressly guaranteed to return the first matching item. I was told that there was no guarantee that assoc would be used.
I pondered the manual some more and found this passage:
However, association lists have their own advantages. Depending on your application, it may be faster to add an association to the front of an association list than to update a property.That is, it is expressly endorsing the technique of adding a new item to the front of an alist in order to override any later item that might have the same key.
After finding that the add-to-the-front technique really did work, I reasoned that if someday Emacs stopped searching alists sequentially, I would not be in any more trouble than I had been today when they removed the aput function.
So I did not take the advice I was given. Instead, I left it pretty much the way it was. I did take the opportunity to clean up the code a bit:
(push '("\\.pl\\'" . cperl-mode) auto-mode-alist)
(push '("\\.t\\'" . cperl-mode) auto-mode-alist)
(push '("\\.cgi\\'" . cperl-mode) auto-mode-alist)
(push '("\\.pm\\'" . cperl-mode) auto-mode-alist)
(push '("\\.blog\\'" . text-mode) auto-mode-alist)
(push '("\\.sml\\'" . sml-mode) auto-mode-alist)
The push function simply appends an element to the front of a
list, modifying the list in-place.But wow, the advice I got was phenomenally bad. It was bad in a really interesting way, too. It reminded me of the advice people get on the #math channel, where some guy comes in with some question about triangles and gets the category-theoretic viewpoint on triangles as natural transformations of something or other. The advice was bad because although it was correct, it was completely devoid of common sense.
[ Addendum 20080124: It has been brought to my attention that the Emacs FAQ endorses my solution, which makes the category-theoretic advice proposed by the #emacs blockheads even less defensible. ]
[ Addendum 20080201: Steve Vinoski suggests replacing the aput function. ]
[Other articles in category /prog] permanent link
Wed, 23 Jan 2008
Smallest state capitals
I think it was James Kushner who first suggested that I consider the
question of which U.S. state capital had the smallest population in
relation to its state's largest city. For example, New York City is
the largest city in the United States, but the state capital of New
York State is Albany, with a population of about 850,000. The
population of New York City exceeds that of Albany by a factor of
around 20.
At the other end of the scale, of course, we have state capitals like Boston, Denver, Atlanta, and Honolulu that are their state's largest cities. For these states, the population quotient is 1, its theoretical minimum.
Well, James, it only took me thirty years, but here it is.
I tried to resolve the question manually a few weeks ago, by browsing Wikipedia for the populations of likely candidates. Today I took a more methodical approach, downloading the U.S. Census Bureau's July 2006 estimates for populations of metropolitan areas, and writing a couple of little programs to grovel the data.
I had to augment the Census Bureau's data with two items: Annapolis, MD, and Montpelier, VT are not large enough to be included in the metropolitan area data file. I used U.S. Census 2006 estimates for these cities as well.
I discarded one conurbation: the Census Bureau includes a "Metropolitan Division" in New Hampshire that consists of Rockingham and Strafford counties; this was the most populous identified area in New Hampshire. It didn't seem entirely germane to the question, so I took it out. On the other hand, including it doesn't change the results much: its population is 416,000, compared with Manchester-Nashua's 402,000.
The results follow.
| State | Capital and its Population | Largest metropolitan area and its population | Quotient | |||
|---|---|---|---|---|---|---|
| MD | Annapolis | 36,408 | Baltimore-Towson | 2,658,405 | 73 | .02 |
| IL | Springfield | 206,112 | Chicago-Naperville-Joliet | 9,505,748 | 46 | .12 |
| NV | Carson City | 55,289 | Las Vegas-Paradise | 1,777,539 | 32 | .15 |
| VT | Montpelier | 7,954 | Burlington-South Burlington | 206,007 | 25 | .90 |
| NY | Albany | 850,957 | New York-Northern New Jersey-Long Island | 18,818,536 | 22 | .11 |
| MO | Jefferson City | 144,958 | St. Louis | 2,796,368 | 19 | .29 |
| KY | Frankfort | 69,068 | Louisville-Jefferson County | 1,222,216 | 17 | .70 |
| FL | Tallahassee | 336,502 | Miami-Fort Lauderdale-Miami Beach | 5,463,857 | 16 | .24 |
| WA | Olympia | 234,670 | Seattle-Tacoma-Bellevue | 3,263,497 | 13 | .91 |
| AK | Juneau | 30,737 | Anchorage | 359,180 | 11 | .69 |
| PA | Harrisburg | 525,380 | Philadelphia-Camden-Wilmington | 5,826,742 | 11 | .09 |
| SD | Pierre | 19,761 | Sioux Falls | 212,911 | 10 | .77 |
| MI | Lansing | 454,044 | Detroit-Warren-Livonia | 4,468,966 | 9 | .84 |
| NJ | Trenton | 367,605 | Edison | 2,308,777 | 6 | .28 |
| CA | Sacramento | 2,067,117 | Los Angeles-Long Beach-Santa Ana | 12,950,129 | 6 | .26 |
| NM | Santa Fe | 142,407 | Albuquerque | 816,811 | 5 | .74 |
| OR | Salem | 384,600 | Portland-Vancouver-Beaverton | 2,137,565 | 5 | .56 |
| DE | Dover | 147,601 | Wilmington | 691,688 | 4 | .69 |
| VA | Richmond | 1,194,008 | Washington-Arlington-Alexandria | 5,290,400 | 4 | .43 |
| ME | Augusta | 121,068 | Portland-South Portland-Biddeford | 513,667 | 4 | .24 |
| TX | Austin | 1,513,565 | Dallas-Fort Worth-Arlington | 6,003,967 | 3 | .97 |
| AL | Montgomery | 361,748 | Birmingham-Hoover | 1,100,019 | 3 | .04 |
| NE | Lincoln | 283,970 | Omaha-Council Bluffs | 822,549 | 2 | .90 |
| WI | Madison | 543,022 | Milwaukee-Waukesha-West Allis | 1,509,981 | 2 | .78 |
| NH | Concord | 148,085 | Manchester-Nashua | 402,789 | 2 | .72 |
| KS | Topeka | 228,894 | Wichita | 592,126 | 2 | .59 |
| MT | Helena | 70,558 | Billings | 148,116 | 2 | .10 |
| ND | Bismarck | 101,138 | Fargo | 187,001 | 1 | .85 |
| NC | Raleigh | 994,551 | Charlotte-Gastonia-Concord | 1,583,016 | 1 | .59 |
| LA | Baton Rouge | 766,514 | New Orleans-Metairie-Kenner | 1,024,678 | 1 | .34 |
| OH | Columbus | 1,725,570 | Cleveland-Elyria-Mentor | 2,114,155 | 1 | .23 |
| AR | Little Rock | 652,834 | Little Rock-North Little Rock | 652,834 | 1 | .00 |
| AZ | Phoenix | 4,039,182 | Phoenix-Mesa-Scottsdale | 4,039,182 | 1 | .00 |
| CO | Denver | 2,408,750 | Denver-Aurora | 2,408,750 | 1 | .00 |
| CT | Hartford | 1,188,841 | Hartford-West Hartford-East Hartford | 1,188,841 | 1 | .00 |
| GA | Atlanta | 5,138,223 | Atlanta-Sandy Springs-Marietta | 5,138,223 | 1 | .00 |
| HI | Honolulu | 909,863 | Honolulu | 909,863 | 1 | .00 |
| IA | Des Moines | 534,230 | Des Moines-West Des Moines | 534,230 | 1 | .00 |
| ID | Boise | 567,640 | Boise City-Nampa | 567,640 | 1 | .00 |
| IN | Indianapolis | 1,666,032 | Indianapolis-Carmel | 1,666,032 | 1 | .00 |
| MA | Boston | 4,455,217 | Boston-Cambridge-Quincy | 4,455,217 | 1 | .00 |
| MN | St. Paul | 3,175,041 | Minneapolis-St. Paul-Bloomington | 3,175,041 | 1 | .00 |
| MS | Jackson | 529,456 | Jackson | 529,456 | 1 | .00 |
| OK | Oklahoma City | 1,172,339 | Oklahoma City | 1,172,339 | 1 | .00 |
| RI | Providence | 1,612,989 | Providence-New Bedford-Fall River | 1,612,989 | 1 | .00 |
| SC | Columbia | 703,771 | Columbia | 703,771 | 1 | .00 |
| TN | Nashville | 1,455,097 | Nashville-Davidson--Murfreesboro | 1,455,097 | 1 | .00 |
| UT | Salt Lake City | 1,067,722 | Salt Lake City | 1,067,722 | 1 | .00 |
| WV | Charleston | 305,526 | Charleston | 305,526 | 1 | .00 |
| WY | Cheyenne | 85,384 | Cheyenne | 85,384 | 1 | .00 |
Vermont is an interesting outlier here. It makes fourth place not because it has a large city, but because its capital, Montpelier, is so very small. I tried doing some scatter plots, to see if anything else jumped out, but they weren't very illuminating. If anything, the data is suprisingly evenly distributed. Here's an example:
[ Addendum 20080129: Some remarks about the format of the Census Bureau's data file. ]
[ Addendum 20090217: A comparison of the relative sizes of each state's largest and second-largest cities. ]
[Other articles in category /misc] permanent link
Sun, 20 Jan 2008
Utterly Useless Book Reviews (#1 in a series?)
This month I'm reading Robert Graves' awesome novel King
Jesus. Here's the utterly useless review I wanted to write: It
does for the Bible what I, Claudius did for Suetonius.
And yeah, if you've read I, Claudius and Suetonius, then
that's all you need to know about King Jesus, and you'll
rush out to read it. But how many of you have read I,
Claudius and Suetonius? Hands? Anyone? Yeah, I didn't think so.
Okay, here's the explanation. Robert Graves was a novelist and a poet. (He himself said he was a poet who wrote novels so that he could earn enough money to write poetry.) I, Claudius is his best-known work. It is a history of the Roman emperors from the end of the reign of Julius Caesar up to the coronation of Claudius, told from the point of view of Claudius, who, though most of the book, is viewed by most of the other characters as harmless and inept, perhaps mentally deficient, or perhaps merely a doofus. It is this inept doofosity that explains his survival and eventual ascension to the Imperial throne at a time when everyone else in line for it was being exiled, burnt, poisoned, or disemboweled. The book is still in print, and in the 1970s, the BBC turned it into an extremely successful TV miniseries starring Derek Jacobi (as Claudius, obviously) and a lot of other actors who subsequently became people you have heard of. (Patrick Stewart! With hair!)
Graves was a classical scholar, and based his novel on the historical accounts available, principally The Twelve Caesars of Suetonius. Suetonius wrote his history after all the people involved were dead, and his book reads like a collection of anecdotes placed in approximately chronological order. Suetonius seems to have dug up and recorded as fact every scurrilous rumor he could find. Some of the rumors are contradictory, and some merely implausible. When Graves turned The Twelve Caesars into I, Claudius, he resolved this mass of unprocessed material into a coherent product. The puzzling trivialities are explained. The contradictions are cleared up. Sometimes the scurrilous rumors are explained as scurrilous rumors; sometimes Claudius explains the grain of truth that lies at their center. Other times the true story, as related by Claudius, is even worse than the watered-down version that came to Suetonius's ears. Suetonius mentions that, as emperor, Claudius tried to introduce three new letters into the alphabet. Huh? In Graves' novel, this is foreshadowed early, and when it finally happens, it makes sense.
In King Jesus, then, Graves has done for the Bible what he did for Suetonius in I, Claudius. He takes a mass of material, much of it misreported, or partly-forgotten stories written down a generation later, and reconstructs a plausible history from which that mass of material could have developed. The miracles are explained, without requiring anything supernatural or magical, but, at the same time, without becoming any less miraculous.
There is a story that Borges tells about the miracles performed by the Buddha, who generally eschewed miracles as being too showy. But Borges tells the story that one day the Buddha had to cross a desert, and seven different gods each gave him a parasol to shade his head. The Buddha did not want to offend any of the gods, so he split himself into seven Buddhas, and each one crossed the desert using a different parasol. He performed a miracle of politeness.
(The trouble with Borges's stories is that you never know which ones he read in some obscure 17th-century book, and which ones he made up himself. I spent a whole year thinking how clever Borges had been to have invented the novelist Adolfo Bioy Casares, with his alphabetical initials, and then one day I was in the bookstore and came upon the Adolfo Bioy Casares section. Oops.)
Anyway, Graves lets Jesus have the miracles, and they are indeed miraculous, but they are miracles of kindness and insight, not miracles of stage magic. When Graves explains the miracles, you say "oh, of course", without then saying "is that all?" I have not yet gotten to the part where Jesus silences the storm and walks on water, but I am looking forward to it. I did get to the loaves and fishes, and it was quite satisfactory. I am not going to spoil the surprise.
I recommend it. Check it out.
[ Addendum 20080201: James
Russell has read both I, Claudius and Twelve
Caesars. ]
[Other articles in category /book]
permanent link
Help, help!
Przemek Klosowski wrote to offer me physics help, and also to ask
about introspection on Perl objects. Specifically, he said that if
you called a nonexistent method on a TCL object, the error message
would include the names of all the methods that would have worked. He
wanted to know if there was a way to get Perl to do something
similar.
There isn't, precisely, because Perl has only a conventional
distinction between methods and subroutines, and you Just Have To Know
which is which, and avoid calling the subroutines as methods, because
the Perl interpreter has no idea which is which. But it does have
enough introspection features that you can get something like what you
want. This article will explain how to do that.
Here is a trivial program that invokes an undefined method on an
object:
Now consider the following program instead:
Some of the items may be intended to be called as functions, and not
as methods. Some may be functions imported from some other module. A
common offender here is Carp, which places a carp
function into another module's namespace; this function will show up
in a list like the one above, without even an "inherited from" note,
even though it is not a method and it does not make sense to call it
on an object at all.
Even when the items in the list really are methods, they may be
undocumented, internal-use-only methods, and may disappear in future
versions of the YAML module.
But even with all these warnings, Help is at least a partial
solution to the problem.
The real reason for this article is to present the code for
Help.pm, not because the module is so intrinsically useful
itself, but because it is almost a catalog of weird-but-useful Perl
module hackery techniques. A full and detailed tour of this module's
30 lines of code would probably make a decent 60- or 90-minute class
for intermediate Perl programmers who want to become wizards. (I have
given many classes on exactly that topic.)
Here's the code:
Typically, a module's import method is inherited from
Exporter, which gets control at this point and arranges to
make some of the module's functions available in the caller's
namespace. So, for example, when you invoke use YAML
'freeze' in your module, Exporter's import
method gets control and puts YAML's "freeze"
function into your module's namespace. But that is not what we are
doing here. Instead, Help has its own import
method:
@Foo::ISA is the array that is searched whenever a method call on a
Foo objects fails because the method doesn't exist. Perl
will search the classes named in @Foo::ISA, in order. It
will search the Help class last. That's important, because
we don't want Help to interfere with Foo's ordinary
inheritance.
Notice the way the variable name Foo::ISA is generated
dynamically by concatenating the value of $class with the
literal string ::ISA. This is how you access a variable
whose name is not known at compile time in Perl. We will see this
technique over and over again in this module.
The backslash in @{"$class\::ISA"} is necessary, because if
we wrote @{"$class::ISA"} instead, Perl would try to
interpolate the value of $ISA variable from the package named
class. We could get around this by writing something like
@{$class . '::ISA'}, but the backslash is easier to read.
But when method search fails, Perl doesn't give up right away.
Instead, it tries the method search a second time, this time looking
for a method named AUTOLOAD. If it finds one, it calls it.
It only throws an exception of there is no AUTOLOAD.
The Help class doesn't have a nosuchmethod method
either, but it does have AUTOLOAD. If Foo or one of
its other parent classes defines an AUTOLOAD, one of those
will be called instead. But if there's no other AUTOLOAD,
then Help's AUTOLOAD will be called as a last
resort.
This pattern match dismantles the contents of $AUTOLOAD into
a class name and a method name:
The AUTOLOAD function is now going to accumulate a table of
all the methods that could have been called on the target
object, print out a report, and throw a fatal exception.
The accumulated table will reside in the private hash
%known_method. Keys in this hash will be method names.
Values will be the classes in which the names were found.
Before the loop actually looks at the methods in the current class
it's searching, it looks to see if the class has any base classes. If
there are any, it pushes them onto the stack to be searched next:
To find out if a name denotes a subroutine, we use
defined(&{subroutine_name}) for each name in the
package symbol table. If there is a subroutine by that name, the program
inserts it and the class name into %known_method. Otherwise,
the name is a variable or filehandle name and is ignored:
If you have any clever techniques for identifying other stuff that
should be omitted from the output, this is where you would put them.
For example, many authors use the convention that functions whose
names have a leading underscore are private to the implementation, and
should not be called by outsiders. We might omit such items from the
output by
adding a line here:
The output for my example would look like this:
You can always force the help message by calling
$object->Help::help. This calls a method named
help, and it starts the inheritance search in the
Help package. Control is transferred to the following
help method:
Calling AUTOLOAD in the normal way, without goto,
would have worked also. I did it this way just to be a fusspot.
It is very common for objects to lack a DESTROY method;
usually nothing additional needs to be done when the object's lifetime
is over. But we do not want the
Help::AUTOLOAD function to be invoked automatically whenever
such an object is destroyed! So Help defines a last-resort
DESTROY method that is called instead; this prevents Perl
from trying the AUTOLOAD search when an object with no
DESTROY method is
destroyed:
Well, this code will not run with "use strict". It does a lot of
stuff on purpose that "strict" was put in specifically to keep you
from doing by accident.
At some point you have to take off the training wheels, kiddies.
Share and enjoy.
[Other articles in category /prog/perl]
permanent link
Major screwups in mathematics
There are many examples of statements that were believed without
proof that turned out to be false, such as any number of decidability
and completeness (non-)theorems. If it turns out that P=NP, this will
be one of those type, but as yet there is no generally accepted proof
to the contrary, so it is not an example. Similarly, if would be
quite surprising to learn that the Goldbach conjecture was false, but
at present mathematicians do not generally believe that it has been
proved to be true, so the Goldbach conjecture is not an example of
this type, and is unlikely ever to be.
There are a lot of results that could have gone one way or another,
such as the three-dimensional kissing number problem. In this case
some people believing they could go one way and some the other, and
then they found that it was one way, but no proof to the contrary was
ever widely accepted.
Then we have results like the independence of the parallel postulate,
where people thought for a long time that it should be implied by the
rest of Euclidean geometry, and tried to prove it, but couldn't, and
eventually it was determined to be independent. But again, there was
no generally accepted proof that it was implied by the other
postulates. So mathematics got the right answer in this case: the
mathematicians tried to prove a false statement, and failed, and then
eventually figured it out.
Alfred Kempe is famous for producing an erroneous proof of the
four-color map theorem, which was accepted for eleven years before the
error was detected. But the four-color map theorem is true. I
want an example of a false statement that was believed for
years because of an erroneous proof.
If there isn't one, that is an astonishing declaration of success for
all of mathematics and for its deductive methods. 2300 years without
one major screwup!
It seems too good to be true. Is it?
(Readers of Planet Haskell
may want to avert their eyes from this compendium of Perl
introspection techniques. Moreover, a very naughty four-letter word
appears, a word that begins with "g" and ends with "o". Let's just
leave it at that.)
use YAML;
my $obj = YAML->new;
$obj->nosuchmethod;
When run, this produces the fatal error:
Can't locate object method "nosuchmethod" via package "YAML" at test.pl line 4.
(YAML in this article is just an example; you don't have to
know what it does. In fact, I don't know what it does.)
use YAML;
use Help 'YAML';
my $obj = YAML->new;
$obj->nosuchmethod;
Now any failed method calls to YAML objects, or objects of
YAML's subclasses, will produce a more detailed error
message:
Unknown method 'nosuchmethod' called on object of class YAML
Perhaps try:
Bless
Blessed
Dump
DumpFile
Load
LoadFile
VALUE
XXX
as_heavy (inherited from Exporter)
die (inherited from YAML::Base)
dumper_class
dumper_object
export (inherited from Exporter)
export_fail (inherited from Exporter)
export_ok_tags (inherited from Exporter)
export_tags (inherited from Exporter)
export_to_level (inherited from Exporter)
field
freeze
global_object
import (inherited from Exporter)
init_action_object
loader_class
loader_object
new (inherited from YAML::Base)
node_info (inherited from YAML::Base)
require_version (inherited from Exporter)
thaw
warn (inherited from YAML::Base)
ynode
Aborting at test.pl line 5
Some of the methods in this list are bogus. For example, the stuff
inherited from Exporter should almost certainly not be
called on a YAML object.
package Help;
use Carp 'croak';
sub import {
my ($selfclass, @classes) = @_;
for my $class (@classes) {
push @{"$class\::ISA"}, $selfclass;
}
}
sub AUTOLOAD {
my ($bottom_class, $method) = $AUTOLOAD =~ /(.*)::(.*)/;
my %known_method;
my @classes = ($bottom_class);
while (@classes) {
my $class = shift @classes;
next if $class eq __PACKAGE__;
unshift @classes, @{"$class\::ISA"};
for my $name (keys %{"$class\::"}) {
next unless defined &{"$class\::$name"};
$known_method{$name} ||= $class;
}
}
warn "Unknown method '$method' called on object of class $bottom_class\n";
warn "Perhaps try:\n";
for my $name (sort keys %known_method) {
warn " $name " .
($known_method{$name} eq $bottom_class
? ""
: "(inherited from $known_method{$name})") .
"\n";
}
croak "Aborting";
}
sub help {
$AUTOLOAD = ref($_[0]) . '::(none)';
goto &AUTOLOAD;
}
sub DESTROY {}
1;
use Help 'Foo'
When any part of the program invokes use Help 'Foo', this
does two things. First, it locates Help.pm, loads it in, and
compiles it, if that has not been done already. And then it
immediately calls Help->import('Foo').
sub import {
my ($selfclass, @classes) = @_;
for my $class (@classes) {
push @{"$class\::ISA"}, $selfclass;
}
}
The $selfclass variable becomes Help and @classes
becomes ('Foo'). Then the module does its first tricky
thing. It puts itself into the @ISA list of another class.
The push line adds Help to @Foo::ISA.AUTOLOAD
So what happens when the program calls $foo->nosuchmethod?
If one of Foo's base classes includes a method with that
name, it will be called as usual. $AUTOLOAD
When Perl calls an AUTOLOAD function, it sets the value of
$AUTOLOAD to include the full name of the method it was
trying to call, the one that didn't exist. In our example,
$AUTOLOAD is set to "Foo::nosuchmethod".
sub AUTOLOAD {
my ($bottom_class, $method) = $AUTOLOAD =~ /(.*)::(.*)/;
The $bottom_class variable contains Foo, and the
$method variable contains nosuchmethod.Accumulating the table of method names
The AUTOLOAD function accumulates this hash by doing a
depth-first search on the @ISA tree, just like Perl's method
resolution does internally. The @classes variable is a stack
of classes that need to be searched for methods but that have not yet
been searched. Initially, it includes only the class on which the
method was actually called, Foo in this case:
my @classes = ($bottom_class);
As long as some class remains unsearched, this loop will continue to
look for more methods. It begins by grabbing the next class off the
stack:
while (@classes) {
my $class = shift @classes;
Foo inherits from Help too, but we don't want our
error message to mention that, so the search skips Help:
next if $class eq __PACKAGE__;
(__PACKAGE__ expands at compile time to the name of the
current package.)
unshift @classes, @{"$class\::ISA"};
Now the real meat of the loop: there is a class name in
$class, say Foo,
and we want the program to find all the methods in that class. Perl
makes the symbol table for the Foo package available in the
hash %Foo::. Keys in this hash are variable, subroutine, and
filehandle names.
for my $name (keys %{"$class\::"}) {
next unless defined &{"$class\::$name"};
$known_method{$name} ||= $class;
}
}
The ||= sets a new value for $name in the hash only
if there was not one already. If a method name appears in more than
one class, it is recorded as being in the first one found in the
search. Since the search is proceeding in the same order that Perl
uses, the one recorded is the one that Perl will actually find. For
example, if Foo inherits from Bar, and both classes
define a this method, the search will find Foo::this
before Bar::this, and that is what will be recorded in the
hash. This is correct, because Foo's this method
overrides Bar's.
next if $name =~ /^_/;
After the loop finishes searching all the base classes, the
%known_method hash looks something like this:
(
this => Foo,
that => Foo,
new => Base,
blookus => Mixin::Blookus,
other => Foo
)
This means that methods this, that, and
other were defined in Foo itself, but that
new is inherited from Base and that blookus
was inherited from Mixin::Blookus.Printing the report
The AUTOLOAD function then prints out some error messages:
warn "Unknown method '$method' called on object of class $bottom_class\n";
warn "Perhaps try:\n";
And at last the payoff: It prints out the list of methods that the
programmer could have called:
for my $name (sort keys %known_method) {
warn " $name " .
($known_method{$name} eq $bottom_class
? ""
: "(inherited from $known_method{$name})") .
"\n";
}
croak "Aborting";
}
Each method name is printed. If the class in which the method was
found is not the bottom class, the name is annotated with the message
(inherited from wherever).
Unknown method 'nosuchmethod' called on object of class Foo:
Perhaps try:
blookus (inherited from Mixin::Blookus)
new (inherited from Base)
other
that
this
Aborting at YourErroneousModule.pm line 679
Finally the function throws a fatal exception. If we had used
die here, the fatal error message would look like
Aborting at Help.pm line 34, which is extremely unhelpful.
Using croak instead of die makes the message look
like Aborting at test.pl line 5 instead. That is, it reports
the error as coming from the place where the erroneous method was
actually called.Synthetic calls
 Suppose you want to force the help message to come out. One way is to
call $object->fgsfds, since probably the object does not
provide a fgsfds method. But this is ugly, and it might not
work, because the object might provide a fgsfds
method. So Help.pm provides another way.
Suppose you want to force the help message to come out. One way is to
call $object->fgsfds, since probably the object does not
provide a fgsfds method. But this is ugly, and it might not
work, because the object might provide a fgsfds
method. So Help.pm provides another way.
sub help {
$AUTOLOAD = ref($_[0]) . '::(none)';
goto &AUTOLOAD;
}
The Help::help method sets up a fake $AUTOLOAD
value and then uses "magic goto" to transfer control to the real
AUTOLOAD function. "Magic goto" is not the evil bad goto
that is Considered Harmful. It is more like a function call. But
unlike a regular function call, it erases the calling function
(help) from the control stack, so that to subsequently
executed code it appears that AUTOLOAD was called directly in
the first place.DESTROY
Whenever a Perl object is destroyed, its DESTROY method is
called, if it has one. If not, method search looks for an
AUTOLOAD method, if there is one, as usual. If this lookup
fails, no fatal exception is thrown; the object is sliently destroyed
and execution continues.
sub DESTROY {}
This DESTROY method restores the default
behavior, which is to do nothing.Living dangerously
Perl has a special package, called UNIVERSAL.
Every class
inherits from UNIVERSAL. If you want to apply Help
to every class at once, you can try:
use Help 'UNIVERSAL';
but don't blame me if something weird happens.About use strict
Whenever I present code like this, I always get questions (or are they
complaints?) from readers about why I omitted "use strict". "Always
use strict!" they say.License
Code in this article is hereby placed in the public domain.
I don't remember how I got thinking about this, but for the past week
or so I've been trying to think of a major screwup in mathematics.
Specifically, I want a statement S such that:
I cannot think of an example.Glossary for non-mathematicians
[ Addendum 20080205: Readers suggested some examples, and I happened
upon one myself. For a summary, see this month's addenda. I also
wrote a detailed article
about a mistake of Kurt Gödel's. ]
[ Addendum 20080206: Another article in this series, asking readers for examples of a different type of screwup. ]
[Other articles in category /math] permanent link
Tue, 08 Jan 2008
Clubbing someone to death with a loaded Uzi
I once had an intern who wrote wrote the following code to process a
web survey form. The form input widgets were named q1,
q2, and so forth:
foreach $k (keys %in) {
if ($k eq q1) {
if ($in{$k} eq agree) {
$count{q10} = $count{q10} + 1;
}
if ($in{$k} eq disaagree) {
$count{q11} = $count{q11} + 1;
}
}
if ($k eq q2) {
@q2split = split(/\0/, $in{$k});
foreach (@q2split) {
$count{$_} = $count{$_} + 1;
}
}
if ($k eq q3) {
$count{$in{$k}} = $count{$in{$k}} + 1;
}
...
}
There is a lot wrong with this code, but it's all trivial compared
with the one big problem, which is the wholly unnecessary loop and
tests. The whole thing could be (and should be, and was) rewritten
as:
if ($in{q1} eq agree) {
$count{q10} = $count{q10} + 1;
}
if ($in{q1} eq disaagree) {
$count{q11} = $count{q11} + 1;
}
@q2split = split(/\0/, $in{q2});
foreach (@q2split) {
$count{$_} = $count{$_} + 1;
}
$count{$in{q3}} = $count{$in{q3}} + 1;
...
After which one could start addressing the smaller problems, like the
fact that "disagree" is misspelled.This is the sort of mistake you expect from an intern. I chuckled and corrected him. But I've seen it several times since from non-interns.
Here's another example. I am not making this up. Whether it's more or less odious than the intern code is up to you to decide:
foreach $location_name (%LOCATION ) {
$location_code = $LOCATION{$location_name};
if ($location_name eq $location ) {
printf FILE "$location_code\,";
printf FILE "%4s", "$min3\,";
printf FILE "%4s", "$max3\,";
printf FILE "%1s", "$wx3\n";
}
}
It could have been written like this:
printf FILE "$LOCATION{$location}\,";
printf FILE "%4s", "$min3\,";
printf FILE "%4s", "$max3\,";
printf FILE "%1s", "$wx3\n";
I started using this problem as an interview question. I'll present
the subject with trivial code like this:
for my $k (keys %hash) {
if ($k eq "name") {
$hash{$k}++;
}
}
and then ask if they have any comments about it. One nice thing about
the question is that it translates naturally into whatever imperative
language they claim expertise in.It's appalling how many supposedly professional programmers see nothing wrong here. They squint at the code, and say "I think you need parentheses around %hash there", or they criticize the choice of variable names.
I first used this as an interview question because the Python code sample submitted by a job applicant contained an example of it. "Weird," I thought, "but maybe she's outgrown that." Since she claimed to be an expert Perl user, I asked her about it in Perl, using code like the example above. After she made a syntactic suggestion, I said "It's not a syntax problem, and it's not a trick question." She criticized the syntax some more. Finally I told her the answer: "Couldn't you just use $hash{name}++?"
"Oh, yeah, I guess so," she said.
A few minutes later we were going over her Python code sample and I pointed out the place where she had done the exact same thing, and asked if she was happy with that loop and wanted to change it. No, she thought it was just fine.
"Doesn't this look like the example I showed you on the whiteboard a little while ago?"
"Oh, I guess it does."
We didn't hire her.
Larry Wall once said that iterating over the keys of a hash is like clubbing someone to death with a loaded Uzi.
I had already realized that you could, in principle, commit this error with a regular array instead of with a hash, but I had never seen an example until today's episode of the Daily WTF. The Daily WTF code is so awful, all the way through, that I was afraid that people might miss this slightly-more subtle gem lurking in the middle, and that was what motivated me to write this article in the first place. Here's the gem:
// Java
for (int a=1;a<=params.size();a++) switch (a)
{
case 1 : if (params.get(0) != null)
this.one=params.get(0).toString();
break;
case 2 : if (params.get(1) != null)
this.two=params.get(1).toString();
break;
...
case 14 : if (params.get(13) != null)
this.fourteen=params.get(13).toString();
break;
}
}
Wow, that is just, uh, stunning.[ Addendum 20080201: A bit more. ]
[ Addendum 20090213: A counterexample. ]
[Other articles in category /prog] permanent link
Sun, 06 Jan 2008
Squillions
A while back I looked up "zillion" in Wikipedia, which is an alias for
the
Wikipedia article about "Indefinite and fictitious numbers". The
article includes a large number of synonyms for "zillion", such as
bajillion, kajillion, gazillion, and so forth. For some reason the
word "squillion" caught my eye, and I noticed that the citation was
from Terry Pratchett: "And you owe me a million billion trillion
zillion squillion dollars." This suggested to me that "squillion"
might be a nonce-word, one made up on the spot by Pratchett for that
one sentence, in which case it should not be in the Wikipedia
article.
Google book search is a good way to answer questions like that, because if "squillion" is widely used, you will find a lot of examples of it. And indeed it is widely used, and I did find a lot of examples of it. So there was no need to remove it from the article.
One of the Google hits was from the Cormac Ó Cuilleanáin translation of Giovanni Boccaccio's Decameron. The Decameron is a great classic of Italian Renaissance literature, probably the greatest classic that Italian has, after Dante's Divine Comedy. It was written around 1350. In this particular chapter (the tenth story on the sixth day, if you want to look it up) Guccio, a priest, is trying to seduce a hideous kitchen-maid:
He sat himself down by the fire—although this was August—and struck up a conversation with the wench in question (Nuta by name), informing her that he was by rights a member of the gentry and had more than a squillion florins in the bank, not counting those he had to give to other people...
The kitchen-maid, by the way, is described as having "a pair of tits like two baskets of manure".
This was amusing, and as I had never read the Decameron, I wanted to read more, and learn how it turned out. But the Google excerpt was limited, so I asked the library to get me a copy of that version of the Decameron. Of course they have many copies on the shelf, but not that particular translation. So I asked the interlibrary loan people for it, and they got it for me.
When it arrived, I was rather dismayed. The ILL people get the book from the most convenient place, and that means that it often comes from the Drexel library, up the street, or the Temple library, across town, or the West Chester Community College library, or Lehigh University, about an hour away in Bethlehem. (Steel Bethlehem, of course, not Jesus Bethlehem.) The farthest I had ever gotten a book from was an extremely obscure quilting manual that Lorrie asked for; it eventually arrived from the Sno-Isles regional library system of Marysville, Washington.
But this copy of the Decameron came from the Sloman library of the University of Essex. I was so shocked that I had to look it up online to make sure that it was not Essex, New Jersey, or something like that. I was not. It was East Saxony. I was upset because I felt that the trouble and effort had been wasted. If I had known that the nearest available copy of Cormac Ó Cuilleanáin's translation was in Essex, I would have been happy to take a different version that was on the shelf. And then to top it off, I had hardly begun to read it before it came due and had to be sent back to Essex.
So I went to the library and got another Decameron, this one translated by Mark Musa and Peter Bondanella. Here is the corresponding passage:
Although it was still August, he took a seat near the fire and began to talk with the girl, whose name was Nuta, telling her that he was a gentleman by procuration, that he had more than a thousand hundreds of florins (not counting those he had to give away to others), ...
And there is a footnote on "thousand hundreds" explaining "Guccio invents this amount, as well as the previous phrase 'by procuration,' in order to impress his lady." By the way, in this version, Nuta has "a pair of tits that looked like two clumps of cowshit".
Anyway, I think I liked "squillions" better than "thousand hundreds", although I suppose "thousand hundreds" is probably a more literal translation.
Well, I can find this out. Of course, one can find the Decameron online in Italian; the copyright expired about five hundred years ago. Here it is in Italian, courtesy of Brown University:
E ancora che d'agosto fosse, postosi presso al fuoco a sedere, cominciò con costei, che Nuta aveva nome, a entrare in parole e dirle che egli era gentile uomo per procuratore e che egli aveva de' fiorini piú di millantanove, senza quegli che egli aveva a dare altrui,...I think the word that is being translated here is "millantanove", although I can't be entirely sure, because I don't know Italian. Once again, though, I am surprised at how easy it is to read a passage in an unintelligible foreign language when I already know what it is going to say. (I wrote about this back in April 2006, and it occurs to me now that that would be a fun topic for an article.)
 The 1903 translation that Brown University provides is "more florins than could be
reckoned", which does not seem to me to capture the flavor of the
original, and does not seem to be a literal translation either.
"Millantanove" seems to me to be a made-up word resembling "mille" =
"thousand". But as I said, I don't know Italian.
The 1903 translation that Brown University provides is "more florins than could be
reckoned", which does not seem to me to capture the flavor of the
original, and does not seem to be a literal translation either.
"Millantanove" seems to me to be a made-up word resembling "mille" =
"thousand". But as I said, I don't know Italian.
Nuta in this version has "a pair of breasts that shewed as two buckets of muck". Feh. The Italian is "con un paio di poppe che parean due ceston da letame". The operative phrase here seems to be "ceston da letame". I don't know what those words mean, but, happily, Italian Wikipedia has an article about letame, and as the picture makes clear, it is indeed manure.
Oh, did you want this article to have a point? Too bad.
I recommend the Decameron. It is funny and salacious. There are a lot of stories about women cheating on their husbands, and then getting away with it through some clever trick, and then everyone who hears the story laughs and admires the cleverness of the ladies. (The counterpoint to this is that there are a number of stories of wife-beating, in which everyone who hears the story laughs and admires the wisdom of the husbands. I don't like that so much.)
There are farcical stories of bed-swapping and wife-swapping, and one story about an abbess who comes out of her cell to berate a nun for having her lover in to visit, but the abbess is wearing a pair of men's trousers on her head instead of her wimple. Oops.
This reminds me of when I was in high school, I was talking to one of my friends, who opted to study French, and this friend told me studying French is fun, because when you get to the third year and start reading real French literature, you read that great classic of French Literature, La Vie de Gargantua et de Pantagruel. If you have not read this master treasure of French culture, I should explain that the first chapter is mainly taken up with Gargantua and Pantagruel having a discussion about what is the best sort of thing to wipe your ass with, and it goes on from there.
I took Latin, and in third-year Latin we read the orations of Cicero against Cataline. Fun stuff, but not the sort of thing that has you rushing to translate the next word.
 I was going to write an article about symmetries of the dodecahedron,
and an interesting problem suggested to me by these balloon displays
that I saw at the local Mazda dealership, but eh, this was a lot
easier.
I was going to write an article about symmetries of the dodecahedron,
and an interesting problem suggested to me by these balloon displays
that I saw at the local Mazda dealership, but eh, this was a lot
easier.
Gargantua and Pantagruel eventually agree that the answer is a live goose.
[ Addendum 20080201: More about 'milliantanove'. ]
[Other articles in category /lang] permanent link
Sat, 05 Jan 2008
Pepys' footballs explained
Walt Mankowski wrote to me with the explanation of Samuel Pepys' footballs: They
are not clods of mud, as I guessed, nor horse droppings, as another
correspondent suggested, but... footballs.
Walt found a reference in Montague Shearman's 1887 book on the history of football in England that specifically mentions this. Folks were playing football in the street, and because of this, Pepys took his coach to Sir Philip Warwicke's, rather than walking.
I didn't ask, but I presume Walt found this by doing some straightforward Google search for "pepys footballs" or something of the sort. For some reason, this did not even occur to me. Once Big Dictionary failed me, I was stumped. Perhaps this marks me as a member of the pre-Internet generation. I imagined this morning that this episode would be repeated, with my daughter Katara in place of Walt. "Oh, Daddy! You're so old-fashioned. Just use a Google search."
Anyway, inspired by Walt's example, or by what I imagined Walt's example to be, I did the search myself, and found the Shearman reference, as well as the following discussion in William Carew Hazlitt's Faiths and Folklore of 1905:
Mission, writing about 1690, says: "In winter foot-ball is a useful and charming exercise. It is a leather ball about as big as one's head, fill'd with wind. This is kick'd about from one to t'other in the streets, by him that can get at it, and that is all the art of it."This book looks like it would be good reading in general. [ Addendum 20080106: This is not the William Hazlitt, but his grandson. Thank you, Wikipedia. ]
Thanks very much, Walt.
[Other articles in category /lang] permanent link
Fri, 04 Jan 2008
Footballs?
The diary of Samuel Pepys for Tuesday, 3 January 1664/5 says:
Up, and by coach to Sir Ph. Warwicke's, the streete being full of footballs, it being a great frost, and found him and Mr. Coventry walking in St. James's Parke."The street being full of footballs?" Huh? I tried looking in the Big Dictionary, and it was no help at all.
My best guess is that it's big chunks of frozen mud that you have to kick out of the way. Do any gentle readers know for sure?
The Diary of Samuel Pepys has a syndication feed you can subscribe to. You get a diary entry every day or so, with all the names and places linked to a glossary. It's fun reading.
[ Addendum 20080105: The answer. ]
[Other articles in category /lang] permanent link
Katara is not a vegetarian
I just had a long vacation and got to spend a lot of time with Katara,
which is why she's popping up so much all of a sudden. I seem to have
gotten into Mimi Smartypants mode. I will return to the
regularly-scheduled discussions of programming and mathematics
shortly. But since I seem to have written two articles in a row
([1] [2])
on the subject of telling kids the difficult truth, I thought I'd try to
finish up this one, which has been mostly done for months now. Also
there was a recent episode that got me thinking about it again.
I went to visit Katara at school last week, and stayed for lunch. I was seated with Katara and three other little girls. As the food was served, one of the girls, Riley, made some joke about how the food cart contained guinea pigs instead. This sort of joke is very funny to preschoolers.
My sense of humor is very close to a preschooler's, and I would have thought that this was funny if she had said that the food cart contained clocks, or nose hairs, or a speech in defense of the Corn Laws, or the Trans-Siberian Railroad, or fish-shaped solid waste. But she said guinea pigs, and instead of laughing, I mused aloud that I had never eaten a guinea pig.
Riley informed me that "You can't eat guinea pigs! They're animals, not food."
"Sure you can," I said. "Meat is made from animals."
Riley got this big grin on her face, the one that preschoolers get when they know that the adults are teasing them, and said "Nawww!"
"Yes," I said. "Meat comes from animals."
Riley shook her head. She knew I was joking. A general discussion ensued, with Katara taking my side, and another girl, Flora, taking Riley's. In the end, I did not convince them.
"Well," I said, mostly to myself, at the end, "you girls are in for a rude awakening someday."
Now, I know that not everyone is as direct as I am. And I know that not all non-vegetarians are as concerned as I am about the ethics of eating meat. But wow. I would have thought that someone would have explained to these girls where meat came from, just as a point of interest if nothing else. Or maybe they would have made the connection between chicken-the-food and chicken-the-farm-animal. I mean, they are constantly getting all these stories set on farms. Since three-year-olds ask about a billion questions a day. they must ask around a thousand questions a day about the farms, so how is it that the subject never came up?
Katara was accidentally exposed to a movie version of Charlotte's Web on an airplane, and the plot of Charlotte's Web is that Charlotte is trying to save Wilbur from being turned into smoked ham. Left to myself I wouldn't have exposed Katara to Charlotte's Web so soon—it is too long for her, for one thing—but my point here is that the world is full of reminders of the true nature of meat, and they can be hard to avoid. So I was very surprised when it turned out that these two age-mates of Katara's were so completely unaware of it.
Anyway, Katara has known from a very early age where meat comes from. Early in her meat-eating career, probably before she was two years old, I specifically explained it to her. I wanted to make sure that she understood that meat comes from animals. Because there are serious ethical issues involved when one eats animals, and I think they must be considered. We may choose to kill and destroy thinking beings to make food, but we should at least be aware that that is what is happening. I'm not sure I think it is evil, but I want to at least be aware of the possibility.
I have never been a vegetarian, but I want to try to face the ethical results of that choice head on, and not pretend that they are not there. I did not want Katara growing up to identify meat with sterile packages in the supermarket. Meat was once alive, moving around with its own agenda, and I think it is important to understand this.
So I made an effort to bring up the subject at home, and then one day when Katara was around twenty months old we went to a Chinese restaurant that has live fish in tanks at the front of the restaurant, and you can ask them to take one of these fish into the kitchen to be cooked for your dinner. Katara has loved to eat fish since she was a tiny baby.
We ordered a striped bass, and then I took Katara to look at the fish in the tanks. I explained to her that these fish swimming in the tanks were for people to eat, and that when we ordered our fish for dinner, a waiter came out and caught one of the fish in a net, took it back to the kitchen, and they killed it and were cooking it for us.
As I said, I had made the point before, but never so directly. We had never before seen the live animals that were turned into food for us. I really did not know how Katara would respond to this. Some people have a very strong negative response when they first learn that meat comes from animals, so negative that they never eat meat again. But I thought Katara should know the truth and make her own decision about how to respond.
Katara's response was to point at one of the striped bass and say "I want to eat that one."
Then she took me to each tank in turn, and told me me which kind of fish she wanted to eat and which ones she did not want to eat. (She favored the fish-looking fish, and rejected the crabs, shrimp, and eels.)
Then when the fish arrived on our table Katara asked if it had been swimming in the tank, and I said it had. "Yum yum," said Katara, and dug in.
[Other articles in category /food] permanent link
Thu, 03 Jan 2008
Note on point-free programming style
This old
comp.lang.functional article by Albert Y. C. Lai, makes
the point that Unix shell pipeline programming is done in an
essentially "point-free" style, using the shell example:
grep '^X-Spam-Level' | sort | uniq | wc -l
and the analogous Haskell code:
length . nub . sort . filter (isPrefixOf "X-Spam-Level")
Neither one explicitly mentions its argument, which is why this is
"point-free". In "point-free" programming, instead of defining a
function in terms of its effect on its arguments, one defines it by
composing the component functions themselves, directly, with
higher-order operators. For example, instead of:
foo x y = 2 * x + yone has, in point-free style:
foo = (+) . (2 *)where (2 *) is the function that doubles its argument, and (+) is the (curried) addition function. The two definitions of foo are entirely equivalent.
As the two examples should make clear, point-free style is sometimes natural, and sometimes not, and the example chosen by M. Lai was carefully selected to bias the argument in favor of point-free style.
Often, after writing a function in pointful style, I get the computer to convert it automatically to point-free style, just to see what it looks like. This is usually educational, and sometimes I use the computed point-free definition instead. As I get better at understanding point-free programming style in Haskell, I am more and more likely to write certain functions point-free in the first place. For example, I recently wrote:
soln = int 1 (srt (add one (neg (sqr soln))))
and then scratched my head, erased it, and replaced it with the equivalent:
soln = int 1 ((srt . (add one) . neg . sqr) soln)
I could have factored out the int 1 too:
soln = (int 1 . srt . add one . neg . sqr) soln
I could even have removed soln from the right-hand side:
soln = fix (int 1 . srt . add one . neg . sqr)
but I am not yet a perfect sage.Sometimes I opt for an intermediate form, one in which some of the arguments are explicit and some are implicit. For example, as an exercise I wrote a function numOccurrences which takes a value and a list and counts the number of times the value occurs in the list. A straightforward and conventional implementation is:
numOccurrences x [] = 0
numOccurrences x (y:ys) =
if (x == y) then 1 + rest
else rest
where rest = numOccurrences x ys
but the partially point-free version I wrote was much better:
numOccurrences x = length . filter (== x)
Once you see this, it's easy to go back to a fully pointful
version:
numOccurrences x y = length (filter (== x) y)
Or you can go the other way, to a point-free version:
numOccurrences = (length .) . filter . (==)
which I find confusing.Anyway, the point of this note is not to argue that the point-free style is better or worse than the pointful style. Sometimes I use the one, and sometimes the other. I just want to point out that the argument made by M. Lai is deceptive, because of the choice of examples. As an equally biased counterexample, consider:
bar x = x*x + 2*x + 1
which the automatic converter informs me can be written in point-free
style as:
bar = (1 +) . ap ((+) . join (*)) (2 *)
Perusal of this example will reveal much to the attentive reader,
including the definitions of join and ap. But I
don't think many people would argue that it is an improvement on the
original. (Maybe I'm wrong, and people would argue that it was an
improvement. I won't know for sure until I have more experience.)For some sort of balance, here is another example where I think the point-free version is at least as good as the pointful version: a recent comment on Reddit suggested a >>> operator that composes functions just like the . operator, but in the other order, so that:
f >>> g = g . f
or, if you prefer:
(>>>) f g x = g(f(x))
The point-free definition of >>> is:
(>>>) = flip (.)
where the flip operator takes a function of two arguments and
makes a new function that does the same thing, but with the arguments
in the opposite order. Whatever your feelings about point-free style,
it is undeniable that the point-free definition makes perfectly clear
that >>> is nothing but . with its arguments in
reverse order.
[Other articles in category /prog/haskell] permanent link
Tue, 01 Jan 2008
Santa Claus
A few years ago I was talking to a woman I worked with, who told me
that she told her kids that Santa Claus was real, "because how could
you not?". She thought she would have been depriving her kids by not
telling them the story. And maybe she would have been; I honestly
don't know. I don't remember what it was like to believe literally in
Santa Claus or how I felt when I learned the truth.
My vocabulary here is failing me. "Telling them the story" is not what I want, because the Santa Claus thing is deceptive, and telling stories is not normally deceptive: "fiction" and "lies" mean different things. When I tell Katara the story of the Little Red Hen, there is no presumption that there is an actual, literal Red Hen. Katara might think there is, or not, or might not think about it at all; I don't know which. Ditto Cinderella, or Olivia the Pig, or any other story I tell or read to her. But when people tell their kids about Santa Claus, they present it not as a story, but as a literal truth. They present it in a way that is calculated to make the kids believe there is actually a fat, benevolent, white-bearded immortal, manufacturing toys in a secret arctic workshop. This is no longer mere fiction; it is a lie. So what I want to say is that this lady thought she would be depriving her kids of the magic of Santa Claus by not telling them this lie.
But I really don't want to use the word "lie" here, because it's so pejorative. It makes it sound as though I think badly of this good woman for telling her kids that Santa Claus was real. But I don't, at all. She is generally wise and honest and I respect her. Parents tell their kids all sorts of awful, appalling lies, which upsets me a lot, but this lie is quite benign by comparison, and bothers me not at all.
Let me be perfectly clear: I have nothing, absolutely nothing, against the Santa Claus story. I have an article in progress about how much I hate the way parents routinely lie to their kids, to manipulate them, and this one isn't in the article, because it doesn't even register. It's just for fun, or nearly so.
Santa Claus seems pretty harmless to me. Unlike many of the pernicious lies children are told, Santa Claus is a great story. It would be really wonderful to believe that I would get presents every year because there was a fat guy manufacturing toys at the North Pole. Delightful! And the only thing wrong with it is that it isn't true. Oh well. There are a lot of pretty stories that aren't true.
Anyway, at the time I had this conversation about Santa Claus, Katara was too young to have heard about Santa Claus anyway, and my co-worker asked if I was planning to tell Katara the Santa Claus story.
Now that I've written this article, it occurs to me what she meant to ask, was not whether I was going to tell Katara the story, but whether I was going to tell her that it was true. Having realized that now, my reply seems a lot more obvious in retrospect than it did at the time.
I hadn't thought about it before, but I said I didn't think I would.
"But what are you going to tell her?"
"The truth, I guess."
The truth, though, is pretty wonderful, although less astonishing. You don't get presents because of the fat guy in the red suit, which is a shame, because wouldn't it be fun if it were true? But you do get them anyway, and it's because your family loves you. As consolation prizes go, that one's pretty good.
So we did tell her the truth. Santa Claus is just a story. Katara will have to grow up without that piece of childhood delight. Sorry, Katara. But she'll also grow up knowing that her parents respect her enough to tell her the truth instead of a pretty lie, and maybe that will be enough of a consolation prize to make up for it.
[Other articles in category /kids] permanent link