Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Tue, 16 Feb 2021
Katara is toiling through A.P. Chemistry this year. I never took A.P. Chemistry but I did take regular high school chemistry and two semesters of university chemistry so it falls to me to help her out when things get too confusing. Lately she has been studying gas equilibria and thermodynamics, in which the so-called ideal gas law plays a central role: $$ PV=nRT$$
This is when you have a gas confined in a container of volume !!V!!. !!P!! is the pressure exerted by the gas on the walls of the container, the !!n!! is the number of gas particles, and the !!T!! is the absolute temperature. !!R!! is a constant, called the “ideal gas constant”. Most real gases do obey this law pretty closely, at least at reasonably low pressures.
The law implies all sorts of interesting things. For example, if you have gas in a container and heat it up so as to double the (absolute) temperature, the gas would like to expand into twice the original volume. If the container is rigid the pressure will double, but if the gas is in a balloon, the balloon will double in size instead. Then if you take the balloon up in an airplane so that the ambient pressure is half as much, the balloon will double in size again.
I had seen this many times and while it all seems reasonable and makes sense, I had never really thought about what it means. Sometimes stuff in physics doesn't mean anything, but sometimes you can relate it to a more fundamental law. For example, in The Character of Physical Law, Feynman points out that the Archimedean lever law is just an expression of the law of conservation of energy, as applied to the potential energy of the weights on the arms of the lever. Thinking about the ideal gas law carefully, for the first time in my life, I realized that it is also a special case of the law of conservation of energy!
The gas molecules are zipping around with various energies, and this kinetic energy manifests on the macro scale as as pressure (when they bump into the walls of the container) and as volume (when they bump into other molecules, forcing the other particles away.)
The pressure is measured in units of dimension !!\frac{\rm force}{\rm area}!!, say newtons per square meter. The product !!PV!! of pressure and volume is $$ \frac{\rm force}{\rm area}\cdot{\rm volume} = \frac{\rm force}{{\rm distance}^2}\cdot{\rm distance}^3 = {\rm force}\cdot{\rm distance} = {\rm energy}. $$ So the equation is equating two ways to measure the same total energy of the gas.
Over on the right-hand side, we also have energy. The absolute temperature !!T!! is the average energy per molecule and the !!n!! counts the number of molecules; multiply them and you get the total energy in a different way.
The !!R!! is nothing mysterious; it's just a proportionality constant required to get the units to match up when we measure temperature in kelvins and count molecules in moles. It's analogous to the mysterious Cookie Constant that relates energy you have to expend on the treadmill with energy you gain from eating cookies. The Cookie Constant is !!1043 \frac{\rm sec}{\rm cookie}!!. !!R!! happens to be around 8.3 joules per mole per kelvin.
(Actually I think there might be a bit more to !!R!! than I said, something about the Boltzmann distribution in there.)
Somehow this got me and Katara thinking about what a mole of chocolate chips would look like. “Better use those mini chips,” said Katara.
[Other articles in category /physics] permanent link
Sun, 09 Feb 2014You sometimes hear people claim that there is no perfectly efficient machine, that every machine wastes some of its input energy in noise or friction.
However, there is a counterexample. An electric space heater is perfectly efficient. Its purpose is to heat the space around it, and 100% of the input energy is applied to this purpose. Even the electrical energy lost to resistance in the cord you use to plug it into the wall is converted to heat.
Wait, you say, the space heater does waste some of its energy. The coils heat up, and they emit not only heat, but also light, which is useless, being a dull orange color. Ah! But what happens when that light hits the wall? Most of it is absorbed, and heats up the wall. Some is reflected, and heats up a different wall instead.
Similarly, a small fraction of the energy is wasted in making a quiet humming noise—until the sound waves are absorbed by the objects in the room, heating them slightly.
Now it's true that some heat is lost when it's radiated from the outside of the walls and ceiling. But some is also lost whenever you open a window or a door, and you can't blame the space heater for your lousy insulation. It heated the room as much as possible under the circumstances.
So remember this when you hear someone complain that incandescent light bulbs are wasteful of energy. They're only wasteful in warm weather. In cold weather, they're free.
[Other articles in category /physics] permanent link
Fri, 06 Feb 2009
Maybe energy is really real
About a year ago I dared to write down my crackpottish musings about
whether energy is a real thing, or whether it is just a mistaken
reification. I made what I thought was a good analogy with the center
of gravity, a useful mathematical abstraction that nobody claims is
actually real.
I call it crackpottish, but I do think I made a reasonable case, and of the many replies I got to that article, I don't think anyone said conclusively that I was a complete jackass. (Of course, it might be that none of the people who really know wanted to argue with a crackpot.) I have thought about it a lot before and since; it continues to bother me.
But I few months ago I did remember an argument that energy is a real thing. Specifically, I remembered Noether's theorem. Noether's theorem, if I understand correctly, claims that for every symmetry in the physical universe, there is a corresponding conservation law, and vice versa.
For example, let's suppose that space itself is uniform. That is, let's suppose that the laws of physics are invariant under a change of position that is a translation. In this special case, Noether's theorem says that the laws must include conservation of momentum: conservation of momentum is mathematically equivalent to the claim that physics is invariant unter a translation transformation.
Perhaps this is a good time to add that I do not (yet) understand Noether's theorem, that I am only parroting stuff that I have read elsewhere, and that my usual physics-related disclaimer applies: I understand just barely enough physics to spin a plausible-sounding line of bullshit.
Anyway, going on with my plausible-sounding bullshit about Noether's theorem, invariance of the laws under a spatial rotation is equivalent to the law of conservation of angular momentum. Actually I think I might have remembered that one wrong. But the crucial one for me I am sure I am not remembering wrong: invariance of physical law under a translation in time rather than in space is equivalent to conservation of energy. Aha.
If this is right, then perhaps there is a good basis for the concept of energy after all, because any physics that is time-invariant must have an equivalent concept of energy. Time-invariance might not be true, but I have no philosophical objection to it, nor do I claim that the notion is incoherent.
So it seems that if I am to understand this properly, I need to understand Noether's theorem. Maybe I'll make that a resolution for 2009. First stop, Wikipedia, to find out what the prerequisites are.
[Other articles in category /physics] permanent link
Sun, 29 Jun 2008
Freshman electromagnetism questions: answer 3
Last year I asked a bunch
of basic questions about electromagnetism. Many readers wrote in with
answers and explanations, which I still hope to write up in detail.
In the meantime, however, I figured out the answer to one of the
questions by myself.
I had asked:
And one day a couple of months ago it occurred to me that yes, of course the electron vibrates up and down, because that is how radio antennas work. The EM wave comes travelling by, and the electrons bound in the metal antenna vibrate up and down. When electrons vibrate up and down in a metal wire, it is called an alternating current. Some gizmo at the bottom end of the antenna detects the alternating current and turns it back into the voice of Don Imus.
- Any beam of light has a time-varying electric field, perpendicular to the direction that the light is travelling. If I shine a light on an electron, why doesn't the electron vibrate up and down in the varying electric field? Or does it?
I thought about it a little more, and I realized that this vibration effect is also how microwave ovens work. The electromagnetic microwave comes travelling by, and it makes the electrons in the burrito vibrate up and down. But these electrons are bound into water molecules, and cannot vibrate freely. Instead, the vibrational energy is dissipated as heat, so the burrito gets warm.
So that's one question out of the way. Probably I have at least three reader responses telling me this exact same thing. And perhaps someday we will all find out together...
[Other articles in category /physics] permanent link
Thu, 15 May 2008
Luminous band-aids
Last night after bedtime Katara asked for a small band-aid for her knee.
I went into the bathroom to get one, and unwrapped it in the dark.
The band-aid itself is circular, about 1.5 cm in diameter. It is sealed between two pieces of paper, each about an inch square, that have been glued together along the four pairs of edges. There is a flap at one edge that you pull, and then you can peel the two glued-together pieces of paper apart to get the band-aid out.
As I peeled apart the two pieces of paper in the dark, there was a thin luminous greenish line running along the inside of the wrapper at the place the papers were being pulled away from each other. The line moved downward following the topmost point of contact between the papers as I pulled the papers apart. It was clearly visible in the dark.
I've never heard of anything like this; the closest I can think of is the thing about how wintergreen Life Savers glow in the dark when you crush them.
My best guess is that it's a static discharge, but I don't know. I don't have pictures of the phenomenon itself, and I'm not likely to be able to get any. But the band-aids look like this:
 |  |
Have any of my Gentle Readers seen anything like this before? A cursory Internet search has revealed nothing of value.
[ Addendum 20180911: The phenomenon is well-known; it is called triboluminescence. Thanks to everyone who has written in over the years to let me know about this. In particular, thanks to Steve Dommett, who wrote to point out that, if done in a vacuum, triboluminescence can produce enough high-energy x-rays to image a person's finger bones! ]
[Other articles in category /physics] permanent link
Fri, 07 Dec 2007
Freshman electromagnetism questions
As I haven't quite managed to mention here before, I have occasionally
been sitting in on one of Penn's first-year physics classes, about
electricity and magnetism. I took pretty much the same class myself
during my freshman year of college, so all the material is quite
familiar to me.
But, as I keep saying here, I do not understand physics very well, and I don't know much about it. And every time I go to a freshman physics lecture I come out feeling like I understand it less than I went in.
I've started writing down my questions in class, even though I don't really have anyone to ask them to. (I don't want to take up the professor's time, since she presumably has her hands full taking care of the paying customers.) When I ask people I know who claim to understand physics, they usually can't give me plausible answers.
Maybe I should mutter something here under my breath about how mathematicians and mathematics students are expected to have a better grasp on fundamental matters.
The last time this came up for me I was trying to understand the phenomenon of dissolving. Specifically, why does it usually happen that substances usually dissolve faster and more thoroughly in warmer solutions than in cooler solutions? I asked a whole bunch of people about this, up to and including a full professor of physical chemistry, and never got a decent answer.
The most common answer, in fact, was incredibly crappy: "the warm solution has higher entropy". This is a virtus dormitiva if ever there was one. There's a scene in a play by Molière in which a candidate for a medical degree is asked by the examiners why opium puts people to sleep. His answer, which is applauded by the examiners, is that it puts people to sleep because it has a virtus dormitiva. That is, a sleep-producing power. Saying that warm solutions dissolve things better than cold ones because they have more entropy is not much better than saying that it is because they have a virtus dormitiva.
The entropy is not a real thing; it is a reification of the power that warmer substances have to (among other things) dissolve solutes more effectively than cooler ones. Whether you ascribe a higher entropy to the warm solution, or a virtus dissolva to it, comes to the same thing, and explains nothing. I was somewhat disgusted that I kept getting this non-answer. (See my explanation of why we put salt on sidewalks when it snows to see what sort of answer I would have preferred. Probably there is some equally useless answer one could have given to that question in terms of entropy.)
(Perhaps my position will seem less crackpottish if I a make an analogy with the concept of "center of gravity". In mechanics, many physical properties can be most easily understood in terms of the center of gravity of some object. For example, the gravitational effect of small objects far apart from one another can be conveniently approximated by supposing that all the mass of each object is concentrated at its center of gravity. A force on an object can be conveniently treated mathematically as a component acting toward the center of gravity, which tends to change the object's linear velocity, and a component acting perpendicular to that, which tends to change its angular velocity. But nobody ever makes the mistake of supposing that the center of gravity has any objective reality in the physical universe. Everyone understands that it is merely a mathematical fiction. I am considering the possibility that energy should be understood to be a mathematical fiction in the same sort of way. From the little I know about physics and physicists, it seems to me that physicists do not think of energy in this way. But I am really not sure.)
Anyway, none of this philosophizing is what I was hoping to discuss in this article. Today I wrote up some of the questions I jotted down in freshman physics class.
- What are the physical interpretations of μ0 and ε0,
the magnetic permeability and electric permittivity of vacuum?
Can these be directly measured? How?
- Consider a simple circuit with a battery, a switch, and a
capacitor. When the switch is closed, the battery will suck
electrons out of one plate of the capacitor and pump them into the
other plate, so the capacitor will charge up.
When we open the switch, the current will stop flowing, and the capacitor will stop charging up.
But why? Suppose the switch is between the capacitor and the positive terminal of the battery. Then the negative terminal is still connected to the capacitor even when the switch is open. Why doesn't the negative terminal of the battery continue to pump electrons into the capacitor, continuing to charge it up, although perhaps less than it would be if the switch were closed?
- Any beam of light has a time-varying electric field, perpendicular
to the direction that the light is travelling. If I shine a light
on an electron, why doesn't the electron vibrate up and down in the
varying electric field? Or does it?
[ Addendum 20080629: I figured out the answer to this one. ]
- Suppose I take a beam of polarized light whose electric field is in
the x direction. I split it in two, delay one of the beams by
exactly half a wavelength, and merge it with the other beam. The
electric fields are exactly out of phase and exactly cancel out.
What happens? Where did the light go? What about conservation of
energy?
- Suppose I have two beams of light whose wavelengths are close but
not exactly the same, say λ and (λ+dλ). I superimpose these. The
electric fields will interfere, and sometimes will be in phase and
sometimes out of phase. There will be regions where the electric
field varies rapidly from the maximum to almost zero, of length on the order of dλ. If I look at the
beam of light only over one of these brief intervals, it should
look just like very high frequency light of wavelength dλ. But
it doesn't. Or does it?
- An electron in a varying magnetic field experiences an
electromotive force. In particular, an electron near a wire that
carries a varying current will move around as the current in the
wire varies.
Now suppose we have one electron A in space near a wire. We will put a very small current into the wire for a moment; this causes electron A to move a little bit.
Let's suppose that the current in the wire is as small as it can be. In fact, let's imagine that the wire is carrying precisely one electron, which we'll call B. We can calculate the amount of current we can attribute to the wire just from B. (Current in amperes is just coulombs per second, and the charge on electron B is some number of coulombs.) Then we can calculate the force on A as a result of this minimal current, and the motion of A that results.
But we could also do the calculation another way ,by forgetting about the wire, and just saying that electron B is travelling through space, and exerts an electrostatic force on A, according to Coulomb's law. We could calculate the motion of A that results from this electrostatic force.
We ought to get the same answer both ways. But do we?
- Suppose we have a beam of light that is travelling along the
x axis, and the electric field is perpendicular to the
x axis, say in the y direction. We learned in
freshman physics how to calculate the vector quantity that
represents the intensity of the electric field at every point on
the x axis; that is, at every point of the form (x,
0, 0). But what is the electric field at (x, 1, 0)? How
does the electric field vary throughout space? Presumably a beam
of light of wavelength λ has a minimum diameter on the order
of λ, but how how does the electric field vary as you move
away from the core? Can you take two such minimum-diameter beams
and overlap them partially?
[ Addendum 20090204: I eventually remembered that Noether's theorem has something to say about the necessity of the energy concept. ]
[Other articles in category /physics] permanent link
Sat, 15 Sep 2007
The Wilkins pendulum mystery resolved
Last March, I pointed out that:
- John Wilkins had defined a natural, decimal system of measurements,
- that he had done this in 1668, about 110 years before the Metric System, and
- that the basic unit of length, which he called the "standard", was almost exactly the same length as the length that was eventually adopted as the meter
This article got some attention back in July, when a lot of people were Google-searching for "john wilkins metric system", because the UK Metric Association had put out a press release making the same points, this time discovered by an Australian, Pat Naughtin.
For example, the BBC Video News says:
According to Pat Naughtin, the Metric System was invented in England in 1668, one hundred and twenty years before the French adopted the system. He discovered this in an ancient and rare book...Actually, though, he did not discover it in Wilkins' ancient and rare book. He discovered it by reading The Universe of Discourse, and then went to the ancient and rare book I cited, to confirm that it said what I had said it said. Remember, folks, you heard it here first.
Anyway, that is not what I planned to write about. In the earlier article, I discussed Wilkins' original definition of the Standard, which was based on the length of a pendulum with a period of exactly one second. Then:
Let d be the distance from the point of suspension to the center of the bob, and r be the radius of the bob, and let x be such that d/r = r/x. Then d+(0.4)x is the standard unit of measurement.(This is my translation of Wilkins' Baroque language.)
But this was a big puzzle to me:
Huh? Why 0.4? Why does r come into it? Why not just use d? Huh?Soon after the press release came out, I got email from a gentleman named Bill Hooper, a retired professor of physics of the University of Virginia's College at Wise, in which he explained this puzzle completely, and in some detail.
According to Professor Hooper, you cannot just use d here, because if you do, the length will depend on the size, shape, and orientation of the bob. I did not know this; I would have supposed that you can assume that the mass of the bob is concentrated at its center of mass, but apparently you cannot.
The usual Physics I calculation that derives the period of a pendulum in terms of the distance from the fulcrum to the center of the bob assumes that the bob is infinitesimal. But in real life the bob is not infinitesimal, and this makes a difference. (And Wilkins specified that one should use the most massive possible bob, for reasons that should be clear.)
No, instead you have to adjust the distance d in the formula by adding I/md, where m is the mass of the bob and I is the moment of intertia of the bob, a property which depends on the shape, size, and mass of the bob. Wilkins specified a spherical bob, so we need only calculate (or look up) the formula for the moment of inertia of a sphere. It turns out that for a solid sphere, I = 2mr2/5. That is, the distance needed is not d, but d + 2r2/5d. Or, as I put it above, d + (0.4)x, where d/r = r/x.
Well, that answers that question. My very grateful thanks to Professor Hooper for the explanantion. I think I might have figured it out myself eventually, but I am not willing to put a bound of less than two hundred years on how long it would have taken me to do so.
One lesson to learn from all this is that those early Royal Society guys were very smart, and when they say something has a mysterious (0.4)x in it, you should assume they know what they are doing. Another lesson is that mechanics was pretty well-understood by 1668.
[Other articles in category /physics] permanent link
Sat, 14 Jul 2007
Evaporation
 I work for the Penn Genomics Institute, mostly doing software work,
but the Institute is run by biologists and also does biology projects.
Last month I taught some perl classes for the four summer interns;
this month they are doing some lab work. Since part of my job
involves dealing with biologists, I thought this would be a good
opportunity to get into the lab, and I got permission from Adam, the
research scientist who was supervising the interns, to let me come
along.
I work for the Penn Genomics Institute, mostly doing software work,
but the Institute is run by biologists and also does biology projects.
Last month I taught some perl classes for the four summer interns;
this month they are doing some lab work. Since part of my job
involves dealing with biologists, I thought this would be a good
opportunity to get into the lab, and I got permission from Adam, the
research scientist who was supervising the interns, to let me come
along.
Since my knowledge of biology is practically nil, Adam was not entirely sure what to do with me while the interns prepared to grow yeasts or whatever it is that they are doing. He set me up with a scale, a set of pipettes, and a beaker of water, with instructions to practice pipetting the water from the beaker onto the scale.
The pipettes came in three sizes. Shown at right is the largest of the ones I used; it can dispense liquid in quantities between 10 and 100 μl, with a precision of 0.1 μl. I used each of the three pipettes in three settings, pipetting water in quantities ranging from 1 ml down to 5 μl. I think the idea here is that I would be able to see if I was doing it right by watching the weight change on the scale, which had a display precision of 1 mg. If I pipette 20 μl of water onto the scale, the measured weight should go up by just about 20 mg.
Sometimes it didn't. For a while my technique was bad, and I didn't always pick up the exact right amount of water. With the small pipette, which had a capacity range of 2–20 μl, you have to suck up the water slowly and carefully, or the pipette tip gets air bubbles in it, and does not pick up the full amount.
With a scale that measures in milligrams, you have a wait around for a while for the scale to settle down after you drop a few μl of water onto it, because the water bounces up and down and the last digit of the scale readout oscillates a bit. Milligrams are much smaller than I had realized.
It turned out that it was pretty much impossible to see if I was picking up the full amount with the smallest pipette. After measuring out some water, I would wait a few seconds for the scale display to stabilize. But if I waited a little longer, it would tick down by a milligram. After another twenty or thirty seconds it would tick down by another milligram. This would continue indefinitely.
I thought about this quietly for a while, and realized that what I was seeing was the water evaporating from the scale pan. The water I had in the scale pan had a very small surface area, only a few square centimeters. But it was evaporating at a measurable rate, around 2 or 3 milligrams per minute.
So it was essentially impossible to measure out five pipette-fuls of 10 μl of water each and end up with 50 mg of water on the scale. By the time I got it done, around 15% of it would have evaporated.
The temperature here was around 27°C, with about 35% relative humidity. So nothing out of the ordinary.
I am used to the idea that if I leave a glass of water on the kitchen counter overnight, it will all be gone in the morning; this was amply demonstrated to me in nursery school when I was about three years old. But to actually see it happening as I watched was a new experience.
I had no idea evaporation was so speedy.
[Other articles in category /physics] permanent link
Sat, 28 Apr 2007
1219.2 feet
In Thursday's article, I
quoted an article about tsunamis that asserted that:
In the Pacific Ocean, a tsunami moves 60.96 feet a second, passing through water that is around 1219.2 feet deep."60.96 feet a second" is an inept conversion of 100 km/h to imperial units, but I wasn't able to similarly identify 1219.2 feet.
Scott Turner has solved the puzzle. 1219.2 feet is an inept conversion of 4000 meters to imperial units, obtained by multiplying 4000 by 0.3048, because there are 0.3048 meters in a foot.
Thank you, M. Turner.
[ Addendum 20070430: 60.96 feet per second is nothing like 100 km/hr, and I have no idea why I said it was. The 60.96 feet per second is a backwards conversion of 200 m/s. ]
[Other articles in category /physics] permanent link
Thu, 26 Apr 2007
Excessive precision
You sometimes read news articles that say that some object is 98.42
feet tall, and it is clear what happened was that the object was
originally reported to be 30 meters tall, and some knucklehead
translated 30 meters to 98.42 feet, instead of to 100 feet as they
should have.
Finding a real example for you was easy: I just did Google search for "62.14 miles", and got this little jewel:
Tsunami waves can be up to 62.14 miles long! They can also be about three feet high in the middle of the ocean. Because of its strong underwater energetic force, the tsunami can rise up to 90 feet, in extreme cases, when they hit the shore! Tsunami waves act like shallow water waves because they are so long. Because it is so long, it can last an hour. In the Pacific Ocean, a tsunami moves 60.96 feet a second, passing through water that is around 1219.2 feet deep.The 60.96 feet per second is actually 100 km/hr, but I'm not sure what's going on with the 1219.2 feet deep. Is it 1/5 nautical mile? But that would be strange. [ Addendum 20070428: the explanation.](.)
Here's another delightful example:
The MiniC.A.T. is very cost-efficient to operate. According to MDI, it costs less than one dollar per 62.14 miles... Given the absence of combustion and the fact that the MiniC.A.T. runs on vegetable oil, oil changes are only necessary every 31,068 miles.(I should add that many of the hits for "62.14 miles" were perfectly legitimate. Many concerned 100-km bicycle races, or the conditions for winning the X-prize. In both cases the distance is in fact 62.14 miles, not 62.13 or 62.15, and the precision is warranted. But I digress.)(eesi.org.)
(Long ago there was a parody of the New York Times which included a parody sports section that announced "FOOTBALL TO GO METRIC". The article revealed that after the change, the end zones would be placed 91.44 meters apart...)
Anyway, similar knuckleheadedness occurs in the well-known value of 98.6 degrees Fahrenheit for normal human body temperature. Human body temperature varies from individual to individual, and by a couple of degrees over the course of the day, so citing the "normal" temperature to a tenth of a degree is ridiculous. The same thing happened here as with the 62.14-mile tsunami. Normal human body temperature was determined to be around 37 degrees Celsius, and then some knucklehead translated 37°C to 98.6°F instead of to 98°F.
When our daughter Katara was on the way, Lorrie and I took a bunch of classes on baby care. Several of these emphasized that the maximum safe spacing for the bars of a crib, rails of a banister, etc., was two and three-eighths inches. I was skeptical, and at one of these classes I was foolish enough to ask if that precision were really required: was two and one-half inches significantly less safe? How about two and seven-sixteenths inches? The answer was immediate and unequivocal: two and one-half inches was too far apart for safety; two and three-eighths inches is the maximum safe distance.
All the baby care books say the same thing. (For example...)
But two and three-eighths inches is 6.0325 cm, so draw your own conclusion about what happened here.
[ Addendum 20070430: 60.96 feet per second is nothing like 100 km/hr, and I have no idea why I said it was. The 60.96 feet per second appears to be a backwards conversion of 200 m/s to ft/s, multiplying by 3.048 instead of dividing. As Scott turner noted a few days ago, a similar error occurs in the conversion of meters to feet in the "1219.2 feet deep" clause. ]
[ Addendum 20220124: the proper spacing of crib slats ]
[Other articles in category /physics] permanent link
Sun, 31 Dec 2006
Daylight chart
My wife is always sad this time of the year because the days are so
short and dark. I made a chart like this one a couple of years ago
so that she could see the daily progress from dark to light as the
winter wore on to spring and then summer.
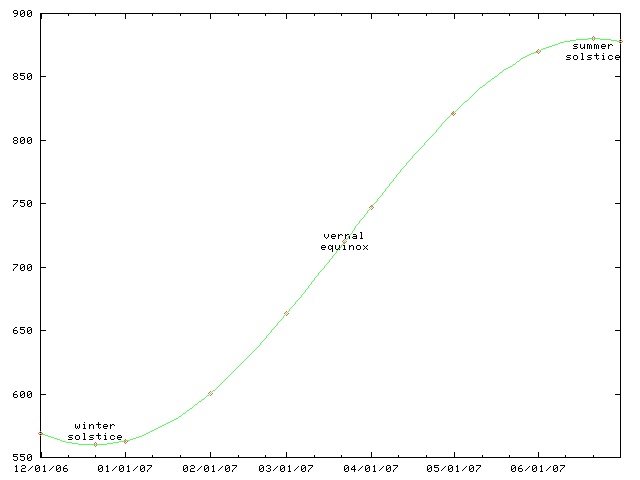
This chart only works for Philadelphia and other places at the same latitude, such as Boulder, Colorado. For higher latitutdes, the y axis must be stretched. For lower latitudes, it must be squished. In the southern hemisphere, the whole chart must be flipped upside-down.
(The chart will work for places inside the Arctic or Antarctic circles, if you use the correct interpretations for y values greater than 1440 minutes and less than 0 minutes.)
This time of year, the length of the day is only increasing by about thirty seconds per day. (Decreasing, if you are in the southern hemishphere.) On the equinox, the change is fastest, about 165 seconds per day. (At latitudes 40°N and 40°S.) After that, the rate of increase slows, until it reaches zero on the summer solstice; then the days start getting shorter again.
As with all articles in the physics section of my blog, readers are cautioned that I do not know what I am talking about, although I can spin a plausible-sounding line of bullshit. For this article, readers are additionally cautioned that I failed observational astronomy twice in college.
[Other articles in category /physics] permanent link
Fri, 21 Apr 2006 Richard P. Feynman says:
When I was in high school, I'd see water running out of a faucet growing narrower, and wonder if I could figure out what determines that curve. I found it was rather easy to do.I puzzled over that one for years; I didn't know how to start. I kept supposing that it had something to do with surface tension and the tendency of the water surface to seek a minimal configuration, and I couldn't understand how it could be "rather easy to do". That stuff all sounded really hard!
 But one day I realized
in a flash that it really is easy. The water accelerates as it
falls. It's moving faster farther down, so the stream must be
narrower, because the rate at which the water is passing a given point
must be constant over the entire stream. (If water is passing a
higher-up point faster than it passes a low point, then the water is
piling up in between—which we know it doesn't do. And vice versa.)
It's easy to calculate the speed of the water at each point in the
stream. Conservation of mass gets us the rest.
But one day I realized
in a flash that it really is easy. The water accelerates as it
falls. It's moving faster farther down, so the stream must be
narrower, because the rate at which the water is passing a given point
must be constant over the entire stream. (If water is passing a
higher-up point faster than it passes a low point, then the water is
piling up in between—which we know it doesn't do. And vice versa.)
It's easy to calculate the speed of the water at each point in the
stream. Conservation of mass gets us the rest.
So here's the calculation. Let's adopt a coordinate system that puts position 0 at the faucet, with increasing position as we move downward. Let R(p) be the radius of the stream at distance p meters below the faucet. We assume that the water is falling smoothly, so that its horizontal cross-section is a circle.
Let's suppose that the initial velocity of the water leaving the faucet is 0. Anything that falls accelerates at a rate g, which happens to be !!9.8 m/s^2!!, but we'll just call it !!g!! and leave it at that. The velocity of the water, after it has fallen for time !!t!!, is !!v = gt!!. Its position !!p!! is !!\frac12 gt^2!!. Thus !!v = (2gp)^{1/2}!!.
Here's the key step: imagine a very thin horizontal disk of water, at distance p below the faucet. Say the disk has height h. The water in this disk is falling at a velocity of !!(2gp)^{1/2}!!, and the disk itself contains volume !!\pi (R(p))^2h!! of water. The rate at which water is passing position !!p!! is therefore !!\pi (R(p))^2h \cdot (2gp)^{1/2}!! gallons per minute, or liters per fortnight, or whatever you prefer. Because of the law of conservation of water, this quantity must be independent of !!p!!, so we have:
$$\pi(R(p))^2h\cdot (2gp)^{1/2} = A$$Where !!A!! is the rate of flow from the faucet. Solving for !!R(p)!!, which is what we really want:
$$R(p) = \left[\frac A{\pi h(2gp)^{1/2}}\right]^{1/2}$$Or, collecting all the constants (!!A, \pi , h,!! and !!g!!) into one big constant !!k!!:
$$R(p) = kp^{-1/4}$$ There's a picture of that over there on the left side of the blog. Looks just about right, doesn't it? Amazing.So here's the weird thing about the flash of insight. I am not a brilliant-flash-of-insight kind of guy. I'm more of a slow-gradual-dawning-of-comprehension kind of guy. This was one of maybe half a dozen brilliant flashes of insight in my entire life. I got this one at a funny time. It was fairly late at night, and I was in a bar on Ninth Avenue in New York, and I was really, really drunk. I had four straight bourbons that night, which may not sound like much to you, but is a lot for me. I was drunker than I have been at any other time in the past ten years. I was so drunk that night that on the way back to where I was staying, I stopped in the middle of Broadway and puked on my shoes, and then later that night I wet the bed. But on the way to puking on my shoes and pissing in the bed, I got this inspiration about what shape a stream of water is, and I grabbed a bunch of bar napkins and figured out that the width is proportional to !!p^{-1/4}!! as you see there to the left.
This isn't only time this has happened. I can remember at least one other occasion. When I was in college, I was freelancing some piece of software for someone. I alternated between writing a bit of code and drinking a bit of whisky. (At that time, I hadn't yet switched from Irish whisky to bourbon.) Write write, drink, write write, drink... then I encountered some rather tricky design problem, and, after another timely pull at the bottle, a brilliant flash of inspiration for how to solve it. "Oho!" I said to myself, taking another swig out of the bottle. "This is a really clever idea! I am so clever! Ho ho ho! Oh, boy, is this clever!" And then I implemented the clever idea, took one last drink, and crawled off to bed.
The next morning I remembered nothing but that I had had a "clever" inspiration while guzzling whisky from the bottle. "Oh, no," I muttered, "What did I do?" And I went to the computer to see what damage I had wrought. I called up the problematic part of the program, and regarded my alcohol-inspired solution. There was a clear and detailed comment explaining the solution, and as I read the code, my surprise grew. "Hey," I said, astonished, "it really was clever." And then I saw the comment at the very end of the clever section: "Told you so."
I don't know what to conclude from this, except perhaps that I should have spent more of my life drinking whiskey. I did try bringing a flask with me to work every day for a while, about fifteen years ago, but I don't remember any noteworthy outcome. But it certainly wasn't a disaster. Still, a lot of people report major problems with this strategy, so it's hard to know what to make of my experience.
[Other articles in category /physics] permanent link
Tue, 18 Apr 2006
It's the radioactive potassium, dude!
A correspondent has informed me that my explanation of the
snow-melting properties of salt is "wrong". I am torn between
paraphrasing the argument, and quoting it verbatim, which may be a
copyright violation and may be impolite. But if I paraphrase, I am
afraid you will inevitably conclude that I have misrepresented his
thinking somehow. Well, here is a brief quotation that summarizes the
heart of the matter:
Anyway the radioactive [isotope of potassium] emits energy (heat) which increases the rate of snow melt.The correspondent informs me that this is taught in the MIT first-year inorganic chemistry class.
So what's going on here? I picture a years-long conspiracy in the MIT chemistry department, sort of a gentle kind of hazing, in which the professors avow with straight faces that the snow-melting properties of rock salt are due to radioactive potassium, and generation after generation of credulous MIT freshmen nod studiously and write it into their notes. I imagine the jokes that the grad students tell about other grad students: "Yeah, Bill here was so green when he first arrived that he still believed the thing about the radioactive potassium!" "I did not! Shut up!" I picture papers, published on April 1 of every year, investigating the phenomenon further, and discoursing on the usefulness of radioactive potassium for smelting ores and frying fish.
Is my correspondent in on the joke, trying to sucker me, so that he can have a laugh about it with his chemistry buddies? Or is he an unwitting participant? Or perhaps there is no such conspiracy, the MIT inorganic chemistry department does not play this trick on their students, and my correspondent misunderstood something. I don't know.
Anyway, I showed this around the office today and got some laughs. It reminds me a little of the passage in Ball Four in which the rules of baseball are going to be amended to increase the height of the pitcher's mound. It is generally agreed that this will give an advantage to the pitcher. But one of the pitchers argues that raising the mound will actually disadvantage him, because it will position him farther from home plate.
You know, the great thing about this theory is that you can get the salt to melt the snow without even taking it out of the bag. When you're done, just pick up the bag again, put it back in the closet. All those people who go to the store to buy extra salt are just a bunch of fools!
Well, it's not enough just to scoff, and sometimes arguments from common sense can be mistaken. So I thought I'd do the calculation. First we need to know how much radioactive potassium is in the rock salt. I don't know what fraction of a bag of rock salt is NaCl and what fraction is KCl, but it must be less than 10% KCl, so let's use that. And it seems that about 0.012% of naturally-occurring potassium is radioactive . So in one kilogram of rock salt, we have about 100g KCl, of which about 0.012g is K40Cl.
Now let's calculate how many K40 atoms there are. KCl has an atomic weight around 75. (40 for the potassium, 35 for the chlorine.) Thus 6.022×1023 atoms of potassium plus that many atoms of chlorine will weigh around 75g. So there are about 0.012 · 6.022×1023 / 75 = 9.6×1019 K40-Cl pairs in our 0.012g sample, and about 9.6×1019 K40 atoms.
Now let's calculate the rate of radioactive decay of K40. It has a half-life of 1.2×109 years. This means that each atom has a (1/2)T probability of still being around after some time interval of length t, where T is t / 1.2×109 years. Let's get an hourly rate of decay by putting t = one hour, which gives T = 9.5×10-14, and the probability of particular K40 atom decaying in any one-hour period is 6.7 × 10-14. Since there are 9.6×1019 K40 atoms in our 1kg sample, around 64,000 will decay each hour.
Now let's calculate the energy released by the radioactive decay. The disintegration energy of K40 is about 1.5 MeV. Multiplying this by 64,000 gets us an energy output of 86.4 GeV per hour.
How much is 86.4 GeV? It's about 3.4×10-9 calories. That's for a kilogram of salt, in an hour.
How big is it? Recall that one calorie is the amount of energy required to raise one gram of water one degree Celsius. 3.4×10-9 calorie is small. Real small.
Note that the energy generated by gravity as the kilogram of rock salt falls one meter to the ground is 9.8 m/s2 · 1000g · 1m = 9.8 joules = 2.3 calories. You get on the order of 750 million times as much energy from dropping the salt as you do from an hour of radioactive decay.
But I think this theory still has some use. For the rest of the month, I'm going to explain all phenomena by reference to radioactive potassium. Why didn't the upgrade of the mail server this morning go well? Because of the radioactive potassium. Why didn't CVS check in my symbolic links correctly? It must have been the radioactive potassium. Why does my article contain arithmetic errors? It's the radioactive potassium, dude!
The nation that controls radioactive potassium controls the world!
[ An earlier version of this article said that the probability of a potassium atom decaying in 1 hour was 6.7 × 10-12 instead of 6.7 × 10-14. Thanks to Przemek Klosowski of the NIST center for neutron research for pointing out this error. ]
[Other articles in category /physics] permanent link
Sat, 15 Apr 2006
Facts you should know
The Minneapolis Star Tribune offers an article on Why is the sky
blue? Facts you should know, subtitled "Scientists offer 10 basic
questions to test your knowledge".
[ The original article has been removed; here
is another copy. ]
I had been planning to write for a
while on why the sky is blue, and how the conventional answers are
pretty crappy. (The short answer is "Rayleigh scattering", but that's
another article for another day. Even crappier are the common
explanations of why the sea is blue. You often hear the explanation that
the sea is blue because it reflects the sky. This is obviously
nonsense. The surface of the sea does reflect the sky, perhaps, but
when the sea is blue, it is a deep, beautiful blue all the way
down. The right answer is, again, Rayleigh scattering.)
The author, Andrea L. Gawrylewski, surveyed a number of scientists and educators and asked them "What is one science question every high school graduate should be able to answer?" The questions follow.
- What percentage of the earth is covered by water?
This is the best question that the guy from Woods Hole Oceanographic Institute can come up with?
It's a plain factual question, something you could learn in two seconds. You can know the answer to this question and still have no understanding whatever of biology, meteorology, geology, oceanography, or any other scientific matter of any importance. If I were going to make a list of the ten things that are most broken about science education, it would be that science education emphasizes stupid trivia like this at the expense of substantive matters.
For a replacement question, how about "Why is it important that three-fourths of the Earth's surface is covered with water?" It's easy to recognize a good question. A good question is one that is quick to ask and long to answer. My question requires a long answer. This one does not.
- What sorts of signals does the brain use to communicate
sensations, thoughts and actions?
This one is a little better. But the answer given, "The single cells in the brain communicate through electrical and chemical signals" is still disappointing. It is an answer at the physical level. A more interesting answer would discuss the protocol layers. How does the brain perform error correction? How is the information actually encoded? I may be mistaken, but I think this stuff is all still a Big Mystery.
The question given asks about how the brain communicates thoughts. The answer given completely fails to answer this question. OK, the brain uses electrical and chemical signals. So how does the brain use electricity and chemicals to communicate thoughts, then?
- Did dinosaurs and humans ever exist at the same time?
Here's another factual question, one with even less information content than the one about the water. This one at least has some profound philosophical implications: since the answer is "no", it implies that people haven't always been on the earth. Is this really the one question every high school graduate should be able to answer? Why dinosaurs? Why not, say, trilobites?
I think the author (Andrew C. Revkin of the New York Times) is probably trying to strike a blow against creationism here. But I think a better question would be something like "what is the origin of humanity?"
- What is Darwin's theory of the origin of species?
At last we have a really substantive question. I think it's fair to say that high school graduates should be able to give an account of Darwinian thinking. I would not have picked the theory of the origin of species, specifically, particularly because the origin of species is not yet fully understood. Instead, I would have wanted to ask "What is Darwin's theory of evolution by natural selection?" And in fact the answer given strongly suggests that this is the question that the author thought he was asking.
But I can't complain about the subject matter. The theory of evolution is certainly one of the most important ideas in all of science.
- Why does a year consist of 365 days, and a day of 24 hours?
I got to this question and sighed in relief. "Ah," I said, "at last, something subtle." It is subtle because the two parts of the question appear to be similar, but in fact are quite different. A year is 365 days long because the earth spins on its axis in about 1/365th the time it takes to revolve around the sun. This matter has important implications. For example, why do we need to have leap years and what would happen if we didn't?
The second part of the question, however, is entirely different. It is not astronomical but historical. Days have 24 hours because some Babylonian thought it would be convenient to divide the day and the night into 12 hours each. It could just as easily have been 1000 hours. We are stuck with 365.2422 whether we like it or not.
The answer given appears to be completely oblivious that there is anything interesting going on here. As far as it is concerned, the two things are exactly the same. "A year, 365 days" it says, "is the time it takes for the earth to travel around the sun. A day, 24 hours, is the time it takes for the earth to spin around once on its axis."
- Why is the sky blue?
I have no complaint here with the question, and the answer is all right, I suppose. (Although I still have a fondness for "because it reflects the sea.") But really the issue is rather tricky. It is not enough to just invoke Rayleigh scattering and point out that the high-frequency photons are scattered a lot more than the low-frequency ones. You need to think about the paths taken by the photons: The ones coming from the sky have, of course, come originally from the sun in a totally different direction, hit the atmosphere obliquely, and been scattered downward into your eyes. The sun itself looks slightly redder because the blue photons that were heading directly toward your eyes are scattered away; this effect is quite pronounced when there is more scattering than usual, as when there are particles of soot in the air, or at sunset.
The explanation doesn't end there. Since the violet photons are scattered even more than the blue ones, why isn't the sky violet? I asked several professors of physics this question and never got a good answer. I eventually decided that it was because there aren't very many of them; because of the blackbody radiation law, the intensity of the sun's light falls off quite rapidly as the frequency increases, past a certain point. And I was delighted to see that the Wikipedia article on Rayleigh scattering addresses this exact point and brings up another matter I hadn't considered: your eyes are much more sensitive to blue light than to violet.
The full explanation goes on even further: to explain the blackbody radiation and the Rayleigh scattering itself, you need to use quantum physical theories. In fact, the failure of classical physics to explain blackbody radiation was the impetus that led Max Planck to invent the quantum theory in the first place.
So this question gets an A+ from me: It's a short question with a really long answer.
- What causes a rainbow?
I have no issue with this question. I don't know if I'd want to select it as the "one science question every high school graduate should be able to answer", but it certainly isn't a terrible choice like some of the others.
- What is it that makes diseases caused by viruses and bacteria hard
to treat?
The phrasing of this one puzzled me. Did the author mean to suggest that genetic disorders, geriatric disorders, and prion diseases are not hard to treat? No, I suppose not. But still, the question seems philosophically strange. Why says that diseases are hard to treat? A lot of formerly fatal bacterial diseases are easy to treat: treating cholera is just a matter of giving the patient IV fluids until it goes away by itself; a course of antibiotics and your case of the bubonic plague will clear right up. And even supposing that we agree that these diseases are hard to treat, how can you rule out "answers" like "because we aren't very clever"? I just don't understand what's being asked here.
The answer gives a bit of a hint about what the question means. It begins "influenza viruses and others continually change over time, usually by mutation." If that's what you're looking for, why not just ask why there's no cure for the common cold?
- How old are the oldest fossils on earth?
Oh boy, another stupid question about how much water there is on the surface of the earth. I guessed a billion years; the answer turns out to be about 3.8 billion years. I think this, like the one about the dinosaurs, is a question motivated by a desire to rule out creationism. But I think it's an inept way of doing so, and the question itself is a loser.
- Why do we put salt on sidewalks when it snows?
Gee, why do we do that? Well, the salt depresses the freezing point of the water, so that it melts at a lower temperature, one, we hope, that is lower than the temperature outside, so that the snow melts. And if it doesn't melt, the salt is gritty and provides some traction when we walk on it.
But why does the salt depress the freezing point? I don't know; I've never understood this. The answer given in the article is no damn good:
Adding salt to snow or ice increases the number of molecules on the ground surface and makes it harder for the water to freeze. Salt can lower freezing temperatures on sidewalks to 15 degrees from 32 degrees.
The second sentence really doesn't add anything at all, and the first one is so plainly nonsense I'm not even sure where to start ridiculing it. (If all that is required is an increase in the number of molecules, why won't it work to add more snow?)So let me think. The water molecules are joggling around, bumping into each other, and the snow is a low-energy crystalline state that they would like to fall into. At low temperatures, even when a molecule manages to joggle its way out of the crystal, it's likely to fall back in pretty quickly, and if not there's probably another molecule around that can fall in instead. At lower temperatures, the molecules joggle less, and there's an equilibrium in this in-and-out exchange that results in more ice and less water than at higher temperatures.
When the salt is around, the salt molecules might fall into the holes in the ice crystal instead, get in the way of the water molecules, and prevent the crystal from re-forming, so that's going to shift the equilibrium in favor of water and against ice. So if you want to reach the same equilibrium that's normally reached at zero degrees, you need to subtract some of the joggling energy, to compensate for the interference of the salt, and that's why the freezing temperature goes down.
I think that's right, or close to it,and it certainly sounds pretty good, but my usual physics disclaimer applies: While I know next to nothing about physics, I can spin a line of bullshit that sounds plausible enough to fool people, including myself, into believing it.
(Is there a such a thing as a salt molecule? Or does it really take the form of isolated sodium and chlorine ions? I guess it doesn't matter much in this instance.)
I think this question is a winner.
[ Addendum 20060416: Allan Farrell's blog Bento Box has another explanation of this. It seems to me that M. Farrell knows a lot more about it than I do, but also that my own explanation was essentially correct. But there may be subtle errors in my explanantion that I didn't notice, so you may want to read the other one and compare.]
[ Addendum 20070204: A correspondent at MIT provided an alternative explanantion. ]
The questions overall were a lot better than the answers, which made me wonder if perhaps M. Gawrylewski had written the answers herself.
[Other articles in category /physics] permanent link
Tue, 28 Mar 2006
The speed of electricity
For some reason I have needed to know this several times in the past
few years: what is the speed of electricity? And for some reason,
good answers are hard to come by.
(Warning: as with all my articles on physics, readers are cautioned that I do not know what I am talking about, but that I can talk a good game and make up plenty of plausible-sounding bullshit that sounds so convincing that I believe it myself. Beware of bullshit.)
If you do a Google search for "speed of electricity", the top hit is Bill Beaty's long discourse on the subject. In this brilliantly obtuse article, Beaty manages to answer just about every question you might have about everything except the speed of electricity, and does so in a way that piles confusion on confusion.
Here's the funny thing about electricity. To have electricity, you need moving electrons in the wire, but the electrons are not themselves the electricity. It's the motion, not the electrons. It's like that joke about the two rabbinical students who are arguing about what makes tea sweet. "It's the sugar," says the first one. "No," disagrees the other, "it's the stirring." With electricity, it really is the stirring.
We can understand this a little better with an analogy. Actually, several analogies, each of which, I think, illuminates the others. They will get progressively closer to the real truth of the matter, but readers are cautioned that these are just analogies, and so may be misleading, particularly if overextended. Also, even the best one is not really very good. I am introducing them primarily to explain why I think M. Beaty's answer is obtuse.
- Consider a
garden hose a hundred feet long. Suppose the hose is already full of
water. You turn on the hose at one end, and water starts coming out
the other end. Then you turn off the hose, and the water stops coming
out. How long does it take for the water to stop coming out? It
probably happens pretty darn fast, almost instantaneously.
This shows that the "signal" travels from one end of the hose to the other at a high speed—and here's the key idea—at a much higher speed than the speed of the water itself. If the hose is one square inch in cross-section, its total volume is about 5.2 gallons. So if you're getting two gallons per minute out of it, that means that water that enters the hose at the faucet end doesn't come out the nozzle end until 156 seconds later, which is pretty darn slow. But it certainly isn't the case that you have to wait 156 seconds for the water to stop coming out after you turn off the faucet. That's just how long it would take to empty the hose. And similarly, you don't have to wait that long for water to start coming out when you turn the faucet on, unless the hose was empty to begin with.
The water is like the electrons in the wire, and electricity is like that signal that travels from the faucet to the nozzle when you turn off the water. The electrons might be travelling pretty slowly, but the signal travels a lot faster.
- You're waiting in the check-in line at the airport. One of the
clerks calls "Can I help who's next?" and the lady at the front of the
line steps up to the counter. Then the next guy in line steps up to
the front of the line. Then the next person steps up. Eventually,
the last person in line steps up. You can imagine that there's a
"hole" that opens up at the front of the line, and the hole travels
backwards through the line to the back end.
How fast does the hole travel? Well, it depends. But one thing is sure: the speed at which the hole moves backward is not the same as the speed at which the people move forward. It might take the clerks another hour to process the sixty people in line. That does not mean that when they call "next", it will take an hour for the hole to move all the way to the back. In fact, the rate at which the hole moves is to a large extent independent of how fast the people in the line are moving forward.
The people in the line are like electrons. The place at which the people are actually moving—the hole—is the electricity itself.
- In the ocean, the waves start far out from shore, and then roll in
toward the shore. But if you look at a cork bobbing on the waves, you
see right away that even though the waves move toward the shore, the
water is staying in pretty much the same place. The cork is
not moving toward the shore; it's bobbing up and down, and it might
well stay in the same place all day, bobbing up and down. It should
be pretty clear that the speed with which the water and the cork are
moving up and down is only distantly related to the speed with which
the waves are coming in to shore. The water is like the electrons,
and the wave is like the electricity.
- A bomb explodes on a hill, and sometime later Ike on the next hill
over hears the bang. This is because the exploding bomb compresses
the air nearby, and then the compressed air expands, compressing the
air a little way away again, and the compressed air expands and
compresses the air a little way farther still, and so there's a wave
of compression that spreads out from the bomb until eventually the air
on the next hill is compressed and presses on Ike's eardrums. It's
important to realize that no individual air molecule has traveled from
hill A to hill B. Each air molecule stays in pretty much the same
place, moving back and forth a bit, like the water in the water waves
or the people in the airport queue. Each person in the airport line
stays in pretty much the same place, even though the "hole" moves all
the way from the front of the line to the back. Similarly, the air
molecules all stay in pretty much the same place even as the
compression wave goes from hill A to hill B. When you speak to
someone across the room, the sound travels to them at a speed of 680
miles per hour, but they are not bowled over by hurricane-force winds.
(Thanks to Aristotle Pagaltzis for suggesting that I point this out.)
Here the air molecules are like the electrons in the wire, and the
sound is like the electricity.
I believe that when someone asks for the speed of electricity, what they are typically after is something like: When I flip the switch on the wall, how long before the light goes on? Or: the ALU in my computer emits some bits. How long before those bits get to the output bus? Or again: I send a telegraph message from Nova Scotia to Ireland on an undersea cable. How long before the message arrives in Ireland? Or again: computers A and B are on the same branch of an ethernet, 10 meters apart. How long before a packet emitted by A's ethernet hardware gets to B's ethernet hardware?
M. Beaty's answer about the speed of the electrons is totally useless as an answer to this kind of question. It's a really detailed, interesting answer to a question to which hardly anyone was interested in the answer.
Here the analogy with the speed of sound really makes clear what is wrong with M. Beaty's answer. I set off a bomb on one hill. How long before Ike on the other hill a mile away hears the bang? Or, in short, "what is the speed of sound?" M. Beaty doesn't know what the speed of sound is, but he is glad to tell you about the speed at which the individual air molecules are moving back and forth, although this actually has very little to do with the speed of sound. He isn't going to tell you how long before the tsunami comes and sweeps away your village, but he has plenty to say about how fast the cork is bobbing up and down on the water.
That's all fine, but I don't think it's what people are looking for when they want the speed of electricity. So the individual charges in the wire are moving at 2.3 mm/s; who cares? As M. Beaty was at some pains to point out, the moving charges are not themselves the electricity, so why bring it up?
I wanted to end this article with a correct and pertinent answer to the question. For a while, I was afraid I was going to have to give up. At first, I just tried looking it up on the web. Many people said that the electricity travels at the speed of light, c. This seemed rather implausible to me, for various reasons. (That's another essay for another day.) And there was widespread disagreement about how fast it really was. For example:
But then I found this page on the characteristic impedance of coaxial cables and other wires, which seems rather more to the point than most of the pages I have found that purport to discuss the "speed of electricity" directly.
From this page, we learn that the thing I have been referring to as the "speed of electricity" is called, in electrical engineering jargon, the "velocity factor" of the wire. And it is a simple function of the "dielectric constant" not of the wire material itself, but of the insulation between the two current-carrying parts of the wire! (In typical physics fashion, the dielectric "constant" is anything but; it depends on the material of which the insulation is made, the temperature, and who knows what other stuff they aren't telling me. Dielectric constants in the rest of the article are for substances at room temperature.) The function is simply:
$$V = {c\over\sqrt{\varepsilon_r}}$$
where V is the velocity of electricity in the wire, and εr is the dielectric constant of the insulating material, relative to that of vacuum. Amazingly, the shape, material, and configuration of the wire doesn't come into it; for example it doesn't matter if the wire is coaxial or twin parallel wires. (Remember the warning from the top of the page: I don't know what I am talking about.) Dielectric constants range from 1 up to infinity, so velocity ranges from c down to zero, as one would expect. This explains why we find so many inconsistent answers about the speed of electricity: it depends on a specific physical property of the wire. But we can consider some common examples.Wikipedia says that the dielectric constant of rubber is about 7 (and this website specifies 6.7 for neoprene) so we would expect the speed of electricity in rubber-insulated wire to be about 0.38c. This is not quite accurate, because the wires are also insulated by air and by the rest of the universe. But it might be close to that. (Remember that warning!)
The dielectric constant of air is very small—Wikipedia says 1.0005, and the other site gives 1.0548 for air at 100 atmospheres pressure—so if the wires are insulated only by air, the speed of electricity in the wires should be very close to the speed of light.
We can also work the calculation the other way: this web page says that signal propagation in an ethernet cable is about 0.66c, so we infer that the dielectric constant for the insulator is around 1/0.662 = 2.3. We look up this number in a a table of dielectric constants and guess from that that the insulator might be polyethylene or something like it. (This inference would be correct.)
What's the lower limit on signal propagation in wires? I found a reference to a material with a dielectric constant of 2880. Such a material, used as an insulator between two wires, would result in a velocity of about 2% of c, which is still 5600 km/s. this page mentions cement pastes with "effective dielectric constants" up around 90,000, yielding an effective velocity of 1/300 c, or 1000 km/s.
Finally, I should add that the formula above only applies for direct currents. For varying currents, such as are typical in AC power lines, the dielectric constant apparently varies with time (some constant!) and the analysis is more complicated.
[ Addendum 20180904: Paul Martin suggests that I link to this useful page about dielectric constants. It includes an extensive table of the εr for various polymers. Mostly they are between 2 and 3. ]
[Other articles in category /physics] permanent link
Fri, 03 Mar 2006
John Wilkins invents the meter
| Buy An Essay Towards a Real Character and a Philosophical Language from Bookshop.org (with kickback) (without kickback) |
In skimming over it, I noticed that Wilkins' language contained words for units of measure: "line", "inch", "foot", "standard", "pearch", "furlong", "mile", "league", and "degree". I thought oh, this was another example of a foolish Englishman mistaking his own provincial notions for universals. Wilkins' language has words for Judaism, Christianity, Islam; everything else is under the category of paganism and false gods, and I thought that the introduction of words for inches and feet was another case like that one. But when I read the details, I realized that Wilkins had been smarter than that.
Wilkins recognizes that what is needed is a truly universal measurement standard. He discusses a number of ways of doing this and rejects them. One of these is the idea of basing the standard on the circumference of the earth, but he thinks this is too difficult and inconvenient to be practical.
But he settles on a method that he says was suggested by Christopher Wren, which is to base the length standard on the time standard (as is done today) and let the standard length be the length of a pendulum with a known period. Pendulums are extremely reliable time standards, and their period depends only their length and on the local effect of gravity. Gravity varies only a very little bit over the surface of the earth. So it was a reasonable thing to try.
Wilkins directed that a pendulum be set up with the heaviest, densest possible spherical bob at the end of lightest, most flexible possible cord, and that the length of the cord be adjusted until the period of the pendulum was as close to one second as possible. So far so good. But here is where I am stumped. Wilkins did not simply take the standard length as the length from the fulcrum to the center of the bob. Instead:
...which being done, there are given these two Lengths, viz. of the String, and of the Radius of the Ball, to which a third Proportional must be found out; which must be as the length of the String from the point of Suspension to the Centre of the Ball is to the Radius of the Ball, so must the said Radius be to this third which being so found, let two fifths of this third Proportional be set off from the Centre downwards, and that will give the Measure desired.Wilkins is saying, effectively: let d be the distance from the point of suspension to the center of the bob, and r be the radius of the bob, and let x be such that d/r = r/x. Then d+(0.4)x is the standard unit of measurement.
Huh? Why 0.4? Why does r come into it? Why not just use d? Huh?
These guys weren't stupid, and there must be something going on here that I don't understand. Can any of the physics experts out there help me figure out what is going on here?
Anyway, the main point of this note is to point out an extraordinary coincidence. Wilkins says that if you follow his instructions above, the standard unit of measurement "will prove to be . . . 39 Inches and a quarter". In other words, almost exactly one meter.
I bet someone out there is thinking that this explains the oddity of the 0.4 and the other stuff I don't understand: Wilkins was adjusting his definition to make his standard unit come out to exactly one meter, just as we do today. (The modern meter is defined as the distance traveled by light in 1/299,792,458 of a second. Why 299,792,458? Because that's how long it happens to take light to travel one meter.) But no, that isn't it. Remember, Wilkins is writing this in 1668. The meter wasn't invented for another 110 years.
[ Addendum 20070915: There is a followup article, which explains the mysterious (0.4)x in the formula for the standard length. ]
Having defined the meter, which he called the "Standard", Wilkins then went on to define smaller and larger units, each differing from the standard by a factor that was a power of 10. So when Wilkins puts words for "inch" and "foot" into his universal language, he isn't putting in words for the common inch and foot, but rather the units that are respectively 1/100 and 1/10 the size of the Standard. His "inch" is actually a centimeter, and his "mile" is a kilometer, to within a fraction of a percent.
Wilkins also defined units of volume and weight measure. A cubic Standard was called a "bushel", and he had a "quart" (1/100 bushel, approximately 10 liters) and a "pint" (approximately one liter). For weight he defined the "hundred" as the weight of a bushel of distilled rainwater; this almost precisely the same as the original definition of the gram. A "pound" is then 1/100 hundred, or about ten kilograms. I don't understand why Wilkins' names are all off by a factor of ten; you'd think he would have wanted to make the quart be a millibushel, which would have been very close to a common quart, and the pound be the weight of a cubic foot of water (about a kilogram) instead of ten cubic feet of water (ten kilograms). But I've read this section over several times, and I'm pretty sure I didn't misunderstand.
Wilkins also based a decimal currency on his units of volume: a "talent" of gold or silver was a cubic standard. Talents were then divided by tens into hundreds, pounds, angels, shillings, pennies, and farthings. A silver penny was therefore 10-5 cubic Standard of silver. Once again, his scale seems off. A cubic Standard of silver weighs about 10.4 metric tonnes. Wilkins' silver penny is about is nearly ten cubic centimeters of metal, weighing 104 grams (about 3.5 troy ounces), and his farthing is 10.4 grams. A gold penny is about 191 grams, or more than six ounces of gold. For all its flaws, however, this is the earliest proposal I am aware of for a fully decimal system of weights and measures, predating the metric system, as I said, by about 110 years.
[Other articles in category /physics] permanent link
Fri, 17 Feb 2006
More on the frequency of vibrations in 1666 and other matters
In a series of earlier posts (1
2
3) I
discussed Robert Hooke's measurement of the frequency of G above
middle C: he determined that it was 272 beats per second. There are
two questions here: first, how did he do that, and second, why is his
answer so badly wrong? (Modern definitions make it about 384 hertz;
17th-century definitions differ, and vary among themselves, but not by
so much as that.)
The article Mr. Birchensha's Ear, by Benjamin Wardhaugh, provides the answers. In 1664, Hooke and the Royal Society set up a vibrating brass wire 136 feet long. It could be seen to vibrate once per second. Hooke divided it in half, and it vibrated twice per second. He truncated it to one foot, and the assembled musicians pronounced the sound to be a G below middle C. Since a wire one foot long vibrates 136 times as fast as one 136 feet long, we have the answer.
And the error? Partly just slop in the dividing and the estimation of the original frequency. Wardhaugh says:
In fact, the frequency is badly wrong (G has a frequency of 196 Hz), probably because Hooke was careless about the length of the pendulum that measured the time. In private he is meticulously precise, but maybe the details don't matter so much for Society showpieces.Pepys wasn't there, which is why he had to learn about it from Hooke in 1666.
The rest of the article is well worth reading:
Passers-by jeer at the useless toy: the pointlessness of the Royal Society's activities is already threatening to become proverbial. (Shadwell later wrote a comedy in which 'the Virtuoso' weighed air, swam on dry land and read by the light of a decaying fish. Poor Hooke went to see it and 'people almost pointed'.)The Royal Society is well-known to be the inspiration for the Grand Academy of Laputa in Gulliver's Travels, one of whose members "had been eight years upon a project for extracting sunbeams out of cucumbers...".
Reading the contents of Derham's 1726 collection of Hooke's papers on Wednesday, I was struck by the title "Hooke's Experiments on Floating of Lead". I was gearing up to write a blog post about how no real scientific paper has ever reminded me quite so much of the Grand Academy. But I abandoned the idea when I remembered that there is nothing unusual or surprising about being reminded of the grand Academy by a Royal Society paper. Also, the title only sounds silly until you learn that the paper itself is about the manner in which solid lead floats on molten lead.
 Final note: while searching for the title of the floating-lead paper
(which I left at home today) I learned something else interesting. In
South Philadelphia there is a playground attached to an antique "shot
tower". I had had no idea what a shot tower was, and I had supposed
it was a place for storing shot and gunpowder. But why build a
tower? It turns out it is the place where lead shot is manufactured.
You melt up a cauldron of lead at the top, then dump it through a
copper sieve and let it fall into a tub of water at the bottom. On
the way down, the molten lead turns into round shot. You sort it for
size and roundness, re-melt the ones that aren't round, and you have
your shot.
Final note: while searching for the title of the floating-lead paper
(which I left at home today) I learned something else interesting. In
South Philadelphia there is a playground attached to an antique "shot
tower". I had had no idea what a shot tower was, and I had supposed
it was a place for storing shot and gunpowder. But why build a
tower? It turns out it is the place where lead shot is manufactured.
You melt up a cauldron of lead at the top, then dump it through a
copper sieve and let it fall into a tub of water at the bottom. On
the way down, the molten lead turns into round shot. You sort it for
size and roundness, re-melt the ones that aren't round, and you have
your shot.
[ Addendum: More about this: [1] [2] [3] ]
[Other articles in category /physics] permanent link
Thu, 16 Feb 2006
More low-tech sound recording
In an
earlier post, I wondered how Robert Hooke could have discovered
the frequency of a vibrating string in 1664. I suggested a device
involving a bristle that traced a sinusoid on a smoked glass plate. I
was sure that I head heard about this somewhere before, and wasn't
making it up.
With the Wonders of the Internet, such things are easy to look up. Google for "bristle" and "smoked glass" and there you have it. The device is called a "phonautograph", and was invented in 1857 by Leon Scott. So the idea does work, but was probably not what Hooke used. My search continues.
The phonautograph was one of Alexander Graham Bell's inspirations for the telephone. Bell, whose principal research area was to improve education of deaf persons, built a phonautograph of his own, using—get this—an actual human ear. The bristle was attached to the ossicles. He cut away the stapes bone, and attached a wheat straw to the incus. I wonder whose ear he used?
I've read that a phonautograph recording survives from around 1860 and is the oldest known sound recording, although there was no way to play it back until recently, when the tracing was digitized and given to a computer to synthesize.
There was some talk a few years ago about the possibility that clay pots might retain recordings of the ambient sounds from the time they were created: they are thrown on potters' wheels that revolve at a uniform speed; they have high recording resolution, and are frequently worked with sharp tools that would have left grooves in them much like the grooves of phonograph records. I saw an exhibit of this in a science museum somewhere, but I could not make anything of the sound that they recovered from the pot, even though it had been specially constructed for the purpose. There are obvious, major problems with the idea, but it's nice to think that we might someday be able to listen to sound recordings of Sumerians chatting in the potter's workshop.
Come to think of it, conventional phonography was pretty low-tech itself, until the introduction of magnetic and later digital media.
[ Addendum: More about this: [1] [2] [4] ]
[Other articles in category /physics] permanent link
The rate of a vibrating string in 1666
In an earlier post, I discussed a report by Samuel Pepys, from 1666,
that Robert
Hooke claimed to be able to tell how often a fly beat its wings,
by comparing the pitch of the sound with that of a known source such
as a vibrating string. But I didn't know how he had determined the
rate at which the string vibrated. I guessed a couple of ways of
measuring this with 17th-century technology.
Clinton Pierce wrote to me with a clever and highly plausible suggestion: build a "buzzer". Take a spoked wheel, and spin it at a known rate, and hold some flexible object against the spokes. If the wheel spins, say, four times per second, and has 64 spokes, the buzzing will be a middle C. It should be possible to space the spokes evenly, and to spin the wheel uniformly at the correct speed.
My own idea involved attaching a bristle to the string, and letting it draw a sinusoid on a smoked glass plate that was drawn past it. The more I thought about the bristle, the more I was sure I had really read about it somewhere. This morning as I made breakfast, I asked myself "What is this 'bristle', anyway? Where do you get one?" and the answer came immediately "You pull it out of a hog." I'm sure I am recalling this and not just making it up. But I liked M. Pierce's suggestion much better than the bristle and smoked glass idea, because it seemed to me much more likely to work. What Hooke actually did, I still have no idea.
I did a little research today, and I have not yet been able to find out how Hooke measured the frequency of a vibrating string. But I have been able to get some information.
Hooke died in 1703. Many of his papers were given to Richard Waller, and in 1705 Waller published Posthumous Works of Dr. Robert Hooke. As an introduction, Waller wrote "The Life of Dr. Robert Hooke", an itemization of every important research or contribution made by Hooke. Two of the entries are as follows:
In July 1664. he produc'd an Experement to shew the number of Vibrations of an extended String, made in a determinate time, requisite to make a certain Tone or Note, by which it was found that a Wire making two hundred seventy two vibrations in one Second of Time, founded G Sol Re Ut in the Scale of all Musick.(We would make it 384 vibrations; 272 is only C#. Whether this is due to a change in the definition of G, or experimental error, or both, I do not know. But it does resolve my question of whether Hooke did have a specific number for the rate at which a fly beat its wings, or whether he just identified it as low D and left it at that.)
[ Addendum 20060216: I realized this morning that it might also be caused by a change in the length of the second. ]
[ Addendum 20070917: I realized sometime later that this was a dumb suggestion. One second is 1/86400 of a day, then as it is now, and the length of the day has not changed significantly since 1664. ]
In July [1680] he shew'd a way of making Musical and other Sounds, by the striking of the Teeth of several Brass Wheels, proportionaly cut as to their numbers, and turned very fast round, in which it was observable, that the equal or proprtional stroaks of the Teeth, that is, 2 to 1, 4 to 3, &c. made the Musical Notes, but the unequal stroaks of the Teeth more answer'd the sound of the Voice in speaking.There we have it: He didn't think of the buzzing rotating wheel until 1680, so he must have been doing something else in 1664. What, I do not yet know.
[ Addendum: More about this: [1] [3] [4] ]
[Other articles in category /physics] permanent link
Tue, 14 Feb 2006 I was leafing through The Diary of Samuel Pepys recently. Pepys, in case you hadn't heard, was an official of the Royal Navy in England in the 17th century. He kept a meticulous diary, in which he recorded all sorts of trivia about what he did, who he saw, what he liked and didn't, what he ate and drank, and so on. It gives a wonderfully clear picture of life in London at the time. (The diary is available online; the version linked to the right is selections only. If you want to buy a paper copy of the complete diary, get it used, or it will be absurdly expensive. I got my copy at a library sale.)The diary is a good book for browsing. Someday I'd like to read a long stretch of it and try to get a sense of the history and continuity of what's going on. But in the meantime, it's still good for browsing. Every few pages you run into something fascinating. Here's what I ran into today:
August 8th, 1666. Discoursed with Mr. Hooke, whom I met in the streete, about the nature of sounds, and he did make me understand the nature of musicall sounds made by strings, mighty prettily; and told me that having come to a certain number of vibrations proper to make any tone, he is able to tell how many strokes a fly makes with her wings (those flies that hum in their flying) by the note that it answers to in musique, during their flying.Mr. Hooke, I hardly need tell you, is Robert Hooke, a groundbreaking scientist, and secretary of the (then newly-formed) Royal Society. (Pepys was later a member of the Society, and, still later, its president.) Hooke is responsible for Hooke's law, which states that the force exerted by a spring is proportional to the distance by which it has been extended or compressed from its natural length. He is also responsible for the use of the word "cell" to describe living cells.
This passage struck me first because it seemed so simple and clever to determine the rate at which a fly's wings beat by comparing the sound with that of a vibrating string. But as I thought about it more, it grew more puzzling. How do you know that a certain string, a middle C, say, is vibrating 256 times per second? How can you measure that with only 17th-century technology?
My first thought was that you can attach a bristle to the string, and then draw a piece of smoked glass under the bristle as the string vibrates; the bristle will leave a track on the glass. I seem to recall having heard of this being done at some time, but I can't remember the details. I'm also not sure that it could be done accurately enough. If you can pull a foot of glass past the bristle in one second, and the string is a middle C, then the bristle will trace a sinusoid whose peaks are about 1/21 inch apart, which is enough to measure. It seems plausible that something like this might be made to work with 17th-century technology. I think the sticking point would be moving the glass at a uniform speed. I don't think they had accurately machined screws yet.
So far the only other thing I have been able to think of is that since the relationship between the mass, tension, length, and pitch of a vibrating string was already known, Hooke measured some slow, massive vibrating rope, and then measured the tension, mass, and length of the string and extrapolated the vibrational rate from that. Perhaps there was a more direct method, but I don't know what it was.
These days you would just hold up a microphone that was plugged into an oscilliscope, or shine an adjustable strobe light on the fly. But you had to be pretty clever to carry out useful physics experiments in 1666.
That's one of the things that always amazes me about historical physics. The equipment was so crappy, it seems almost miraculous that they figured out anything at all. Consider the Greeks, who figured out that the moon shines by the reflected light of the sun. Presumably this idea originated in the observation that the lit side of the moon always faces the sun. But that's not all they did. They observed that the shape of the illuminated area was consistent with the shape you would see if part of a sphere was illuminated from without. Who the heck noticed that? They could presumably make spheres out of clay, but they didn't have any reliable, steady, directed light source. Candles flicker. So who got the idea to look at partially illuminated spherical wads of clay, and then went to the trouble of setting up the light source so they could examine the shape of the illuminated area?
[ Addendum: More about this: [2] [3] [4] ]
[Other articles in category /physics] permanent link
Mon, 16 Jan 2006It's with some trepidation that I'm starting this section of my blog, because I really don't understand physics very well. Most of it, I suspect, will be about how little I understand. But I'm going to give it a whirl.
Sometime this summer it occurred to me that the phenomenon of transparency is more more complex than one might initially think, and more so than most people realize. I went around asking people with more physics education than I had if they could explain to me why things like glass and water are transparent, and it seemed to me that not only did they not understand it any better than I did, but they didn't realize that they didn't understand it.
A common response, for example, was that media like glass and water are transparent because the light passes through them unimpeded. This is clearly wrong. We can see that it's wrong because both glass and water have a tendency to refract incident light. Unimpeded photons always travel in straight lines. If light is refracted by a medium, it is because the photons couple with electrons in the medium, are absorbed, and then new photons are emitted later, going in a different direction. So the photons are being absorbed; they are not passing through the water unimpeded. (Similarly, light passes more slowly though glass and water than it does through vacuum, because of the time taken up by the interactions between the photons and the electrons. If the photons were unimpeded by electromagnetic effects, they would pass through with speed c.)
Sometimes the physics students tell me that some of the photons interact, but the rest pass through unimpeded. This is not the case either. If some of the photons were unimpeded when passing through water or glass, then you would see two images of the other side: one refracted, and one not. But you don't; you see only one image. (Some photons are reflected completely, so you do see two images: a reflected one, and a transmitted one. But if photons were refracted internally as well as being transmitted unimpeded, there would be two transmitted images.) This demonstrates that all the photons are interacting with the medium.
The no-interference explanation is correct for a vacuum, of course. Vacuum is transparent because the photons pass through it with no interaction. So there are actually two separate phenomena that both go by the name of "transparency". The way in which vacuum is transparent is physically different from the way in which glass is transparent. I don't know which of these phenomena is responsible for the transparency of air.
Now, here is the thing that was really puzzling me about glass and water. For transparency, you need the photons to come out of the medium going in the same direction as they went in. If photons are scattered in all different directions, you get a translucent or opaque medium. Transparency is only achieved when the photons that come out have the same velocity and frequency as those going in, or at least when the outgoing velocity depends in some simple fashion on the incoming velocity, as with a lens.
Since the photon that comes out of glass is going in the exact same direction as the photon that went in, something very interesting is happening inside the glass. The photon reaches the glass and is immediately absorbed by an electron. Sometime later, the electron emits a new photon. The new photon is travelling in exactly the same direction as the old photon. The new photon is absorbed by the next electron, which later emits another photon, again travelling in the exact same direction. This process repeats billions of times until the final photon is ejected on the other side of the glass, still in the exact same direction, and goes on its way.
Even a tiny amount of random scattering of the photons would disrupt the transparency completely. So, I thought, I would expect to find transparency in media that have a very rigid crystalline structure, so that the electromagnetic interactions would be exactly the same at each step. But in fact we find transparency not in crystalline substances, such as metals, but rather in amorphous ones, like glass and water! This was the big puzzle for me. How can it be that the photon always comes out in the same direction that it went in, even though it was wandering about inside of glass or water, which have random internal structures?
Nobody has been able to give me a convincing explanation of this. After much pondering, I have decided that it is probably due to conservation of relativistic momentum. Because of quantum constraints, the electron can only emit a new photon of the same energy as the incoming photon. Because the electron is bound in an atom, its own momentum cannot change, so conservation of momentum requires that the outgoing photon have the same velocity as the incoming one.
I would like to have this confirmed by someone who really understands physics. So far, though, I haven't met anyone like that! I'm thinking that I should start attending physics colloquia at the University of Pennsylvania and see if I can buttonhole a couple of solid-state physics professors. Even if I don't buttonhole anyone, going to the colloquia might be useful and interesting. I should write a blog post about why it's easier to learn stuff from a colloquium than from a book.
[ Update 20231128: Jez Humble posted (in 2007) [an answer to this](https://jezhumble.net/2007/01/07/the-nature-of-transparency.html). If I understand it correctly, the answer is, in fact, because of the conservation of momentum as I guessed above. See the next-to-last paragraph of M. Humble's explanation. ][Other articles in category /physics] permanent link



