Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sat, 02 Dec 2023
Content warning: grumpy complaining. This was a frustrating month.
Need an intuitive example for how "P is necessary for Q" means "Q⇒P"?
This kind of thing comes up pretty often. Why are there so many ways that the logical expression !!Q\implies P!! can appear in natural language?
- If !!Q!!, then !!P!!
- !!Q!! implies !!P!!
- !!P!! if !!Q!!
- !!Q!! is sufficient for !!P!!
- !!P!! is necessary for !!Q!!
Strange, isn't it? !!Q\land P!! is much simpler: “Both !!Q!! and !!P!! are true” is pretty much it.
Anyway this person wanted an intuitive example of “!!P!! is necessary for !!Q!!”
I suggested:
Suppose that it is necessary to have a ticket (!!P!!) in order to board a certain train (!!Q!!). That is, if you board the train (!!Q!!), then you have a ticket (!!P!!).
Again this follows the principle that rule enforcement is a good thing when you are looking for intuitive examples. Keeping ticketless people off the train is something that the primate brain is wired up to do well.
My first draft had “board a train” in place of “board a certain train”. One commenter complained:
many people travel on trains without a ticket, worldwide
I was (and am) quite disgusted by this pettifogging.
I said “Suppose that…”. I was not claiming that the condition applies to every train in all of history.
OP had only asked for an example, not some universal principle.
Does ...999.999... = 0?
This person is asking one of those questions that often puts Math StackExchange into the mode of insisting that the idea is completely nonsensical, when it is actually very close to perfectly mundane mathematics. (Previously: [1] [2] [3] ) That didn't happen this time, which I found very gratifying.
Normally, decimal numerals have a finite integer part on the left of the decimal point, and an infinite fractional part on the right of the decimal point, as with (for example) !!\frac{13}{3} = 4.333\ldots!!. It turns out to work surprisingly well to reverse this, allowing an infinite integer part on the left and a finite fractional part on the right, for example !!\frac25 = \ldots 333.4!!. For technical reasons we usually do this in base !!p!! where !!p!! is prime; it doesn't work as well in base !!10!!. But it works well enough to use: If we have the base-10 numeral !!\ldots 9999.0!! and we add !!1!!, using the ordinary elementary-school right-to-left addition algorithm, the carry in the units place goes to the tens place as usual, then the next carry goes to the hundreds place and so on to infinity, leaving us with !!\ldots 0000.0!!, so that !!\ldots 9999.0!! can be considered a representation of the number !!-1!!, and that means we don't need negation signs.
In fact this system is fundamental to the way numbers are represented in computer arithmetic. Inside the computer the integer !!-1!! is literally represented as the base-2 numeral !!11111111\;11111111\;11111111\;11111111!!, and when we add !!1!! to it the carry bit wanders off toward infinity on the left. (In the computer the numeral is finite, so we simulate infinity by just discarding the carry bit when it gets too far away.)
Once you've seen this a very reasonable next question is whether you can have numbers that have an infinite sequence of digits on both sides. I think something goes wrong here — for one thing it is no longer clear how to actually do arithmetic. For the infinite-to-the-left numerals arithmetic is straightforward (elementary-school algorithms go right-to-left anyway) and for the standard infinite-to-the-right numerals we can sort of fudge it. (Try multiplying the infinite decimal for !!\sqrt 2!! by itself and see what trouble you get into. Or simpler: What's !!4.666\ldots \times 3!!?)
OP's actual question was: If !!\ldots 9999.0 !! can be considered to represent !!-1!!, and if !!0.9999\ldots!! can be considered to represent !!1!!, can we add them and conclude that !!\ldots 9999.9999\ldots = 0!!?
This very deserving question got a good answer from someone who was not me. This was a relief, because my shameful answer was pure shitpostery. It should have been heavily downvoted, but wasn't. The gods of Math SE karma are capricious.
Why define addition with successor?
Ugh, so annoying. OP had read (Bertrand Russell's explanation of) the Peano definition of addition, and did not understand it. Several people tried hard to explain, but communication was not happening. Or, perhaps, OP was more interested in having an argument than in arriving at an understanding. I lost a bit of my temper when they claimed:
Russell's so-called definition of addition (as quoted in my question) is nothing but a tautology: ….
I didn't say:
If you think Bertrand Russell is stupid, it's because you're stupid.
although I wanted to at first. The reply I did make is still not as measured as I would like, and although it leaves this point implicit, the point is still there. I did at least shut up after that. I had answered OP's question as well as I was able, and carrying on a complex discussion in the comments is almost never of value.
Why is Ramanujan considered a great mathematician?
This was easily my best answer of the month, but the question was deleted, so you will only be able to see it if you have enough Math SE reputation.
OP asked a perfectly reasonable question: Ramanujan gets a lot of media hype for stuff like this:
$${\sqrt {\phi +2}}-\phi ={\cfrac {e^{{-2\pi /5}}}{1+{\cfrac {e^{{-2\pi }}}{1+{\cfrac {e^{{-4\pi }}}{1+{\cfrac {e^{{-6\pi }}}{1+\,\cdots }}}}}}}}$$
which is not of any obvious use, so “why is it given such high regard?”
OP appeared to be impugning a famous mathematician, and Math SE always responds badly to that; their heroes must not be questioned. And even worse, OP mentioned the notorious non-fact that $$1+2+3+\ldots =-\frac1{12}$$ which drives Math SE people into a frothing rage.
One commenter argued:
Mathematics is not inherently about its "usefulness". Even if you can't find practical use for those formulas, you still have to admit that they are by no means trivial
I think this is fatuous. OP is right here, and the commenter is wrong. Mathematicians are not considered great because they produce wacky and impractical equations. They are considered great because they solve problems, invent techniques that answer previously impossible questions, and because they contribute insights into deep and complex issues.
Some blockhead even said:
Most of the mathematical results are useless. Mathematics is more like an art.
Bullshit. Mathematics is about trying to understand stuff, not about taping a banana to the wall. I replied:
I don't think “mathematics is not inherently about its usefulness" is an apt answer here. Sometimes mathematical results have application to physics or engineering. But for many mathematical results the application is to other parts of mathematics, and mathematicians do judge the ‘usefulness’ of results on this basis. Consider for example Mochizuki's field of “inter-universal Teichmüller theory”. This was considered interesting only as long as it appeared that it might provide a way to prove the !!abc!! conjecture. When that hope collapsed, everyone lost interest in it.
My answer to OP elaborated on this point:
The point of these formulas wasn't that they were useful in themselves. It's that in order to find them he had to have a deep understanding of matters that were previously unknown. His contribution was the deep understanding.
I then discussed Hardy's book on the work he did with Ramanujan and Hardy's own estimation of Ramanujan's work:
The first chapter is somewhat negative, as it summarizes the parts of Ramanujan's work that he felt didn't have lasting value — because Hardy's next eleven chapters are about the work that he felt did have value.
So if OP wanted a substantive and detailed answer to their question, that would be the first place to look.
I also did an arXiv search for “Ramanujan” and found many recent references, including one with “applications to the Ramanujan !!τ!!-function”, and concluded:
The !!\tau!!-function is the subject of the entire chapter 10 of Hardy's book and appears to still be of interest as recently as last Monday.
The question was closed as “opinion-based” (a criticism that I think my answer completely demolishes) and then it was deleted. Now if someone else trying to find out why Ramanujan is held in high regard they will not be able to find my factual, substantive answer.
Screw you, Math SE. This month we both sucked.
[Other articles in category /math/se] permanent link
Fri, 24 Nov 2023
Math SE report 2023-09: Sense and reference, Wason tasks, what is a sequence?
Proving there is only one proof?
OP asks:
In mathematics, is it possible to prove that there is only one (shortest) proof of a given theorem (say, in ZFC)?
This was actually from back in July, when there was a fairly substantive answer. But it left out what I thought was a simpler, non-substantive answer: For a given theorem !!T!! it's actually quite simple to prove that there is (or isn't) only one proof of !!T!!: just generate all possible proofs in order by length until you find the shortest proofs of !!T!!, and then stop before you generate anything longer than those. There are difficult and subtle issues in provability theory, but this isn't one of them.
I say “non-substantive” because it doesn't address any of the possibly interesting questions of why a theorem would have only one proof, or multiple proofs, or what those proofs would look like, or anything like that. It just answers the question given: is it possible to prove that there is only one shortest proof.
So depending on what OP was looking for, it might be very unsatisfying. Or it might be hugely enlightening, to discover that this seemingly complicated question actually has a simple answer, just because proofs can be systematically enumerated.
This comes in handy in more interesting contexts. Gödel showed that arithmetic contains a theorem whose shortest proof is at least one million steps long! He did it by constructing an arithmetic formula !!G!! which can be interpreted as saying:
!!G!! cannot be proved in less than one million steps.
If !!G!! is false, it can be proved (in less than one million steps) and our system is inconsistent. So assuming that our axioms are consistent, then !!G!! is true and either:
- There is no proof of at all of !!G!!, or
- There are proofs of !!G!! but the shortest one is at least a million steps
Which is it? It can't be (1) because there is a proof of !!G!!: simply generate every single proof of one million steps or fewer, and check at the last line of each one to make sure that it is not !!G!!. So it must be (2).
What counts as a sequence, and how would we know that it isn't deceiving?
This is a philosophical question: What is a sequence, really? And:
if I write down random numbers with no pattern at all except for the fact that it gets larger, is it a viable sequence?
And several other related questions that are actually rather subtle: Is a sequence defined by its elements, or by some external rule? If the former how can you know when a sequence is linear, when you can only hope to examine a finite prefix?
I this is a great question because I think a sequence, properly construed, is both a rule and its elements. The definition says that a sequence of elements of !!S!! is simply a function !!f:\Bbb N\to S!!. This definition is a sort of spherical cow: it's a nice, simple model that captures many of the mathematical essentials of the thing being modeled. It works well for many purposes, but you get into trouble if you forget that it's just a model. It captures the denotation, but not the sense. I wouldn't yak so much about this if it wasn't so often forgotten. But the sense is the interesting part. If you forget about it, you lose the ability to ask questions like
Are sequences !!s_1!! and !!s_2!! the same sequence?
If all you have is the denotation, there's only one way to answer this question:
By definition, yes, if and only if !!s_1!! and !!s_2!! are the same function.
and there is nothing further to say about it. The question is pointless and the answer is useless. Sometimes the meaning is hidden a little deeper. Not this time. If we push down into the denotation, hoping for meaning, we find nothing but more emptiness:
Q: What does it mean to say that !!s_1!! and !!s_2!! are the same function?
A: It means that the sets $$S_1 = \{ \langle i, s_1(i) \rangle \mid i\in \Bbb N\}$$ and $$S_2 = \{ \langle i, s_2(i) \rangle \mid i\in \Bbb N\}$$ have exactly the same elements.
We could keep going down this road, but it goes nowhere and having gotten to the end we would have seen nothing worth seeing.
But we do ask and answer this kind of question all the time. For example:
- !!S_1(n)!! is the infinite sequence of odd numbers starting at !!1!!
- !!S_2(n)!! is the infinite sequence of numbers that are the difference between a square and its previous square, starting at !!1^2-0^2!!
Are sequences !!S_1!! and !!S_2!! the same sequence? Yes, yes, of course they are, don't focus on the answer. Focus on the question! What is this question actually asking?
The real essence of the question is not about the denotation, about just the elements. Rather: we're given descriptions of two possible computations, and the question is asking if these two computations will arrive at the same results in each case. That's the real question.
Well, I started this blog article back in October and it's still not ready because I got stuck writing about this question. I think the answer I gave on SE is pretty good, OP asked what is essentially a philosophical question and the backbone of my answer is on the level of philosophy rather than mathematics.
[ Addendum: On review, I am pleasantly surprised that this section of the blog post turned out both coherent and relevant. I really expected it to be neither. A Thanksgiving miracle! ]
Can inequalities be added the way that equations can be added?
OP says:
Suppose you have !!x + y > 6!! and !!x - y > 4!!. Adding the inequalities, the !!y!! terms cancel and you end up with … !!x > 5!!. It is not intuitively obvious to me that this holds true … I can see that you can't subtract inequalities, but is it always okay to add them?
I have a theory that if someone is having trouble with the intuitive meaning of some mathematical property, it's a good idea to turn it into a question about fair allocation of resources, or who has more of some commodity, because human brains are good at monkey tasks like seeing who got cheated when the bananas were shared out.
About ten years ago someone asked for an intuitive explanation of why you could add !!\frac a2!! to both sides of !!\frac a2 < \frac b2!! to get !!\frac a2+\frac a2 < \frac a2 + \frac b2!!. I said:
Say I have half a bag of cookies, that's !!\frac a2!! cookies, and you have half a carton of cookies, that's !!\frac b2!! cookies, and the carton is bigger than the bag, so you have more than me, so that !!\frac a2 < \frac b2!!.
Now a friendly djinn comes along and gives you another half a bag of cookies, !!\frac a2!!. And to be fair he gives me half a bag too, also !!\frac a2!!.
So you had more cookies before, and the djinn gave each of us an extra half a bag. Then who has more now?
I tried something similar this time around:
Say you have two bags of cookies, !!a!! and !!b!!. A friendly baker comes by and offers to trade with you: you will give the baker your bag !!a!! and in return you will get a larger bag !!c!! which contains more cookies. That is, !! a \lt c !!. You like cookies, so you agree.
Then the baker also trades your bag !!b!! for a bigger bag !!d!!.
Is it possible that you might not have more cookies than before you made the trades? … But that's what it would mean if !! a\lt c !! and !! b\lt d !! but not !! a+b \lt c+d !! too.
Someday I'll write up a whole blog article about this idea, that puzzles in arithmetic sometimes become intuitively obvious when you turn them into questions about money or commodities, and that puzzles in logic sometimes become intuitively obvious when you turn them into questions about contract and rule compliance.
I don't remember why I decided to replace the djinn with a baker this time around. The cookies stayed the same though. I like cookies. Here's another cookie example, this time to explain why !!1\div 0.5 = 2!!.
What is the difference between "for all" and "there exists" in set builder notation?
This is the same sort of thing again. OP was was asking about
$$B = \{n \in \mathbb{N} : \forall x \in \mathbb{N} \text{ and } n=2^x\}$$
but attempting to understand this is trying to swallow two pills at once. One pill is the logic part (what role is the !!\forall!! playing) and the other pill is the arithmetic part having to do with powers of !!2!!. If you're trying to understand the logic part and you don't have an instantaneous understanding of powers of !!2!!, it can be helpful to simplify matters by replacing the arithmetic with something you understand intuitively. In place of the relation !!a = 2^b!! I like to use the relation “!!a!! is the mother of !!b!!”, which everyone already knows.
Are infinities included in the closure of the real set !!\overline{\mathbb{R}}!!
This is a good question by the Chip Buchholtz criterion: The answer is much longer than the question was. OP wants to know if the closure of !!\Bbb R!! is just !!\Bbb R!! or if it's some larger set like !![-\infty, \infty]!!. They are running up against the idea that topological closure is not an absolute notion; it only makes sense in the context of an enclosing space.
I tried to draw an analogy between the closure and the complement of a set: Does the complement of the real numbers include the number !!i!!? Well, it depends on the context.
OP preferred someone else's answer, and I did too, saying:
I thought your answer was better because it hit all the important issues more succinctly!
I try to make things very explicit, but the downside of that is that it makes my answers longer, and shorter is generally better than longer. Sometimes it works, and sometimes it doesn't.
Vacuous falsehood - does it exist, and are there examples?
I really liked this question because I learned something from it. It brought me up short: “Huh,” I said. “I never thought about that.” Three people downvoted the question, I have no idea why.
I didn't know what a vacuous falsity would be either but I decided that since the negation of a vacuous truth would be false it was probably the first thing to look at. I pulled out my stock example of vacuous truth, which is:
All my rubies are red.
This is true, because all rubies are red, but vacuously so because I don't own any rubies.
Since this is a vacuous truth, negating it ought to give us a vacuous falsity, if there is such a thing:
I have a ruby that isn't red.
This is indeed false. And not in the way one would expect! A more typical false claim of this type would be:
I have a belt that isn't leather.
This is also false, in rather a different way. It's false, but not vacuously so, because to disprove it you have to get my belts out of the closet and examine them.
Now though I'm not sure I gave the right explanation in my answer. I said:
In the vacuously false case we don't even need to read the second half of the sentence:
there is a ruby in my vault that …… The irrelevance of the “…is not red” part is mirrored exactly in the irrelevance of the “… are red” part in the vacuously true statement:
all the rubies in my vault are …
But is this the right analogy? I could have gone the other way:
In the vacuously false case we don't even need to read the first half of the sentence:
there is a ruby … that is not red… The irrelevance of the “… in my vault …” part is mirrored exactly in the irrelevance of the “… are red” part in the vacuously true statement:
all the rubies in my vault are …
Ah well, this article has been drying out on the shelf for a month now, I'm making an editorial decision to publish it without thinking about it any more.
[Other articles in category /math/se] permanent link
Tue, 05 Sep 2023
Math SE report 2023-06: funky-looking Hasse diagrams, and what is a polynomial anyway?
Is !!x^4-x^4 = 0!! a fourth-degree equation?
This is actually a really good question! (You can tell because it's quick to ask and complicated to answer.) It goes back to a very fundamental problem that beginners in mathematics, which is that there is a difference between an object's true nature and the way it happens to be written down. And often these problems are compounded because there is no way to talk about the object except by referring to how it is written down.
OP says:
The best definition I could find for the degree of an equation is the following:
The highest power of the unknown term whose coefficient isn't zero in a given equation
And they are bothered by this, and rightly so. I was almost derailed at this point into writing an article about what an equation is, but I'm going to put it off for another day, because I think to get to this person's question what we really need to do is to say what a polynomial is.
One way is to describe it as an expression in a certain form, but this is a bit roundabout. It's like describing a rational number as an expression of the form !!\frac n d!! where !!n!! and !!d!! are relatively prime integers. Under this sort of definition, !!x^4-x^4!! isn't a polynomial at all, because it's not an expression of the correct form.
But I think the right way to define a polynomial is that it's an element of the free ring over some ring !!C!! of coefficients. This leaves completely open the question of how a polynomial is written, or what it looks like. It becomes a theorem that polynomials are in one-to-one correspondence with finite sequences of elements of !!C!!. Then we can say that the “degree” of a polynomial is one less than the length of the corresponding finite sequence, or something like that.
[ Sometimes we make an exception for the zero polynomial and say its degree is !!-\infty!!, to preserve the law !!\operatorname{deg}(pq) = \operatorname{deg}(p)+\operatorname{deg}(q)!!.) ]
In this view the zero polynomial is simply the zero element of the ring. The polynomial called “!!x^4!!” is the fourth power of the free element !!x!!.
Since the polynomials are elements of a ring, addition, subtraction, and multiplication come along automatically, and we can discuss the value of the expression !!x^4-x^4!!, which by the usual properties of !!-!! is also the zero polynomial.
Anyway that all is pretty much what I said:
!!x^4-x^4!! is just a way to write the polynomial !!0!!, which is not a fourth-degree polynomial. Similarly !!x^5+x^4-x^5!! is not a fifth-degree polynomial.
There's an underlying reality here, the abstract elements of the ring !!R[x]!!. And then there's a representation theorem, which is that elements of !!R[x]!! are in one-to-one correspondence with finite sequences of elements of !!R!!. The ring laws give us ways to normalize arbitrary expressions involving polynomials. And then there's also the important functor that turns every polynomial ring into a ring of functions, turning the polynomial !!x^4!! into the function !!x\mapsto x^4!!.
This kind of abstract approach isn't usually explained in secondary or tertiary education, and I'm not sure it would be an improvement if it were. (You'd have to explain rings, for one thing.) But the main conceptual point is that there is a difference between the thing itself (say, !!x^4!!) and the way we happen to write the thing (say, !!x^5+x^4-x^5!!), and some properties are properties of the thing itself and others are properties of expressions, of the way the thing has been written. The degree of a polynomial is a property of the thing itself, not of the way it happens to be written, so both of those expressions are ways to write the same polynomial, which is fourth-degree, regardless of the fact that in one of them, “the highest power of the unknown term whose coefficient isn't zero” is five.
There is one example of this abstraction that everyone learns in childhood, rational numbers. I lean hard on this example, because most people know it pretty well, even if they don't realize it yet. !!\frac15!! and !!\frac6{30}!! are the same thing, written in two different ways. Mathematicians will, without even thinking about it, speak of the numerator of a rational number, and without batting an eyelash will say that the numerator of the rational number !!\frac{6}{30}!! is !!1!!. The fraction !!\frac6{30}!! is a mere notation that represents a rational number, in this case the rational number !!\frac15!!, and this rational number has a numerator of !!1!!.
Beginning (and intermediate) computer programmers also have this issue, that the thing itself, usually some embedding of data in the computer's memory, may be serialized into a string in multiple ways. There's a string that represents the thing, and then there's the thing itself, but it's hard to talk about the thing itself because anything you can write is a string. I wish this were made explicit in CS education. Computer programmers who don't pick up on this crucial point, at least on an intuitive level, do not progress past intermediate.
What are the names given to statements that can be true or false?
I think I totally flubbed this one. OP is really concerned with open and closed formulas. For example, “!!x > 2!!” is true, or false, depending on the value of !!x!!. And OP astutely noted that while “!!x>4 \to x> 2!!” is always true, its meaning still depends on the value of !!x!!.
I did get around to explaining that part of the issue, eventually. The crucial point, which is that there are formulas which may have free variables and then there are statements which do not, is buried at the end after a lot of barely-relevant blather about Quinian quasiquotation. What was I thinking? Perhaps I should go back and shorten the answer to just the relevant part.
How does one identify the weakest preconditions in Hoare triples?
I wrote a detailed explanation of how one identifies weakest
preconditions in Hoare triples, before realizing that actually OP
understood this perfectly, and their
confusion was because their book wrote “{x≠1}” where it should have
had “{x≠-1}”.
Sheesh.
Artifacts of mathematical logic
This was fun. OP wants actual physical artifacts that embody concepts from mathematical logic, the way one models of the platonic solids embody concepts from solid geometry.
I couldn't think of anything good, but then Michael Weiss brought up Lewis Carroll's Game of Logic. This reminded me that Martin Gardner had written a book about embodiments of simple logic, including the Carroll one, so I mentioned that. It's a fun book. Check out the account of Ramon Llull, who missed being canonized because his martyrdom looked a bit too much like FAFO.
I find this answer a little unsatisfying though. The logic machines in Gardner's book do only a little boolean algebra, or maybe at best a tiny bit of predicate logic. But I'd love to see a physical system that somehow encapsulated sequent calculus or natural deduction or something like that. Wouldn't it be cool to have blocks stuck together with magnets or physical couplings, and if you could physically detach the !!B!! from !!A\to B!! only if you already had an assemblage that matched !!A!! exactly? I have no idea how you'd do it. Maybe a linear logic model would be more feasible: once you used !!A!! with !!A\to B!! to get !!B!!, you wouldn't be able to use either one again.
We need some genius to come and invent some astonishing mechanism that formerly seemed impossible. I wonder if Ernő Rubik is available?
Joachim Breitner's Incredible Proof Machine is a fun thing along these lines, but it's not at all an artifact.
Is there a name for this refinement of the subset ordering?
This was my question. I've never seen this ordering elsewhere, but it has a simple description. We start with a totally ordered finite set !!S!!. Then if !!A!! and !!B!! are subsets of !!S!!, we deem !!A \preceq B!! if there is an injective mapping !!f:A\to B!! where !!a \le f(a)!! for each !!a\in A!!.
So for example, if !!S!! has three elements !!a\lt b\lt c!! then the ordering I want, on !!2^S!!, has this Hasse diagram:
!!\{b\}\prec\{a,b\}!! because we can match the !!b!!'s. And !!\{a,b\}\prec \{a, c\}!! because we can match !!a!! with !!a!! and !!b!! with !!c!!. But !!\{c\}\not\prec\{a, b\}!! because we can't match !!c!! with either !!a!! or with !!b!!, and !!\{a,b\}\not\prec\{c\}!! because, while we can match either of !!a!! or !!b!! with !!c!!, we aren't allowed to match both of them with !!c!!.
Here's the corresponding Hasse diagram for !!|S|=4!!:
Maybe a better way to describe this is: the bottom element is !!\varnothing!!. To go up the lattice one step, you either increment one of the elements of the current set, or you insert an !!a!! if there isn't one already. So from !!\{b,d\}!! you can either increment the !!b!! to move up to !!\{c, d\}!! or you can insert an !!a!! to move up to !!\{a, b, d\}!!.
This ordering comes up in connection with a problem I've thought about a lot: Say you have a number !!N!! and you want to find !!AB=N!! with !!A!! and !!B!! as close together as possible. Even if you have the prime factorization of !!N!! available, it's not usually clear what the answer is. (In general it's NP-hard.)
If !!N!! is the product of two primes, !!N=p_1p_2!! the answer is obvious. And if !!N!! is a product of three primes !!N =p_1p_2p_3!! there is a definitive answer. Without loss of generality, !!p_1 ≤ p_2 ≤ p_3!!, and the answer is simply that !!A=p_1p_2, B=p_3!! is always optimal.
But if !!N =p_1p_2p_3p_4!! it can go two different ways. Assuming !!p_1 ≤ p_2 ≤ p_3 ≤ p_4!!, it usually turns out that the optimal solution is !!A=p_1p_4, B=p_2p_3!!. But sometimes the optimal solution is !!A=p_1p_2p_3, B=p_4!!. These are the only two possibilities.
Which ways of splitting the prime factors might be optimal relates to those Hasse diagrams above. The possibly-optimal splits between !!A!! and !!B!! correspond to nodes that are just at the boundary of the left and right halves of the diagram.
Nobody had an answer for what this order was called, so I could not look it up. This is OK, I will figure it all out eventually.
[Other articles in category /math/se] permanent link
Fri, 09 Jun 2023
Math SE report 2023-05: Arguments that don't work, why I am a potato, and set theory as a monastery
How to shift a power series to be centered at !!a!!?
OP observed that while the Taylor series for !!\sin x!!, centered at zero, is a good approximation near !!x=0!!, it is quite inaccurate for computing !!\sin 4!!:
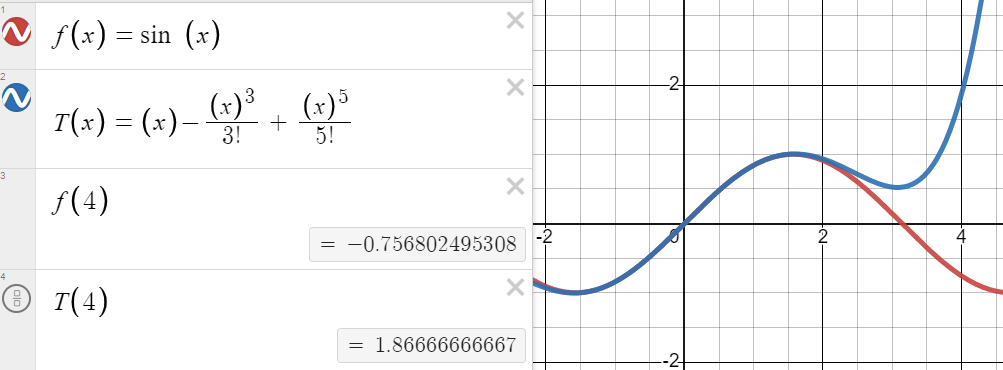
They wanted to know how to use it to compute a good approximation for !!\sin 4!!. But the Taylor series centered around !!4!! is no good for this, because it only tells you that when !!x!! is close to !!4!!, $$\sin x \approx \sin 4 + (x-4)\cos 4 + \ldots, $$ which is obviously useless: put !!x=4!! and you get !!\sin 4 = \sin 4!!.
I'd written about Taylor series centering at some length before, but that answer was too long and detailed to repeat this time. It was about theory (why do we do it at all) and not about computation.
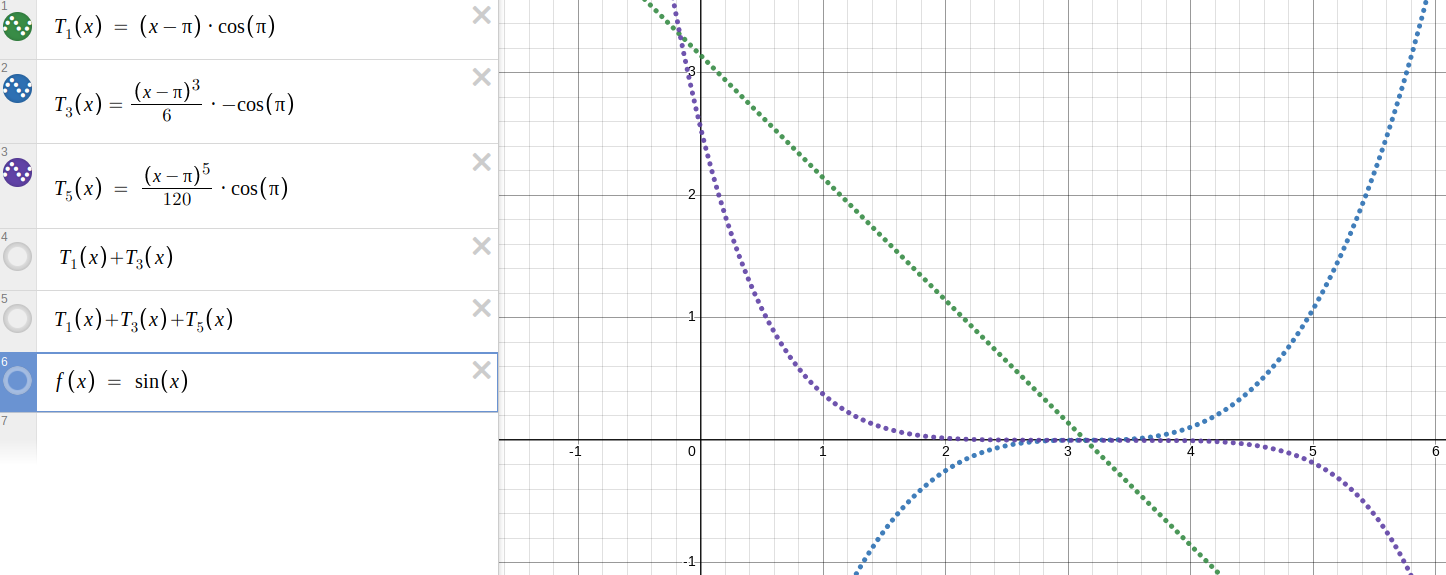
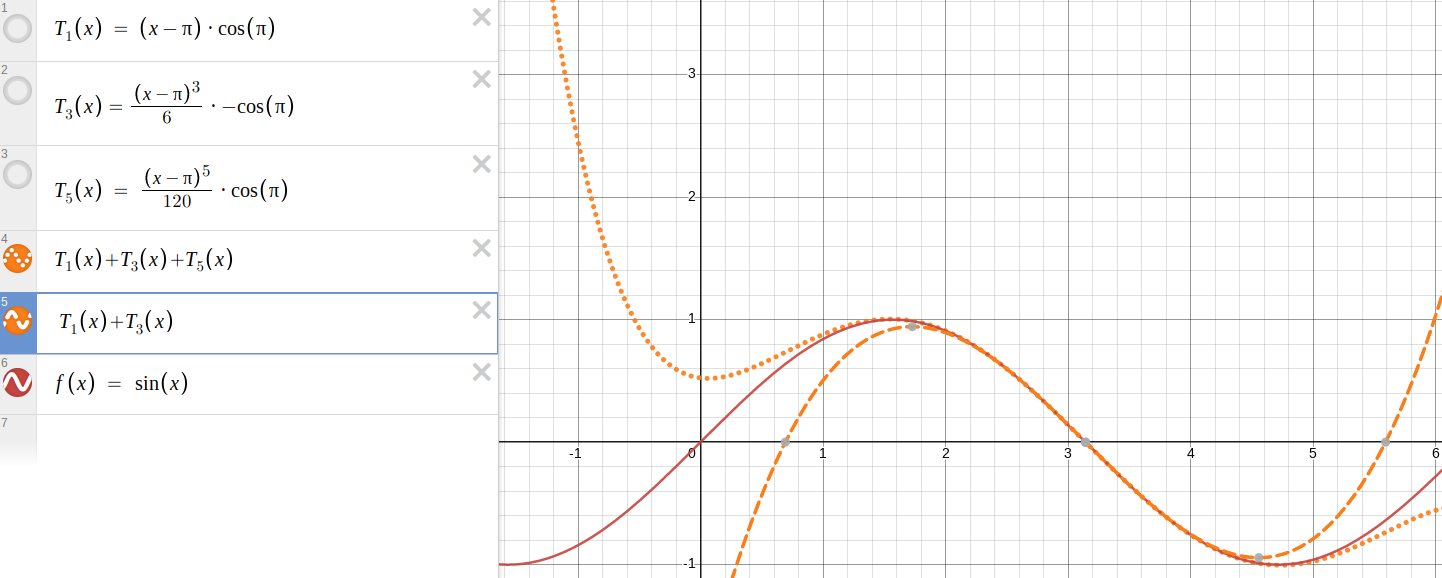
So I took a good suggestion from the comments, which is that if you want to compute !!\sin 4!! you should start with the Taylor series centered around !!π!!:
$$\begin{align} \sin x & \approx \sin \pi + (x-\pi)\cos \pi - \frac{(x-\pi)^2}{2}\sin \pi - \frac{(x-\pi)^3}{6}\cos \pi + \ldots \\ & = -(x-\pi) + \frac{(x-\pi)^3}{6} - \frac{(x-\pi)^5}{120} + \ldots \end{align} $$
because the !!\sin \pi!! terms vanish and !!\cos \pi = -1!!. I did some nice rainbow-colored graphs in Desmos.
I just realized I already wrote this up last month. And do you know why? It's because I copied this article from last month's, forgot to change the subject line from “2023-04” to “2023-05”, and because of that forgot that I was doing May and not April. Wheeee! This is what comes of writing blog articles at 3 AM.
Well anyway, continuing with May, we have…
Rational solutions for !!x^3+y^3=1!! where both x and y are non-negative
OP wanted solutions to $$x^3 + y^3 = 1,$$ and had done some research, finding a relevant blog post that they didn't understand, which observed that if !!x!! and !!y!! were solutions, so too would be certain functions of !!x!! and !!y!!, and this allows an infinite family of solutions to be developed if one knows a solution to begin with.
Unfortunately, there are no nontrivial rational solutions to !!x^3 + y^3 = 1!!, as has been known for some time. The blog post that OP found was discussing !!x^3 + y^3 = 9!!, for which !!\langle x, y\rangle = \langle 1, 2\rangle !! is an obvious starting point.
OP asked a rather odd question in the comments:
Why is !!(0, 1)!! not a start?
Had they actually tried this, they would have seen that if they started with !!\langle x, y\rangle = \langle 0, 1\rangle !!, when they computed the two functions that were supposed to give them another solution, they got !!\langle 0, 1\rangle !! back again. I told OP to try it and see what happened. (Surprising how often people forget this. Lower Mathematics!)
This reminds me a bit of a post I replied to long ago that asked why we can't use induction to prove the Goldbach conjecture. Well, what happens when you try? The base case is trivial, so far so good. The induction case says here you go, for every even number !!k < n!! I give you primes !!p_k!! and !!q_k!! with !!p_k+q_k = k!!. Your job is to use these to find primes !!p_{k+2}!! and !!q_{k+2}!! with !!p_{k+2}+q_{k+2} = k+2!!. Uhhh? What now?
Proving !!n(n^2+5)!! is always even
Mathematicially this is elementary, but the pedagogy is interesting.
OP had already proved this by considering even and odd cases separately, but wanted to know if an induction proof was possible. They had started one, but gotten stuck.
Three people, apparently not reading the question, provided proofs by considering even and odd cases separately. One other provided a proof by induction that was “a bit hairy”. But I think a better answer engages with OP's attempt at an induction proof: Instead of “here's a way it could be done”, it's better to provide “here's how you could have made your way work”.
I used a trick, which is that instead of taking !!\Phi(x)!! to mean “!!f(x)!! is even”, and proving !!\Phi(x)!! for all !!x!! by induction, I took !!\Phi(x)!! to mean “!!f(x)!! is even and !!f(x+1)!! is also even”. You have to prove more, but you have more to work with. For a similar approach to a similar problem, see Proof that every third Fibonacci number is even.
The key feature that makes this a good answer is where it says:
For !!f(n+2)!! we will use your method. …. Subtracting !!n(n^2+5) = n^3 + 5n!! as you suggested ….
It's important to point out to the student when their idea would have worked. This is important in code reviews too. The object is not to make the junior programmer do it the same way you would have, it's to help them make their own idea work well. I ought to write an article about that.
Is an argument valid if assuming its premises and conclusion leads to no contradiction?
This was one of those questions where OP proposed some logical principle that was totally invalid and asked why it isn't allowed, something about why you can't assume the conclusion and show that it satisfies the required properties.
It's a curious question because there's such a failure of instruction here: OP has not grasped what it means to be a valid deduction, that the logic used in mathematics is the same logic that is used everywhere else, and that mathematical arguments are valid or invalid for the same reasons that those same arguments are valid or invalid when thinking about anything else: the invalid arguments lead you to the wrong conclusions!
Anyway, I don't want to quote my whole answer here, but you should check it out, it's amusing. OP didn't like it though.
Proving or disproving that if !!A^2X=λ^2X!! then !!AX=λX!!
OP did like this one, and so do I, it's hilarious. The question is apparently something about linear transformations and eigenvalues and stuff like that, which I never learned as well as I should have, owing to my undergraduate linear algebra class being very poor. (Ugh, so many characteristic polynomials.)
Someone else posted a linear algebra (dis)proof which was very reasonable and which got several upvotes. But I realized that this is not actually a question about eigenvalues! It is elementary algebra: If you have an example where !!A^2X=λ^2X!!, then !!-\lambda!! has this property also and is a counterexample to the claim. OP was pleased with this and accepted my answer instead of the smart one with the upvotes.
This kind of thing is why my Math SE avatar is a potato.
Can we treat two equal sets as being distinct mathematical objects?
There was an answer to this that I felt was subtly wrong. It said:
The axiom that answers your question is known as Extensionality: Sets are uniquely determined by their elements.
and then started talking about ZFC, which seems to me to be an irrelevant confusion.
The formal idea of sets comes from the axioms, but the axioms themselves come from a sort of preformal idea of sets. We want to study what happens when we have these things-that-have-elements, and when we ignore any other properties that they might have. The axiom is just a more formal statement of that. Do sets have properties, such as identities, other than their elements? It's tempting to say “no” as this other person did. But I think the more correct answer is “it doesn't matter”.
Think of a monastery where, to enter, you must renounce all your worldly possessions. Must you legally divest yourself of the possessions in order to enter the monastery? Will the monks refuse you entry if, in the view of the outside world, you still own a Lamborghini? No, they won't, because they don't care. The renunciation is what counts. If you are a monk and you ask another monk whether you still own the Lamborgini, they will just be puzzled. You have renounced your possessions, so why are you asking this? Monks are not concerned with Lamborghinis.
Set theory is a monastery where the one requirement for entry is that you must renounce your interest in properties of sets other than those that come from their elements. Whether a set owns a Lamborghini is of no consequence to set theorists.
[Other articles in category /math/se] permanent link
Fri, 28 Apr 2023
Show how the student could have solved it
A few days ago I offered these maxims about pedagogy:
It's not enough to show the student the answer; you should try to show them how to find the answer.
It's not enough to show the student how you can find the answer; you should try to show them how they could have found the answer.
A nice illustration popped up on Math SE this morning. OP asks:
If all eigenvalues of a matrix are 0 or 1, does that imply the matrix is idempotent?
Shortly afterward a comment from PrincessEev said, opaquely:
The matrices $$\left[\begin{matrix} 0&x\\ 0&0 \end{matrix}\right]$$ are obvious counterexamples for !!x\ne 0!!.
Uh, they are? It wasn't obvious to me. I mean, I think I see why the eigenvalues must be zero, without doing the calculation. But where did this example come from?
But then later they redeemed themselves by adding another comment:
it was just my first instinct to try a few examples with what felt like a bold claim: matrices with enough well-placed zeroes tend to vanish when raising them to powers
I understand now! Yeah, I could have thought of that, but didn't. So the second comment actually taught me something, not what the answer is, which not very useful, because who cares?, but how to find the answer, which contains knowledge that might be generally useful.
[Other articles in category /math/se] permanent link
Thu, 20 Apr 2023
Math SE report 2023-04: Simplest-possible examples, pointy regions, and nearly-orthogonal vectors
Polyhedra has more corners than facets
This one was a bit puzzling because it asked:
Is it true that [a polyhedron] has always more/as many corners than facets? I haven't found a counterexample…
(By ‘facets’ I assume OP meant ‘faces’.)
This is puzzling because there are so many counterexamples. For example, every dipyramid has this property. A dipyramid is what you get if you take two pyramids and glue their bases together. Maybe you want to say this is obscure, but an octahedron is a dipyramid and one might expect anyone asking about polyhedra to know about octahedra. I wonder what examples this person did consider?
In fact, for any polyhedron with !!F!! faces and !!V!! vertices, there is a corresponding “dual” polyhedron with !!V!! faces and !!F!! vertices, so for almost any polyhedron you can think of, if that polyhedron is not already a counterexample, then its dual is. A cube is not, but its dual is — this is the octahedron again.
Finding sets !!A!!, !!B!!, and !!C!! such that !!A\in B!!, !!B \in C!!, but !!A \notin C!!
I thought this one was pedagogically interesting. OP made a mistake in their approach that is quite common:
The problem tells us !!B = \{A,b_1,b_2,\ldots\}!! and !!C = \{B,c_1,c_2\}!!.
The mistake OP made here was to start by trying to find the most general possible example. Yes, if !!A\in B!! then in general !!B = \{A,b_1,b_2,\ldots\}!!. This might be a more helpful observation if the question had asked for some universal property of all such !!A, B, C!!. Then you could add constraints to the general case and see if you had anything left at the end. But this problem only asked for one example. So instead of considering the most general case of !!A\in B!!, and therefore the most complex form of the idea, the first thing one should try is the simplest possible example of !!A\in B!!, which is just !!B = \{A\}.!!
Then similarly one should try !!C = \{B\}!!. Obviously the required properties !!A\in B!! and !!B\in C!! are satisfied. What about !!A\notin C!!?
Since the only element of !!C!! is !!B!!, the answer is easy: !!A\notin C!! unless !!A=B = \{A\}!!
So now we just have to avoid !!A=\{A\}!!. Again let's try the simplest thing that could possibly work: !!A=\emptyset!!. And then we win, because indeed !!\emptyset\ne \{\emptyset\}!!, since the left side is empty and the right side isn't.
Did we get lucky here? No! The axiom of foundation guarantees that literally any !!A!! will work. But you don't have to know that to find an example, because literally any !!A!! will work.
This is Lower Mathematics in action. The abstract approach is useful if you are trying to prove some theorem, but if all you want is to find an example, the abstract approach is overkill.
Volume obtained by rotating a region around two different lines
OP considered the region bounded by the curves !!y=x^2!! and !!y=\sqrt x!! for !!0\le x, y\le 1!!, and then the solids of revolution obtained by revolving this region around the lines !!y=0!! and !!y=1!!. They said:
I expected the volume obtained by rotating about !!y=1!! to be identical with the volume obtained by rotating about the !!x!!-axis. To my surprise, calculation shows different results.
Many people would have posted an answer to this that simply did the calculation, sometimes one with no words in it. But I think this misses the point of the question, which is about OP's intuition. Why were they wrong?
Something that has been on my mind lately is an elaboration of a certain principle of pedagogy. Everyone knows the principle:
It's not enough to show the student the answer; you should try to show them how to find the answer.
Not everyone follows this, but at least most people are aware of it.
But my decades of experience watching people teach math have led me to believe that this is insufficient. There's a higher-order version of this principle that is also important:
It's not enough to show the student how you can find the answer; you should try to show them how they could have found the answer.
And by ‘they’ I don't mean ‘a student’; I mean the student, the specific one sitting in front of you, who knows what they know and can do what they can do.
This is hard.
(I think the !!A\in B, B\in C, A\notin C!! thing above is another example of this. Three people answered that question by pulling solutions out of thin air, but how much does that help OP solve the next problem of this type?)
Anyway, I digress. The region in question looks like this:
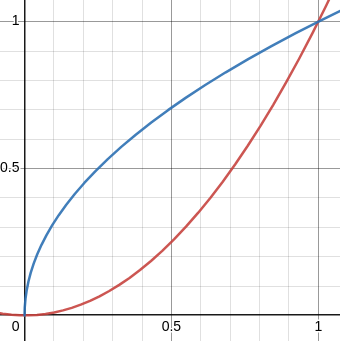
I observed that the upper end is much narrower than the lower end. You could count boxes to verify this, but I think it's obvious, and said:
Which end would you rather be poked with?
Then I pointed out that if you revolve the region around !!y=1!!, the thick end travels a long way and sweeps out a large volume, whereas if you revolve it around !!y=0!! the thick end is closer to the axis of revolution, so does not sweep out so much volume. So just from looking at the picture, one might guess that the volume will be larger when revolved around !!y=1!!, which is what OP originally reported.
I did not actually do the calculation, so it's conceivable that I was utterly wrong, but I suspect not.
Definition of Graph Isomorphism
This was not that interesting, but it is a demonstration of a couple of things:
Finding the simplest possible example
Because it's usually easier for someone to understand a simple example well enough to generalize it than it is for them to understand an abstract, general construction well enough to specialize it to an example.
Math SE will often ignore subtle answers to challenging questions, while giving many upvotes to trivialities
This post and the octahedron one were my most upvoted posts of the month and also the most trivial. This is why one should ignore upvotes: they are not correlated with anything of real importance.
Help understanding proof: classifying groups of order 21
I may have kinda blown this one. My answer was way too long. OP was asking about specific steps in some group theory proof, ultimately related to the formula $$(aba^{-1})^n = ab^na^{-1}.$$
Algebraically this is quite easy to show, and I did. But it also has deep and essential intuitive content, which I summarized like this:
It says that if you are going to repeat several times the operation of turning your head, then doing !!b!!, then turning your head back, you can skip some of the head-turning and just turn your head once, do operation !!b!! repeatedly, and turn your head back at the end.
This !!aba^{-1}!! thing, called “conjugation”, is incredibly important in group theory, and I have often felt that my group theory course did not make this clear. As I recall the course observed that the mapping !!\varphi_a : x\mapsto axa^{-1}!! is always a group automorphism, went on from there. Which indeed it is, but so what? Why do we care about that particular transformation, anyway?
But the intuitive content of the statement about the automophism is that the symmetries of an object don't change when you turn your head. That's why it's important!
When are two rotations of a sphere conjugate? Exactly when they rotate by the same amount around their respective axes. (“Turn your head!”)
Why are two permutations conjugate if and only if they have the same cycle structure? Because this exactly when they are equivalent under renaming of the objects being permuted; renaming the objects is analogous to "turning your head" for this kind of symmetry.
So whenever the topic of conjugation comes up, I am tempted to launch into a long explanation of the significance of conjugation and its intuitive understanding. Which might have been helpful in this case, but it might have been a completely unnecessary distraction, and I should probably have resisted.
What definition of "nearly orthogonal" would result in "In a 10,000-dimensional space there are millions of nearly orthogonal vectors"?
This was one of those cases where OP asked a very slightly under-baked question and several people jumped in to say it made no mathematical sense at all. (“It's a figure of speech” says one comment. No, it isn't. “I doubt that reference is to a precisely defined concept”, says another. There are more things in heaven and earth, Horatio… “I call bullshit, or imprecise speech,” says a third. Heavens, such foul language!)
I have complained about this at length in the past: I think Math SE persons are too quick to jump from “I have not heard of that” to “it does not exist” and then to “it cannot exist”, or from “I don't quite understand that” to “nobody can understand that” and then to “that is incomprehensible nonsense”.
Two vectors !!u!! and !!v!! are said to be orthogonal if their inner product !!\langle u,v\rangle!! is exactly zero. So if you don't know what “nearly orthogonal” means, you might guess that it means that the inner product is nearly zero: $$\left\lvert \langle u,v\rangle \right\rvert < \epsilon$$ for some small specified !!\epsilon!!. The angle between !!u!! and !!v!! would then be approximately between !!\frac\pi2 - \epsilon!! and !!\frac\pi2 + \epsilon!!, which is nearly a right angle; hence “nearly orthogonal”. This is not exactly subtle thinking.
Another user helpfully linked to a Math Overflow post that discussed essentially the same question, with the title “Almost orthogonal vectors”. So bullshit it isn't, and the question there was sufficiently clear that six people thought it was worth answering, including some guy named Tim Gowers.
I didn't know the answer (although I do now!), but if you don't know the answer, you can still sometimes be useful by writing up the answers of other people who are smarter than yourself, that is called “scholarship”.
In writing it up I almost made a horrible mistake. At one point my draft said something like:
The top answer there gives a bound and claims it is implied by the Johnson-Lindenstrauss lemma. I think the bound might not be quite correct, because the Johnson-Lindenstrauss lemma seems to apply to a somewhat different situation, and…
Fortunately, I realized before posting that that person who had written that answer that was in fact William B. Johnson after whom the Johnson-Lindenstrauss lemma was named, and there was quite a good chance that he did not misapply his own theorem. Heh. Yikes.
It's funny now, but if I had actually made that mistake I would have been mortified.
Also
I have an article with pretty diagrams about how to expand a Taylor series around !!x=\pi!!, with a nice Desmos demonstration that you might enjoy playing with. Press the little ▶️ button in the box that defines the parameter !!a!! and watch the cubic polynomials whip back and forth.
[ Addendum 20230421: Eric Roode says that the animation reminds him of “the robot from Lost in Space sliding back and forth, waving its arms wildly, and saying ‘Danger, Will Robinson! Danger!’”. Same. ]
I have already written a separate article about this post that asks how to compute the integral $$\int_0^{2000} e^{x/2-\lfloor x/2\rfloor}\; dx$$
which you might like to read if you didn't already.
[Other articles in category /math/se] permanent link
Sat, 15 Apr 2023
I liked this simple calculus exercise
A recent Math SE question asked for help computing the value of $$\int_0^{2000} e^{x/2-\left\lfloor x/2\right\rfloor}\; dx.\tag{$\star$}$$
(!!\left\lfloor \frac x2 \right\rfloor!! means !!\frac x2!! rounded down to the nearest integer.)
Often when I see someone's homework problems I exclaim “what blockhead TA assigned this?” But I think this is a really good exercise. Here's why.
In a calculus class, some people will have learned to integrate common functions by rote manipulatation of the expressions. They have learned a set of rules for converting $$\int_a^b x^k\; dx$$ to $$\left.\frac{x^{k+1}}{k+1}\right\rvert_a^b$$ and then to $$\frac{b^{k+1}}{k+1}- \frac{a^{k+1}}{k+1}$$ and such like, and they grind through the algebra. If this is all someone knows how to do, they are going to have a lot of trouble with !!(\star)!!. They might say “But nobody ever taught us how to integrate functions with !!\left\lfloor \frac x2\right\rfloor!!”.
A calculus tyro trying to deal with this analytically might also try rewriting $$e^{x/2-\left\lfloor x/2\right\rfloor}$$ as $$\frac{e^{x/2}}{e^{\left\lfloor x/2\right\rfloor}}$$ but that makes the problem harder, not easier.
To solve this, the student has to actually understand what the integral is computing, and if they don't they will have to learn something about it. The integral is computing the area under a curve. if you graph the function $$\frac x2-\left\lfloor \frac x2\right\rfloor$$
you find that it looks like this:
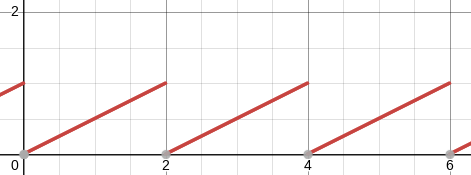
If the interval of integration in !!(\star)!! were only !!(0,2)!! instead of !!(0, 2000)!!, the problem would be very easy because, on this interval, the complicated exponent is identically equal to !!\frac x2!!:
$$\begin{align} \int_0^2 e^{x/2-\left\lfloor x/2\right\rfloor}\; dx & = \int_0^2 e^{x/2}\; dx \\ & = \left. 2e^{x/2} \right\rvert_0^2 \\ & = 2e-2 \end{align} $$
Since the function is completely periodic, integrating over any of the !!1000!! intervals of length !!2!! will produce the same value, so the final answer is simply $$1000\cdot (2e-2).$$
But just pushing around the symbols won't get you there, to solve this problem you have to actually know something about calculus.
The student who overcomes this problem might learn the following useful techniques:
If some expression looks complicated, try graphing it and see if you get any insight into how it behaves.
Some complicated functions can be understood by breaking them into simple parts and dealing with the parts separately.
Piecewise-continuous functions can be integrated by breaking them into continuous intervals and integrating the intervals separately.
You can exploit symmetry to reduce the amount of calculation required.
None of this is deep stuff, but it's all valuable technique. Also they might make the valuable observation that not every problem should be solved by pushing around the symbols.
[Other articles in category /math/se] permanent link
Sun, 19 Feb 2023I had an unusually interesting batch of Math Stack Exchange posts recently.
I think all of my answers to these questions are worth reading in full, and if you like the math posts on my blog, you will like reading these SE posts also. Well, most of them. Maybe.
Summaries follow.
Confusion about equality: mathematical objects versus the symbols that describe them
This one is from last September but I'm really happy with it because it thoroughly addresses up a very common misconception about mathematical notation:
Based on my understanding of equality, the statement !!(1+1)+1=1!!, contains no mathematical content beyond !!1=1!!, since the group element !!(1+1)+1!! literally is the group element !!1!!. This bothers me...
My answer begins with
It should; it's wrong.
I'm frequently surprised by how often this fallacy shows up on Math SE, often asserted as an obvious truth by people I thought would know better. So it's worth explaining in detail. I expect I'll be able to refer people to this answer when it comes up in the future.
A brief summary of my answer is:
- Mathematical expressions denote computations, not values.
- !!A=B!! means that that two computations eventually produce the same value.
- This does not, in general, mean that the computations have the same meaning.
What does italic i mean in integral calculator?
The i means the imaginary unit, that !!i^2=-1!! thing. No surprise there. But the reason was a bit interesting. OP had Wolfram α compute some horrendous double integral:

and the answer should have been a real number, so what was !!i!! doing in there?
The answer: Floating-point roundoff error. Check out Claude Leibovici's detailed explanation of where the roundoff error comes from, it's much smarter than what I said, which was to mumble something about how Wolfram α's “probably … used … some advanced technique …” which sounds wise but actually I had no idea what it might have done. Claude Leibovici actually has an explanation.
I was going to leave this out but I wanted to remind you all how much I despise floating-point arithmetic.
Can Peano's 9th axiom be expressed using a self-referential set definition?
This is one of those not-quite-baked questions where the initial answers act like it does not make sense (tier 4 or 5). But it does make sense and there is a good answer (tier 1).
The question asks if you can define the set of natural numbers by saying something like
If !!K = \{0\} \cup \{S(k)\mid k \in K\}!!, then !!K=\mathbb{N}!!.
The initial comments said no, it's self-referential. But so is:
$$ n! = \begin{cases} 1, & \text{if $n$ = 0} \\ n\cdot (n-1)!& \text{otherwise} \end{cases} $$
and nobody bats an eyelash at that. (The author of the comments later retracted his rejection.)
In fact it requires only a little bit of elaboration to make sense of such “circular” definitions. To interpret $$X = f(X)$$ you need to do two things. First, think of !!f!! as a mapping, and ask if it has any fixed points, any arguments !!x!! for which !!x=f(x)!! holds. And then, from the set of fixed points, find some unambiguous way to identify one of the fixed points as the one you want. If !!f!! is a mapping from sets to sets, it often happens that the family of fixed points is closed under intersections, and you can select the unique minimal fixed point that is a proper subset of all the others.
This was all formalized by Dana Scott in the 1960s and it continues to underlie formal treatments of programming language semantics.
Is there a scenario for when changing the order of different quantifiers in a nested quantifier retain the original meaning?
This is interesting because some of the replies make the mistake of conflating the meaning of an expression with its value, a problem I discussed above in connection with something else. Two expressions of first-order logic may be logically equivalent, but this does not imply that they have the same meaning.
The question also looks superficially like “What is the difference between !!\forall x\exists y. R(x,y)!! and !!\exists y\forall x. R(x,y)!!, which is a FAQ. But it is not that question.
The question concerned expressions of the type !!\forall x.\exists y.P(x,y)!! and was further complicated by the implicit quantifier on the !!P!!. Are we asking if !!\forall x.\exists y.P(x,y)!! always has a different meaning from !!\forall y.\exists x.P(x,y)!! for all !!P!!? Or for a particular !!P!!? There are several similar-sounding questions that could be asked here, and my thinking about the variations is still not clear to me.
English (and standard mathematical terminology) is not well-equipped to discuss this sort of thing intelligibly. Or perhaps I just don't know how to do it. I had to work hard to write something I was satisfied with.
Cantor set - is it made of !![a,b]!! intervals or exclusively of singletons?
This question is a bit confused (every set is made of singletons) and I was worried that some know-it-all would jump in and tell this person that really the Cantor set is very simple. When actually the Cantor set is really weird and this is why it is such an important counterexample to so many plausible-seeming conjectures. As Von Neumann supposedly said, in mathematics one doesn't understand things, one just gets used to them. It can be hard for people who have gotten used to the Cantor set to remember what it is like for people who are grappling with it for the first time — or to remember that they themselves may not understand as well as they imagine they do.
When I write an answer to a question like this, in which I need to say “your idea is somewhat confused”, I like to place that remark in close proximity to “… because the situation is a confusing one” so that OP doesn't feel that they are the only person in the world who is puzzled by the Cantor set.
(Sometimes they are the only person in the world who is puzzled by whatever it is, and then it's okay for them to feel that way. I wouldn't lie and say that the situation was a confusing one when I thought it wasn't. If the matter is actually simple it's better to say so, because that can be valuable information. Beginners often overthink simple issues. But the Cantor set is not one of those situations!)
A valuable pedagogical strategy is finding a simpler example. The Cantor set does not have all the same properties as !!\Bbb Q!!. But !!\Bbb Q!! does seem to share with the Cantor set the specific properties that were troubling this person. Does !!\Bbb Q!! contain any intervals? Like the Cantor set, no. Is !!\Bbb Q!! a union of singletons? It's not clear what OP meant by this, but, uh, probably? And if not we can at least find out more about what OP thought they meant, by asking about !!\Bbb Q!!. So it's a good idea to take the focus off of the Cantor set, which is weird, complicated, and unfamiliar, and put it on !!\Bbb Q!!, which is much less weird, somewhat less complicated, and much more familiar. Then with that foundation laid, you are in a better position to climb up to !!\Bbb R\setminus\Bbb Q!! (Similar to !!\Bbb Q!!, but uncountable) and then to the Cantor set itself.
Here I am talking about the Cantor set.
Deriving that a cube has six sides via a square and combinatorics
This is probably my favorite question of the month, because it seems quite half-baked, but there is an excellent answer available. As often happens with half-baked questions, the people who don't know the answer jump to the conclusion that no answer is possible, and say dumb stuff like:
What is the definition of a "cube" in your problem?
This is going the wrong direction. The point is to find the ‘right’ definition of the cube; if OP could define “cube” in the way they wanted, they wouldn't need to ask the question.
A better way to answer this question is to understand that what OP is looking for is actually a suitable definition of “cube”. A more mathematically sophisticated person might have asked:
How can we understand the cube as a combinatorial object, developed from the square?
The word “cube” in this question does not mean some specific mathematical object, but rather the informal intuitive cube. A correct answer will explain how to approach the informal idea of the cube in a mathematical way.
There is a nice (tier 1!) answer in this case: A segment is composed of an interior !!i!! and two endpoints, so we can represent it as !!S=i+2!!. Then !!S^3!! is a cube and its analogous combinatorial description is !!(i+2)^3 =i^3+6i^2+12i+8!!. Ta daa! The answer has a more detailed explanation.
There were a couple of followup comments that annoyed me, objecting that what I had presented was not a proof. That was a feature, not a bug. The question hadn't asked for a proof, and I had not tried to provide one.
One of the comments went further, and called it “a nice coincidence”. It's not, it's just generating functions.
I think the “coincidence” person has a profound misunderstanding of how mathematics operates. I wrote several hundred words explaining why but then realized that I had finally been able to articulate an idea I've been groping around to get hold of for decades. This is too precious to me to stick in at the tail end of an anthology article; it deserves its own article. So I am saving the next five paragraphs for next week. Or next year. Whenever I can do it justice.
Algebraic descriptions of the cube.
Thanks for reading.
[ Addendum 20230221: The original question also wanted to identify the faces of a cube with pairs of something there were four of, maybe the sides or the corners of a square. I did find a way to identify faces of a cube with pairs of something interesting. ]
[Other articles in category /math/se] permanent link
Mon, 11 Apr 2022
At last, an internet commenter I can agree with
Browsing around Math StackExchange today, I encountered this question, ‘Unique’ doesn't have a unique meaning, which pointed out that the phrase “Every boy has a unique shirt” is at least confusing. (Do all the boys share a single shirt?)
“Aha,” I said. “I know what's wrong there: it should be ‘every boy has a distinct shirt’.” I scrolled down to see if I should write that as an answer. But I noticed that the question had been posted in 2012, and guessed that probably someone had already said what I was going to say. Indeed, when I looked at the comments, I saw that the third one said:
If I meant that no shirt belongs to two boys, I would say "every boy has a distinct shirt".
Okay, that saves me the trouble of replying at least. I went to click the upvote button on the comment, but there was no button,
because
the comment had been posted, in August of 2012, by me.
[Other articles in category /math/se] permanent link
Wed, 09 Mar 2022
Bad but interesting mathematical notation idea
Zaz Brown showed up on Math SE yesterday with a proposal to make mathematical notation more uniform. It's been pointed out several times that the expressions
$$y^n = x \qquad n = \log_y x \qquad y=\sqrt[n]x $$
all mean the same thing, and yet look completely different. This has led to proposals to try to unify the three notations, although none has gone anywhere. (For example, this Math SE thread .)
!!\def\o{\overline}\def\u{\underline}!!
In this new thread, M. Brown has an interesting observation: exponentiation also unifies addition and multiplication. So write !!\o x!! to mean !!e^x!!, and !!\u x!! to mean !!\ln x!!, and leave multiplication as it is. Now !!x^y!! can be written as !!\o{\u x y}!! and !!x+y!! can be written as !!\u{\bar x \! \bar y}!!.
Well, this is a terrible idea, and I'll explain why I think so in some detail. But I really hope nobody will think I mean this as any sort of criticism of its author. I have a lot of ideas too, and most of them are amazingly bad, way worse than this one. Having bad ideas doesn't make someone a bad person. And just because an idea is bad, doesn't mean it wasn't worth considering; thinking about ideas is how you decide which ones are bad and which aren't. M. Brown's idea was interesting enough for me to think about it and write an article. That's a compliment, not a criticism.
I'm deeply interested in notation. I think mathematicians don't yet understand the power of mathematical notation and what it does. We use it, but we don't understand it. I've observed before that you can solve algebraic equations or calculus problems just by “pushing around the symbols”. But why can you do that? Where is the meaning, and how do the symbols capture the meaning? How does that work? The fact that symbols in general can somehow convey meaning is a deep philosophical mystery, not just in mathematics but in all communication, and nobody understands how it works. Mathematical symbols can be even more amazing: they don't just tell you what other people were thinking, they tell you things themselves. You rearrange them in a certain way and they smile and whisper secrets: “now you can see this function is everywhere zero”, “this is evidently unbounded” or “the result is undefined when !!\lvert x_1\rvert > \frac 23!!”. It's almost as if the symbols are doing some of the thinking for you.
Anyway this particular idea is not good, but maybe we can learn something from its failure modes?
Here's how you would write !!x^2+x!!: $$\u{\o{\o{2\u x}}{\o x}}$$
Zaz Brown suggested that this expression might be better written as !!x{\u{\o x \o 1}}!!, which is analogous to !!x(x+1)!!, but I think that reply misses a very important point: you need to be able to write both expressions so that you can equate them, or transform one into the other. The expression !!x(x+1)!! is useful because you can see at a glance that it is composite for all integer !!x!! larger than 1, and actually twice a composite for sufficiently large !!x!!. (This is the kind of thing I had in mind when I said the symbols whisper secrets to you.) !!x^2+x!! is useful in different ways: you can see that it's !!\Theta(x^2)!! and it's !!(x+1)^2 - (x+1)!! and so on. Both are useful and you need to be able to turn one into the other easily. Good notation facilitates that sort of conversion.
M. Brown's proposal actually has at least two components. One component is its choice of multiplication, exponentials and logarithms as the only first-class citizens. The other is the specific way that was chosen to write these, with the over- and underbars. This second component is no good at all, for purely typographic reasons. These three expressions look almost identical but have completely different meanings: $$ \u{\o a\, \o c}\qquad \u{\o { ac}} \qquad \o{\u a\, \u c}.$$
In fact, the two on the right were almost indistinguishable until I told MathJax to put in some extra space. I'm sure you can imagine similar problems with !!\u{\o{\o{2\u x}}}{\o x}!! turning into !!\u{\o{\o{2\u x x}}}!! or !!\u{\o{\o{2\u x }x}}!! or whatever. Think of how easy it is to drop a minus sign; this is much worse.
[ Addendum 20220308: Earlier, I had said that !!x+y!! could be written as !!\u{\bar x\bar y}!!. A Gentle Reader pointed out that the bar on the bottom wasn't connected but should have been, as on the far right of this screenshot:

I meant it to be connected and what I wrote asked for it to be connected, but MathJax, which formats the math formulas on the blog, didn't connect it. To remove the gap, I had to explicitly subtract space between the !!x!! and the !!y!!. ]
But maybe the other component of the proposal has something to it and we will find out what it is if we fix the typographic problem with the bars. What's a good alternative?
Maybe !!\o x = x^\bullet!! and !!\u x = x_\bullet!! ? On the one hand we get the nice property that !!x^\bullet_\bullet = x!!. But I think the dots would make my head swim. Perhaps !!\o x = x\top!! and !!\u x = x\bot!!? Let's try.
Good notation facilitates transformation of expressions into equal expressions. The !!\top\bot!! notation allows us to easily express the simple identities $$a\top\bot \quad = \quad a\bot\top \quad = \quad a.$$ That kind of thing is good, although the dots did it better. But I couldn't find anything else like it.
Let's see what the distributive law looks like. In standard notation it is $$a(b+c) = ab + ac.$$ In the original bar notation it was $$a\u{\o b\o c} = \u{\o{ab}\, \o{ac}}.$$ This looks uncouth but perhaps would not be worse once one got used to it.
With the !!\top\bot!! idea we have
$$ a(b\top c\top)\bot = ((ab)\top(ac)\top)\bot. $$
I had been hoping that by making the !!\top!! and !!\bot!! symbols postfix we'd be able to avoid parentheses. That didn't happen: without the parentheses you can't distinguish between !!(ab)\top!! and !!a(b\top)!!. Postfix notation is famous for allowing you to omit parentheses, but that's only if your operators all have fixed arity. Here the invisible variadic multiplication ruins that. And making it visible dyadic multiplication is not really an improvement:
$$ ab\top c\top\cdot\cdot\bot = ab\cdot\top ac\cdot \top\cdot \bot. $$
You know what I think would happen if we actually tried to use this idea? Someone would very quickly invent an abbreviation for !!\u{\o {x_1}\, \o {x_2} \cdots \o{x_k}}!!, I don't know, something like “!!x_1 + x_2 + \ldots + x_k!!” maybe. (It looks crazy, I know, but it might just work.) Because people might like to discuss the fact that $$ \u{\o 2\, \o 3 } = 5$$ and without an addition sign there seems to be no way to explain why this should be.
Well, I have been turning away from the real issue for a while now, but !!a(b\top c\top)\bot = !! !!((ab)\top(ac)\top)\bot!! forces me to confront it. The standard expression of the distributive law equates a computation with two operations and another with three. The computations expressed by the new notation involve five and six operations respectively. Put this way, the distributive law is no longer simple!
This reminds me of the earlier suggestion that if !!x^2+x!! is too complicated, one can write !!x(x+1)!! instead. But expressions don't only express a result, they express a way of arriving at that result. The purpose of an equation is to state that two different computations arrive at the same result. Yes, it's true that $$a+b = \ln e^ae^b,$$ but the two computations are not the same! If they were, the statement would be vacuous. Instead, it says that the simple computation on the left arrives at the same result as the complicated one on the right, an interesting thing to know. “!!2+3=5!!” might imply that !!e^2\cdot e^3=e^5!! but it doesn't say the same thing.
Here's my takeaway from consideration of the Zaz Brown proposal:
It's not sufficient for a system of notation to have a way of expressing every result; it has to be able to express every possible computation.
Put that way, other instructive examples come to mind. Consider Egyptian fractions. It's known that every rational number between !!0!! and !!1!! can be written in the form $$\frac1{a_1} + \frac1{a_2} + \ldots + \frac1{a_n}$$ where !!\{ a_i\}!! is a strictly increasing sequence of positive integers. For example $$\frac 7{23} = \frac 14 + \frac1{19} + \frac1{583} + \frac1{1019084}$$ or with a bit more ingenuity, $$\frac7{23} = \frac16 + \frac1{12} + \frac1{23} + \frac1{138} + \frac1{276},$$ longer but less messy. The ancient Egyptians did in fact write numbers this way, and when they wanted to calculate !!2\cdot\frac17!!, they had to look it up in a table, because writing !!\frac27!! was not an expressible computation, it had to be expressed in terms of reciprocals and sums, so !!2\cdot\frac 17 = \frac14 + \frac1{28}!!. They could write all the numbers, but they couldn't write all the ways of making the numbers.
(Neither can we. We can write the real root of !!x^3-2!! as !!\sqrt[3]2!!, but there is no effective notation for the real root of !!x^5+x-1!!. The best we can do is something like “!!0.75488\ldots!!”, which is even less effective than how the Egyptians had to write !!\frac27!! as !!\frac14+\frac1{28}!!.)
Anyway I think my conclusion from all this is that a practical mathematical notation really must have a symbol for addition, which is not at all surprising. But it was fun and interesting to see what happened without it. It didn't work well, but maybe the next idea will be better.
Thanks again, Zaz Brown.
[ Addendum 20230422: I discussed the Egyptians’ table of !!\frac 2n!! a couple of years ago, and why a more general table wasn't needed. ]
[Other articles in category /math/se] permanent link
Sat, 26 Feb 2022
I vent my rage at dumbass Math SE comments
[ Content warning: ranting ]
An article I've had in progress for a while is an essay about the dogmatic slogan that “infinity is not a number”. As research for that article I got Math Stack Exchange to disgorge all the comments that used that phrase. There were several dozen.
Most of them were just inane, or ill-considered; some contained genuine technical errors. But this one was so annoying that I have paused to complain about it individually:
One thing many laypeople do not understand or realize is that infinity is not a number, it's not equal to any number, and that two infinities can be different (or the same) in size from one another."
That is not “one thing”. It is three things.
A person who is unclear on the distinction between !!1!! and !!3!! should withhold their opinions about the nature of infinity.
[ Addendum 20220301: I did not clearly communicate which side of the “infinity is not a number” issue I am on. Here's my preliminary statement on the matter: The facile and prevalent claim that “infinity is not a number”, to the extent that it isn't inane, is false. I hope this is sufficiently clear. ]
[Other articles in category /math/se] permanent link
Thu, 30 Dec 2021
A little more about the pedagogy of what it means to be transcendental
[ This is a followup to In simple English, what does it mean to be transcendental? ]
A while back a Math SE user posted a comment on my simple explanation of transcendental and algebraic numbers that asked why my explanation had contained some redundancies:
Are there any numbers for which division is necessary? I can't think of any. Likewise, subtracting integers is redundant; I believe all you need is "you can add any integer; you can multiply by any non-zero integer; you can multiply by x."
This is true! I had said:
We will play a game. Suppose you have some number !!x!!. You start with !!x!! and then you can add, subtract, multiply, or divide by any integer, except zero. You can also multiply by !!x!!. You can do these things as many times as you want. If the total becomes zero, you win.
and you don't need subtraction or division. (The underlying mathematical fact that motivated this answer is that integer polynomials are the free ring over the integers. For a ring you only need addition and multiplication.) So why did I mention subtraction and division? They're not mathematically necessary, doesn't it make the answer more complicated to put them in?
I had considered this carefully, and had decided it was simpler this way. The target audience is a person with no significant mathematical training. To a mathematician, it's obvious that inclusion of integers includes subtraction as a special case because you can simply add a negative integer. But non-mathematicians are not used to thinking this way. They have been taught that there are four arithmetic operations. If I mention all four, they will understand that all the operations of basic arithmetic are allowed. But if I had said only "addition and multiplication" many people would have been distracted and wondered "why just those two? Why not some other two?". Including all four avoids this distraction.
I could have said only “addition and multiplication” and later on explained that allowing subtraction and division doesn't change anything. I think this would have been an inferior choice. It's best to get to the point as quickly as possible. In this case the point is that all the operations of basic arithmetic are allowed. The fact that you can omit two is not relevant. My version is shorter and clearer, and avoids the whole issue.
If my version were less technically correct, that would be a major drawback. Sacrificing correctness for clarity is a seductive but usually harmful choice. The result may appear more clear, when it actually isn't, because of the subtle errors that have been papered over. In this case, though, nothing was sacrificed. It's 100% correct both ways. Mathematicians might prefer the minimal statement, but whole point of this answer is that it is correct even though it is not written in the way that a mathematician would prefer.
I'd like to boil this down to a pithy maxim, but I'm not sure I can do it without being inane. There's something in it about how, when you write something for non mathematicians, you should try to write every part of it for non-mathematicians, not just at the surface presentation but in the deeper layers too.
There's also something about how you should be very careful to distinguish the underlying mathematical truth on the one hand, from the practices that mathematicians have developed to help them in their day-to-day business, or to help them communicate with other mathematicians, or that are merely historical accidents, on the other. The underlying truth is the important part. The rest can be jettisoned.
[Other articles in category /math/se] permanent link
Thu, 18 Nov 2021
In simple English, what does it mean to be transcendental?
I've been meaning to write this up for a while, but somehow never got around to it. In my opinion, it's the best Math Stack Exchange post I've ever written. And also remarkable: its excellence was widely recognized. Often I work hard and write posts that I think are really good, and they get one or two upvotes; that's okay, because the work is its own reward. And sometimes I write posts that are nothing at all that get a lot of votes anyway, and that is okay because the Math SE gods are fickle. But this one was great and it got what it deserved.
I am really proud of it, and in this post I am going to boast as shamelessly as I can.
The question was:
There were several answers posted immediately that essentially recited the definition, some better than others. At the time I arrived, the most successful of these was by Akiva Weinberger, which already had around fifty upvotes.
… Numbers like this, that satisfy polynomial equations, are called algebraic numbers. … A real (or complex) number that's not algebraic is called transcendental.
If you're going to essentially quote the definition, I don't think you can do better than to explain it the way Akiva Weinberger did. It was a good answer!
Once one answer gets several upvotes, it moves to the top of the list, right under the question itself. People see it first, and they give it more votes. A new answer has zero votes, and is near the bottom of the page, so people tend it ignore it. It's really hard for new answers to surpass a highly-upvoted previous answer. And while fifty upvotes on some stack exchanges is not a large number, on Math SE fifty is a lot; less than 0.2% of answers score so high.
I was unhappy with the several quoting-the-definition answers. Because honestly "numbers… that satisfy polynomial equations" is not “simple English” or “layman's terms” as the OP requested. Okay, transcendental numbers have something to do with polynomial equations, but why do we care about polynomial equations? It's just explaining one obscure mathematical abstraction in terms of second one.
I tried to think a little deeper. Why do we care about polynomials? And I decided: it's because the integer polynomials are the free ring over the integers. That's not simple English either, but the idea is simple and I thought I could explain it simply. Here's what I wrote:
We will play a game. Suppose you have some number !!x!!. You start with !!x!! and then you can add, subtract, multiply, or divide by any integer, except zero. You can also multiply by !!x!!. You can do these things as many times as you want. If the total becomes zero, you win.
For example, suppose !!x!! is !!\frac23!!. Multiply by !!3!!, then subtract !!2!!. The result is zero. You win!
Suppose !!x!! is !!\sqrt[3] 7!!. Multiply by !!x!!, then by !!x!! again, then subtract !!7!!. You win!
Suppose !!x!! is !!\sqrt2 +\sqrt3!!. Here it's not easy to see how to win. But it turns out that if you multiply by !!x!!, subtract 10, multiply by !!x!! twice, and add !!1!!, then you win. (This is not supposed to be obvious; you can try it with your calculator.)
But if you start with !!x=\pi!!, you cannot win. There is no way to get from !!\pi!! to !!0!! if you add, subtract, multiply, or divide by integers, or multiply by !!\pi!!, no matter how many steps you take. (This is also not supposed to be obvious. It is a very tricky thing!)
Numbers like !!\sqrt 2+ \sqrt 3!! from which you can win are called algebraic. Numbers like !!\pi!! with which you can't win are called transcendental.
Why is this interesting? Each algebraic number is related arithmetically to the integers, and the winning moves in the game show you how so. The path to zero might be long and complicated, but each step is simple and there is a path. But transcendental numbers are fundamentally different: they are not arithmetically related to the integers via simple steps.
This answer was an immediate hit. It rocketed past the previous top answer into the stratosphere. Of 190,000 Math SE, answers, there are twenty with scores over 500; mine is 13th.
The original version left off the final paragraph (“Why is this interesting?”). Fortunately, someone posted a comment pointing out the lack. They were absolutely right, and I hastened to fix it.
I love this answer for several reasons:
It's not as short as possible, but it's short enough.
It's almost completely jargonless. It doesn't use the word “coefficient”. You don't have to know what a polynomial is. You only have to understand grade-school arithmetic. You don't even need to know what a square root is; you can still try the example if you have a calculator with a square root button.
Sometimes to translate a technical concept into plain language, one must sacrifice perfect accuracy, or omit important details. This explanation is technically flawless.
One often sees explanations of “irrational number” that refer to the fact such a number has a nonrepeating decimal expansion. While this is true, it's a not what irrationality is really about, but a secondary property. The true core of the matter is that an irrational number is not the ratio of any two integers.
My post didn't use the word “polynomial” and took a somewhat different path than the typical explanation, but it nevertheless hit directly at the core of the topic, not at a side issue. The “path to zero” thing isn't some property that algebraic numbers happen to have, it's the crucial issue, only phrased a little differently.
Also I had some unusually satisfying exchanges with critical commenters. There are a few I want to call out for triumphant mockery, but I have a policy of not mocking private persons on this blog, and this is just the kind of situation I intended to apply it to.
This is some good work. When I stand in judgment and God asks me if I did my work as well as I could, this is going to be one of the things I bring up.
[ Addendum 20211230: More about one of the finer points of this answer's pedagogical approach. ]
[Other articles in category /math/se] permanent link
Fri, 12 Nov 2021
Stack Exchange is a good place to explain initial and terminal objects in the category of sets
The fact that singleton sets are terminal in the category of sets, and the empty set is initial, is completely elementary, so it's often passed over without discussion. But understanding it requires understanding the behavior of empty functions, and while there is nothing complex about that, novices often haven't thought it through, because empty functions are useless except for the important role they play in Set. So it's not unusual to see questions like this one:
I have trouble understanding the difference between initial and terminal objects in category theory. … Why there can be morphism from empty set to any other set? And why there is not morphism to empty set as well?
I'm happy with the following answer, which is of the “you already knew this, you only thought you didn't” type. It doesn't reveal any new information, it doesn't present any insights. All it does is connect together some things that the querent hasn't connected before.
This kind of connecting is an important part of pedagogy, one that Math Stack Exchange is uniquely well-suited to deal with. It is not well-handled by the textbook (which should not be spending time or space on such an elementary issue) or in lectures (likewise). In practice it's often handled by the TA (or the professor), during office hours, which isn't a good way to do it: the TA will get bored after the second time, and most students never show up to office hours anyway. It can be well-handled if the class has a recitation section where a subset of the students show up at a set time for a session with the TA, but upper-level classes like category theory don't usually have enough students to warrant this kind of organization. When I taught at math camp, we would recognize this kind of thing on the fly and convene a tiny recitation section just to deal with the one issue, but again, very few category theory classes take place at math camp.
Stack Exchange, on the other hand, is a great place to do this. There are no time or space limitations. One person can write up the answer, and then later querents can be redirected to the pre-written answer.
Your confusion seems to be not so much about initial and terminal objects, but about what those look like in the category of sets. Looking at the formal definition of “function” will help make clear some of the unusual cases such as functions with empty domains.
A function from !!A!! to !!B!! can be understood as a set of pairs $$\langle a,b\rangle$$ where !!a\in A!! and !!b\in B!!. And:
There must be exactly one pair !!\langle a,b\rangle!! for each element !!a!! of !!A!!.
Exactly one, no more and no less, or the set of pairs is not a function.
For example, the function that takes an integer !!n!! and yields its square !!n^2!! can be understood as the (infinite) set of ordered pairs:
$$\{ \ldots ,\langle -2, 4\rangle, \langle -1, 1\rangle, \langle 0, 0\rangle ,\langle 1, 1\rangle, \langle 2, 4\rangle\ldots\}$$
And for each integer !!n!! there is exactly one pair !!\langle n, n^2\rangle!!. Some numbers can be missing on the right side (for example, there is no pair !!\langle n, 3\rangle!!) and some numbers can be repeated on the right (for example the function contains both !!\langle -2, 4\rangle!! and !!\langle 2, 4\rangle!!) but on the left each number appears exactly once.
Now suppose !!A!! is some set !!\{a_1, a_2, \ldots\}!! and !!B!! is a set with only one element !!\{b\}!!. What does a function from !!A!! to !!B!! look like? There is only one possible function: it must be: $$\{ \langle a_1, b\rangle, \langle a_2, b\rangle, \ldots\}.$$ There is no choice about the left-side elements of the pairs, because there must be exactly one pair for each element of !!A!!. There is also no choice about the right-side element of each pair. !!B!! has only one element, !!b!!, so the right-side element of each pair must be !!b!!.
So, if !!B!! is a one-element set, there is exactly one function from !!A!! to !!B!!. This is the definition of “terminal”, and one-element sets are terminal.
Now what if it's !!A!! that has only one element? We have !!A=\{a\}!! and !!B=\{b_1, b_2, \ldots\}!!. How many functions are there now? Only one?
One function is $$\{\langle a, b_1\rangle\}$$ another is $$\{\langle a, b_2\rangle\}$$ and another is $$\{\langle a, b_3\rangle\}$$ and so on. Each function is a set of pairs where the left-side elements come from !!A!!, and each element of !!A!! is in exactly one pair. !!A!! has only one element, so there can only be one pair in each function. Still, the functions are all different.
You said:
I would find it more intuitive if one-element set would be initial object too.
But for a one-element set !!A!! to be initial, there must be exactly one function !!A\to B!! for each !!B!!. And we see above that usually there are many functions !!A\to B!!.
Now we do functions on the empty set. Suppose !!A!! is !!\{a_1, a_2, \ldots\}!! and !!B!! is empty. What does a function from !!A\to B!! look like? It must be a set of pairs, it must have exactly one pair for each element of !!a!!, and the right-side of each pair must be an element of !!B!!. But !!B!! has no elements, so this is impossible: $$\{\langle a_1, ?\rangle, \langle a_2, ?\rangle, \ldots\}.$$
There is nothing to put on the right side of the pairs. So there are no functions !!A\to\varnothing!!. (There is one exception to this claim, which we will see in a minute.)
What if !!A!! is empty and !!B!! is not, say !!\{b_1, b_2, \ldots\}!!? A function !!A\to B!! is a set of pairs that has exactly one pair for each element of !!A!!. But !!A!! has no elements. No problem, the function has no pairs! $$\{\}$$
A function is a set of pairs, and the set can be empty. This is called the “empty function”. When !!A!! is the empty set, there is exactly one function from !!A\to B!!, the empty function, no matter what !!B!! is. This is the definition of “initial”, so the empty set is initial.
Does the empty set have an identity morphism? It does; the empty function !!\{ \}!! is its identity morphism. This is the one exception to the claim that there are no functions from !!A\to\varnothing!!: if !!A!! is also empty, the empty function is such a function, the only one.
The issue for topological spaces is exactly the same:
- When !!B!! has only one element, there is exactly one continuous map !!A\to B!! for every !!A!!.
- When !!A!! is empty, there is exactly one continuous map !!A\to B!! for every !!B!!: the empty function is the homeomorphism.
- When !!A!! has only one element, there are usually many continuous maps !!A\to B!!, one different one for each element of !!B!!.
There are categories in which the initial and terminal objects are the same:
In the category of groups, the trivial group (with one element) is both initial and terminal.
A less important but simpler example is Set*, the category of pointed sets, whose objects are nonempty sets in which one element has been painted red. The morphisms of Set* are ordinary functions that map the red element in the domain to the red element of the codomain.
I hope this was some help.
[ Thanks to Rupert Swarbrick for pointing out that I wrote “homeomorphism” instead of “continuous map” ]
[Other articles in category /math/se] permanent link
Sat, 01 Aug 2020
How are finite fields constructed?
Here's another recent Math Stack Exchange answer I'm pleased with.
I know this question has been asked many times and there is good information out there which has clarified a lot for me but I still do not understand how the addition and multiplication tables for !!GF(4)!! is constructed?
I've seen [links] but none explicity explain the construction and I'm too new to be told "its an extension of !!GF(2)!!"
The only “reasonable” answer here is “get an undergraduate abstract algebra text and read the chapter on finite fields”. Because come on, you can't expect some random stranger to appear and write up a detailed but short explanation at your exact level of knowledge.
But sometimes Internet Magic Lightning strikes and that's what you do get! And OP set themselves up to be struck by magic lightning, because you can't get a detailed but short explanation at your exact level of knowledge if you don't provide a detailed but short explanation of your exact level of knowledge — and this person did just that. They understand finite fields of prime order, but not how to construct the extension fields. No problem, I can explain that!
I had special fun writing this answer because I just love constructing extensions of finite fields. (Previously: [1] [2])
For any given !!n!!, there is at most one field with !!n!! elements: only one, if !!n!! is a power of a prime number (!!2, 3, 2^2, 5, 7, 2^3, 3^2, 11, 13, \ldots!!) and none otherwise (!!6, 10, 12, 14\ldots!!). This field with !!n!! elements is written as !!\Bbb F_n!! or as !!GF(n)!!.
Suppose we want to construct !!\Bbb F_n!! where !!n=p^k!!. When !!k=1!!, this is easy-peasy: take the !!n!! elements to be the integers !!0, 1, 2\ldots p-1!!, and the addition and multiplication are done modulo !!n!!.
When !!k>1!! it is more interesting. One possible construction goes like this:
The elements of !!\Bbb F_{p^k}!! are the polynomials $$a_{k-1}x^{k-1} + a_{k-2}x^{k-2} + \ldots + a_1x+a_0$$ where the coefficients !!a_i!! are elements of !!\Bbb F_p!!. That is, the coefficients are just integers in !!{0, 1, \ldots p-1}!!, but with the understanding that the addition and multiplication will be done modulo !!p!!. Note that there are !!p^k!! of these polynomials in total.
Addition of polynomials is done exactly as usual: combine like terms, but remember that the coefficients are added modulo !!p!! because they are elements of !!\Bbb F_p!!.
Multiplication is more interesting:
a. Pick an irreducible polynomial !!P!! of degree !!k!!. “Irreducible” means that it does not factor into a product of smaller polynomials. How to actually locate an irreducible polynomial is an interesting question; here we will mostly ignore it.
b. To multiply two elements, multiply them normally, remembering that the coefficients are in !!\Bbb F_p!!. Divide the product by !!P!! and keep the remainder. Since !!P!! has degree !!k!!, the remainder must have degree at most !!k-1!!, and this is your answer.
Now we will see an example: we will construct !!\Bbb F_{2^2}!!. Here !!k=2!! and !!p=2!!. The elements will be polynomials of degree at most 1, with coefficients in !!\Bbb F_2!!. There are four elements: !!0x+0, 0x+1, 1x+0, !! and !!1x+1!!. As usual we will write these as !!0, 1, x, x+1!!. This will not be misleading.
Addition is straightforward: combine like terms, remembering that !!1+1=0!! because the coefficients are in !!\Bbb F_2!!:
$$\begin{array}{c|cccc} + & 0 & 1 & x & x+1 \\ \hline 0 & 0 & 1 & x & x+1 \\ 1 & 1 & 0 & x+1 & x \\ x & x & x+1 & 0 & 1 \\ x+1 & x+1 & x & 1 & 0 \end{array} $$
The multiplication as always is more interesting. We need to find an irreducible polynomial !!P!!. It so happens that !!P=x^2+x+1!! is the only one that works. (If you didn't know this, you could find out easily: a reducible polynomial of degree 2 factors into two linear factors. So the reducible polynomials are !!x^2, x·(x+1) = x^2+x!!, and !!(x+1)^2 = x^2+2x+1 = x^2+1!!. That leaves only !!x^2+x+1!!.)
To multiply two polynomials, we multiply them normally, then divide by !!x^2+x+1!! and keep the remainder. For example, what is !!(x+1)(x+1)!!? It's !!x^2+2x+1 = x^2 + 1!!. There is a theorem from elementary algebra (the “division theorem”) that we can find a unique quotient !!Q!! and remainder !!R!!, with the degree of !!R!! less than 2, such that !!PQ+R = x^2+1!!. In this case, !!Q=1, R=x!! works. (You should check this.) Since !!R=x!! this is our answer: !!(x+1)(x+1) = x!!.
Let's try !!x·x = x^2!!. We want !!PQ+R = x^2!!, and it happens that !!Q=1, R=x+1!! works. So !!x·x = x+1!!.
I strongly recommend that you calculate the multiplication table yourself. But here it is if you want to check:
$$\begin{array}{c|cccc} · & 0 & 1 & x & x+1 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & x & x+1 \\ x & 0 & x & x+1 & 1 \\ x+1 & 0 & x+1 & 1 & x \end{array} $$
To calculate the unique field !!\Bbb F_{2^3}!! of order 8, you let the elements be the 8 second-degree polynomials !!0, 1, x, \ldots, x^2+x, x^2+x+1!! and instead of reducing by !!x^2+x+1!!, you reduce by !!x^3+x+1!!. (Not by !!x^3+x^2+x+1!!, because that factors as !!(x^2+1)(x+1)!!.) To calculate the unique field !!\Bbb F_{3^2}!! of order 27, you start with the 27 third-degree polynomials with coefficients in !!{0,1,2}!!, and you reduce by !!x^3+2x+1!! (I think).
The special notation !!\Bbb F_p[x]!! means the ring of all polynomials with coefficients from !!\Bbb F_p!!. !!\langle P \rangle!! means the ring of all multiples of polynomial !!P!!. (A ring is a set with an addition, subtraction, and multiplication defined.)
When we write !!\Bbb F_p[x] / \langle P\rangle!! we are constructing a thing called a “quotient” structure. This is a generalization of the process that turns the ordinary integers !!\Bbb Z!! into the modular-arithmetic integers we have been calling !!\Bbb F_p!!. To construct !!\Bbb F_p!!, we start with !!\Bbb Z!! and then agree that two elements of !!\Bbb Z!! will be considered equivalent if they differ by a multiple of !!p!!.
To get !!\Bbb F_p[x] / \langle P \rangle!! we start with !!\Bbb F_p[x]!!, and then agree that elements of !!\Bbb F_p[x]!! will be considered equivalent if they differ by a multiple of !!P!!. The division theorem guarantees that of all the equivalent polynomials in a class, exactly one of them will have degree less than that of !!P!!, and that is the one we choose as a representative of its class and write into the multiplication table. This is what we are doing when we “divide by !!P!! and keep the remainder”.
A particularly important example of this construction is !!\Bbb R[x] / \langle x^2 + 1\rangle!!. That is, we take the set of polynomials with real coefficients, but we consider two polynomials equivalent if they differ by a multiple of !!x^2 + 1!!. By the division theorem, each polynomial is then equivalent to some first-degree polynomial !!ax+b!!.
Let's multiply $$(ax+b)(cx+d).$$ As usual we obtain $$acx^2 + (ad+bc)x + bd.$$ From this we can subtract !!ac(x^2 + 1)!! to obtain the equivalent first-degree polynomial $$(ad+bc) x + (bd-ac).$$
Now recall that in the complex numbers, !!(b+ai)(d + ci) = (bd-ac) + (ad+bc)i!!. We have just constructed the complex numbers,with the polynomial !!x!! playing the role of !!i!!.
[ Note to self: maybe write a separate article about what makes this a good answer, and how it is structured. ]
[Other articles in category /math/se] permanent link
Fri, 31 Jul 2020
What does it mean to expand a function “in powers of x-1”?
A recent Math Stack Excahnge post was asked to expand the function !!e^{2x}!! in powers of !!(x-1)!! and was confused about what that meant, and what the point of it was. I wrote an answer I liked, which I am reproducing here.
You asked:
I don't understand what are we doing in this whole process
which is a fair question. I didn't understand this either when I first learned it. But it's important for practical engineering reasons as well as for theoretical mathematical ones.
Before we go on, let's see that your proposal is the wrong answer to this question, because it is the correct answer, but to a different question. You suggested: $$e^{2x}\approx1+2\left(x-1\right)+2\left(x-1\right)^2+\frac{4}{3}\left(x-1\right)^3$$
Taking !!x=1!! we get !!e^2 \approx 1!!, which is just wrong, since actually !!e^2\approx 7.39!!. As a comment pointed out, the series you have above is for !!e^{2(x-1)}!!. But we wanted a series that adds up to !!e^{2x}!!.
As you know, the Maclaurin series works here:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3$$
so why don't we just use it? Let's try !!x=1!!. We get $$e^2\approx 1 + 2 + 2 + \frac43$$
This adds to !!6+\frac13!!, but the correct answer is actually around !!7.39!! as we saw before. That is not a very accurate approximation. Maybe we need more terms? Let's try ten:
$$e^{2x} \approx 1+2x+2x^2+\frac{4}{3}x^3 + \ldots + \frac{8}{2835}x^9$$
If we do this we get !!7.3887!!, which isn't too far off. But it was a lot of work! And we find that as !!x!! gets farther away from zero, the series above gets less and less accurate. For example, take !!x=3.1!!, the formula with four terms gives us !!66.14!!, which is dead wrong. Even if we use ten terms, we get !!444.3!!, which is still way off. The right answer is actually !!492.7!!.
What do we do about this? Just add more terms? That could be a lot of work and it might not get us where we need to go. (Some Maclaurin series just stop working at all too far from zero, and no amount of terms will make them work.) Instead we use a different technique.
Expanding the Taylor series “around !!x=a!!” gets us a different series, one that works best when !!x!! is close to !!a!! instead of when !!x!! is close to zero. Your homework is to expand it around !!x=1!!, and I don't want to give away the answer, so I'll do a different example. We'll expand !!e^{2x}!! around !!x=3!!. The general formula is $$e^{2x} \approx \sum \frac{f^{(i)}(3)}{i!} (x-3)^i\tag{$\star$}\ \qquad \text{(when $x$ is close to $3$)}$$
The !!f^{(i)}(x)!! is the !!i!!'th derivative of !! e^{2x}!! , which is !!2^ie^{2x}!!, so the first few terms of the series above are:
$$\begin{eqnarray} e^{2x} & \approx& e^6 + \frac{2e^6}1 (x-3) + \frac{4e^6}{2}(x-3)^2 + \frac{8e^6}{6}(x-3)^3\\ & = & e^6\left(1+ 2(x-3) + 2(x-3)^2 + \frac34(x-3)^3\right)\\ & & \qquad \text{(when $x$ is close to $3$)} \end{eqnarray} $$
The first thing to notice here is that when !!x!! is exactly !!3!!, this series is perfectly correct; we get !!e^6 = e^6!! exactly, even when we add up only the first term, and ignore the rest. That's a kind of useless answer because we already knew that !!e^6 = e^6!!. But that's not what this series is for. The whole point of this series is to tell us how different !!e^{2x}!! is from !!e^6!! when !!x!! is close to, but not equal to !!3!!.
Let's see what it does at !!x=3.1!!. With only four terms we get $$\begin{eqnarray} e^{6.2} & \approx& e^6(1 + 2(0.1) + 2(0.1)^2 + \frac34(0.1)^3)\\ & = & e^6 \cdot 1.22075 \\ & \approx & 492.486 \end{eqnarray}$$
which is very close to the correct answer, which is !!492.7!!. And that's with only four terms. Even if we didn't know an exact value for !!e^6!!, we could find out that !!e^{6.2}!! is about !!22.075\%!! larger, with hardly any calculation.
Why did this work so well? If you look at the expression !!(\star)!! you can see: The terms of the series all have factors of the form !!(x-3)^i!!. When !!x=3.1!!, these are !!(0.1)^i!!, which becomes very small very quickly as !!i!! increases. Because the later terms of the series are very small, they don't affect the final sum, and if we leave them out, we won't mess up the answer too much. So the series works well, producing accurate results from only a few terms, when !!x!! is close to !!3!!.
But in the Maclaurin series, which is around !!x=0!!, those !!(x-3)^i!! terms are !!x^i!! terms intead, and when !!x=3.1!!, they are not small, they're very large! They get bigger as !!i!! increases, and very quickly. (The !! i! !! in the denominator wins, eventually, but that doesn't happen for many terms.) If we leave out these many large terms, we get the wrong results.
The short answer to your question is:
Maclaurin series are only good for calculating functions when !!x!! is close to !!0!!, and become inaccurate as !!x!! moves away from zero. But a Taylor series around !!a!! has its “center” near !!a!! and is most accurate when !!x!! is close to !!a!!.
[Other articles in category /math/se] permanent link
Fri, 18 Dec 2015I only posted three answers in August, but two of them were interesting.
In why this !!\sigma\pi\sigma^{-1}!! keeps apearing in my group theory book? (cycle decomposition) the querent asked about the “conjugation” operation that keeps cropping up in group theory. Why is it important? I sympathize with this; it wasn't adequately explained when I took group theory, and I had to figure it out a long time later. Unfortunately I don't think I picked the right example to explain it, so I am going to try again now.
Consider the eight symmetries of the square. They are of five types:
- Rotation clockwise or counterclockwise by 90°.
- Rotation by 180°.
- Horizontal or vertical reflection
- Diagonal reflection
- The trivial (identity) symmetry
What is meant when I say that a horizontal and a vertical reflection are of the same ‘type’? Informally, it is that the horizontal reflection looks just like the vertical reflection, if you turn your head ninety degrees. We can formalize this by observing that if we rotate the square 90°, then give it a horizontal flip, then rotate it back, the effect is exactly to give it a vertical flip. In notation, we might represent the horizontal flip by !!H!!, the vertical flip by !!V!!, the clockwise rotation by !!\rho!!, and the counterclockwise rotation by !!\rho^{-1}!!; then we have
$$ \rho H \rho^{-1} = V$$
and similarly
$$ \rho V \rho^{-1} = H.$$
Vertical flips do not look like diagonal flips—the diagonal flip leaves two of the corners in the same place, and the vertical flip does not—and indeed there is no analogous formula with !!H!! replaced with one of the diagonal flips. However, if !!D_1!! and !!D_2!! are the two diagonal flips, then we do have
$$ \rho D_1 \rho^{-1} = D_2.$$
In general, When !!a!! and !!b!! are two symmetries, and there is some symmetry !!x!! for which
$$xax^{-1} = b$$
we say that !!a!! is conjugate to !!b!!. One can show that conjugacy is an equivalence relation, which means that the symmetries of any object can be divided into separate “conjugacy classes” such that two symmetries are conjugate if and only if they are in the same class. For the square, the conjugacy classes are the five I listed earlier.
This conjugacy thing is important for telling when two symmetries are group-theoretically “the same”, and have the same group-theoretic properties. For example, the fact that the horizontal and vertical flips move all four vertices, while the diagonal flips do not. Another example is that a horizontal flip is self-inverse (if you do it again, it cancels itself out), but a 90° rotation is not (you have to do it four times before it cancels out.) But the horizontal flip shares all its properties with the vertical flip, because it is the same if you just turn your head.
Identifying this sameness makes certain kinds of arguments much simpler. For example, in counting squares, I wanted to count the number of ways of coloring the faces of a cube, and instead of dealing with the 24 symmetries of the cube, I only needed to deal with their 5 conjugacy classes.
The example I gave in my math.se answer was maybe less perspicuous. I considered the symmetries of a sphere, and talked about how two rotations of the sphere by 17° are conjugate, regardless of what axis one rotates around. I thought of the square at the end, and threw it in, but I wish I had started with it.
How to convert a decimal to a fraction easily? was the month's big winner. OP wanted to know how to take a decimal like !!0.3760683761!! and discover that it can be written as !!\frac{44}{117}!!. The right answer to this is of course to use continued fraction theory, but I did not want to write a long treatise on continued fractions, so I stripped down the theory to obtain an algorithm that is slower, but much easier to understand.
The algorithm is just binary search, but with a twist. If you are looking for a fraction for !!x!!, and you know !!\frac ab < x < \frac cd!!, then you construct the mediant !!\frac{a+c}{b+d}!! and compare it with !!x!!. This gives you a smaller interval in which to search for !!x!!, and the reason you use the mediant instead of using !!\frac12\left(\frac ab + \frac cd\right)!! as usual is that if you use the mediant you are guaranteed to exactly nail all the best rational approximations of !!x!!. This is the algorithm I described a few years ago in your age as a fraction, again; there the binary search proceeds down the branches of the Stern-Brocot tree to find a fraction close to !!0.368!!.
I did ask a question this month: I was looking for a simpler version of the dogbone space construction. The dogbone space is a very peculiar counterexample of general topology, originally constructed by R.H. Bing. I mentioned it here in 2007, and said, at the time:
[The paper] is on my desk, but I have not read this yet, and I may never.
I did try to read it, but I did not try very hard, and I did not understand it. So my question this month was if there was a simpler example of the same type. I did not receive an answer, just a followup comment that no, there is no such example.
[Other articles in category /math/se] permanent link
Sun, 16 Aug 2015My overall SE posting volume was down this month, and not only did I post relatively few interesting items, I've already written a whole article about the most interesting one. So this will be a short report.
I already wrote up Building a box from smaller boxes on the blog here. But maybe I have a couple of extra remarks. First, the other guy's proposed solution is awful. It's long and complicated, which is forgivable if it had answered the question, but it doesn't. And the key point is “blah blah blah therefore code a solver which visits all configurations of the search space”. Well heck, if this post had just been one sentence that ended with “code a solver which visits all configurations of the search space” I would not have any complaints about that.
As an undergraduate I once gave a talk on this topic. One of my examples was the problem of packing 31 dominoes into a chessboard from which two squares have been deleted. There is a simple combinatorial argument why this is impossible if the two deleted squares are the same color, say if they are opposite corners: each domino must cover one square of each color. But if you don't take time to think about the combinatorial argument you could waste a lot of time on computer search learning that there is no solution in that case, and completely miss the deeper understanding that it brings you. So this has been on my mind for a long time.
I wrote a few posts this month where I thought I gave good hints. In How to scale an unit vector !!u!! in such way that !!a u\cdot u=1!! where !!a!! is a scalar I think I did a good job identifying the original author's confusion; he was conflating his original unit vector !!u!! and the scaled, leading him to write !!au\cdot u=1!!. This is sure to lead to confusion. So I led him to the point of writing !!a(bv)\cdot(bv)=1!! and let him take it from there. The other proposed solution is much more rote and mechanical. (“Divide this by that…”)
In Find numbers !!\overline{abcd}!! so that !!\overline{abcd}+\overline{bcd}+\overline{cd}+d+1=\overline{dcba}!! the OP got stuck partway through and I specifically addressed the stuckness; other people solved the problem from the beginning. I think that's the way to go, if the original proposal was never going to work, especially if you stop and say why it was never going to work, but this time OP's original suggestion was perfectly good and she just didn't know how to get to the next step. By the way, the notation !!\overline{abcd}!! here means the number !!1000a+100b+10c+d!!.
In Help finding the limit of this series !!\frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \cdots!! it would have been really easy to say “use the formula” or to analyze the series de novo, but I think I almost hit the nail on the head here: it's just like !!1+\frac12 + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \cdots!!, which I bet OP already knows, except a little different. But I pointed out the wrong difference: I observed that the first sequence is one-fourth the second one (which it is) but it would have been simpler to observe that it's just the second one without the !!1+\frac12!!. I had to review it just now to give the simpler explanation, but I sure wish I'd thought of it at the time. Nobody else pointed it out either. Best of all, would have been to mention both methods. If you can notice both of them you can solve the problem without the advance knowledge of the value of !!1+\frac12+\frac14+\ldots!!, because you have !!4S = 1+\frac12 + S!! and then solve for !!S!!.
In Visualization of Rhombus made of Radii and Chords it seemed that OP just needed to see a diagram (“I really really don't see how two circles can form a rhombus?”), so I drew one.
[Other articles in category /math/se] permanent link
Sat, 18 Jul 2015[ Notice: I originally published this report at the wrong URL. I moved it so that I could publish the June 2015 report at that URL instead. If you're seeing this for the second time, you might want to read the June article instead. ]
A lot of the stuff I've written in the past couple of years has been on Mathematics StackExchange. Some of it is pretty mundane, but some is interesting. I thought I might have a little meta-discussion in the blog and see how that goes. These are the noteworthy posts I made in April 2015.
Languages and their relation : help is pretty mundane, but interesting for one reason: OP was confused about a statement in a textbook, and provided a reference, which OPs don't always do. The text used the symbol !!\subset_\ne!!. OP had interpreted it as meaning !!\not\subseteq!!, but I think what was meant was !!\subsetneq!!.
I dug up a copy of the text and groveled over it looking for the explanation of !!\subset_\ne!!, which is not standard. There was none that I could find. The book even had a section with a glossary of notation, which didn't mention !!\subset_\ne!!. Math professors can be assholes sometimes.
Is there an operation that takes !!a^b!! and !!a^c!!, and returns !!a^{bc}!! is more interesting. First off, why is this even a reasonable question? Why should there be such an operation? But note that there is an operation that takes !!a^b!! and !!a^c!! and returns !!a^{b+c}!!, namely, multiplication, so it's plausible that the operation that OP wants might also exist.
But it's easy to see that there is no operation that takes !!a^b!! and !!a^c!! and returns !!a^{bc}!!: just observe that although !!4^2=2^4!!, the putative operation (call it !!f!!) should take !!f(2^4, 2^4)!! and yield !!2^{4\cdot4} = 2^{16} = 65536!!, but it should also take !!f(4^2, 4^2)!! and yield !!4^{2\cdot2} = 2^4 = 256!!. So the operation is not well-defined. And you can take this even further: !!2^4!! can be written as !!e^{4\log 2}!!, so !!f!! should also take !!f(e^{2\log 4}, e^{2\log 4})!! and yield !!e^{4(\log 4)^2} \approx 2180.37!!.
They key point is that the representation of a number, or even an integer, in the form !!a^b!! is not unique. (Jargon: "exponentiation is not injective".) You can raise !!a^b!!, but having done so you cannot look at the result and know what !!a!! and !!b!! were, which is what !!f!! needs to do.
But if !!f!! can't do it, how can multiplication do it when it multiplies !!a^b!! and !!a^c!! and gets !!a^{b+c}!!? Does it somehow know what !!a!! is? No, it turns out that it doesn't need !!a!! in this case. There is something magical going on there, ultimately related to the fact that if some quantity is increasing by a factor of !!x!! every !!t!! units of time, then there is some !!t_2!! for which it is exactly doubling every !!t_2!! units of time. Because of this there is a marvelous group homomophism $$\log : \langle \Bbb R^+, \times\rangle \to \langle \Bbb R ,+\rangle$$ which can change multiplication into addition without knowing what the base numbers are.
In that thread I had a brief argument with someone who thinks that operators apply to expressions rather than to numbers. Well, you can say this, but it makes the question trivial: you can certainly have an "operator" that takes expressions !!a^b!! and !!a^c!! and yields the expression !!a^{bc}!!. You just can't expect to apply it to numbers, such as !!16!! and !!16!!, because those numbers are not expressions in the form !!a^b!!. I remembered the argument going on longer than it did; I originally ended this paragraph with a lament that I wasted more than two comments on this guy, but looking at the record, it seems that I didn't. Good work, Mr. Dominus.
how 1/0.5 is equal to 2? wants a simple explanation. Very likely OP is a primary school student. The question reminds me of a similar question, asking why the long division algorithm is the way it is. Each of these is a failure of education to explain what division is actually doing. The long division answer is that long division is an optimization for repeated subtraction; to divide !!450\div 3!! you want to know how many shares of three cookies each you can get from !!450!! cookies. Long division is simply a notation for keeping track of removing !!100!! shares, leaving !!150!! cookies, then !!5\cdot 10!! further shares, leaving none.
In this question there was a similar answer. !!1/0.5!! is !!2!! because if you have one cookie, and want to give each kid a share of !!0.5!! cookies, you can get out two shares. Simple enough.
I like division examples that involve giving cookies to kids, because cookies are easy to focus on, and because the motivation for equal shares is intuitively understood by everyone who has kids, or who has been one.
There is a general pedagogical principle that an ounce of examples are worth a pound of theory. My answer here is a good example of that. When you explain the theory, you're telling the student how to understand it. When you give an example, though, if it's the right example, the student can't help but understand it, and when they do they'll understand it in their own way, which is better than if you told them how.
How to read a cycle graph? is interesting because hapless OP is asking for an explanation of a particularly strange diagram from Wikipedia. I'm familiar with the eccentric Wikipedian who drew this, and I was glad that I was around to say "The other stuff in this diagram is nonstandard stuff that the somewhat eccentric author made up. Don't worry if it's not clear; this author is notorious for that."
In Expected number of die tosses to get something less than 5, OP calculated as follows: The first die roll is a winner !!\frac23!! of the time. The second roll is the first winner !!\frac13\cdot\frac23!! of the time. The third roll is the first winner !!\frac13\cdot\frac13\cdot\frac23!! of the time. Summing the series !!\sum_n \frac23\left(\frac13\right)^nn!! we eventually obtain the answer, !!\frac32!!. The accepted answer does it this way also.
But there's a much easier way to solve this problem. What we really want to know is: how many rolls before we expect to have seen one good one? And the answer is: the expected number of winners per die roll is !!\frac23!!, expectations are additive, so the expected number of winners per !!n!! die rolls is !!\frac23n!!, and so we need !!n=\frac32!! rolls to expect one winner. Problem solved!
I first discovered this when I was around fifteen, and wrote about it here a few years ago.
As I've mentioned before, this is one of the best things about mathematics: not that it works, but that you can do it by whatever method that occurs to you and you get the same answer. This is where mathematics pedagogy goes wrong most often: it proscribes that you must get the answer by method X, rather than that you must get the answer by hook or by crook. If the student uses method Y, and it works (and if it is correct) that should be worth full credit.
Bad instructors always say "Well, we need to test to see if the student knows method X." No, we should be testing to see if the student can solve problem P. If we are testing for method X, that is a failure of the test or of the curriculum. Because if method X is useful, it is useful because for some problems, it is the only method that works. It is the instructor's job to find one of these problems and put it on the test. If there is no such problem, then X is useless and it is the instructor's job to omit it from the curriculum. If Y always works, but X is faster, it is the instructor's job to explain this, and then to assign a problem for the test where Y would take more time than is available.
I see now I wrote the same thing in 2006. It bears repeating. I also said it again a couple of years ago on math.se itself in reply to a similar comment by Brian Scott:
If the goal is to teach students how to write proofs by induction, the instructor should damned well come up with problems for which induction is the best approach. And if even then a student comes up with a different approach, the instructor should be pleased. ... The directions should not begin [with "prove by induction"]. I consider it a failure on the part of the instructor if he or she has to specify a technique in order to give students practice in applying it.
[Other articles in category /math/se] permanent link
Thu, 18 Jun 2015A lot of the stuff I've written in the past couple of years has been on math.StackExchange. Some of it is pretty mundane, but some is interesting. My summary of April's interesting posts was well-received, so here are the noteworthy posts I made in May 2015.
What matrix transforms !!(1,0)!! into !!(2,6)!! and tranforms !!(0,1)!! into !!(4,8)!!? was a little funny because the answer is $$\begin{pmatrix}2 & 4 \\ 6 & 8 \end{pmatrix}$$ and yeah, it works exactly like it appears to, there's no trick. But if I just told the guy that, he might feel unnecessarily foolish. I gave him a method for solving the problem and figured that when he saw what answer he came up with, he might learn the thing that the exercise was designed to teach him.
Is a “network topology'” a topological space? is interesting because several people showed up right away to say no, it is an abuse of terminology, and that network topology really has nothing to do with mathematical topology. Most of those comments have since been deleted. My answer was essentially: it is topological, because just as in mathematical topology you care about which computers are connected to which, and not about where any of the computers actually are.
Nobody constructing a token ring network thinks that it has to be a geometrically circular ring. No, it only has to be a topologically circular ring. A square is fine; so is a triangle; topologically they are equivalent, both in networking and in mathematics. The wires can cross, as long as they don't connect at the crossings. But if you use something that isn't topologically a ring, like say a line or a star or a tree, the network doesn't work.
The term “topological” is a little funny. “Topos” means “place” (like in “topography” or “toponym”) but in topology you don't care about places.
Is there a standard term for this generalization of the Euler totient function? was asked by me. I don't include all my answers in these posts, but I think maybe I should have a policy of including all my questions. This one concerned a simple concept from number theory which I was surprised had no name: I wanted !!\phi_k(n)!! to be the number of integers !!m!! that are no larger than !!n!! for which !!\gcd(m,n) = k!!. For !!k=1!! this is the famous Euler totient function, written !!\varphi(n)!!.
But then I realized that the reason it has no name is that it's simply !!\phi_k(n) = \varphi\left(\frac n k\right)!! so there's no need for a name or a special notation.
As often happens, I found the answer myself shortly after I asked the question. I wonder if the reason for this is that my time to come up with the answer is Poisson-distributed. Then if I set a time threshold for how long I'll work on the problem before asking about it, I am likely to find the answer to almost any question that exceeds the threshold shortly after I exceed the threshold. But if I set the threshold higher, this would still be true, so there is no way to win this particular game. Good feature of this theory: I am off the hook for asking questions I could have answered myself. Bad feature: no real empirical support.
how many ways can you divide 24 people into groups of two? displays a few oddities, and I think I didn't understand what was going on at that time. OP has calculated the first few special cases:
1:1 2:1 3:3 4:3 5:12 6:15
which I think means that there is one way to divide 2 people into groups of 2, 3 ways to divide 4 people, and 15 ways to divide 6 people. This is all correct! But what could the 1:1, 3:3, 5:12 terms mean? You simply can't divide 5 people into groups of 2. Well, maybe OP was counting the extra odd person left over as a sort of group on their own? Then odd values would be correct; I didn't appreciate this at the time.
But having calculated 6 special cases correctly, why can't OP calculate the seventh? Perhaps they were using brute force: the next value is 48, hard to brute-force correctly if you don't have a enough experience with combinatorics.
I tried to suggest a general strategy: look at special cases, and not by brute force, but try to analyze them so that you can come up with a method for solving them. The method is unnecessary for the small cases, where brute force enumeration suffices, but you can use the brute force enumeration to check that the method is working. And then for the larger cases, where brute force is impractical, you use your method.
It seems that OP couldn't understand my method, and when they tried to apply it, got wrong answers. Oh well, you can lead a horse to water, etc.
The other pathology here is:
I think I did what you said and I got 1.585times 10 to the 21
for the !!n=24!! case. The correct answer is $$23\cdot21\cdot19\cdot17\cdot15\cdot13\cdot11\cdot9\cdot7\cdot5\cdot3\cdot1 = 316234143225 \approx 3.16\cdot 10^{11}.$$ OP didn't explain how they got !!1.585\cdot10^{21}!! so there's not much hope of correcting their weird error.
This is someone who probably could have been helped in person, but on the Internet it's hopeless. Their problems are Internet communication problems.
Lambda calculus typing isn't especially noteworthy, but I wrote a fairly detailed explanation of the algorithm that Haskell or SML uses to find the type of an expression, and that might be interesting to someone.
I think Special representation of a number is the standout post of the month. OP speculates that, among numbers of the form !!pq+rs!! (where !!p,q,r,s!! are prime), the choice of !!p,q,r,s!! is unique. That is, the mapping !!\langle p,q,r,s\rangle \to pq+rs!! is reversible.
I was able to guess that this was not the case within a couple of minutes, replied pretty much immediately:
I would bet money against this representation being unique.
I was sure that a simple computer search would find counterexamples. In fact, the smallest is !!11\cdot13 + 19\cdot 29 = 11\cdot 43 + 13\cdot 17 = 694!! which is small enough that you could find it without the computer if you are patient.
The obvious lesson to learn from this is that many elementary conjectures of this type can be easily disproved by a trivial computer search, and I frequently wonder why more amateur mathematicians don't learn enough computer programming to investigate this sort of thing. (I wrote recently on the topic of An ounce of theory is worth a pound of search , and this is an interesting counterpoint to that.)
But the most interesting thing here is how I was able to instantly guess the answer. I explained in some detail in the post. But the basic line of reasoning goes like this.
Additive properties of the primes are always distributed more or less at random unless there is some obvious reason why they can't be. For example, let !!p!! be prime and consider !!2p+1!!. This must have exactly one of the three forms !!3n-1, 3n,!! or !!3n+1!! for some integer !!n!!. It obviously has the form !!3n+1!! almost never (the only exception is !!p=3!!). But of the other two forms there is no obvious reason to prefer one over the other, and indeed of the primes up to 10,000, 611 are of the type !!3n!! and and 616 are of the type !!3n-1!!.
So we should expect the value !!pq+rs!! to be distributed more or less randomly over the set of outputs, because there's no obvious reason why it couldn't be, except for simple stuff, like that it's obviously almost always even.
So we are throwing a bunch of balls at random into bins, and the claim is that no bin should contain more than one ball. For that to happen, there must be vastly more bins than balls. But the bins are numbers, and primes are not at all uncommon among numbers, so the number of bins isn't vastly larger, and there ought to be at least some collisions.
In fact, a more careful analysis, which I wrote up on the site, shows that the number of balls is vastly larger—to have them be roughly the same, you would need primes to be roughly as common as perfect squares, but they are far more abundant than that—so as you take larger and larger primes, the number of collisions increases enormously and it's easy to find twenty or more quadruples of primes that all map to the same result. But I was able to predict this after a couple of minutes of thought, from completely elementary considerations, so I think it's a good example of Lower Mathematics at work.
This is an example of a fairly common pathology of math.se questions: OP makes a conjecture that !!X!! never occurs or that there are no examples with property !!X!!, when actually !!X!! almost always occurs or every example has property !!X!!.
I don't know what causes this. Rik Signes speculates that it's just wishful thinking: OP is doing some project where it would be useful to have !!pq+rs!! be unique, so posts in hope that someone will tell them that it is. But there was nothing more to it than baseless hope. Rik might be right.
[ Addendum 20150619: A previous version of this article included the delightful typo “mathemativicians”. ]
[Other articles in category /math/se] permanent link
Sun, 14 Jun 2015[ This page originally held the report for April 2015, which has moved. It now contains the report for June 2015. ]
Is “smarter than” a transitive relationship? concerns a hypothetical "is smarter than" relation with the following paradoxical-seeming property:
most X's are smarter than most Y's, but most Y's are such that it is not the case that most X's are smarter than it.
That is, if !!\mathsf Mx.\Phi(x)!! means that most !!x!! have property !!\Phi!!, then we want both $$\mathsf Mx.\mathsf My.S(x, y)$$ and also $$\mathsf My.\mathsf Mx.\lnot S(x, y).$$
“Most” is a little funny here: what does it mean? But we can pin it down by supposing that there are an infinite number of !!x!!es and !!y!!s, and agreeing that most !!x!! have property !!P!! if there are only a finite number of exceptions. For example, everyone should agree that most positive integers are larger than 7 and that most prime numbers are odd. The jargon word here is that we are saying that a subset contains “most of” the elements of a larger set if it is cofinite.
There is a model of this property, and OP reports that they asked the prof if this was because the "smarter than" relation !!S(x,y)!! could be antitransitive, so that one might have !!S(x,y), S(y,z)!! but also !!S(z,x)!!. The prof said no, it's not because of that, but the OP want so argue that it's that anyway. But no, it's not because of that; there is a model that uses a perfectly simple transitive relation, and the nontransitive thing nothing but a distraction. (The model maps the !!x!!es and !!y!!s onto numbers, and says !!x!! is smarter than !!y!! if its number is bigger.) Despite this OP couldn't give up the idea that the model exists because of intransitive relations. It's funny how sometimes people get stuck on one idea and can't let go of it.
How to generate a random number between 1 and 10 with a six-sided die? was a lot of fun and attracted several very good answers. Top-scoring is Jack D'Aurizio's, which proposes a completely straightforward method: roll once to generate a bit that selects !!N=0!! or !!N=5!!, and then roll again until you get !!M\ne 6!!, and the result is !!N+M!!.
But several other answers were suggested, including two by me, one explaining the general technique of arithmetic coding, which I'll probably refer back to in the future when people ask similar questions. Don't miss NovaDenizen's clever simplification of arithmetic coding, which I want to think about more, or D'Aurizio's suggestion that if you threw the die into a V-shaped trough, it would land with one edge pointing up and thus select a random number from 1 to 12 in a single throw.
Interesting question: Is there an easy-to-remember mapping from edges to numbers from 1–12? Each edge is naturally identified by a pair of distinct integers from 1–6 that do not add to 7.
The oddly-phrased Category theory with objects as logical expressions over !!{\vee,\wedge,\neg}!! and morphisms as? asks if there is a standard way to turn logical expressions into a category, which there is: you put an arrow from !!A\to B!! for each proof that !!A!! implies !!B!!; composition of arrows is concatenation of proofs, and identity arrows are empty proofs. The categorial product, coproduct, and exponential then correspond to !!\land, \lor, !! and !!\to!!.
This got me thinking though. Proofs are properly not lists, they are trees, so it's not entirely clear what the concatenation operation is. For example, suppose proof !!X!! concludes !!A!! at its root and proof !!Y!! assumes !!A!! in more than one leaf. When you concatenate !!X!! and !!Y!! do you join all the !!A!!'s, or what? I really need to study this more. Maybe the Lambek and Scott book talks about it, or maybe the Goldblatt Topoi book, which I actually own. I somehow skipped most of the Cartesian closed category stuff, which is an oversight I ought to correct.
In Why is the Ramsey`s theorem a generalization of the Pigeonhole principle I gave what I thought was a terrific answer, showing how Ramsey's graph theorem and the pigeonhole principle are both special cases of Ramsey's hypergraph theorem. This might be my favorite answer of the month. It got several upvotes, but OP preferred a different answer, with fewer details.
There was a thread a while back about theorems which are generalizations of other theorems in non-obvious ways. I pointed out the Yoneda lemma was a generalization of Cayley's theorem from group theory. I see that nobody mentioned the Ramsey hypergraph theorem being a generalization of the pigeonhole principle, but it's closed now, so it's too late to add it.
In Why does the Deduction Theorem use Union? I explained that the English word and actually has multiple meanings. I know I've seen this discussed in elementary logic texts but I don't remember where.
Finally, Which is the largest power of natural number that can be evaluated by computers? asks if it's possible for a computer to calculate !!7^{120000000000}!!. The answer is yes, but it's nontrivial and you need to use some tricks. You have to use the multiplying-by-squaring trick, and for the squarings you probably want to do the multiplication with DFT. OP was dissatistifed with the answer, and seemed to have some axe to grind, but I couldn't figure out what it was.
[Other articles in category /math/se] permanent link




