Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 31 Dec 2007
Harriet Tubman
Katara and I had a pretty heavy conversation in the car on the way home
from school last week. I should begin by saying that Philadelphia has a lot of murals.
More murals than any other city in the world, in fact. The mural arts
people like to put up murals on large, otherwise ugly party walls.
That is, when you have two buildings that share a wall, and one of
them is torn down, leaving a vacant lot with a giant blank wall, the
mural arts people see it as a prime location and put a mural there.
On the way back from Katara's school we drive through Mantua, which is
not one of the rosier Philadelphia neighborhoods, and has a lot of
vacant lots, and so a lot of murals. We sometimes count the murals on
the way home, and usually pass four or five.
Katara pointed out a mural she liked, and I observed that there was construction on the adjacent vacant lot, which is likely to mean that the mural will be covered up soon by the new building. I mentioned that my favorite Philadelphia mural of all had been on the side of a building that was torn down in 2002.
Katara asked me to tell her about it, so I did. It was the giant mural of Harriet Tubman that used to be on the side of the I. Goldberg building at 9th and Chestnut Streets. It was awesome. There was 40-foot-high painting of Harriet Tubman raising her lantern at night, leading a crowd of people through a dark tunnel (Underground Railroad, obviously) into a beautiful green land beyond, and giant chains that had once barred the tunnel, but which were now shattered.
It's hard to photograph a mural well. The scale and the space do not translate to photographs. It looked something like this:

Here's a detail:

Anyway, I said that my favorite mural had been the Harriet Tubman one, and that it had been torn down before she was born. (As you can see from the picture, the building was located next to a parking lot. The owners of the building ripped it down to expand the parking lot.)
But then Katara asked me to tell her about Harriet Tubman, and that was something of a puzzle, because Katara is only three and a half. But the subject is not intrinsically hard to understand; it's just unpleasant. And I don't believe that it's my job to shield her from the unpleasantness of the world, but it is my job to try to answer her questions, if I can. So I tried.
"Okay, you know how you own stuff, and you can do what you want, because it's yours?"
Sure, she understands that. We have always been very clear in distinguishing between her stuff and our stuff, and in defending her property rights against everyone, including ourselves.
"But you know that you can't own other people, right?"
This was confusing, so I tried an example. "Emily is your friend, and sometimes you ask her to do things, and maybe she does them. But you can't make her do things she doesn't want to do, because she gets to decide for herself what she does."
Sure, of course. Now we're back on track. "Well, a long time ago, some people decided that they owned some other people, called slaves, and that the slaves would have to do whatever their owners said, even if they didn't want to."
Katara was very indignant. I believe she said "That's not nice!" I agreed; I said it was terrible, one of the most terrible things that had ever happened in this country. And then we were over the hump. I said that slaves sometimes tried to run away from the owners, and get away to a place where they could do whatever they wanted, and that Harriet Tubman helped slaves escape.
There you have Harriet Tubman in a nutshell for a three-and-a-half year-old. It was a lot easier than the time she asked me why ships in 1580 had no women aboard.
I did not touch the racial issue at all. When you are explaining something complicated, it is important to keep it in bite-sized chunks, and to deal with them one at a time, and I thought slavery was already a big enough chunk. Katara is going to meet this issue head-on anyway, probably sooner than I would like, because she is biracial.
I explained about the Underground Railroad, and we discussed what a terrible thing slavery must have been. Katara wanted to know what the owners made the slaves do, and there my nerve failed me. I told her that I didn't want to tell her about it because it was so awful and frightening. I had pictures in my head of beatings, and of slaves with their teeth knocked out so that they could be forced to eat, to break hunger strikes, and of rape, and families broken up, and I just couldn't go there. Well, I suppose it is my job to shield her from some the unpleasantness of the world, for a while.
I realize now I could have talked about slaves forced to do farm work, fed bad food, and so on, but I don't think that would really have gotten the point across. And I do think I got the point across: the terrible thing about being a slave is that you have to do what you are told, whether you want to or not. All preschoolers understand that very clearly, whereas for Katara, toil and neglect are rather vague abstractions. So I'm glad I left it where I did.
But then a little later Katara asked some questions about family relations among the slaves, and if slaves had families, and I said yes, that if a mother had a child, then her child belonged to the same owner, and sometimes the owner would take the child away from its mother and sell it to someone else and they would never see each other again. Katara, of course, was appalled by this.
I'm not sure I had a point here, except that Katara is a thoughtful kid, who can be trusted with grown-up issues even at three and a half years old, and I am very proud of her.
That seems like a good place to end the year. Thanks for reading.
[ Addendum 20080201: The mural was repainted in a new location, at 2950 Germantown Avenue! ]
[ Addendum 20160420: The Germantown Avenue mural is by the same artist, Sam Donovan, but is not the same design. The model was Kat Lindsey. Donovan’s web site provides a better picture. ]
[Other articles in category /kids] permanent link
Sun, 30 Dec 2007
Welcome to my ~/bin
In the previous article I
mentioned "a conference tutorial about the contents of my
~/bin directory". Usually I have a web page about each
tutorial, with a description, and some sample slides, and I wanted to
link to the page about this tutorial. But I found to my surprise that
I had forgotten to make the page about this one.
So I went to fix that, and then I couldn't decide which sample slides to show. And I haven't given the tutorial for a couple of years, and I have an upcoming project that will prevent me from giving it for another couple of years. Eh, figuring out what to put online is more trouble than it's worth. I decided it would be a lot less toil to just put the whole thing online.
The materials are copyright © 2004 Mark Jason Dominus, and are not under any sort of free license.
But please enjoy them anyway.
I think the title is an accidental ripoff of an earlier class by Damian Conway. I totally forgot that he had done a class on the same subject, and I think he used the same title. But that just makes us even, because for the past few years he has been making money going around giving talks on "Conference Presentation Aikido", which is a blatant (and deliberate) ripoff of my 2002 Perl conference talk on Conference Presentation Judo. So I don't feel as bad as I might have.
Welcome to my ~/bin complete slides and other materials.
I hereby wish you a happy new year, unless you don't want one, in which case I wish you a crappy new year instead.
[Other articles in category /prog/perl] permanent link
Thu, 20 Dec 2007
Another trivial utility: accumulate
As usual, whenever I write one of these things, I wonder why it took
me so long to get off my butt and put in the five minutes of work that
were actually required. I've wanted something like this for
years. It's called accumulate. It reads an input of
this form:
k1 v1
k1 v2
k2 v3
k1 v4
k2 v5
k3 v6
and writes it out in this format:
k1 v1 v2 v4
k2 v3 v5
k3 v6
I wanted it this time because I had a bunch of files that included some
duplicates, and wanted to get rid of the duplicates. So:
md5sum * | accumulate | perl -lane 'unlink @F[2..$#F]'
(Incidentally, people sometimes argue that Perl's .. operator
should count backwards when the left operand exceeds the right one.
These people are wrong. There is only one argument that needs to be
made to refute this idea; maybe it is the only argument that
can be made. And examples of it abound. The code above is one
such example.)I'm afraid of insulting you by showing the source code for accumulate, because of course it is so very trivial, and you could write it in five minutes, as I did. But who knows; maybe seeing the source has some value:
#!/usr/bin/perl
use Getopt::Std;
my %opt = (k => 1, v => 2);
getopts('k:v:', \%opt) or usage();
for (qw(k v)) {
$opt{$_} -= 1 if $opt{$_} > 0;
}
while (<>) {
chomp;
my @F = split;
push @{$K{$F[$opt{k}]}}, $F[$opt{v}];
}
for my $k (keys %K) {
print "$k @{$K{$k}}\n";
}
It's tempting to add a -F option to tell it that the input is
not delimited by white space, or an option to change the output
format, or blah blah blah, but I managed to restrain myself, mostly.Several years ago I wrote a conference tutorial about the contents of my ~/bin directory. The clearest conclusion that transpired from my analysis was that the utilities I write have too many features that I don't use. The second-clearest was that I waste too much time writing custom argument-parsing code instead of using Getopt::Std. I've tried to learn from this. One thing I found later is that a good way to sublimate the urge to put in some feature is to put in the option to enable it, and to document it, but to leave the feature itself unimplemented. This might work for you too if you have the same problem.
I did put in -k and -v options to control which input columns are accumulated. These default to the first and second columns, naturally. Maybe this was a waste of time, since it occurs to me now that accumulate -k k -v v could be replaced by cut -fk,v | accumulate, if only cut didn't suck quite so badly. Of course one could use awk {print "$k $v" } | accumulate to escape cut's suckage. And some solution of this type obviates the need for accumulate's putative -F option also. Well, I digress.
The accumulate program itself reminds me of a much more ambitious project I worked on for a while between 1998 and 2001, as does the yucky line:
push @{$K{$F[$opt{k}]}}, $F[$opt{v}];
The ambitious project was tentatively named "twingler".Beginning Perl programmers often have trouble with compound data structures because Perl's syntax for the nested structures is so horrendous. Suppose, for example, that you have a reference to a two-dimensional array $aref, and you want to produce a hash, such that each value in the array appears as a key in the hash, associated with a list of strings in the form "m,n" indicating where in the array that value appeared. Well, of course it is obviously nothing more than:
for my $a1 (0 .. $#$aref) {
for my $a2 (0 .. $#{$aref->[$a1]}) {
push @{$hash{$aref->[$a1][$a2]}}, "$a1,$a2";
}
}
Obviously. <sarcasm>Geez, a child could see
that.</sarcasm>The idea of twingler was that you would specify the transformation you wanted declaratively, and it would then write the appropriate Perl code to perform the transformation. The interesting part of this project is figuring out the language for specifying the transformation. It must be complex enough to be able to express most of the interesting transformations that people commonly want, but if it isn't at the same time much simpler than Perl itself, it isn't worth using. Nobody will see any point in learning a new declarative language for expressing Perl data transformations unless it is itself simpler to use than just writing the Perl would have been.
[ Addendum 20150508: I dumped all my Twingler notes on the blog last year. ]
There are some hard problems here: What do people need? What subset of this can be expressed simply? How can we design a simple, limited language that people can use to express their needs? Can the language actually be compiled to Perl?
I had to face similar sorts of problems when I was writing linogram, but in the case of linogram I was more successful. I tinkered with twingler for some time and made several pages of (typed) notes but never came up with anything I was really happy with.
[ Addendum 20150508: I dumped all my Twingler notes on the blog last year. ]
At one point I abandoned the idea of a declarative language, in favor of just having the program take a sample input and a corresponding sample output, and deduce the appropriate transformation from there. For example, you would put in:
[ [ A, B ],
[ C, B ],
[ D, E ] ]
and
{ B => [A, C],
E => [D],
}
and it would generate:
for my $a1 (@$input) {
my ($e1, $e2) = @$a1;
push @{$output{$e2}}, $e1;
}
And then presumably you could eyeball this, and if what you really
wanted was @{$a1}[0, -1] instead of @$a1 you could
tinker it into the form you needed without too much extra trouble.
This is much nicer from a user-experience point of view, but at the
same time it seems more difficult to implement. I had some ideas. One idea was to have it generate a bunch of expressions for mapping single elements from the input to the output, and then to try to unify those expressions. But as I said, I never did figure it out.
It's a shame, because it would have been pretty cool if I had gotten it to work.
The MIT CS grad students' handbook used to say something about how you always need to have several projects going on at once, because two-thirds of all research projects end in failure. The people you see who seem to have one success after another actually have three projects going on all the time, and you only see the successes. This is a nice example of that.
[Other articles in category /prog] permanent link
Tue, 18 Dec 2007
Happy birthday Perl!
In case you hadn't yet heard, today is the 20th anniversary of the
first release of Perl.
[Other articles in category /anniversary] permanent link
Mon, 17 Dec 2007
Strangest Asian knockoff yet
A few years ago Lorrie and I had brunch at the very trendy
Philadelphia restaurant "Striped Bass". I guess it wasn't too
impressive, because usually if the food is really good I will remember
what I ate, even years later, and I do not. But the plates
were awesome. They were round, with an octagonal depression in the
center, a rainbow-colored pattern around the edge, garnished with
pictures of ivy leaves.
Good plates have the name of the maker on the back. These were made by Villeroy & Boch. Some time later, we visited the Villeroy & Boch outlet in Woodbury, New York, and I found the pattern I wanted, "Pasadena". The cool circular plates from Striped Bass were only for sale to restaurants, but the standard ones were octagonal, which is also pretty cool. So I bought a set. (57% off list price! Whee!)
(The picture gets much bigger when you click it.)
They no longer make these plates. If you broke one, and wanted a replacement, you could buy one online for $43.99. Ouch! But there is another option, if you are not too fussy.
Many years after I bought my dishes, I was shopping in one of the big Asian grocery stores on Washington Avenue. They have a kitchenware aisle. I found this plate:
The real VB plate is made of porcelain. The Washington Avenue knockoff is made of plastic.
Of course I bought it. It is hilarious! And it only cost two dollars.
[ Addendum 20170131: A challenger appears! ]
[Other articles in category /food] permanent link
Tue, 11 Dec 2007
More notes on power series
It seems I wasn't done thinking about this. I pointed out in yesterday's article that,
having defined the cosine function as:
coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])
one has the choice to define the sine function analogously:
sins = zipWith (*) (cycle [0,1,0,-1]) (map ((1/) . fact) [0..])
or in a totally different way, by reference to cosine:
sins = (srt . (add one) . neg . sqr) coss
Here is a third way. Sine and cosine are solutions of the
differential equation f = -f''. Since I now have enough
infrastructure to get Haskell to solve differential equations, I can
use this to define sine and cosine:
solution_of_equation f0 f1 = func
where func = int f0 (int f1 (neg func))
sins = solution_of_equation 0 1
coss = solution_of_equation 1 0
The constants f0 and f1 specify the initial
conditions of the differential equation, values for f(0) and
f'(0), respectively.Well, that was fun.
One problem with the power series approach is that the answer you get is not usually in a recognizable form. If what you get out is
[1.0,0.0,-0.5,0.0,0.0416666666666667,0.0,-0.00138888888888889,0.0,2.48015873015873e-05,0.0,...]
then you might recognize it as the cosine function. But last night I
couldn't sleep because I was wondering about the equation
f·f' = 1, so I got up and put it in, and out
came:
[1.0,1.0,-0.5,0.5,-0.625,0.875,-1.3125,2.0625,-3.3515625,5.5859375,-9.49609375,16.40234375,...]
Okay, now what? Is this something familiar? I'm wasn't sure. One
thing that might help a bit is to get the program to disgorge rational
numbers rather than floating-point numbers. But even that won't
completely solve the problem. One thing I was thinking about in the shower is doing Fourier analysis; this should at least identify the functions that are sinusoidal. Suppose that we know (or believe, or hope) that some power series a1x + a3x3 + ... actually has the form c1 sin x + c2 sin 2x + c3 sin 3x + ... . Then we can guess the values of the ci by solving a system of n equations of the form:
$$\sum_{i=1}^n i^kc_i = k!a_k\qquad{\hbox{($k$ from 1 to $n$)}}$$
And one ought to be able to do something analogous, and more general, by including the cosine terms as well. I haven't tried it, but it seems like it might work.But what about more general cases? I have no idea. If you have the happy inspiration to square the mystery power series above, you get [1, 2, 0, 0, 0, ...], so it is √(2x+1), but what if you're not so lucky? I wasn't; I solved it by a variation of Gareth McCaughan's method of a few days ago: f·f' is the derivative of f2/2, so integrate both sides of f·f' = 1, getting f2/2 = x + C, and so f = √(2x + C). Only after I had solved the equation this way did I try squaring the power series, and see that it was simple.
I'll keep thinking.
[Other articles in category /math] permanent link
Mon, 10 Dec 2007
Lazy square roots of power series return
In an earlier article I
talked about wanting to use lazy streams to calculate the power series
expansion of the solution of this differential equation:
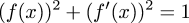
At least one person wrote to ask me for the Haskell code for the power series calculations, so here's that first off.
A power series a0 + a1x + a2x2 + a3x3 + ... is represented as a (probably infinite) list of numbers [a0, a1, a2, ...]. If the list is finite, the missing terms are assumed to be all 0.
The following operators perform arithmetic on functions:
-- add functions a and b
add [] b = b
add a [] = a
add (a:a') (b:b') = (a+b) : add a' b'
-- multiply functions a and b
mul [] _ = []
mul _ [] = []
mul (a:a') (b:b') = (a*b) : add (add (scale a b')
(scale b a'))
(0 : mul a' b')
-- termwise multiplication of two series
mul2 = zipWith (*)
-- multiply constant a by function b
scale a b = mul2 (cycle [a]) b
neg a = scale (-1) a
And there are a bunch of other useful utilities:
-- 0, 1, 2, 3, ... iota = 0 : zipWith (+) (cycle [1]) iota -- 1, 1/2, 1/3, 1/4, ... iotaR = map (1/) (tail iota) -- derivative of function a deriv a = tail (mul2 iota a) -- integral of function a -- c is the constant of integration int c a = c : (mul2 iotaR a) -- square of function f sqr f = mul f f -- constant function con c = c : cycle [0] one = con 1
| Buy Structure and Interpretation of Computer Programs from Bookshop.org (with kickback) (without kickback) |
-- reciprocal of argument function inv (s0:st) = r where r = r0 : scale (negate r0) (mul r st) r0 = 1/s0 -- divide function a by function b squot a b = mul a (inv b) -- square root of argument function srt (s0:s) = r where r = r0 : (squot s (add [r0] r)) r0 = sqrt(s0)We can define the cosine function as follows:
coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])We could define the sine function analogously, or we can say that sin(x) = √(1 - cos2(x)):
sins = (srt . (add one) . neg . sqr) cossThis works fine.
Okay, so as usual that is not what I wanted to talk about; I wanted to show how to solve the differential equation. I found I was getting myself confused, so I decided to try to solve a simpler differential equation first. (Pólya says: "Can you solve a simpler problem of the same type?" Pólya is a smart guy. When the voice talking in your head is Pólya's, you better pay attention.) The simplest relevant differential equation seemed to be f = f'. The first thing I tried was observing that for all f, f = f0 : mul2 iotaR f'. This yields the code:
f = f0 : mul2 iotaR (deriv f)
This holds for any function, and so it's unsolvable. But if you
combine it with the differential equation, which says that f =
f', you get:
f = f0 : mul2 iotaR f
where f0 = 1 -- or whatever the initial conditions dictate
and in fact this works just fine. And then you can observe that this
is just the definition of int; replacing the definition with
the name, we have:
f = int f0 f
where f0 = 1 -- or whatever
This runs too, and calculates the power series for the
exponential function, as it should. It's also transparently obvious,
and makes me wonder why it took me so long to find. But I was looking
for solutions of the form:
f = deriv f
which Haskell can't figure out. It's funny that it only handles
differential equations when they're expressed as integral equations. I
need to meditate on that some more.It occurs to me just now that the f = f0 : mul2 iotaR (deriv f) identity above just says that the integral and derivative operators are inverses. These things are always so simple in hindsight.
Anyway, moving along, back to the original problem, instead of f = f', I want f2 + (f')2 = 1, or equivalently f' = √(1 - f2). So I take the derivative-integral identity as before:
f = int f0 (deriv f)
and put in √(1 - f2) for deriv f:
f = int f0 ((srt . (add one) . neg . sqr) f)
where f0 = sqrt 0.5 -- or whatever
And now I am done; Haskell cheerfully generates the power series
expansion for f for any given initial condition. (The
parameter f0 is precisely the desired value of f(0).)
For example, when f(0) = √(1/2), as above, the calculated
terms show the function to be exactly
√(1/2)·(sin(x) + cos(x)); when f(0)
= 0, the output terms are exactly those of sin(x). When
f(0) = 1, the output blows up and comes out as [1, 0, NaN, NaN,
...]. I'm not quite sure why yet, but I suspect it has something to
do with there being two different solutions that both have f(0) = 1. All of this also works just fine in Perl, if you build a suitable lazy-list library; see chapter 6 of HOP for complete details. Sample code is here. For a Scheme implementation, see SICP. For a Java, Common Lisp, Python, Ruby, or SML implementation, do the obvious thing.
But anyway, it does work, and I thought it might be nice to blog about something I actually pursued to completion for a change. Also I was afraid that after my week of posts about Perl syntax, differential equations, electromagnetism, Unix kernel internals, and paint chips in the shape of Austria, the readers of Planet Haskell, where my blog has recently been syndicated, were going to storm my house with torches and pitchforks. This article should mollify them for a time, I hope.
[ Addendum 20071211: Some additional notes about this. ]
[Other articles in category /math] permanent link
Sun, 09 Dec 2007
Four ways to solve a nonlinear differential equation
In a recent article I
mentioned the differential equation:
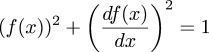
I got interested in this a few weeks ago when I was sitting in on a freshman physics lecture at Penn. I took pretty much the same class when I was a freshman, but I've never felt like I really understood physics. Sitting in freshman physics class again confirms this. Every time I go to a class, I come out with bigger questions than I went in.
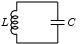 The instructor was
talking about LC circuits, which are simple circuits with a capacitor
(that's the "C") and an inductor (that's the "L", although I don't
know why). The physics people claim that in such a circuit the
capacitor charges up, and then discharges again, repeatedly. When one
plate of the capacitor is full of electrons, the electrons want to
come out, and equalize the charge on the plates, and so they make a
current flowing from the negative to the positive plate. Without the inductor, the current
would fall off exponentially, as the charge on the plates equalized.
Eventually the two plates would be equally charged and nothing more
would happen.
The instructor was
talking about LC circuits, which are simple circuits with a capacitor
(that's the "C") and an inductor (that's the "L", although I don't
know why). The physics people claim that in such a circuit the
capacitor charges up, and then discharges again, repeatedly. When one
plate of the capacitor is full of electrons, the electrons want to
come out, and equalize the charge on the plates, and so they make a
current flowing from the negative to the positive plate. Without the inductor, the current
would fall off exponentially, as the charge on the plates equalized.
Eventually the two plates would be equally charged and nothing more
would happen.
But the inductor generates an electromotive force that tends to resist any change in the current through it, so the decreasing current in the inductor creates a force that tends to keep the electrons moving anyway, and this means that the (formerly) positive plate of the capacitor gets extra electrons stuffed into it. As the charge on this plate becomes increasingly negative, it tends to oppose the incoming current even more, and the current does eventually come to a halt. But by that time a whole lot of electrons have moved from the negative to the positive plate, so that the positive plate has become negative and the negative plate positive. Then the electrons come out of the newly-negative plate and the whole thing starts over again in reverse.
In practice, of course, all the components offer some resistance to the current, so some of the energy is dissipated as heat, and eventually the electrons stop moving back and forth.
Anyway, the current is nothing more nor less than the motion of the electrons, and so it is proportional to the derivative of the charge in the capacitor. Because to say that current is flowing is exactly the same as saying that the charge in the capacitor is changing. And the magnetic flux in the inductor is proportional to rate of change of the current flowing through it, by Maxwell's laws or something.
The amount of energy in the whole system is the sum of the energy stored in the capacitor and the energy stored in the magnetic field of the inductor. The former turns out to be proportional to the square of the charge in the capacitor, and the latter to the square of the current. The law of conservation of energy says that this sum must be constant. Letting f(t) be the charge at time t, then df/dt is the current, and (adopting suitable units) one has:
$$(f(x))^2 + \left(df(x)\over dx\right)^2 = 1$$
which is the equation I was considering.Anyway, the reason for this article is mainly that I wanted to talk about the different methods of solution, which were all quite different from each other. Michael Lugo went ahead with the power series approach I was using. Say that:
$$ \halign{\hfil $\displaystyle #$&$\displaystyle= #$\hfil\cr f & \sum_{i=0}^\infty a_{i}x^{i} \cr f' & \sum_{i=0}^\infty (i+1)a_{i+1}x^{i} \cr } $$
Then:
$$ \halign{\hfil $\displaystyle #$&$\displaystyle= #$\hfil\cr f^2 & \sum_{i=0}^\infty \sum_{j=0}^{i} a_{i-j} a_j x^{i} \cr (f')^2 & \sum_{i=0}^\infty \sum_{j=0}^{i} (i-j+1)a_{i-j+1}(j+1)a_{j+1} x^{i} \cr } $$
And we want the sum of these two to be equal to 1.Equating coefficients on both sides of the equation gives us the following equations:
| !!a_0^2 + a_1^2!! | = | 1 |
| !!2a_0a_1 + 4a_1a_2!! | = | 0 |
| !!2a_0a_2 + a_1^2 + 6a_1a_3 + 4a_2^2!! | = | 0 |
| !!2a_0a_3 + 2a_1a_2 + 8a_1a_4 + 12a_2a_3!! | = | 0 |
| !!2a_0a_4 + 2a_1a_3 + a_2^2 + 10a_1a_5 + 16a_2a_4 + 9a_3^2!! | = | 0 |
| ... | ||
Now take the next line from the table, 2a0a2 + a12 + 6a1a3 + 4a22. This can be separated into the form 2a2(a0 + 2a2) + a1(a1 + 6a3). The left-hand term is zero, by the previous paragraph, and since the whole thing equals zero, we have a3 = -a1/6.
Continuing in this way, we can conclude that a0 = -2!a2 = 4!a4 = -6!a6 = ..., and that a1 = -3!a3 = 5!a5 = ... . These should look familiar from first-year calculus, and together they imply that f(x) = a0 cos(x) + a1 sin(x), where (according to the first line of the table) a02 + a12 = 1. And that is the complete solution of the equation, except for the case we omitted, when either a0 or a1 is zero; these give the trivial solutions f(x) = ±1.
Okay, that was a lot of algebra grinding, and if you're not as clever as M. Lugo, you might not notice that the even terms of the series depend only on a0 and the odd terms only on a1; I didn't. I thought they were all mixed together, which is why I alluded to "a bunch of not-so-obvious solutions" in the earlier article. Is there a simpler way to get the answer?
Gareth McCaughan wrote to me to point out a really clever trick that solves the equation right off. Take the derivative of both sides of the equation; you immediately get 2ff' + 2f'f'' = 0, or, factoring out f', f'(f + f'') = 0. So there are two solutions: either f'=0 and f is a constant function, or f + f'' = 0, which even the electrical engineers know how to solve.
David Speyer showed a third solution that seems midway between the two in the amount of clever trickery required. He rewrote the equation as:
$${df\over dx} = \sqrt{1 - f^2}$$
$${df\over\sqrt{1 - f^2} } = dx$$
The left side is an old standby of calculus I classes; it's the derivative of the arcsine function. On integrating both sides, we have:$$\arcsin f = x + C$$
so f = sin(x + C). This is equivalent to the a0 cos(x) + a1 sin(x) form that we got before, by an application of the sum-of-angles formula for the sine function. I think M. McCaughan's solution is slicker, but M. Speyer's is the only one that I feel like I should have noticed myself.Finally, Walt Mankowski wrote to tell me that he had put the question to Maple, which disgorged the following solution after a few seconds:
f(x) = 1, f(x) = -1, f(x) = sin(x - _C1), f(x) = -sin(x - _C1).This is correct, except that the appearance of both sin(x + C) and -sin(x + C) is a bit odd, since -sin(x + C) = sin(x + (C + π)). It seems that Maple wasn't clever enough to notice that. Walt says he will ask around and see if he can find someone who knows what Maple did to get the solution here.
I would like to add a pithy and insightful conclusion to this article, but I've been working on it for more than a week now, and also it's almost lunch time, so I think I'll have to settle for observing that sometimes there are a lot of ways to solve math problems.
Thanks again to everyone who wrote in about this.
[Other articles in category /math] permanent link
Sat, 08 Dec 2007
Corrections about sync(2)
I made some errors in today's post
about sync and fsync.
Most important, I said that "the sync() system call marks all the kernel buffers as dirty". This is totally wrong, and doesn't even make sense. Dirty buffers are those with data that needs to be written out. Marking a non-dirty buffer as dirty is a waste of time, since nothing has changed in the buffer, but it will now be rewritten anyway. What sync() does is schedule all the dirty buffers to be written as soon as possible.
On some recent systems, sync() actually waits for all the dirty buffers to be written, and a bunch of people tried to correct me about this. But my original article was right: historically, it was not so, and even today it's not universally true. In former times, sync() would schedule the buffers for writing, and then return before the data was actually written.
I said that one of the duties of init was to call sync() every thirty seconds, but this was mistaken. That duty actually fell to a separate program, known as update. While discussing this with one of the readers who wrote to correct me, I looked up the source for Version 7 Unix, to make sure I was right, and it's so short I thought I might as well show it here:
/*
* Update the file system every 30 seconds.
* For cache benefit, open certain system directories.
*/
#include <signal.h>
char *fillst[] = {
"/bin",
"/usr",
"/usr/bin",
0,
};
main()
{
char **f;
if(fork())
exit(0);
close(0);
close(1);
close(2);
for(f = fillst; *f; f++)
open(*f, 0);
dosync();
for(;;)
pause();
}
dosync()
{
sync();
signal(SIGALRM, dosync);
alarm(30);
}
The program is so simple I don't have much more to say about it. It
initially invokes dosync(), which calls sync() and
then schedules another call to dosync() in 30 seconds. Note
that the 0 in the second argument to open had not
yet been changed to O_RDONLY. The pause() call is
equivalent to sleep(0): it causes the process to relinquish
its time slice whenever it is active.In various systems more recent than V7, the program was known by various names, but it was update for a very long time.
Several people wrote to correct me about the:
# sync
# sync
# sync
# halt
thing, some saying that I had the reason wrong, or that it did not make
sense, or that only two syncs were used, rather than three.
But I had it right. People did use three, and they did it for the
reason I said, whether that makes sense or not. (Some of the people
who miscorrected me were unaware that sync() would finish and
exit before the data was actually written.) But for example, see this
old Usenet thread for a discussion of the topic that confirms what
I said.Nobody disputed my contention that Linus was suffering from the promptings of the Evil One when he tried to change the semantics of fsync(), and nobody seems to know the proper name of the false god of false efficiency. I'll give this some thought and see what I can come up with.
Thanks to Tony Finch, Dmitry Kim, and Stefan O'Rear for discussion of these points.
[Other articles in category /Unix] permanent link
Dirty, dirty buffers!
One side issue that arose during my talk on Monday about
inodes was the write-buffering normally done by Unix kernels. I
wrote a pretty long note to the PLUG mailing list about it, and
I thought I'd repost it here.
When your process asks the kernel to write data:
int bytes_written = write(file_descriptor,
buffer,
n_bytes);
the kernel normally copies the data from your buffer into a kernel
buffer, and then, instead of writing out the data to disk, it marks
its buffer as "dirty" (that is, as needing to be written eventually),
and reports success back to the process immediately, even though the
dirty buffer has not yet been written, and the data is not yet on the disk.Normally, the kernel writes out the dirty buffer in due time, and the data makes it to the disk, and you are happy because your process got to go ahead and do some more work without having to wait for the disk, which could take milliseconds. ("A long time", as I so quaintly called it in the talk.) If some other process reads the data before it is written, that is okay, because the kernel can give it the updated data out of the buffer.
But if there is a catastrophe, say a power failure, then you see the bad side of this asynchronous writing technique, because the data, which your process thought had been written, and which the kernel reported as having been written, has actually been lost.
There are a number of mechanisms in place to deal with this. The oldest is the sync() system call, which marks all the kernel buffers as dirty. All Unix systems run a program called init, and one of init's principal duties is to call sync() every thirty seconds or so, to make sure that the kernel buffers get flushed to disk at least every thirty seconds, and so that no crash will lose more than about thirty seconds' worth of data.
(There is also a command-line program sync which just does a sync() call and then exits, and old-time Unix sysadmins are in the habit of halting the system with:
# sync
# sync
# sync
# halt
because the second and third syncs give the kernel time to actually
write out the
buffers that were marked dirty by the first sync. Although I
suspect that few of them know why they do this. I swear I am not
making this up.)But for really crucial data, sync() is not enough, because, although it marks the kernel buffers as dirty, it still does not actually write the data to the disk.
So there is also an fsync() call; I forget when this was introduced. The process gives fsync() a file descriptor, and the call demands that the kernel actually write the associated dirty buffers to disk, and does not return until they have been. And since, unlike write(), it actually waits for the data to go to the disk, a successful return from fsync() indicates that the data is truly safe.
The mail delivery agent will use this when it is writing your email to your mailbox, to make sure that no mail is lost.
Some systems have an O_SYNC flag than the process can supply when it opens the file for writing:
int fd = open("blookus", O_WRONLY | O_SYNC);
This sets the O_SYNC flag in the kernel file pointer
structure, which means that whenever data is
written to this file pointer, the kernel, contrary to its usual
practice, will implicitly fsync() the descriptor.Well, that's not what I wanted to write about here. What I meant to discuss was...
No, wait. That is what I wanted to write about. How about that?
Anyway, there's an interesting question that arises in connection with fsync(): suppose you fsync() a file. That guarantees that the data will be written. But does it also guarantee that the mtime and the file extent of the file will be updated? That is, does it guarantee that the file's inode will be written?
On most systems, yes. But on some versions of Linux's ext2 filesystem, no. Linus himself broke this as a sacrifice to the false god of efficiency, a very bad decision in my opinion, for reasons that should be obvious to everyone but those in the thrall of Mammon. (Mammon's not right here. What is the proper name of the false god of efficiency?)
Sanity eventually prevailed. Recent versions of Linux have an fsync() call, which updates both the data and the inode, and a fdatasync() call, which only guarantees to update the data.
[ Addendum 20071208: Some of this is wrong. I posted corrections. ]
[Other articles in category /Unix] permanent link
Fri, 07 Dec 2007
Freshman electromagnetism questions
As I haven't quite managed to mention here before, I have occasionally
been sitting in on one of Penn's first-year physics classes, about
electricity and magnetism. I took pretty much the same class myself
during my freshman year of college, so all the material is quite
familiar to me.
But, as I keep saying here, I do not understand physics very well, and I don't know much about it. And every time I go to a freshman physics lecture I come out feeling like I understand it less than I went in.
I've started writing down my questions in class, even though I don't really have anyone to ask them to. (I don't want to take up the professor's time, since she presumably has her hands full taking care of the paying customers.) When I ask people I know who claim to understand physics, they usually can't give me plausible answers.
Maybe I should mutter something here under my breath about how mathematicians and mathematics students are expected to have a better grasp on fundamental matters.
The last time this came up for me I was trying to understand the phenomenon of dissolving. Specifically, why does it usually happen that substances usually dissolve faster and more thoroughly in warmer solutions than in cooler solutions? I asked a whole bunch of people about this, up to and including a full professor of physical chemistry, and never got a decent answer.
The most common answer, in fact, was incredibly crappy: "the warm solution has higher entropy". This is a virtus dormitiva if ever there was one. There's a scene in a play by Molière in which a candidate for a medical degree is asked by the examiners why opium puts people to sleep. His answer, which is applauded by the examiners, is that it puts people to sleep because it has a virtus dormitiva. That is, a sleep-producing power. Saying that warm solutions dissolve things better than cold ones because they have more entropy is not much better than saying that it is because they have a virtus dormitiva.
The entropy is not a real thing; it is a reification of the power that warmer substances have to (among other things) dissolve solutes more effectively than cooler ones. Whether you ascribe a higher entropy to the warm solution, or a virtus dissolva to it, comes to the same thing, and explains nothing. I was somewhat disgusted that I kept getting this non-answer. (See my explanation of why we put salt on sidewalks when it snows to see what sort of answer I would have preferred. Probably there is some equally useless answer one could have given to that question in terms of entropy.)
(Perhaps my position will seem less crackpottish if I a make an analogy with the concept of "center of gravity". In mechanics, many physical properties can be most easily understood in terms of the center of gravity of some object. For example, the gravitational effect of small objects far apart from one another can be conveniently approximated by supposing that all the mass of each object is concentrated at its center of gravity. A force on an object can be conveniently treated mathematically as a component acting toward the center of gravity, which tends to change the object's linear velocity, and a component acting perpendicular to that, which tends to change its angular velocity. But nobody ever makes the mistake of supposing that the center of gravity has any objective reality in the physical universe. Everyone understands that it is merely a mathematical fiction. I am considering the possibility that energy should be understood to be a mathematical fiction in the same sort of way. From the little I know about physics and physicists, it seems to me that physicists do not think of energy in this way. But I am really not sure.)
Anyway, none of this philosophizing is what I was hoping to discuss in this article. Today I wrote up some of the questions I jotted down in freshman physics class.
- What are the physical interpretations of μ0 and ε0,
the magnetic permeability and electric permittivity of vacuum?
Can these be directly measured? How?
- Consider a simple circuit with a battery, a switch, and a
capacitor. When the switch is closed, the battery will suck
electrons out of one plate of the capacitor and pump them into the
other plate, so the capacitor will charge up.
When we open the switch, the current will stop flowing, and the capacitor will stop charging up.
But why? Suppose the switch is between the capacitor and the positive terminal of the battery. Then the negative terminal is still connected to the capacitor even when the switch is open. Why doesn't the negative terminal of the battery continue to pump electrons into the capacitor, continuing to charge it up, although perhaps less than it would be if the switch were closed?
- Any beam of light has a time-varying electric field, perpendicular
to the direction that the light is travelling. If I shine a light
on an electron, why doesn't the electron vibrate up and down in the
varying electric field? Or does it?
[ Addendum 20080629: I figured out the answer to this one. ]
- Suppose I take a beam of polarized light whose electric field is in
the x direction. I split it in two, delay one of the beams by
exactly half a wavelength, and merge it with the other beam. The
electric fields are exactly out of phase and exactly cancel out.
What happens? Where did the light go? What about conservation of
energy?
- Suppose I have two beams of light whose wavelengths are close but
not exactly the same, say λ and (λ+dλ). I superimpose these. The
electric fields will interfere, and sometimes will be in phase and
sometimes out of phase. There will be regions where the electric
field varies rapidly from the maximum to almost zero, of length on the order of dλ. If I look at the
beam of light only over one of these brief intervals, it should
look just like very high frequency light of wavelength dλ. But
it doesn't. Or does it?
- An electron in a varying magnetic field experiences an
electromotive force. In particular, an electron near a wire that
carries a varying current will move around as the current in the
wire varies.
Now suppose we have one electron A in space near a wire. We will put a very small current into the wire for a moment; this causes electron A to move a little bit.
Let's suppose that the current in the wire is as small as it can be. In fact, let's imagine that the wire is carrying precisely one electron, which we'll call B. We can calculate the amount of current we can attribute to the wire just from B. (Current in amperes is just coulombs per second, and the charge on electron B is some number of coulombs.) Then we can calculate the force on A as a result of this minimal current, and the motion of A that results.
But we could also do the calculation another way ,by forgetting about the wire, and just saying that electron B is travelling through space, and exerts an electrostatic force on A, according to Coulomb's law. We could calculate the motion of A that results from this electrostatic force.
We ought to get the same answer both ways. But do we?
- Suppose we have a beam of light that is travelling along the
x axis, and the electric field is perpendicular to the
x axis, say in the y direction. We learned in
freshman physics how to calculate the vector quantity that
represents the intensity of the electric field at every point on
the x axis; that is, at every point of the form (x,
0, 0). But what is the electric field at (x, 1, 0)? How
does the electric field vary throughout space? Presumably a beam
of light of wavelength λ has a minimum diameter on the order
of λ, but how how does the electric field vary as you move
away from the core? Can you take two such minimum-diameter beams
and overlap them partially?
[ Addendum 20090204: I eventually remembered that Noether's theorem has something to say about the necessity of the energy concept. ]
[Other articles in category /physics] permanent link
Thu, 06 Dec 2007
What's a File?
Almost every December since 2001 I have given a talk to the
local Linux users' group on some aspect of Unix internals. My
first talk was on the
internals of the ext2 filesystem. This year I was under
a lot of deadline pressure at work, so I decided I would give the 2001
talk again, maybe with a few revisions.
Actually I was under so much deadline pressure that I did not have time to revise the talk. I arrived at the user group meeting without a certain idea of what talk I was going to give.
Fortunately, the meeting structure is to have a Q&A and discussion period before the invited speaker gives his talk. The Q&A period always lasts about an hour. In that hour before I had to speak, I wrote a new talk called What's a File?. It mostly concerns the Unix "inode" structure, and what the kernel uses it for. It uses the output of the well-known ls -l command as a jumping-off point, since most of the ls -l information comes from the inode.
Then I talk about how files are opened and permissions are checked, how the filesystem is organized, how the kernel reads and writes data, how directories are structured, how it's possible to have one file with two names, how symbolic links work, and what that mysterious field is in the ls -l output between the permissions and the owner.
The talk was quite successful, much more so than I would have expected, given how quickly I wrote it and my complete inability to edit or revise it. Of course, it does help that I know this material backwards and forwards and standing on my head, and also that I could reuse all the diagrams and illustrations from the 2001 version of the talk.
I would not, however, recommend this technique.
As my talks have gotten better over the years, I find that less and less of the talk material is captured in the slides, and so the slides become less and less representative of the talk itself. But I put them online anyway, and here they are.
Here's a .tgz file in case you want to download it all at once.
[Other articles in category /Unix] permanent link
Tue, 04 Dec 2007
An Austrian coincidence
Only one of these depicts a location in my obstetrician's
waiting room where the paint is chipped.

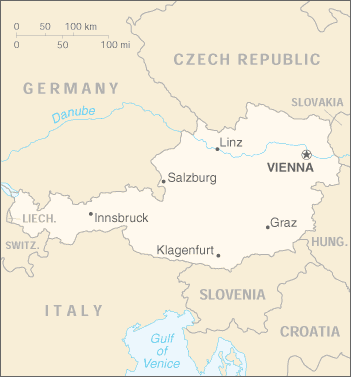
[Other articles in category /misc] permanent link
Sat, 01 Dec 2007
19th-century elementary arithmetic
In grade school I read a delightful story, by C. A.
Stephens, called The Jonah. In the story, which
takes place in 1867, Grandma and Grandpa are away for the weekend,
leaving the kids alone on the farm. The girls make fried pies for
lunch.
They have a tradition that one or two of the pies are "Jonahs": they look the same on the outside, but instead of being filled with fruit, they are filled with something you don't want to eat, in this case a mixture of bran and cayenne pepper. If you get the Jonah pie, you must either eat the whole thing, or crawl under the table to be a footstool for the rest of the meal.
Just as they are about to serve, a stranger knocks at the door. He is an old friend of Grandpa's. They invite him to lunch, of course removing the Jonahs from the platter. But he insists that they be put back, and he gets the Jonah, and crawls under the table, marching it around the dining room on his back. The ice is broken, and the rest of the afternoon is filled with laughter and stories.
Later on, when the grandparents return, the kids learn that the elderly visitor was none other than Hannibal Hamlin, formerly Vice-President of the United States.
A few years ago I tried to track this down, and thanks to the Wonders of the Internet, I was successful. Then this month I had the library get me some other C. A. Stephens stories, and they were equally delightful and amusing.
In one of these, the narrator leaves the pump full of water overnight, and the pipe freezes solid. He then has to carry water for forty head of cattle, in buckets from the kitchen, in sub-freezing weather. He does eventually manage to thaw the pipe. But why did he forget in the first place? Because of fractions:
I had been in a kind of haze all day over two hard examples in complex fractions at school. One of them I still remember distinctly:At that point I had to stop reading and calculate the answer, and I recommend that you do the same.
$${7\over8} \; {\rm of} \; {60 {5\over10} \over 10 {3\over8}} \; {\rm of} \; {8\over 5} \; \div \; 8{68\over 415} = {\rm What?}$$
I got the answer wrong, by the way. I got 25/64 or 64/25 or something of the sort, which suggests that I flipped over an 8/5 somewhere, because the correct answer is exactly 1. At first I hoped perhaps there was some 19th-century precedence convention I was getting wrong, but no, it was nothing like that. The precedence in this problem is unambiguous. I just screwed up.
Entirely coincidentally (I was investigating the spelling of the word "canceling") I also recently downloaded (from Google Books) an arithmetic text from the same period, The National Arithmetic, on the Inductive System, by Benjamin Greenleaf, 1866. Here are a few typical examples:
Some of these are rather easy, but others are a long slog. For example, #1 and #3 here (actually #1 and #25 in the book) can be solved right off, without paper. But probably very few people have enough skill at mental arithmetic to carry off $612/(83 3/7) * (14 7/10) in their heads.
- If 7/8 of a bushel of corn cost 63 cents, what cost a bushel? What cost 15 bushels?
- When 14 7/8 tons of copperas are sold for $500, what is the value of 1 ton? what is the value of 9 11/12 tons?
- If a man by laboring 15 hours a day, in 6 days can perform a certain piece of work, how many days would it require to do the same work by laboring 10 hours a day?
- Bought 87 3/7 yards of broadcloth for $612; what was the value for 14 7/10 yards?
- If a horse eat 19 3/7 bushels of oats in 87 3/7 days, how many will 7 horses eat in 60 days?
The "complex fractions" section, which the original problem would have fallen under, had it been from the same book, includes problems like this: "Add 1/9, 2 5/8, 45/(94 7/11), and (47 5/9)/(314 3/5) together." Such exercises have gone out of style, I think.
In addition to the complicated mechanical examples, there is some good theory in the book. For example, pages 227–229 concern continued fraction expansions of rational numbers, as a tool for calculating simple rational approximations of rationals. Pages 417–423 concern radix-n numerals, with special attention given to the duodecimal system. A typical problem is "How many square feet in a floor 48 feet 6 inches long, and 24 feet 3 inches broad?" The remarkable thing here is that the answer is given in the form 1176 sq. feet. 1' 6'', where the 1' 6'' actually means 1/12 + 6/144 square feet— that is, it is a base-12 "decimal".
I often hear people bemoaning the dumbing-down of the primary and secondary school mathematics curricula, and usually I laugh at those people, because (for example) I have read a whole stack of "College Algebra" books from the early 20th century, which deal in material that is usually taken care of in 10th and 11th grades now. But I think these 19th-century arithmetics must form some part of an argument in the other direction.
On the other hand, those same people often complain that students' time is wasted by a lot of "new math" nonsense like base-12 arithmetic, and that we should go back to the tried and true methods of the good old days. I did not have an example in mind when I wrote this paragraph, but two minutes of Google searching turned up the following excellent example:
Most forms of life develop random growths which are best pruned off. In plants they are boles and suckerwood. In humans they are warts and tumors. In the educational system they are fashionable and transient theories of education created by a variety of human called, for example, "Professor Of The Teaching Of Mathematics."(Smart Machines, by Lawrence J. Kamm; chapter 11, "Smart Machines in Education".)When the Russians launched Sputnik these people came to the rescue of our nation; they leapfrogged the Russians by creating and imposing on our children the "New Math."
They had heard something about digital computers using base 2 arithmetic. They didn't know why, but clearly base 10 was old fashioned and base 2 was in. So they converted a large fraction of children's arithmetic education to learning how to calculate with any base number and to switch from base to base. But why, teacher? Because that is the modern way. No one knows how many potential engineers and scientists were permanently turned away by this inanity.
Fortunately this lunacy has now petered out.
Pages 417–423 of The National Arithmetic, with their problems on the conversion from base-6 to base-11 numerals, suggest that those people may not know what they are talking about.
[Other articles in category /math] permanent link
Fri, 30 Nov 2007
Lazy square roots of power series
Lately for various reasons I have been investigating the differential
equation:
$$(f(x))^2 + (f'(x))^2 = 1$$
where !!f'!! is the derivative of !!f!!. This equation has a couple of obvious solutions (!!f(x) = 1!!; !!f(x) = \sin(x)!!) and a bunch of not-so-obvious ones. Since I couldn't solve the equation symbolically, I decided to fall back on power series. Representing !!f(x)!! as !!a_0 + a_1x + a_2x^2 + \ldots!!, one can manipulate the power series and solve for !!a_0, a_1, a_2!!, etc. In fact, this is exactly the application for which mathematicians first became intersted in power series. The big question is "once you have found !!a_0, a_1!!, etc., do these values correspond to a real function? And for what !!x!! does the power series expression actually make sense?" This question, springing from a desire to solve intractable differential equations, motivates a lot of the theoretical mathematics of the last hundred and fifty years.I decided to see if I could use the power series methods of chapter 6 of Higher-Order Perl to calculate !!a_0!!, etc. So far, not yet, although I am getting closer. The key is that if $series is the series you want, and if you can calculate at least one term at the front of the series, and then express the rest of $series in terms of $series, you win. For example:
# Perl
my $series;
$series = node(1, promise { scale(2, $series) } );
This is perfectly well-defined code; it runs fine and sets
$series to be the series !![1,2,4,8,16...]!!. In Haskell this is
standard operating procedure:
-- Haskell
series = 1 : scale 2 series
But in Perl it's still a bit outré.Similarly, the book shows, on page 323, how to calculate the reciprocal of a series !!s!!. Any series can be expressed as the sum of the first term and the rest of the terms:
$$s = s_H + xs_T$$ Now suppose that !!r=\frac1s!!. $$ r = r_H + xr_T$$ We have: $$ \begin{array}{rcl} rs & = & 1 \\ (r_H + xr_T)(s_H+xs_T) & = & 1 \\ r_Hs_H + xr_Hs_T + xr_Ts_H + x^2r_Ts_T & = & 1 \end{array} $$ Equating the constant terms on both sides gives !!r_Hs_H=1!!, so !!r_H = \frac1{s_H}!!. Then equating the non-constant terms gives:
$$\begin{array}{rcl} xr_Hs_T + xr_Ts_H + x^2r_Ts_T & = & 0 \\ x\frac1{s_H}s_T + xr_Ts_H + x^2r_Ts_T & = & 0 \\ \frac1{s_H}s_T + r_Ts_H + xr_Ts_T & = & 0 \\ r_T & = & \frac{-\frac1{s_H}s_T}{s_H+xs_T} \\ r_T & = & \frac{-\frac1{s_H}s_T}s \\ r_T & = & {-\frac1{s_H}s_T}r \end{array} $$ and we win. This same calculation appears on page 323, in a somewhat more confused form. (Also, I considered only the special case where !!s_H = 1!!.) The code works just fine.
To solve the differential equation !!f^2 + (f')^2 = 1!!, I want to do something like this:
$$f = \sqrt{1 - {(f')}^{2}}$$
so I need to be able to take the square root of a power series. This does not appear in the book, and I have not seen it elsewhere. Here it is.Say we want !!r^2 = s!!, where !!s!! is known. Then write, as usual:
$$\begin{array}{rcl} s &=& \operatorname{head}(s) + x·\operatorname{tail}(s) \\ r &=& \operatorname{head}(r) + x·\operatorname{tail}(r) \\ \end{array} $$ as before, and, since !!r^2 = s!!, we have:
$$ (\operatorname{head}(r))^2 + 2x \operatorname{head}(r) \operatorname{tail}(r) + x^2(\operatorname{tail}(r))^2 = \operatorname{head}(s) + x·\operatorname{tail}(s) $$ so, equating coefficients on both sides, !!(\operatorname{head}(r))^2 = \operatorname{head}(s)!!, and !!\operatorname{head}(r) = \sqrt{\operatorname{head}(s)}!!.
Subtracting the !!\operatorname{head}(s)!! from both sides, and dividing by !!x!!:
$$\begin{array}{rcl} 2\operatorname{head}(r) \operatorname{tail}(r) + x·(\operatorname{tail}(r))^2 &=& \operatorname{tail}(s) \\ \operatorname{tail}(r)·(2·\operatorname{head}(r) + x·\operatorname{tail}(r)) &=& \operatorname{tail}(s) \\ \operatorname{tail}(r)·(\operatorname{head}(r) + r) &=& \operatorname{tail}(s) \\ \operatorname{tail}(r) &=& \frac{\operatorname{tail}(s)}{\operatorname{head}(r) + r} \end{array}$$ and we win. Or rather, we win once we write the code, which would be something like this:
# Perl
sub series_sqrt {
my $s = shift;
my ($s0, $st) = (head($s), tail($s));
my $r0 = sqrt($s0);
my $r;
$r = node($r0,
promise {
divide($st,
add2(node($r0, undef),
$r))
});
return $r;
}
I confess I haven't tried this in Perl yet, but I have high
confidence that it will work. I actually did the implementation in
Haskell:
-- Haskell
series_sqrt (s0:st) = r
where r = r0 : (divide st (add [r0] r))
r0 = sqrt(s0)
And when I asked it for the square root of !![1,1,0,0,0,\ldots]!! (that is,
of !!1+x!!) it gave me back !![1, 0.5, -0.125, -0.0625, \ldots]!!, which is
indeed correct.
The Perl code is skankier than I wish it were. A couple of years ago I said in an interview that "I wish Perl's syntax were less verbose." Some people were surprised by this at the time, since Perl programmers consider Perl's syntax to be quite terse. But comparison of the Perl and Haskell code above demonstrates the sort of thing I mean.
Part of ths issue here, of course, is that the lazy list data structure is built in to Haskell, but I have to do it synthetically in Perl, and so every construction of a lazy list structure in Perl is accompanied by a syntactic marker (such as node(...) or promise { ... }) that is absent, or nearly absent, from the Haskell.
But when I complained about Perl's verbose syntax in 2005, one thing I had specifically in mind was Perl's argument acquisition syntax, here represented by my $s = shift;. Haskell is much terser, with no loss of expressiveness. Haskell gets another win in the automatic destructuring bind: instead of explicitly calling head() and tail() to acquire the values of s0 and st, as in the Perl code, they are implicitly called by the pattern match (s0:st) in the Haskell code, which never mentions s at all. It is quite fair to ascribe this to a failure of Perl's syntax, since there's no reason in principle why Perl couldn't support this, at least for built-in data structures. For example, consider the Perl code:
sub blah {
my $href = shift();
my $a = $href->{this};
my $tmp = $href->{that};
my $b = $tmp->[0];
my $c = $tmp->[2];
# Now do something with $a, $b, $c
}
It would be much more convenient to write this as:
sub blah {
my { this => $a, that => [$b, undef, $c] } = shift();
# Now do something with $a, $b, $c
}
This is a lot easier to understand. There are a number of interesting user-interface issues to ask about here: What if the assigned value is not in the expected form? Are $a, $b, and $c copied from $href or are they aliases into it? And so on. One easy way to dispense with all of these interesting questions (perhaps not in the best way) is to assert that this notation is just syntactic sugar for the long version.
I talked to Chip Salzenberg about this at one time, and he said he thought it would not be very hard to implement. But even if he was right, what is not very hard for Chip Salzenberg to do can turn out to be nearly impossible for us mortals.
[ Addendum 20071209: There's a followup article that shows several different ways of solving the differential equation, including the power-series method. ]
[ Addendum 20071210: I did figure out how to get Haskell to solve the differential equation. ]
[Other articles in category /math] permanent link
Mon, 29 Oct 2007
Undefined behavior in Perl and other languages
Miles Gould wrote what I thought was an interesting
article on implementation-defined languages, and cited Perl as an
example. One of his points was that a language that is defined by its
implementation, as Perl is, rather than by a standards document,
cannot have any "undefined behavior".
- Undefined behavior
- Perl: the static variable hack
- Perl: modifying a hash in a loop
- Perl: modifying an array in a loop
- Haskell: n+k patterns
- XML screws up
Undefined behavior
For people unfamiliar with this concept, I should explain briefly. The C standard is full of places that say "if the program contains x, the behavior is undefined", which really means "C programs do not contain x, so If the program contains x, it is not written in C, and, as this standard only defines the meaning of programs in C, it has nothing to say about the meaning of your program." There are around a couple of hundred of these phrases, and a larger number of places where it is implied.For example, everyone knows that it means when you write x = 4;, but what does it mean if you write 4 = x;? According to clause 6.3.2.1[#1], it means nothing, and this is not a C program. The non-guarantee in this case is extremely strong. The C compiler, upon encountering this locution, is allowed to abort and spontaneously erase all your files, and in doing so it is not violating the requirements of the standard, because the standard does not require any particular behavior in this case.
The memorable phrase that the comp.lang.c folks use is that using that construction might cause demons to fly out of your nose.
[ Addendum 20071030: I am informed that I misread the standard here, and that the behavior of this particular line is not undefined, but requires a compiler diagnostic. Perhaps a better example would have been x = *(char *)0. ]
I mentioned this in passing in one of my recent articles about a C program I wrote:
unsigned strinc(char *s)
{
char *p = strchr(s, '\0') - 1;
while (p >= s && *p == 'A' + colors - 1) *p-- = 'A';
if (p < s) return 0;
(*p)++;
return 1;
}
Here the pointer p starts at the end of the string s,
and the loop might stop when p points to the position just
before s. Except no, that is forbidden, and the program might
at that moment cause demons to fly out of your nose. You are allowed
to have a pointer that points to the position just after an
object, but not one that points just before. Well anyway, I seem to have digressed. My point was that M. Gould says that one advantage of languages like Perl that are defined wholly by their (one) implementation is that you never have "undefined behavior". If you want to know what some locution does, you type it in and see what it does. Poof, instant definition.
Although I think this is a sound point, it occurred to me that that is not entirely correct. The manual is a specification of sorts, and even if the implementation does X in situation Y, the manual might say "The implementation does X in situation Y, but this is unsupported and may change without warning in the future." Then what you have is not so different from Y being undefined behavior. Because the manual is (presumably) a statement of official policy from the maintainers, and, as a communiqué from the people with the ultimate authority to define the future meaning of the language, it has some of the same status that a formal specification would.
Perl: the static variable hack
Such disclaimers do appear in the Perl documentation. Probably the most significant example of this is the static variable hack. For various implementation reasons, the locution my $static if 0 has a strange and interesting effect:
sub foo {
my $static = 42 if 0;
print "static is now $static\n";
$static++;
}
foo() for 1..5;
This makes $static behave as a "static" variable, and persist
from call to call of foo(). Without the ... if 0,
the code would print "static is now 42" five times. But with
... if 0, it prints:
static is now
static is now 1
static is now 2
static is now 3
static is now 4
This was never an intentional feature. It arose accidentally, and
then people discovered it and started using it. Since the behavior
was the result of a strange quirk of the implementation, caused by the
surprising interaction of several internal details, it was officially
decided by the support group that this behavior would not be supported
in future versions. The manual was amended to say that this behavior
was explicitly undefined, and might change in the future. It can be
used in one-off programs, but not in any important program, one that
might have a long life and need to be run under several different
versions of Perl. Programs that use pointers that point outside the
bounds of allocated storage in C are in a similar position. It might
work on today's system, with today's compiler, today, but you can't do
that in any larger context.Having the "undefined behavior" be determined by the manual, instead of by a language standard, has its drawbacks. The language standard is fretted over by experts for months. When the C standard says that behavior is undefined, it is because someone like Clive Feather or Doug Gwyn or P.J. Plauger, someone who knows more about C than you ever will, knows that there is some machine somewhere on which the behavior is unsupported and unsupportable. When the Perl manual says that some behavior is undefined, you might be hearing from the Perl equivalent of Doug Gwyn, someone like Nick Clark or Chip Salzenberg or Gurusamy Sarathy. Or you might be hearing from a mere nervous-nellie who got their patch into the manual on a night when the release manager had stayed up too late.
Perl: modifying a hash in a loop
Here is an example of this that has bothered me for a long time. One can use the each() operator to loop lazily over the contents of a hash:
while (my $key = each %hash) {
# do something with $key and $hash{$key}
}
What happens if you modify the hash in the middle of the loop? For
various implementation reasons, the manual forbids this.For example, suppose the loop code adds a new key to the hash. The hash might overflow as a result, and this would trigger a reorganization that would move everything around, destroying the ordering information. The subsequent calls to each() would continue from the same element of the hash, but in the new order, making it likely that the loop would visit some keys more than once, or some not at all. So the prohibition in that case makes sense: The each() operator normally guarantees to produce each key exactly once, and adding elements to a hash in the middle of the loop might cause that guarantee to be broken in an unpredictable way. Moreover, there is no obvious way to fix this without potentially wrecking the performance of hashes.
But the manual also forbids deleting keys inside the loop, and there the issue does not come up, because in Perl, hashes are never reorganized as the result of a deletion. The behavior is easily described: Deleting a key that has already been visited will not affect the each() loop, and deleting one that has not yet been visited will just cause it to be skipped when the time comes.
Some people might find this general case confusing, I suppose. But the following code also runs afoul of the "do not modify a hash inside of an each loop" prohibition, and I don't think anyone would find it confusing:
while (my $key = each %hash) {
delete $hash{$key} if is_bad($hash{$key});
}
Here we want to delete all the bad items from the hash. We do this by
scanning the hash and deleting the current item whenever it is bad.
Since each key is deleted only after it is scanned by each,
we should expect this to visit every key in the hash, as indeed it
does. And this appears to be a useful thing to write. The only
alternative is to make two passes, constructing a list of bad keys on
the first pass, and deleting them on the second pass. The code would
be more complicated and the time and memory performance would be much
worse.There is a potential implementation problem, though. The way that each() works is to take the current item and follow a "next" pointer from it to find the next item. (I am omitting some unimportant details here.) But if we have deleted the current item, the implementation cannot follow the "next" pointer. So what happens?
In fact, the implementation has always contained a bunch of code, written by Larry Wall, to ensure that deleting the current key will work properly, and that it will not spoil the each(). This is nontrivial. When you delete an item, the delete() operator looks to see if it is the current item of an each() loop, and if so, it marks the item with a special flag instead of deleting it. Later on, the next time each() is invoked, it sees the flag and deletes the item after following the "next" pointer.
So the implementation takes some pains to make this work. But someone came along later and forbade all modifications of a hash inside an each loop, throwing the baby out with the bathwater. Larry and perl paid a price for this feature, in performance and memory and code size, and I think it was a feature well bought. But then someone patched the manual and spoiled the value of the feature. (Some years later, I patched the manual again to add an exception for this case. Score!)
Perl: modifying an array in a loop
Another example is the question of what happens when you modify an array inside a loop over the array, as with:
@a = (1..3);
for (@a) {
print;
push @a, $_ + 3 if $_ % 2 == 1;
}
(This prints 12346.) The internals are simple, and the semantics are
well-defined by the implementation, and straightforward, but the
manual has the heebie-jeebies about it, and most of the Perl community
is extremely superstitious about this, claiming that it is "entirely
unpredictable". I would like to support this with a quotation from
the manual, but I can't find it in the enormous and disorganized mass
that is the Perl documentation.[ Addendum: Tom Boutell found it. The perlsyn page says "If any part of LIST is an array, foreach will get very confused if you add or remove elements within the loop body, for example with splice. So don't do that." ]
The behavior, for the record, is quite straightforward: On the first iteration, the loop processes the first element in the array. On the second iteration, the loop processes the second element in the array, whatever that element is at the time the second iteration starts, whether or not that was the second element before. On the third iteration, the loop processes the third element in the array, whatever it is at that moment. And so the loop continues, terminating the first time it is called upon to process an element that is past the end of the array. We might imagine the following pseudocode:
index = 0;
while (index < array.length()) {
process element array[index];
index += 1;
}
There is nothing subtle or difficult about this, and claims that the
behavior is "entirely unpredictable" are probably superstitious
confessions of ignorance and fear.Let's try to predict the "entirely unpredictable" behavior of the example above:
@a = (1..3);
for (@a) {
print;
push @a, $_ + 3 if $_ % 2 == 1;
}
Initially the array contains (1, 2, 3), and so the first iteration
processes the first element, which is 1. This prints 1, and, since 1
is odd, pushes 4 onto the end of the array.The array now contains (1, 2, 3, 4), and the loop processes the second element, which is 2. 2 is printed. The loop then processes the third element, printing 3 and pushing 6 onto the end. The array now contains (1, 2, 3, 4, 6).
On the fourth iteration, the fourth element (4) is printed, and on the fifth iteration, the fifth element (6) is printed. That is the last element, so the loop is finished. What was so hard about that?
Haskell: n+k patterns
My blog was recently inserted into the feed for planet.haskell.org, and of course I immediately started my first streak of posting code-heavy articles about C and Perl. This is distressing not just because the articles were off-topic for Planet Haskell—I wouldn't give the matter two thoughts if I were posting my usual mix of abstract math and stuff—but it's so off-topic that it feels weird to see it sitting there on the front page of Planet Haskell. So I thought I'd make an effort to talk about Haskell, as a friendly attempt to promote good relations between tribes. I'm not sure what tribe I'm in, actually, but what the heck. I thought about Haskell a bit, and a Haskell example came to mind.Here is a definition of the factorial function in Haskell:
fact 0 = 1
fact n = n * fact (n-1)
I don't need to explain this to anyone, right?Okay, now here is another definition:
fact 0 = 1
fact (n+1) = (n+1) * fact n
Also fine, and indeed this is legal Haskell. The pattern n+1
is allowed to match an integer that is at least 1, say 7, and doing so binds n to
the value 6. This is by a rather peculiar special case in the
specification of Haskell's pattern-matcher. (It is section 3.17.2#8
of Haskell 98 Language and Libraries: The Revised
Report, should you want to look it up.) This peculiar
special case is known sometimes as a "successor pattern" but more
often as an "n+k pattern".The spec explicitly deprecates this feature:
Many people feel that n+k patterns should not be used. These patterns may be removed or changed in future versions of Haskell.
(Page 33.) One wonders why they put it in at all, if they were going to go ahead and tell you not to use it. The Haskell committee is usually smarter than this.
 I have a vague recollection that there was an argument between people
who wanted to use Haskell as a language for teaching undergraduate
programming, and those who didn't care about that, and that this was
the compromise result. Like many compromises, it is inferior to both
of the alternatives that it interpolates between. Putting the feature
in complicates the syntax and the semantics of the language, disrupts
its conceptual purity, and bloats the
spec—see the Perlesque yikkity-yak on pages 57–58 about
how x + 1 = ... binds a meaning to +, but (x +
1) = ... binds a meaning to x. Such complication is
worth while only if there is a corresponding payoff in terms of
increased functionality and usability in the language. In this case,
the payoff is a feature that can only be used in one-off programs.
Serious programs must avoid it, since the patterns "may be removed or
changed in future versions of Haskell". The Haskell committee
purchased this feature at a certain cost, and it is debatable whether
they got their money's worth. I'm not sure which side of that issue I
fall on. But having purchased the feature, the committee then threw
it in the garbage, squandering their sunk costs. Oh well. Not even
the Haskell committee is perfect.
I have a vague recollection that there was an argument between people
who wanted to use Haskell as a language for teaching undergraduate
programming, and those who didn't care about that, and that this was
the compromise result. Like many compromises, it is inferior to both
of the alternatives that it interpolates between. Putting the feature
in complicates the syntax and the semantics of the language, disrupts
its conceptual purity, and bloats the
spec—see the Perlesque yikkity-yak on pages 57–58 about
how x + 1 = ... binds a meaning to +, but (x +
1) = ... binds a meaning to x. Such complication is
worth while only if there is a corresponding payoff in terms of
increased functionality and usability in the language. In this case,
the payoff is a feature that can only be used in one-off programs.
Serious programs must avoid it, since the patterns "may be removed or
changed in future versions of Haskell". The Haskell committee
purchased this feature at a certain cost, and it is debatable whether
they got their money's worth. I'm not sure which side of that issue I
fall on. But having purchased the feature, the committee then threw
it in the garbage, squandering their sunk costs. Oh well. Not even
the Haskell committee is perfect.
I think it might be worth pointing out that the version of the program with the n+k pattern is technically superior to the other version. Given a negative integer argument, the first version recurses forever, possibly taking a long time to fail and perhaps taking out the rest of the system on which it is running. But the n+k version fails immediately, because the n+1 pattern will only match an integer that is at least 1.
XML screws up
The "nasal demons" of the C standard are a joke, but a serious one. The C standard defines what C compilers must do when presented with C programs; it does not define what they do when presented with other inputs, nor what other software does when presented with C programs. The authors of C standard clearly understood the standard's role in the world.Earlier versions of the XML standard were less clear. There was a particularly laughable clause in the first edition of the XML 1,0 standard:
XML documents may, and should, begin with an XML declaration which specifies the version of XML being used. For example, the following is a complete XML document, well-formed but not valid:
<?xml version="1.0"?> <greeting>Hello, world!</greeting>...
The version number "1.0" should be used to indicate conformance to this version of this specification; it is an error for a document to use the value "1.0" if it does not conform to this version of this specification.
(Emphasis is mine.) The XML 1.0 spec is just a document. It has no power, except to declare that certain files are XML 1.0 and certain files are not. A file that complies with the requirements of the spec is XML 1.0; all other files are not XML 1.0. But in the emphasized clause, the spec says that certain behavior "is an error" if it is exhibited by documents that do not conform to the spec. That is, it is declaring certain non-XML-1.0 documents "erroneous". But within the meaning of the spec, "erroneous" simply means that the documents are not XML 1.0. So the clause is completely redundant. Documents that do not conform to the spec are erroneous by definition, whether or not they use the value "1.0".
It's as if the Catholic Church issued an edict forbidding all rabbis from wearing cassocks, on pain of excommunication.
I am happy to discover that this dumb error has been removed from the most recent edition of the XML 1.0 spec.
[Other articles in category /prog/perl] permanent link
Sat, 27 Oct 2007
Where's that blog?
I haven't posted in a couple of weeks, and I was wondering why. So I
took a look at the test version of the blog, which displays all the
unpublished articles as well as the published ones, and the reason
was obvious: In the past ten days I've written seven articles that are
unfinished or that didn't work. Usually only about a third of my
articles flop; this month a whole bunch flopped in a row. What can I
say? Sometimes the muse delivers, and sometimes she doesn't.
I said a while back that I would try to publish more regularly, and not wait until every article was perfect. But I don't want to publish the unfinished articles yet. So I thought instead I'd publish a short summary of what I've been thinking about lately.
I hope to get at least one or two of these done by the end of the month.
Simplified Poker
I recently played a computer poker game that uses a 24-card deck, with only the nine through ace of each suit. This changes the game drastically. For example, a flush is less likely than a four of a kind. (The game uses the standard hand rankings anyway.) It is very easy to compute optimal strategies for this game, because there are so few possible hands (42,504) that you can brute-force all the calculations with a computer.This got me thinking again of something I started writing up last year and never finished: The game of "Simplified Poker", which was an attempt to do for Poker what the λ-calculus does for computation: the simplest possible model that nevertheless captures all the essential features of the original. Simplified Poker is played with an infinite deck in which half the cards are kings and half are jacks. Each hand contains only two cards. Nevertheless, bluffing is still possible.
The Annoying Boxes Puzzle
This is a logic puzzle in which you deduce which box contains the treasure, but with a twist. I thought it up many years ago, and then in the course of trying to write up an explanation about five years ago, I consulted Raymond Smullyan's book What is the Name of This Book? in order to get a citation to prove a certain fact about the form that such puzzles usually take. In doing so, I discovered that Smullyan actually presented the annoying boxes puzzle (in slightly different form) in that book!It's primarily waiting for me to take a photograph to accompany the puzzle.
[ Addendum 20160319: I did eventually post this, but it took me until 2015 to do it: The annoying boxes puzzle. ]
Undefined behavior
I have a pretty interesting article on the concept of "undefined behavior", which is a big deal in the C world, but which means something rather different, and is much less important, in Perl.[ Addendum 20071029: This is ready now. ]
Tootle
My daughter Katara has become interested in the book Tootle, by Gertrude Crampton, which is the third-best-selling hardback children's book of all time. A few years back I wrote some brief literary criticism of Tootle, which I included when I wrote the Wikipedia article about the book. This criticism was quite rightly deleted later on, as uncited original research. It needs a new home, and that home is obviously here.
Periodicity without Fourier Series
Suppose I have tabulated the number of blog posts I made every day for two years. I want to find if there is any discernible periodicity to this data. Do I tend to post in 26-day cycles, for example?One way to do this is to take the Fourier transform of the data. For various reasons, I don't like this technique, and I'm trying to invent something new. I think I have what I want, although it took several tries to find it. Unfortunately, the blog posting data shows no periodicity whatsoever.
Emacs and auto-mode-alist
The elisp code I've been using for the past fifteen years to set the default mode for Perl editing in Emacs broke last week. My search for a replacement turned up some very bizarre advice on IRC.
Van der Waerden's problem
Also still pending is the rest of my van der Waerden problem series. I have written about four programs so far, and I have two to go.
[Other articles in category /meta] permanent link
Sun, 14 Oct 2007
Van der Waerden's problem: programs 3 and 4
In this series of articles I'm analyzing five versions of a
program that I wrote around 1988, and then another program that does
the same thing that I wrote last month without referring to the 1988
code. (I said before that it was four versions, but apparently I'm not so
good at counting to five.)
If you don't remember what the program does, here's an explanation.
Here is program 1, which was an earlier attempt to do the same thing. Here's program 2.
Program 3
Complete source code for this version.I said of the previous program:
The problem is all in the implementation. You see, this program actually constructs the entire tree in memory.Somewhere along the line it dawned on me that constructing the tree was unnecessary, so I took that machinery out, and the result was version 3.
Consequently, this program is easy to explain once you have seen the previous version: almost all I have to do is list the stuff that I took out.
Since this program does not construct a tree of node structures, it omits the definition of the node structure and the macro for manufacturing nodes. Since it gets rid of the node allocation, it also gets rid of the memory leak of the previous version, and so omits the customized memory allocation functions Malloc and Free that performed memory tracking.
The previous program had a compiled-in limit on the number of colors it would handle, because at the time I didn't know how to do a dynamic array. In this program, I got rid of the node structures, so there was no array of node structures, so no need for a limit on the number of node structures in the array. And all the code that enforced the limit is gone.
The apchk function, which checks to see if a string is good, remains unchanged from the previous version.
The makenodes function, which was the principal function in the previous program, remains, but has lost a lot of code. It is simpler to call, too; the node argument is gone:
makenodes(maxlen,"");
I got rid of the silly !howfar test in favor of a more
easily-understood howfar == 0 test. There are lots of times
when ! is appropriate, but testing whether a non-negative
integer has reached zero is not one of them. I was going to comment
earlier about what a novice error this is, and I'm glad to see that I
fixed it.The main use of apchk in the previous program had if (!apchk(...)) { ... }. That was okay, because apchk returns a Boolean result. But the negation is annoying. It suggests that apchk's return value is backward. (Instead of returning true for a bad string, it should return true for a good string.) This is not very much a big deal, and I only brought it up so that I could diffidently confess that these days I would probably have done:
#define unless(c) if(!(c))
...
unless (is_bad(...)) {
}
There are a lot of stories of doofus Pascal programmers who do:
#define begin {
#define end }
and Fortran programmers who do:
#define GT >
#define GE >=
#define LT <
#define LE <=
and I find, to my shame, that I have become one of them. Anyone
seeing #define unless(c) if(!(c)) would snort and say "Oh,
this was obviously written by a Perl programmer."But at least I was a C programmer first.
Actually I was a Fortran programmer first. But I was never a big enough doofus to #define GE >=.
The big flaw in the current program is the string argument to makenodes. Each call to makenodes copies this string so that it can append a character to the end. I discussed this at some length in the previous article, so I don't want to make too much of it now; I'll just say that a better technique would have reused the string buffer from call to call. This obviously saves a little memory, and since most of the contents of the string doesn't change, it also saves a lot of time.
This might be worth seeing, since it seems to me now to be a marvel of wasted code:
ls = strlen(s);
newarg = STRING(ls + 1);
if (!newarg)
{
fprintf(stderr,"Couldn't get %d bytes for newarg in makenodes\n",ls+2);
fprintf(stderr,"Total get was %d.\n",gotten);
fprintf(stderr,"P\n L\n O\n P\n !\n");
abort();
}
strcpy(newarg,s);
newarg[ls+1] = '\0';
newarg[ls] = 'A' + i;
makenodes(howfar-1,newarg);
free(newarg);
The repeated strlen, for example, when ls could be
calculated as maxlen - howfar. The excessively verbose
failure message, which should be inside the STRING macro
anyway. (The code that maintains gotten has gone away with
the debugging allocation routines, so the second fprintf is
superfluous.) And why did I think abort was the right
thing to call on an out-of-memory condition?Oh well, you live and learn.
Program 4
Complete source code for this version.The fourth version of the program is even more trimmed-down. In this version of the program I did get the idea to reuse the string buffer instead of copying the string on every recursive call. But I also got an even better idea, and eliminated the recursive call. The makenodes function is now down to one argument, which tells it how deep a tree to search.
void
makenodes(maxdepth)
int maxdepth;
{
int apchk(), depth = 0;
char curlet, *curstring = STRING(maxdepth);
curstring[0] = '\0';
curlet = 'A';
while (depth >= 0)
{
while (curlet <= 'A' - 1 + colors)
{
#ifdef DIAG
printf("%s makenoding with string %s%c, depth %d.\n",
TABS+12-depth,curstring,curlet,depth);
#endif
if (apchk(curstring,curlet))
curlet++;
else
if (depth < maxdepth)
{
curstring[depth] = curlet;
curstring[depth+1] = '\0';
depth += 1;
curlet = 'A';
}
else
{
printf("%s%c\n",curstring,curlet);
curlet++;
}
}
depth -= 1;
curlet = curstring[depth] + 1;
curstring[depth] = '\0';
}
}
This is a better job all around, and not very different from what I
wrote last month to do the same thing. I was going to title this
series of articles "I have become a better programmer!", and now that
I see this version, I'm glad I didn't, because there's no evidence
here that I am much better. This version of the program gets a solid
A from my older self.The value depth scans forward in the string when the search is going well, and is decremented again when the search needs to backtrack. If depth == maxdepth, a witness of the desired length has been found, and is printed out.
The curlet ("current letter") variable tracks which branch of the current tree node we are "recursing" down. After the function recurses down, by incrementing depth, curlet is set to 'A' to visit the first sub-node of the new current node. The curstring buffer tracks the path through the tree to the current node. When the function needs to backtrack, it restores the state of curlet from the last character in the buffer and then trims that character off the end of the path.
I'd only want to make two changes to this code. One would be to make depth a pointer into the curstring buffer instead of an index into it. Then again, the compiler may well have optimized it into one anyway. But it would also allow me to eliminate curlet in favor of just using *depth everywhere.
The other change would address a more serious defect: the contents of curstring are kept properly zero-terminated at all times, whenever depth is advanced or retracted. This zero-termination is unnecessary, since curstring is never used as a string except when depth == maxdepth. When printfing curstring, I could have used something like:
printf("%.*s%c\n",curstring,maxlen,curlet);
which prints exactly maxlen characters from the buffer,
regardless of whether it is zero-terminated. It would, however, have required that I know about %.*s, which I'm sure I did not. Was %.*s even available in 1988? I forget, and my copy of K&R First Edition is in a box somewhere since my recent move. Anyway, if %.*s was unavailable for whatever reason, the code could have had a single curstring[maxdepth] = 0 up front, which would have been quite sufficient for the one printf it needed to do.
Coming next: one very different program to solve the same problem, and a comparison with last month's effort.
[Other articles in category /prog] permanent link
Fri, 12 Oct 2007
The square of the Catalan sequence
Yesterday I went to a talk by Val Tannen about his work on "provenance
semirings".
The idea is that when you calculate derived data in a database, such as a view or a selection, you can simultaneously calculate exactly which input tuples contributed to each output tuple's presence in the output. Each input tuple is annotated with an identifier that says who was responsible for putting it there, and the output annotations are polynomials in these identifiers. (The complete paper is here.)
A simple example may make this a bit clearer. Suppose we have the following table R:
| R | |
| a | a |
| a | b |
| a | c |
| b | c |
| c | e |
| d | e |
| S | |
| a | a |
| a | b |
| a | c |
| a | e |
| b | e |
If you annotate the tuples of R with identifiers like this:
| R | ||
| a | a | u |
| a | b | v |
| a | c | w |
| b | c | x |
| c | e | y |
| d | e | z |
| S | ||
| a | a | u2 |
| a | b | uv |
| a | c | uw + xv |
| a | e | wy |
| b | e | xy |
| S | ||
| a | a | u2 |
| a | b | 0 |
| a | c | uw |
| a | e | wy |
| b | e | xy |
This assignment of polynomials generalizes a lot of earlier work on tuple annotation. For example, suppose each tuple in R is annotated with a probability of being correct. You can propagate the probabilities to S just by substituting the appropriate numbers for the variables in the polynomials. Or suppose each tuple in R might appear multiple times and is annotated with the number of times it appears. Then ditto.
If your queries are recursive, then the polynomials might be infinite. For example, suppose you are calculating the transitive closure T of relation R. This is like the previous example, except that instead of having S(x, z) = R(x, y) and R(y, z), we have T(x, z) = R(x, z) or (T(x, y) and R(y, z)). This is a recursive equation, so we need to do a fixpoint solution for it, using certain well-known techniques. The result in this example is:
| T | ||
| a | a | u+ |
| a | b | u*v |
| a | c | u*(vx+w) |
| a | e | u*(vx+w)y |
| b | c | x |
| b | e | xy |
| d | e | z |
| 1 | a |
| 2 | (a + b) |
| 3 | ((a + b) + c) |
| (a + (b + c)) | |
| 4 | (((a + b) + c) + d) |
| ((a + (b + c)) + d) | |
| ((a + b) + (c + d)) | |
| (a + ((b + c) + d)) | |
| (a + (b + (c + d))) | |
| 5 | ((((a + b) + c) + d) + e) |
| (((a + (b + c)) + d) + e) | |
| (((a + b) + (c + d)) + e) | |
| (((a + b) + c) + (d + e)) | |
| ((a + ((b + c) + d)) + e) | |
| ((a + (b + (c + d))) + e) | |
| ((a + (b + c)) + (d + e)) | |
| ((a + b) + ((c + d) + e)) | |
| ((a + b) + (c + (d + e))) | |
| (a + (((b + c) + d) + e)) | |
| (a + ((b + (c + d)) + e)) | |
| (a + ((b + c) + (d + e))) | |
| (a + (b + ((c + d) + e))) | |
| (a + (b + (c + (d + e)))) |
Anyway, in his talk, Val referred to the sequence as "bizarre", and I had to jump in to point out that it was not at all bizarre, it was the Catalan numbers, which are just what you would expect from a relation like V = s + V2, blah blah, and he cut me off, because of course he knows all about the Catalan numbers. He only called them bizarre as a rhetorical flourish, meant to echo the presumed puzzlement of the undergraduates in the room.
(I never know how much of what kind of math to expect from computer science professors. Sometimes they know things I don't expect at all, and sometimes they don't know things that I expect everyone to know.
(This was indeed what was going on, and the professor seemed to think it was a surprising insight. I am not relating this boastfully, because I truly don't think it was a particularly inspired guess.
(Now that I think about it, maybe the answer here is that computer science professors know more about math than I expect, and less about computation.)
Anyway, I digress, and the whole article up to now was not really what I wanted to discuss anyway. What I wanted to discuss was that when I started blathering about Catalan numbers, Val said that if I knew so much about Catalan numbers, I should calculate the coefficient of the x59 term in V2, which also appeared as one of the annotations in his example.
So that's the puzzle, what is the coefficient of the x59 term in V2, where V = 1 + s + 2s2 + 5s3 + 14s4 + ... ?
After I had thought about this for a couple of minutes, I realized that it was going to be much simpler than it first appeared, for two reasons.
The first thing that occurred to me was that the definition of multiplication of polynomials is that the coefficient of the xn term in the product of A and B is Σaibn-i. When A=B, this reduces to Σaian-i. Now, it just so happens that the Catalan numbers obey the relation cn+1 = Σ cicn-i, which is exactly the same form. Since the coefficients of V are the ci, the coefficients of V2 are going to have the form Σcicn-i, which is just the Catalan numbers again, but shifted up by one place.
The next thing I thought was that the Catalan numbers have a pretty simple generating function f(x). This just means that you pretend that the sequence V is a Taylor series, and figure out what function it is the Taylor series of, and use that as a shorthand for the whole series, ignoring all questions of convergence and other such analytic fusspottery. If V is the Taylor series for f(x), then V2 is the Taylor series for f(x)2. And if f has a compact representation, say as sin(x) or something, it might be much easier to square than the original V was. Since I knew in this case that the generating function is simple, this seemed likely to win. In fact the generating function of V is not sin(x) but (1-√(1-4x))/2x. When you square this, you get almost the same thing back, which matches my prediction from the previous paragraph. This would have given me the right answer, but before I actually finished that calculation, I had an "oho" moment.
The generating function is known to satisfy the relation f(x) = 1 + xf(x)2. This relation is where the (1-√(1-4x))/2x thing comes from in the first place; it is the function that satisfies that relation. (You can see this relation prefigured in the equation that Val had, with V = s + V2. There the notation is a bit different, though.) We can just rearrange the terms here, putting the f(x)2 by itself, and get f(x)2 = (f(x)-1)/x.
Now we are pretty much done, because f(x) = V = 1 + x + 2x2 + 5x3 + 14x4 + ... , so f(x)-1 = x + 2x2 + 5x3 + 14x4 + ..., and (f(x)-1)/x = 1 + 2x + 5x2 + 14x3 + ... . Lo and behold, the terms are the Catalan numbers again.
So the answer is that the coefficient of the x59 term is just c(60), calculation of which is left as an exercise for the reader.
I don't know what the point of all that was, but I thought it was fun how the hairy-looking problem seemed likely to be simple when I looked at it a little more carefully, and then how it did turn out to be quite simple.
This blog has had a recurring dialogue between subtle technique and the sawed-off shotgun method, and I often favor the sawed-off shotgun method. Often programmers' big problem is that they are very clever and learned, and so they want to be clever and learned all the time, even when being a knucklehead would work better. But I think this example provides some balance, because it shows a big win for the clever, learned method, which does produce a lot more understanding.
Then again, it really doesn't take long to whip up a program to multiply infinite polynomials. I did it in chapter 6 of Higher-Order Perl, and here it is again in Haskell:
data Poly a = P [a] deriving Show
instance (Eq a) => Eq (Poly a)
where (P x) == (P y) = (x == y)
polySum x [] = x
polySum [] y = y
polySum (x:xs) (y:ys) = (x+y) : (polySum xs ys)
polyTimes [] _ = []
polyTimes _ [] = []
polyTimes (x:xs) (y:ys) = (x*y) : more
where
more = (polySum (polySum (map (x *) ys) (map (* y) xs))
(0 : (polyTimes xs ys)))
instance (Num a) => Num (Poly a)
where (P x) + (P y) = P (polySum x y)
(P x) * (P y) = P (polyTimes x y)
[Other articles in category /math] permanent link
Tue, 09 Oct 2007
Relatively prime polynomials over Z2
Last week Wikipedia was having a discussion on whether the subject of
"mathematical
quilting" was notable enough to deserve an article. I remembered
that there had been a mathematical quilt on the cover of some journal
I read last year, and I went to the Penn math library to try to find
it again. While I was there, I discovered that the June 2007 issue of
Mathematics Magazine had a cover story about the
probability that two randomly-selected polynomials over Z2 are relatively prime. ("The
Probability of Relatively Prime Polynomials", Arthur T. Benjamin and
Curtis D Bennett, page 196).
Polynomials over Z2 are one of my favorite subjects, and the answer to the question turned out to be beautiful. So I thought I'd write about it here.
First, what does it mean for two polynomials to be relatively prime? It's analogous to the corresponding definition for integers. For any numbers a and b, there is always some number d such that both a and b are multiples of d. (d = 1 is always a solution.) The greatest such number is called the greatest common divisor or GCD of a and b. The GCD of two numbers might be 1, or it might be some larger number. If it's 1, we say that the two numbers are relatively prime (to each other). For example, the GCD of 100 and 28 is 4, so 100 and 28 are not relatively prime. But the GCD of 100 and 27 is 1, so 100 and 27 are relatively prime. One can prove theorems like these: If p is prime, then either a is a multiple of p, or a is relatively prime to p, but not both. And the equation ap + bq = 1 has a solution (in integers) if and only if p and q are relatively prime.
The definition for polynomials is just the same. Take two polynomials over some variable x, say p and q. There is some polynomial d such that both p and q are multiples of d; d(x) = 1 is one such. When the only solutions are trivial polynomials like 1, we say that the polynomials are relatively prime. For example, consider x2 + 2x + 1 and x2 - 1. Both are multiples of x+1, so they are not relatively prime. But x2 + 2x + 1 is relatively prime to x2 - 2x + 1. And one can prove theorems that are analogous to the ones that work in the integers. The analog of "prime integer" is "irreducible polynomial". If p is irreducible, then either a is a multiple of p, or a is relatively prime to p, but not both. And the equation a(x)p(x) + b(x)q(x) = 1 has a solution for polynomials a and b if and only if p and q are relatively prime.
One uses Euclid's algorithm to calculate the GCD of two integers. Euclid's algorithm is simple: To calculate the GCD of a and b, just subtract the smaller from the larger, repeatedly, until one of the numbers becomes 0. Then the other is the GCD. One can use an entirely analogous algorithm to calculate the GCD of two polynomials. Two polynomials are relatively prime just when their GCD, as calculated by Euclid's algorithm, has degree 0.
Anyway, that was more introduction than I wanted to give. The article in Mathematics Magazine concerned polynomials over Z2, which means that the coefficients are in the field Z2, which is just like the regular integers, except that 1+1=0. As I explained in the earlier article, this implies that a=-a for all a, so there are no negatives and subtraction is the same as addition. I like this field a lot, because subtraction blows. Do you have trouble because you're always dropping minus signs here and there? You'll like Z2; there are no minus signs.
Here is a table that shows which pairs of polynomials over Z2 are relatively prime. If you read this blog through some crappy aggregator, you are really missing out, because the table is awesome, and you can't see it properly. Check out the real thing.
| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | c0 | c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | d0 | d1 | ||
| 0 | [a0] | ||||||||||||||||||||||||||||||||
| 1 | [a1] | ||||||||||||||||||||||||||||||||
| x | [a2] | ||||||||||||||||||||||||||||||||
| x + 1 | [a3] | ||||||||||||||||||||||||||||||||
| x2 | [a4] | ||||||||||||||||||||||||||||||||
| x2 + 1 | [a5] | ||||||||||||||||||||||||||||||||
| x2 + x | [a6] | ||||||||||||||||||||||||||||||||
| x2 + x + 1 | [a7] | ||||||||||||||||||||||||||||||||
| x3 | [a8] | ||||||||||||||||||||||||||||||||
| x3 + 1 | [a9] | ||||||||||||||||||||||||||||||||
| x3 + x | [b0] | ||||||||||||||||||||||||||||||||
| x3 + x + 1 | [b1] | ||||||||||||||||||||||||||||||||
| x3 + x2 | [b2] | ||||||||||||||||||||||||||||||||
| x3 + x2 + 1 | [b3] | ||||||||||||||||||||||||||||||||
| x3 + x2 + x | [b4] | ||||||||||||||||||||||||||||||||
| x3 + x2 + x + 1 | [b5] | ||||||||||||||||||||||||||||||||
| x4 | [b6] | ||||||||||||||||||||||||||||||||
| x4 + 1 | [b7] | ||||||||||||||||||||||||||||||||
| x4 + x | [b8] | ||||||||||||||||||||||||||||||||
| x4 + x + 1 | [b9] | ||||||||||||||||||||||||||||||||
| x4 + x2 | [c0] | ||||||||||||||||||||||||||||||||
| x4 + x2 + 1 | [c1] | ||||||||||||||||||||||||||||||||
| x4 + x2 + x | [c2] | ||||||||||||||||||||||||||||||||
| x4 + x2 + x + 1 | [c3] | ||||||||||||||||||||||||||||||||
| x4 + x3 | [c4] | ||||||||||||||||||||||||||||||||
| x4 + x3 + 1 | [c5] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x | [c6] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x + 1 | [c7] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x2 | [c8] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x2 + 1 | [c9] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x2 + x | [d0] | ||||||||||||||||||||||||||||||||
| x4 + x3 + x2 + x + 1 | [d1] | ||||||||||||||||||||||||||||||||
 A pink square means that the polynomials are relatively prime; a white square
means that they are not.
Another version of this table appeared on the cover of
Mathematics Magazine. It's shown at right.
A pink square means that the polynomials are relatively prime; a white square
means that they are not.
Another version of this table appeared on the cover of
Mathematics Magazine. It's shown at right.
The thin black lines in the diagram above divide the polynomials of different degrees. Suppose you pick two degrees, say 2 and 2, and look at the corresponding black box in the diagram:
| a4 | a5 | a6 | a7 | ||
| x2 | [a4] | ||||
| x2 + 1 | [a5] | ||||
| x2 + x | [a6] | ||||
| x2 + x + 1 | [a7] | ||||
The proof of this is delightful. If you run Euclid's algorithm on two relatively prime polynomials over Z2, you get a series of intermediate results, terminating in the constant 1. Given the intermediate results and the number of steps, you can run the algorithm backward and find the original polynomials. If you run the algorithm backward starting from 0 instead of from 1, for the same number of steps, you get two non-relatively-prime polynomials of the same degrees instead. This establishes a one-to-one correspondence between pairs of relatively prime polynomials and pairs of non-relatively-prime polynomials of the same degrees. End of proof. (See the paper for complete details.)
You can use basically the same proof to show that the probability that two randomly-selected polynomials over Zp is 1-1/p. The argument is the same: Euclid's algorithm could produce a series of intermediate results terminating in 0, in which case the polynomials are not relatively prime, or it could produce the same series of intermediate results terminating in something else, in which case they are relatively prime. The paper comes to an analogous conclusion about monic polynomials over Z.
Some folks I showed the diagram to observed that it
looks like a quilt pattern. My wife did actually make a quilt that
tabulates the GCD function for integers, which I mentioned in the
Wikipedia discussion of the notability of the Mathematical Quilting
article. That seems to have brought us back to where the article
started, so I'll end here.

[Other articles in category /math] permanent link
Mon, 08 Oct 2007
[Other articles in category /math] permanent link
Fri, 05 Oct 2007
Van der Waerden's problem: program 2
In this series of articles I'm going to analyze four versions of a
program that I wrote around 1988, and then another program that does
the same thing that I wrote last month without referring to the 1988
code.
If you don't remember what the program does, here's an explanation.
Here is program 1, which was an earlier attempt to do the same thing.
Program 2
In yesterday's article I wrote about a crappy program to search for "good" strings in van der Waerden's problem. It was crappy because it searched the entire space of all 327 strings, with no pruning.I can't remember whether I expected this to be practical at the time. Did I really think it would work? Well, there was some sense to it. It does work just fine for the 29 case. I think probably my idea was to do the simplest thing that could possibly work, and get as much information out of it as I could. On my current machine, this method proves that V(3,3) > 19 by finding a witness (RRBRRBBYYRRBRRBBYYB) in under 10 seconds. If we estimate that the computer I had then was 10,000 times slower, then I could have produced the same result in about 28 hours. I was at college, and there was plenty of free computing power available, so running a program for 28 hours was easily done. While I was waiting for it to finish, I could work on a better program.
Excerpts of the better program follow. The complete source code is here.
The idea behind this program is that the strings of length less than V form a tree, with the empty string as the root, and the children of string s are obtained from s by appending a single character to the end of s. If the string at a node is bad, so will be all the strings under it, and we can prune the entire branch at that node. This leaves us with a tree of all the good strings. The ones farthest from the root will be the witnesses we seek for the values of V(n, C), and we can find these by doing depth-first search on the tree,
There is nothing wrong with this idea in principle; that's the way my current program works too. The problem is all in the implementation. You see, this program actually constructs the entire tree in memory:
#define NEWN ((struct tree *) Malloc(sizeof(struct tree)));\
printf("*")
struct tree {
char bad;
struct tree *away[MAXCOLORS];
} *root;
struct tree is a tree node structure. It represents a
string s, and has a flag to record whether s is bad. It
also has pointers to its subnodes, which will represents strings
sA,
sB,
and so on.MAXCOLORS is a compiled-in limit on the number of different symbols the strings can contain, an upper bound on C. Apparently I didn't know the standard technique for avoiding this inflexibility. You declare the array as having length 1, but then when you allocate the structure, you allocate enough space for the array you are actually planning to use. Even though the declared size of the array is 1, you are allowed to refer to node->away[37] as long as there is actually enough space in the allocated chunk. The implementation would look like this:
struct tree {
char bad;
struct tree *away[1];
} ;
struct tree *make_tree_node(char bad, unsigned n_subnodes)
{
struct tree *t;
unsigned i;
t = malloc(sizeof(struct tree)
+ (n_subnodes-1) * sizeof(struct tree *));
if (t == NULL) return NULL;
t->bad = bad;
for (i=0; i < n_subnodes; i++) t->away[i] = NULL;
return t;
}
(Note for those who are not advanced C programmers: I give you my
solemn word of honor that I am not doing anything dodgy or bizarre
here; it is a standard, widely-used, supported technique, guaranteed
to work everywhere.)(As before, this code is in a pink box to indicate that it is not actually part of the program I am discussing.)
Another thing I notice is that the NEWN macro is very weird. Note that it may not work as expected in a context like this:
for(i=0; i<10; i++)
s[i] = NEWN;
This allocates ten nodes but prints only one star, because it expands
to:
for(i=0; i<10; i++)
s[i] = ((struct tree *) Malloc(sizeof(struct tree)));
printf("*");
and the for loop does not control the printf. The
usual fix for multiline macros like this is to wrap them in
do...while(0), but that is not appropriate here.
Had I been writing this today, I would have made NEWN a
function, not a macro. Clevermacroitis is a common disorder of
beginning C programmers, and I was no exception.The main business of the program is in the makenodes function; the main routine does some argument processing and then calls makenodes. The arguments to the makenodes function are the current tree node, the current string that that node represents, and an integer howfar that says how deep a tree to construct under the current node.
There's a base case, for when nothing needs to be constructed:
if (!howfar)
{
for (i=0; i<colors; i++)
n->away[i] = NULL;
return;
}
But in general the function calls itself recursively:
for (i=0; i<colors; i++)
{
n->away[i] = NEWN;
n->away[i]->bad = 0;
if (apchk(s,'A'+i))
{
n->away[i]->bad = 1;
}
else
...
Recall that apchk checks a string for an arithmetic
progression of equal characters. That is, it checks to see if a
string is good or bad. If the string is bad, the function prunes the
tree at the current node, and doesn't recurse further.Unlike the one in the previous program, this apchk doesn't bother checking all the possible arithmetic progressions. It only checks the new ones: that is, the ones involving the last character. That's why it has two arguments. One is the old string s and the other is the new symbol that we want to append to s.
If s would still be good with symbol 'A'+i appended to the end, the function recurses:
...
else
{
ls = strlen(s);
newarg = STRING(ls + 1);
strcpy(newarg,s);
newarg[ls+1] = '\0';
newarg[ls] = 'A' + i;
makenodes(n->away[i],howfar-1,newarg);
Free(newarg,ls+2);
Free(n->away[i],sizeof(struct tree));
}
}
}
The entire string is copied here into a new buffer. A better
technique sould have been to allocate a single buffer back up in
main, and to reuse that buffer over again on each call to
makenodes. It would have looked something like this:
char *s = String(maxlen);
memset(s, 0, maxlen+1);
makenodes(s, s, maxlen);
void
makenodes(char *start, char *end, unsigned howfar)
{
...
for (i=0; i<colors; i++) {
*end = 'A' + i;
makenodes(start, end+1, howfar-1);
}
*end = '\0';
...
}
This would have saved a lot of consing, ahem, I mean a lot of
mallocing. Also a lot of string copying. We could avoid the
end pointer by using start+maxlen-howfar instead,
but this way is easier to understand.I was thinking this afternoon how it's intersting the way I wrote this. It's written the way it would have been done, had I been using a functional programming language. In a functional language, you would never mutate the same string for each function call; you always copy the old structure and construct a new one, just as I did in this program. This is why C programmers abominate functional languages.
Had I been writing makenodes today, I would probably have eliminated the other argument. Instead of passing it a node and having it fill in the children, I would have had it construct and return a complete node. The recursive call would then have looked like this:
struct tree *new = NEWN;
...
for (i=0; i<colors; i++) {
new->away[i] = makenodes(...);
...
}
return new;
One thing I left out of all this was the diagnostic printfs;
you can see them in the complete code if you want. But there's one I
thought was worth mentioning anyway:
#define TABS " "
....
#ifdef DIAG
printf("%s makenoding with string %s, depth %d.\n",
TABS+12-maxlen+howfar,s,maxlen-howfar);
#endif
The interesting thing here is the
TABS+12-maxlen+howfar
argument, which indents the display depending on how far the recursion
has progressed. In Perl, which has nonaddressable strings, I usually
do something like this:
my $TABS = " " x (maxlen - howfar);
print $TABS, "....";
The TABS trick here is pretty clever, and I'm a bit surprised
that I thought of it in 1988, when I had been programming in C for
only about a year. It makes an interesting contrast to my failure to
reuse the string buffer in makenodes earlier.(Peeking ahead, I see that in the next version of the program, I did reuse the string buffer in this way.)
TABS is actually forty spaces, not tabs. I suspect I used tabs when I tested it with V(2, 3), where maxlen was only 9, and then changed it to spaces for calculating V(3, 3), where maxlen was 27.
The apchk function checks to see if a string is good. Actually it gets a string, qq, and a character, q, and checks to see if the concatenation of qq and q would be good. This reduces its running time to O(|qq|) rather than O(|qq|2).
int
apchk(qq,q)
char *qq ,q;
{
int lqq, f, s, t;
t = lqq = strlen(qq);
if (lqq < 2) return NO;
for (f=lqq % 2; f <= lqq - 2; f += 2)
{
s = (f + t) / 2;
if ((qq[f] == qq[s]) && (qq[s] == q))
return YES;
}
return NO;
}
It's funny that it didn't occur to me to include an extra parameter to
avoid the strlen, or to use q instead of
qq[s] in the first == test. Also, as in the previous
program, I seem unaware of the relative precedences of
&& and ==. This is probably a hangover from
my experience with Pascal, where the parentheses are required.It seems I hadn't learned yet that predicate functions like apchk should be named something like is_bad, so that you can understand code like if (is_bad(s)) { ... } without having to study the code of is_bad to figure out what it returns.
I was going to write that I hated this function, and that I could do it a lot better now. But then I tried to replace it, and wasn't as successful as I expected I would be. My replacement was:
unsigned
is_bad(char *qq, int q)
{
size_t qql = strlen(qq);
char *f = qq + qql%2;
char *s = f + qql/2;
while (f < s) {
if (*f == q && *s == q) return 1;
f += 2; s += 1;
}
return 0;
}
I could simplify the initializations of f and s,
which are the parts I dislike most here, by making the pointers move
backward instead of forward, but then the termination test becomes
more complicated:
unsigned
is_bad(char *qq, int q)
{
char *s = strchr(qq, '\0')-1;
char *f = s-1;
while (1) {
if (*f == q && *s == q) return 1;
if (f - qq < 2) break;
f -= 2; s -= 1;
}
return 0;
}
Anyway, I thought I could improve it, but I'm not sure I did. On the
one hand, I like the
f -= 2; s -= 1;, which I think is pretty clear. On the other
hand, s = (f + t) / 2 is pretty clear too; s is
midway between f and t. I'm willing to give
teenage Dominus a passing grade on this one.Someone probably wants to replace the while loop here with a for loop. That person is not me.
The Malloc and Free functions track memory usage and were presumably introduced when I discovered that my program used up way too much memory and crashed—I think I remember that the original version omitted the calls to free. They aren't particularly noteworthy, except perhaps for this bit, in Malloc:
if (p == NULL)
{
fprintf(stderr,"Couldn't get %d bytes.\n",c);
fprintf(stderr,"Total get was %d.\n",gotten);
fprintf(stderr,"P\n L\n O\n P\n !\n");
abort();
}
Plop!It strikes me as odd that I was using void in 1988 (this is before the C90 standard) but still K&R-style function declarations. I don't know what to make of that.
Behavior
This program works, almost. On my current machine, it can find the length-26 witnesses for V(3, 3) in no time. (In 1998, it took several days to run on a Sequent Balance 21000.) The major problem is that it gobbles memory: the if (!howfar) base case in makenodes forgets to release the memory that was allocated for the new node. I wonder if the Malloc and Free functions were written in an unsuccessful attempt to track this down.Sometime after I wrote this program, while I was waiting for it to complete, it occurred to me that it never actually used the tree for anything, and I could take it out.
I have this idea that one of the principal symptoms of novice programmers is that they take the data structures too literally, and always want to represent data the way it will appear when it's printed out. I haven't developed the idea well enough to write an article about it, but I hope it will show up here sometime in the next three years. This program, which constructs an entirely unnecessary tree structure, may be one of the examples of this idea.
I'll show the third version sometime in the next few days, I hope.
[ Addendum 20071014: Here is part 3. ]
[Other articles in category /prog] permanent link
Thu, 04 Oct 2007
The world's worst macro preprocessor: postmortem
I see that the world's worst macro processor, subject of a previous
article, is a little over a year old. A year ago I said that it
was a huge success. I think it's time for a
postmortem analysis.
My overall assessment is that it has been a huge success, and that if I were doing it over I would do it the same way.
A recent article contained a bunch of red and blue dots:
Well, clearly you can do four: • • • •. And then you can add another red one on the end: • • • • •. And then another that could be either red or blue: • • • • • •. And then the next can be either color, say blue: • • • • • • •.I typed this using these macros:
#define R* <span style="color: red">•</span>
#define B* <span style="color: blue">•</span>
#define Y* <span style="color: yellow">•</span>
Without the macro processor, I would have had to suffer a lot. Then,
a little while later, I needed to prepare this display:
•••••••••••••••••••••••••• •••••••••••••••••••••••••• •••••••••••••••••••••••••• •••••••••••••••••••••••••• •••••••••••••••••••••••••• •••••••••••••••••••••••••• •••••••••••••••••••••••••• ••••••••••••••••••••••••••No problem; the lines just look like R*R*B*B*R*R*B*Y*B*Y*Y*R*Y*R*R*B*R*B*B*Y*R*Y*Y*B*Y*B*.
Some time later I realized that this display would be totally illegible to the blind, the color-blind, and people using text-only browsers. So I just changed the macros:
#define R* <span style="color: red">R</span>
#define B* <span style="color: blue">B</span>
#define Y* <span style="color: yellow">Y</span>
Problem solved. • • • • • • • instantly becomes
R R B B R B B. And a good thing, too, because I
discovered afterward that a lot of aggregators, like bloglines and
feedburner, discard the color information.I find that I've used the macro feature 114 times so far. The most common use has been:
#define ^2 <sup>2</sup>But I also have files with:
#define r2 √2
#define R2 √2
#define s2 √2
#define S2 √2
That last one appears in three files. Clearly, making the macros
local to files was a good decision.Those uses are pretty typical. A less typical one is:
#define <OVL> <span style="text-decoration: overline">
#define </OVL> </span>
This is the sort of thing that you can get away with on a one-time
basis, but which you wouldn't want to make a convention of. Since the
purpose of the macro processor is to enable such hacks for the
duration of a single article, it's all good.I did run into at least one problem: I was writing an article in which I had defined ^i to abbreviate <sup><i>i</i></sup>. And then several paragraphs later I had a TeX formula that contained the ^i sequence in its TeX meaning. This was being replaced with a bunch of HTML, which was then passed to TeX, which then produced the wrong output.
One can solve this by reordering the plugins. If I had put the TeX plugin before the macro plugin, the problem would have gone away, because the TeX plugin would have replaced the TeX formula with an image element before the macro plugin ever saw the ^i.
This approach has many drawbacks. One is that it would no longer have been possible to use Blosxom macros in a TeX formula. I wasn't willing to foreclose this possibility, and I also wasn't sure that I hadn't done it somewhere. If I had, the TeX formula that depended on the macro expansion would have broken. And this is a risk whenever you move the macro plugin: if you move it from before plugin X to after plugin X, you have to worry that maybe something in some article depended on the text passed to X having been macro-processed.
When I installed the macro processor, I placed it first in plugin order for precisely this reason. Moving the macro substitution later would have required me to remember which plugins would be affected by the macro substitutions and which not. With the macro processing first, the question has a simple answer: all of them are affected.
Also, I didn't ever want to have to worry that some macro definition might mangle the output of some plugin. What if you are hacking on some plugin, and you change it to return <span style="Foo"> instead of <span style="foo">, and then discover that three articles you wrote back in 1997 are now totally garbled because they contained #define Foo >WUGGA<? It's just too unpredictable. Having the macro processing occur first means that you can always see in the original article file just what might be macro-replaced.
So I didn't reorder the plugins.
Another way to solve the TeX ^i problem would have been to do something like this:
#define ^i <sup><i>i</i></sup>
#define ^*i ^i
with the idea that I could write ^*i in the TeX formula, and
the macro processor would replace it with ^i after it
was done replacing all the ^i's. At present the macro processor does not define any order to macro replacements, but it does guarantee to replace each string only once. That is, the results of macro replacement are not themselves searched for macro replacement. This limits the power of the macro system, but I think that is a good thing. One of the powers that is thus proscribed is the power to get stuck in an infinite loop.
It occurs to me now that although I call it the world's worst macro system, perhaps that doesn't give me enough credit for doing good design that might not have been obvious. I had forgotten about my choice of single-substituion behavior, but looking back on it a year later, I feel pleased with myself for it, and imagine that a lot of people would have made the wrong choice instead.
(A brief digression: unlimited, repeated substitution is a bad move here because it is complex—much more complex than it appears. A macro system with single substitution is nothing much, but a macro system with repeated substitution is a programming language. The semantics of the λ-calculus is nothing more than simple substitution, repeated as necessary, and the λ-calculus is a maximally complex computational engine. Term-rewriting systems are a more obvious theoretical example, and TeX is a better-known practical example of this phenomenon. I was sure I did not want my macro system to be a programming language, so I avoided repeated substitution.)
Because each input text is substituted at most once, the processor's refusal to define the order of the replacements is not something you have to think about, as long as your macros are prefix-unique. (That is, as long as none is a prefix of another.) So you shouldn't define:
#define foo bar #define fool idiotbecause then you don't know if foolish turns into barlish or idiotish. This is not a big deal in practice.
Well, anyway, I did not solve the problem with #define ^*i ^i. I took a much worse solution, which was to hack a #undefall directive into the macro processor. In my original article, I boasted that the macro processor "has exactly one feature". Now it has two, and it's not an improvement. I disliked the new feature at the time, and now that I'm reviewing the decision, I think I'm going to take it out.
I see that I did use the double-macro solution elsewhere. In the article about Gödel and the U.S. Constitution, I macroed an abbreviation for the umlaut:
#define Godel Gödel
But this sequence also ocurred in the URLs in the link elements, and
the substitution broke the links. I should probably have changed this
to:
#define Go:del Gödel
But instead I added:
#define GODEL Godel
and then used GODEL in the URLs. Oh well, whatever works, I
guess.Perhaps my favorite use so far is in an (unfinished) article about prosopagnosia. I got tired of writing about prosopagnosia and prosopagnosiacs, so
#define PAa prosopagnosia
#define PAic prosopagnosiac
Note that with these definitions, I get PAa's,
and PAics for free. I could use PAac instead of defining
PAic, but that would prevent me from deciding later that
prosopagnosiac should be spelled "prosopagnosic".
[Other articles in category /prog] permanent link
Wed, 03 Oct 2007
Van der Waerden's problem: program 1
In this series of articles I'm going to analyze four versions of a
program that I wrote around 1988, and then another program that does
the same thing that I wrote last month without referring to the 1988
code.
If you don't remember what the program does, here's an explanation.
Program 1
I'm going to discuss the program a bit at a time. The complete program is here.This program does an unpruned exhaustive search of the string space. Since for V(3, 3) the string space contains 327 = 7,625,597,484,987 strings, it takes a pretty long time to finish. I quickly realized that I was wasting my time with this program.
The program is invoked with a length argument and an optional colors argument, which defaults to 2. It then looks for good strings of the specified length, printing those it finds. If there are none, one then knows that V(3, colors) > length. Otherwise, one knows that V(3, colors) ≤ length, and has witness strings to prove it.
I don't want to spend a lot of time on it because there are plenty of C programming style guides you can read if you care for that. But already on lines 4–5 we have something I wouldn't write today:
#define NO 0
#define YES !NO
Oh well.The program wants to iterate through all Cn strings. How does it know when it's done? It's not easy to make a program as slow as this one even slower, but I found a way to do it.
last = STRING(length);
stuff(last,'A' - 1 + colors);
for (i=0; i<colors; i++)
last[i] = 'A' + i;
for (; strcmp(seq,last); strinc(seq))
...
It manufactures the string ABCDDDDDDDDD....D and compares the
current string to that one every time through the loop. A much simpler
method is to detect completion while incrementing the target string.
The function that does the increment looks like this:
void
strinc(s)
char *s;
{
int i;
for (i= length - 1; i>=0; i--)
{
if (s[i] != 'A' - 1 + colors)
{
s[i]++;
return;
}
s[i] = 'A';
}
return;
}
Had I been writing it today, it would have looked more like this:
unsigned strinc(char *s)
{
char *p = strchr(s, '\0') - 1;
while (p >= s && *p == 'A' + colors - 1) *p-- = 'A';
if (p < s) return 0;
(*p)++;
return 1;
}
(This code is in a pink box to show that it is not actually part of
the program I am discussing in this article.)The function returns true on success and false on failure. A false return can be taken by the caller as the signal to terminate the program.
This replacement function invokes undefined behavior, because there is no guarantee that p is allowed to run off the beginning of the string in the way that it does. But there is no need to check the strings in lexicographic order. Instead of scanning the strings in the order AAA, AAB, ABA, ABB, BAA, etc., one can scan them in reverse lexicographic order: AAA, BAA, ABA, BBA, AAB, etc. Then instead of running off the beginning of the string, p runs off the end, which is allowed. This fixes the undefined behavior problem and also eliminates the call to strchr that finds the end of the string. This is likely to produce a significant speedup:
unsigned strinc(char *s)
{
while (*s == 'A' + colors - 1) *s++ = 'A';
if (!*s) return 0;
(*s)++;
return 1;
}
Here we're depending on the optimizer to avoid recomputing the value
of 'A' + colors - 1 every time through the loop.The heart of the program is the apchk() function, which checks whether a string q contains an arithmetic progression of length 3:
int
apchk(q)
char *q;
{
int f, s, t;
for (f=0; f <= length - 3; f++)
for (s=f+1; s <= length - 2; s++)
{
t = s+s-f;
if (t >= length) break;
if ((q[f] == q[s]) && (q[s] == q[t])) return YES;
}
return NO;
}
I hesitate to say that this is the biggest waste of time in the whole
program, since after all it is a program whose job is to examine
7,625,597,484,987 strings. But look. 2/3 of the
calls to this function are asking it to check a string that differs
from the previous string in the final character only. Nevertheless,
it still checks all 49 possible arithmetic progressions, even the ones
that didn't change.The t ≥ length test is superfluous, or if it isn't, it should be.
Also notice that I wasn't sure of the precendence in the final test.
It didn't take me long to figure out that this program was not going to finish in time. I wrote a series of others, which I hope to post here in coming days. The next one sucks too, but in a completely different way.
[ Addendum 20071005: Here is part 2. ]
[ Addendum 20071014: Here is part 3. ]
[Other articles in category /prog] permanent link
Tue, 02 Oct 2007
Van der Waerden's problem
In this series of articles I'm going to analyze four versions of a
program that I wrote around 1988, and then another program that does
the same thing that I wrote last month without referring to the 1988
code.
First I'll explain what the programs are about.
Van der Waerden's problem
Color each of a row of dots red or blue, so that no three evenly-spaced dots are the same color. (That is, if dots n and n+i are the same color, dot n+2i must be a different color.) How many dots can you do?Well, clearly you can do four: R R B B. And then you can add another red one on the end: R R B B R. And then another that could be either red or blue: R R B B R B. And then the next can be either color, say blue: R R B B R B B.
But now you are at the end, because if you make the next dot red, then dots 2, 5, and 8 will all be red (R R B B R B B R), and if you make the next dot blue then dots 6, 7, and 8 will be blue (R R B B R B B B).
But maybe we made a mistake somewhere earlier, and if the first seven dots were colored differently, we could have made a row of more than 7 that obeyed the no-three-evenly-spaced-dots requirement. In fact, this is so: R R B B R R B B is an example.
But this is the end of the line. Any coloring of a row of 9 dots contains three evenly-spaced dots of the same color. (I don't know a good way to prove this, short of an enumeration of all 512 possible arrangements of dots. Well, of course it is sufficient to enumerate the 256 that begin with R, but that is pretty much the same thing.)
[Addendum 20141208: In this post I give a simple argument that !!V(3,2)\le 9!!.]
Van der Waerden's theorem says that for any number of colors, say C, a sufficiently-long row of colored dots will contain n evenly-spaced same-color dots for any n. Or, put another way, if you partition the integers into C disjoint classes, at least one class will contain arbitrarily long arithmetic progressions.The proof of van der Waerden's theorem works by taking C and n and producing a number V such that a row of V dots, colored with C colors, is guaranteed to contain n evenly-spaced dots of a single color. The smallest such V is denoted V(n, C). For example V(3, 2) is 9, because any row of 9 dots of 2 colors is guaranteed to contain 3 evenly-spaced dots of the same color, but this is not true of such row of only 8 dots.
Van der Waerden's theorem does not tell you what V(n, C) actually is; it provides only an upper bound. And here's the funny thing about van der Waerden's theorem: the upper bound is incredibly bad.
For V(3, 2), the theorem tells you only that V(3, 2) ≤ 325. That is, it tells you that any row of 325 red and blue dots must contain three evenly spaced dots of the same color. This is true, but oh, so sloppy, since the same is true of any row of 9 dots.
For V(3, 3), the question is how many red, yellow, and blue dots do you need to guarantee three evenly-spaced same-colored dots. The theorem helpfully suggests that:
$$V(3,3) \leq 7(2\cdot3^7+1)(2\cdot3^{7(2\cdot3^7+1)}+1)$$
This is approximately 5.79·1014613. But what is the actual value of V(3, 3)? It's 27. Urgggh.In fact, there is a rather large cash prize available to be won by the first person who comes up with a general upper bound for V(n, C) that is smaller than a tower of 2's of height n. (That's 222... with n 2's.)
In the rest of this series, a string which does not contain three evenly-spaced equal symbols will be called good, and one which does contain three such symbols will be called bad. Then a special case of Van der Waerden's theorem, with n=3, says that, for any fixed number of symbols, all sufficiently long strings are bad.
In college I wanted to investigate this a little more. In particular, I wanted to calculate V(3, 3). These days you can just look it up on Wikipedia, but in those benighted times such information was hard to come by. I also wanted to construct the longest possible good strings, witnesses of length V(3, 3)-1. Although I did not know it at the time, V(3, 3) = 27, so a witness should have length 26. It turns out that there are exactly 48 witnesses of length 26. Here are the 1/6 of them that begin with RB or RRB:
RRBBRRBYBYYRYRRBRBBYRYYBYB RRBBYRRYRYBBYYBBYRYRRYBBRR RRBYBRRYRYBBYYBBYRYRRBYBRR RBRRBRBYYBBYYBRBRRBYYRRYRY RBRBBRRYBBYBYRRYYRRYBYBBYR RBRBBRRYBBYBYRRYYRRYBYBBYB RBRBBYBRRYRYYBYBBRBRYYRRYY RBYYBYBRRBBRRBYBYYBRRYYRYR
The rest of the witnesses may be obtained by permuting the colors in these eight.
I wrote a series of C programs around 1988 to exhaustively search for good strings. Last month I was in a meeting and I decided to write the program again for some reason. I wrote a much better program. This series of articles will compare the five programs. I will post the first one tomorrow.
[ Addendum 20071003: Here is part 1. ]
[ Addendum 20071005: Here is part 2. ]
[ Addendum 20071005: I made a mistake in the expression I gave for the upper bound on V(3,3) and left out a factor of 7 in the exponent on the last 3. I had said that the upper bound was around 102092, but actually it is more like the seventh power of this. ]
[ Addendum 20071014: Here is part 3. ]
[Other articles in category /prog] permanent link
Sun, 16 Sep 2007
Thank you very much for that bulletin
I'm about to move house, and so I'm going through a lot of old stuff
and throwing it away. I just unearthed the decorations from my office
door circa 1994. I want to record one of these here before I throw it
away and forget about it. It's a clipping from the front page of the
New York Times from 11 April, 1992. It is noteworthy for
its headline, which only one column wide, but at the very top of
page A1, above the fold. It says:
FIGHTING IMPERILS
EFFORTS TO HALT WAR
IN YUGOSLAVIA
No. If you read the article it turned out that it was about how darn hard it was to end the war when folks kept shooting at each other, dad gum it.
I hear that the headline the following week was DOG BITES MAN, but I don't have a clipping of that.
Addendum 20200507: Here's a thumbnail image. ]
[Other articles in category /lang] permanent link
Sat, 15 Sep 2007
The Wilkins pendulum mystery resolved
Last March, I pointed out that:
- John Wilkins had defined a natural, decimal system of measurements,
- that he had done this in 1668, about 110 years before the Metric System, and
- that the basic unit of length, which he called the "standard", was almost exactly the same length as the length that was eventually adopted as the meter
This article got some attention back in July, when a lot of people were Google-searching for "john wilkins metric system", because the UK Metric Association had put out a press release making the same points, this time discovered by an Australian, Pat Naughtin.
For example, the BBC Video News says:
According to Pat Naughtin, the Metric System was invented in England in 1668, one hundred and twenty years before the French adopted the system. He discovered this in an ancient and rare book...Actually, though, he did not discover it in Wilkins' ancient and rare book. He discovered it by reading The Universe of Discourse, and then went to the ancient and rare book I cited, to confirm that it said what I had said it said. Remember, folks, you heard it here first.
Anyway, that is not what I planned to write about. In the earlier article, I discussed Wilkins' original definition of the Standard, which was based on the length of a pendulum with a period of exactly one second. Then:
Let d be the distance from the point of suspension to the center of the bob, and r be the radius of the bob, and let x be such that d/r = r/x. Then d+(0.4)x is the standard unit of measurement.(This is my translation of Wilkins' Baroque language.)
But this was a big puzzle to me:
Huh? Why 0.4? Why does r come into it? Why not just use d? Huh?Soon after the press release came out, I got email from a gentleman named Bill Hooper, a retired professor of physics of the University of Virginia's College at Wise, in which he explained this puzzle completely, and in some detail.
According to Professor Hooper, you cannot just use d here, because if you do, the length will depend on the size, shape, and orientation of the bob. I did not know this; I would have supposed that you can assume that the mass of the bob is concentrated at its center of mass, but apparently you cannot.
The usual Physics I calculation that derives the period of a pendulum in terms of the distance from the fulcrum to the center of the bob assumes that the bob is infinitesimal. But in real life the bob is not infinitesimal, and this makes a difference. (And Wilkins specified that one should use the most massive possible bob, for reasons that should be clear.)
No, instead you have to adjust the distance d in the formula by adding I/md, where m is the mass of the bob and I is the moment of intertia of the bob, a property which depends on the shape, size, and mass of the bob. Wilkins specified a spherical bob, so we need only calculate (or look up) the formula for the moment of inertia of a sphere. It turns out that for a solid sphere, I = 2mr2/5. That is, the distance needed is not d, but d + 2r2/5d. Or, as I put it above, d + (0.4)x, where d/r = r/x.
Well, that answers that question. My very grateful thanks to Professor Hooper for the explanantion. I think I might have figured it out myself eventually, but I am not willing to put a bound of less than two hundred years on how long it would have taken me to do so.
One lesson to learn from all this is that those early Royal Society guys were very smart, and when they say something has a mysterious (0.4)x in it, you should assume they know what they are doing. Another lesson is that mechanics was pretty well-understood by 1668.
[Other articles in category /physics] permanent link
Fri, 14 Sep 2007
Why spiders hang with their heads down
Katara asked me last week why spiders hang in their webs with their
heads downwards, and I said I would try to find out. After a cursory
Google search, I was none the wiser, so I tried asking the Wikipedia
"reference desk" page. I did not learn anything useful about the
spiders, but I did learn that the reference desk page is full of
people who know even less about spiders than I do who are nevertheless
willing to post idle speculations.
Fortunately, I was at a meeting this week in Durham that was also attended by three of the world's foremost spider experts. I put the question to Jonathan A. Coddington, curator of arachnids for the Smithsonian Institution.
 Professor Coddington told me that it was because the spider prefers
(for obvious mechanical and dynamic reasons) to attack its prey from
above, and so it waits
the upper part of the web and constructs the web so that the principal
prey-catching portion is below. When prey is caught in the web, the
spider charges down and attacks it.
Professor Coddington told me that it was because the spider prefers
(for obvious mechanical and dynamic reasons) to attack its prey from
above, and so it waits
the upper part of the web and constructs the web so that the principal
prey-catching portion is below. When prey is caught in the web, the
spider charges down and attacks it.
I had mistakenly thought that spiders in orb webs (which are the circular webs you imagine when you try to think of the canonical spiderweb) perched in the center. But it is only the topological center, and geometrically it is above the midline, as the adjacent picture should make clear. Note that more of the radial threads are below the center than are above it.
[Other articles in category /bio] permanent link
Thu, 13 Sep 2007
Girls of the SEC
I'm in the Raleigh-Durham airport, and I just got back from the
newsstand, where I learned that the pictorial in this month's
Playboy magazine this month is "Girls of the SEC". On
seeing this, I found myself shaking my head in sad puzzlement.
This isn't the first time I've had this reaction on learning about a Playboy pictorial; last time was probably in August 2002 when I saw the "Women of Enron" cover. (I am not making this up.) I wasn't aware of the December 2002 feature, "Women of Worldcom" (I swear I'm not making this up), but I would have had the same reaction if I had been.
I know that in recent years the Playboy franchise has fallen from its former heights of glory: circulation is way down, the Playboy Clubs have all closed, few people still carry Playboy keychains. But I didn't remember that they had fallen quite so far. They seem to have exhausted all the plausible topics for pictorial features, and are now well into the scraping-the-bottom-of-the-barrel stage. The June 1968 feature was "Girls of Scandinavia". July 1999, "Girls of Hawaiian Tropic". Then "Women of Enron" and now "Girls of the SEC".
How many men have ever had a fantasy about sexy SEC employees, anyway? How can you even tell? Sexy flight attendants, sure; they wear recognizable uniforms. But what characterizes an SEC employee? A rumpled flannel suit? An interest in cost accounting? A tendency to talk about the new Basel II banking regulations? I tried to think of a category that would be less sexually inspiring than "SEC employees". It's difficult. My first thought was "Girls of Wal-Mart." But no, Wal-Mart employees wear uniforms.
If you go too far in that direction you end up in the realm of fetish. For example, Playboy is unlikely to do a feature on "girls of the infectious disease wards". But if they did, there is someone (probably on /b/), who would be extremely interested. It is hard to imagine anyone with a similarly intense interest in SEC employees.
So what's next for Playboy? Girls of the hospital gift shops? Girls of State Farm Insurance telephone customer service division? Girls of the beet canneries? Girls of Acadia University Grounds and Facilities Services? Girls of the DMV?
[ Pre-publication addendum: After a little more research, I figured out that SEC refers here to "Southeastern Conference" and that Playboy has done at least two other features with the same title, most recently in October 2001. I decided to run the article anyway, since I think I wouldn't have made the mistake if I hadn't been prepared ahead of time by "Women of Enron". ]
[ Addendum 20070913: This article is now on the first page of Google searches for "girls of the sec playboy". ]
[ Addendum 20070915: The article has moved up from tenth to third place. Truly, Google works in mysterious ways. ]
[Other articles in category /misc] permanent link
Wed, 12 Sep 2007
The loophole in the U.S. Constitution: the answer
In the previous
article, I wondered what "inconsistency in the Constitution" Gödel
might have found that would permit the United States to become a dictatorship.
Several people wrote in to tell me that Peter Suber addresses this in his book The Paradox of Self-Amendment, which is available online. (Suber also provides a provenance for the Gödel story.)
Apparently, the "inconsistency" noted by Gödel is simply that the Constitution provides for its own amendment. Suber says: "He noticed that the AC had procedural limitations but no substantive limitations; hence it could be used to overturn the democratic institutions described in the rest of the constitution." I am gravely disappointed. I had been hoping for something brilliant and subtle that only Gödel would have noticed.
Thanks to Greg Padgett, Julian Orbach, Simon Cozens, and Neil Kandalgaonkar for bringing this to my attention.
M. Padgett also pointed out that the scheme I proposed for amending the constitution, which I claimed would require only the cooperation of a majority of both houses of Congress, 218 + 51 = 269 people in all, would actually require a filibuster-proof majority in the Senate. He says that to be safe you would want all 100 senators to conspire; I'm not sure why 60 would not be sufficient. (Under current Senate rules, 60 senators can halt a filibuster.) This would bring the total required to 218 + 60 = 278 conspirators.
He also pointed out that the complaisance of five Supreme Court justices would give the President essentially dictatorial powers, since any legal challenge to Presidential authority could be rejected by the court. But this train of thought seems to have led both of us down the same path, ending in the idea that this situation is not really within the scope of the original question.
As a final note, I will point out what I think is a much more serious loophole in the Constitution: if the Vice President is impeached and tried by the Senate, then, as President of the Senate, he presides over his own trial. Article I, section 3 contains an exception for the trial of the President, where the Chief Justice presides instead. But the framers inexplicably forgot to extend this exception to the trial of the Vice President.
[ Addendum 20090121: Jeffrey Kegler has discovered Oskar Morgenstern's lost eyewitness account of Gödel's citizenship hearing. Read about it here. ]
[ Addendum 20110525: As far as I know, there is no particular reason to believe that Peter Suber's theory is correct. Morgenstern knew, but did not include it in his account. ]
[ Addendum 20160315: I thought of another interesting loophole in the Constitution: The Vice-President can murder the President, and then immediately pardon himself. ]
[ Addendum 20210210: As a result of this year's impeachment trial, it has come to my attention that the vice-president need not preside over senate impeachment trials. The senate can appoint anyone it wants to preside. ]
[Other articles in category /law] permanent link
Sun, 09 Sep 2007
The loophole in the U.S. Constitution
Gödel took the matter of citizenship with great solemnity, preparing for the exam by making a close study of the United States Constitution. On the eve of the hearing, he called [Oskar] Morgenstern in an agitated state, saying he had found an "inconsistency" in the Constitution, one that could allow a dictatorship to arise.(Holt, Jim. Time Bandits, The New Yorker, 29 February 2005.)
I've wondered for years what "inconsistency" was.
I suppose the Attorney General could bring some sort of suit in the Supreme Court that resulted in the Court "interpreting" the Constitution to find that the President had the power to, say, arbitrarily replace congresspersons with his own stooges. This would require only six conspirators: five justices and the President. (The A.G. is a mere appendage of the President and is not required for the scheme anyway.)
But this seems outside the rules. I'm not sure what the rules are, but having the Supreme Court radically and arbitrarily "re-interpret" the Constitution isn't an "inconsistency in the Constitution". The solution above is more like a coup d'etat. The Joint Chiefs of Staff could stage a military takeover and institute a dictatorship, but that isn't an "inconsistency in the Constitution" either. To qualify, the Supreme Court would have to find a plausible interpretation of the Constitution that resulted in a dictatorship.
The best solution I have found so far is this: Under Article IV, Congress has the power to admit new states. A congressional majority could agree to admit 150 trivial new states, and then propose arbitrary constitutional amendments, to be ratified by the trivial legislatures of the new states.
This would require a congressional majority in both houses. So Gödel's constant, the smallest number of conspirators required to legally transform the United States into a dictatorship, is at most 269. (This upper bound would have been 267 in 1948 when Gödel became a citizen.) I would like to reduce this number, because I can't see Gödel getting excited over a "loophole" that required so many conspirators.
[ Addendum 20070912: The answer. ]
[ Addendum 20090121: Jeffrey Kegler has discovered Oskar Morgenstern's lost eyewitness account of Gödel's citizenship hearing. Read about it here. ]
[ Addendum 20160129: F.E. Guerra-Pujol has written an article speculating on this topic, “Gödel’s Loophole”. Guerra-Pujol specifically rejects my Article IV proposal for requiring too many conspirators. ]
[ Addendum 20200116: The Harvard Law Review has published an article that proposes my scheme. ]
[Other articles in category /law] permanent link
Sat, 08 Sep 2007
The missing deltahedron
I recently wrote about the convex deltahedra,
which are the eight polyhedra whose faces are all congruent
equilateral triangles:
| Name | Faces | Edges | Vertices |
| Tetrahedron | 4 | 6 | 4 |
| Triangular dipyramid | 6 | 9 | 5 |
| Octahedron | 8 | 12 | 6 |
| Pentagonal dipyramid | 10 | 15 | 7 |
| Snub disphenoid | 12 | 18 | 8 |
| Triaugmented triangular prism | 14 | 21 | 9 |
| Gyroelongated square dipyramid | 16 | 24 | 10 |
| Icosahedron | 20 | 30 | 12 |
The number of edges that meet at a vertex is its valence. Vertices in convex deltahedra have valences of 3, 4, or 5. The valence can't be larger than 5 because only six equilateral triangles will fit, and if you fit 6 then they lie flat and the polyhedron is not properly convex.
Let V3, V4, and V5 be the number of vertices of valences 3, 4, and 5, respectively. Then:
| What | V3 | V4 | V5 |
| D4 | 4 | ||
| D6 | 2 | 3 | |
| D8 | 6 | ||
| D10 | 5 | 2 | |
| D12 | 4 | 4 | |
| D14 | 3 | 6 | |
| D16 | 2 | 8 | |
| D20 | 12 |
Well, this is all oversubtle, I realized later, because you don't need to do the V3–V4–V5 analysis to see that something is missing. There are convex deltahedra with 4, 6, 8, 10, 12, 14, and 20 faces; what happened to 18?
Still, I did a little work on a more careful analysis that might shed some light on the 18-hedron situation. I'm still in the middle of it, but I'm trying to continue my policy of posting more frequent, partial articles.
Let V be the number of vertices in a convex deltahedron, E be the number of edges, and F be the number of faces.
We then have V = V3 + V4 + V5. We also have E = ½(3V3 + 4V4 + 5V5). And since each face has exactly 3 edges, we have 3F = 2E.
By Euler's formula, F + V = E + 2. Plugging in the stuff from the previous paragraph, we get 3V3 + 2V4 + V5 = 12.
It is very easy to enumerate all possible solutions of this equation. There are 19:
| V3 | V4 | V5 | What |
| 4 | 0 | 0 | D4 |
| 3 | 1 | 1 | |
| 3 | 0 | 3 | |
| 2 | 3 | 0 | D6 |
| 2 | 2 | 2 | |
| 2 | 1 | 4 | |
| 2 | 0 | 6 | |
| 1 | 4 | 1 | |
| 1 | 3 | 3 | |
| 1 | 2 | 5 | |
| 1 | 1 | 7 | |
| 1 | 0 | 9 | |
| 0 | 6 | 0 | D8 |
| 0 | 5 | 2 | D10 |
| 0 | 4 | 4 | D12 |
| 0 | 3 | 6 | D14 |
| 0 | 2 | 8 | D16 |
| 0 | 1 | 10 | |
| 0 | 0 | 12 | D20 |
(3,1,1) fails completely because to have V5 > 0 you need V ≥ 6. There isn't even a graph with (V3, V4, V5) = (3,1,1), much less a polyhedron.
There is a graph with (3,0,3), but it is decidedly nonplanar: it contains K3,3, plus an additional triangle. But the graph of any polyhedron must be planar, because you can make a little hole in one of the faces of the polyhedron and flatten it out without the edges crossing.
Another way to think about (3,0,3) is to consider it as a sort of triangular tripyramid. Each of the V5s shares an edge with each of the other five vertices, so the three V5s are all pairwise connected by edges and form a triangle. Each of the three V3s must be connected to each of the three vertices of this triangle. You can add two of the required V3s, by erecting a triangular pyramid on the top and the bottom of the triangle. But then you have nowhere to put the third pyramid.
 On Thursday I didn't know what went wrong with (2,2,2); it seemed
fine. (I found it a little challenging to embed it in the plane, but
I'm not sure if it would still be challenging if it hadn't been the
middle of the night.) I decided that when I got into the office on
Friday I would try making a model of it with my magnet toy and see
what happened.
On Thursday I didn't know what went wrong with (2,2,2); it seemed
fine. (I found it a little challenging to embed it in the plane, but
I'm not sure if it would still be challenging if it hadn't been the
middle of the night.) I decided that when I got into the office on
Friday I would try making a model of it with my magnet toy and see
what happened.
It turned out that nothing goes wrong with (2,2,2). It makes a perfectly good non-convex deltahedron. It's what you get when you glue together three tetrahedra, face-to-face-to-face. The concavity is on the underside in the picture.
 (2,0,6) was a planar graph too, and so the problem had to be
geometric, not topological. When I got to the office, I put it
together. It also worked fine, but the result is not a polyhedron.
The thing you get could be described as a gyroelongated triangular
dipyramid. That is, you take an octahedron and glue tetrahedra to two
of its opposite faces. But then the faces of the tetrahedra are
coplanar with the faces of the octahedron to which they abut, and this
is forbidden in polyhedra. When that happens you're supposed to
eliminate the intervening edge and consider the two faces to be a
single face, a rhombus in this case.
(2,0,6) was a planar graph too, and so the problem had to be
geometric, not topological. When I got to the office, I put it
together. It also worked fine, but the result is not a polyhedron.
The thing you get could be described as a gyroelongated triangular
dipyramid. That is, you take an octahedron and glue tetrahedra to two
of its opposite faces. But then the faces of the tetrahedra are
coplanar with the faces of the octahedron to which they abut, and this
is forbidden in polyhedra. When that happens you're supposed to
eliminate the intervening edge and consider the two faces to be a
single face, a rhombus in this case.
 The resulting thing is not a
polyhedron with 12 triangular faces, but one with six rhombic faces (a
rhombohedron), essentially a squashed cube. In fact, it's exactly
what you get if you make a cube from the magnet toy and then try to
insert another unit-length rod into the diagonal of each of the six
faces. You have to squash the cube to do this, of course, since the
diagonals had length √2 before and length 1 after.
The resulting thing is not a
polyhedron with 12 triangular faces, but one with six rhombic faces (a
rhombohedron), essentially a squashed cube. In fact, it's exactly
what you get if you make a cube from the magnet toy and then try to
insert another unit-length rod into the diagonal of each of the six
faces. You have to squash the cube to do this, of course, since the
diagonals had length √2 before and length 1 after.
So there are several ways in which the triples (V3,V4,V5) can fail to
determine a convex deltahedron: There is an utter topological
failure, as with
(3,1,1).
There is a planarity failure, which is also topological, but less severe, as with (3,0,3). (3,0,3) also fails because you can't embed it into R3. (I mean that you cannot embed its 3-skeleton. Of course you can embed its 1-skeleton in R3, but that is not sufficient for the thing to be a polyhedron.) I'm not sure if this is really different from the previous failure; I need to consider more examples. And (3,0,3) fails in yet another way: you can't even embed its 1-skeleton in R3 without violating the constraint that says that the edges must all have unit length. The V5s must lie at the vertices of an equilateral triangle, and then the three unit spheres centered at the V5s intersect at exactly two points of R3. You can put two of the V3s at these points, but this leaves nowhere for the third V3. Again, I'm not sure that this is a fundamentally different failure mode than the other two.
Another failure mode is that the graph might be embeddable into R3, and might satisfy the unit-edge constraint, but in doing so it might determine a concave polyhedron, like (2,2,2) does, or a non-polyhedron, like (2,0,6) does.
I still have six (V3,V4,V5) triples to look into. I wonder if there are any other failure modes?
I should probably think about (0,1,10) first, since the whole point of all this was to figure out what happened to D18. But I'm trying to work up from the simple cases to the harder ones.
I suppose the next step is to look up the proof that there are only eight convex deltahedra and see how it goes.
I suspect that (2,1,4) turns out to be nonplanar, but I haven't looked at it carefully enough to actually find a forbidden minor.
One thing that did occur to me today was that a triple (V3, V4, V5) doesn't necessarily determine a unique graph, and I need to look into that in more detail. I'll be taking a plane trip on Sunday and I plan to take the magnet toy with me and continue my investigations on the plane.
In other news, Katara and I went to my office this evening to drop off some books and pick up some stuff for the trip, including the magnet toy. Katara was very excited when she saw the collection of convex deltahedron models on my desk, each in a different color, and wanted to build models just like them. We got through all of them, except D10, because we ran out of ball bearings. By the end Katara was getting pretty good at building the models, although I think she probably wouldn't be able to do it without directions yet. I thought it was good work, especially for someone who always skips from 14 to 16 when she counts.
On the way home in the car, we were talking about how she was getting older and I rhapsodized about how she was learning to do more things, learning to do the old things better, learning to count higher, and so on. Katara then suggested that when she is older she might remember to include 15.
[Other articles in category /math] permanent link
Fri, 07 Sep 2007
Families of scalars
I'm supposedly in the midst of writing a book about fixing common
errors in Perl programs, and my canonical example is the family of scalar variables. For
instance, code like this:
if ($FORM{'h01'}) {$checked01 = " CHECKED "}
if ($FORM{'h02'}) {$checked02 = " CHECKED "}
if ($FORM{'h03'}) {$checked03 = " CHECKED "}
if ($FORM{'h04'}) {$checked04 = " CHECKED "}
if ($FORM{'h05'}) {$checked05 = " CHECKED "}
if ($FORM{'h06'}) {$checked06 = " CHECKED "}
(I did not make this up; I got it from here.)
The flag here is the family
$checked01,
$checked02, etc. Such code is almost always improved by
replacing the family with an array, and the repeated code with a
loop:
$checked[$_] = $FORM{"h$_"} for "01" .. "06";
Actually in this particular case a better solution was to eliminated
the checked variables entirely, but that is not what I
was planning to discuss. Rather, I planned to discuss a recent
instance in which I wrote some code with a family of variables myself,
and the fix was somewhat different.The program I was working on was a digester for the qmail logs, translating them into a semblance of human-readable format. (This is not a criticism; log files need not be human-readable; they need to be easy to translate, scan, and digest.) The program scans the log, gathering information about each message and all the attempts to deliver it to each of its recipient addresses. Each delivery can be local or remote.
Normally the program prints information about each message and all its deliveries. I was adding options to the program to allow the user to specify that only local deliveries or only remote deliveries were of interest.
The first thing I did was to add the option-processing code:
...
} elsif ($arg eq "--local-only" || $arg eq '-L') {
$local_only = 1;
} elsif ($arg eq "--remote-only" || $arg eq '-R') {
$remote_only = 1;
As you see, this is where I made my mistake, and introduced a
(two-member) family of variables. The conventional fix says that this
should have been something like $do_only{local} and
$do_only{remote}. But I didn't notice my mistake right away.Later on, when processing a message, I wanted to the program to scan its deliveries, and skip all processing and display of the message unless some of its deliveries were of the interesting type:
if ($local_only || $remote_only) {
...
}
I had vague misgivings at this point about the test, which seemed
redundant, but I pressed on anyway, and found myself in minor trouble.
Counting the number of local or remote deliveries was complicated:
if ($local_only || $remote_only) {
my $n_local_deliveries =
grep $msg->{del}{$_}{lr} eq "local", keys %{$msg->{del}};
my $n_remote_deliveries =
grep $msg->{del}{$_}{lr} eq "remote", keys %{$msg->{del}};
...
}
There is a duplication of code here. Also, there is a waste of CPU
time, since the program never needs to have both numbers available.
This latter waste could be avoided at the expense of complicating the
code, by using something like $n_remote_deliveries = keys(%{$msg->{del}}) -
$n_local_deliveries, but that is not a good solution.Also, the complete logic for skipping the report was excessively complicated:
if ($local_only || $remote_only) {
my $n_local_deliveries =
grep $msg->{del}{$_}{lr} eq "local", keys %{$msg->{del}};
my $n_remote_deliveries =
grep $msg->{del}{$_}{lr} eq "remote", keys %{$msg->{del}};
return if $local_only && $local_deliveries == 0
|| $remote_only && $remote_deliveries == 0;
}
I could have saved the wasted CPU time (and the repeated tests of the
flags) by rewriting the code like this:
if ($local_only) {
return unless
grep $msg->{del}{$_}{lr} eq "local", keys %{$msg->{del}};
} elsif ($remote_only) {
return unless
grep $msg->{del}{$_}{lr} eq "remote", keys %{$msg->{del}};
}
but that is not addressing the real problem, which was the family of
variables, $local_only and $remote_only, which
inevitably lead to duplicated code, as they did here.Such variables are related by a convention in the programmer's mind, and nowhere else. The language itself is as unaware of the relationship as if the variables had been named $number_of_nosehairs_on_typical_goat and $fusion_point_of_platinum. A cardinal rule of programming is to make such conventional relationships explicit, because then the programming system can give you some assistance in dealing with them. (Also because then they are apparent to the maintenance programmer, who does not have to understand the convention.) Here, the program was unable to associate $local_only with the string "local" and $remote_only with "remote", and I had to make up the lack by writing additional code.
For families of variables, the remedy is often to make the relationship explicit by using an aggregate variable, such as an array or a hash, something like this:
if (%use_only) {
my ($only_these) = keys %use_only;
return unless
grep $msg->{del}{$_}{lr} eq $only_these, keys %{$msg->{del}};
}
Here the relationship is explicit because $use_only{"remote"}
indicates an interest in remote deliveries and
$use_only{"local"} indicates an interest in local deliveries,
and the program can examine the key in the hash to determine what to
look for in the {lr} data.But in this case the alternatives are disjoint, so the %use_only hash will never contain more than one element. The tipoff is the bizarre ($only_these) = keys ... line. Since the hash is really storing a single scalar, it can be replaced with a scalar variable:
} elsif ($arg eq "--local-only" || $arg eq '-L') {
$only_these = "local";
} elsif ($arg eq "--remote-only" || $arg eq '-R') {
$only_these = "remote";
Then the logic for skipping uninteresting messages becomes:
if ($only_these) {
return unless
grep $msg->{del}{$_}{lr} eq $only_these, keys %{$msg->{del}};
}
Ahh, better.A long time ago I started to suspect that flag variables themselves are a generally bad practice, and are best avoided, and I think this example is evidence in favor of that theory. I had a conversation about this yesterday with Aristotle Pagaltzis, who is very thoughtful about this sort of thing. One of our conclusions was that although the flag variable can be useful to avoid computing the same boolean value more than once, if it is worth having, it is because your program uses it repeatedly, and so it is probably testing the same boolean value more than once, and so it is likely that the program logic would be simplified if one could merge the blocks that would have been controlled by those multiple tests into one place, thus keeping related code together, and eliminating the repeated tests.
[Other articles in category /prs] permanent link
Thu, 06 Sep 2007
Followup notes about dice and polyhedra
I got a lot of commentary about these geometric articles, and started
writing up some followup notes. But halfway through I got stuck in
the middle of making certain illustrations, and then I got sick, and
then I went to a conference in Vienna. So I decided I'd better
publish what I have, and maybe I'll get to the other fascinating
points later.
- Regarding a die whose sides appear with probabilities 1/21 ... 6/21
- Several people wrote in to cast doubt on my assertion that the
probability of an irregular die showing a certain face is
proportional to the solid angle subtended by that face from the
die's center of gravity. But nobody made the point more clearly
than Robert Young, who pointed out that if I were right, a coin
would have a 7% chance of landing on its edge. I hereby recant
this claim.
- John Berthels suggested that my analysis might be correct if the
die was dropped into an inelastic medium like mud that would
prevent it from bouncing.
- Jack Vickeridge referred me to this web
site, which has a fairly extensive discussion of seven-sided
dice. The conclusion: if you want a fair die, you have no choice
but to use something barrel-shaped.
- Michael Lugo wrote a
detailed followup in which he discusses this and related
problems. He says "What makes Mark's problem difficult is the
lack of symmetry; each face has to be different." Quite so.
- Several people wrote in to cast doubt on my assertion that the
probability of an irregular die showing a certain face is
proportional to the solid angle subtended by that face from the
die's center of gravity. But nobody made the point more clearly
than Robert Young, who pointed out that if I were right, a coin
would have a 7% chance of landing on its edge. I hereby recant
this claim.
- Regarding alternate labelings for standard dice
- Aaron Crane says that these dice (with faces {1,2,2,3,3,4} and
{1,3,4,5,6,8}) are sometimes known as "Sicherman dice", after the
person who first brought them to the attention of Martin Gardner.
Can anyone confirm that this was Col. G.L. Sicherman? I have no
reason to believe that it was, except that it would be so very
unsurprising if it were true.
- Addendum 20070905: I now see that the Wikipedia article
attributes the dice to "Colonel George Sicherman," which is
sufficiently clear that I would feel embarrassed to write to the
Colonel to ask if it is indeed he. I also discovered that the
Colonel has a
Perl program on his web site that will calculate "all pairs of
n-sided dice that give the same sums as standard
n-sided dice".
- M. Crane also says that it is an interesting question
which set of dice is better for backgammon. Both sets have
advantages: the standard set rolls doubles 1/6 of the time,
whereas the Sicherman dice only roll doubles 1/9 of the time. (In
backgammon, doubles count double, so that whereas a player who
rolls a–b can move the pieces a total of
a+b points, a player who rolls a–a
can move pieces a total of 4a points.) The standard dice
permit movement of 296/36 points per roll, and the Sicherman dice
only 274/36 points per roll.
Ofsetting this disadvantage is the advantage that the Sicherman dice can roll an 8. In backgammon, one's own pieces may not land on a point occupied by more than one opposing piece. If your opponent occupies six conscutive points with two pieces each, they form an impassable barrier. Such a barrier is passable to a player using the Sicherman dice, because of the 8.
- Doug Orleans points out that in some
contexts one might prefer to use a Sicherman variant dice {2,3,3,4,4,5} and
{0,2,3,4,5,7}, which retain the property that opposite faces sum
to 7, and so that each die shows 3.5 pips on average. Such dice
roll doubles as frequently as do standard dice.
- The Wikipedia article on dice asserts that the {2, 3, 3,
4, 4, 5} die is used in some wargames to express the strength of
"regular" troops, and the standard {1, 2, 3, 4, 5, 6} die to
express the strength of "irregular" troops. This makes the
outcome of battles involving regular forces more predictable than
those involving irregular forces.
- Aaron Crane says that these dice (with faces {1,2,2,3,3,4} and
{1,3,4,5,6,8}) are sometimes known as "Sicherman dice", after the
person who first brought them to the attention of Martin Gardner.
Can anyone confirm that this was Col. G.L. Sicherman? I have no
reason to believe that it was, except that it would be so very
unsurprising if it were true.
- Regarding deltahedra and the snub disphenoid
- Several people proposed alternative constructions for the snub
disphenoid.
- Brooks Moses suggested the following construction: Take a square
antiprism, squash the top square into a rhombus, and insert a
strut along the short diagonal of the rhombus. Then squash and
strut the bottom square similarly.
It seems, when you think about this, that there are two ways to do the squashing. Suppose you squash the bottom square horizontally in all cases. The top square is turned 45° relative to the bottom (because it's an antiprism) and so you can squash it along the -45° diagonal or along the +45° diagonal, obtaining a left- and a right-handed version of the final solid. But if you do this, you find that the two solids are the same, under a 90° rotation.
This construction, incidentally, is equivalent to the one I described in the previous article: I said you should take two rhombuses and connect corresponding vertices. I had a paragraph that read:
But this is where I started to get it wrong. The two wings have between them eight edges, and I had imagined that you could glue a rhombic antiprism in between them. . . .
But no, I was right; you can do exactly this, and you get a snub disphenoid. What fooled me was that when you are looking at the snub disphenoid, it is very difficult to see where the belt of eight triangles from the antiprism got to. It winds around the polyhedron in a strange way. There is a much more obvious belt of triangles around the middle, which is not suitable for an antiprism, being shaped not like a straight line but more like the letter W, if the letter W were written on a cylinder and had its two ends identified. I was focusing on this belt, but the other one is there, if you know how to see it.The snub disphenoid has four vertices with valence 4 and four with valence 5. Of its 12 triangular faces, four have two valence-4 vertices and one valence-5 vertex, and eight have one valence-4 vertex and two valence-5 vertices. These latter eight form the belt of the antiprism.
- M. Moses also suggested taking a triaugmented triangular
prism, which you will recall is a triangular prism with a square
pyramid erected on each of its three square faces, removing one of
the three pyramids, and then squashing the exposed square face
into a rhombus shape, adding a new strut on the diagonal. This
one gives me even less intuition about what is going on, and it
seems even more strongly that it shou,ld matter whether you put in
the extra strut from upper-left to lower-right, or from
upper-right to lower-left. But it doesn't matter; you get the
same thing either way.
- Jacob Fugal pointed out that you can make a
snub disphenoid as follows: take a pentagonal dipyramid, and
replace one of the equatorial *----*----* figures with a rhombus.
This is simple, but unfortunately gives very little intuition for
what the disphenoid is like. It is obvious from the construction
that there must be pentagons on the front and back, left over from
the dipyramid. But it is not at all clear that there are now two
new upside-down pentagons on the left and right sides, or that the
disphenoid has a vertical symmetry.
- Brooks Moses suggested the following construction: Take a square
antiprism, squash the top square into a rhombus, and insert a
strut along the short diagonal of the rhombus. Then squash and
strut the bottom square similarly.
- A few people asked me where John Batzel got they magnet toy
that I was using to construct the models. It costs only
$5! John gave me his set, and I bought three more, and I now
have a beautiful set of convex deltahedra and a stellated
dodecahedron on my desk. (Actually, it is not precisely a
stellated dodecahedron, since the star faces are not quite planar,
but it is very close. If anyone knows the name of this thing,
which has 32 vertices, 90 edges, and 60 equilateral triangular
faces, I would be pleased to hear about it.) Also I brought my
daughter Katara into my office a few weekends ago to show
her the stella
octangula ("I wanna see the stella octangula, Daddy! Show me
the stella octangula!") which she enjoyed; she then stomped on
it, and then we built another one together.
- [ Addendum 20070908: More about deltahedra. ]
- Several people proposed alternative constructions for the snub
disphenoid.
[Other articles in category /math] permanent link
Tue, 07 Aug 2007
Different arrangements for standard dice
Gaal Yahas wrote to refer me to an article
about a pair of dice that never roll seven. It sounded cool, but
but it was too late at night for me to read it, so I put it on the
to-do list. But it reminded me of a really nice puzzle, which is to
find a nontrivial relabeling of a pair of standard dice that gives the
same probability of throwing any sum from 2 to 12. It's a happy (and
hardly inevitable) fact that there is a solution.
To understand just what is being asked for here, first observe that a standard pair of dice throws a 2 exactly 1/36 of the time, a 3 exactly 2/36 of the time, and so forth:
| 2 | 1/36 |
| 3 | 2/36 |
| 4 | 3/36 |
| 5 | 4/36 |
| 6 | 5/36 |
| 7 | 6/36 |
| 8 | 5/36 |
| 9 | 4/36 |
| 10 | 3/36 |
| 11 | 2/36 |
| 12 | 1/36 |
The standard dice have faces numbered 1, 2, 3, 4, 5, and 6. It should be clear that if one die had {0,1,2,3,4,5} instead, and the other had {2,3,4,5,6,7}, then the probabilities would be exactly the same. Similarly you could subtract 3.7 from every face of one die, giving it labels {-2.7, -1.7, -0.7, 0.3, 1.3, 2.3}, and if you added the 3.7 to every face of the other die, giving labels {4.7, 5.7, 6.7, 7.7, 8.7, 9.7}, you'd still have the same chance of getting any particular total. For example, there are still exactly 2 ways out of 36 possible rolls to get the total 3: you can roll -2.7 + 5.7, or you can roll -1.7 + 4.7. But the question is to find a nontrivial relabeling.
Like many combinatorial problems, this one is best solved with generating functions. Suppose we represent a die as a polynomial. If the polynomial is Σaixi, it represents a die that has ai chances to produce the value i. A standard die is x6 + x5 + x4 + x3 + x2 + x, with one chance to produce each integer from 1 to 6. (We can deal with probabilities instead of "chances" by requiring that Σai = 1, but it comes to pretty much the same thing.)
The reason it's useful to adopt this representation is that rolling the dice together corresponds to multiplication of the polynomials. Rolling two dice together, we multiply (x6 + x5 + x4 + x3 + x2 + x) by itself and get P(x) = x12 + 2x11 + 3x10 + 4x9 + 5x8 + 6x7 + 5x6 + 4x5 + 3x4 + 2x3 + x2, which gives the chances of getting any particular sum; the coefficient of the x9 term is 4, so there are 4 ways to roll a 9 on two dice.
What we want is a factorization of this 12th-degree polynomial into two polynomials Q(x) and R(x) with non-negative coefficients. We also want Q(1) = R(1) = 6, which forces the corresponding dice to have 6 faces each. Since we already know that P(x) = (x6 + x5 + x4 + x3 + x2 + x)2, it's not hard; we really only have to factor x6 + x5 + x4 + x3 + x2 + x and then see if there's any suitable way of rearranging the factors.
x6 + x5 + x4 + x3 + x2 + x = x(x4 + x2 + 1)(x + 1) = x(x2 + x + 1)(x2 - x + 1)(x + 1). So P(x) has eight factors:
| x | x2 + x + 1 | x2 - x + 1 | x + 1 |
| x | x2 + x + 1 | x2 - x + 1 | x + 1 |
We want to combine these into two products Q(x) and R(x) such that Q(1) = R(1) = 6. If we calculate f(1) for each of these, we get 1, 3 (pink), 1, and 2 (blue). So each of Q and R will require one of the factors that has f(1) = 3 and one that has f(1) = 2; we can distribute the f(1) = 1 factors as needed. For normal dice the way we do this is to assign all the factors in each row to one die. If we want alternative dice, our only real choice is what to do with the x2 - x + 1 and x factors.
Redistributing the lone x factors just corresponds to subtracting 1 from all the faces of one die and adding it back to all the faces of the other, so we can ignore them. The only interesting question is what to do with the x2 - x + 1 factors. The normal distribution assigns one to each die, and the only alternative is to assign both of them to a single die. This gives us the two polynomials:
| x(x2 + x + 1)(x + 1) | = | x4 + 2x3 + 2x2 + x |
| x(x2 + x + 1)(x +
1)(x2 - x + 1)2 | = | x8 + x6 + x5 + x4 + x3 + x |
And so the solution is that one die has faces {1,2,2,3,3,4} and the other has faces {1,3,4,5,6,8}:
| 1 | 2 | 2 | 3 | 3 | 4 | |
| 1 | 2 | 3 | 3 | 4 | 4 | 5 |
| 3 | 4 | 5 | 5 | 6 | 6 | 7 |
| 4 | 5 | 6 | 6 | 7 | 7 | 8 |
| 5 | 6 | 7 | 7 | 8 | 8 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 10 |
| 8 | 9 | 10 | 10 | 11 | 11 | 12 |
Counting up entries in the table, we see that there are indeed 6 ways to throw a 7, 4 ways to throw a 9, and so forth.
One could apply similar methods to the problem of making a pair of dice that can't roll 7. Since there are six chances in 36 of rolling 7, we need to say what will happen instead in these 6 cases. We might distribute them equally among some of the other possibilities, say 2, 4, 6, 8, 10, and 12, so that we want the final distribution of results to correspond to the polynomial 2x12 + 2x11 + 4x10 + 4x9 + 6x8 + 6x6 + 4x5 + 4x4 + 2x3 + 2x2. The important thing to notice here is that the coefficient of the x7 term is 0.
Now we want to factor this polynomial and proceed as before. Unfortunately, it is irreducible. (Except for the trivial factor of x2.) Several other possibilities are similarly irreducible. It's tempting to reason from the dice to the algebra, and conjecture that any reducible polynomial that has a zero x7 term must be rather exceptional in other ways, such as by having only even exponents. But I'm not sure it will work, because the polynomials are more general than the dice: the polynomials can have negative coefficients, which are meaningless for the dice. Still, I can fantasize that there might be some result of this type available, and I can even imagine a couple of ways of getting to this result, one combinatorial, another based on Fourier transforms. But I've noticed that I have a tendency to want to leave articles unpublished until I finish exploring all possible aspects of them, and I'd like to change that habit, so I'll stop here, for now.
[ Addendum 20070905: There are some followup notes. ]
[Other articles in category /math] permanent link
Mon, 06 Aug 2007
Standard analytic polyhedra
If you want to consider a cube analytically, you have an easy job.
The vertices lie at the points:
(0,0,0)And you can see at a glance whether two vertices share an edge (they are the same in two of their three components) or are opposite (they differ in all three components).
(0,0,1)
(0,1,0)
(0,1,1)
(1,0,0)
(1,0,1)
(1,1,0)
(1,1,1)
Last week I was reading the Wikipedia article about the computer game "Hunt the Wumpus", which I played as a small child. For the Guitar Hero / WoW generation I should explain Wumpus briefly.
The object of "Wumpus" is to kill the Wumpus, which hides in a network of twenty caves arranged in a dodecahedron. Each cave is thus connected to three others. On your turn, you may move to an adjacent cave or shoot a crooked arrow. The arrow can pass through up to five connected caves, and if it enters the room where the Wumpus is, it kills him and you win. Two of the caves contain bottomless pits; to enter these is death. Two of the caves contain giant bats, which will drop you into another cave at random; if it contains a pit, too bad. If you are in a cave adjacent to a pit, you can feel a draft; if you are adjacent to bats, you can hear them. If you are adjacent to the Wumpus, you can smell him. If you enter the Wumpus's cave, he eats you. If you shoot an arrow that fails to kill him, he wakes up and moves to an adjacent cave; if he enters you cave, he eats you. You have five arrows.
I did not learn until much later that the caves are connected in a dodecahedron; indeed, at the time I probably didn't know what a dodecahedron was. The twenty caves were numbered, so that cave 1 was connected to 2, 5, and 8. This necessitated a map, because otherwise it was too hard to remember which room was connected to which.
Or did it? If the map had been a cube, the eight rooms could have been named 000, 001, 010, etc., and then it would have been trivial to remember: 011 is connected to 111, 001, and 010, obviously, and you can see it at a glance. It's even easy to compute all the paths between two vertices: the paths from 011 to 000 are 011–010–000 and 011–001–000; if you want to allow longer paths you can easily come up with 011–111–110–100–000 for example.
And similarly, the Wumpus source code contains a table that records which caves are connected to which, and consults this table in many places. If the caves had been arranged in a cube, no table would have been required. Or if one was wanted, it could have been generated algorithmically.
So I got to wondering last week if there was an analogous nomenclature for the vertices of a dodecahedron that would have obviated the Wumpus map and the table in the source code.
I came up with a very clever proof that there was none, which would have been great, except that the proof also worked for the tetrahedron, and the tetrahedron does have such a convenient notation: you can name the vertices (0,0,0), (0,1,1), (1,0,1), and (1,1,0), where there must be an even number of 1 components. (I mentioned this yesterday in connection with something else and promised to come back to it. Here it is.) So the proof was wrong, which was good, and I kept thinking about it.
The next-simplest case is the octahedron, and I racked my brains trying to come up with a convenient notation for the vertices that would allow one to see at a glance which were connected. When I finally found it, I felt like a complete dunce. The octahedron has six vertices, which are above, below, to the left of, to the right of, in front of, and behind the center. Their coordinates are therefore (1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) and (0,0,-1). Two vertices are opposite when they have two components the same (necessarily both 0) and one different (necessarily negatives). Otherwise, they are connected by an edge. This is really simple stuff.
Still no luck with the dodecahedron. There are nice canonical representations of the coordinates of the vertices—see the Wikipedia article, for example—but I still haven't looked at it closely enough to decide if there is a simple procedure for taking two vertices and determining their geometric relation at a glance. Obviously, you can check for adjacent vertices by calculating the distance between them and seeing if it's the correct value, but that's not "at a glance"; arithmetic is forbidden.
It's easy to number the vertices in layers, say by calling the top five vertices A1 ... A5, then the five below that B1 ... B5, and so on. Then it's easy to see that A3 will be adjacent to A2, A4, and B3, for example.
But this nomenclature, unlike the good ones above, is not isometric: it has a preferred orientation of the dodecahedron. It's obvious that A1, A2, A3, A4, and A5 form a pentagonal face, but rather harder to see that A2, A3, B2, B3, and C5 do. With the cube, it's easy to see what a rotation or a reflection looks like. For example, rotation of 120° around an axis through a pair of vertices of the cube takes vertex (a, b, c) to (c, a, b); rotation of 90° around an axis through a face takes it to (1-b, a, c). Similarly, rotations and reflections of the tetrahedron correspond to simple permutations of the components of the vertices. Nothing like this exists for the A-B-C-D nomenclature for the dodecahedron.
I'll post if I come up with anything nice.
[Other articles in category /math] permanent link
Sun, 05 Aug 2007
Sub-blogs and the math sub-blog
I notice that a number of people have my blog included in lists of
"math blogs", which is fine with me, but I got a bit worried when I
saw someone's web site that actually includes a lot of "math
blog" articles, including mine, which is only ever about one-fourth
math, the rest being given over to random other stuff. So the "math
blog" section of this guy's web site is carrying my ill-informed
articles about evolutionary biology and notes about the Frances the
Badger books.
If you really do want just the math articles for some reason, you can subscribe to the feeds at http://blog.plover.com/math/index.rss or http://blog.plover.com/math/index.atom. I've been generating these sub-feed files since the blog began, and I know nobody uses them. But perhaps someone would like to.
Similarly, there are sub-feeds for other subsections of the blog, for example "physics". Most of these topic areas receive many fewer updates than does the "math" section:
| 64 | math |
| 16 | lang |
| 14 | physics |
| 14 | oops |
| 14 | linogram |
| 14 | book |
| 14 | prog |
| 10 | bio |
| 7 | lang/etym |
| 6 | meta |
Personally I feel that the eclecticism of the blog is one of its attractions, and I gather that a lot of other people do too, but perhaps not everyone agrees.
[Other articles in category /meta] permanent link
The 123456 die
As a result of my recent
article on the snub disphenoid, Paul Keir wrote to me to ask about
non-equiprobable dice. Specifically, he wanted a die that, because it
was irregular, was twice as likely to land on one face as on any of the
others.
That got me thinking about the problem in general. For some reason I've been trying to construct a die whose faces come up with probabilities 1/21, 2/21, 3/21, 4/21, 5/21, and 6/21 respectively.
Unless there is a clever insight I haven't had, I think this will be rather difficult to do explicitly. (Approximation methods will probably work fairly easily though, I think.) I started by trying to make a hexahedron with faces that had areas 1, 2, 3, 4, 5, 6, and even this has so far evaded me. This will not be sufficient to solve the problem, because the probability that the hexahedron will land on face F is not proportional to the area of F, but rather to the solid angle subtended by F from the hexahedron's center of gravity.
Anyway, I got interested in the idea of making a hexahedron whose faces had areas 1..6. First I tried just taking a bunch of simple shapes (right triangles and the like) of the appropriate sizes and fitting them together geometrically; so far that hasn't worked. So then I thought maybe I could get what I wanted by taking a tetrahedron or a disphenoid or some such and truncating a couple of the corners.
As Polya says, if you can't solve the problem, you should try solving a simpler problem of the same sort, so I decided to see if it was possible to take a regular tetrahedron and chop off one vertex so that the resulting pentahedron had faces with areas 1, 2, 3, 4, 5. The regular tetrahedron is quite tractable, geometrically, because you can put its vertices at (0,0,0), (0,1,1), (1,0,1), and (1,1,0), and then a plane that chops off the (0,0,0) vertex cuts the three apical edges at points (0,a,a), (b,0,b), and (c,c,0), for some 0 ≤ a, b, c ≤ 1. The chopped-off areas of the three faces are simply ab√3/4, bc√3/4, ca√3/4, and the un-chopped base has area √3/4, so if we want the three chopped faces to have areas of 2/5, 3/5 and 4/5 times √3/4, respectively, we must have ab = 3/5, bc = 2/5, and ca = 1/5, and we can solve for a, b, c. (We want the new top face to have area 1/5 · √3/4, but that will have to take care of itself, since it is also determined by a, b, and c.) Unfortunately, solving these equations gives b = √6/√5, which is geometrically impossible. We might fantasize that there might be some alternate solution, say with the three chopped faces having areas of 1/5, 2/5 and 4/5 times √3/4, and the top face being 3/5 · √3/4 instead of 1/5 · √3/4, but none of those will work either.
Oh well, it was worth a shot. I do think it's interesting that if you know the areas of the bottom four faces of a truncated regular tetrahedron, that completely determines the apical face. Because you can solve for the lengths of the truncated apical edges, as above, and then that gives you the coordinates of the three apical vertices.
I had a brief idea about truncating a square pyramid to get the hexahedron I wanted in the first place, but that's more difficult, because you can't just pick the lengths of the four apical edges any way you want; their upper endpoints must be coplanar.
The (0,a,a), (b,0,b), (c,c,0) thing has been on my mind anyway, and I hope to write tomorrow's blog article about it. But I've decided that my articles are too long and too intermittent, and I'm going to try to post some shorter, more casual ones more frequently. I recently remembered that in the early days of the blog I made an effort to post every day, and I think I'd like to try to resume that.
[ Addendum 20070905: There are some followup notes. ]
[Other articles in category /math] permanent link
Wed, 01 Aug 2007
The snub disphenoid
 The snub
disphenoid is pictured at left. I do not know why it is called that,
and I ought to know, because I am the principal author (so far) of the
Wikipedia article on the disphenoid. Also,
I never quite figured out what "snub" means in this context, despite
perusing that section of H.S.M. Coxeter's book on polytopes at some
length. It has something to do with being halfway between what you
get when you cut all the corners off, and what you get when you cut all
the corners off again.
The snub
disphenoid is pictured at left. I do not know why it is called that,
and I ought to know, because I am the principal author (so far) of the
Wikipedia article on the disphenoid. Also,
I never quite figured out what "snub" means in this context, despite
perusing that section of H.S.M. Coxeter's book on polytopes at some
length. It has something to do with being halfway between what you
get when you cut all the corners off, and what you get when you cut all
the corners off again.

 Anyway, earlier this week I was visiting John Batzel, who works
upstairs from me, and discovered that he had obtained a really cool
toy. It was a collection of large steel ball bearings and colored
magnetic rods, which could be assembled into various polyhedra and
trusses. This is irresistible to me. The pictures at right, taken around
2002, show me modeling a dodecahedron with less suitable
materials.
Anyway, earlier this week I was visiting John Batzel, who works
upstairs from me, and discovered that he had obtained a really cool
toy. It was a collection of large steel ball bearings and colored
magnetic rods, which could be assembled into various polyhedra and
trusses. This is irresistible to me. The pictures at right, taken around
2002, show me modeling a dodecahedron with less suitable
materials.
The first thing I tried to make out of John's magnetic sticks and balls was a regular dodecahedron, because it is my favorite polyhedron. (Isn't it everyone's?) This was unsuccessful, because it wasn't rigid enough, and kept collapsing. It's possible that if I had gotten the whole thing together it would have been stable, but holding the 50 separate magnetic parts in the right place long enough to get it together was too taxing, so I tried putting together some other things.
A pentagonal dipyramid worked out well, however. To understand this solid, imagine a regular pyramid, such as the kind that entombs the pharaohs or collects mystical energy. This sort of pyramid is known as a square pyramid, because it has a square base, and thus four triangular sides. Imagine that the base was instead a pentagon, so that there were five triangular sides sides instead of only four. Then it would be a pentagonal pyramid. Now take two such pentagonal pyramids and glue the pentagonal bases together. You now have a pentagonal dipyramid.
The success of the pentagonal dipyramid gave me the idea that rigid triangular lattices were the way to go with this toy, so I built an octahedron (square dipyramid) and an icosahedron to be sure. Even the icosahedron (thirty sticks and twelve balls) held together and supported its own weight. So I had John bring up the Wikipedia article about deltahedra. A deltahedron is just a polyhedron whose faces are all equilateral triangles.
Four of the deltahedra are the tetrahedron (triangular pyramid, with 4 faces), triangular dipyramid (6 faces), octahedron (square dipyramid, 8 faces), and pentagonal dipyramid (10 faces).
 Another is the icosahedron. Imagine making a belt of 10 triangles,
alternating up and down, and then connect the ends of the belt. The result is a
shape called a pentagonal
antiprism, shown at left. The edges of the down-pointing triangles form a
pentagon on the top of the antiprism, and the edges of the up-pointing
triangles form one on the bottom. Attach a pentagonal pyramid to each
of these pentagons, and you have an icosahedron, with a total of 20
faces.
Another is the icosahedron. Imagine making a belt of 10 triangles,
alternating up and down, and then connect the ends of the belt. The result is a
shape called a pentagonal
antiprism, shown at left. The edges of the down-pointing triangles form a
pentagon on the top of the antiprism, and the edges of the up-pointing
triangles form one on the bottom. Attach a pentagonal pyramid to each
of these pentagons, and you have an icosahedron, with a total of 20
faces.
The other three deltahedra are less frequently seen. One is the
result of taking a triangular prism and appending a square pyramid to
each of its three square faces. (Wikipedia calls this a "triaugmented
triangular prism"; I don't know how standard that name is.) Since the
prism had two triangular faces to begin with, and we have added four
more to each of the three square faces of the original prism, the
total is 14 faces.
Another deltahedron is the "gyroelongated square dipyramid". You get this by taking two square pyramids, as with the octahedron. But instead of gluing their square bases together directly, you splice a square antiprism in between. The two square faces of the antiprism are not aligned; they are turned at an angle of 45° to each other, so that when you are looking at the top pyramid face-on, you are looking at the bottom pyramid edge-on, and this is the "gyro" in "gyroelongated". (The icosahedron is a gyroelongated pentagonal dipyramid.) I made one of these in John's office, but found it rather straightforward.
The last deltahedron, however, was quite a puzzle. Wikipedia calls it a "snub disphenoid", and as I mentioned before, the name did not help me out at all. It took me several tries to build it correctly. It contains 12 faces and 8 vertices. When I finally had the model I still couldn't figure it out, and spent quite a long time rotating it and examining it. It has a rather strange symmetry. It is front-back and left-right symmetric. And it is almost top-bottom symmetric: If you give it a vertical reflection, you get the same thing back, but rotated 90° around the vertical axis.
When I planned this article I thought I understood it better. Imagine sticking together two equilateral triangles. Call the common edge the "rib". Fold the resulting rhombus along the rib so that the edges go up, down, up, down in a zigzag. Let's call the resulting shape a "wing"; it has a concave side and a convex side. Take two wings. Orient them with the concave sides facing each other, and with the ribs not parallel, but at right angles. So far, so good.
But this is where I started to get it wrong. The two wings have between them eight edges, and I had imagined that you could glue a rhombic antiprism in between them. I'm not convinced that there is such a thing as a rhombic antiprism, but I'll have to do some arithmetic to be sure. Anyway, supposing that there were such a thing, you could glue it in as I said, but if you did the wings would flatten out and what you would get would not be a proper polyhedron because the two triangles in each wing would be coplanar, and polyhedra are not allowed to have abutting coplanar faces. (The putative gyroelongated triangular dipyramid fails for this reason, I believe.)
To make the snub disphenoid, you do stick eight triangles in between the two wings, but the eight triangles do not form a rhombic antiprism. Even supposing that such a thing exists.
I hope to have some nice renderings for you later. I have been doing some fun work in rendering semiregular polyhedra, and I am looking forward to discussing it here. Advance peek: suppose you know how the vertices are connected by edges. How do you figure out where the vertices are located in 3-space?
If you would like to investigate this, the snub disphenoid has 8 vertices, which we can call A, B, ... H. Then:
| This vertex: | is connected to these: |
| A | B C E F H |
| B | A C D E |
| C | A B D H |
| D | B C E G H |
| E | F G A B D |
| F | E G H A |
| G | E F H D |
| H | F G A C D |
Here is a list of the eight deltahedra, with links to the corresponding Wikipedia articles:
| Name | Faces | Edges | Vertices |
| Tetrahedron | 4 | 6 | 4 |
| Triangular dipyramid | 6 | 9 | 5 |
| Octahedron | 8 | 12 | 6 |
| Pentagonal dipyramid | 10 | 15 | 7 |
| Snub disphenoid | 12 | 18 | 8 |
| Triaugmented triangular prism | 14 | 21 | 9 |
| Gyroelongated square dipyramid | 16 | 24 | 10 |
| Icosahedron | 20 | 30 | 12 |
[ Addendum 20070908: More about deltahedra. ]
[Other articles in category /math] permanent link
Sat, 28 Jul 2007
Lightweight Database Strategies for Perl
Several years ago I got what I thought was a great idea for a
three-hour conference tutorial: lightweight data storage techniques.
When you don't have enough data to be bothered using a
high-performance database, or when your data is simple enough that you
don't want to bother with a relational database, you stick it in a
flat file and hack up some file code to read it. This is the sort of
thing that people do all the time in Perl, and I thought it
would be a big seller. I was wrong.
I don't know why. I tried giving the class a snappier title, but that didn't help. I'm really bad at titles. Maybe people are embarrassed to think about all the lightweight data storage hackery they do in Perl, and feel that they "should" be using a relational database, and don't want to commit more resources to lightweight database techniques. Or maybe they just don't think there is very much to know about it.
But there is a lot to know; with a little bit of technique you can postpone the day when you need to go to an RDB, often for quite a long time, and often forever. Many of the techniques fall into the why-didn't-I-think-of-that category, stuff that isn't too weird to write or maintain, but that you might not have thought to try.
I think it's a good class, but since it never sold well, I've decided it would do more good (for me and for everyone else) if I just gave away the materials for free.
Table of Contents
The class is in three sections. The first section is about using plain text files and talks about a bunch of useful techniques, such as how to do binary search on sorted text files (this is nontrivial) and how to replace records in-place, when they might not fit.The second section is about the Tie::File module, which associates a flat text file with a Perl array.
The third section is about DBM files, with a comparison of the five major implementations. It finishes up with a discussion of some of Berkeley DB's lesser-known useful features, such as its DB_BTREE file type, which offers fast access like a hash but keeps the records in sorted order
- Text Files
- Rotating log file; deleting a user
- Copy the File
- -i.bak
- Using -i inside a program
- Problems with -i
- Atomicity issues
- Essential problem with files; fundamental operations; seeking
- Sorted files
- In-place modification of records
- Overwriting records
- Bytes vs. positions
- Gappy Files
- Fixed-length records
- Numeric indices
- Case study: lastlog
- Indexing
- Void fields
- Generic text indices
- Packed offsets
- Tie::File
- Tie::File Examples
- delete_user revisited
- uppercase_username revisited
- Rotating log file revisited
- Most important thing to know about Tie::File
- Indexing with Tie::File
- Tie::File Internals
- Caching
- Record modification
- Immediate vs. Deferred Writing
- Autodeferring
- Miscellaneous Features
- DBM
- Common DBM Implementations
- What DBM Does
- Small DBMs: ODBM, NDBM, and SDBM
- GDBM
- DB_File
- Indexing revisited
- Ordered hashes
- Partial matching
- Sequential access
- Multiple values
- Filters
- BerkeleyDB
Online materials
- Class slides:

This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.- PDF files:
- Browse slides online
- Sample source code referred to in the class:

Example source code from Lightweight Databases class is licensed under a Creative Commons Public Domain License. - People sometimes ask what use Tie::File is when Berkeley DB has a DB_RECNO option that appears to be the same thing. This document explains why.
[Other articles in category /prog/perl] permanent link
Fri, 27 Jul 2007
Conference talk brochure descriptions
I just got back from doing some
tutorials at OSCON, which were generally well-received. Sometimes
it goes better than other times; this time it went pretty well, I
thought, except that I was seven minutes late to the Tuesday morning
one, through a tremendous series of fuckups beginning with the
conference hotel not being able to find my reservation on Saturday
night, continuing with my barely missing two unrelated streetcars on
Tuesday morning, and, let's not leave out the most important part, my
forgetting that the class started at 8:30 and not at 9:00 until about
8:00.
I've written before about the general worthlessness of the attendee evaluations, so maybe I won't go into detail about them again. What I want to complain about here is the descriptions of the classes that appear in the conference brochure and on the web site.
One of the things that Nat (the program committee chair) and I have commiserated about in the past is that no matter how hard you try to make a clear, concise, accurate description of the class, you are doomed, because people do not use the descriptions in a rational way. For example, suppose I happen to be giving the same class two years in a row. The class title is the same both years. The 250-word description in the brochure and on the web site is word-for-word identical both years. Nevertheless, you can be sure that someone will hand in an evaluation the second year that complains bitterly that the class was a waste of time, because they took the class the year before and there was no new material. I vented about this to Nat once, and the look of exhausted disgust on his face was something to see. Because I only have to read my own stupid evaluations, but Nat has to read all the stupid evaluations, and he probably sees that same idiotic complaint ten times a year.
Here's one I was afraid I'd get this year, and, who knows. It may yet happen. I sent the program committee seven proposals. They accepted three. One was for the Advanced techniques for Parsing class; one for for Higher-Order Perl. There was significant overlap between these two classes; the last third of the Higher-Order Perl class is about higher-order parser combinators, which are the principal subject of the advanced parsing class. This puts me in a difficult position. The program committee has accepted two classes that overlap. I have to deliver the material that I promised in the brochure, which people paid money to hear. I cannot unilaterally eliminate the overlap, say by substituting a different topic into Higher-Order Perl, because then someone in that class might quite rightly complain that they had been promised a section on parsing techniques, had paid for a section on parsing techniques, but had not been delivered a section on parsing techniques. But some people will sign up for both classes, and then will inevitably complain about the overlap, even though it should have been clear from the brochure that the classes would overlap.
The only way out for me is to try to get the program committee to agree beforehand to let me change around one of the classes to remove the overlap, write one-third of a new class, and document the change in the brochure description before it is published. That is a lot of work to do in a short time. Some people write their class slides the night before they give the class. I don't; I take weeks over it, revising extensively, and then I give a practice session, and then I revise again. So the classes overlapped, and I'm sure there were complaints about it that I haven't seen yet.
My favorite complaint of all time was from the guy who took Tricks of the Wizards and then complained that the material was too advanced.
This year I had the opposite problem. I gave a class on Advanced techniques for Parsing, and the following day I read a blog article from someone who had been disappointed that it was insufficiently advanced. This is a fair and legitimate criticism, and deserves a reasonable response. The response is not, however, to change the class content, because I think I have a pretty good idea of how sophisticated the conference attendees are, and of what is useful, and if I made the class a lot more advanced than it is, hardly anyone would understand it. But I did feel bad that this blogger had mistakenly wasted hours in my class and gotten nothing out of it. That should have been avoidable.
The first thing I did was to check the brochure description, to see if perhaps it was misleading, or if it promised extra-advanced material that I then didn't deliver. This sometimes happens. The deadline for proposals is far in advance of the deadline for the class materials themselves. So what happens is that you write up a proposal for a class you think you can do, that people will like, and that will appeal to the program committee, and you send it in. A few months later, it is accepted, and you start work on the class. Then sometimes you discover that even though you proposed a class about A, B, and C, there is only enough time to do A and B properly, and to cover all three in a three-hour class would just be a mess. So you write a class that covers A and B properly, and has an abbreviated discussion of C. But then there will be some people who came to the class specifically for the discussion of C, and who are disappointed. It is a tough problem.
Anyway, I thought this time I had done a reasonably good job of writing a class that actually matched the brochure description. So I wrote to the blogger to ask how the description could have been better: what would I have needed to say in it that would have tipped him off that the class would not have had whatever it was he was looking for?
The answer: nothing. He had not read the description. He attended the class solely because of the title, Advanced techniques for Parsing, and then after two hours figured out that it was not as advanced as he wanted it to be.
Not my fault! Not my fault!
[Other articles in category /talk] permanent link
Sat, 21 Jul 2007
Homosexuality is not hereditary
A just read a big pile of blog comments that all said that
homosexuality couldn't be hereditary, because if it were, natural
selection would have gotten rid of it by now.
But natural selection is more interesting than that. This article will ignore the obvious notion of homosexuals who breed anyway. Here is one way in which homosexuality could be entirely hereditary and still be favored by natural selection.
Suppose that human sexuality is extremely complicated, which should not be controversial. Suppose, just for concreteness, that there are 137 different genes that can affect whether an individual turns out heterosexual or homosexual. Say that each of these can either be either in state Q or state S, and that and that any individual will turn out homosexual if any 93 of the 137 genes are in state Q, heterosexual otherwise.
The over-simplistic argument from natural selection says that the Q states will be bred out of the population, and that S will be increasingly predominant over time.
Now let's consider an individual, X, whose family members tend to carry a lot of Q genes.
Suppose X's parents have a lot of Q genes, around 87 or 90. X's parents' siblings, who resemble them, will also have a lot of Q genes, and have a high probability of being homosexual. Having no children of their own, they may contribute to X's welfare, maybe by caring for X or by finding food for X.
In short, for every gay uncle X has, that is one additional set of cousins with whom X does not have to compete for scarce resources.
This could well turn out to be a survival advantage for X over someone from a family of people without a lot of Q genes, someone who is competing for food with a passel of cousins, none of whom ever really get enough to eat, someone whose aunt might even try to kill them in order to benefit her own children.
Perhaps X turns out to be homosexual and never breeds, but X probably has some siblings, in which case X might be an advantageous gay uncle or lesbian aunt to one of his or her own nieces or nephews, who, remember, are carrying a lot of the same genes, including the Q genes.
It might not actually work this way, of course, and in most ways it probably doesn't. The only point here is to show that natural selection does not necessarily rule out the idea of inherited homosexuality; people who think it must, have not exercised enough imagination.
(Now that I have finished writing this article, it occurs to me that the same argument applies to bees and ants; most individuals in a bee or ant colony are sterile. Who would be foolish enough to argue that this trait will soon be bred out of the colony?)
The moral of this story:
Time and time again, biologists baffled by some apparently futile or maladroit bit of bad design in nature have eventually come to see that they have underestimated the ingenuity, the sheer brilliance, the depth of insight to be disovered in one of Mother Nature's creations. Francis Crick has mischievously baptized this trend in the name of his colleague Leslie Orgel, speaking of what he calls "Orgels Second Rule: Evolution is cleverer than you are."Daniel Dennett, Darwin's Dangerous Idea, p. 74.
[Other articles in category /bio] permanent link
Fri, 20 Jul 2007
Tough questions
It's easy to recognize a good question: a good question is one that
takes a lot longer to answer than it does to ask. Chip Buchholtz's
example is "what is a byte?" To answer that you have to get into the
nitty gritty of computer architecture and how, although the
information in the computer is stored by the bit, the memory bus can
only address it by the byte.
One of the biology interns asked a me a good one a couple of weeks ago: he asked how, if Perl runs Perl scripts, and the OS is running Perl, what is running the OS? Now that is a tough question to answer. I explained about logic gates, and how the logic gates are built into trivial arithmetic and memory circuits, how these are then built up into ALUs and memories, and how these in turn are controlled by microcode, and finally how the logical parts are assembled into a computer. I don't know how understandable it was, but it was the best I could do in five minutes, and I think I got some of the idea across. But I started and finished by saying that it was basically miraculous.
My daughter Katara asks a ton of questions, some better than others. On any given evening she is likely to ask "Daddy, what are you doing?" about fifteen times, and "why?" about fifteen million times. "Why" can be a great question, but sometimes it's not so great; Katara asks both kinds. Sometimes it's in response to "I'm eating a sandwich." Then the inevitable "why?" is rather annoying.
Some of the "why" questions are nearly impossible to answer. For example, we see a lady coming up the street toward us. "Is that Susanna?" "No." "Why is it not Susanna?"
I think what's happening here is that having discovered this magic word that often produces interesting information, Katara is employing it whenever possible, even when it doesn't make sense, because she hasn't yet learned when it works and when not. Why is that not Susanna? Hey, you never know when you might get an interesting answer. But there might be something else going on that I don't appreciate.
But the nice thing about Katara's incessant questions is that she listens to and remembers the answers, ponders them deeply, and then is likely to come back with an insightful followup when you least expect it.
This weekend we went to visit my parents in New York, and as we drove down the Henry Hudson Parkway, we passed the North River wastewater treatment plant. Three-year-olds are fascinated with poop, so I took the opportunity to point out the plant to Katara. I said that although it had a park with trees on the roof, the inside was a giant machine for turning poop into garden soil; they cleaned it and mixed with with wood chips and it composted like the stuff in our composter. (I later found that some of these details were not quite accurate, but the general idea is correct. See the official site for the official story. My wife provided the helpful analogy with the composter.) As I expected, Katara was interested, and thought this over; she confirmed that they turned poop into soil, and then asked what they made pee into. I was not prepared for that one, and I had to promise her I would find out later. It took me some Internet research time to find out about denitrogenation.
Speaking of poop, last month Katara asked a puzzler: why don't birds use toilets? I think this was motivated by our earlier discussion of bird poop on our car.
In Make Way for Ducklings there's a picture of the friendly policeman Michael, running back to his police box to order a police escort to help the ducklings across Beacon Street. He's holding his billy club. Katara asked what that was for. I thought a moment, and then said "It's for hitting people with." Later I wondered if I had given an inaccurate or incomplete answer, so I asked around, and did some reading. It appears I got that one right. Some folks I know suggested that I should have said it was for hitting bad people, but I'd rather stick to the plain facts, and leave out the editorializing.
So I was reading the Mattingly book this evening, and Katara was eating and playing with Play-Doh on the kitchen floor. After the eleventh repetition of "Daddy, what are you doing?" "Reading." I decided to tell Katara what I was reading about. I said that I was reading about ships, that ships are big boats; they carry lots of men and guns. Katara asked why they carried guns, and I explained that often the ships carried treasure, like spices or gold or jewels or cloth, and that pirates tried to steal it. Katara asked if the cloth was like a wash cloth, and I said no, it was more like the kind of cloth that Mommy makes quilts from, or like the silk that her silk dress is made of. I explained about the pirates, which she seemed to understand, because toddlers know all about people who try to take stuff that isn't theirs. And then she asked the question I couldn't answer: Why were there men on the ships, but no women?
I was totally stumped; I don't even know where to begin explaining to a three-year-old why there are no women on ships in 1588. The only answers I could think of had to do with women's traditional roles, with European mores, social constructions of gender, and so on, all stuff that wouldn't help. Sometimes women were smuggled aboard ship, but I wasn't going to say that either.
I don't usually give up, but this time I gave up. This is a tough question of the first order, easy to ask, hard to answer. It's a lot easier to explain wastewater treatment.
[Other articles in category /misc] permanent link
"More intuitive" programming language syntax
Chromatic wrote an article today about The
Broken Metric of "Intuitive to the Uneducated" Language
Syntax in which he addresses the very common argument that
some language syntax is better than some other because it is "more
intuitive" or "easier for beginners to understand".
Chromatic says that these arguments are bunk because programming language syntax is much less important than programming language semantics. But I think that is straining at a gnat and swallowing a camel.
To argue that a certain programming language feature is bad because it is confusing to beginners, you have to do two things. You have to successfully argue that being confusing to beginners is an important metric. Chromatic's article tries to refute this, saying that it is not an important metric.
But before you even get to that stage, you first have to show that the programming language feature actually is confusing to beginners.
But these arguments are never presented with any evidence at all, because no such evidence exists. They are complete fabrications, pulled out of the asses of their propounders, and made of equal parts wishful thinking and bullshit.
Addendum 20070720:
|
To support my assertion that nobody knows what makes programming hard
for beginners, I wanted to cite this paper, The
camel has two humps, by Dehnadi and Bornat, which I was
rereading recently, but I couldn't find my copy and couldn't remember
the title or authors. Happily, I eventually remembered. The abstract begins:
Learning to program is notoriously difficult. A substantial minority of students fails in every introductory programming course in every UK university. Despite heroic academic effort, the proportion has increased rather than decreased over the years. Despite a great deal of research into teaching methods and student responses, we have no idea of the cause.But the situation isn't completely hopeless; the abstract also says:
We have found a test for programming aptitude, of which we give details. We can predict success or failure even before students have had any contact with any programming language with very high accuracy, and by testing with the same instrument after a few weeks of exposure, with extreme accuracy. We present experimental evidence to support our claim. certain to succeed.What's the secret? Read and learn. |
http://retractionwatch.com/2014/07/18/the-camel-doesnt-have-two-humps-programming-aptitude-test-canned-for-overzealous-conclusion/ Addendum 20160518: Bornat has retracted the paper mentioned above, which was never published. He says:
In 2006 I wrote an intemperate description of the results of an experiment carried out by Saeed Dehnadi. Many of the extravagant claims I made were insupportable, and I retract them. I continue to believe, however, that Dehnadi had uncovered the first evidence of an important phenomenon in programming learners. Later research seems to confirm that belief.In particular, Bornat says “There wasn’t and still isn’t an aptitude test for programming based on Dehnadi’s work.” This retracts the specific claim that I quoted above. The entire retraction is worth reading.
[Other articles in category /prog] permanent link
Thu, 19 Jul 2007
More about fixed points and attractors
A while back I talked about a
technique for calculating √2 where you pick a function that has √2
as a fixed point (that is, f(√2) = √2) and then see what
happens when you consider the sequence x, f(x),
f(f(x)), ..., for various initial values of
x. For some such functions the sequence diverges, but often it
converges to √2.
I picked a few example functions, some of which worked and some of which didn't.
One glaring omission from the article was that I forgot to mention the so-called "Babylonian method" for calculating square roots. The Babylonian method for calculating √n is simply to iterate the function x → ½(x + n/x). (This is a special case of the Newton-Raphson method for finding the zeroes of a function. In this case the function whose zeroes are being found is is x → x2 - n.) The Babylonian method converges quickly for almost all initial values of x. As I was writing the article, at 3 AM, I had the nagging feeling that I was leaving out an important example function, and then later on realized what it was. Oops.
But there's a happy outcome, which is that the Babylonian method points the way to a nice general extension of this general technique. Suppose you've found a function f that has your target value, say √2, as a fixed point, but you find that iterating f doesn't work for some reason. For example, one of the functions I considered in the article was x → 2/x. No matter what initial value you start with (other than √2 and -√2) iterating the function gets you nowhere; the values just hop back and forth between x and 2/x forever.
But as I said in the original article, functions that have √2 as a fixed point are easy to find. Suppose we have such a function, f, which is badly-behaved because the fixed point repels, or because of the hopping-back-and-forth problem. Then we can perturb the function by trying instead x → ½(x + f(x)), which has the same fixed points, but which might be better-behaved. (More generally, x → (ax + bf(x)) / (a + b) has the same fixed points as f for any nonzero a and b, but in this article we'll leave a = b = 1.) Applying this transformation to the function x → 2/x gives us the Babylonian method.
I tried applying this transform to the other example I used in the original article, which was x → x2 + x - 2. This has √2 as a fixed point, but the √2 is a repelling fixed point. √2 ± ε → √2 ± (1 + 2√2)ε, so the error gets bigger instead of smaller. I hoped that perturbing this function might improve its behavior, and at first it seemed that it didn't. The transformed version is x → ½(x + x2 + x - 2) = x2/2 + x - 1. That comes to pretty much the same thing. It takes √2 ± ε → √2 + (1 + √2)ε, which has the same problem. So that didn't work; oh well.
But actually things had improved a bit. The original function also has -√2 as a fixed point, and again it's one that repels from both sides, because -√2 ± ε → -√2 ± (1 - 2√2)ε, and |1 - 2√2| > 1. But the transformed function, unlike the original, has -√2 as an attractor, since it takes -√2 ± ε → -√2 ± (1 - √2)ε and |1 - √2| < 1.
So the perturbed function works for calculating √2, in a slightly backwards way; you pick a value close to -√2 and iterate the function, and the iterated values get increasingly close to -√2. Or you can get rid of the minus signs entirely by transforming the function again, and considering -f(-x) instead of f(x). This turns x2/2 + x - 1 into -x2/2 + x + 1. The fixed points change places, so now √2 is the attractor, and -√2 is the repeller, since √2 ± ε → √2 ± (1 - √2)ε. Starting with x = 1, we get:
| 1.5 |
| 1.375 |
| 1.4296875 |
| 1.40768433 |
| 1.41689675 |
| 1.41309855 |
| 1.41467479 |
| 1.41402241 |
| 1.41429272 |
| 1.41418077 |
| 1.41422714 |
| 1.41420794 |
| 1.41421589 |
| 1.41421260 |
| 1.41421396 |
| 1.41421340 |
| 1.41421363 |
I had meant to write about Möbius transformations, but that will have to wait until next week, I think.
[ Addendum 20201018: Another followup article, but I never did get around to discussing the Möbius transformations. ]
[Other articles in category /math] permanent link
Wed, 18 Jul 2007
God Plays Dice
Lately my favorite blog is God Plays Dice. If you
like my blog, I think you will probably like that one too.
[Other articles in category ] permanent link
Sat, 14 Jul 2007
Evaporation
 I work for the Penn Genomics Institute, mostly doing software work,
but the Institute is run by biologists and also does biology projects.
Last month I taught some perl classes for the four summer interns;
this month they are doing some lab work. Since part of my job
involves dealing with biologists, I thought this would be a good
opportunity to get into the lab, and I got permission from Adam, the
research scientist who was supervising the interns, to let me come
along.
I work for the Penn Genomics Institute, mostly doing software work,
but the Institute is run by biologists and also does biology projects.
Last month I taught some perl classes for the four summer interns;
this month they are doing some lab work. Since part of my job
involves dealing with biologists, I thought this would be a good
opportunity to get into the lab, and I got permission from Adam, the
research scientist who was supervising the interns, to let me come
along.
Since my knowledge of biology is practically nil, Adam was not entirely sure what to do with me while the interns prepared to grow yeasts or whatever it is that they are doing. He set me up with a scale, a set of pipettes, and a beaker of water, with instructions to practice pipetting the water from the beaker onto the scale.
The pipettes came in three sizes. Shown at right is the largest of the ones I used; it can dispense liquid in quantities between 10 and 100 μl, with a precision of 0.1 μl. I used each of the three pipettes in three settings, pipetting water in quantities ranging from 1 ml down to 5 μl. I think the idea here is that I would be able to see if I was doing it right by watching the weight change on the scale, which had a display precision of 1 mg. If I pipette 20 μl of water onto the scale, the measured weight should go up by just about 20 mg.
Sometimes it didn't. For a while my technique was bad, and I didn't always pick up the exact right amount of water. With the small pipette, which had a capacity range of 2–20 μl, you have to suck up the water slowly and carefully, or the pipette tip gets air bubbles in it, and does not pick up the full amount.
With a scale that measures in milligrams, you have a wait around for a while for the scale to settle down after you drop a few μl of water onto it, because the water bounces up and down and the last digit of the scale readout oscillates a bit. Milligrams are much smaller than I had realized.
It turned out that it was pretty much impossible to see if I was picking up the full amount with the smallest pipette. After measuring out some water, I would wait a few seconds for the scale display to stabilize. But if I waited a little longer, it would tick down by a milligram. After another twenty or thirty seconds it would tick down by another milligram. This would continue indefinitely.
I thought about this quietly for a while, and realized that what I was seeing was the water evaporating from the scale pan. The water I had in the scale pan had a very small surface area, only a few square centimeters. But it was evaporating at a measurable rate, around 2 or 3 milligrams per minute.
So it was essentially impossible to measure out five pipette-fuls of 10 μl of water each and end up with 50 mg of water on the scale. By the time I got it done, around 15% of it would have evaporated.
The temperature here was around 27°C, with about 35% relative humidity. So nothing out of the ordinary.
I am used to the idea that if I leave a glass of water on the kitchen counter overnight, it will all be gone in the morning; this was amply demonstrated to me in nursery school when I was about three years old. But to actually see it happening as I watched was a new experience.
I had no idea evaporation was so speedy.
[Other articles in category /physics] permanent link
Thu, 12 Jul 2007
New York tourism
Anil Dash recently blogged about touristy
stuff in New York that you should skip. I grew up in New York, so
I know something about this.
Top of Anil's list: the Statue of Liberty. He advises taking the Staten Island Ferry instead. I couldn't agree more. The Statue is great, but it's just as great seen from a distance, and you get a superb view of it from the Ferry. The Ferry is cheap (Anil says it's free; it was fifty cents last time I took it) and the view of lower Manhattan is unbeatable.
Similarly, you should avoid the Circle Line, which is a boat trip all the way around Manhattan Island. That sounds good, but it takes all day and you spend a lot of it cruising the not-so-scenic Harlem River. The high point of the trip is the view of lower Manhattan and the harbor. You can get the best parts of the Circle Line trip by taking the Staten Island Ferry, which is much cheaper and omits the dull bits.
Ten years ago I would have said to skip the World Trade Center in favor of the Empire State Building. Well, so much for that suggestion.
Anil says to skip Katz's and the Carnegie Deli, that they're tourist traps. I've never been to Katz's. I would not have advised skipping the Carnegie. I have not been there since 1995, so my view may be out of date, and the place may have changed. But in 1995 I would have said that although it is indeed a tourist trap, the pastrami sandwich is superb nevertheless. At no time, however, would I have advised anyone to eat anything else from there. Get the sandwich and eat it in the comfort of your hotel room, perhaps. But quickly, before it gets cold.
Also in the "go there but only eat one thing" department is Junior's Restaurant, at (I think) Atlantic and De Kalb avenues in Brooklyn. Now here's the thing about Junior's: their cheesecake is justly famous. They guarantee it. It is not your usual guarantee. A typical guarantee would be that if you are not happy with the cheesecake, they will refund your money. That is not Junior's guarantee. No. Junior's guarantees your money back unless their cheesecake is the best you have ever eaten.
Lorrie and I once ordered a cheesecake from Junior's. They ship it overnight, packed in dry ice. Our order was delayed in transit; we called the next day to ask where it was. They apologized and immediately overnighted us a second cheesecake, free, with no further discussion. The next day the two cheesecakes arrived in the mail. Both of them were the best cheesecake I have ever eaten.
But I once went to have dinner at Junior's. This was a mistake. Their cheesecake is so stupendous, I thought, how could their other food possibly fail? As usual, the cheesecake was the best I have ever eaten. But dinner? Not so hot. Do go to Junior's. You don't even have to schlep out to Atlantic Avenue, since they have opened restaurants in Times Square and at Grand Central Station. Get the cheesecake. But eat dinner somewhere else.
Anil says not to eat in the goddamn Olive Garden, and of course he is right. What on earth is the point of going to New York, food capital of this half of the Earth, and eating in the goddamn Olive Garden? You could have done that in Dubuque or Tallahassee or whatever crappy Olive-Garden-loving burg you came from.
If you don't know where to eat in New York, here's my advice: Take the subway to 42nd street, get out, and walk to 9th Avenue. Choose a side of the street by coin flip. Walk north on 9th avenue. Make a note of every interesting-seeming restaurant you pass. After three blocks, you will have passed at least ten interesting-seeming restaurants. Walk back to the most interesting-seeming one and go in, or select one at random. I promise you will have a win, probably a big win. That stretch of 9th Avenue is a paradise of inexpensive but superb restaurants.
I have played the 9th Avenue game many times and it has never failed.
Speaking of "things to skip", I suggest skipping the giant Times Square New Year's Eve celebration, unless you are a pickpocket, in which case you should get there early. Instead, have dinner on 9th Avenue. As you pass each cross-street walking down 9th Avenue, you will be able to see the Times Square crowd two blocks east, and you can pause a moment to think how clever you are to not to be part of it; feeling smugly superior to the writhing mass of humanity is an authentically New York experience. Then have an awesome dinner on 9th Avenue, and take the subway home.
Anil's whole series is pretty good, and as a native New Yorker I found little to disagree with. But I think he may be a little misleading when he says "the natives are friendly and helpful." I would say not. Neither are they unfriendly or unhelpful. What they mostly are, in my experience, is brusque and in a hurry. They will not go out of their way to abuse, harass, or ridicule you; nor will they go out of their way to advise or assist you. The New Yorkers' outlook on the world is that they have important business to attend to, and so, presumably, do you, and everything will run smoothly as long as everyone just stays out of each others' way and attends to their own important business.
In Boston, people will take you personally. I was once thrown out of a liquor store in Boston for daring to ask for a bottle of rye in a manner that the proprietor found offensive. This would never happen in New York. New Yorkers don't have time to be offended by your stupid demands, and they will not throw you out, because they want your money, and if dealing with your stupid demands is what they have to do to get it, well, they will just deal with your stupid demands as quickly as possible. A New York liquor store owner is not in the business of getting offended, and he has more important things to do than to throw you out. He is in the business of taking your money, and if he throws you out, it is because you are getting in the way of his next customer and preventing him from taking his money. Most likely, if you ask for rye, the New York liquor store owner will take your money and give you the rye.
There is a story about Hitler and Goebbels having an argument, with Hitler arguing that the Jews were too inferior to pose any sort of threat, and Goebbels disputing with him, saying that Jews are devious and cunning. To prove his point, Goebbels takes Hitler to a Jewish-run hardware and sundries store and asks the proprietor for a left-handed teapot. The proprietor hesitates a moment, says "let me check in the back room," and returns carrying a teapot in his left hand. "Yes," he says, "I had just one left." As Goebbels and Hitler leave the shop with their left-handed teapot, Goebbels says "I told you the Jews were cunning." Hitler replies "What's so cunning about having one left?"
A Bostonian would have told those two assholes where they could stick their left-handed teapot. That Jew emigrated from Germany, and he did not go to Boston. He went to New York, as did his fifty devious cousins.
But I digress.
In some cities I have visited, there is no convention about which side of the subway stairs are for going up and which are for going down. People just go up whichever side they feel like. In New York, you always travel on the right-hand side of the stairs. Everyone does this, because everyone knows that if they don't they will just get in the way and hold everyone up, including themselves. They have no time for this disorganized nonsense in which people go up whatever side of the stairs suits them.
New Yorkers do not stop and stand in doorways. When New Yorkers need to open their umbrellas, they step aside, and do it out of the way.
New Yorkers are orderly queuers. Disorganized queuing just wastes everyone's time. You don't want to waste everyone's time, do you? So get in line and shut the hell up!
Here in Philadelphia, we waste a lot of time trying to flag down cabs that turn out to be full. New Yorkers would never tolerate such slack management. In New York, taxicabs have a lamp on top that is wired to the taximeter; it lights up when the taxi is empty. That is good business for drivers, for riders, for everyone. I like Philadelphia well enough to have lived here for seventeen years, but it's no New York, let me tell you.
Hong Kong, on the other hand, is a very satisfactory New York. A few years back I visited Hong Kong, food capital of the other half of the Earth, on business, and loved it there. Not least because of the food. The Cantonese are the best cooks in the world, cooks so gifted and brilliant that people all over the world line up on the weekends to eat Cantonese-style garbage, and then come back next weekend to eat it again, because Cantonese garbage, which they call dim sum, but if you think about it for a minute you will realize that dim sum is the week's leftovers, served up in a not-too-subtle disguise, dim sum is more delicious than other cuisines' delicacies. And Hong Kong has the best Cantonese food in the world.
People had warned me beforehand that the Hongkongians were known for being brusque and rude. And that is what I found. Several times in Hong Kong I called up someone or other to try to get something done, and the conversation went roughly like this: I would start my detailed explanation of what I wanted, and why, and the person on the other end of the phone would cut me off mid-sentence, saying something like "You need x; I do y. OK? OK! <click>" and that was the end of it.
As a New Yorker, I recognized immediately what was going on. Brusque, yes, but not rude. I knew that the person on the other end of the phone was thinking that their time was valuable, that I presumably considered my own time valuable, and that we would both be best served if each of us wasted as little of our valuable time as possible in idle chitchat. New Yorkers are just like that too. I gather some people are offended by this behavior, and want the person on the phone to be polite and friendly. I just want them to shut up and do the thing I want done, and in Hong Kong that is what I got.
So if you are a tourist in New York, please try to remember: New Yorkers may appear to be trying to get rid of you as quickly as they can, and if it seems that way, it is probably because they are trying to get rid of you as quickly as they can. But they are doing it because they are trying to help, because they have your best interests at heart. And also because they want to get rid of you as quickly as they can.
[Other articles in category /food] permanent link
Another useful utility
Every couple of years I get a good idea for a simple utility that will
make my life easier. Last time it was the following triviality, which
I call f:
#!/usr/bin/perl
my $field = shift or usage();
$field -= 1 if $field > 0;
$|=1;
while (<>) {
chomp;
my @f = split;
print $f[$field], "\n";
}
sub usage {
print STDERR "$0 fieldnumber\n";
exit 1;
}
I got tired of writing awk '{print $11}' when I wanted to
extract the 11th field of some stream of data in a Unix pipeline,
which is something I do about six thousand times a day. So
I wrote this tiny thing. It was probably the most useful piece of
software I wrote in that calendar year, and as you can see from the
length, it certainly had the best cost-to-benefit ratio. I use it
every day.The point here is that you can replace awk '{print $11}' with just f 11. For example, f 11 access_log finds out the referrer URLs from my Apache httpd log. I also frequently use f -1, which prints the last field in each line. ls -l | grep '^l' | f -1 prints out the targets of all the symbolic links in the current directory.
Programs like this won't win me any prizes, but they certainly are useful.
Anyway, today's post was inspired by another similarly tiny utility that I expect will be similarly useful that I just finished. It's called runN:
#!/usr/bin/perl
use Getopt::Std;
my %opt;
getopts('r:n:c:v', \%opt) or usage();
$opt{n} or usage();
$opt{c} or usage();
@ARGV = shuffle(@ARGV) if $opt{r};
my $N = $opt{n};
my %pid;
while (@ARGV) {
if (keys(%pid) < $N) {
$pid{spawn($opt{c}, split /\s+/, shift @ARGV)} = 1;
} else {
delete $pid{wait()};
}
}
1 while wait() >= 0;
sub spawn {
my $pid = fork;
die "fork: $!" unless defined $pid;
return $pid if $pid;
exec @_;
die "exec: $!";
}
You can tell I just finished it because the shuffle() and
usage() functions are unimplemented.The idea is that you execute the program like this:
runN -n 3 -c foo arg1 arg2 arg3 arg4...and it runs the commands foo arg1, foo arg2, foo arg3, foo arg4, etc., simultaneously, but with no more than 3 running at a time.
The -n option says how many commands to run simultaneously; after running that many the main control waits until one has exited before starting another.
If I had implemented shuffle(), then -r would run the commands in random order, instead of in the order specified. Probably I should get rid of -c and just have the program take the first argument as the command name, so that the invocation above would become runN -n 3 foo arg1 arg2 arg3 arg4.... The -v flag, had I implemented it, would put the program into verbose mode.
I find that it's best to defer the implementation of features like -r and -v until I actually need them, which might be never. In the past I've done post-analyses of the contents of ~mjd/bin, and what I found was that my tendency was to implement a lot more features than I needed or used.
In the original implementation, the -n is mandatory, because I couldn't immediately think of a reasonable default. The only obvious choice is 1, but since the point of the program was to run programs concurrently, 1 is not reasonable. But it occurs to me now that if I let -n default to 1, then this command would replace many of my current invocations of:
for i in ...; do cmd $i donewhich I do quite a lot. Typing runN cmd ... would be a lot quicker and easier. As I've written before, when a feature you put in turns out to have unanticipated uses, it's a sign of a good, modular design.
The code itself makes me happy for two reasons. One is that the program worked properly on the first try, which does not happen very often for me. When I was in elementary school, my teachers always complained that although I was very bright, I made a lot of careless mistakes because I was not methodical enough. They tried hard to fix this personality flaw. They did not succeed.
The other thing I like about the code is that it's so very brief. Not to say that it is any briefer than it should be; I think it's just about perfect. One of the recurring themes of my study of programming for the last few years is that beginner programmers use way more code than is necessary, just like beginning writers use way too many words. The process and concurrency management turned out to be a lot easier than I thought they would be: the default Unix behavior was just exactly what I needed. I am particularly pleased with delete $pid{wait()}. Sometimes these things just come together.
The 1 while wait() >= 0 line is a non-obfuscated version of something I wrote in my prize-winning obfuscated program, of all places. Sometimes the line between the sublime and the ridiculous is very fine indeed.
Despite my wariness of adding unnecessary features, there is at least one that I will put in before I deploy this to ~mjd/bin and start using it. I'll implement usage(), since experience has shown that I tend to forget how to invoke these things, and reading the usage message is a quicker way to figure it out than is rereading the source code. In the past, usage messages have been good investments.
I'm tempted to replace the cut-rate use of split here with something more robust. The problem I foresee is that I might want to run a command with an argument that contains a space. Consider:
runN -n 2 -c ls foo bar "-l baz"This runs ls foo, then ls bar, then ls -l baz. Without the split() or something like it, the third command would be equivalent to ls "-l baz" and would fail with something like -l baz: no such file or directory. (Actually it tries to interpret the space as an option flag, and fails for that reason instead.) So I put the split in to enable this usage. (Maybe this was a you-ain't-gonna-need-it moment; I'm not sure.) But this design makes it difficult or impossible to apply the command to an argument with a space in it. Suppose I'm trying to do ls on three directories, one of which is called old stuff. The natural thing to try is:
runN -n 2 -c ls foo bar "old stuff"But the third command turns into ls old stuff and produces:
ls: old: No such file or directory ls: stuff: No such file or directoryIf the split() were omitted, it would just work, but then the ls -l baz example above would fail. If the split() were replaced by the correct logic, I would be able to get what I wanted by writing something like this:
runN -n 2 -c ls foo bar "'old stuff'"But as it is this just produces another error:
ls: 'old: No such file or directory ls: stuff': No such file or directoryPerl comes standard with a library called ShellWords that is probably close to what I want here. I didn't use it because I wasn't sure I'd actually need it—only time will tell—and because shell parsing is very complicated and error-prone, more so when it is done synthetically rather than by the shell, and even more so when it is done multiple times; you end up with horrible monstrosities like this:
s='q=`echo "$s" | sed -e '"'"'s/'"'"'"'"'"'"'"'"'/'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'"'/g'"'"'`; echo "s='"'"'"$q"'"'"'"; echo $s' q=`echo "$s" | sed -e 's/'"'"'/'"'"'"'"'"'"'"'"'/g'`; echo "s='"$q"'"; echo $sSo my fear was that by introducing a double set of shell-like interpretation, I'd be opening a horrible can of escape character worms and weird errors, and my hope was that if I ignored the issue the problems might be simpler, and might never arise in practice. We'll see.
[ Addendum 20080712: Aaron Crane wrote a thoughtful followup. Thank you, M. Crane. ]
[Other articles in category /prog] permanent link
Sat, 30 Jun 2007
How to calculate the square root of 2
A few weeks ago I
mentioned the following recurrence:
| p0 = 1 | q0 = 1 |
| pi+1 = pi + 2qi | qi+1 = pi + qi |
I said that this formula comes from consideration of continued fractions. But I was thinking about it a little more, and I realized that there is a way to get such a recurrence for pretty much any algebraic constant you want.
Consider for a while the squaring function s : x → x2. This function has two obvious fixed points, namely 0 and 1, by which I mean that s(0) = 0 and s(1) = 1. Actually it has a third fixed point, ∞.
If you consider the behavior on some x in the interval (0, 1), you see that s(x) is also in the same interval. But also, s(x) < x on this interval. Now consider what happens when you iterate s on this interval, calculating the sequence s(x), s(s(x)), and so on. The values must stay in (0, 1), but must always decrease, so that no matter what x you start with, the sequence converges to 0. We say that 0 is an "attracting" fixed point of s, because any starting value x, no matter how far from 0 it is (as long as it's still in (0, 1)), will eventually be attracted to 0. Similarly, 1 is a "repelling" fixed point, because any starting value of x, no matter how close to 1, will be repelled to 0.
Consideration of the interval (1, ∞) is similar. 1 is a repeller and ∞ is an attractor.
Fixed points are not always attractors or repellers. The function x → 1/x has fixed points at ±1, but these points are neither attractors nor repellers.
Also, a fixed point might attract from one side and repel from the other. Consider x → x/(x+1). This has a fixed point at 0. It maps the interval (0, ∞) onto (0, 1), which is a contraction, so that 0 attracts values on the right. On the other hand, 0 repels values on the left, because 1/-n goes to 1/(-n+1). -1/4 goes to -1/3 goes to -1/2 goes to -1, at which point the whole thing blows up and goes to -∞.
The idea about the fixed point attractors is suggestive. Suppose we were to pick a function f that had √2 as a fixed point. Then √2 might be an attractor, in which case iterating f will get us increasingly accurate approximations to √2.
So we want to find some function f such that f(√2) = √2. Such functions are very easy to find! For example, take √2. square it, and divide by 2, and add 1, and take the square root, and you have √2 again. So x → √(1+x2/2) is such a function. Or take √2. Take the reciprocal, double it, and you have √2 again. So x → 2/x is another such function. Or take √2. Add 1 and take the reciprocal. Then add 1 again, and you are back to √2. So x → 1 + 1/(x+1) is a function with √2 as a fixed point.
Or we could look for functions of the form ax2 + bx + c. Suppose √2 were a fixed point of this function. Then we would have 2a + b√2 + c = √2. We would like a, b, and c to be simple, since the whole point of this exercise is to calculate √2 easily. So let's take a=b=1, c=-2. The function is now x → x2 + x - 2.
Which one to pick? It's an embarrasment of riches.
Let's start with the polynomial, x → x2 + x - 2. Well, unfortunately this is the wrong choice. √2 is a fixed point of this function, but repels on both sides: √2 ± ε → √2 ± ε(1 + 2√2), which is getting farther away.
The inverse function of x → x2 + x - 2 will have √2 as an attractor on both sides, but it is not so convenient to deal with because it involves taking square roots. Still, it does work; if you iterate ½(-1 + √(9 + 4x)) you do get √2.
Of the example functions I came up with, x → 2/x is pretty simple too, but again the fixed points are not attractors. Iterating the function for any initial value other than the fixed points just gets you in a cycle of length 2, bouncing from one side of √2 to the other forever, and not getting any closer.
But the next function, x → 1 + 1/(x+1), is a winner. (0, ∞) is crushed into (1, 2), with √2 as the fixed point, so √2 attracts from both sides.
Writing x as a/b, the function becomes a/b → 1 + 1/(a/b+1), or, simplifying, a/b → (a + 2b) / (a + b). This is exactly the recurrence I gave at the beginning of the article.
We did get a little lucky, since the fixed point of interest, √2, was the attractor, and the other one, -√2, was the repeller. ((-∞, -1) is mapped onto (-∞, 1), with -√2 as the fixed point; -√2 repels on both sides.) But had it been the other way around we could have exchanged the behaviors of the two fixed points by considering -f(-x) instead. Another way to fix it is to change the attractive behavior into repelling behavior and vice versa by running the function backwards. When we tried this for x → x2 + x - 2 it was a pain because of the square roots. But the inverse of x → 1 + 1/(x+1) is simply x → (-x + 2) / (x - 1), which is no harder to deal with.
The continued fraction stuff can come out of the recurrence, instead of the other way around. Let's iterate the function x → 1 + 1/(1+x) formally, repeatedly replacing x with 1 + 1/(1+x). We get:
1 + 1/(1+x)So we might expect the fixed point, if there is one, to be 1 + 1/(2 + 1/(2 + 1/(2 + ...))), if this makes sense. Not all such expressions do make sense, but this one is a continued fraction, and continued fractions always make sense. This one is eventually periodic, and a theorem says that such continued fractions always have values that are quadratic surds. The value of this one happens to be √2. I hope you are not too surprised.
1 + 1/(1+1 + 1/(1+x))
1 + 1/(1+1 + 1/(1+1 + 1/(1+x)))
...
In the course of figuring all this out over the last two weeks or so, I investigated many fascinating sidetracks. The x → 1 + 1/(x+1) function is an example of a "Möbius transformation", which has a number of interesing properties that I will probably write about next month. Here's a foretaste: a Möbius transformation is simply a function x → (ax + b) / (cx + d) for some constants a, b, c, and d. If we agree to abbreviate this function as !!{ a\, b \choose c\,d}!!, then the inverse function is also a Möbius transformation, and is in fact !!{a\, b\choose c\,d}^{-1}!!.
[ Addendum 20070719: There is a followup article to this one. ] [ Addendum 20201018: Another followup article. ]
[Other articles in category /math] permanent link
Sun, 24 Jun 2007
Do you dream in color?
People have occasionally asked me whether I dreamt in color or on
black-and-white, by which I suppose they meant grayscale. This
question was strange to me the first time I heard it, because up to
then it had not occurred to me that anyone did not dream in color. I
still find it strange, and I had to do a Google search to verify that
there really are people who claim not to dream in color.
One time, when I replied that I did dream in color, my interlocutor asked me if I was sure: perhaps I dreamt in black and white, but only remembered it as being in color later.
I am sure I dream in color, because on more than one occasion I have had discussions in dreams about colors of objects. I can't remember any examples right now, but it was something like this: "Give me the red apple." "Okay, here." "That is not the red apple, that is the green apple!" And then I looked and saw that the apple I had thought was red was really green.
One could still argue that I wasn't really dreaming in color, that it only seemed like that, or something. It's a delicate philosophical point. One could also argue that I didn't have any dream at all, I only thought I did after I woke up. I suppose the only refutations of such an argument either appeal to neurology or involve a swift kick in the pants.
And then suppose I have a dream in which I take LSD and have marvelous hallucinations. Did I really have hallucinations? Or did I only dream them? If I dream that I kill someone, we agree that it wasn't real, that a dream murder is not a real murder; it is only in your head. But hallucinations, by definition, are only in your head even when they are real, so don't dream hallucinations have as much claim to reality as waking hallucinations?
One might argue that dreamt LSD hallucinations are likely to be qualitatively very different from real LSD hallucinations—less like real LSD hallucinations, say, and more like, well, dreams. But this only refutes the claim that the dream hallucinations were LSD hallucinations. And nobody was going to claim that they were LSD hallucinations anyway, since no actual LSD was involved. So this doesn't address the right question.
Stickier versions of the same problem are possible. For example, suppose I give Bill a little piece of paper and tell him it is impregnated with LSD. It is not, but because of the placebo effect, Bill believes himself to be having an LSD trip and reports hallucinations. There was no LSD involved, so the hallucinations were only imaginary. But even real hallucinations are only imaginary. Are we really justified in saying that Bill is mistaken, that he did not actually hallucinate, but only imagined that he did? That seems like a very difficult position to defend.
I seem to have wandered from the main point, which is that I had another dream last night that supports my contention that I dream in color. I was showing my friend Peter some little homunculi that had been made long ago from colored pipe cleaners, shiny paper, and sequins by my grandmother's friend Kay Seiler. Originally there had been ten of these, but in the dream I had only five. When my grandmother had died, my sister and I had split the set, taking five each. In place of the five originals I was missing, I had five copies, which were identifiable as such because they were in grayscale. Presumably my sister had grayscale copies of the originals I retained. I explained this to Peter, drawing his attention to the five full-color homunculi and the five grayscale ones.
So yes, barring philosophical arguments that I think deserve a kick in the pants, I am sure that I dream in color.
[Other articles in category /brain] permanent link
Sun, 17 Jun 2007
Square triangular numbers
A while back I made the erroneous assertion that no numbers
are both square and triangular. As I noted in a followup, this is
a rather stupid thing to say, since both 0 and 1 are obvious
counterexamples. (36 is a nontrivial counterexample.) Also, a few
years before I had actually investigated this very question and had
determined that the set of such numbers is infinite. Whoops.
I no longer remember how I solved the problem the first time around, but I was tinkering around with it today and came up with an approach that I think is instructive, or at least interesting.
We want to find non-negative integers a and b such that ½(a2 + a) = b2. Or, equivalently, we want a and b such that √(a2 + a) = b√2.
Now, √(a2 + a) is pretty nearly a + ½. So suppose we could find p and q with a + ½ = b·p/q, and p/q a bit larger than √2. a + ½ is a bit too large to be what we want on the left, but p/q is a bit larger than what we want on the right too. Perhaps the fudging on both sides would match up, and we would get √(a2 + a) = b√2 anyway.
If this magic were somehow to occur, then a and b would be the numbers we wanted.
Finding p/q that is a shade over √2 is a well-studied problem, and one of the things I have in my toolbox, because it seems to come up over and over in the solution of other problems, such as this one. It has interesting connections to several other parts of mathematics, and I have written about it here before.
The theoretical part of finding p/q close to √2 is some thing about continued fractions that I don't want to get into today. But the practical part is very simple. The following recurrence generates all the best rational approximations to √2; the farther you carry it, the better the approximation:
| p0 = 1 | q0 = 1 |
| pi+1 = pi + 2qi | qi+1 = pi + qi |
| p | q | p/q |
| 1 | 1 | 1.0 |
| 3 | 2 | 1.5 |
| 7 | 5 | 1.4 |
| 17 | 12 | 1.416666666666667 |
| 41 | 29 | 1.413793103448276 |
| 99 | 70 | 1.414285714285714 |
| 239 | 169 | 1.414201183431953 |
| 577 | 408 | 1.41421568627451 |
| 1393 | 985 | 1.414213197969543 |
| 3363 | 2378 | 1.41421362489487 |
Now, we want a + ½ = b·p/q, or equivalently (2a + 1)/2b = p/q. This means we can restrict our attention to the rows of the table that have q even. This is a good thing, because we need p/q a bit larger than √2, and those are precisely the rows with even q. The rows that have q odd have p/q a bit smaller than √2, which is not what we need. So everything is falling into place.
Let's throw away the rows with q odd, put a = (p - 1)/2 and b = q/2, and see what we get:
| p | q | a | b | ½(a2+a) = b2 |
| 3 | 2 | 1 | 1 | 1 |
| 17 | 12 | 8 | 6 | 36 |
| 99 | 70 | 49 | 35 | 1225 |
| 577 | 408 | 288 | 204 | 41616 |
| 3363 | 2378 | 1681 | 1189 | 1413721 |
I have two points to make about this. One is that I have complained in the past about mathematical pedagogy, how the convention is to come up with some magic-seeming guess ahead of time, as when pulling a rabbit from a hat, and then at the end it is revealed to be the right choice, but what really happened was that the author worked out the whole thing, then saw at the end what he would need at the beginning to make it all work, and went back and filled in the details.
That is not what happened here. My apparent luck was real luck. I really didn't know how it was going to come out. I was really just exploring, trying to see if I could get some insight into the answer without necessarily getting all the way there; I thought I might need to go back and do a more careful analysis of the fudge factors, or something. But sometimes when you go exploring you stumble on the destination by accident, and that is what happened this time.
The other point I want to make is that I've written before about how a mixture of equal parts of numerical sloppiness and algebraic tinkering, with a dash of canned theory, can produce useful results, in a sort of alchemical transmutation that turns base metals into gold, or at least silver. Here we see it happen again.
[Other articles in category /math] permanent link
Sat, 16 Jun 2007
Frances Trollope arrives in America
More than a year ago
I mentioned Frances Trollope's book Domestic Manners of the
Americans, which I have at long last checked out of the library
and begun to read. I am only at page 40 or so, but it is easy going,
and entertaining.
Trollope's book begins with her arrival from Europe in New Orleans. I was drawn in early on by the following passage, which appears on page 5:
The land is defended from the encroachments of the river by a high embankment which is called the Levée; without which the dwellings would speedily disappear, as the river is evidently higher than the banks would be without it. . . . She was looking so mighty, and so unsubdued all the time, that I could not help fancying she would some day take the matter into her own hands again, and if so, farewell to New Orleans.
The book was published in 1832.
[Other articles in category /book] permanent link
Thu, 14 Jun 2007
Harry Potter and the Goblet of Fire
I have not been too impressed with the Harry Potter
books. I read them all, one at a time, on airplanes. They are good
for this because they are fat, undemanding, and readily available in
airport bookshops for reasonable prices. In a lot of ways they are
badly constructed, but there is really no point in dwelling on their
flaws. The Potter books have been widely criticized already from all
directions, and so what? People keep buying them.
But The Goblet of Fire has been bothering me for years now, because its plot is so very stupid. I am complaining about it here in my blog because it continues to annoy me, and I hope to forget about it after I write this. The rest of this article will contain extensive spoilers, and I will assume that you either know it all already or that you don't care.
The bad guys want to kill Harry Potter, the protagonist. The Triwizard Tournament is being held at Harry's school. In the tournament, the school champions must overcome several trials, the last of which is to race through a maze and grab the enchanted goblet at the center of the maze. The bad guys' plan is this: they will enter Harry in the tournament. They will interfere subtly in the tournament, to ensure that Harry is first to lay hands on the goblet. They will enchant the goblet so that it is a "portkey", and whoever first touches it will be transported into their evil clutches.
They need an evil-doer on the spot, to interfere in the competition in Harry's favor; if he is eliminated early, or fails to touch the goblet first, all their plotting will be for naught. So they abduct and imprison Mad-eye Moody, a temporary faculty member and a famous capturer of evil-doers, and enchant one of their own to impersonate him for the entire school year.
The badness of this plan is just mind-boggling. Moody is a tough customer. If they fail to abduct him, or if he escapes his year-long captivity, their plans are in the toilet. If the substitution is detected, their plans are in the toilet. Their fake Moody will be teaching a class in "Defense Against the Dark Arts", a subject in which the real Moody has real expertise that the substitute lacks; the substitute somehow escapes detection on this front. For several months the fake Moody will be eating three meals a day with a passel of witches and wizards who are old friends with the real Moody, and among whom is Albus Dumbledore, who supposedly is not a complete idiot; the substitute somehow escapes detection on this front as well.
Even with the substitution accomplished, the bad guys' task is far from easy. Harry procrastinates everything he can and it's all they can do to arrange that he is not eliminated from the tournament. None of the other champions are either, and the villains have a tough problem to make sure that he is first through the maze.
Here is an alternative plan, which apparently did not occur to the fearsome Lord Voldemort: instead of making the Goblet of Fire into a portkey, he should enchant a common object, say a pencil. We know this is possible, since it has been explicitly established that absolutely any object can be a portkey, and the first instance of one that we see appears to be an abandoned boot. Then, since fake Moody is teaching Harry's class, sometime during the first week of the term he should ask Harry to stay behind on some pretext, and then say "Oh, Harry, would you please pass me that pencil over there?" After Harry is dead, fake Moody can disappear. A little thought will no doubt reveal similar plans that involve no substitutions or imprisonments: send Harry a booby-trapped package in the mail, or enchant his socks, or something of the sort.
In fact, they do something like this in one of the later books; they sell another character, I think Ginny Weasley, some charm that puts her under their control. This is a flub already, because they should have sold it to Harry instead—duh—and then had him kill himself. Or they could have sold him a portkey. Or an exploding candy. But I don't want to belabor the point.
Normally I have no trouble suspending my disbelief in matters like this. I can forgive a little ineptness on the part of the master schemers, because I am such an inept schemer that I usually don't notice. When evil plots seem over-elaborate and excessively risky to me, I just imagine that it seems that way because evil plots are so far outside my area of expertise, and read on. But in The Goblet of Fire I couldn't do this. My enjoyment of the book was disrupted by the extreme ineptness of the evil scheme.
One of Rowling's recurring themes is the corruption and ineptness of the ostensibly benevolent government. But perhaps this incompetence is a good thing. If the good guys had been less incompetent in the past, the bad guys might have had to rise to the occasion, and would have stomped Harry flat in no time. Lulled into complacency by years of ineffective opposition, they become so weak and soft that they are defeated by a gang of teenagers.
Okay, that's off my chest now. Thanks for your forbearance.
[Other articles in category /book] permanent link
Wed, 13 Jun 2007
How to calculate binomial coefficients, again
Yesterday's article about how to
calculate binomial coefficients was well-received. It was posted
on Reddit, and to my surprise and gratification, the comments were
reasonably intelligent. Usually when a math article of mine shows up
on Reddit, all the megacretins come out of the woodwork to say what an
idiot I am, and why don't I go back to school and learn basic logic.
A couple of people pointed out that, contrary to what I asserted, the
algorithm I described can in fact overflow even when the final result
is small enough to fit in a machine word. Consider
 for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps.
for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps.
Perhaps more concretely, !!35\choose11!! is 417,225,900, which is small enough to fit in a 32-bit unsigned integer, but the algorithm I wrote wants to calculate this as !!35{34\choose10}\over11!!, and the numerator here is 4,589,484,900, which does not fit.
One Reddit user suggested that you can get around this as follows: To multiply r by a/b, first check if b divides r. If so, calculate (r/b)·a; otherwise calculate (r·a)/b. This should avoid both overflow and fractions.
Unfortunately, it does not. A simple example is !!{14\choose4} = {11\over1}{12\over2}{13\over3}{14\over4}!!. After the first three multiplications one has 286. One then wants to multiply by 14/4. 4 does not divide 286, so the suggestion calls for multiplying 286 by 14/4. But 14/4 is 3.5, a non-integer, and the goal was to use integer arithmetic throughout.
| Buy The Art of Computer Programming: Volume 2, Seminumerical Algorithms from Bookshop.org (with kickback) (without kickback) |
I haven't looked, but it is hard to imagine that Volume II of Knuth doesn't discuss this in exhaustive detail, including all the stuff I just said, plus a bunch of considerations that hadn't occurred to any of us.
A few people also pointed out that you can save time when n
> m/2 by calculating !!m\choose m-n!! instead of  . For example, instead of calculating !!100\choose98!!, calculate
. For example, instead of calculating !!100\choose98!!, calculate 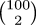 . I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.
. I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.
[Other articles in category /math] permanent link
Tue, 12 Jun 2007
How to calculate binomial coefficients
The binomial coefficient !!n\choose
k!! is usually defined as:
$${n\choose k} = {n!\over k!(n-k)!}$$
This is a fine definition, brief, closed-form, easy to prove theorems about. But these good qualities seduce people into using it for numerical calculations:
fact 0 = 1
fact (n+1) = (n+1) * fact n
choose n k = (fact n) `div` ((fact k)*(fact (n-k)))
(Is it considered bad form among Haskellites to use the
n+k patterns? The Haskell Report is decidedly
ambivalent about them.)
Anyway, this is a quite terrible way to calculate binomial
coefficients. Consider calculating !!100\choose 2!!, for example. The result
is only 4950, but to get there the computer has to calculate 100! and
98! and then divide these two 150-digit numbers. This requires the
use of bignums in languages that have bignums, and causes an
arithmetic overflow in languages that don't. A straightforward
implementation in C, for example, drops dead with an arithmetic
exception; using doubles instead, it claims that the value of 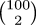 is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
Even in the best case, !!2n\choose n!!, the result is only on the order of 4n, but the algorithm has to divide a numerator of about 4nn2n by a denominator of about n2n to get it.
A much better way to calculate values of 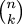 is to use the following recurrence:
is to use the following recurrence:
$${n+1\choose k+1} = {n+1\over k+1}{n\choose k}$$
This translates to code as follows:
choose n 0 = 1
choose 0 k = 0
choose (n+1) (k+1) = (choose n k) * (n+1) `div` (k+1)
This calculates !!8\choose 4!! as
!!{5\over1}{6\over2}{7\over3}{8\over4}
!!. None of the intermediate results are larger than the
final answer.An iterative version is also straightforward:
unsigned choose(unsigned n, unsigned k) {
unsigned r = 1;
unsigned d;
if (k > n) return 0;
for (d=1; d <= k; d++) {
r *= n--;
r /= d;
}
return r;
}
This is speedy, and it cannot cause an arithmetic overflow unless the
final result is too large to be represented.It's important to multiply by the numerator before dividing by the denominator, since if you do this, all the partial results are integers and you don't have to deal with fractions or floating-point numbers or anything like that. I think I may have mentioned before how much I despise floating-point numbers. They are best avoided.
I ran across this algorithm last year while I was reading the Lilavati, a treatise on arithmetic written about 850 years ago in India. The algorithm also appears in the article on "Algebra" from the first edition of the Encyclopaedia Britannica, published in 1768.
So this algorithm is simple, ancient, efficient, and convenient. And the problems with the other algorithm are obvious, or should be. Why isn't this better known?
[ Addendum 20070613: There is a followup article to this one. ]
[Other articles in category /math] permanent link
Sun, 10 Jun 2007 One of the books in the bedtime-reading rotation for my daughter Katara is A Bargain for Frances, by Russell and Lillian Hoban. (Russell Hoban is also the author of a number of acclaimed novels for adults, most notably Riddley Walker.) The plot and character relationships in A Bargain for Frances are quite complex, probably about at the limit of what a two-year-old can handle. I will try to summarize.Frances the badger is having a tea party with her friend Thelma, who has previously behaved abusively to her. Thelma's tea set is plastic, with red flowers. Frances is saving up her money for a real china tea set with blue pictures. Thelma asserts that those tea sets are no longer made, and that they are prohibitively expensive. She offers to sell Frances her own tea set, in return for Frances's savings of $2.17. Frances agrees. End of act I.
When Frances returns home with the plastic tea set, her little sister Gloria criticizes it, saying repeatedly that it is "ugly". She reports that the china kind with blue pictures is available in the local candy store for $2.07, and that Thelma knows this. Frances rushes to the candy store, where she witnesses Thelma buying a china tea set with her money. End of act II.
There is an act III, but I do not want to spoil the ending.
There is quite a lot here to engage the mind of a two-year-old: what does it mean to make a trade, for example? And Thelma is quite devious in the way she talks up the benefits of her plastic tea set ("It does not break, unless you step on it") while dissembling her own desire for a china one. Katara has not yet learned to deceive others for her own benefit, and I think this is her first literary exposure to the idea.
I mentioned at one point that Thelma had told a lie: she had said "I don't think they make that kind [of tea set] anymore" when she knew that the very tea set was available at the candy store. Katara was very interested by this observation. She asked me repeatedly, over a period of a several weeks, to explain to her what a lie was. I had some trouble, because I did not have any good examples to draw on. Katara does not do it yet, and Lorrie and I do not lie to Katara either.
One time I tried to explain lies by telling Katara about how people sometimes tell children that if they do not behave, goblins will come and take them away. Of course, this didn't work. First I had to explain what goblins were. Katara was very disturbed at the thought of goblins that might take her away. I had to reassure Katara that there were no goblins. We got completely sidetracked on a discussion of goblins. I should have foreseen this, but it was the best example I was able to come up with on the spur of the moment.
Later I thought of a better example, with no distracting goblins: suppose Katara asks for raspberries, and I know there are some in the refrigerator, but I tell her that we have none, because I want to eat them myself. I think this was just a little bit too complicated for Katara. It has four parts, and I try to keep explanations to three parts, which seems to be about the maximum that she can follow at once. (Two parts is even better.) I think Katara attached too much significance to the raspberries; for a while she seemed to think that lying had something to do with raspberries.
Oh well, at least I tried. She will catch on soon enough, I am sure.
Perhaps the most complex idea in the book is this: when Frances and Thelma agree to trade money for tea set, they agree on "no backsies". This is an important plot point. After the second or third reading, Katara asked me what "no backsies" meant.
I had to think about this carefully before I answered, because it is quite involved, and until I thought it through, I was not sure I understood it myself. You might want to think about this before reading on. Remember that it's not enough to understand it; you have to be able to explain it.
My understanding of "no backsies" was that normally, when friends trade, there is an assumption that the exchange may be unilaterally voided by either party, as long as this is done timely. You can come back the next day and say you have changed your mind, and your friend, being your friend, is expected to consent. Specifying "no backsies" establishes an advance agreement that this is not the case. If you come back the next day, your friend can protest "but we said there were no backsies on this" and refuse to undo the trade. (The trade can, of course, be voided later if both parties agree.)
So to understand this, you must first understand what it means to trade, and why. Katara took this in early on, and fairly easily. You also have to understand the idea that one or both parties might want to change their minds later; this is also something Katara can get her head around. Toddlers know all about what it means to change one's mind.
But then you have to understand that one party might want to annul the agreement and the other party might not. Tracking two people's independent and conflicting desires is probably a little too hard for Katara at this stage. She can sometimes understand another person's point of view, by identification. ("You sometimes feel like x; here this other person feels the same way.") And similarly she can immerse herself in the world-view of the protagonist of a book, and understand that the protagonist's desires might be frustrated by another character. But to immerse herself in both world-views simultaneously is beyond her.
"No backsies" goes beyond this: you have to understand the idea that an agreement might have default, unspoken conventions, and that the participants will adhere to these conventions even if they don't want to; this is not something that two-year-olds are good at doing yet. You have to understand the idea of an explicit modification to the default conditions; that part is not too hard, and everyday examples abound. But then you have to understand what the unspoken convention actually is, and how it is being modified, and the difference between a unilateral annulment of an agreement and a bilateral one. Again, I think it's the bilaterality that's hard for Katara to understand. She is still genuinely puzzled when I tell her we should leave the public restroom clean for the next person.
Really, though, the main difficulty is just that the idea is very complicated. Maybe I'm wrong about which parts are harder and which parts are easier, and perhaps Katara can understand any of the pieces separately. But at two years old she can't yet sustain a train of thought as complicated as the one required to pull together all the pieces of "no backsies". This sort of understanding is one of the essential components of being an adult, and she will get it sooner or later; probably sooner.
This is not the only part of the book that repays careful thought. At one point, during Thelma's monologue about the unavailability of china tea sets, she says:
I know another girl who saved up for that tea set. Her mother went to every store and could not find one. Then that girl lost some of her money and spent the rest on candy. She never got the tea set. A lot of girls never do get tea sets. So maybe you won't get one.One evening my wife Lorrie asked me who I thought Thelma was speaking about in that passage. I replied that I had always understood it as a pure fabrication, and that there was no "other girl".
Lorrie said that she thought that Thelma had been speaking about herself, that Thelma had saved up her money, and her mother had gone looking for a china tea set, been unable to find one, and had brought home the plastic set as a consolation prize.
The crucial clue was the detail about how the "other girl" spent the rest of her money on candy, which is just a bit too specific for a mere fabrication.
Once you try out the hypothesis that Thelma is speaking personally, a lot of other details fall into place. For example, her assertion that "A lot of girls never do get tea sets" is no longer a clever invention on her part: she is repeating something her mother told her to shut her up when she expressed her disappointment over receiving a plastic instead of a china tea set. Her sales pitch to Frances about why a plastic tea set is better than a china one can be understood as an echo of her mother's own attempts to console her.
My wife is very clever, and was an English major to boot. She is skilled at noticing such things both by native talent and by long training of that talent.
Good children's literature does reward a close reading, and like good adult literature, reveals additional depths on multiple readings. It seems to me that books for small children are more insipid than they used to be, but that could just be fuddy-duddyism, or it could be selection bias: I no longer remember the ones I loved as a child that would now seem insipid precisely because they would now seem insipid.
But the ability to produce good literature at any level is rare, so it is probably just that there only a few great writers in every generation can do it. Russell Hoban was one of the best here.
[Other articles in category /book] permanent link
Fri, 08 Jun 2007
Counting transitive relations
A relation on a set S is merely a subset of
S×S. For example, the relation < on the set
{1,2,3} can be identified as {(1,2), (1,3), (2,3)}, the set of all (a,
b) with a < b.
A relation is transitive if, whenever it has both (a, b) and (b, c), it also has (a, c).
For the last week I've been trying to find a good way to calculate the number of transitive relations on a set with three elements.
There are 13 transitive relations on a set with 2 elements. This is easy to see. There are 16 relations in all. The only way a relation can fail to be transitive is to contain both (1, 2) and (2, 1). There are clearly four such relations. Of these four, the only one that is transitive has (1, 1) and (2, 2) also. Similarly it's quite easy to see that there are only 2 relations on a 1-element set, and both are transitive.
There are 512 relations on a set with 3 elements. How many are transitive?
It would be very easy to write a computer program to check them all and count the transitive ones. That is not what I am after here. In fact, it would also be easy to enumerate the transitive relations by hand; 512 is not too many. That is not what I am after either. I am trying to find some method or technique that scales reasonably well, well enough that I could apply it for larger n.
No luck so far. Relations on 3-sets can fail to be transitive in all sorts of interesting ways. Say that a relation has the Fabc property if it contains (a,b) and (b,c) but not (a,c). Such a relation is intransitive.
Now clearly there are 64 Fabc relations for each distinct choice of a, b, and c. But some of these properties overlap. For example, {(a,b), (b,c), (c,a)} has not only the Fabc property but also the Fbca and Fcab properties.
Of the 64 relations with the Fabc property, 16 have the Fbca property also. 16 have the Faba property. None have the Facb property. There are 12 of these properties, and they overlap in a really complicated way.
After a week I gave in and looked in the literature. I have a couple of papers in my bag I haven't read yet. But it seems that there is no simple solution, which is reassuring.
One problem is that the number of relations on n elements grows very rapidly (it's 2n2) and the number of transitive relations is a good-sized fraction of these.
[Other articles in category /math] permanent link
Wed, 16 May 2007
Moziz Addums
Last July at a porch sale I obtained a facsimile copy of
Housekeeping in Old Virginia, by M.C. Tyree, originally
published in 1879. I had been trying to understand the purpose of
ironing. Ironing makes the clothes look nice, but it must have also
served some important purpose, essential for life, that I don't now
understand. In the Laura Ingalls Wilder Little House
books, Laura recounts a common saying that scheduled the week's
work:
Wash on Monday
Iron on Tuesday
Mend on Wednesday
Churn on Thursday
Clean on Friday
Bake on Saturday
Rest on Sunday
You bake on Saturday so that you have fresh bread for Sunday dinner. You wash on Monday because washing is backbreaking labor and you want to do it right after your day of rest. You iron the following day before the washed clothes are dirty again. But why iron at all? If you don't wash the clothes or clean the house, you'll get sick and die. If you don't bake, you won't have any bread, and you'll starve. But ironing? In my mind it was categorized with dusting, as something people with nice houses in the city might do, but not something that Ma Ingalls, three miles from the nearest neighbor, would concern herself with.
But no. Ironing, and starching with the water from boiled potatoes, was so important that it got a whole day to itself, putting it on par with essential activities like cleaning and baking. But why?
A few months later, I figured it out. In this era of tumble-drying and permanent press, I had forgotten what happens to fabrics that are air dried, and did not understand until I was on a trip and tried to air-dry a cotton bath towel. Air-dried fabrics come out not merely wrinkled but corrugated, like an accordion, or a washboard, and are unusable. Ironing was truly a necessity.
Anyway, I was at this porch sale, and I hoped that this 1879 housekeeping book might provide the answer to the ironing riddle. It turned out to be a cookbook. There is plenty to say about this cookbook anyway. It comes recommended by many notable ladies, including Mrs. R.B. Hayes. (Her husband was President of the United States.) She is quoted on the flyleaf as being "very much pleased" with the cookbook.
Some of the recipes are profoundly unhelpful. For example, p.106 has:
Boiled salmon. After the fish has been cleaned and washed, dry it and sew it up in a cloth; lay in a fish-kettle, cover with warm water, and simmer until done and tender.Just how long do I simmer it? Oh, until it is "done" and "tender". All right, I will just open up the fish kettle and poke it to see. . . except that it is sewed up in a cloth. Hmmm.
You'd think that if I'm supposed to simmer this fish that has been sewn up in a cloth, the author of the recipe might advise me on how long until it is "done". "Until tender" is a bit of a puzzle too. In my experience, fish become firmer and less tender the longer you simmer them. Well, I have a theory about this. The recipe is attributed to "Mrs. S.T.", and consulting the index of contributors, I see that it is short for "Mrs. Samuel Tyree", presumably the editor's mother-in-law. Having a little joke at her expense, perhaps?
There are a lot of other interesting points, which may appear here later. For example, did you know that the most convenient size hog for household use is one of 150 to 200 pounds? And the cookbook contains recipes not only for tomato catsup, but also pepper catsup, mushroom catsup, and walnut catsup.
But the real reason I brought all this up is that page 253–254 has the following item, attributed to "Moziz Addums":
Resipee for cukin kon-feel Pees. Gether your pees 'bout sun-down. The folrin day, 'bout leven o'clock, gowge out your pees with your thum nale, like gowgin out a man's ey-ball at a kote house. Rense your pees, parbile them, then fry 'erm with some several slices uv streekd middlin, incouragin uv the gravy to seep out and intermarry with your pees. When modritly brown, but not scorcht, empty intoo a dish. Mash 'em gently with a spune, mix with raw tomarters sprinkled with a little brown shugar and the immortal dish ar quite ready. Eat a hepe. Eat mo and mo. It is good for your genral helth uv mind and body. It fattens you up, makes you sassy, goes throo and throo your very soul. But why don't you eat? Eat on. By Jings. Eat. Stop! Never, while thar is a pee in the dish.This was apparently inserted for humorous effect. Around the time the cookbook was written, there was quite a vogue for dialectal humor of this type, most of which has been justly forgotten. Probably the best-remembered practitioner of this brand of humor was Josh Billings, who I bet you haven't heard of anyway. Tremendously popular at the time, almost as much so as Mark Twain, his work is little-read today; the joke is no longer funny. The exceptionally racist example above is in many ways typical of the genre.
One aspect of this that is puzzling to us today (other than the obvious "why was this considered funny?") is that it's not clear exactly what was supposed to be going on. Is the idea that Moziz Addums wrote this down herself, or is this a transcript by a literate person of a recipe dictated by Moziz Addums? Neither theory makes sense. Where do the misspellings come from? In the former theory, they are Moziz Addums' own misspellings. But then we must imagine someone literate enough to spell "intermarry" and "immortal" correctly, but who does not know how to spell "of".
In the other theory, the recipe is a transcript, and the misspellings have been used by the anonymous, literate transcriber to indicate Moziz Addums' unusual or dialectal pronunciations, as with "tomarters", perhaps. But "uv" is the standard (indeed, the only) pronunciation of "of", which wrecks this interpretation. (Spelling "of" as "uv" was the signature of Petroleum V. Nasby, another one of those forgotten dialectal humorists.) And why did the transcriber misspell "peas" as "pees"?
So what we have here is something that nobody could possibly have written or said, except as an inept parody of someone else's speech. I like my parody to be rather less artificial.
All of this analysis would be spoilsportish if the joke were actually funny. E.B. White famously said that "Analyzing humor is like dissecting a frog. Few people are interested and the frog dies of it." Here, at least, the frog had already been dead for a hundred years dead before I got to it.
[ Addendum 20100810: In case you were wondering, "kon-feel pees" are actually "cornfield peas", that is, peas that have been planted in between the rows of corn in a cornfield. ]
[Other articles in category /lang] permanent link
Tue, 15 May 2007
Ambiguous words and dictionary hacks
A Mexican gentleman of my acquaintance, Marco Antonio Manzo, was
complaining to me (on IRC) that what makes English hard was the large
number of ambiguous words. For example, English has the word "free"
where Spanish distinguishes "gratis" (free like free beer) from
"libre" (free like free speech).
I said I was surprised that he thought that was unique to English, and said that probably Spanish had just as many "ambiguous" words, but that he just hadn't noticed them. I couldn't think of any Spanish examples offhand, but I knew some German ones: in English, "suit" can mean a lawsuit, a suit of clothes, or a suit of playing cards. German has different words for all of these. In German, the suit of a playing card is its "farbe", its color. So German distinguishes between suit of clothes and suit of playing cards, which English does not, but fails to distinguish between colors of paint and suit of playing cards, which English does.
Every language has these mismatches. Korean has two words for "thin", one meaning thin like paper and the other meaning thin like string. Korean distinguishes father's sister ("komo") from mother's sister ("imo") where English has only "aunt".
Anyway, Sr. Manzo then went to lunch, and I wanted to find some examples of concepts distinguished by English but not by Spanish. I did this with a dictionary hack.
A dictionary hack is when you take a plain text dictionary and do some sort of rough-and-ready processing on it to get an 80% solution to some problem. The oldest dictionary hack I know of is the old Unix rhyming dictionary hack:
rev /usr/dict/words | sort | rev > rhyming.txt
This takes the Unix word list and turns it into a semblance of a
rhyming dictionary. It's not an especially accurate semblance, but
you can't beat the price.
...
ugh Marlborough choreograph Guelph Wabash
Hugh Scarborough lithograph Adolph cash
McHugh thorough electrocardiograph Randolph dash
Pugh trough electroencephalograph Rudolph leash
laugh sough nomograph triumph gash
bough tough tomograph lymph hash
cough tanh seismograph nymph lash
dough Penh phonograph philosoph clash
sourdough sinh chronograph Christoph eyelash
hough oh polarograph homeomorph flash
though pharaoh spectrograph isomorph backlash
although Shiloh Addressograph polymorph whiplash
McCullough pooh chromatograph glyph splash
furlough graph autograph anaglyph slash
slough paragraph epitaph petroglyph mash
enough telegraph staph myrrh smash
rough radiotelegrap aleph ash gnash
through calligraph Joseph Nash Monash
breakthrough epigraph caliph bash rash
borough mimeograph Ralph abash brash
...
It figures out that "clash" rhymes with "lash" and "backlash", but not
that "myrrh" rhymes with "purr" or "her" or "sir". You can of
course, do better, by using a text file that has two columns, one for
orthography and one for pronunciation, and sorting it by reverse
pronunciation. But like I said, you won't beat the price.But I digress. Last week I pulled an excellent dictionary hack. I found the Internet Dictionary Project's English-Spanish lexicon file on the web with a quick Google search; it looks like this:
a un, uno, una[Article]
aardvark cerdo hormiguero
aardvark oso hormiguero[Noun]
aardvarks cerdos hormigueros
aardvarks osos hormigueros
ab prefijo que indica separacio/n
aback hacia atras
aback hacia atr´s,take aback, desconcertar. En facha.
aback por sopresa, desprevenidamente, de improviso
aback atra/s[Adverb]
abacterial abacteriano, sin bacterias
abacus a/baco
abacuses a/bacos
abaft A popa (towards stern)/En popa (in stern)
abaft detra/s de[Adverb]
abalone abulo/n
abalone oreja de mar (molusco)[Noun]
abalone oreja de mar[Noun]
abalones abulones
abalones orejas de mar (moluscos)[Noun]
abalones orejas de mar[Noun]
abandon abandonar
abandon darse por vencido[Verb]
abandon dejar
abandon desamparar, desertar, renunciar, evacuar, repudiar
abandon renunciar a[Verb]
abandon abandono[Noun]
abandoned abandonado
abandoned dejado
...
Then I did:
sort +1 idengspa.txt |
perl -nle '($ecur, $scur) = split /\s+/, $_, 2;
print "$eprev $ecur $scur"
if $sprev eq $scur &&
substr($eprev, 0, 1) ne substr($ecur, 0, 1);
($eprev, $sprev) = ($ecur, $scur)'
The sort sorts the lexicon into Spanish order instead of English order. The Perl thing comes out looking a lot more complicated than it ought. It just says to look and print consecutive items that have the same Spanish, but whose English begins with different letters. The condition on the English is to filter out items where the Spanish is the same and the English is almost the same, such as:
| blond | blonde | rubio |
| cake | cakes | tarta |
| oceanographic | oceanographical | oceanografico[Adjective] |
| palaces | palazzi | palacios[Noun] |
| talc | talcum | talco |
| taxi | taxicab | taxi |
It does filter out possible items of interest, such as:
| carefree | careless | sin cuidado |
But since the goal is just to produce some examples, and this cheap hack was never going to generate an exhaustive list anyway, that is all right.
The output is:
at letter a
actions stock acciones[Noun]
accredit certify acreditar
around thereabout alrededor
high tall alto
comrade pal amigo[Noun]
antecedents backgrounds antecedentes
(...complete output...)
A lot of these are useless, genuine synonyms. It would be silly to
suggest that Spanish fails to preserve the English distinction between
"marry" and "wed", between "ale" and "beer", between "desire" and
"yearn", or between "vest" and "waistcoat". But some good
possibilities remain.Of these, some probably fail for reasons that only a Spanish-speaker would be able to supply. For instance, is "el pastel" really the best translation of both "cake" and "pie"? If so, it is an example of the type I want. But perhaps it's just a poor translation; perhaps Spanish does have this distinction; say maybe "torta" for "cake" and "empanada" for "pie". (That's what Google suggests, anyway.)
Another kind of failure arises because of idioms. The output:
exactly o'clock en punto
is of this type. It's not that Spanish fails to distinguish between
the concepts of "exactly" and "o'clock"; it's that "en punto" (which
means "on the point of") is used idiomatically to mean both of those
things: some phrase like "en punto tres" ("on the point of three")
means "exactly three" and so, by analogy, "three o'clock". I don't
know just what the correct Spanish phrases are, but I can guess that
they'll be something like this.Still, some of the outputs are suggestive:
| high | tall | alto |
| low | small | bajo[Adjective] |
| babble | fumble | balbucear[Verb] |
| jealous | zealous | celoso |
| contest | debate | debate[Noun] |
| forlorn | stranded | desamparado[Adjective] |
| docile | meek | do/cil[Adjective] |
| picture | square | el cuadro |
| fourth | room | el cuarto |
| collar | neck | el cuello |
| idiom | language | el idioma[Noun] |
| clock | watch | el reloj |
| floor | ground | el suelo |
| ceiling | roof | el techo |
| knife | razor | la navaja |
| feather | pen | la pluma |
| cloudy | foggy | nublado |
I put some of these to Sr. Manzo, and he agreed that some were indeed ambiguous in Spanish. I wouldn't have known what to suggest without the dictionary hack.
[Other articles in category /lang] permanent link
Mon, 14 May 2007
Bryan and his posse
Today upon the arrival of a coworker and his associates, I said "Oh,
here comes Bryan and his posse". My use of "posse" here drew some
comment. I realized I was not completely sure what "posse" meant. I
mostly knew it from old West contexts: the Big Dictionary has quotes
like this one, from 1901:
A pitched battle was fought..at Rockhill, Missouri, between the Sheriff's posse and the miners on strike.I first ran across the word in J.D. Fitzgerald's Great Brain books. At least in old West contexts, the word refers to a gang of men assembled by some authority such as a sheriff or a marshal, to perform some task, such as searching for a lost person, apprehending an outlaw, or blasting some striking miners. This much was clear to me before.
From the context and orthography, I guessed that it was from Spanish. But no, it's not. It's Latin! "Posse" is the Latin verb "to be able", akin to English "possible" and ultimately to "potent" and related words. I'd guessed something like this, supposing English "posse" was akin to some Spanish derivative of the Latin. But it isn't; it's direct from Latin: "posse" in English is short for posse comitatus, "force of the county".
The Big Dictionary has citations for "posse comitatus" back to 1576:
Mr. Sheryve meaneth in person to repayre thither & with force to bryng hym from Aylesham, Whomsoever he fyndeth to denye the samet & suerly will with Posse Comitatus fetch hym from this new erected pryson to morrow.
"Sheryve" is "Sheriff". (If you have trouble understanding this, try reading it aloud. English spelling changed more than its pronunciation since 1576.)
I had heard the phrase before in connection with the Posse Comitatus Act of U.S. law. This law, passed in 1878, is intended to prohibit the use of the U.S. armed forces as Posse Comitatus—that is, as civilian law enforcement. Here the use is obviously Latin, and I hadn't connected it before with the sheriff's posse. But they are one and the same.
[Other articles in category /lang/etym] permanent link
Mon, 30 Apr 2007
Woodrow Wilson on bloggers
Last weekend my family and I drove up to New York. On the way we
stopped in the Woodrow Wilson Service Area on the New Jersey
Turnpike, which has a little plaque on the wall
commemorating Woodrow Wilson and providing some quotations, such as:
Uncompromising thought is the luxury of the closeted recluse.
(Part of a speech at the University of Tennessee in 17 June, 1890).
Bloggers beware; Woodrow Wilson has your number.
[Other articles in category /meta] permanent link
Sun, 29 Apr 2007
Your age as a fraction, again
In a recent article, I
discussed methods for calculating your age as a fractional year, in
the style of (a sophisticated) three-and-a-half-year-old. For
example, as of today, Richard M. Stallman is (a sophisticated)
54-and-four-thirty-thirds-year-old; tomorrow he'll be a
54-and-one-eighth-year-old.
I discussed several methods of finding the answer, including a clever but difficult method that involved fiddling with continued fractions, and some dead-simple brute force methods that take nominally longer but are much easier to do.
But a few days ago on IRC, a gentleman named Mauro Persano said he thought I could use the Stern-Brocot tree to solve the problem, and he was absolutely right. Application of a bit of clever theory sweeps away all the difficulties of the continued-fraction approach, leaving behind a solution that is clever and simple and fast.
Here's the essence of it: We consider a list of intervals that covers all the positive rational numbers; initially, the list contains only the interval (0/1, 1/0). At each stage we divide each interval in the list in two, by chopping it at the simplest fraction it contains.
To chop the interval (a/b, c/d), we split it into the two intervals (a/b, (a+c)/(b+d)), ((a+c)/(b+d)), c/d). The fraction (a+c)/(b+d) is called the mediant of a/b and c/d. It's not obvious that the mediant is always the simplest possible fraction in the interval, but it is true.
So we start with the interval (0/1, 1/0), and in the first step we split it at (0+1)/(1+0) = 1/1. It is now two intervals, (0/1, 1/1) and (1/1, 1/0). At the next step, we split these two intervals at 1/2 and 2/1, respectively; the resulting four intervals are (0/1, 1/2), (1/2, 1/1), (1/1, 2/1), and (2/1, 1/0). We split these at 1/3, 2/3, 3/2, and 3/1. The process goes on from there:
| 0/1 | 1/0 | ||||||||||||||||||||||||||||||
| 0/1 | 1/1 | 1/0 | |||||||||||||||||||||||||||||
| 0/1 | 1/2 | 1/1 | 2/1 | 1/0 | |||||||||||||||||||||||||||
| 0/1 | 1/3 | 1/2 | 2/3 | 1/1 | 3/2 | 2/1 | 3/1 | 1/0 | |||||||||||||||||||||||
| 0/1 | 1/4 | 1/3 | 2/5 | 1/2 | 3/5 | 2/3 | 3/4 | 1/1 | 4/3 | 3/2 | 5/3 | 2/1 | 5/2 | 3/1 | 4/1 | 1/0 |
Or, omitting the repeated items at each step:
| 0/1 | 1/0 | ||||||||||||||||||||||||||||||
| 1/1 | |||||||||||||||||||||||||||||||
| 1/2 | 2/1 | ||||||||||||||||||||||||||||||
| 1/3 | 2/3 | 3/2 | 3/1 | ||||||||||||||||||||||||||||
| 1/4 | 2/5 | 3/5 | 3/4 | 4/3 | 5/3 | 5/2 | 4/1 |
If we disregard the two corners, 0/1 and 1/0, we can see from this diagram that the fractions naturally organize themselves into a tree. If a fraction is introduced at step N, then the interval it splits has exactly one endpoint that was introduced at step N-1, and this is its parent in the tree; conversely, a fraction introduced at step N is the parent of the two step-N+1 fractions that are introduced to split the two intervals of which it is an endpoint.
This process has many important and interesting properties. The splitting process eventually lists every positive rational number exactly once, as a fraction in lowest terms. Every fraction is simpler than all of its descendants in the tree. And, perhaps most important, each time an interval is split, it is divided at the simplest fraction that the interval contains. ("Simplest" just means "has the smallest denominator".)
This means that we can find the simplest fraction in some interval simply by doing binary tree search until we find a fraction in that interval.
For example, Placido Polanco had a .368 batting average last season. What is the smallest number of at-bats he could have had? We are asking here for the denominator of the simplest fraction that lies in the interval [.3675, .3685).
- We start at the root, which is 1/1. 1 is too big, to we move left down the tree to 1/2.
- 1/2 = .5000 and is also too big, so we move left down the tree to 1/3.
- 1/3 = .3333 and is too small, so we move right down the tree to 2/5.
- 2/5 = .4000 and is too big, so go left to 3/8, which is the mediant of 1/3 and 2/5.
- 3/8 = .3750, so go left to 4/11, the mediant of 1/3 and 3/8.
- 4/11 = .3636, so go right to 7/19, the mediant of 3/8 and 4/11.
- 7/19 = .3684, which is in the interval, so we are done.
Calculation of mediants is incredibly simple, even easier than adding fractions. Tree search is simple, just compare and then go left or right. Calculating whether a fraction is in an interval is simple too. Everything is simple simple simple.
Our program wants to find the simplest fraction in some interval, say (L, R). To do this, it keeps track of l and r, initially 0/1 and 1/0, and repeatedly calculates the mediant m of l and r. If the mediant is in the target interval, the function is done. If the mediant is too small, set l = m and continue; if it is too large set r = m and continue:
# Find and return numerator and denominator of simplest fraction
# in the range [$Ln/$Ld, $Rn/$Rd)
#
sub find_simplest_in {
my ($Ln, $Ld, $Rn, $Rd) = @_;
my ($ln, $ld) = (0, 1);
my ($rn, $rd) = (1, 0);
while (1) {
my ($mn, $md) = ($ln + $rn, $ld + $rd);
# print " $ln/$ld $mn/$md $rn/$rd\n";
if (isin($Ln, $Ld, $mn, $md, $Rn, $Rd)) {
return ($mn, $md);
} elsif (isless($mn, $md, $Ln, $Ld)) {
($ln, $ld) = ($mn, $md);
} elsif (islessequal($Rn, $Rd, $mn, $md)) {
($rn, $rd) = ($mn, $md);
} else {
die;
}
}
}
(In this program, rn and rd are the numerator and
the denominator of r.)The isin, isless, and islessequal functions are simple utilities for comparing fractions.
# Return true iff $an/$ad < $bn/$bd
sub isless {
my ($an, $ad, $bn, $bd) = @_;
$an * $bd < $bn * $ad;
}
# Return true iff $an/$ad <= $bn/$bd
sub islessequal {
my ($an, $ad, $bn, $bd) = @_;
$an * $bd <= $bn * $ad;
}
# Return true iff $bn/$bd is in [$an/$ad, $cn/$cd).
sub isin {
my ($an, $ad, $bn, $bd, $cn, $cd) = @_;
islessequal($an, $ad, $bn, $bd) and isless($bn, $bd, $cn, $cd);
}
The asymmetry between
isless and islessequal is because I want to deal with
half-open intervals.Just add a trivial scaffold to run the main function and we are done:
#!/usr/bin/perl
my $D = shift || 10;
for my $N (0 .. $D-1) {
my $Np1 = $N+1;
my ($mn, $md) = find_simplest_in($N, $D, $Np1, $D);
print "$N/$D - $Np1/$D : $mn/$md\n";
}
Given the argument 10, the program produces this output:
0/10 - 1/10 : 1/11
1/10 - 2/10 : 1/6
2/10 - 3/10 : 1/4
3/10 - 4/10 : 1/3
4/10 - 5/10 : 2/5
5/10 - 6/10 : 1/2
6/10 - 7/10 : 2/3
7/10 - 8/10 : 3/4
8/10 - 9/10 : 4/5
9/10 - 10/10 : 9/10
This says that the simplest fraction in the range [0/10, 1/10) is
1/11; the simplest fraction in the range [3/10, 4/10) is 1/3, and so
forth. The simplest fractions that do not appear are 1/5, which is
beaten out by the simpler 1/4 in the [2/10, 3/10) range, and 3/5,
which is beaten out by 2/3 in the [6/10, 7/10) range.Unlike the programs from the previous article, this program is really fast, even in principle, even for very large arguments. The code is brief and simple. But we had to deploy some rather sophisticated number theory to get it. It's a nice reminder that the sawed-off shotgun doesn't always win.
This is article #200 on my blog. Thanks for reading.
[Other articles in category /math] permanent link
Sat, 28 Apr 2007
1219.2 feet
In Thursday's article, I
quoted an article about tsunamis that asserted that:
In the Pacific Ocean, a tsunami moves 60.96 feet a second, passing through water that is around 1219.2 feet deep."60.96 feet a second" is an inept conversion of 100 km/h to imperial units, but I wasn't able to similarly identify 1219.2 feet.
Scott Turner has solved the puzzle. 1219.2 feet is an inept conversion of 4000 meters to imperial units, obtained by multiplying 4000 by 0.3048, because there are 0.3048 meters in a foot.
Thank you, M. Turner.
[ Addendum 20070430: 60.96 feet per second is nothing like 100 km/hr, and I have no idea why I said it was. The 60.96 feet per second is a backwards conversion of 200 m/s. ]
[Other articles in category /physics] permanent link
Thu, 26 Apr 2007
Excessive precision
You sometimes read news articles that say that some object is 98.42
feet tall, and it is clear what happened was that the object was
originally reported to be 30 meters tall, and some knucklehead
translated 30 meters to 98.42 feet, instead of to 100 feet as they
should have.
Finding a real example for you was easy: I just did Google search for "62.14 miles", and got this little jewel:
Tsunami waves can be up to 62.14 miles long! They can also be about three feet high in the middle of the ocean. Because of its strong underwater energetic force, the tsunami can rise up to 90 feet, in extreme cases, when they hit the shore! Tsunami waves act like shallow water waves because they are so long. Because it is so long, it can last an hour. In the Pacific Ocean, a tsunami moves 60.96 feet a second, passing through water that is around 1219.2 feet deep.The 60.96 feet per second is actually 100 km/hr, but I'm not sure what's going on with the 1219.2 feet deep. Is it 1/5 nautical mile? But that would be strange. [ Addendum 20070428: the explanation.](.)
Here's another delightful example:
The MiniC.A.T. is very cost-efficient to operate. According to MDI, it costs less than one dollar per 62.14 miles... Given the absence of combustion and the fact that the MiniC.A.T. runs on vegetable oil, oil changes are only necessary every 31,068 miles.(I should add that many of the hits for "62.14 miles" were perfectly legitimate. Many concerned 100-km bicycle races, or the conditions for winning the X-prize. In both cases the distance is in fact 62.14 miles, not 62.13 or 62.15, and the precision is warranted. But I digress.)(eesi.org.)
(Long ago there was a parody of the New York Times which included a parody sports section that announced "FOOTBALL TO GO METRIC". The article revealed that after the change, the end zones would be placed 91.44 meters apart...)
Anyway, similar knuckleheadedness occurs in the well-known value of 98.6 degrees Fahrenheit for normal human body temperature. Human body temperature varies from individual to individual, and by a couple of degrees over the course of the day, so citing the "normal" temperature to a tenth of a degree is ridiculous. The same thing happened here as with the 62.14-mile tsunami. Normal human body temperature was determined to be around 37 degrees Celsius, and then some knucklehead translated 37°C to 98.6°F instead of to 98°F.
When our daughter Katara was on the way, Lorrie and I took a bunch of classes on baby care. Several of these emphasized that the maximum safe spacing for the bars of a crib, rails of a banister, etc., was two and three-eighths inches. I was skeptical, and at one of these classes I was foolish enough to ask if that precision were really required: was two and one-half inches significantly less safe? How about two and seven-sixteenths inches? The answer was immediate and unequivocal: two and one-half inches was too far apart for safety; two and three-eighths inches is the maximum safe distance.
All the baby care books say the same thing. (For example...)
But two and three-eighths inches is 6.0325 cm, so draw your own conclusion about what happened here.
[ Addendum 20070430: 60.96 feet per second is nothing like 100 km/hr, and I have no idea why I said it was. The 60.96 feet per second appears to be a backwards conversion of 200 m/s to ft/s, multiplying by 3.048 instead of dividing. As Scott turner noted a few days ago, a similar error occurs in the conversion of meters to feet in the "1219.2 feet deep" clause. ]
[ Addendum 20220124: the proper spacing of crib slats ]
[Other articles in category /physics] permanent link
Sat, 21 Apr 2007
Degrees of algebraic numbers
An algebraic number x is said to have degree n if it is
the zero of some irreducible nth-degree polynomial P with
integer coefficients.
For example, all rational numbers have degree 1, since the rational number a/b is a zero of the first-degree polynomial bx - a. √2 has degree 2, since it is a zero of x2 - 2, but (as the Greeks showed) not of any first-degree polynomial.
It's often pretty easy to guess what degree some number has, just by looking at it. For example, the nth root of a prime number p has degree n. !!\sqrt{1 + \sqrt 2}!! has a square root of a square root, so it's fourth-degree number. If you write !!x = \sqrt{1 + \sqrt 2}!! then eliminate the square roots, you get x4 - 2x2 - 1, which is the 4th-degree polynomial satisfied by this 4th-degree number.
But it's not always quite so simple. One day when I was in high
school, I bumped into the fact that !!\sqrt{7 + 4 \sqrt 3}!!, which looks
just like a 4th-degree number, is actually a 2nd-degree number.
It's numerically equal to !!2 + \sqrt 3!!. At the time,
I was totally boggled. I couldn't believe it at first, and I had to
get out my calculator and calculate both values numerically to be sure
I wasn't hallucinating. I was so sure that the nested square
roots in 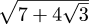 would force it to be
4th-degree.
would force it to be
4th-degree.
If you eliminate the square roots, as in the other example, you get
the 4th-degree polynomial
x4 - 14x2 + 1, which is satisfied
by 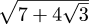 . But unlike the previous
4th-degree polynomial, this one is reducible. It factors into
(x2 + 4x + 1)(x2 - 4x + 1). Since
. But unlike the previous
4th-degree polynomial, this one is reducible. It factors into
(x2 + 4x + 1)(x2 - 4x + 1). Since
 is a zero of the polynomial, it
must be a zero of one of the two factors, and so it is
second-degree. (It is a zero of the second factor.)
is a zero of the polynomial, it
must be a zero of one of the two factors, and so it is
second-degree. (It is a zero of the second factor.)
I don't know exactly why I was so stunned to discover this. Clearly, the square of any number of the form a + b√c is another number of the same form (namely (a2 + b2c) + 2ab√c), so it must be the case that lots of a + b√c numbers must be squares of other such, and so that lots of !!\sqrt{a + b \sqrt c}!! numbers must be second-degree. I must have known this, or at least been capable of knowing it. Socrates says that the truth is within us, and we just don't know it yet; in this case that was certainly true. I think I was so attached to the idea that the nested square roots signified fourth-degreeness that I couldn't stop to realize that they don't always.
In the years since, I came to realize that recognizing the degree of an algebraic number could be quite difficult. One method, of course, is the one I used above: eliminate the radical signs, and you have a polynomial; then factor the polynomial and find the irreducible factor of which the original number is a root. But in practice this can be very tricky, even before you get to the "factor the polynomial" stage. For example, let x = 21/2 + 21/3. Now let's try to eliminate the radicals.
Proceeding as before, we do x - 21/3 = 21/2 and then square both sides, getting x2 - 2·21/3x + 22/3 = 2, and then it's not clear what to do next.
So we try the other way, starting with x - 21/2 = 21/3 and then cube both sides, getting x3 - 3·21/2x2 + 6x - 2·21/2 = 2. Then we move all the 21/2 terms to the other side: x3 + 6x - 2 = (3x2 + 2)·21/2. Now squaring both sides eliminates the last radical, giving us x6 + 12x4 - 4x3 + 36x2 - 24x + 4 = 18x4 + 12x2 + 8. Collecting the terms, we see that 21/2 + 21/3 is a root of x6 - 6x4 - 4x3 + 12x2 - 24x - 4. Now we need to make sure that this polynomial is irreducible. Ouch.
In the course of writing this article, though, I found a much better method. I'll work a simpler example first, √2 + √3. The radical-eliminating method would have us put x - √2 = √3, then x2 - 2√2x + 2 = 3, then x2 - 1 = 2√2x, then x4 - 2x2 + 1 = 8x2, so √2 + √3 is a root of x4 - 10x2 + 1.
The new improved method goes like this. Let x = √2 + √3. Now calculate powers of x:
| x0 = | 1 | |||
| x1 = | √2 + | √3 | ||
| x2 = | 2√6 + | 5 | ||
| x3 = | 11√2 + | 9√3 | ||
| x4 = | 20√6 + | 49 |
That's a lot of calculating, but it's totally mechanical.
All of the powers of x have the form a6√6 + a2√2 + a3√3 + a1. This is easy to see if you write p for √2 and q for √3. Then x = p + q and powers of x are polynomials in p and q. But any time you have p2 you replace it with 2, and any time you have q2 you replace it with 3, so your polynomials never have any terms in them other than 1, p, q, and pq.
This means that you can think of the powers of x as being vectors in a 4-dimensional vector space whose canonical basis is {1, √2, √3, √6}. Any four vectors in this space, such as {1, x, x2, x3}, are either linearly independent, and so can be combined to total up to any other vector, such as x4, or else they are linearly dependent and three of them can be combined to make the fourth. In the former case, we have found a fourth-degree polynomial of which x is a root, and proved that there is no simpler such polynomial; in the latter case, we've found a simpler polynomial of which x is a root.
To complete the example above, it is evident that {1, x, x2, x3} are linearly independent, but if you don't believe it you can use any of the usual mechanical tests. This proves that √2 + √3 has degree 4, and not less. Because if √2 + √3 were of degree 2 (say) then we would be able to find a, b, c such that ax2 + bx + c = 0, and then the x2, x1, and x0 vectors would be dependent. But they aren't, so we can't, so it isn't.
Instead, there must be a, b, c, and d such that x4 = ax3 + bx2 + cx + d. To find these we need merely solve a system of four simultaneous equations, one for each column in the table:
| 2 b | = | 20 |
| 11 a + c | = | 0 |
| 9 a + c | = | 0 |
| 5 b + d | = | 49 |
And we immediately get a=0, b=10, c=0, d=-1, so x4 = 10x2 - 1, and our polynomial is x4 - 10x2 + 1, as before.
Yesterday's draft of this article said:
I think [21/2 + 21/3] turns out to be degree 6, but if you try to work it out in the straightforward way, by equating it to x and then trying to get rid of the roots, you get a big mess. I think it turns out that if two numbers have degrees a and b, then their sum has degree at most ab, but I wouldn't even want to swear to that without thinking it over real carefully.Happily, I'm now sure about all of this. I can work through the mechanical method on it. Putting x = 21/2 + 21/3, we get:
| x0 = | [0 | 0 | 0 | 0 | 0 | 1] |
| x1 = | [0 | 0 | 0 | 1 | 1 | 0] |
| x2 = | [0 | 1 | 2 | 0 | 0 | 2] |
| x3 = | [3 | 0 | 0 | 6 | 2 | 2] |
| x4 = | [0 | 12 | 8 | 2 | 8 | 4] |
| x5 = | [20 | 2 | 10 | 20 | 4 | 40] |
| x6 = | [12 | 60 | 24 | 60 | 80 | 12] |
Where the vector [a, b, c, d, e, f] is really shorthand for a21/2·22/3 + b22/3 + c21/2·21/3 + d21/3 + e21/2 + f.
x0...x5 turn out to be linearly independent, almost by inspection, so 21/2 + 21/3 has degree 6. To express x6 as a linear combination of x0...x5, we set up the following equations:
| 20a | + 3c | = 12 | ||||
| 2a | + 12b | + d | = 60 | |||
| 10a | + 8b | + 2d | = 24 | |||
| 20a | + 2b | + 6c | + e | = 60 | ||
| 4a | + 8b | + 2c | + e | = 80 | ||
| 40a | + 4b | + 2c | + 2d | + f | = 12 |
Solving these gives [a, b, c, d, e, f]= [0, 6, 4, -12, 24, 4], so x6 = 6x4 + 4x3 - 12x2 + 24x + 4, and 21/2 + 21/3 is a root of x6 - 6x4 - 4x3 + 12x2 - 24x - 4, which is irreducible.
And similarly, using this method, one can calculate in a few minutes that 21/2 + 21/4 has degree 4 and is a root of x4 - 4x2 - 8x + 2.
I wish I had figured this out in high school; it would have delighted me.
[Other articles in category /math] permanent link
Sun, 15 Apr 2007
Happy birthday Leonhard Euler
Leonhard Euler, one of the greatest and most prolific mathematicians
ever to walk the earth, was born 300 years ago today in Basel,
Switzerland.
Euler named the constant e (not for himself; he used vowels for constants and had already used a for something else), and discovered the astonishing formula !!e^{ix} = \cos x + i \sin x!!, which is known as Euler's formula. A special case of this formula is the Euler identity: !!e^{i\pi} + 1 = 0!!.
I never really understood what was going on there until last year, when I read the utterly brilliant book Visual Complex Analysis, by Tristan Needham. This was certainly the best math book I read in all of 2006, and probably the best one I've read in the past five years. (Many thanks to Dan Schmidt for rcommending it.)
The brief explanantion is something like this: the exponential function ect is exactly the function that satisfies the differential equation df/dt = cf(t). That is, it is the function that describes the motion of a particle whose velocity is proportional to its position at all times.
Imagine a particle moving on the real line. If its velocity is proportional to its position, it will speed away from the origin at an exponentially increasing rate. Or, if the proportionality constant is negative, it will rapidly approach the origin, getting closer (but never quite reaching it) at an exponentially increasing rate.
Now, suppose we consider a particle moving on the complex plane instead of on the real line, again with velocity proportional to position. If the proportionality constant is real, the particle will speed away from the origin (or towards it, if the constant is negative), as before. But what if the proportionality constant is imaginary?
A proportionality constant of i means that the velocity of the particle is at right angles to the position, because multiplication by i in the complex plane corresponds to a counterclockwise rotation by 90°, as always. In this case, the path of the particle is a circle, and so its position as a function of t is described by something like cos t + i sin t. But this function must satisfy the differential equation also, with c = i, and we have Euler's formula.
Another famous and important formula named after Euler is also called Euler's formula, and states that for any simply-connected polyhedron with F faces, E edges, and V vertices, F - E + V = 2. For example, the cube has 6 faces, 12 edges, and 8 vertices, and indeed 6 - 12 + 8 = 2. The formula also holds for all planar graphs and is the fundamental result of planar graph theory.
Spheres in this case behave like planes, and graphs that cover spheres also satisfy F - E + V = 2. One then wonders whether the theorem holds for more complex surfaces, such as tori; this is equivalent to asking about polyhedra that have a single hole. In this case, the theorem is a little different, and the identity becomes F - E + V = 0.
It turns out that every surface S has a value χ(S), called the Euler characteristic, such that graphs on the surface all satisfy F - E + V = χ(S).
Euler also discovered that the sum of the first n terms of the harmonic series, 1 + 1/2 + 1/3 + ... + 1/n, is approximately log n. We might like to say that it becomes arbitrarily close to log n, as so many things do, but it does not. It is always a bit larger than log n, and you cannot make it as close as you want. The more terms you take, the closer the sum gets to log n + γ, where γ is approximately 0.577216. This γ is Euler's constant:
$$\gamma = \lim_{n\rightarrow\infty}\left({\sum_{i=1}^n {1\over i} - \ln n}\right)$$
This is one of those numbers that shows up all over the place, and is easy to calculate, but is a big fat mystery. Is it rational? Everyone would be shocked if it were, but nobody knows for sure.The Euler totient function φ(x) counts the number of integers less than x that have no divisors in common with x. It is of tremendous importance in combinmatorics and number theory. One of the most fundamental and astonishing facts about the totient function is Euler's theorem: aφ(n) - 1 is a multiple of n whenever a and n have no divisors in common. For example, since &phi(9) = 6, a6 - 1 is a multiple of 9, except when a is divisible by 3:
| 16 - 1 | = | 0· | 9. |
| 26 - 1 | = | 7· | 9. |
| 46 - 1 | = | 455· | 9. |
| 56 - 1 | = | 1736· | 9. |
| 76 - 1 | = | 13072· | 9. |
Euler's solution in 1736 of the "bridges of Königsberg" problem is often said to have begun the study of topology. It is also the source of the term "Eulerian path".
Wikipedia lists forty more items that are merely named for Euler. The list of topics that he discovered, invented, or contributed to would be far too large to actually construct.
Happy birthday, Leonhard Euler.
[Other articles in category /anniversary] permanent link
Thu, 12 Apr 2007
A security problem in a CGI program: addenda
Shell-less piping in Perl
In my previous article, I said:
Unfortunately, there is no easy way to avoid the shell when running a command that is attached to the parent process via a pipe. Perl provides open "| command arg arg arg...", which is what I used, and which is analogous to [system STRING], involving the shell. But it provides nothing analogous to [system ARGLIST], which avoids the shell. If it did, then I probably would have used it, writing something like this:Several people wrote to point out that, as of Perl 5.8.0, Perl does provide this, with a syntax almost identical to what I proposed:
open M, "|", $MAILER, "-fnobody\@plover.com", $addre;and the whole problem would have been avoided.
open M, "|-", $MAILER, "-fnobody\@plover.com", $addre;
Why didn't I use this? The program was written in late 2002, and Perl
5.8.0 was released in July 2002, so I expect it's just that I wasn't
familiar with the new feature yet. Why didn't I mention it in the
original article? As I said, I just got back from Asia, and I am
still terribly jetlagged.(Jet lag when travelling with a toddler is worse than normal jet lag, because nobody else can get over the jet lag until the toddler does.)
Jeff Weisberg also pointed out that even prior to 5.8.0, you can write:
open(F, "|-") || exec("program", "arg", "arg", "arg");
Why didn't I use this construction? I have run out of excuses.
Perhaps I was jetlagged in 2002 also.
RFC 822
John Berthels wrote to point out that my proposed fix, which rejects all inputs containing spaces, also rejects some RFC822-valid addresses. Someone whose address was actually something like "Mark Dominus"@example.com would be unable to use the web form to subscribe to the mailing list.Quite so. Such addresses are extremely rare, and people who use them are expected to figure out how to subscribe by email, rather than using the web form.
qmail
Nobody has expressed confusion on this point, but I want to expliticly state that, in my opinion, the security problem I described was entirely my fault, and was not due to any deficiency in the qmail mail system, or in its qmail-inject or qmail-queue components.Moreover, since I have previously been paid to give classes at large conferences on how to avoid exactly this sort of problem, I deserve whatever scorn and ridicule comes my way because of this.
Thanks to everyone who wrote in.
[Other articles in category /oops] permanent link
Wed, 11 Apr 2007
A security problem in a CGI program
<sarcasm>No! Who could possibly have predicted such a
thing?</sarcasm>
I was away in Asia, and when I got back I noticed some oddities in my mail logs. Specifically, Yahoo! was rejecting mail.plover.com's outgoing email. In the course of investigating the mail logs, I discovered the reason why: mail.plover.com had been relaying a ton of outgoing spam.
It took me a little while to track down the problem. It was a mailing list subscription form on perl.plover.com:
The form took the input email address and used it to manufacture an email message, requesting that that address be subscribed to the indicated lists:
my $MAILER = '/var/qmail/bin/qmail-inject';
...
for (@lists) {
next unless m|^perl-qotw[\-a-z]*|;
open M, "|$MAILER" or next;
print M "From: nobody\@plover.com\n";
print M "To: $_-subscribe-$addre\@plover.com\n";
print M "\nRequested by $ENV{REMOTE_ADDR} at ", scalar(localtime), "\n";
close M or next;
push @DONE, $_;
}
The message was delivered to the list management software, which
interpreted it as a request to subscribe, and generated an appropriate
confirmation reply. In theory, this doesn't open any new security
holes, because a malicious remote user could also forge an identical
message to the list management software without using the form.The problem is the interpolated $addre variable. The value of this variable is essentially the address from the form. Interpolating user input into a string like this is always fraught with peril. Daniel J. Bernstein has one of the most succinct explanantions of this that I have ever seen:
The essence of user interfaces is parsing: converting an unstructured sequence of commands, in a format usually determined more by psychology than by solid engineering, into structured data.In this case, I interpolated user data without quoting, and suffered the consequences.When another programmer wants to talk to a user interface, he has to quote: convert his structured data into an unstructured sequence of commands that the parser will, he hopes, convert back into the original structured data.
This situation is a recipe for disaster. The parser often has bugs: it fails to handle some inputs according to the documented interface. The quoter often has bugs: it produces outputs that do not have the right meaning. Only on rare joyous occasions does it happen that the parser and the quoter both misinterpret the interface in the same way.
When the original data is controlled by a malicious user, many of these bugs translate into security holes.
The malicious remote user supplied an address of the following form:
into9507@plover.com
Content-Transfer-Encoding: quoted-printable
Content-Type: text/plain
From: Alwin Bestor <Morgan@plover.com>
Subject: Enhance your love life with this medical marvel
bcc: hapless@example.com,recipients@example.com,of@example.net,
spam@example.com,...
Attention fellow males..
If you'd like to have stronger, harder and larger erections,
more power and intense orgasms, increased stamina and
ejaculatory control, and MUCH more,...
.
(Yes, my system was used to send out penis enlargement spam. Oh, the
embarrassment.) The address contained many lines of data, separated by CRNL, and a complete message header. Interpolated into the subscription message, the bcc: line caused the qmail-inject user ineterface program to add all the "bcc" addresses to the outbound recipient list.
Several thoughts occur to me about this.
User interfaces and programmatic interfaces
The problem would probably not have occurred had I used the qmail-queue progam, which provides a programmatic interface, rather than qmail-inject, which provides a user interface. I originally selected qmail-inject for convenience: it automatically generates Date and Message-ID fields, for example. The qmail-queue program does not try to parse the recipient information from the message header; it takes recipient information in an out-of-band channel.
Perl piped open is deficient
Perl's system and exec functions have two modes. One mode looks like this:
system "command arg arg arg...";
If the argument string contains shell metacharacters or certain other
constructions, Perl uses the shell to execute the command; otherwise
it forks and execs the command directly. The shell is the cause of
all sorts of parsing-quoting problems, and is best avoided in programs
like this one. But Perl provides an alternative:
system "command", "arg", "arg", "arg"...;
Here Perl never uses the shell; it always forks and execs the command
directly. Thus, system "cat *" prints the contents of all
the files in the current working directory, but system "cat",
"*" prints only the contents of the file named "*", if
there is one.qmail-inject has an option to take the envelope information from an out-of-band channel: you can supply it in the command-line arguments. I did not use this option in the original program, because I did not want to pass the user input through the Unix shell, which is what Perl's open FH, "| command args..." construction would have required.
Unfortunately, there is no easy way to avoid the shell when running a command that is attached to the parent process via a pipe. Perl provides open "| command arg arg arg...", which is what I used, and which is analogous to the first construction, involving the shell. But it provides nothing analogous to the second construction, which avoids the shell. If it did, then I probably would have used it, writing something like this:
open M, "|", $MAILER, "-fnobody\@plover.com", $addre;
and the whole problem would have been avoided.A better choice would have been to set up the pipe myself and use Perl's exec function to execute qmail-inject, which bypasses the shell. The qmail-inject program would always have received exactly one receipient address argument. In the event of an attack like the one above, it would have tried to send mail to into9507@plover.com^M^JContent-Transfer-Encoding:..., which would simply have bounced.
Why didn't I do this? Pure laziness.
qmail-queue more vulnerable than qmail-inject in this instance
Rather strangely, an partial attack is feasible with qmail-queue, even though it provides a (mostly) non-parsing interface. The addresses to qmail-queue are supplied to it on file descriptor 1 in the form:
Taddress1@example.com^@Taddress2@example.com^@Taddress3@example.com^@...^@
If my program were to talk to qmail-queue instead of to qmail-inject, the program would have
contained code that looked like this:
print QMAIL_QUEUE_ENVELOPE "T$addre\0";
qmail-queue parses only to the extent of dividing up its input at the ^@
characters. But even this little bit of parsing is a problem.
By supplying an appropriately-formed address string, a malicious user
could still have forced my program to send mail to many addresses. But still the recipient addresses would have been out of the content of the message. If the malicious user is unable to affect the content of the message body, the program is not useful for spamming.
But using qmail-queue, my program would have had to generate the To field itself, and so it would have had to insert the user-supplied address into the content of the message. This would have opened the whole can of worms again.
My program attacked specifically
I think some human put real time into attacking this particular program. There are bots that scour the web for email submission forms, and then try to send spam through them. Those bots don't successfully attack this program, because the recipient address is hard-wired. Also, the program refuses to send email unless at least one of the checkboxes is checked, and form-spam bots don't typically check boxes. Someone had to try some experiments to get the input format just so. I have logs of the experiments.A couple of days after the exploit was discovered, a botnet started using it to send spam; 42 different IP addresses sent requests. I fixed the problem last night around 22:30; there were about 320 more requests, and by 09:00 this morning the attempts to send spam stopped.
Perl's "taint" feature would not have prevented this
Perl offers a feature that is designed specifically for detecting and preventing exactly this sort of problem. It tracks which data are possibly under control of a malicious user, and whether they are used in unsafe operations. Unsafe operations include most file and process operations.One of my first thoughts was that I should have enabled the tainting feature to begin with. However, it would not have helped in this case. Although the user-supplied address would have been flagged as "tainted" and so untrustworthy; by extension, the email message string into which it was interpolated would have been tainted. But Perl does not consider writing a tainted string to a pipe to be an "unsafe" operation and so would not have signalled a failure.
The fix
The short-range fix to the problem was simple:
my $addr = param('addr');
$addr =~ s/^\s+//;
$addr =~ s/\s+$//;
...
if ($addr =~ /\s/) {
sleep 45 + rand(45);
print p("Sorry, addresses are not allowed to contain spaces");
fin();
}
Addresses are not allowed to contain whitespace, except leading or
trailing whitespace, which is ignored. Since whitespace inside an
address is unlikely to be an innocent mistake, the program waits
before responding, to slow down the attacker.
Summary
Dammit.[ Addendum 20070412: There is a followup article to this one. ]
[Other articles in category /oops] permanent link
Thu, 05 Apr 2007[ Note: because this article is in the oops section of my blog, I intend that you understand it as a description of a mistake that I have made. ]
Abhijit Menon-Sen wrote to me to ask for advice in finding the smallest triangular number that has at least 500 divisors. (That is, he wants the smallest n such that both n = (k2 + k)/2 for some integer k and also ν(n) ≥ 500, where ν(n) is the number of integers that divide n.) He said in his note that he believed that brute-force search would take too long, and asked how I might trim down the search.
The first thing that occurred to me was that ν is a multiplicative function, which means that ν(ab) = ν(a)ν(b) whenever a and b are relatively prime. Since n and n-1 are relatively prime, we have that ν(n(n-1)) = ν(n)·ν(n-1), and so if T is triangular, it should be easy to calculate ν(T). In particular, either n is even, and ν(T) = ν(n/2)·ν(n-1), or n is odd, and ν(T) = ν(n)·ν((n-1)/2).
So I wrote a program to run through all possible values of n, calculating a table of ν(n), and then the corresponding ν(n(n-1)/2), and then stopping when it found one with sufficiently large ν.
my $N = 1;
my $max = 0;
while (1) {
my $n = $N % 2 ? divisors($N) : divisors($N/2);
my $np1 = $N % 2 ? divisors(($N+1)/2) : divisors($N+1);
if ($n * $np1 > $max) {
$max = $n * $np1;
print "N=$N; T=", $N*($N+1)/2, "; nd()=$max\n";
}
last if $max >= 500;
$N++;
}
There may be some clever way to quickly calculate ν(n) in
general, but I don't know it. But if you have the prime factorization
of n, it's easy: if n =
p1a1p2a2...
then ν(n) = (a1 + 1)(a2
+ 1)... . This is a consequence of the multiplicativity of ν and
the fact that ν(pn) is clearly
n+1. Since I expected that n wouldn't get too big, I
opted to factor n and to calculate ν from the prime
factorization:
my @nd;
sub divisors {
my $n = shift;
return $nd[$n] if $nd[$n];
my @f = factor($n);
my $ND = 1;
my $cur = 0;
my $curct = 0;
while (@f) {
my $next = shift @f;
if ($next != $cur) {
$cur = $next;
$ND *= $curct+1;
$curct = 1;
} else {
$curct++;
}
}
$ND *= $curct+1;
return $ND;
}
Unix comes with a factor program that factors numbers pretty
quickly, so I used that:
sub factor {
my $r = qx{factor $_[0]};
my @f = split /\s+/, $r;
shift @f;
return @f;
}
This found the answer, 76,576,500, in about a minute and a half.
(76,576,500 = 1 + 2 + ... + 12,375, and has 576 factors.) I sent this
off to Abhijit.I was rather pleased with myself, so I went onto IRC to boast about my cleverness. I posed the problem, and rather than torment everyone there with a detailed description of the mathematics, I just said that I had come up with some advice about how to approach the problem that turned out to be good advice.
A few minutes later one of the gentlemen on IRC, who goes by "jeek", (real name T.J. Eckman) asked me if 76,576,500 was the right answer. I said that I thought it was and asked how he'd found it. I was really interested, because I was sure that jeek had no idea that ν was multiplicative or any of that other stuff. Indeed, his answer was that he used the simplest possible brute force search. Here's jeek's program:
$x=1; $y=0;
while(1) {
$y += $x++; $r=0;
for ($z=1; $z<=($y ** .5); $z++) {
if (($y/$z) == int($y/$z)) {
$r++;
if (($y/$z) != ($z)) { $r++; }
}
}
if ($r>499) {print "$y\n";die}
}
(I added whitespace, but changed nothing else.)In this program, the variable $y holds the current triangular number. To calculate ν(y), this program just counts $z from 1 up to √y, incrementing a counter every time it discovers that z is a divisor of y. If the counter exceeds 499, the program prints y and stops. This takes about four and a half minutes.
It takes three times as long, but uses only one-third the code. Beginners may not see this as a win, but it is a huge win. It is a lot easier to reduce run time than it is to reduce code size. A program one-third the size of another is almost always better—a lot better.
In this case, we can trim up some obvious inefficiencies and make the program even smaller. For example, the tests here can be omitted:
if (($y/$z) != ($z)) { $r++; }
It can yield false only if
y is the square of z. But y is triangular, and
triangular numbers are never square. And we can optimize away the
repeated square root in the loop test, and use a cheaper and simpler
$y % $z == 0 divisibility test in place of the complicated one.
while(1) {
$y += $x++; $r=0;
for $z (1 .. sqrt($y)) {
$y % $z == 0 and $r+=2;
}
if ($r>499) {print "$x $y\n";die}
}
The program is now one-fifth the size of mine and runs in 75
seconds. That is, it is now smaller and faster than mine.This shows that jeek's approach was the right one and mine was wrong, wrong, wrong. Simple programs are a lot easier to speed up than complicated ones. And I haven't even consider the cost of the time I wasted writing my complicated program when I could have written Jeek's six-liner that does the same thing.
So! I had to write back to my friend to tell him that my good advice was actually bad advice.
The sawed-off shotgun wins again!
[ Addendum 20070405: Robert Munro pointed out an error in the final version of the program, which I have since corrected. ]
[ Addendum 20070405: I said that triangular numbers are never square, which is manifestly false, since 1 is both, as is 36. I should have remembered this, since some time in the past three years I investigated this exact question and found the answer. But it hardly affects the program. The only way it could cause a failure is if there were a perfect square triangular number with exactly 499 factors; such a number would be erroneously reported as having 500 factors instead. But the program reports a number with 576 factors instead. Conceivably this could actually be a misreported perfect square with only 575 factors, but regardless, the reported number is correct. ]
[ Addendum 20060617: I have written an article about triangular numbers that are also square. ]
[Other articles in category /oops] permanent link
Thu, 22 Mar 2007
Symmetric functions
I used to teach math at the John Hopkins CTY program, which is a
well-regarded summer math camp. Kids would show up and finish a year
(or more) of high-school math in three weeks. We'd certify them by
giving them standardized tests, which might carry some weight with
their school. But before they were allowed to take the standardized
test, they had to pass a much more difficult and comprehensive exam
that we'd made up ourselves.
The most difficult question on the Algebra III exam presented the examinee with some intractable third degree polynomial—say x3 + 4x2 - 2x + 6—and asked for the sum of the cubes of its roots.
You might like to match your wits against the Algebra III students before reading the solution below.
In the three summers I taught, only about two students were able to solve this problem, which is rather tricky. Usually they would start by trying to find the roots. This is doomed, because the Algebra III course only covers how to find the roots when they are rational, and the roots here are totally bizarre.
Even clever students didn't solve the problem, which required several inspired tactics. First you must decide to let the roots be p, q, and r, and, using Descartes' theorem, say that
x3 + bx2 + cx + d = (x - p)(x - q)(x - r)
This isn't a hard thing to do, and a lot of the kids probably did try it, but it's not immediately clear what the point is, or that it will get you anywhere useful, so I think a lot of them never took it any farther.But expanding the right-hand side of the equation above yields:
x3 + bx2 + cx + d = x3 - (p + q + r)x2 + (pq + pr + qr)x - pqr
And so, equating coefficients, you have:| b | = | -(p + q + r) |
| c | = | pq + pr + qr |
| d | = | -pqr |
| -b3 | = | p3 + q3 + r3 + 3p2q + 3p2r + 3q2r + 3pq2 + 3pr2 + 3qr2 + 6pqr |
| p3 + q3 + r3 | = | -b3 + 3bc - 3d |
Or, to take an example that we can actually check, consider x3 - 6x2 + 11x - 6, whose roots are 1, 2, and 3. The sum of the cubes is 1 + 8 + 27 = 36, and indeed -b3 + 3bc - 3d = 63 + 3·(-6)·11 + 18 = 216 - 198 + 18 = 36.
This was a lot of algebra III, but once you have seen this example, it's not hard to solve a lot of similar problems. For instance, what is the sum of the squares of the roots of x2 + bx + c? Well, proceeding as before, we let the roots be p and q, so x2 + bx + c = (x - p)(x - q) = x2 - (p + q)x + pq, so that b = -(p + q) and c = pq. Then b2 = p2 + 2pq+ q2, and b2 - 2c = p2 + q2.
In general, if F is any symmetric function of the roots of a polynomial, then F can be calculated from the coefficients of the polynomial without too much difficulty.
Anyway, I was tinkering around with this at breakfast a couple of days ago, and I got to thinking about b2 - 2c = p2 + q2. If roots p and q are both integers, then b2 - 2c is the sum of two squares. (The sum-of-two-squares theorem is one of my favorites.) And the roots are integers only when the discriminant of the original polynomial is itself a square. But the discriminant in this case is b2 - 4c. So we have the somewhat odd-seeming statement that when b2 - 4c is a square, then b2 - 2c is a sum of two squares.
I found this surprising because it seemed so underconstrained: it says that you can add some random even number to a fairly large class of squares and the result must be a sum of two squares, even if the even number you added wasn't a square itself. But after I tried a few examples to convince myself I hadn't made a mistake, I was sure there had to be a very simple, direct way to get to the same place.
It took some fiddling, but eventually I did find it. Say that b2 - 4c = a2. Then b and a must have the same parity, so p = (b + a)/2 is an integer, and we can write b = p + q and a = p - q where p and q are both integers.
Then c = (b2 - a2)/4 is just pq, and b2 - 2c = p2 + q2.
So that's where that comes from.
It seems like there ought to be an interesting relationship between the symmetric functions of roots of a polynomial and their expression in terms of the coefficients of the polynomial. The symmetric functions of degree N are all linear combinations of a finite set of symmetric functions. For example, any second-degree symmetric function of two variables has the form a(p2 + q2) + 2bpq. We can denote these basic symmetric functions of two variables as Fi,j(p, q) = Σpiqj. Then we have identities like (F1,0)2 = F2,0 + F1,1 and (F1,0)3 = F3,0 + 3F2,1.
Maybe I'll do an article about this in a week or two.
[Other articles in category /math] permanent link
Tue, 20 Mar 2007
How big is a five-gallon jug?
Office water coolers in the United States commonly take five-gallon
jugs of water. You are probably familiar with these jugs, but here is
a picture of a jug, to refresh your memory. A random graduate student
has been provided for scale:
Here's today's riddle: Can you estimate the volume of the jug in cubic feet? "Estimate" means by eyeballing it, not by calculating, measuring, consulting reference works, etc. But feel free to look at an actual jug if you have one handy.
Once you've settled on your estimate, compare it with the correct answer, below.
Answer:
| It is about 2/3 of a cubic foot. One gallon contains about 231 cubic inches. Five gallons contain about 1155 cubic inches. One cubic foot contains 12×12×12 = 1728 cubic inches. |
Hard to believe, isn't it? ("Strange but true.") I took one of these jugs around my office last year, asking everyone to guess how big it was; nobody came close. People typically guessed that it was about three times as big as it actually is.
This puzzle totally does not work anywhere except in the United States. The corresponding puzzle for the rest of the world is "Here is a twenty-liter jug. Can you guess the volume of the jug in liters?" I suppose this is an argument in favor of the metric system.
[Other articles in category /tech] permanent link
Mon, 19 Mar 2007
Your age as a fraction
Little kids often report their ages as "two and a half" or sometimes
even "three and three quarters". These evaluations are usually based
on whole months: if you were born on April 2, 1969, then on October
2, 1971 you start reporting your age as "two and a half", and, if you
choose to report your age as "three and three quarters", you
conventionally may begin on January 2, 1973.
However, these reports are not quite accurate. On January 2, 1973, exactly 3 years and 9 months from your birthday, you would be 1,371 days old, or 3 years plus 275 days. 275/365 = 0.7534. On January 1, you were only 3 + 274/365 days old, which is 3.7507 years, and so January 1 is the day on which you should have been allowed to start reporting your age as "three and three quarters". This slippage between days and months occurs in the other direction as well, so there may be kids wandering around declaring themselves as "three and a half" a full day before they actually reach that age.
Clearly this is one of the major problems facing our society, so I wanted to make up a table showing, for each number of days d from 1 to 365, what is the simplest fraction a/b such that when it is d days after your birthday, you are (some whole number and) a/b years. That is, I wanted a/b such that d/365 ≤ a/b < (d+1)/365.
Then, by consulting the table each day, anyone could find out what new fraction they might have qualified for, and, if they preferred the new fraction to the old, they might start reporting their age with that fraction.
There is a well-developed branch of mathematics that deals with this problem. To find simple fractions that approximate any given rational number, or lie in any range, we first expand the bounds of the range in continued fraction form. For example, suppose it has been 208 days since your birthday. Then today your age will range from y plus 208/365 years up to y plus 209/365 years.
Then we expand 208/365 and 209/365 as continued fractions:
208/365 = [0; 1, 1, 3, 12, 1, 3]Where [0; 1, 1, 3, 12, 1, 3] is an abbreviation for the typographically horrendous expression:
209/365 = [0; 1, 1, 2, 1, 16, 1, 2]
$$ 0 + {1\over \displaystyle 1 + {\strut 1\over\displaystyle 1 + {\strut 1\over\displaystyle 3 + {\strut 1\over\displaystyle 12 + {\strut 1\over\displaystyle 1 + {\strut 1\over\displaystyle 3 }}}}}}$$
And similarly the other one. (Oh, the suffering!)Then you need to find a continued fraction that lies numerically in between these two but is as short as possible. (Shortness of continued fractions corresponds directly to simplicity of the rational numbers they represent.) To do this, take the common initial segment, which is [0; 1, 1], and then apply an appropriate rule for the next place, which depends on whether the numbers in the next place differ by 1 or by more than 1, whether the first difference occurs in an even position or an odd one, mumble mumble mumble; in this case the rules say we should append 3. The result is [0; 1, 1, 3], or, in conventional notation:
$$ 0 + {1\over \displaystyle 1 + {\strut 1\over\displaystyle 1 + {\strut 1\over\displaystyle 3 }}} $$
which is equal to 4/7. And indeed, 4/7 of a year is 208.57 days, so sometime on the 208th day of the year, you can start reporting your age as (y and) 4/7 years.Since I already had a library for calculating with continued fractions, I started extending it with functions to handle this problem, to apply all the fussy little rules for truncating the continued fraction in the right place, and so on.
Then I came to my senses, and realized there was a better way, at least for the cases I wanted to calculate. Given d, we want to find the simplest fraction a/b such that d/365 ≤ a/b < (d+1)/365. Equivalently, we want the smallest integer b such that there is some integer a with db/365 ≤ a < (d+1)b/365. But b must be in the range (2 .. 365), so we can easily calculate this just by trying every possible value of b, from 2 on up:
use POSIX 'ceil', 'floor';
sub approx_frac {
my ($n, $d) = @_;
for my $b (1 .. $d) {
my ($lb, $ub) = ($n*$b/$d, ($n+1)*$b/$d);
if (ceil($lb) < ceil($ub) && ceil($ub) > $ub) {
return (int($ub), $b);
}
}
return ($n, $d);
}
The fussing with ceil() in the main test is to make the
ranges open on the upper end: 2/5 is not in the range
[3/10, 4/10), but it is in the range
[4/10, 5/10). Then we can embed this in a simple report-printing
program:
my $N = shift || 365;
for my $i (1..($N-1)) {
my ($a, $b) = approx_frac($i, $N);
print "$i/$N: $a/$b\n";
}
For tenths, the simplest fractions are:
| 1/10 ≤ | 1/6 | < 2/10 | (0.1667) |
| 2/10 ≤ | 1/4 | < 3/10 | (0.2500) |
| 3/10 ≤ | 1/3 | < 4/10 | (0.3333) |
| 4/10 ≤ | 2/5 | < 5/10 | (0.4000) |
| 5/10 ≤ | 1/2 | < 6/10 | (0.5000) |
| 6/10 ≤ | 2/3 | < 7/10 | (0.6667) |
| 7/10 ≤ | 3/4 | < 8/10 | (0.7500) |
| 8/10 ≤ | 4/5 | < 9/10 | (0.8000) |
| 9/10 ≤ | 9/10 | < 10/10 | (0.9000) |
This works fine, and it is a heck of a lot simpler than all the continued fraction stuff. The more so because the continued fraction library is written in C.
For the application at hand, an alternative algorithm is to go through all fractions, starting with the simplest, placing each one into the appropriate d/365 slot, unless that slot is already filled by a simpler fraction:
my $N = shift || 365;
my $unfilled = $N;
DEN:
for my $d (2 .. $N) {
for my $n (1 .. $d-1) {
my $a = int($n * $N / $d);
unless (defined $simple[$a]) {
$simple[$a] = [$n, $d];
last DEN if --$unfilled == 0;
}
}
}
for (1 .. $N-1) {
print "$_/$N: $simple[$_][0]/$simple[$_][1]\n";
}
A while back I wrote an article about using the sawed-off
shotgun approach instead of the subtle technique approach. This
is another case where the simple algorithm wins big. It is an
n2 algorithm, whereas I think the continued fraction
one is n log n in the worst case. But unless you're
preparing enormous tables, it really doesn't matter much. And the
proportionality constant on the O() is surely a lot smaller for
the simple algorithms.(It might also be that you could optimize the algorithms to go faster: you can skip the body of the loop in the slot-filling algorithm whenever $n and $d have a common factor, which means you are executing the body only n log n times. But testing for common factors takes time too...)
I was going to paste in a bunch of tabulations, but once again I remembered that it makes more sense to just let you run the program for yourself. Here is a form that will generate the table for all the fractions 1/N .. (N-1)/N; use N=365 to generate a table of year fractions for common years, and N=366 to generate the table for leap years:
[ Addendum 20070429: There is a followup to this article. ]
[Other articles in category /math] permanent link
Wed, 14 Mar 2007 The subject of really narrow buildings came up on Reddit last week, and my post about the "Spite House" was well-received. Since pictures of it seem to be hard to come by, I scanned the pictures from New York's Architectural Holdouts by Andrew Alpern and Seymour Durst.The book is worth checking out, particularly if you are familiar with New York. The canonical architectural holdout occurs when a developer is trying to assemble a large parcel of land for a big building, and a little old lady refuses to sell her home. The book is full of astonishing pictures: skyscrapers built with holdout buildings embedded inside them and with holdout buildings wedged underneath them. Skyscrapers built in the shape of the letter E (with the holdouts between the prongs), the letter C (with the holdout in the cup), and the letter Y (with the holdout in the fork).
 |
| Photo credit: Jerry Callen |
 But
anyway, the Spite House. The story, as told by Alpern and Durst, is
that around 1882, Patrick McQuade wanted to build some houses on 82nd
Street at Lexington Avenue. The adjoining parcel of land, around the
corner on Lexington, was owned by Joseph Richardson, shown at left.
If McQuade could acquire this parcel, he would be able to extend his
building all the way to Lexington Avenue, and put windows on that side
of the building. No problem: the parcel was a strip of land 102 feet
long and five feet wide along Lexington, useless for any other
purpose. Surely Richardson would sell.
But
anyway, the Spite House. The story, as told by Alpern and Durst, is
that around 1882, Patrick McQuade wanted to build some houses on 82nd
Street at Lexington Avenue. The adjoining parcel of land, around the
corner on Lexington, was owned by Joseph Richardson, shown at left.
If McQuade could acquire this parcel, he would be able to extend his
building all the way to Lexington Avenue, and put windows on that side
of the building. No problem: the parcel was a strip of land 102 feet
long and five feet wide along Lexington, useless for any other
purpose. Surely Richardson would sell.
McQuade offered $1,000, but Richardson demanded $5,000. Unwilling to pay, McQuade started building his houses anyway, complete with windows looking out on Richardson's five-foot-wide strip, which was unbuildable. Or so he thought.
Richardson built a building five
feet wide and 102 feet long, blocking McQuade's Lexington Avenue
windows. (Click the pictures for large versions.)
The building soon became known as the "Spite House". The photograph above was taken around 1895. Lexington Avenue is torn up for maintenance in this picture.
Richardson took advantage of a clause in the building codes that allowed him to build bay window extensions in his building. This allowed him to extend its maximum width 2'3" beyond the boundary of the lot. (Alpern and Durst say "In those days, such encroachments on the public sidewalks were not prohibited.") The rooms of the Spite House were in these bay window extensions, connected by extremely narrow hallways:
 After construction was completed, Richardson moved into the Spite
House and lived there until he died in 1897. The pictures below and
at left are from that time.
After construction was completed, Richardson moved into the Spite
House and lived there until he died in 1897. The pictures below and
at left are from that time.
The edge-on photograph below, showing the Spite House's 3'4" frontage on 82nd Street, was taken in 1912.
The Spite House was demolished in 1915.
Picture credits
The photograph of the Macy's Herald Square store is copyright ©2004 Jerry Callen, and is used with permission.All other pictures and photographs are in the public domain. I took them from pages 122–124 of the book New York's Architectural Holdouts, by Alpern and Durst. The original sources, as given by Alpern and Durst, are as follows:

| Collection of Andrew Alpern. |
 
| January 1897 issue of Scientific American.
|
  
| New York Journal, 5 June 1897 |

| New York Public Service Commission |
[Other articles in category /tech] permanent link
Fri, 09 Mar 2007
Bernoulli processes
A family has four children. Assume that the sexes of the four
children are independent, and that boys and girls are equiprobable.
What's the most likely distribution of boys and girls?
Well,it depends how you count. Are there three possibilities or five?
|
|
| Boys | Girls | Probability |
|---|---|---|
| 0 | 4 | 0.0625 |
| 1 | 3 | 0.25 |
| 2 | 2 | 0.375 |
| 3 | 1 | 0.25 |
| 4 | 0 | 0.0625 |
This distribution is depicted in the graph at right. Individually, (3, 1) and (1, 3) are less likely than (2, 2). But "three-and-one" includes both (1, 3) and (3, 1), whereas "two-and-two" includes only (2, 2). So if you group outcomes into three categories, as in the green division above left, "three-and-one" comes out more frequent overall than "two-and-two":
| One sex | The other | Total probability |
|---|---|---|
| 4 | 0 | 0.125 |
| 3 | 1 | 0.5 |
| 2 | 2 | 0.375 |
It makes a difference whether you specify the sexes in the
distribution. If a "distribution" is a thing like "b of the
children are boys and g are girls", then the most frequent
distribution is (2, 2). But if a distribution is "x of one sex
and y of the other", then the most frequent distribution [3, 1],
where I've used square brackets to show that the order is not
important. [3, 1] is the same as [1, 3].
This is true in general. Suppose someone has 1,000 kids. What's the most likely distribution of sexes? It's 500 boys and 500 girls, which I've been writing (500, 500). This is more likely than either (499, 501) or (501, 499). But if you consider "Equal numbers" versus "501-to-499", which I've been writing as [500, 500] and [501, 499], then [501, 499] wins:
| Boys | Girls | Probability |
|---|---|---|
| 501 | 499 | 0.02517 |
| 500 | 500 | 0.02522 |
| 499 | 501 | 0.02517 |
| One sex | The other | Total probability |
|---|---|---|
| 501 | 499 | 0.05035 |
| 500 | 500 | 0.02522 |
|
Why is this? [4, 3, 3, 3] covers the four most frequent distributions: (4, 3, 3, 3), (3, 4, 3, 3), (3, 3, 4, 3), and (3, 3, 3, 4). But [4, 4, 3, 2] covers twelve quite frequent distributions: (4, 4, 3, 2), (4, 3, 2, 4), and so on. Even though the individual distributions aren't as common as (4, 4, 4, 3), there are twelve of them instead of 4. This gives [4, 4, 3, 2] the edge.
[5, 4, 3, 1] includes 24 distributions, and ends up tied for second place. A complete table is in the sidebar at left.
(For 5-card poker hands, the situation is much simpler. [2, 2, 1, 0] is most common, followed by [2, 1, 1, 1] and [3, 1, 1, 0] (tied), then [3, 2, 0, 0], [4, 1, 0, 0], and [5, 0, 0, 0].)
This same issue arose in my
recent article on Yahtzee roll probabilities. There we had six
"suits", which represented the six possible rolls of a die, and I
asked how frequent each distribution of "suits" was when five dice
were rolled. For distribution [p1,
p2, ...], we let ni be the
number of p's that are equal to i. Then the expression
for probability of the distribution has a factor of 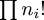 in the denominator, with the result that
distributions with a lot of equal-sized parts tend to appear less
frequently than you might otherwise expect.
in the denominator, with the result that
distributions with a lot of equal-sized parts tend to appear less
frequently than you might otherwise expect.
I'm not sure how I got so deep into this end of the subject, since I didn't really want to compare complex distributions to each other so much as to compare simple distributions under different conditions. I had originally planned to discuss the World Series, which is a best-four-of-seven series of baseball games that we play here in the U.S. and sometimes in that other country to the north. Sometimes one team wins four games in a row ("sweeps"); other times the Series runs the full seven games.
You might expect that even splits would tend to occur when the two teams playing were evenly matched, but that when one team was much better than the other, the outcome would be more likely to be a sweep. Indeed, this is generally so. The chart below graphs the possible outcomes. The x-axis represents the probability of the Philadelphia Phillies winning any individual game. The y-axis is the probability that the Phillies win the entire series (red line), which in turn is the sum of four possible events: the Phillies win in 4 games (green), in 5 games (dark blue), in 6 games (light blue), or in 7 games (magenta). The probabilities of the Nameless Opponents winning are not shown, because they are exactly the opposite. (That is, you just flip the whole chart horizontally.)
Clearly, the Phillies have a greater-than-even chance of winning the Series if and only if they have a greater-than-even chance of winning each game. If they are playing a better team, they are likely to lose, but if they do win they are most likely to do so in 6 or 7 games. A sweep is the most likely outcome only if the Opponents are seriously overmatched, and have a less than 25% chance of winning each game. (The lines for the 4-a outcome and the 4-b outcome cross at 1-(pa / pb)1/(b-a), where pi is 1, 4, 10, 20 for i = 0, 1, 2, 3.)
If we consider just the first four games of the World Series, there are five possible outcomes, ranging from a Phillies sweep, through a two-and-two split, to an Opponents sweep. Let p be the probability of the Phillies winning any single game. As p increases, so does the likelihood of a Phillies sweep. The chart below plots the likelihood of each of the five possible outcomes, for various values of p, charted here on the horizontal axis:
When is the 2-2 split the most likely outcome? Only when the Phillies and the Opponents are approximately evenly matched, with neither team no more than 60% likely to win any game.
But just as with the sexes of the four kids, we get a different result if we consider the outcomes that don't distinguish the teams. For the first four games of the World Series, there are only three outcomes: a sweep (which we've been writing [4, 0]), a [3, 1] split, and a [2, 2] split:
Here are the corresponding charts for series of various lengths.
| Series length (games) | Distinguish teams | Don't distinguish teams |
|---|---|---|
| 2 | 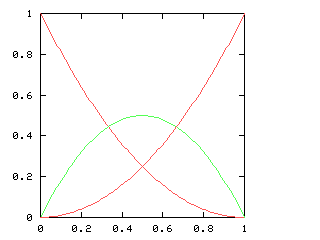
| 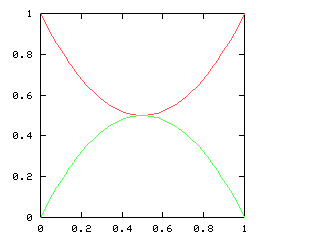
|
| 3 | 
| 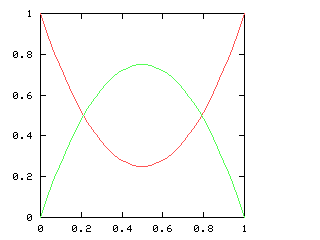
|
| 4 | 
| 
|
| 5 | 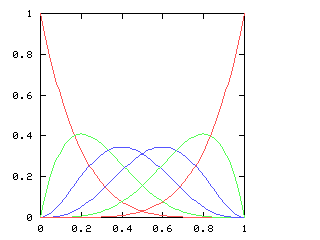
| 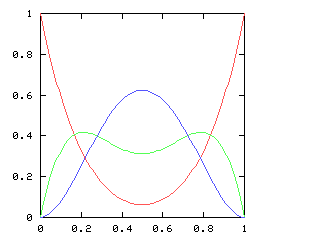
|
| 6 | 
| 
|
| 7 | 
| 
|
| 8 | 
| 
|
| 9 | 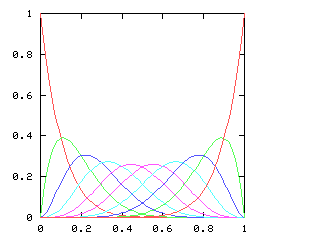
| 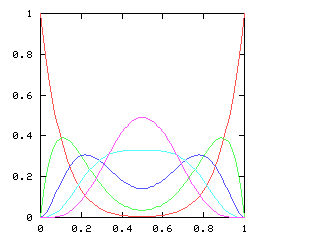
|
| 10 | 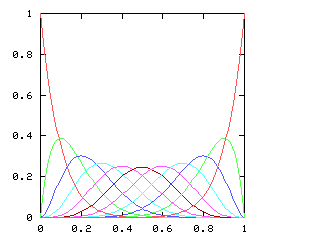
| 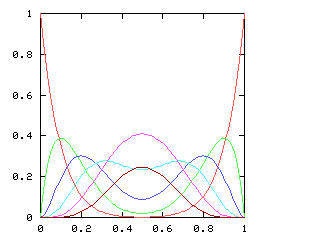
|
I have no particular conclusion to announce about this; I just thought that the charts looked cool.
Coming later, maybe: reasoning backwards: if the Phillies sweep the World Series, what can we conclude about the likelihood that they are a much better team than the Opponents? (My suspicion is that you can conclude a lot more by looking at the runs scored and runs allowed totals.)
(Incidentally, baseball players get a share of the ticket money for World Series games, but only for the first four games. Otherwise, they could have an an incentive to prolong the series by playing less well than they could, which is counter to the ideals of sport. I find this sort of rule, which is designed to prevent conflicts of interest, deeply satisfying.)
[Other articles in category /math] permanent link
Mon, 05 Mar 2007
An integer partition puzzle
Last month I wrote an article
about calculating Yahtzee probabilities and another one about counting
permutations in which integer partitions came up. An integer
partition of some integer N is an unordered sequence of
positive integers that sums to N. For example, there are 5
different integer partitions of 4:
| 1 1 1 1 |
| 2 1 1 |
| 2 2 |
| 3 1 |
| 4 |
Here's one interesting fact: it's quite easy to calculate the number of partitions of N. Let P(n, k) be the number of partitions of n into parts that are at least k. Then it's easy to see that:
$$P(n, k) = \sum_{i=k}^{n-1} P(n-i, k)$$
And there are simple boundary conditions: P(n, n) = 1; P(n, k) = 0 when k > n, and so forth. And P(n), the number of partitions of n into parts of any size, is just P(n, 1). So a program to calculate P(n) is very simple:
my @P;
sub P {
my ($n, $k) = @_;
return 0 if $n < 0;
return 1 if $n == 0;
return 0 if $k > $n;
my $r = $P[$n] ||= [];
return $r->[$k] if defined $r->[$k];
return $r->[$k] = P($n-$k, $k) + P($n, $k+1);
}
sub part {
P($_[0], 1);
}
for (1..100) {
printf "%3d %10d\n", $_, part($_);
}
I had a funny conversation once with someone who ought to have known
better: I remarked that it was easy to calculate P(n),
and disagreed with me, asking why Rademacher's
closed-form expression for P(n) had been such a
breakthrough. But the two properties are independent; the same is
true for lots of stuff. Just because you can calculate something
doesn't mean you understand it. Calculating ζ(2) is quick and
easy, but it was a major breakthrough when Euler discovered that it
was equal to π2/6. Calculating ζ(3) is even
quicker and easier, but nobody has any idea what the value
represents.Similarly, P(n) is easy to calculate, but harder to understand. Ramanujan observed, and proved, that P(5k+4) is always a multiple of 5, which had somehow escaped everyone's notice until then. And there are a couple of other similar identities which were proved later: P(7k+5) is always a multiple of 7; P(11k+6) is always a multiple of 11. Based on that information, any idiot could conjecture that P(13k+7) would always be a multiple of 13; this conjecture is wrong. (P(7) = 15.)
Anyway, all that is just leading up to the real point of this note, which is that I was tabulating the number of partitions of n into exactly k parts, which is also quite easy. Let's call this Q(n, k). And I discovered that Q(13, 4) = Q(13, 5). There are 18 ways to divide a pile of 13 beans into 4 piles, and also 18 ways to divide the beans into 5 piles.
|
|
So far, I haven't turned anything up; it seems to be a coincidence. A simpler problem of the same type is that Q(8, 3) = Q(8, 4); that seems to be a coincidence too:
|
|
Oh well, sometimes these things don't work out the way you'd like.
[Other articles in category /math] permanent link
"Go ahead, throw your vote away!"
I noticed this back in November right afer the election, when I was
reading the election returns in the newspaper. There were four
candidates for the office of U.S. Senator in Nevada. One of these was
Brendan Trainor, running for the Libertarian party.
Trainor received a total of 5,269 votes, or 0.90% of votes cast.
A fifth choice, "None of these candidates", was available. This choice received 8,232 votes, or 1.41%.
Another candidate, David Schumann, representing the Independent American Party, was also defeated by "None of these candidates".
I'm not sure what conclusion to draw from this. I am normally sympathetic to the attempts of independent candidates and small parties to run for office, and I frequently vote for them. But when your candidate fails to beat out "None of the above", all I can think is that you must be doing something terribly wrong.
[ Addendum 20200723: [Wikipedia's article on Nevada's “None of These Candidates” option](WPREF/None_of_These_Candidates). ]
[Other articles in category /politics] permanent link
Wed, 21 Feb 2007
A bug in HTML generation
A few days ago I hacked on the TeX plugin I wrote for Blosxom so that
it would put the TeX source code into the ALT attributes of the image
elements it generated.
But then I started to see requests in the HTTP error log for URLs like this:
/pictures/blog/tex/total-die-rolls.gif$${6/choose%20k}k!{N!/over%20/prod%20{i!}^{n_i}{n_i}!}/qquad%20/hbox{/rm%20where%20$k%20=%20/sum%20n_i$}$$.gif
Someone must be referring people to these incorrect URLs, and it is
presumably me. The HTML version of the blog looked okay, so I checked
the RSS and Atom files, and found that, indeed, they were malformed.
Instead of <img src="foo.gif" alt="$TeX$">, they
contained codes for <img src="foo.gif$TeX$">.I tracked down and fixed the problem. Usually when I get a bug like this, I ask myself what I could learn from it. This one is unusual. I can't think of much. Here's the bug.
The <img> element is generated by a function called imglink. The arguments to imglink are the filename that contains the image (for use in the SRC attribute) and the text for the ALT attribute. The ALT text is optional. If it is omitted, the function tries to locate the TeX source code and fetch it. If this attempt fails, it continues anyway, and omits the ALT attribute. Then it generates and returns the HTML:
sub imglink {
my $file = shift;
...
my $alt = shift || fetch_tex($file);
...
$alt = qq{alt="$alt"} if $alt;
qq{<img $alt border=0 src="$url">};
}
This function is called from several places in the plugin. Sometimes
the TeX source code is available at the place from which the call
comes, and the code has return imglink($file, $tex);
sometimes it isn't and the code has
return imglink($file) and hopes that the imglink
function can retrieve the TeX.One such place is the branch that handles generation of tags for every type of output except HTML. When generating the HTML output, the plugin actually tries to run TeX and generate the resulting image file. For other types of output, it assumes that the image file is already prepared, and just calls imglink to refer to an image that it presumes already exists:
return imglink($file, $tex) unless $blosxom::flavour eq "html";The bug was that I had written this instead:
return imglink($file. $tex) unless $blosxom::flavour eq "html";The . here is a string concatenation operator.
It's a bit surprising that I don't make more errors like this than I do. I am a very inaccurate typist.
Stronger type checking would not have saved me here. Both arguments are strings, concatenation of strings is perfectly well-defined, and the imglink function was designed and implemented to accept either one or two arguments.
The function did note the omission of the $tex argument, attempted to locate the TeX source code for the bizarrely-named file, and failed, but I had opted to have it recover and continue silently. I still think that was the right design. But I need to think about that some more.
The only lesson I have been able to extract from this so far is that I need a way of previewing the RSS and Atom outputs before publishing them. I do preview the HTML output, but in this case it was perfectly correct.
[Other articles in category /prog/bug] permanent link
Tue, 20 Feb 2007
A polynomial trivium
A couple of months ago I calculated the following polynomial—I
forget why—and wrote
it on my whiteboard. I want to erase the whiteboard, so I'm recording
the polynomial here instead.
$${9\over 8}x^4 - {45\over 4}x^3 + 39{3\over8}x^2 - 54{1\over4}x + 27$$
The property this polynomial was designed to have is this: at x = 1, 2, 3, 4, it takes the values 2, 4, 6, 8. But at x=5 it gives not 10 but 37.
[Other articles in category /math] permanent link
Addenda to Apostol's proof that sqrt(2) is irrational
Yesterday I posted Tom
Apostol's wonderful proof that √2 is irrational. Here are some
additional notes about it.
- Gareth McCaughan observed that:
It's equivalent to the following simple algebraic proof: if a/b is the "simplest" integer ratio equal to √2 then consider (2b-a)/(a-b), which a little manipulation shows is also equal to √2 but has smaller numerator and denominator, contradiction.
- According to Cut-the-knot, the proof was anticipated in 1892 by A. P. Kiselev and appeared on page 121 of his book Geometry.
[Other articles in category /math] permanent link
Mon, 19 Feb 2007
A new proof that the square root of 2 is irrational
Last week I ran into this totally brilliant proof that √2 is
irrational. The proof was discovered by Tom M. Apostol, and was
published as
"Irrationality of the Square Root of Two - A Geometric Proof"
in the American Mathematical Monthly, November
2000, pp. 841–842.
In short, if √2 were rational, we could construct an isosceles right triangle with integer sides. Given one such triangle, it is possible to construct another that is smaller. Repeating the construction, we could construct arbitrarily small integer triangles. But this is impossible since there is a lower limit on how small a triangle can be and still have integer sides. Therefore no such triangle could exist in the first place, and √2 is irrational.
In hideous detail: Suppose that √2 is rational. Then by scaling up the isosceles right triangle with sides 1, 1, and √2 appropriately, we obtain the smallest possible isosceles right triangle whose sides are all integers. (If √2 = a/b, where a/b is in lowest terms, then the desired triangle has legs with length b and hypotenuse a.) This is ΔOAB in the diagram below:
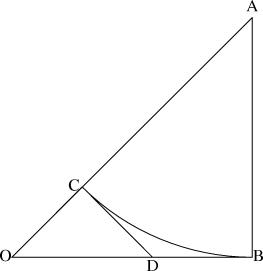
Now construct arc BC, whose center is at A. AC and AB are radii of the same circle, so AC = AB, and thus AC is an integer. Since OC = OA - CA, OC is also an integer.
Let CD be the perpendicular to OA at point C. Then ΔOCD is also an isosceles right triangle, so OC = CD, and CD is an integer. CD and BD are tangents to the same arc from the same point D, so CD = BD, and BD is an integer. Since OB and BD are both integers, so is OD.
Since OC, CD, and OD are all integers, ΔOCD is another isosceles right triangle with integer sides, which contradicts the assumption that OAB was the smallest such.
The thing I find amazing about this proof is not just how simple it is, but how strongly geometric. The Greeks proved that √2 was irrational a long time ago, with an argument that was essentially arithmetical. The Greeks being who they were, their essentially arithmetical argument was phrased in terms of geometry, with all the numbers and arithmetic represented by operations on line segments. The Tom Apostol proof is much more in the style of the Greeks than is the one that the Greeks actually found!
[ 20070220: There is a short followup to this article. ]
[Other articles in category /math] permanent link
Sun, 18 Feb 2007
ALT attributes in formula image elements
I have a Blosxom plugin that recognizes
<formula>...</formula> elements in my blog article files,
interprets the contents as TeX, converts the results to a gif file,
and then replaces the whole thing with an inline image tag to inline
the gif file.
Today I fixed the plugin to leave the original TeX source code in the ALT attribute of the IMG tag. I should have done this in the first place.
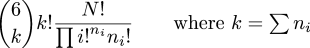
[Other articles in category /meta] permanent link
Fri, 16 Feb 2007
Yahtzee probability
In the game of Yahtzee, the players roll five dice and try to generate
various combinations, such as five of a kind, or full house (a
simultaneous pair and a three of a kind.) A fun problem is to
calculate the probabilities of getting these patterns. In Yahtzee,
players get to re-roll any or all of the dice, twice, so the probabilities
depend in part on the re-rolling strategy you choose. But the first
step in computing the probabilities is to calculate the chance of
getting each pattern in a single roll of all five dice.
A related problem is to calculate the probability of certain poker hands. Early in the history of poker, rules varied about whether a straight beat a flush; players weren't sure which was more common. Eventually it was established that straights were more common than flushes. This problem is complicated by the fact that the deck contains a finite number of each card. With cards, drawing a 6 reduces the likelihood of drawing another 6; this is not true when you roll a 6 at dice.
With three dice, it's quite easy to calculate the likelihood of rolling various patterns:
| Pattern | Probability | |
| A A A | 6 | / 216 |
| A A B | 90 | / 216 |
| A B C | 120 | / 216 |
A high school student would have no trouble with this. For pattern AAA, there are clearly only six possibilities. For pattern AAB, there are 6 choices for what A represents, times 5 choices for what B represents, times 3 choices for which die is B; this makes 90. For pattern ABC, there are 6 choices for what A represents times 5 choices for what B represents times 4 choices for what C represents; this makes 120. Then you check by adding up 6+90+120 to make sure you get 63 = 216.
It is perhaps a bit surprising that the majority of rolls of three dice have all three dice different. Then again, maybe not. In elementary school I was able to amaze some of my classmates by demonstrating that I could flip three coins and get a two-and-one pattern most of the time. Anyway, it should be clear that as the number of dice increases, the chance of them all showing all different numbers decreases, until it hits 0 for more than 6 dice.
The three-die case is unusually simple. Let's try four dice:
| Pattern | Probability | |
| A A A A | 6 | / 1296 |
| A A A B | 120 | / 1296 |
| A A B B | 90 | / 1296 |
| A A B C | 720 | / 1296 |
| A B C D | 360 | / 1296 |
There are obviously 6 ways to throw the pattern AAAA. For pattern AAAB there are 6 choices for A × 5 choices for B × 4 choices for which die is the B = 120. So far this is no different from the three-die case. But AABB has an added complication, so let's analyze AAAA and AAAB a little more carefully.
First, we count the number of ways of assigning numbers of pips on the dice to symbols A, B, and so on. Then we count the number of ways of assigning the symbols to actual dice. The total is the product of these. For AAAA there are 6 ways of assigning some number of pips to A, and then one way of assigning A's to all four dice. For AAAB there are 6×5 ways of assigning pips to symbols A and B, and then four ways of assigning A's and B's to the dice, namely AAAB, AABA, ABAA, and BAAA. With that in mind, let's look at AABB and AABC.
For AABB, There are 6 choices for A and 5 for B, as before. And there are !!4\choose2!! = 6 choices for which dice are A and which are B. This would give 6·5·6 = 180 total. But of the 6 assignments of A's and B's to the dice, half are redundant. Assignments AABB and BBAA, for example, are completely equivalent. Taking A=2 B=4 with pattern AABB yields the same die roll as A=4 B=2 with pattern BBAA. So we have double-counted everything, and the actual total is only 90, not 180.
Similarly, for AABC, we get 6 choices for A × 5 choices for B × 4 choices for C = 120. And then there seem to be 12 ways of assigning dice to symbols:
| AABC | AACB |
| ABAC | ACAB |
| ABCA | ACBA |
| BAAC | CAAB |
| BACA | CABA |
| BCAA | CBAA |
But no, actually there are only 6, because B and C are entirely equivalent, and so the patterns in the left column cover all the situations covered by the ones in the right column. The total is not 120×12 but only 120×6 = 720.
Then similarly for ABCD we have 6×5×4×3 = 360 ways of assigning pips to the symbols, and 24 ways of assigning the symbols to the dice, but all 24 ways are equivalent, so it's really only 1 way of assigning the symbols to the dice, and the total is 360.
The check step asks if 6 + 120 + 90 + 720 + 360 = 64 = 1296, which it does, so that is all right.
Before tackling five dice, let's try to generalize. Suppose the we have N dice and the pattern has k ≤ N distinct symbols which occur (respectively) p1, p2, ... pk times each.
There are !!{6\choose k}k!!! ways to assign the pips to the symbols. (Note for non-mathematicians: when k > 6, !!{6\choose k}!! is zero.)
Then there are !!N\choose p_1 p_2
\ldots p_k!! ways to assign the symbols to the dice, where
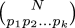 denotes the so-called multinomial
coefficient, equal to !!{N!\over
p_1!p_2!\ldots p_k!}!!.
denotes the so-called multinomial
coefficient, equal to !!{N!\over
p_1!p_2!\ldots p_k!}!!.
But some of those pi might be equal, as with
AABB, where p1 =
p2 = 2, or with AABC, where
p2 =
p3 = 1. In such cases
case some of the
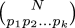 assignments are redundant.
assignments are redundant.
So rather than dealing with the pi directly, it's convenient to aggregate them into groups of equal numbers. Let's say that ni counts the number of p's that are equal to i. Then instead of having pi = (3, 1, 1, 1, 1) for AAABCDE, we have ni = (4, 0, 1) because there are 4 symbols that appear once, none that appear twice, and one ("A") that appears three times.
We can re-express
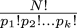 in terms of the ni:
in terms of the ni:
$$N!\over {1!}^{n_1}{2!}^{n_2}\ldots{k}!^{n_k}$$
And the reduced contribution from equivalent patterns is easy to express too; we need to divide by !!\prod {n_i}!!!. So we can write the total as:
$$ {6\choose k}k! {N!\over \prod {i!}^{n_i}{n_i}!} \qquad \text{where $k = \sum n_i$} $$
Note that k, the number of distinct symbols, is merely the sum of the ni.To get the probability, we just divide by 6N. Let's see how that pans out for the Yahtzee example, which is the N=5 case:
| Pattern | ni | Probability | |||||
| 1 | 2 | 3 | 4 | 5 | |||
| A A A A A | 1 | 6 | / 7776 | ||||
| A A A A B | 1 | 1 | 150 | / 7776 | |||
| A A A B B | 1 | 1 | 300 | / 7776 | |||
| A A A B C | 2 | 1 | 1200 | / 7776 | |||
| A A B B C | 1 | 2 | 1800 | / 7776 | |||
| A A B C D | 3 | 1 | 3600 | / 7776 | |||
| A B C D E | 5 | 720 | / 7776 | ||||
6 + 150 + 300 + 1,200 + 1,800 + 3,600 + 720 = 7,776, so this checks out. The table is actually not quite right for Yahtzee, which also recognizes "large straight" (12345 or 23456) and "small straight" (1234X, 2345X, or 3456X.) I will continue to disregard this.
The most common Yahtzee throw is one pair, by a large margin. (Any Yahtzee player could have told you that.) And here's a curiosity: a full house (AAABB), which scores 25 points, occurs twice as often as four of a kind (AAAAB), which scores at most 29 points and usually less.
The key item in the formula is the factor of !!{N!\over \prod {i!}^{n_i}{n_i}!}!! on the right. This was on my mind because of the article I wrote a couple of days ago about counting permutations by cycle class. The key formula in that article was:
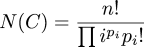
Anyway, I digress. We can generalize the formula above to work for S-sided dice;
this is a simple matter of replacing the 6 with an S. We
don't even need to recalculate the ni.
And since the key factor of 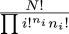 does not involve S, we can easily
precalculate it for some pattern and then plug it into the rest of the
formula to get the likelihood of rolling that pattern with different
kinds of dice. For example, consider the two-pairs pattern AABBC.
This pattern has n1 = 1,
n2 = 2, so the key factor comes out to be 15.
Plugging this into the rest of the formula, we see that the probability of
rolling AABBC with five S-sided dice is
!!90 {S \choose 3} S^{-5}!!.
Here is a tabulation:
does not involve S, we can easily
precalculate it for some pattern and then plug it into the rest of the
formula to get the likelihood of rolling that pattern with different
kinds of dice. For example, consider the two-pairs pattern AABBC.
This pattern has n1 = 1,
n2 = 2, so the key factor comes out to be 15.
Plugging this into the rest of the formula, we see that the probability of
rolling AABBC with five S-sided dice is
!!90 {S \choose 3} S^{-5}!!.
Here is a tabulation:
| 
| |||||||||||||||||||||||||||||||||||||
The graph is quite typical, and each pattern has its own favorite kind of dice. Here's the corresponding graph and table for rolling the AABBCDEF pattern on eight dice:
| 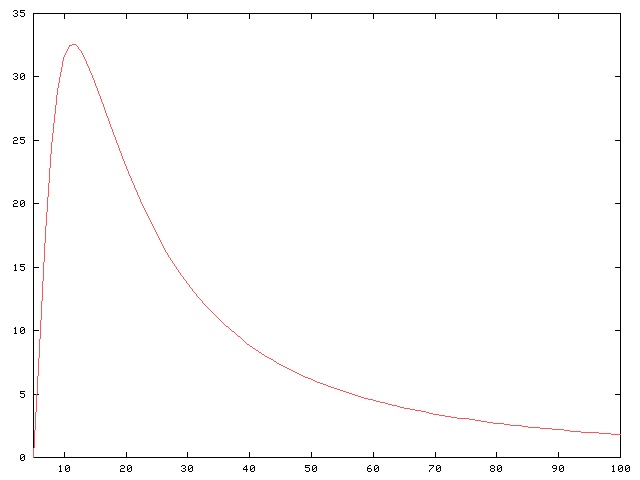
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Returning to the discussion of poker hands, we might ask what the ranking of poker hands whould be, on the planet where a poker hand contains six cards instead of five. Does four of a kind beat three pair? Using the methods in this article, we can get a quick approximation. It will be something like this:
- Two trips (AAABBB)
- Overfull house (AAAABB)
- Three pair
- Four of a kind
- Full house (AAABBC)
- Three of a kind
- Two pair
- One pair
- No pair
I was going to end the article with tabulations of the number of different ways to roll each possible pattern, and the probabilities of getting them, but then I came to my senses. Instead of my running the program and pasting in the voluminous output, why not just let you run the program yourself, if you care to see the answers?
[Other articles in category /math] permanent link
Wed, 14 Feb 2007
Subtlety or sawed-off shotgun?
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
There's a line in one of William Gibson's short stories about how some situations call for a subtle and high-tech approach, and others call for a sawed-off shotgun. I think my success as a programmer, insofar as I have any, comes from knowing when to deploy each kind of approach.
In a recent article I needed to produce the table that appears at left.This was generated by a small computer program. I learned a long time ago that although it it tempting to hack up something like this by hand, you should usually write a computer program to do it instead. It takes a little extra time up front, and that time is almost always amply paid back when you inevitably decide that that table should have three columns instead of two, or the lines should alternate light and dark gray, or that you forgot to align the right-hand column on the decimal points, or whatever, and then all you have to do is change two lines of code and rerun the program, instead of hand-editing all 34 lines of the output and screwing up two of them and hand-editing them again. And again. And again.
When I was making up the seating chart for my wedding, I used this approach. I wrote a raw data file, and then a Perl program to read the data file and generate LaTeX output. The whole thing was driven by make. I felt like a bit of an ass as I wrote the program, wondering if I wasn't indulging in an excessive use of technology, and whether I was really going to run the program more than once or twice. How often does the seating chart need to change, anyway?
Gentle readers, that seating chart changed approximately one million and six times.
The Nth main division of the table at left contains one line for every partition of the integer N. The right-hand entry in each line (say 144) is calculated by a function permcount, which takes the left-hand entry (say [5, 1]) as input. The permcount function in turn calls upon fact to calculate factorials and choose to calculate binomial coefficients.
But how is the left-hand column generated? In my book, I spent quite a lot of time discussing generation of partitions of an integer, as an example of iterator techniques. Some of these techniques are very clever and highly scalable. Which of these clever partition-generating techniques did I use to generate the left-hand column of the table?
Why, none of them, of course! The left-hand column is hard-wired into
the program:
while (<DATA>) {
chomp;
my @p = split //;
...
}
...
__DATA__
1
11
2
111
12
3
...
51
6
I guessed that it would take a lot longer to write code to generate
partitions, or even to find it already written and use it, than it
would just to generate the partitions out of my head and type them in.
This guess was correct.
The only thing wrong with my approach is that it doesn't scale. But
it doesn't need to scale.
The sawed-off shotgun wins!
[ Addendum 20190920: The Gibson story is Johnny Mnemonic, which begins:
I put the shotgun in an Adidas bag and padded it out with four pairs of tennis socks, not my style at all, but that was what I was aiming for: If they think you're crude, go technical; if they think you're technical, go crude. I'm a very technical boy. So I decided to get as crude as possible.The rest of the paragraph somewhat undercuts my point: Shotguns were so long obsolete that Johnny had to manufacture the cartridges himself. ]
[Other articles in category /prog] permanent link
Tue, 13 Feb 2007
Cycle classes of permutations
I've always had trouble sleeping. In high school I would pass the
time at night by doing math. Math is a good activity for insomniacs:
It's quiet and doesn't require special equipment.
This also makes it a good way to pass the time on trains and in boring meetings. I've written before about the time-consuming math problems I use to pass time on trains.
Today's article is about another entertainment I've been using lately in meetings: count the number of permutations in each cycle class.In case you have forgotten, here is a brief summary: a permutation is a mapping from a set to itself. A cycle of a permutation is a subset of the set for which the elements fall into a single orbit. For example, the permutation:
$$ \pmatrix{1&2&3&4&5&6&7&8\cr 1&4&2&8&5&7&6&3\cr}$$
can be represented by the following diagram:
We can sort the permutations into cycle classes by saying that two permutations are in the same cycle class if the lengths of the cycles are all the same. This effectively files the numeric labels off the points in the diagrams. So, for example, the permutations of {1,2,3} fall into the three following cycle classes:
| Cycle lengths | Permutations | How many? | |
 | 1 1 1 | () | 1 |
 | 2 1 | (1 2) (1 3) (2 3) | 3 |
 | 3 | (1 2 3) (1 3 2) | 2 |
| Cycle lengths | Permutations | How many? | |
 | 1 1 1 1 | () | 1 |
 | 2 1 1 | (1 2) (1 3) (1 4) (2 3) (2 4) (1 4) | 6 |
 | 2 2 | (1 2)(3 4) (1 3)(2 4) (1 4)(2 3) | 3 |
 | 3 1 | (1 2 3) (1 2 4) (1 3 2) (1 3 4) (1 4 2) (1 4 3) (2 3 4) (2 4 3) | 8 |
 | 4 | (1 2 3 4) (1 2 4 3) (1 3 2 4) (1 3 4 2) (1 4 2 3) (1 4 3 2) | 6 |
It is not too hard a problem, and would probably only take fifteen or twenty minutes outside of a meeting, but this is exactly what makes it a good problem for meetings, where you can give the problem only partial and intermittent attention. Now that I have a simple formula, the enumeration of cycle classes loses all its entertainment value. That's the way the cookie crumbles.
Here's the formula. Suppose we want to know how many permutations of {1,...,n} are in the cycle class C. C is a partition of the number n, which is to say it's a multiset of positive integers whose sum is n. If C contains p1 1's, p2 2's, and so forth, then the number of permutations in cycle class C is:
$$ N(C) = {n! \over {\prod i^{p_i}{p_i}!}} $$
This can be proved by a fairly simple counting argument, plus a bit of algebraic tinkering. Note that if any of the pi is 0, we can disregard it, since it will contribute a factor of i0·0! = 1 in the denominator.For example, how many permutations of {1,2,3,4,5} have one 3-cycle and one 2-cycle? The cycle class is therefore {3,2}, and all the pi are 0 except for p2 = p3 = 1. The formula then gives 5! in the numerator and factors 2 and 3 in the denominator, for a total of 120/6 = 20. And in fact this is right. (It's equal to !!2{5\choose3}!!: choose three of the five elements to form the 3-cycle, and then the other two go into the 2-cycle. Then there are two possible orders for the elements of the 3-cycle.)
How many permutations of {1,2,3,4,5} have one 2-cycle and three 1-cycles? Here we have p1 = 3, p2 = 1, and the other pi are 0. Then the formula gives 120 in the numerator and factors of 6 and 2 in the denominator, for a total of 10.
Here are the breakdowns of the number of partitions in each cycle class for various n:
1
| | 1 | 1
| 2
| | 1 1 | 1
| | 2 | 1
| 3
| | 1 1 1 | 1
| | 1 2 | 3
| | 3 | 2
| 4
| | 1 1 1 1 | 1
| | 1 1 2 | 6
| | 2 2 | 3
| | 3 1 | 8
| | 4 | 6
| 5
| | 1 1 1 1 1 | 1
| | 2 1 1 1 | 10
| | 2 2 1 | 15
| | 3 1 1 | 20
| | 3 2 | 20
| | 4 1 | 30
| | 5 | 24
| 6
| | 1 1 1 1 1 1 | 1
| | 2 1 1 1 1 | 15
| | 2 2 1 1 | 45
| | 2 2 2 | 15
| | 3 1 1 1 | 40
| | 3 2 1 | 120
| | 3 3 | 40
| | 4 1 1 | 90
| | 4 2 | 90
| | 5 1 | 144
| | 6 | 120
| | ||||||||||||
Incidentally, the thing about the average permutation having exactly one fixed point is quite easy to prove. Consider a permutation of N things. Each of the N things is left fixed by exactly (N-1)! of the permutations. So the total number of fixed points in all the permutations is N!, and we are done.
A similar but slightly more contorted analysis reveals that the average number of 2-cycles per permutation is 1/2, the average number of 3-cycles is 1/3, and so forth. Thus the average number of total cycles per permutation is !!\sum_{i=1}^n{1\over i} = H_n!!. For example, for n=4, examination of the table above shows that there is 1 permutation with 4 independent cycles (the identity permutation), 6 with 3 cycles, 11 with 2 cycles, and 6 with 1 cycle, for an average of (4+18+22+6)/24 = 50/24 = 1 + 1/2 + 1/3 + 1/4.
The 1, 6, 11, 6 are of course the Stirling numbers of the first kind; the identity !!\sum{n\brack i}i = n!H_n!! is presumably well-known.
[Other articles in category /math] permanent link
Fri, 09 Feb 2007What to make of this?
- Sentence 2 is false.
- Sentence 1 is true.
Many answers are possible. The point of this note is to refute one particular common answer, which is that the whole thing is just meaningless.
This view is espoused by many people who, it seems, ought to know better. There are two problems with this view.
The first problem is that it involves a theory of meaning that appears to have nothing whatsoever to do with pragmatics. You can certainly say that something is meaningless, but that doesn't make it so. I can claim all I want to that "jqgc ihzu kenwgeihjmbyfvnlufoxvjc sndaye" is a meaningful utterance, but that does not avail me much, since nobody can understand it. And conversely, I can say as loudly and as often as I want to that the utterance "Snow is white" is meaningless, but that doesn't make it so; the utterance still means that snow is white, at least to some people in some contexts.
Similarly, asserting that the sentences are meaningless is all very well, but the evidence is against this assertion. The meaning of the utterance "sentence 2 is false" seems quite plain, and so does the meaning of the utterance "sentence 1 is true". A theory of meaning in which these simple and plain-seeming sentences are actually meaningless would seem to be at odds with the evidence: People do believe they understand them, do ascribe meaning to them, and, for the most part, agree on what the meaning is. Saying that "snow is white" is meaningless, contrary to the fact that many people agree that it means that snow is white, is foolish; saying that the example sentences above are meaningless is similarly foolish.
I have heard people argue that although the sentences are individually meaningful, they are meaningless in conjunction. This position is even more problematic. Let us refer to a person who holds this position as P. Suppose sentence 1 is presented to you in isolation. You think you understand its meaning, and since P agrees that it is meaningful, he presumably would agree that you do. But then, a week later, someone presents you with sentence 2; according to P's theory, sentence 1 now becomes meaningless. It was meaningful on February 1, but not on February 8, even though the speaker and the listener both think it is meaningful and both have the same idea of what it means. But according to P, as midnight of February 8, they are suddenly mistaken.
The second problem with the notion that the sentences are meaningless comes when you ask what makes them meaningless, and how one can distinguish meaningful sentences from sentences like these that are apparently meaningful but (according to the theory) actually meaningless.
The answer is usually something along the lines that sentences that
contain self-reference are meaningless. This answer is totally
inadequate, as has been demonstrated many times by many people,
notably W.V.O. Quine. In the example above, the self-reference
objection is refuted simply by observing that neither sentence is
self-referent. One might try to construct an argument about
reference loops, or something of the sort, but none of this will
avail, because of Quine's example:
But all of this is peripheral to the main problem with the argument
that sentences that contain self-reference are meaningless. The main
problem with this argument is that it cannot be true. The
sentence "sentences that contain self-reference are meaningless" is
itself a sentence, and therefore refers to itself, and is therefore
meaningless under its own theory. If the assertion is true, then the
sentence asserting it is meaningless under the assertion itself; the
theory deconstructs itself. So anyone espousing this theory has
clearly not thought through the consequences. (Graham Priest says that
people advancing this theory are subject to a devastating ad
hominem attack. He doesn't give it specifically, but many such
come to mind.)
In fact, the self-reference-implies-meaninglessness theory obliterates
not only itself, but almost all useful statements of logic. Consider
for example "The negation of a true sentence is false and the negation
of a false sentence is true." This sentence, or a variation of it, is
probably found in every logic textbook ever written. Such a sentence
refers to itself, and so, in the
self-reference-implies-meaninglessness theory, is meaningless. So too
with most of the other substantive assertions of our logic textbooks,
which are principally composed of such self-referent sentences about
properties of sentences; so much for logic.
The problems with ascribing meaninglessness to self-referent sentences
run deeper still. If a sentence is meaningless, it cannot be
self-referent, because, being meaningless, it cannot refer to anything
at all. Is "jqgc ihzu kenwgeihjmbyfvnlufoxvjc sndaye" self-referent?
No, because it is meaningless. In order to conclude that it was
self-referent, we would have to understand it well enough to ascribe a
meaning to it, and this would prove that it was meaningful.
So the position that the example sentences 1 and 2 are "meaningless"
has no logical or pragmatic validity at all; it is totally
indefensible. It is the philosophical equivalent of putting one's
fingers in one's ears and shouting "LA LA LA I CAN'T HEAR YOU!"
[Other articles in category /math/logic]
permanent link
Fondue
Lorrie was in charge of buying the ingredients. I did not read the
label on the wine before I opened and tasted it, and so was startled
to discover that it was a Riesling, which is very much not a dry wine,
as is traditional. Riesling is is a very sweet and fruity wine.
I asked Lorrie how she chose the wine, and she said she had gotten
Riesling because she prefers sweet wines. I remarked that dry wines
are traditional for fondue. But it was what we had, and I made the
fondue with it. Anyway, as Lorrie pointed out, fondue is often
flavored with a dash of kirsch, which is a cherry liqueur, and not at
all dry. I never have kirsch in the house, and usually use port or
sherry instead. Since we were using Riesling, I left that stuff
out.
The fondue was really outstanding, easily the most delicious fondue
I've ever made. Using Riesling totally changed the character of the
dish. The Riesling gave it a very rich and complex flavor. I'm going
to use Riesling in the future too. Give it a try.
Transfer to a caquelon (fondue pot) and serve with chunks of crusty
French bread and crisp apples.
[Other articles in category /food]
permanent link
Mnemonics
The
Wikipedia article about the number e mentions a very silly
mnemonic for remembing the digits of e: "2.7-Andrew
Jackson-Andrew Jackson-Isosceles Right Triangle". Apparently, Andrew
Jackson was elected President in 1828. When I saw this, my immediate
thought was "that's great; from now on I'll always remember when
Andrew Jackson was elected President."
In high school, I had a math teacher who pointed out that a mnemonic
for the numerical value of √3 was to recall that George
Washington was born in the year 1732. And indeed, since that day I
have never forgotten that Washington was born in 1732.
[Other articles in category /math]
permanent link
Software archaeology
This lack is exacerbated by several unfortunate facts: creation times
are available on Windows systems; the Unix inode contains three
timestamps, one of which is called the "ctime", and the "c" is
suggestive of the wrong thing; Perl's built-in stat function
overloads the return value to return the Windows creation time in the
same position (on Windows) as it returns the ctime (on Unix).
So we see questions like this one, which appeared this week on the
Philadelphia Linux Users' Group mailing list:
But anyway, that got me thinking about ctimes in general, and I did
some research into the history and semantics of the thing, and made
some rather surprising discoveries.
One good reference for the broad outlines of early Unix is the paper that
Dennis Ritchie and Ken Thompson published in Communications of
the ACM in 1974. This was updated in 1978, but the part
I'm quoting wasn't revised and is current to 1974. Here is what it
has to say about the relevant parts of the inode structure:
Now how about that?
When did the ctime change from being called a "creation time" to a
"change time"? Did the semantics change too, or was the "creation
time" description a misnomer? If I can't find out, I might write to
Ritchie to ask. But this is, of course, a last resort.
In the meantime, I do have the source code for the fifth edition
kernel, but it appears that, around that time (1975 or so), there was
no creation time. At least, I can't find one.
The inode operations inside the kernel are defined to operate on struct
inodes:
We can see an example of this in the stat1 function, which is
the backend for the stat and fstat system calls:
14 words are copied from the inode structure starting from this
position, including the device and i-number fields, the mode, the link
count, and so on, up through the addresses of the data or indirect
blocks. (In modern Unixes, the stat call omits these addresses.)
Then four words are copied out of the cp buffer, which has been
read from the inode actually on the disk; these eight bytes are at
position 24 in the inode, and ought to contain the mtime and the
ctime. The question is, which is which? This simple question turns
out to have a surprisingly complicated answer.
When an inode is modified, the IUPD flag is
set in the i_flag member. For example, here is
chmod, which modifies the inode but not the underlying data.
On a modern unix system, we would expect this to update the ctime, but
not the mtime. Let's see what it does in version 5:
Lines 16–17 copy the mode, link count, uid, gid, "size", and
"addr" fields from the in-memory copy of the inode into the block
buffer that will be written back to the disk. Lines 18–22
update the atime if the IACC flag is set, or skip it if not.
Then, if the IUPD flag is set, lines 24–25 write the
tm value into the next slot in the buffer, where the mtime is
stored. The bwrite call on line 27 commits the data to the
disk; this results in a call into the appropriate device driver
code.
There is no sign of updating the ctime field, but recall that we
started this search by looking at what the chmod call does;
it sets IUPD, which eventually results in the updating of the
mtime field. So the mtime field is not really an mtime field as we
now know it; it is doing the job that is now done by the ctime field.
And in fact, the dump command predicates its decision about
whether to dump a file on the contents of the mtime field. Which is
really the ctime field. So functionally, dump is doing the
same thing it does now.
It's possible that I missed it, but I cannot find the advertised
creation time anywhere. The logical place to look is in the
maknode function, which allocates new inodes. The
maknode function calls ialloc to get an unused inode
from the device, and this initializes its mode (as specified by the
user), its link count (to 1), and its uid and gid (to the current
process's uid and gid). It does not set a creation time. The
ialloc function is fairly complicated, but as far as I can
tell it is not setting any creation time either.
Working it from the other end, asking who might look at the
ctime field, we have the find command, which has a
-mtime option, but no -ctime option. The
dump command, as noted before, uses the mtime. Several
commands perform stat calls and declare structs to hold the
result. For example, pr, which prints files with nice
pagination, declares a struct inode, which is the inode as
returned by stat, as opposed to the inode as used internally
by the kernel—what we would call a struct stat now.
There was no /usr/include in the fifth edition, so the
pr command contains its own declaration of the struct
inode. It looks like this:
So the creation time advertised by the CACM paper (1974)
and the version 1 manual (1971) seems to have disappeared by the time
of version 5 (1975), if indeed it ever existed.
But there was some schizophrenia in the version 5 system about whether
there was a third date in addition to the atime and the mtime. The
stat call copied it into the stat buffer, and some commands
assumed that it would be there, although they weren't sure what it
would be for, and none of them seem look at it. It's quite possible
that there was at one time a creation date, which had been eliminated
by the time of the fifth edition, leaving behind the vestigial remains
we saw in commands like ln and prof and in the code
of the stat1 function.
Oh, what the hell; I have the version 7 source code; I may as well
look at it. Yes, by this time the /usr/include/sys/stat.h
file had been invented, and does indeed include all three times in the
struct stat. So the mtime (as we now know it) appears to
have been introduced in v7.
One sometimes hears that early Unix had atime and mtime, and that
ctime was introduced later. But actually, it appears that early Unix
had atime and ctime, and it was the mtime that was introduced later.
The confusion arises because in those days the ctime was called
"mtime".
Addendum: It occurs to me now that the version 5 mtime is not
precisely like the modern ctime, because it can be set via the
smdate call, which is analogous to the modern utime
call. The modern ctime cannot be set at all.
(Totally peripheral addendum: Google search for
dmr puts Dennis M. Ritchie in fourth position, not
the first. Is this grave insult to our community to be tolerated? I
think not! It must be avenged! With fire and steel!)
[ Addendum 20070127: Unix source code prior to the fifth edition is
lost. The manuals for the third and fourth editions are
available from the Unix Heritage
Society. The manual for the third edition (February 1973) mentions the
creation time, but by the fourth edition (November 1973) the
stat(2) man page no longer mentions a creation time. In
v4, the two dates in the stat structure are called actime
(modern atime) and modtime (modern mtime/ctime). ]
[Other articles in category /Unix]
permanent link
Environmental manipulations
The nohup basically does signal(NOHUP, SIG_IGN)
before calling execvp(COMMAND, ARGV) to execute the
command.
Similarly, there is a chroot command, run as chroot
new-root-directory command args..., which
runs the specified command with its default root inode set to
somewhere else. And there is a nice command, run as nice
nice-value-adjustment command args..., which
runs the specified command with its "nice" value changed. And there
is an env environment-settings command
args... which runs the specified command with new
variables installed into the environment. The standard sudo
command could also be considered to be of this type.
I have also found it useful to write trivial commands called
indir, which runs a command after chdir-ing to a new
directory, and stopafter, which runs a command after setting
the alarm timer to a specified amount, and, just today,
with-umask, which runs a command after setting the umask to a
particular value.
I could probably have avoided indir and with-umask.
Instead of indir DIR COMMAND, I could use sh -c 'cd DIR;
exec COMMAND', for example. But indir avoids an extra
layer of horrible shell quotes, which can be convenient.
Today it occurred to me to wonder if this proliferation of commands
was really the best way to solve the problem. The sh -c
'...' method solves it partly, for those parts of the process
user area to which correspond shell builtin commands. This includes
the working directory, umask, and environment variables, but not the
signal table, the alarm timer, or the root directory.
There is no standardized interface to all of these things at any
level. At the system call level, the working directory is changed by
the chdir system call, the root directory by chroot,
the alarm timer by alarm, the signal table by a bunch of
OS-dependent nonsense like signal or sigaction, the
nice value by setpriority, environment variables by a
potentially complex bunch of memory manipulation and pointer banging,
and so on.
Since there's no single interface for controlling all these things, we
might get a win by making an abstraction layer for dealing with them.
One place to put this abstraction layer is at the system level, and
might look something like this:
You can also put the abstraction layer at the C library level. This
has fewer drawbacks. It no longer requires kernel hacking, and can
provide a method for modifying the environment. But you still need to
write the command that uses the library.
We may as well put the abstraction layer at the Unix command level.
This means writing a command in some language, like Perl or C, which
offers a shell-level interface to manipulating the process
environment, perhaps something like this:
[Other articles in category /Unix]
permanent link
Length of baseball games
The canonical game, of course, lasts 9 innings. However, if the score
is tied at the end of 9 innings, the game can, and often does, run
longer, because the game is extended to the end of the first complete
inning in which one team is ahead. So some games run longer than 9
innings: games of 10 and 11 innings are quite common, and the
major-league record is 25.
Counterbalancing this effect, however, are two factors. Most important is
that when the home team is ahead after the first half of the ninth
inning, the second half is not played, since it would be a waste of
time. So nearly half of all games are only 8 1/2 innings long. This
depresses the average considerably. Together with the games that are
stopped early on account of rain or other environmental conditions,
the contribution from the extra-inning tie games is almost exactly
cancelled out, and the average ends up close to 9.
[Other articles in category /games]
permanent link
Here's a random example:
Anyway, somewhere in the process of all this I learned that Hobbes had
some mathematical works, and spent a little time hunting them down.
The Penn library has links to online versions of some, so I got to
read a little with hardly any investment of effort. One that
particularly grabbed my attention was "Three papers presented to the
Royal Society against Dr. Wallis".
Wallis was a noted mathematician of the 17th century, a contemporary
of Isaac Newton, and a contributor to the early development of the
calculus. These days he is probably best known for the remarkable
formula:
$${\pi\over2} =
{2\over1}{2\over3}{4\over3}{4\over5}{6\over5}{6\over7}{8\over7}\cdots$$
Hobbes, of course, is totally wrong here. He's so totally wrong that
it might seem hard to believe that he even put such a totally wrong
notion into print. One wants to imagine that maybe we have
misunderstood Hobbes here, that he meant something other than what he
said. But no, he is perfectly lucid as always. That is a drawback of
being such an extremely clear writer: when you screw up, you cannot
hide in obscurity.
Here is the original document,
in case you cannot believe it.
I picture the members of the Royal Society squirming in their seats as
Hobbes presents this "confutation" of Wallis. There is a reason why
John Wallis is a noted mathematician of the 17th century, and Hobbes
is not a noted mathematician at all. Oh well!
Wallis presented a rebuttal sometime later, which I was not going to
mention, since I think everyone will agree that Hobbes is totally
wrong. But it was such a cogent rebuttal that I wanted to quote a bit
from it:
[Other articles in category /math]
permanent link
Linogram circular problems
When I first tried this, it didn't work because linogram
didn't understand that a labeled_curve with N = 4
control points would also have four instances of circ, four
of circ.c, four of circ.c.x, and so on. It did
understand that the labeled curve would have four instances of
s, but the multiplicity wasn't being propagated to the
subobjects of s.
I fixed this up in pretty short order.
But the same bug persisted for circ.r, and this is not
so easy to fix. The difference is that while circ.c is a
full subobject, subject to equation solving, and expected to be
unknown, circ.r is a parameter, which much be specified in
advance.
N, the number of spots and control points, is another such
parameter. So there's a first pass through the object hierarchy to
collect the parameters, and then a later pass figures out the
subobjects. You can't figure out the subobjects without the
parameters, because until you know the value of parameters like
N, you don't know how many subobjects there are in arrays like
s[N].
For subobjects like S[N].circ.c.x, there is no issue. The
program gathers up the parameters, including N, and then
figures out the subobjects, including S[0].circ.c.x and so
on. But S[0].circ.r, is a parameter, and I can't say that
its value will be postponed until after the values of the parameters
are collected. I need to know the values of the parameters before I
can figure out what the parameters are.
This is not a show-stopper. I can think of at least three ways
forward. For example, the program could do a separate pass for
param index parameters, resolving those first. Or I could do
a more sophisticated dependency analysis on the parameter values; a
lot of the code for this is already around, to handle things like
param number a = b*2, b=4, c=a+b+3, d=c*5+b. But I need to
mull over the right way to proceed.
Consider this oddity in the meantime:
When you invent a new kind of program, there is an interesting
tradeoff between what you want to allow, what you actually do allow,
and what you know how to implement. I definitely want to allow the
labeled_curve thing. But I'm quite willing to let the
snark-boojum example turn into some sort of run-time failure.
[Other articles in category /linogram]
permanent link
Recent Linogram development update
Then I said "duh", because I already have a syndication feed for this page, so why not just
post the stuff here?
So that is what I will do. I am about to copy a bunch of stuff from
that page to this one, backdating it to match when I posted it.
The new items are:
[1]
[2]
[3]
[4]
[5].
People who only want to hear about linogram, and not about
anything else, can subscribe to
[Other articles in category /linogram]
permanent link
Another Linogram success story
Here was today's surprise. For a long time, my demo diagram has been
a rough rendering of one of the figures from Higher-Order
Perl:
I wanted component k in the middle of the diagram to be a
curved line, but since I didn't have curved lines yet, I used two
straight lines instead, as shown below:
I now needed to replace this with a curved line. This meant
removing all the references to start, end,
upper and so forth, since curves don't have any of those
things. A significant rewrite, in other words.
But then I had a happy thought. I added the following definition to
the file:
I then replaced:
I didn't foresee this when I designed the linogram language.
Sometimes when you try a new kind of program for the first time, you
keep getting unpleasant surprises. You find things you realize you
didn't think through, or that have unexpected consequences, or
features that turn out not to be as powerful as you need, or that mesh
badly with other features. Then you have to go back and revisit your
design, fix problems, try to patch up mismatches, and so forth. In
contrast, the appearance of the sort of pleasant surprise like the one
in this article is exactly the opposite sort of situation, and makes
me really happy.
[Other articles in category /linogram]
permanent link
Linogram development: 20070120 Update
The regular polygons are working pretty well, and the curves are
working pretty well. Here are some simple examples:
One interesting design problem turned up that I had not foreseen. I
had planned for the curve object to be specified by 2 or more
control points. (The control points are marked by little circles in
the demo pictures above.) The first and last controlpoints would be
endpoints, and the curve would start at point 0, then head toward
point 1, veer off toward point 2, then veer off toward point 3, etc.,
until it finally ended at point N. You can see this in the
pictures.
This is like the behavior of pic, which has good-looking
curves. You don't want to require that the curve pass through
all the control points, because that does not give it enough freedom
to be curvy. And this behavior is easy to get just by using a
degree-N Bézier curve, which was what I planned to
do.
However, PostScript surprised me. I had thought that it had
degree-N Bézier curves, but it does not. It has only
degree-3 ("cubic") Bézier curves. So then I was left with the
puzzle of how to use PostScript's Bézier curves to get what I
wanted. Or should I just change the definition of curve in
linogram to be more like what PostScript wanted? Well, I
didn't want to do that, because linogram is supposed to be
generic, not a front-end to PostScript. Or, at least, not a front-end
only to PostScript.
I did figure out a compromise. The curves generated by the PostScript
drawer are made of PostScript's piecewise-cubic curves, but, as you
can see from the demo pictures, they still have the behavior I want.
The four control points in the small demos above actually turn into
two PostScript cubic Bézier curves, with a total of seven control points.
If you give linogram the points
A,
B,
C, and
D, the PostScript engine draws two cubic Bézier curves, with control
points
{A,
B,
B,
(B + C)/2} and
{(B + C)/2,
C,
C,
D}, respectively. Maybe I'll write a blog article about why I
chose to do it this way.
One drawback of this approach is that the curves turn rather sharply
near the control points. I may tinker with the formula later to
smooth out the curves a bit, but I think for now this part is good
enough for beta testing.
[Other articles in category /linogram]
permanent link
Linogram development: 20070117 Update
All of the equations are rather trivial. All the difficulty is in
generating the equations in the first place. The program must
recognize that the variable i in the polygon
definition is a dummy iterator variable, and that it is associatated
with the parameter N in the polygon definition. It must
propagate the specification of N to the right place, and then
iterate the equations appropriately, producing something like:
Open figures still don't work properly. I don't think this will take
too long to fix.
The code is very messy. For example, all the Type classes
are in a file whose name is not Type.pm but
Chunk.pm. I plan to have a round of cleanup and consolidation
after the 2.0 release, which I hope will be soon.
[Other articles in category /linogram]
permanent link
R3 is not a square
It would be rather surprising if there were, since you could then
describe any point in space unambiguously by giving its two
coordinates from X. This would mean that in some sense, R3
could be thought of as two-dimensional. You would expect that any
such X, if it existed at all, would have to be extremely
peculiar.
I had been wondering about this rather idly for many years, but last
week a gentleman on IRC mentioned to me that there had been a proof in
the American Mathematical Monthly a couple of years back that
there was in fact no such X. So I went and looked it up.
The paper was "Another Proof That R3 Has No Square Root", Sam
B. Nadler, Jr., American Mathematical Monthly vol 111
June–July 2004, pp. 527–528. The proof there is
straightforward enough, analyzing the topological dimension of
X and arriving at a contradiction.
But the Nadler paper referenced an earlier paper which has a much
better proof. The proof in "R3 Has No Root", Robbert Fokkink,
American Mathematical Monthly vol 109 March 2002, p. 285, is
shorter, simpler, and more general. Here it is.
A linear map Rn → Rn can be understood to preserve or reverse
orientation, depending on whether its determinant is +1 or -1. This
notion of orientation can be generalized to arbitrary homeomorphisms,
giving a "degree" deg(m) for every homeomorphism which is +1 if
it is orientation-preserving and -1 if it is orientation-reversing.
The generalization has all the properties that one would hope for. In
particular, it coincides with the corresponding notions for linear
maps and differentiable maps, and it is multiplicative: deg(f
o g) = deg(f)·deg(g) for all homeomorphisms
f and g. In particular ("fact 1"), if h is any
homeomorphism whatever, then h o h is an
orientation-preserving map.
Now, suppose that h : X2 → R3 is a homeomorphism.
Then X4 is homeomorphic to R6, and we can view
quadruples (a,b,c,d) of elements of
X as equivalent to sextuples
(p,q,r,s,t,u)
of elements of R.
Consider the map s on X4 which takes
(a,b,c,d) →
(d,a,b,c). Then s o s is the map (a,b,c,d)
→ (c,d,a,b). By fact 1 above, s o s must be an
orientation-preserving map.
But translated to the putatively homeomorphic space R6, the
map (a,b,c,d) →
(c,d,a,b) is just the linear map on
R6 that takes
(p,q,r,s,t,u) →
(s,t,u,p,q,r). This map is
orientation-reversing, because its determinant is -1. This is a
contradiction. So X4 must not be homeomorphic to R6,
and X2 therefore not homeomorphic to R3.
The same proof goes through just fine to show that
R2n+1 = X2 is false for all n,
and similarly for open subsets of R2n+1.
The paper also refers to an earlier paper ("The cartesian product of a
certain nonmanifold and a line is E4", R.H. Bing,
Annals of Mathematics series 2 vol 70 1959
pp. 399–412) which constructs an extremely pathological
space B, called the "dogbone space", not even a manifold, which
nevertheless has B × R3 = R4. This is on my
desk, but I have not read this yet, and I may never.
[Other articles in category /math]
permanent link
State of the Blog 2006
The longest article was the one about
finite extension fields of Z2; the shortest was
the MadHatterDay
commemorative. Other long articles included some math ones (metric spaces, the Pólya-Burnside
theorem) and some non-math ones (how
Forbes magazine made a list of the top 20 tools and
omitted the hammer, do
aliens feel disgust?).
I drew, generated, or appropriated about 300 pictures, diagrams, and
other illustrations, plus 66 mathematical formulas. This does not
count the 50 pictures of books that I included, but it does include
108 little colored squares for the article on the Pólya-Burnside
counting lemma.
None of the book links earned me any money from kickbacks. However,
the blog did generate some income. When Aaron Swartz struck oil, he
offered to give away money to web sites that needed it. Mine didn't
need it, but a little later he published a list of web sites he'd
given money to, and I decided that I was at least as deserving as some
of them. So I stuck a "donate" button on my blog and invited Aaron to
use it. He did. Thanks, Aaron!
I now invite you to use that button yourself. Here are two versions
that both do the same thing:
My MacArthur Fellowship check has apparently been held up in the
mail.
The followup to the Design
Patterns article was very popular also. Other popular articles
were on risk, the envelope paradox, the invention of the = sign, and
ten science questions every
high school graduate should be able to answer.
My own personal favorites are the articles about alien disgust, the manufacture of round objects, and
what makes π so peculiar. In
that last one, I think I was skating on the thin edge of crackpotism.
The article about Forbes' tool list
was mentioned in The New York Times.
The blog attracted around five hundred email messages, most of which
were intelligent and thoughtful, and most of which I answered. But my
favorite email message was from the guy who tried to convince me that
rock salt melts snow because
it contains radioactive potassium.
Moving the blog has probably cost me a lot of readers. I know from
the logs that many of them have not moved from newbabe to Dreamhost.
Traffic on the new site just after the move was about 25% lower than
on the old site just before the move. Oh well.
If the blog hadn't moved so many times, it would be listed by
Technorati as one of the top ten blogs on math and science, and one of
the top few thousand overall. As it is, the incoming links (which are
what Technorati uses to judge blog importance) are scattered across
three different sites, so it appears to be three semi-popular blogs
rather than one very popular blog. This would bother me, if
Technorati rankings weren't so utterly meaningless.
I think I've upheld this vow pretty well, and although there have been
occasions on which I've called people knuckleheaded assholes, it has
always been either a large group (like Biblical literalists) or
people who were dead (like this pinhead) or
both.
Another vow I made was that I wasn't going to include any tedious
personal crap, like what music I was listening to, or whether the
grocery store was out of Count Chocula this week. I think I did okay
on that score. There are plenty of bloggers who will tell you about
the fight they had with their girlfriend last night, but very few that
will analyze abbreviations
in Medieval Latin. So I have the Medieval Latin abbreviations
audience pretty much to myself. I am a bit surprised at how
thoroughly I seem to have communicated my inner life, in spite of
having left out any mention of Count Chocula. This is a blog of what
I've thought, not what I've done.
The longest of these unpublished articles was written some time after
my article on the envelope
paradox hit the front page of Reddit. Most of the Reddit comments
were astoundingly obtuse. There were about nine responses of the type
"That's cute, but the fallacy is...", each one proposing a
different fallacy. All of the proposed fallacies were
completely wrong; most of them were obviously wrong. (There is no
fallacy; the argument is correct.) I decided against posting this
rebuttal article for several reasons:
The article about metric spaces
was supposed to be one of a three-part series, which I still hope to
finish eventually. I made several attempts to write another part in
this series, about the real numbers and why we have them at all. This
requires explanation, because the reals are mathematically and
philosophically quite artificial and problematic. (It took me a lot
of thought to convince myself that they were mathematically
inevitable, and that the aliens would have them too, but that is
another article.) The three or four drafts I wrote on this topic
total about 2,100 words, but I still haven't quite got it where I want
it, so it will have to wait.
I wrote 2,000 words about oddities in my brain, what it's good at and
what not, and put it on the shelf because I decided it was too
self-absorbed. I wrote a complete "frequently-asked questions" post
which answered the (single) question "Why don't you allow comments?"
and then suppressed it because I was afraid it was too self-absorbed.
Then I reread it a few months later and thought it was really funny,
and almost relented. Then I read it again the next month and decided
it was better to keep it suppressed. I'm not indecisive; I'm just
very deliberate.
I finished a 2,000-word article about how to derive the formulas for
least-squares linear regression and put it on the shelf because I
decided that it was boring. I finished a 1,300-word article about
quasiquotation in Lisp and put it on the shelf because I decided it
was boring. (Here's the payoff from the quasiquotation article: John
McCarthy, the inventor of Lisp, took both the concept and the name directly
from W.V.O. Quine, who invented it in 1940.)
Had I been writing this blog in 2005, there would have been a bunch of
articles about Sir Thomas Browne, but I was pretty much done with him
by the time I started the blog. (I'm sure I will return someday.)
There would have been a bunch of articles about John Wilkins's book on
the Philosophical Language, and some on his book about cryptography.
(The Philosophical Language crept in a bit anyway.) There would have
been an article about Charles Dickens's book Great
Expectations, which I finished reading about a year and a half
ago.
An article about A Christmas Carol is in the works, but I
seem to have missed the seasonal window on that one, so perhaps I'll
save it for next December. I wrote an article about how to calculate
the length of the day, and writing a computer progam to tell time by
the old Greek system, which divides the daytime into twelve equal
hours and the nighttime into twelve equal hours, so that the night
hours are longer than the day ones in the winter, and shorter in the
summer. But I missed the target date (the solstice) for that one, so
it'll have to wait until at least the next solstice. I wrote part of
an article about Hangeul (the Korean alphabet), planning to publish it
on Hangeul Day (the Koreans have a national holiday celebrating
Hangeul) but I couldn't find the quotations I wanted from 1445, so I
put it on the shelf. This week I'm reading Gari Ledyard's doctoral
thesis, The Korean Language Reform of 1446, so I may
acquire more information about that and be able to finish the article.
(I highly recommend the Ledyard thing; it's really well-written.) I
recently wrote about 1,000 words about Vernor Vinge's new novel
Rainbows End, but that's not finished yet.
A followup to the article about why
you don't have one ear in the middle of your face is in progress.
It's delayed by two things: first, I made a giant mistake in the
original article, and I need to correct it, but that means I have to
figure out what the mistake is and how to correct it. And second, I
have to follow up on a number of fascinating references about
directional olfaction.
Sometimes these followups eventually arrive,as the one about ssh-agent
did, and sometimes they stall. A followup to my early article about the
nature of transparency, about the behavior of light, and the
misconception of "the speed of light in glass", ran out of steam after
a page when I realized that my understanding of light was so poor that
I would inevitably make several gross errors of fact if I finished
it.
I spent a lot of the summer reading books about inconsistent
mathematics, including Graham Priest's book In
Contradiction, but for some reason no blog articles came of it.
Well, not exactly. What has come out is an unfinished 1,230-word
article against the idea that mathematics is properly understood as
being about formal systems, an unfinished 1,320-word article about the
ubiquity of the Grelling-Nelson paradox, an unfinished 1,110-word
article about the "recursion theorem" of computer science, and an
unfinished 1,460-word article about paraconsistent logic and the liar
paradox.
I have an idea that I might inaugurate a new section of the blog,
called "junkheap", where unfinished articles would appear after aging
in the cellar for three years, regardless what sort of crappy
condition they are in. Now that the blog is a year old, planning
something two years out doesn't seem too weird.
I also have an ideas file with a couple hundred notes for future
articles, in case I find myself with time to write but can't think of
a topic. Har.
I was not expecting that so many of my articles would take the form
"ABCDEFG. But none of this is really germane to the real point
of this article, which is ... HIJKLMN." But the more articles
I write in this style, the more comfortable I am with it. Perhaps in
a hundred years graduate students will refer to an essay of this type,
with two loosely-coupled sections of approximately the same length,
linked by an apologetic phrase, as "Dominus-style".
However, I do know that the phrase "I don't know" (and variations,
like "did not know") appears 67 times, in 44 of the 161 articles. I
would like to think that this is one of the things that will set my
blog apart from others, and I hope to improve these numbers in the
coming years.
[Other articles in category /meta]
permanent link
ssh-agent, revisited
Other machines trust B, but not A, so credential
forwarding is not the solution here either.
I concluded that the identifying information, 711505562, was useless.
Aaron Crane corrected me on this; you can find it listed in
/proc/net/unix, which gives the pathname in the
filesystem:
I had suggested that the kernel probably maintained no direct mapping
from the socket i-number to the filesystem path, and that obtaining
this information would require difficult grovelling of the kernel data
structures. But apparently to whatever extent that is true, it is
irrelevant, since the /proc/net/unix driver has already been
written to do it.
[Other articles in category /Unix]
permanent link
Messages from the future
This is completely unnecessary. You can wait until you have evidence
of messages from the future before you do this.
Here's what you should do. If someone contacts you, claiming to be
your future self, have them send you a copy of some document—the
Declaration of Independence, for example, or just a letter of
introduction from themselves to you, but really it doesn't need to be
more than about a hundred characters long—encrypted with a
one-time pad. The message, being encrypted, will appear to be complete
gibberish.
Then pull a coin out of your pocket and start flipping it. Use the
coin flips as the one-time pad to decrypt the message; record the pad
as you obtain it from the coin.
Don't do the decryption all at once.
Use several coins, in several different places, over a period of
several weeks.
Don't even use coins. Say to yourself one day, on a whim, "I think
I'll decrypt the next bit of the message by looking out the window and
counting red cars that go by. If an odd number of red cars go by in
the next minute, I'll take that as a head, and if an even number of
red cars go by, I'll take that as a tail." Go to the museum and use
their Geiger counter for the next few bits. Use the stock market
listings for a few of the bits, and the results of the World Series
for a couple.
If the message is not actually from your future self, the coin flips
and other random bits you generate will not decrypt it, and you will
get complete gibberish.
But if the coin flips and other random bits miraculously turn out to
decrypt the message perfectly, you can be quite sure that you are dealing
with a person from the future, because nobody else could possibly have
predicted the random bits.
Now you need to make sure the person from the future is really you.
Make up a secret password. Encrypt the one-time pad with a
conventional secret-key method, using your secret password as the key.
Save the encrypted pad in several safe places, so that you can get it
later when you need it, and commit the password to memory. Destroy
the unencrypted version of the pad. (Or just memorize the pad. It's
not as hard as you think.)
Later, when the time comes to send a message into the past, go get the
pad from wherever you stashed it and decrypt it with the secret key
you committed to memory. This gives you a complete record of the
results of the coin flips and other events that the past-you used to
decrypt your message. You can then prepare your encrypted message
accordingly.
[Other articles in category /CS]
permanent link
"snow is white" is false when you change "is" to "is not".
Or similarly:
If a sentence is false, then its negation is true.
Nevertheless, Quine's sentence is an antinomy of the same sort as the
example sentences at the top of the article.
Lorrie and I had fondue for dinner two nights ago. To make cheese
fondue, you melt a lot of Swiss cheese into a cup of dry white wine,
then serve hot and dunk chunks of bread into the melted cheese with
long forks. Recipe
Rub the inside of a heavy saucepan with a cut garlic clove. Heat 1
cup Riesling over medium heat in the saucepan. When the surface of
the wine is covered with fine bubbles, add 1 tablespoon corn starch
and stir until dissolved. Reduce heat and slowly add 3/4 lb grated
emmenthaler and 3/4 lb grated gruyere cheeses, stirring constantly
until completely melted.
A while back I recounted the joke about the plover's egg: A teenage
girl, upon hearing that the human testicle is the size of a plover's
egg, remarks "Oh, so that's how big a plover's egg is." I believe this
was considered risqué in 1974, when it was current. But today
I was reminded of it in a rather different context.
For appropriate values of "everyone", everyone knows that Unix files
do not record any sort of "creation time". A fairly frequently asked
question in Unix programming forums, and other related forums, such as
Perl programming forums, is how to get the creation date of a file;
the answer is that you cannot do that because it is not there.
How does one check and change ctime?
And when questioned as to why he or she wanted to do this, this person
replied:
We are looking to change the creation time. From what I understand,
ctime is the closest thing to creation time.
There is something about this reply that irritates me, but I'm not
quite sure what it is. Several responses come to mind: "Close" is
not sufficient in system programming; the ctime is not "close" to a
creation time, in any sense; before you go trying to change the thing,
you ought to do a minimal amount of research to find out what it is.
It is a perfect example of the Wrong Question, on the same order as
that poor slob all those years ago who wanted to know how to tell if a
file was a hard link or a soft link.
An error? I don't think so. Here is corroborating evidence, the
stat man page from the first edition of Unix, from 1971:IV. IMPLEMENTATION OF THE FILE SYSTEM
... The entry found thereby (the file's i-node) contains the
description of the file:
...
time of creation, last use, and last modification
NAME stat -- get file status
SYNOPSIS sys stat; name; buf / stat = 18.
DESCRIPTION name points to a null-terminated string naming a file; buf is the
address of a 34(10) byte buffer into which information is placed
concerning the file. It is unnecessary to have any permissions at all
with respect to the file, but all directories leading to the file
must be readable.
After stat, buf has the following format:
buf, +1 i-number
+2, +3 flags (see below)
+4 number of links
+5 user ID of owner size in bytes
+6,+7 size in bytes
+8,+9 first indirect block or contents block
...
+22,+23 eighth indirect block or contents block
+24,+25,+26,+27 creation time
+28,+29, +30,+31 modification time
+32,+33 unused
(Dennis Ritchie provides the Unix
first edition manual; the stat page is in section
2.1.)
struct inode {
char i_flag;
char i_count;
int i_dev;
int i_number;
int i_mode;
char i_nlink;
char i_uid;
char i_gid;
char i_size0;
char *i_size1;
int i_addr[8];
int i_lastr;
} inode[NINODE];
The i_lastr field is what we would now call the atime. (I
suppose it stands for "last read".) The mtime and ctime are not
there, because they are not stored in the in-memory copy of the inode.
They are fetched directly from the disk when needed.
1 stat1(ip, ub)
2 int *ip;
3 {
4 register i, *bp, *cp;
5
6 iupdat(ip, time);
7 bp = bread(ip->i_dev, ldiv(ip->i_number+31, 16));
8 cp = bp->b_addr + 32*lrem(ip->i_number+31, 16) + 24;
9 ip = &(ip->i_dev);
10 for(i=0; i<14; i++) {
11 suword(ub, *ip++);
12 ub =+ 2;
13 }
14 for(i=0; i<4; i++) {
15 suword(ub, *cp++);
16 ub =+ 2;
17 }
18 brelse(bp);
19 }
ub is the user buffer into which the stat data will be
deposited. ip is the inode structure from which most of
this data will be copied. The
suword utility copies a two-byte unsigned integer ("short
unsigned word") from source to destination. This is done starting at
the i_dev field (line 9), which effectively skips the two
earlier fields, i_flag and i_count, which are
internal kernel matters that are none of the user's business.
1 chmod()
2 {
3 register *ip;
4
5 if ((ip = owner()) == NULL)
6 return;
7 ip->i_mode =& ~07777;
8 if (u.u_uid)
9 u.u_arg[1] =& ~ISVTX;
10 ip->i_mode =| u.u_arg[1]&07777;
11 ip->i_flag =| IUPD;
12 iput(ip);
13 }
Line 10 is the important one; it sets the mode on the in-memory copy
of the inode to the argument supplied by the user. Then line 11 sets
the IUPD flag to indicate that the inode has been modified.
Line 12 calls iput, whose principal job is to maintain the
kernel's internal reference count of the number of file descriptors
that are attached to this inode. When this number reaches zero, the
inode is written back to disk, and discarded from the kernel's open
file table. The iupdat function, called from iput,
is the one that actually writes the modified inode back to the
disk:
1 iupdat(p, tm)
2 int *p;
3 int *tm;
4 {
5 register *ip1, *ip2, *rp;
6 int *bp, i;
7
8 rp = p;
9 if((rp->i_flag&(IUPD|IACC)) != 0) {
10 if(getfs(rp->i_dev)->s_ronly)
11 return;
12 i = rp->i_number+31;
13 bp = bread(rp->i_dev, ldiv(i,16));
14 ip1 = bp->b_addr + 32*lrem(i, 16);
15 ip2 = &rp->i_mode;
16 while(ip2 < &rp->i_addr[8])
17 *ip1++ = *ip2++;
18 if(rp->i_flag&IACC) {
19 *ip1++ = time[0];
20 *ip1++ = time[1];
21 } else
22 ip1 =+ 2;
23 if(rp->i_flag&IUPD) {
24 *ip1++ = *tm++;
25 *ip1++ = *tm;
26 }
27 bwrite(bp);
28 }
29 }
What is going on here? p is the in-memory copy of the inode
we want to update. It is immediately copied into a register, and
called by the alias rp thereafter. tm is the time
that the kernel should write into the mtime field of the inode.
Usually this is the current time, but the smdate system call
("set modified date") supplies it from the user instead.
struct inode {
int dev;
...
int atime[2];
int mtime[2];
};
No sign of the ctime, which would have been after the mtime
field. (Of course, it could be there anyway, unmentioned in the
declaration, since it is last.) And similarly, the ls command
has:
struct ibuf {
int idev;
int inum;
...
char *iatime[2];
char *imtime[2];
};
A couple of commands have extremely misleading declarations. Here's
the struct inode from the prof command, which prints
profiling reports:
struct inode {
int idev;
...
int ctime[2];
int mtime[2];
int fill;
};
The atime field has erroneously been called ctime here, but
it seems that since prof does not use the atime, nobody
noticed the bug. And there's a mystery fill field at the
end, as if prof is expecting one more field, but doesn't know
what it will be for. The declaration of ibuf in the
ln command has similar oddities.
Unix is full of little utility programs that run some other program in
a slightly modified environment. For example, the nohup
command:
SYNOPSIS
nohup COMMAND [ARG]...
DESCRIPTION
Run COMMAND, ignoring hangup signals.
/* declares USERAREA_* constants,
int userarea_set(int, ...)
and void *userarea_get(int)
*/
#include <sys/userarea.h>
userarea_set(USERAREA_NICE, 12);
userarea_set(USERAREA_CWD, "/tmp");
userarea_set(USERAREA_SIGNAL, SIGHUP, SIG_IGN);
userarea_set(USERAREA_UMASK, 0022);
...
This has several drawbacks. One is that it requires kernel hacking.
A subitem of this is that it will never become widespread, and that if
you can't (or don't want to) replace your kernel, it cannot be made to
work for you. Another is that it does not work for the environment
variables, which are not really administered by the kernel. Another
is that it does not fully solve the original problem, which is to
obviate the plethora of nice, nohup, sudo,
and env commands. You would still have to write a command
to replace them. I had thought of another drawback, but forgot it while I
was writing the last two sentences.
newenv nice=12 cwd=/tmp signal=HUP:IGNORE umask=0022 -- command args...
Then newenv has a giant dispatch table inside it to process
the settings accordingly:
...
nice => sub { setpriority(PRIO_PROCESS, $$, $_) },
cwd => sub { chdir($_) },
signal => sub {
my ($name, $result) = split /:/;
$SIG{$name} = $result;
},
umask => sub { umask(oct($_)) },
...
One question to ask is whether something like this already exists.
Another is, if not, whether it's because there's some reason why it's
a bad idea, or because there's a simpler solution, or just because
nobody has done it yet.
In an earlier
article, I asserted that the average length of a baseball game was
very close to 9 innings. This is a good rule of thumb, but it is also
something of a coincidence, and might not be true in every year.
And as in arithmetic unpractised men must, and professors themselves
may often, err, and cast up false; so also in any other subject of
reasoning, the ablest, most attentive, and most practised men may
deceive themselves, and infer false conclusions; not but that reason
itself is always right reason, as well as arithmetic is a certain and
infallible art: but no one man's reason, nor the reason of any one
number of men, makes the certainty; no more than an account is
therefore well cast up because a great many men have unanimously
approved it. And therefore, as when there is a controversy in an
account, the parties must by their own accord set up for right reason
the reason of some arbitrator, or judge, to whose sentence they will
both stand, or their controversy must either come to blows, or be
undecided, for want of a right reason constituted by Nature; so is it
also in all debates of what kind soever: and when men that think
themselves wiser than all others clamour and demand right reason for
judge, yet seek no more but that things should be determined by no
other men's reason but their own, it is as intolerable in the society
of men, as it is in play after trump is turned to use for trump on
every occasion that suit whereof they have most in their hand. For
they do nothing else, that will have every of their passions, as it
comes to bear sway in them, to be taken for right reason, and that in
their own controversies: bewraying their want of right reason by the
claim they lay to it.
Gosh, that is so true. Leviathan is of course
available online at many locations; here
is one such.
Hobbes says, in short, that the square root of 100 squares is not 10
unit lengths, but 10 squares. That is his whole argument.The Theoreme.
The four sides of a Square, being divided into any
number of equal parts, for example into 10; and straight lines being
drawn through opposite points, which will divide the Square into 100
lesser Squares; The received Opinion, and which Dr. Wallis commonly
useth, is, that the root of those 100, namely 10, is the side of the
whole Square.The Confutation.
The Root 10 is a number of those Squares,
whereof the whole containeth 100, whereof one Square is an Unitie;
therefore, the Root 10, is 10 Squares: Therefore the root of 100 Squares is 10 Squares, and
not the side of any Square; because the side of a Square is
not a Superfices, but a Line.
Like as 10 dozen is the root, not of 100 dozen, but of 100 dozen
dozen. ... But, says he, the root of 100 soldiers, is 10 soldiers.
Answer: No such matter, for 100 soldiers is not the product of 10
soldiers into 10 soldiers, but of 10 soldiers into the number 10: And
therefore neither 10, nor 10 soldiers, is the root of it.
Post scriptum: The remarkable blog Giornale Nuovo
recently had an
article about engraved title pages of English books, and mentioned
Leviathan's famous illustration specifically. Check it out.
The problems are not related to geometric circles; the are logically
circular. 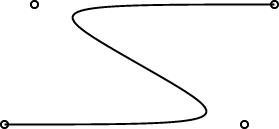 In the course of preparing my sample curve diagrams, one of which is
shown at right, I ran into several related bugs in the way that arrays
were being handled. What I really wanted to do was to define a
labeled_curve object, something like this:
In the course of preparing my sample curve diagrams, one of which is
shown at right, I ran into several related bugs in the way that arrays
were being handled. What I really wanted to do was to define a
labeled_curve object, something like this:
define labeled_curve extends curve {
spot s[N];
constraints { s[i] = control[i]; }
}
That is, it is just like an ordinary curve, except that it also has a
"spot" at each control point. A "spot" is a graphic element that
marks the control point, probably with a small circle or something of
the sort:
define spot extends point {
circle circ(r=0.05);
constraints {
circ.c.x = x; circ.c.y = y;
}
}
A spot is like a point, and so it has an x
and a y coordinate. But it also has a circle, circ,
which is centered at this location. (circ.c is the center of
the circle.)
define snark {
param number p = 3;
}
define boojum {
param number N = s[2].p;
snark s[N];
}
Here the program needs to know the value of N in order to
decide how many snarks are in a boojum. But the number N itself is
determined by examining the p parameter in snark 2, which
itself will not exist if N is less than 3. Should this sort of
nonsense be allowed? I'm not sure yet.
Lately most of my spare time (and some not-spare time) has been going
to linogram. I've been posting updates pretty regularly at
the main linogram page. But I don't know if
anyone ever looks at that page. That got me thinking that it was not
convenient to use, even for people who are interested in
linogram, and that maybe I should have an RSS/Atom feed for
that page so that people who are interested do not have to keep
checking back.  this RSS feed
or
this RSS feed
or
 this Atom feed.
this Atom feed.
I've been saying for a while that a well-designed system surprises
even the designer with its power and expressiveness. Every time
linogram surprises me, I feel a flush of satisfaction because
this is evidence that I designed it well. I'm beginning to think that
linogram may be the best single piece of design I've
ever done.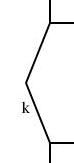
define bentline {
line upper, lower;
param number depth = 0.2;
point start, end, center;
constraints {
center = upper.end = lower.start;
start = upper.start; end = lower.end;
start.x = end.x = center.x + depth;
center.y = (start.y + end.y)/2;
}
}
...
bentline k;
label klbl(text="k") = k.upper.center - (0.1, 0);
...
constraints {
...
k.start = plus.sw; k.end = times.nw;
...
}
So I had defined a thing called a bentline, which is a line
with a slight angle in it. Or more precisely, it's two
approximately-vertical lines joined end-to-end. It has three
important reference points: start, which is the top point,
end, the bottom point, which is directly under the top
point, and center, halfway in between, but displaced
leftward by depth.
require "curve";
define bentline_curved extends bentline {
curve c(N=3);
constraints {
c.control[0] = start;
c.control[1] = center;
c.control[2] = end;
}
draw { c; }
}
A bentline_curved is now the same as a bentline, but
with an extra curved line, called c, which has three control
points, defined to be identical with start, center,
and end. These three points inherit all the same constraints
as before, and so are constrained in the same way and positioned in
the same way. But instead of drawing the two lines, the
bentline_curved draws only the curve.
bentline k;
with:
bentline_curved k;
and recompiled the diagram. The result is below:
To make this change, I didn't have to edit or understand the
definition of bentline, except to understand a bit about its
interface: begin, end, and center. I could
build a new definition atop it that allowed the rest of the program to
use it in exactly the same way, although it was drawn in a completely
different way.
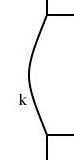
The array feature is working, pending some bug fixes. I have not yet
found all the bugs, I think. But the feature has definitely moved
from the does-not-work-at-all phase into the mostly-works phase. That
is, I am spending most of my time tracking down bugs, rather than
writing large amount of code. The test suite is expanding rapidly.
Here's
a more complicated curve demo.
The array feature is almost complete, perhaps entirely complete.
Fully nontrivial tests are passing. For example, here is test
polygon002 from the distribution:
require "polygon";
polygon t1(N=3), t2(N=3);
constraints {
t1.v[0] = (0, 0);
t1.v[1] = (1, 1);
t1.v[2] = (2, 3);
t2.v[i] = t1.v[i-1];
}
This defines two polygons, t1 and
t2, each with three sides. The three vertices of
t1 are specified explicitly. Triangle
t2 is the same, but with the vertices numbered
differently: t2.v0 =
t1.v2,
t2.v1 =
t1.v0, and
t2.v2 =
t1.v1. Each of the triangles also
has three edges, defined implicitly by the definition in
polygon.lino:
require "point";
require "line";
define polygon {
param index N;
point v[N];
line e[N];
constraints {
e[i].start = v[i];
e[i].end = v[i+1];
}
}
All together, there are 38 values here: 2 coordinates for each of
three vertices of each of the two triangles makes 12; 2 coordinates
for each of two endpoints of each of three edges of each of the two
triangles is another 24, and the two N values themselves
makes a total of 12 + 24 + 2 = 38.
e0.end = v0+1
Then it must fold the constants in the subscripts and apply the
appropriate overflow semantics—in this case, 2+1=0.
e1.end = v1+1
e2.end = v2+1
I haven't done a math article for a while. The most recent math
things I read were some papers on the following theorem: Obviously,
there is a topological space X such that X3 =
R3, namely, X = R. But is there a space
X such that X2 = R3? ("=" here denotes
topological homeomorphism.)
This is the end of the first year of my blog. The dates on the early
articles say that I posted a few in 2005, but they are deceptive. I
didn't want a blog with only one post in it, so I posted a bunch of
stuff that I had already written, and backdated it to the dates on
which I had written it. The blog first appeared on 8 January, 2006,
and this was the date on which I wrote its first articles.Output
Not counting this article, I posted 161 articles this year, totalling
about 172,000 words, which I think is not a bad output. About 1/4 of
this output was about mathematics.Financial
I incurred the costs of Dreamhosting (see below). But these costs are
offset because I am also using the DreamHost as a remote backup for
files. So it has some non-blog value, and will also result in a tax
deduction.
I could not decide whether to go with the cute and pathetic begging
approach (shown right) or the brusque and crass demanding approach
(left).
Popularity
The most popular article was certainly the one on Design Patterns of 1972.
I had been thinking this one over for years, and I was glad it
attracted as much attention as it did. Ralph Johnson (author of the
Design Patterns book) responded to it, and I learned that
Design Patterns is not the book that Johnson thought it
was. Gosh, I'm glad I didn't write that book.
System administration
I moved the blog twice. It originally resided on
www.plover.com, which is in my house. I had serious network
problems in July and August, Verizon's little annual gift to me. When
I realized that the blog was be much more popular than I expected, and
that I wanted it to be reliably available, I moved it to
newbabe.pobox.com, which I'd had an account on for years but
had never really used. This account was withdrawn a few months later,
so I rented space at Dreamhost, called blog.plover.com, and
moved it there. I expect it will stay at Dreamhost for quite a
while.Policy
I made a couple of vows when I started the blog. A number of years
ago on my use.perl.org journal I complained extensively about
some people I worked with. They deserved everything I said, but the
remarks caused me a lot of trouble and soured me on blogs for many
years. When I started this blog, I vowed that I wouldn't insult
anyone personally, unless perhaps they were already dead and couldn't
object. Some people have no trouble with this, but for someone like
me, who is a seething cauldron of bile, it required a conscious
effort.What I didn't post this year
My blog directory contains 55 unpublished articles, totalling 39,500
words, in various states of incompleteness; compare this with the 161
articles I did complete.
So that was one long article that never made it;
had it been published, it would have been longer than any other except
the Z2 article.Surprises
I got a number of unpredictable surprises when I started the blog.
One was that I wasn't really aware of LiveJournal, and its "friends"
pages. I found it really weird to see my equation-filled articles on
subvocal reading and Baroque scientific literature appearing on these
pages, sandwiched between posts about Count Chocula from people named
"Taldin the Blue Unicorn". Okay, whatever.Wrong wrong wrong!
I do not have a count of the number of mistakes and errors I made that
I corrected in later articles, although I wish I did. Nor do I have a
count of the number of mistakes that I did not correct.Thanks
Thanks to all my readers for their interest and close attention, and
for making my blog a speedy success.
My recent article about reusing
ssh-agent processes attracted a lot of mail, most of it very
interesting.
Thanks to everyone who wrote in on this matter.
lrwx------ 1 mjd users 64 Dec 12 23:34 3 -> socket:[711505562]
% grep 711505562 /proc/net/unix
ce030540: 00000002 00000000 00010000 0001 01 711505562 /tmp/ssh-tNT31655/agent.31655
I read a pretty dumb article today about passwords that your future
self could use when communicating with you backwards in time, to
authenticate his identity to you. The idea was that you should make
up a password now and commit it to memory so that you can use it later
in case you need to communicate backwards in time.