Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 01 Aug 2007
The snub disphenoid
 The snub
disphenoid is pictured at left. I do not know why it is called that,
and I ought to know, because I am the principal author (so far) of the
Wikipedia article on the disphenoid. Also,
I never quite figured out what "snub" means in this context, despite
perusing that section of H.S.M. Coxeter's book on polytopes at some
length. It has something to do with being halfway between what you
get when you cut all the corners off, and what you get when you cut all
the corners off again.
The snub
disphenoid is pictured at left. I do not know why it is called that,
and I ought to know, because I am the principal author (so far) of the
Wikipedia article on the disphenoid. Also,
I never quite figured out what "snub" means in this context, despite
perusing that section of H.S.M. Coxeter's book on polytopes at some
length. It has something to do with being halfway between what you
get when you cut all the corners off, and what you get when you cut all
the corners off again.

 Anyway, earlier this week I was visiting John Batzel, who works
upstairs from me, and discovered that he had obtained a really cool
toy. It was a collection of large steel ball bearings and colored
magnetic rods, which could be assembled into various polyhedra and
trusses. This is irresistible to me. The pictures at right, taken around
2002, show me modeling a dodecahedron with less suitable
materials.
Anyway, earlier this week I was visiting John Batzel, who works
upstairs from me, and discovered that he had obtained a really cool
toy. It was a collection of large steel ball bearings and colored
magnetic rods, which could be assembled into various polyhedra and
trusses. This is irresistible to me. The pictures at right, taken around
2002, show me modeling a dodecahedron with less suitable
materials.
The first thing I tried to make out of John's magnetic sticks and balls was a regular dodecahedron, because it is my favorite polyhedron. (Isn't it everyone's?) This was unsuccessful, because it wasn't rigid enough, and kept collapsing. It's possible that if I had gotten the whole thing together it would have been stable, but holding the 50 separate magnetic parts in the right place long enough to get it together was too taxing, so I tried putting together some other things.
A pentagonal dipyramid worked out well, however. To understand this solid, imagine a regular pyramid, such as the kind that entombs the pharaohs or collects mystical energy. This sort of pyramid is known as a square pyramid, because it has a square base, and thus four triangular sides. Imagine that the base was instead a pentagon, so that there were five triangular sides sides instead of only four. Then it would be a pentagonal pyramid. Now take two such pentagonal pyramids and glue the pentagonal bases together. You now have a pentagonal dipyramid.
The success of the pentagonal dipyramid gave me the idea that rigid triangular lattices were the way to go with this toy, so I built an octahedron (square dipyramid) and an icosahedron to be sure. Even the icosahedron (thirty sticks and twelve balls) held together and supported its own weight. So I had John bring up the Wikipedia article about deltahedra. A deltahedron is just a polyhedron whose faces are all equilateral triangles.
Four of the deltahedra are the tetrahedron (triangular pyramid, with 4 faces), triangular dipyramid (6 faces), octahedron (square dipyramid, 8 faces), and pentagonal dipyramid (10 faces).
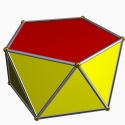
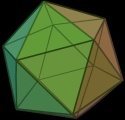 Another is the icosahedron. Imagine making a belt of 10 triangles,
alternating up and down, and then connect the ends of the belt. The result is a
shape called a pentagonal
antiprism, shown at left. The edges of the down-pointing triangles form a
pentagon on the top of the antiprism, and the edges of the up-pointing
triangles form one on the bottom. Attach a pentagonal pyramid to each
of these pentagons, and you have an icosahedron, with a total of 20
faces.
Another is the icosahedron. Imagine making a belt of 10 triangles,
alternating up and down, and then connect the ends of the belt. The result is a
shape called a pentagonal
antiprism, shown at left. The edges of the down-pointing triangles form a
pentagon on the top of the antiprism, and the edges of the up-pointing
triangles form one on the bottom. Attach a pentagonal pyramid to each
of these pentagons, and you have an icosahedron, with a total of 20
faces.
The other three deltahedra are less frequently seen. One is the
result of taking a triangular prism and appending a square pyramid to
each of its three square faces. (Wikipedia calls this a "triaugmented
triangular prism"; I don't know how standard that name is.) Since the
prism had two triangular faces to begin with, and we have added four
more to each of the three square faces of the original prism, the
total is 14 faces.
Another deltahedron is the "gyroelongated square dipyramid". You get this by taking two square pyramids, as with the octahedron. But instead of gluing their square bases together directly, you splice a square antiprism in between. The two square faces of the antiprism are not aligned; they are turned at an angle of 45° to each other, so that when you are looking at the top pyramid face-on, you are looking at the bottom pyramid edge-on, and this is the "gyro" in "gyroelongated". (The icosahedron is a gyroelongated pentagonal dipyramid.) I made one of these in John's office, but found it rather straightforward.
The last deltahedron, however, was quite a puzzle. Wikipedia calls it a "snub disphenoid", and as I mentioned before, the name did not help me out at all. It took me several tries to build it correctly. It contains 12 faces and 8 vertices. When I finally had the model I still couldn't figure it out, and spent quite a long time rotating it and examining it. It has a rather strange symmetry. It is front-back and left-right symmetric. And it is almost top-bottom symmetric: If you give it a vertical reflection, you get the same thing back, but rotated 90° around the vertical axis.
When I planned this article I thought I understood it better. Imagine sticking together two equilateral triangles. Call the common edge the "rib". Fold the resulting rhombus along the rib so that the edges go up, down, up, down in a zigzag. Let's call the resulting shape a "wing"; it has a concave side and a convex side. Take two wings. Orient them with the concave sides facing each other, and with the ribs not parallel, but at right angles. So far, so good.
But this is where I started to get it wrong. The two wings have between them eight edges, and I had imagined that you could glue a rhombic antiprism in between them. I'm not convinced that there is such a thing as a rhombic antiprism, but I'll have to do some arithmetic to be sure. Anyway, supposing that there were such a thing, you could glue it in as I said, but if you did the wings would flatten out and what you would get would not be a proper polyhedron because the two triangles in each wing would be coplanar, and polyhedra are not allowed to have abutting coplanar faces. (The putative gyroelongated triangular dipyramid fails for this reason, I believe.)
To make the snub disphenoid, you do stick eight triangles in between the two wings, but the eight triangles do not form a rhombic antiprism. Even supposing that such a thing exists.
I hope to have some nice renderings for you later. I have been doing some fun work in rendering semiregular polyhedra, and I am looking forward to discussing it here. Advance peek: suppose you know how the vertices are connected by edges. How do you figure out where the vertices are located in 3-space?
If you would like to investigate this, the snub disphenoid has 8 vertices, which we can call A, B, ... H. Then:
| This vertex: | is connected to these: |
| A | B C E F H |
| B | A C D E |
| C | A B D H |
| D | B C E G H |
| E | F G A B D |
| F | E G H A |
| G | E F H D |
| H | F G A C D |
Here is a list of the eight deltahedra, with links to the corresponding Wikipedia articles:
| Name | Faces | Edges | Vertices |
| Tetrahedron | 4 | 6 | 4 |
| Triangular dipyramid | 6 | 9 | 5 |
| Octahedron | 8 | 12 | 6 |
| Pentagonal dipyramid | 10 | 15 | 7 |
| Snub disphenoid | 12 | 18 | 8 |
| Triaugmented triangular prism | 14 | 21 | 9 |
| Gyroelongated square dipyramid | 16 | 24 | 10 |
| Icosahedron | 20 | 30 | 12 |
[ Addendum 20070908: More about deltahedra. ]
[Other articles in category /math] permanent link


