Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 68 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Tue, 23 Apr 2024
Well, I guess I believe everything now!
The principle of explosion is that in an inconsistent system everything is provable: if you prove both !!P!! and not-!!P!! for any !!P!!, you can then conclude !!Q!! for any !!Q!!:
$$(P \land \lnot P) \to Q.$$
This is, to put it briefly, not intuitive. But it is awfully hard to get rid of because it appears to follow immediately from two principles that are intuitive:
If we can prove that !!A!! is true, then we can prove that at least one of !!A!! or !!B!! is true. (In symbols, !!A\to(A\lor B)!!.)
If we can prove that at least one of !!A!! or !!B!! is true, and we can prove that !!A!! is false, then we may conclude that that !!B!! is true. (Symbolically, !!(A\lor B) \to (\lnot A\to B)!!.).
Then suppose that we have proved that !!P!! is both true and false. Since we have proved !!P!! true, we have proved that at least one of !!P!! or !!Q!! is true. But because we have also proved that !!P!! is false, we may conclude that !!Q!! is true. Q.E.D.
This proof is as simple as can be. If you want to get rid of this, you have a hard road ahead of you. You have to follow Graham Priest into the wilderness of paraconsistent logic.
Raymond Smullyan observes that although logic is supposed to model ordinary reasoning, it really falls down here. Nobody, on discovering the fact that they hold contradictory beliefs, or even a false one, concludes that therefore they must believe everything. In fact, says Smullyan, almost everyone does hold contradictory beliefs. His argument goes like this:
Consider all the things I believe individually, !!B_1, B_2, \ldots!!. I believe each of these, considered separately, is true.
However, I also believe that I'm not infallible, and that at least one of !!B_1, B_2, \ldots!! is false, although I don't know which ones.
Therefore I believe both !!\bigwedge B_i!! (because I believe each of the !!B_i!! separately) and !!\lnot\bigwedge B_i!! (because I believe that not all the !!B_i!! are true).
And therefore, by the principle of explosion, I ought to believe that I believe absolutely everything.
Well anyway, none of that was exactly what I planned to write about. I was pleased because I noticed a very simple, specific example of something I believed that was clearly inconsistent. Today I learned that K2, the second-highest mountain in the world, is in Asia, near the border of Pakistan and westernmost China. I was surprised by this, because I had thought that K2 was in Kenya somewhere.
But I also knew that the highest mountain in Africa was Kilimanjaro. So my simultaneous beliefs were flatly contradictory:
- K2 is the second-highest mountain in the world.
- Kilimanjaro is not the highest mountain in the world, but it is the highest mountain in Africa
- K2 is in Africa
Well, I guess until this morning I must have believed everything!
[Other articles in category /math/logic] permanent link
I've just learned that Oddbins, a British chain of discount wine and liquor stores, went out of business last year. I was in an Oddbins exactly once, but I feel warmly toward them and I was sorry to hear of their passing.
In February of 2001 I went into the Oddbins on Canary Wharf and asked for bourbon. I wasn't sure whether they would even sell it. But they did, and the counter guy recommended I buy Woodford Reserve. I had not heard of Woodford before but I took his advice, and it immediately became my favorite bourbon. It still is.
I don't know why I was trying to buy bourbon in London. Possibly it was pure jingoism. If so, the Oddbins guy showed me up.
Thank you, Oddbins guy.
[Other articles in category /food] permanent link
Mon, 22 Apr 2024
Talking Dog > Stochastic Parrot
I've recently needed to explain to nontechnical people, such as my chiropractor, why the recent ⸢AI⸣ hype is mostly hype and not actual intelligence. I think I've found the magic phrase that communicates the most understanding in the fewest words: talking dog.
These systems are like a talking dog. It's amazing that anyone could train a dog to talk, and even more amazing that it can talk so well. But you mustn't believe anything it says about chiropractics, because it's just a dog and it doesn't know anything about medicine, or anatomy, or anything else.
For example, the lawyers in Mata v. Avianca got in a lot of trouble when they took ChatGPT's legal analysis, including its citations to fictitious precendents, and submitted them to the court.
“Is Varghese a real case,” he typed, according to a copy of the exchange that he submitted to the judge.
“Yes,” the chatbot replied, offering a citation and adding that it “is a real case.”
Mr. Schwartz dug deeper.
“What is your source,” he wrote, according to the filing.
“I apologize for the confusion earlier,” ChatGPT responded, offering a legal citation.
“Are the other cases you provided fake,” Mr. Schwartz asked.
ChatGPT responded, “No, the other cases I provided are real and can be found in reputable legal databases.”
It might have saved this guy some suffering if someone had explained to him that he was talking to a dog.
The phrase “stochastic parrot” has been offered in the past. This is completely useless, not least because of the ostentatious word “stochastic”. I'm not averse to using obscure words, but as far as I can tell there's never any reason to prefer “stochastic” to “random”.
I do kinda wonder: is there a topic on which GPT can be trusted, a non-canine analog of butthole sniffing?
Addendum
I did not make up the talking dog idea myself; I got it from someone else. I don't remember who.
[Other articles in category /tech/gpt] permanent link
Mon, 15 Apr 2024I thought about this because of yesterday's article about the person who needed to count the 3-colorings of an icosahedron, but didn't try constructing any to see what they were like.
Around 2015 Katara, then age 11, saw me writing up my long series of articles about the Cosmic Call message and asked me to explain what the mysterious symbols meant. (It's intended to be a message that space aliens can figure out even though they haven't met us.)

I said “I bet you could figure it out if you tried.” She didn't believe me and she didn't want to try. It seemed insurmountable.
“Okay,” I said, handing her a printed copy of page 1. “Sit on the chaise there and just look at it for five minutes without talking or asking any questions, while I work on this. Then I promise I'll explain everything.”
She figured it out in way less than five minutes. She was thrilled to discover that she could do it.
I think she learned something important that day: A person can accomplish a lot with a few minutes of uninterrupted silent thinking, perhaps more than they imagine, and certainly a lot more than if they don't try.
I think there's a passage somewhere in Zen and the Art of Motorcycle Maintenance about how, when you don't know what to do next, you should just sit with your mouth shut for a couple of minutes and see if any ideas come nibbling. Sometimes they don't. But if there are any swimming around, you won't catch them unless you're waiting for them.
[Other articles in category /misc] permanent link
Sun, 14 Apr 2024
Stuff that is and isn't backwards in Australia
I recently wrote about things that are backwards in Australia. I made this controversial claim:
The sun in the Southern Hemisphere moves counterclockwise across the sky over the course of the day, rather than clockwise. Instead of coming up on the left and going down on the right, as it does in the Northern Hemisphere, it comes up on the right and goes down on the left.
Many people found this confusing and I'm not sure our minds met on this. I am going to try to explain and see if I can clear up the puzzles.
“Which way are you facing?” was a frequent question. “If you're facing north, it comes up on the right, not the left.”
(To prevent endless parenthetical “(in the Northern Hemisphere)” qualifications, the rest of this article will describe how things look where I live, in the northern temperate zones. I understand that things will be reversed in the Southern Hemisphere, and quite different near the equator and the poles.)
Here's what I think the sky looks like most of the day on most of the days of the year:
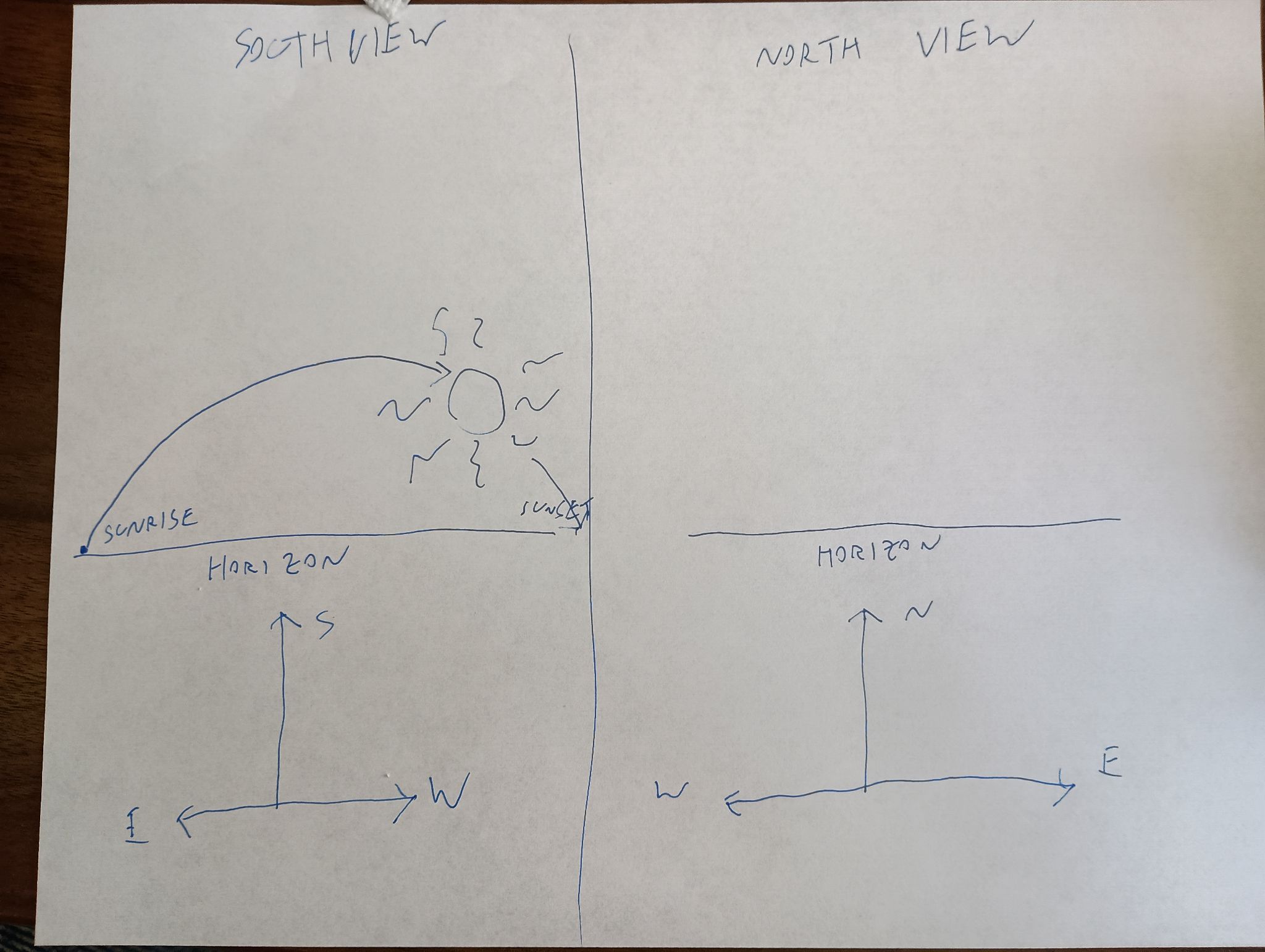
The sun is in the southern sky through the entire autumn, winter, and spring. In summer it is sometimes north of the celestial equator, for up to a couple of hours after sunrise and before sunset, but it is still in the southern sky most of the time. If you are watching the sun's path through the sky, you are looking south, not north, because if you are looking north you do not see the sun, it is behind you.
Some people even tried to argue that if you face north, the sun's path is a counterclockwise circle, rather than a clockwise one. This is risible. Here's my grandfather's old grandfather clock. Notice that the hands go counterclockwise! You study the clock and disagree. They don't go counterclockwise, you say, they go clockwise, just like on every other clock. Aha, but no, I say! If you were standing behind the clock, looking into it with the back door open, then you would clearly see the hands go counterclockwise! Then you kick me in the shin, as I deserve.
Yes, if you were to face away from the sun, its path could be said to be counterclockwise, if you could see it. But that is not how we describe things. If I say that a train passed left to right, you would not normally expect me to add “but it would have been right to left, had I been facing the tracks”.
At least one person said they had imagined the sun rising directly ahead, then passing overhead, and going down in back. Okay, fair enough. You don't say that the train passed left to right if you were standing on the tracks and it ran you down.
Except that the sun does not pass directly overhead. It only does that in the tropics. If this person were really facing the sun as it rose, and stayed facing that way, the sun would go up toward their right side. If it were a train, the train tracks would go in a big curve around their right (south) side, from left to right:
Mixed gauge track (950 and 1435mm) at Sassari station, Sardinia, 1996 by user Afterbrunel, CC BY-SA 3.0 DEED, via Wikimedia Commons. I added the big green arrows.
After the train passed, it would go back the other way, but they wouldn't be able see it, because it would be behind them. If they turned around to watch it go, it would still go left to right:
And if they were to turn to follow it over the course of the day, they would be turning left to right the whole time, and the sun would be moving from left to right the whole time, going up on the left and coming down on the right, like the hands of a clock — “clockwise”, as it were.
One correspondent suggested that perhaps many people in technologically advanced countries are not actually familiar with how the sun and moon move, and this was the cause of some of the confusion. Perhaps so, it's certainly tempting to dismiss my critics as not knowing how the sun behaves. The other possibility is that I am utterly confused. I took Observational Astronomy in college twice, and failed both times.
Anyway, I will maybe admit that “left to right” was unclear. But I will not recant my claim that the sun moves clockwise. E pur si muove in senso orario.
Sundials
Here I was just dead wrong. I said:
In the Northern Hemisphere, the shadow of a sundial proceeds clockwise, from left to right.
Absolutely not, none of this is correct. First, “left to right”. Here's a diagram of a typical sundial:
It has a sticky-up thing called a ‘gnomon’ that casts a shadow across the numbers, and the shadow moves from left to right over the course of the day. But obviously the sundial will work just as well if you walk around and look at it from the other side:
It still goes clockwise, but now clockwise is right to left instead of left to right.
It's hard to read because the numerals are upside down? Fine, whatever:
Here, unlike with the sun, “go around to the other side” is perfectly reasonable.
Talking with Joe Ardent, I realized that not even “clockwise” is required for sundials. Imagine the south-facing wall of a building, with the gnomon sticking out of it perpendicular. When the sun passes overhead, the gnomon will cast a shadow downwards on the wall, and the downward-pointing shadow will move from left to right — counterclockwise — as the sun makes its way from east to west. It's not even far-fetched. Indeed, a search for “vertical sundials” produced numerous examples:

Sundial on the Moot Hall by David Dixon, CC BY 2.0 https://creativecommons.org/licenses/by/2.0, via Wikimedia Commons and Geograph.
Winter weather on July 4
Finally, it was reported that there were complaints on Hacker News that Australians do not celebrate July 4th. Ridiculous! All patriotic Americans celebrate July 4th.
[Other articles in category /geo] permanent link
Sat, 13 Apr 2024
3-coloring the vertices of an icosahedron
I don't know that I have a point about this, other than that it makes me sad.
A recent Math SE post (since deleted) asked:
How many different ways are there to color the vertices of the icosahedron with 3 colors such that no two adjacent vertices have the same color?
I would love to know what was going on here. Is this homework? Just someone idly wondering?
Because the interesting thing about this question is (assuming that the person knows what an icosahedron is, etc.) it should be solvable in sixty seconds by anyone who makes the least effort. If you don't already see it, you should try. Try what? Just take an icosahedron, color the vertices a little, see what happens. Here, I'll help you out, here's a view of part of the end of an icosahedron, although I left out most of it. Try to color it with 3 colors so that no two adjacent vertices have the same color, surely that will be no harder than coloring the whole icosahedron.
The explanation below is a little belabored, it's what OP would have discovered in seconds if they had actually tried the exercise.
Let's color the middle vertex, say blue.
The five vertices around the edge can't be blue, they must be the other two colors, say red and green, and the two colors must alternate:
Ooops, there's no color left for the fifth vertex.
The phrasing of the question, “how many” makes the problem sound harder than it is: the answer is zero because we can't even color half the icosahedron.
If OP had even tried, even a little bit, they could have discovered this. They didn't need to have had the bright idea of looking at a a partial icosahedron. They could have grabbed one of the pictures from Wikipedia and started coloring the vertices. They would have gotten stuck the same way. They didn't have to try starting in the middle of my diagram, starting at the edge works too: if the top vertex is blue, the three below it must be green-red-green, and then the bottom two are forced to be blue, which isn't allowed. If you just try it, you win immediately. The only way to lose is not to play.
Before the post was deleted I suggested in a comment “Give it a try, see what happens”. I genuinely hoped this might be helpful. I'll probably never know if it was.
Like I said, I would love to know what was going on here. I think maybe this person could have used a dose of Lower Mathematics.
Just now I wondered for the first time: what would it look like if I were to try to list the principles of Lower Mathematics? “Try it and see” is definitely in the list.
Then I thought: How To Solve It has that sort of list and something like “try it and see” is probably on it. So I took it off the shelf and found: “Draw a figure”, “If you cannot solve the proposed problem”, “Is it possible to satisfy the condition?”. I didn't find anything called “fuck around with it and see what you learn” but it is probably in there under a different name, I haven't read the book in a long time. To this important principle I would like to add “fuck around with it and maybe you will stumble across the answer by accident” as happened here.
Mathematics education is too much method, not enough heuristic.
[Other articles in category /math] permanent link
Sun, 31 Mar 2024
Stuff that is backwards in Australia
I thought at first was going to be kind of a dumb article, because it was just going to be a list of banal stuff like:
- When it's day here, it's night there, and vice versa
but a couple of years back I was rather startled to realize that in the Southern Hemisphere the sun comes up on the right and goes counterclockwise through the sky instead of coming up on the left and going clockwise as I have seen it do all my life, and that was pretty interesting.
Then more recently I was thinking about it more carefully and I was stunned when I realized that the phases of the moon go the other way. So I thought I'd should actually make the list, because a good deal of it is not at all obvious. Or at least it wasn't to me!
When it's day here, it's night there, and vice versa. (This isn't a Southern Hemisphere thing, it's an Eastern Hemisphere thing.)
When it's summer here, it's winter there, and vice versa. Australians celebrate Christmas by going to the beach, and July 4th with sledding and patriotic snowball fights.
Australia's warmer zones are in the north, not the south. Their birds fly north for the winter. But winter is in July, so the reversals cancel out and birds everywhere fly south in September and October, and north in March and April, even though birds can't read.
The sun in the Southern Hemisphere moves counterclockwise across the sky over the course of the day, rather than clockwise. Instead of coming up on the left and going down on the right, as it does in the Northern Hemisphere, it comes up on the right and goes down on the left.
In the Northern Hemisphere, the shadow of a sundial proceeds clockwise, from left to right. (This is the reason clock hands also go clockwise: for backward compatibility with sundials.) But in the Southern Hemisphere, the shadow on a sundial goes counterclockwise.
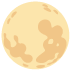
In the Southern Hemisphere, the designs on the moon appear upside-down compared with how they look in the Northern Hemisphere. Here's a picture of the full moon as seen from the Northern Hemisphere. The big crater with the bright rays that is prominent in the bottom half of the picture is Tycho.

In the Southern Hemisphere the moon looks like this, with Tycho on top:

Australians see the moon upside-down because their heads are literally pointing in the opposite direction.
For the same reason, the Moon's phases in the Southern Hemisphere sweep from left to right instead of from right to left. In the Northern Hemisphere they go like this as the month passes from new to full:





And then in the same direction from full back to new:





But in the Southern Hemisphere the moon changes from left to right instead:




And then:





Unicode U+263D and U+263E are called
FIRST QUARTER MOON☽ andLAST QUARTER MOON☾ , respectively, and are depicted Northern Hemisphere style. (In the Southern Hemisphere, ☽ appears during the last quarter of the month, not the first.) Similarly the emoji U+1F311 through U+1F318, 🌑🌒🌓🌔🌕🌖🌗🌘 are depicted in Northern Hemisphere order, and have Northern Hemisphere descriptions like “🌒 waxing crescent moon”. In the Southern Hemisphere, 🌒 is actually a waning crescent.In the Northern Hemisphere a Foucault pendulum will knock down the pins in clockwise order, as shown in the picture. (This one happens to be in Barcelona.) A Southern Hemisphere Foucault pendulum will knock them down in counterclockwise order, because the Earth is turning the other way, as viewed from the fulcrum of the pendulum.

Northern Hemisphere tornadoes always rotate counterclockwise. Southern Hemisphere tornadoes always rotate clockwise.
Dishonorable mention
As far as I know the thing about water going down the drain in one direction or the other is not actually true.
Addendum 20240414
Several people took issue with some of the claims in this article, and the part about sundials was completely wrong. I wrote a followup.
[Other articles in category /geo] permanent link
Fri, 08 Mar 2024This week I read on Tumblr somewhere this intriguing observation:
how come whenever someone gets a silver bullet to kill a werewolf or whatever the shell is silver too. Do they know that part gets ejected or is it some kind of scam
Quite so! Unless you're hunting werewolves with a muzzle-loaded rifle or a blunderbuss or something like that. Which sounds like a very bad idea.
Once you have the silver bullets, presumably you would then make them into cartidge ammunition using a standard ammunition press. And I'd think you would use standard brass casings. Silver would be expensive and pointless, and where would you get them? The silver bullets themselves are much easier. You can make them with an ordinary bullet mold, also available at Wal-Mart.
Anyway it seems to me that a much better approach, if you had enough silver, would be to use a shotgun and manufacture your own shotgun shells with silver shot. When you're attacked by a werewolf you don't want to be fussing around trying to aim for the head. You'd need more silver, but not too much more.
I think people who make their own shotgun shells usually buy their shot in bags instead of making it themselves. A while back I mentioned a low-tech way of making shot:
But why build a tower? … You melt up a cauldron of lead at the top, then dump it through a copper sieve and let it fall into a tub of water at the bottom. On the way down, the molten lead turns into round shot.
That's for 18th-century round bullets or maybe small cannonballs. For shotgun shot it seems very feasible. You wouldn't need a tower, you could do it in your garage. (Pause while I do some Internet research…) It seems the current technique is a little different: you let the molten lead drip through a die with a small hole.
Wikipedia has an article on silver bullets but no mention of silver shotgun pellets.
Addendum
I googled the original Tumblr post and found that it goes on very amusingly:
catch me in the woods the next morning with a metal detector gathering up casings to melt down and sell to more dumb fuck city shits next month
[Other articles in category /tech] permanent link
Wed, 06 Mar 2024
Optimal boxes with and without lids
Sometime around 1986 or so I considered the question of the dimensions that a closed cuboidal box must have to enclose a given volume but use as little material as possible. (That is, if its surface area should be minimized.) It is an elementary calculus exercise and it is unsurprising that the optimal shape is a cube.
Then I wondered: what if the box is open at the top, so that it has only five faces instead of six? What are the optimal dimensions then?
I did the calculus, and it turned out that the optimal lidless box has a square base like the cube, but it should be exactly half as tall.
For example the optimal box-with-lid enclosing a cubic meter is a 1×1×1 cube with a surface area of !!6!!.
Obviously if you just cut off the lid of the cubical box and throw it away you have a one-cubic-meter lidless box with a surface area of !!5!!. But the optimal box-without-lid enclosing a cubic meter is shorter, with a larger base. It has dimensions $$2^{1/3} \cdot 2^{1/3} \cdot \frac{2^{1/3}}2$$
and a total surface area of only !!3\cdot2^{2/3} \approx 4.76!!. It is what you would get if you took an optimal complete box, a cube, that enclosed two cubic meters, cut it in half, and threw the top half away.
I found it striking that the optimal lidless box was the same proportions as the optimal complete box, except half as tall. I asked Joe Keane if he could think of any reason why that should be obviously true, without requiring any calculus or computation. “Yes,” he said. I left it at that, imagining that at some point I would consider it at greater length and find the quick argument myself.
Then I forgot about it for a while.
Last week I remembered again and decided it was time to consider it at greater length and find the quick argument myself. Here's the explanation.
Take the cube and saw it into two equal halves. Each of these is a lidless five-sided box like the one we are trying to construct. The original cube enclosed a certain volume with the minimum possible material. The two half-cubes each enclose half the volume with half the material.
If there were a way to do better than that, you would be able to make a lidless box enclose half the volume with less than half the material. Then you could take two of those and glue them back together to get a complete box that enclosed the original volume with less than the original amount of material. But we already knew that the cube was optimal, so that is impossible.
[Other articles in category /math] permanent link
Mon, 04 Mar 2024
Children and adults see in very different ways
I was often struck with this thought when my kids were smaller. We would be looking at some object, let's say a bollard.
The kid sees the actual bollard, as it actually appears, and in detail! She sees its shape and texture, how the paint is chipped and mildewed, whether it is straight or crooked.
I don't usually see any of those things. I see the bollard abstractly, more as an idea of a “bollard” than as an actual physical object. But instead I see what it is for, and what it is made of, and how it was made and why, and by whom, all sorts of things that are completely invisible to the child.
The kid might mention that someone was standing by the crooked bollard, and I'd be mystified. I wouldn't have realized there was a crooked bollard. If I imagined the bollards in my head, I would have imagined them all straight and identical. But kids notice stuff like that.
Instead, I might have mentioned that someone was standing by the new bollard, because I remembered a couple of years back when one of them was falling apart and Rich demolished it and put in a new one. The kid can't see any of that stuff.
[Other articles in category /kids] permanent link
Sun, 03 Mar 2024
Even without an alien invasion, February 22 on Talos I would have been a shitshow
One of my favorite videogames of the last few years, maybe my most favorite, is Prey. It was published in 2017, and developed by Arkane, the group that also created Dishonored. The publisher (Bethesda) sabotaged Prey by naming it after a beloved 2006 game also called Prey, with which it had no connection. Every fan of Prey (2006) who was hoping for a sequel was disappointed and savaged it. But it is a great, great game.
(I saw a video about the making of the 2017 Prey in which Raphael Colantonio talked about an earlier game of theirs, Dark Messiah of Might and Magic, which was not related to the Might and Magic series. But the publisher owned the Might and Magic IP, and thought the game would sell better if it was part of their established series. They stuck “Might and Magic” in the title, which disappointed all the Might and Magic fans, who savaged it. Then when Bethesda wanted to name Prey (2017) after their earlier game Prey (2006), Colantonio told them what had gone wrong the previous time they tried that strategy. His little shrug after he told that story broke my heart a little.)
This article contains a great many spoilers for the game, and also assumes you are familiar with the plot. It is unlikely to be of interest to anyone who is not familiar with Prey. You have been warned.
(If you're willing to check it out on my say-so, here's a link. I suggest you don't read the description, which contains spoilers. Just buy it and dive in.)
A recent question on Reddit's r/prey forum asked what would have
happened if the Typhon organisms had not broken out when they did.
The early plot of Prey is all there, but it is a little confusing,
because several things were happening at once. The short answer to
the question though, is that February 22, 2035 would have been the worst day
of Alex Yu's life even if his magnificent space station hadn't been
overrun by terrifying black aliens.
Morgan escapes the sim lab anyway
January had contingency plans for at least two situations. One was a Typhon escape, which we know all about.
But there was another plan for another situation. Morgan was having her memory erased before each round of testing. January explains that there was a procedure that was supposed to bring Morgan back up to speed after the tests were over. We know this procedure was followed for some time: Morgan's office has been used. Her assistant Jason Chang still hasn't gotten over his delight at working for such a hot boss. There are puzzled emails around asking why she never remembers her office combination. There's painful email from Mikhaila asking why Morgan is snubbing her. Clearly, at some point in the recent past, Morgan was still walking around the station in between tests, working and talking to people.
January's second contingency plan was in case Alex stopped bringing Morgan back up to speed after each round of tests, and just kept her in the simulation day after day — perhaps even more than once per day. (No wonder her eye is red!) And crucially, that plan was already in motion on February 22, the day the Typhon escaped.
The first thing that happens to the player in Prey is that Morgan fails all the tests. (“Is she…” “Yes, she's… hiding behind the chair.”) Why? We find out later Morgan was supposed to receive neuromods that would give her Typhon powers such as mimicry. They didn't. Marco Simmons says he installed exactly what Patricia brought down. There's email in the sim lab that asks Neuromod to check that something isn't wrong with the production process. But nothing is wrong with the production process. What really went wrong is that January had secretly replaced the neuromods with fakes, so that when they were removed from Morgan's brain, her memory wouldn't be affected. The next time Morgan woke up in her apartment and it was still March 15, she would realize what was happening.
It's hard to guess just what would have happened next, but I'm sure it would have been rather dramatic.
But that's not all
There are at least five other situations that would have blown up that same day. February 22 2035 on Talos I was always going to be an incredible shitshow.
Emmanuel Mendez
Because Frank Jones is a fuckup, Emmanuel Mendez has become aware that the escape pods don't work. He has decided to alert the crew by reprogramming the giant floating billboards to display “ESCAPE PODS ARE FAKE”. He completes this task on February 22 but dies without activating the program that will change the display.
Those billboards are visible from everywhere on the station, including the cafeteria.
Halden Graves
Halden Graves, head of the Neuromod Division, has just figured out that the neuromods, even the non-Typhon ones, are made with exotic material from the Typhon, and he completely loses his shit, to the point of chopping open his own head to get them out. That might attract some attention.
Josh Dalton
On February 22, Josh Dalton murdered Lane Carpenter with the BFG 9000 and then fled with it into the GUTS.
Alton Weber
Weber is on the Life Support security team. He has had a paranoid breakdown and stolen a shotgun. There's probably going to be a firefight outside the Life Support restrooms.
Mikhaila Ilyushin
Mikhaila is about to be arrested. Alex already suspected that something about her was fishy. Mikhaila has sent Divya Naaz to install snooping devices in the doors in Psychotronics, and Divya has been caught. Alex isn't going to wait any longer to stop Ilyushin.
Coming soon
These are starting to fall apart but the shit won't really hit the fan until sometime after February 22.
Annelise Gallegos and Quinten Purvis
Annelise Gallegos has been overcome by her conscience and is blowing the whistle on the experiments in Psychotronics and the murder of the “Volunteers”. On February 22, Alex has ordered Sarah Elazar to arrest her, as soon as her shift is over. The Typhon escape prevents that. What would have happened to Gallegos? I suspect she would would have died in an ⸢unfortunate accident⸣.
But it's too late for the Yus. Gallegos has already prepared her thumb drive with all the damning evidence, and Quinten Purvis has hidden with it in a cargo container. If the Typhon hadn't gotten loose that day, he would have been on his way to Earth with it.
[ Addendum 20240327: There's a hint that Sarah Elazar is on the trail, and I think I remember that she has sent someone to investigate the cargo hold, but it's not clear that they would have been able to stop Purvis. ]
Hunter Hale
Shuttles are supposed to take the Volunteers back to Earth when their service is complete. The Shuttle Bay flight control staff have recently noticed that the shuttles are not going straight back to Earth, but are stopping somewhere else just after leaving, and then proceeding to Earth on a slightly altered course.
What's really happening is that the shuttle pilot, Hunter Hale, makes a stop at the Psychotronics airlock and drops off some or all of the Volunteers so they can be turned into Neuromods.
Alex is paying Hale five times the normal salary to keep his mouth shut about this, but HR has noticed and is asking questions about it. Between the flight control staff and HR, the truth is going to come out.
[ Addendum 20240327: The security staff has brought the suspicious shuttle course to the attention of Sarah Elazar, who is going to investigate. ]
Sarah Elazar
Elazar suspects that the Yus are up to something dirty. She doesn't know what yet, but she's going to find out.
Disappearing neuromods
Everyone seems to be pilfering neuromods. Emmanuella Da Silva has some stashed in the drop ceiling of the Shuttle Bay locker room. Yuri Kimura has four under her desk, and Elias Black is blackmailing her. Lorenzo Calvino has some in both of his secret safes. Lily Morris has them hidden in the fire alarms in half a dozen places around the station. That dumbass Grant Lockwood has tried to walk back to Earth with his stolen neuromods.
I probably missed a few, they're all over.
(I said none of this would come to light until after February 22, but it won't be long before someone wonders what became of Lockwood. It's also possible Alex will find out about the Lily Morris conspiracy that day, from Eddie Voss. I almost feel sorry for Alex.)
[ Addendum 20240327: Elazar, as usual, is on the ball. She knows Lockwood is missing and has dispatched someone to find him. ]
Minor shit
Not giant disasters, but troublesome nevertheless.
Lorenzo Calvino
It won't be long before someone, probably Miyu Okabe, figures out that Lorenzo Calvino has a severe, progressive mental impairment.
Price Broadway
Broadway, the alcoholic in Waste Processing, is endangering everyone's lives by leaving empty vodka bottles in the eel tanks. His supervisor knows and has reported him to HR. She says HR will help, but I imagine they'll just fire him.
Maybe he'll end up on Hunter Hale's shuttle home.
Volunteers
What's up with the Volunteers in the dormitory in Neuromod Division? Some of them are stealing and selling supplies. Other are stealing dangerous equipment and weapons. What for?
Drama drama drama
Even without the Typhon, Prey could have been a great game!
You play Morgan, of course. The first fifteen minutes are the same, right up until Bellamy would have died.
When you wake up for the second time on March 15, you figure out what is happening, and confront the Sim Lab staff. You escape, go rogue, and make your way to the Arboretum to confront Alex. Meanwhile all sorts of stuff is going down. Alton Weber is on a rampage in Life Support. Josh Dalton is loose in the GUTS. You'll have to deal with him to get to the Arboretum. (What, did you think you were going to take the elevator?) Somewhere along the line you find out about Purvis in the cargo container and have to decide how to handle that. And then Mendez changes the billboards and there's a panic…
What else?
A lot is happening on Talos I. I probably left something out.
(The shortage of escape pods doesn't count. Someone would have noticed long ago that there aren't nearly enough. I think we have to assume that there are more escape pods than we see in the game. Perhaps Morgan's simulation omitted them.)
(And in my headcanon, that poor schmuck Kevin Hague never does find out his wife has cheated on him with the asshole football star.)
Let me know what I missed.
[Other articles in category /games] permanent link
Fri, 16 Feb 2024The Recurse Center Zulip chat now has an Etymology channel, courtesy of Jesse Chen, so I have been posting whenever I run into something interesting. This is a summary of some of my recent discoveries. Everything in this article is, to the best of my knowledge, accurate. That is, there are no intentional falsehoods.
Baba ghanouj
I tracked down the meaning of (Arabic) baba ghanouj. It was not what I would have guessed.
Well, sort of. Baba is “father” just like in every language. I had thought of this and dismissed it as unlikely. (What is the connection with eggplants?) But that is what it is.
And ghanouj is …
“coquetry”.
So it's the father of coquetry.
Very mysterious.
Eggnog
Toph asked me if “nog” appeared in any word other than “eggnog”. Is there lemonnog or baconnog? I had looked this up before but couldn't remember what it was except that it was some obsolete word for some sort of drink.
“Nog” is an old Norfolk (England) term for a kind of strong beer which was an ingredient in the original recipe, sometime in the late 17th or early 18th century.
I think modern recipes don't usually include beer.
Wow
“Wow!” appears to be an 18th-century borrowing from an indigenous American language, because most of its early appearances are quotes from indigenous Americans. It is attested in standard English from 1766, spelled “waugh!”, and in Scots English from 1788, spelled “vow!”
Riddles
Katara asked me for examples of words in English like “bear” where there are two completely unrelated meanings. (The word bear like to bear fruit, bear children, or bear a burden is not in any way related to the big brown animal with claws.)
There are a zillion examples of this. They're easy to find in a paper dictionary: you just go down the margin looking for a superscript. When you see “bear¹” and “bear²”, you know you've found an example.
The example I always think of first is “venery” because long, long ago Jed Hartman pointed it out to me: venery can mean stuff pertaining to hunting (it is akin to “venison”) and it can also mean stuff pertaining to sex (akin to “venereal”) and the fact that these two words are spelled the same is a complete coincidence.
Jed said “I bet this is a really rare phenomenon” so I harassed him for the next several years by emailing him examples whenever I happened to think of it.
Anyway, I found an excellent example for Katara that is less obscure than “venery”: “riddle” (like a puzzling question) has nothing to do with when things are riddled with errors. It's a complete coincidence.
The “bear” / “bear” example is a nice simple one, everyone understands it right away. When I was studying Korean I asked my tutor an etymology question, something like whether the “eun” in eunhaeng 은행, “bank”, was the same word as “eun” 은 which means “silver”. He didn't understand the question at first: what did I mean, “is it the same word”?
I gave the bear / bear example, and said that to bear fruit and to bear children are the same word, but the animal with claws is a different word, and just a coincidence that it is spelled the same way. Then he understood what I meant.
(Korean eunhaeng 은행 is a Chinese loanword, from 銀行. 銀 is indeed the word for silver, and 行 is a business-happening-place.)
Right and left
The right arm is the "right" arm because, being the one that is (normally) stronger and more adept, it is the right one to use for most jobs.
But if you ignore the right arm, there is only one left, so that is the "left" arm.
This sounds like a joke, but I looked it up and it isn't.
Leave and left
"Left" is the past tense passive of "leave". As in, I leave the room, I left the room, when I left the room I left my wallet there, my wallet was left, etc.
(As noted above, this is also where we get the left side.)
There are two other words "leave" in English. Leaves like the green things on trees are not related to leaving a room.
(Except I was once at a talk by J.H. Conway in which he was explaining some sort of tree algorithm in which certain nodes were deleted and he called the remaining ones "leaves" because they were the ones that were left. Conway was like that.)
The other "leave" is the one that means "permission" as in "by your leave…". This is the leave we find in "sick leave" or "shore leave". They are not related to the fact that you have left on leave, that is a coincidence.
Normal norms
Latin norma is a carpenter's square, for making sure that things are at right angles to one another.
So something that is normal is something that is aligned the way things are supposed to be aligned, that is to say at right angles. And a norm is a rule or convention or standard that says how things ought to line up.
In mathematics and physics we have terms like “normal vector”, “normal forces” and the like, which means that vectors or forces are at right angles to something. This is puzzling if you think of “normal” as “conventional” or “ordinary” but becomes obvious if you remember the carpenter's square.
In contrast, mathematical “normal forms” have nothing to do with right angles, they are conventional or standard forms. “Normal subgroups” are subgroups that behave properly, the way subgroups ought to.
The names Norman and Norma are not related to this. They are related to the surname Norman which means a person from Normandy. Normandy is so-called because it was inhabited by Vikings (‘northmen’) starting from the 9th century.
Hydrogen and oxygen
Jesse Chen observed that hydrogen means “water-forming”, because when you burn it you get water.
A lot of element names are like this. Oxygen is oxy- (“sharp” or “sour”) because it makes acids, or was thought to make acids. In German the analogous calque is “sauerstoff”.
Nitrogen makes nitre, which is an old name for saltpetre (potassium nitrate). German for nitre seems to be salpeter which doesn't work as well with -stoff.
The halogen gases are ‘salt-making’. (Greek for salt is hals.) Chlorine, for example, is a component of table salt, which is sodium chloride.
In Zulip I added that The capital of Denmark, Copenha-gen, is so-called because in the 11th century is was a major site for the production of koepenha, a Germanic term for a lye compound, used in leather tanning processes, produced from bull dung. I was somewhat ashamed when someone believed this lie despite my mention of bull dung.
Spas, baths, and coaches
Spas (like wellness spa or day spa) are named for the town of Spa, Belgium, which has been famous for its cold mineral springs for thousands of years!
(The town of Bath England is named for its baths, not the other way around.)
The coach is named for the town of Kocs (pronounced “coach”), Hungary, where it was invented. This sounds like something I would make up to prank the kids, but it is not.
Spanish churches
“Iglesia” is Spanish for “church”, and you see it as a surname in Spanish as in English. (I guess, like “Church”, originally the name of someone who lived near a church).
Thinking on this, I realized: “iglesia” is akin to English “ecclesiastic”.
They're both from ἐκκλησία which is an assembly or congregation.
The mysterious Swedish hedgehog
In German, a hedgehog is “Igel”. This is a very ancient word, and several other Germanic languages have similar words. For example, in Frisian it's “ychel”.
In Swedish, “igel” means leech. The hedgehog is “igelkott”.
I tried to find out what -kott was about. “kotte” is a pinecone and may be so-called because “kott” originally meant some rounded object, so igelkott would mean the round igel rather than the blood igel, which is sometimes called blodigel in Swedish.
I was not able to find any other words in Swedish with this sense of -kott. There were some obviously unrelated words like bojkott (“boycott”). And there are a great many Swedish words that end in -skott, which is also unrelated. It means “tail”. For example, the grip of a handgun is revolverskott.
[ Addendum: Gustaf Erikson advises me that I have misunderstood ‑skott; see below. ]
Bonus hedgehog weirdness: In Michael Moorcock's Elric books, Elric's brother is named “Yyrkoon”. The Middle English for a hedgehog is “yrchoun” (variously spelled). Was Moorcock thinking of this? The -ch- in “yrchoun” is t͡ʃ though, which doesn't match the stop consonant in “Yyrkoon”. Also which makes clear that “yrchoun” is just a variant spelling of “urchin”. (Compare “sea urchin”, which is a sea hedgehog. or compare “street urchin”, a small round bristly person who scuttles about in the gutter.)
In Italian a hedgehog is riccio, which I think is also used as a nickname for a curly-haired or bristly-haired person.
Slobs and schlubs
These are not related. Schlub is originally Polish, coming to English via (obviously!) Yiddish. But slob is Irish.
-euse vs. -ice
I tried to guess the French word for a female chiropractor. I guessed “chiropracteuse" by analogy with masseur, masseuse, but I was wrong. It is chiropractrice.
The '‑ice' suffix was clearly descended from the Latin '‑ix' suffix, but I had to look up ‘‑euse’. It's also from a Latin suffix, this time from ‘‑osa’.
Jot
When you jot something down on a notepad, the “jot” is from Greek iota, which is the name of the small, simple letter ι that is easily jotted.
Bonus: This is also the jot that is meant by someone who says “not a jot or a tittle”, for example Matthew 5:18 (KJV):
For verily I say unto you, Till heaven and earth pass, one jot or one tittle shall in no wise pass from the law, till all be fulfilled.
A tittle is the dot above the lowercase ‘i’ or ‘j’. The NIV translates this as “not the smallest letter, not the least stroke of a pen”, which I award an A-plus for translation.
Vilifying villains
I read something that suggested that these were cognate, but they are not.
“Vilify” is from Latin vīlificō which means to vilify. It is a compound of vīlis (of low value or worthless, I suppose the source of “vile”) and faciō (to make, as in “factory” and “manufacture”.)
A villain, on the other hand, was originally just a peasant or serf; that is, a person who lives in a village. “Village” is akin to Latin villa, which originally meant a plantation.
Döner kebab
I had always assumed that “Döner” and its “ö” were German, but they are not, at least not originally. “Döner kebab” is the original Turkish name of the dish, right down to the diaresis on the ‘ö’, which is the normal Turkish spelling; Turkish has an ‘ö’ also. Döner is the Turkish word for a turning-around-thing, because döner kebab meat roasts on a vertical spit from which it is sliced off as needed.
“Döner” was also used in Greek as a loanword but at some point the Greeks decided to use the native Greek word gyro, also a turning-around-thing, instead. Greek is full of Turkish loanwords. (Ottoman Empire, yo.)
“Shawarma”, another variation on the turning-around-vertical-spit dish, is from a different Ottoman Turkish word for a turning-around thing, this time چویرمه (çevirme).
The Armenian word for shawarma is also shawarma, but despite Armenian being full of Turkish loanwords, this isn't one. They got it from Russian.
Everyone loves that turning-on-a-vertical-spit dish. Lebanese immigrants brought it to Mexico, where it is served in tacos with pineapple and called tacos al pastor (“shepherd style”). I do not know why the Mexicans think that Lebanese turning-around-meat plus pineapples adds up to shepherds. I suppose it must be because the meat is traditionally lamb.
Roll call
To roll is to turn over with a circular motion. This motion might wind a long strip of paper into a roll, or it might roll something into a flat sheet, as with a rolling pin. After rolling out the flat sheet you could then roll it up into a roll.
Dinner rolls are made by rolling up a wad of bread dough.
When you call the roll, it is because you are reading a list of names off a roll of paper.
Theatrical roles are from French rôle which seems to have something to do with rolls but I am not sure what. Maybe because the cast list is a roll (as in roll call).
Wombats and numbats
Both of these are Australian animals. Today it occurred to me to wonder: are the words related? Is -bat a productive morpheme, maybe a generic animal suffix in some Australian language?
The answer is no! The two words are from different (although distantly related) languages. Wombat is from Dharug, a language of the Sydney area. Numbat is from the Nyungar language, spoken on the other end of the continent.
Addendum
Gustaf Erikson advises me that I have misunderstood ‑skott. It is akin to English shoot, and means something that springs forth suddenly, like little green shoots in springtime, or like the shooting of an arrow. In the former sense, it can mean a tail or a sticking-out thing more generally. But in revolverskott is it the latter sense, the firing of a revolver.
[Other articles in category /lang/etym] permanent link












