Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 10 Dec 2007
Lazy square roots of power series return
In an earlier article I
talked about wanting to use lazy streams to calculate the power series
expansion of the solution of this differential equation:
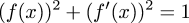
At least one person wrote to ask me for the Haskell code for the power series calculations, so here's that first off.
A power series a0 + a1x + a2x2 + a3x3 + ... is represented as a (probably infinite) list of numbers [a0, a1, a2, ...]. If the list is finite, the missing terms are assumed to be all 0.
The following operators perform arithmetic on functions:
-- add functions a and b
add [] b = b
add a [] = a
add (a:a') (b:b') = (a+b) : add a' b'
-- multiply functions a and b
mul [] _ = []
mul _ [] = []
mul (a:a') (b:b') = (a*b) : add (add (scale a b')
(scale b a'))
(0 : mul a' b')
-- termwise multiplication of two series
mul2 = zipWith (*)
-- multiply constant a by function b
scale a b = mul2 (cycle [a]) b
neg a = scale (-1) a
And there are a bunch of other useful utilities:
-- 0, 1, 2, 3, ... iota = 0 : zipWith (+) (cycle [1]) iota -- 1, 1/2, 1/3, 1/4, ... iotaR = map (1/) (tail iota) -- derivative of function a deriv a = tail (mul2 iota a) -- integral of function a -- c is the constant of integration int c a = c : (mul2 iotaR a) -- square of function f sqr f = mul f f -- constant function con c = c : cycle [0] one = con 1
| Buy Structure and Interpretation of Computer Programs from Bookshop.org (with kickback) (without kickback) |
-- reciprocal of argument function inv (s0:st) = r where r = r0 : scale (negate r0) (mul r st) r0 = 1/s0 -- divide function a by function b squot a b = mul a (inv b) -- square root of argument function srt (s0:s) = r where r = r0 : (squot s (add [r0] r)) r0 = sqrt(s0)We can define the cosine function as follows:
coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])We could define the sine function analogously, or we can say that sin(x) = √(1 - cos2(x)):
sins = (srt . (add one) . neg . sqr) cossThis works fine.
Okay, so as usual that is not what I wanted to talk about; I wanted to show how to solve the differential equation. I found I was getting myself confused, so I decided to try to solve a simpler differential equation first. (Pólya says: "Can you solve a simpler problem of the same type?" Pólya is a smart guy. When the voice talking in your head is Pólya's, you better pay attention.) The simplest relevant differential equation seemed to be f = f'. The first thing I tried was observing that for all f, f = f0 : mul2 iotaR f'. This yields the code:
f = f0 : mul2 iotaR (deriv f)
This holds for any function, and so it's unsolvable. But if you
combine it with the differential equation, which says that f =
f', you get:
f = f0 : mul2 iotaR f
where f0 = 1 -- or whatever the initial conditions dictate
and in fact this works just fine. And then you can observe that this
is just the definition of int; replacing the definition with
the name, we have:
f = int f0 f
where f0 = 1 -- or whatever
This runs too, and calculates the power series for the
exponential function, as it should. It's also transparently obvious,
and makes me wonder why it took me so long to find. But I was looking
for solutions of the form:
f = deriv f
which Haskell can't figure out. It's funny that it only handles
differential equations when they're expressed as integral equations. I
need to meditate on that some more.It occurs to me just now that the f = f0 : mul2 iotaR (deriv f) identity above just says that the integral and derivative operators are inverses. These things are always so simple in hindsight.
Anyway, moving along, back to the original problem, instead of f = f', I want f2 + (f')2 = 1, or equivalently f' = √(1 - f2). So I take the derivative-integral identity as before:
f = int f0 (deriv f)
and put in √(1 - f2) for deriv f:
f = int f0 ((srt . (add one) . neg . sqr) f)
where f0 = sqrt 0.5 -- or whatever
And now I am done; Haskell cheerfully generates the power series
expansion for f for any given initial condition. (The
parameter f0 is precisely the desired value of f(0).)
For example, when f(0) = √(1/2), as above, the calculated
terms show the function to be exactly
√(1/2)·(sin(x) + cos(x)); when f(0)
= 0, the output terms are exactly those of sin(x). When
f(0) = 1, the output blows up and comes out as [1, 0, NaN, NaN,
...]. I'm not quite sure why yet, but I suspect it has something to
do with there being two different solutions that both have f(0) = 1. All of this also works just fine in Perl, if you build a suitable lazy-list library; see chapter 6 of HOP for complete details. Sample code is here. For a Scheme implementation, see SICP. For a Java, Common Lisp, Python, Ruby, or SML implementation, do the obvious thing.
But anyway, it does work, and I thought it might be nice to blog about something I actually pursued to completion for a change. Also I was afraid that after my week of posts about Perl syntax, differential equations, electromagnetism, Unix kernel internals, and paint chips in the shape of Austria, the readers of Planet Haskell, where my blog has recently been syndicated, were going to storm my house with torches and pitchforks. This article should mollify them for a time, I hope.
[ Addendum 20071211: Some additional notes about this. ]
[Other articles in category /math] permanent link



