Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 31 Aug 2024
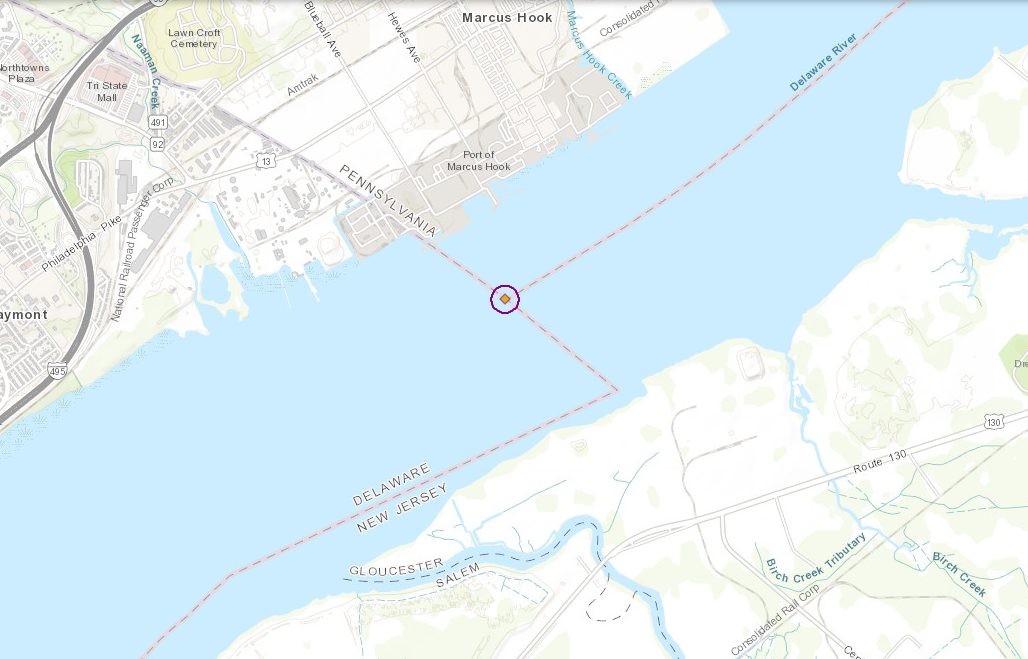
Another corner of Pennsylvania
A couple of years back I wrote:
I live in southeastern Pennsylvania, so the Pennsylvania-New Jersey-Delaware triple point must be somewhere nearby. I sat up and got my phone so I could look at the map, and felt foolish.
As you can see, the triple point is in the middle of the Delaware River, as of course it must be; the entire border between Pennsylvania and New Jersey, all the hundreds of miles from its northernmost point (near Port Jervis) to its southernmost (shown above), runs right down the middle of the Delaware.
I briefly considered making a trip to get as close as possible, and photographing the point from land. That would not be too inconvenient. Nearby Marcus Hook is served by commuter rail. But Marcus Hook is not very attractive as a destination. Having been to Marcus Hook, it is hard for me to work up much enthusiasm for a return visit.
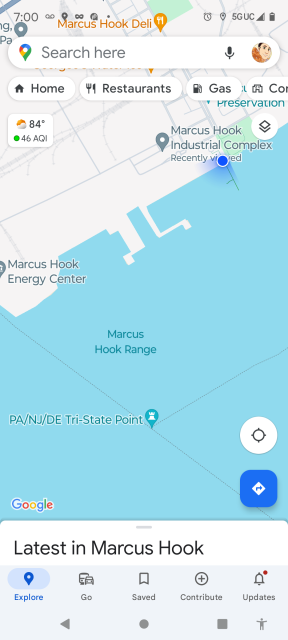
I was recently passing by Marcus Hook on the way back from Annapolis, so I thought what the heck, I'd stop in and see if I could get a look in the direction of the tripoint. As you can see from this screencap, I was at least standing in the right place, pointed in the right direction.
I didn't quite see the tripoint itself because this buoyancy-operated aquatic transport was in the way. I don't mind, it was more interesting to look at than open water would have been.
Thanks to the Wonders of the Internet, I have learned that this is an LPG tanker. Hydrocarbons from hundreds of miles away are delivered to the refinery in Marcus Hook via rail, road, and pipeline, and then shipped out on vessels like this one. Infrastructure fans should check it out.
I was pleased to find that Marcus Hook wasn't as dismal as I remembered, it's just a typical industrial small town. I thought maybe I should go back and look around some more. If you hoped I might have something more interesting or even profound to say here, sorry.
Oh, I know. Here, I took this picture in Annapolis:
Perhaps he who is worthy of honor does not die. But fame is fleeting. Even if he who is worthy of honor does get a plinth, the grateful populace may not want to shell out for a statue.
[Other articles in category /misc] permanent link
Sat, 24 Aug 2024Marnanel Thurman reported the following item that they found in an 1875 book titled How to Entertain a Social Party:
To Make a Loaf of Bread Dance on the Table.
— Having a quill filled with quicksilver and stopped close, you secretly thrust it into a hot roll or loaf, which will put it in motion.
(Bottom of page 46.) No further explanation is given.
This may remind you of an episode from Huckleberry Finn:
Well, then I happened to think how they always put quicksilver in loaves of bread and float them off, because they always go right to the drownded carcass and stop there.
When I first read this I assumed it was a local Southern superstition, characteristic of that place and time. But it seems not! According to this article by Dan Rolph of the Historical Society of Pennsylvania, the belief was longstanding and widespread, lasting from at least 1767 to 1872, and appearing also in London and in Pennsylvania.
Details of the dancing bread trick are lacking. I guess the quicksilver stays inside the stopped-up quill. (Otherwise, there would be no need to “stop it close”.) Then perhaps on being heated by the bread, the quicksilver expands lengthwise as in a thermometer, and then… my imagination fails me.
The procedure for making drowned-body-finding bread is quite different. Rolph's sources all agree: you poke in your finger and scoop out a bit of the inside, pour the quicksilver into the cavity, and then plug up the hole. So there's no quill; the quicksilver is just sloshing around loose in there. Huckleberry Finn agrees:
I took out the plug and shook out the little dab of quicksilver…
Does anyone have more information about this? Does hot bread filled with mercury really dance on the table, and if so why? Is the supersition about bread finding drowned bodies related to this, or is it a coincidence?
Also, what song did the sirens sing, and by what name was Achilles called when he hid among women?
[Other articles in category /misc] permanent link
Thu, 22 Aug 2024
(Source: XKCD “Exam numbers”.)
This post is about the bottom center panel, “Game Theory final exam”.
I don't know much about game theory and I haven't seen any other discussion of this question. But I have a strategy I think is plausible and I'm somewhat pleased with.
(I assume that answers to the exam question must be real numbers — not !!\infty!! — and that “average” here is short for 'arithmetic mean'.)
First, I believe the other players and I must find a way to agree on what the average will be, or else we are all doomed. We can't communicate, so we should choose a Schelling point and hope that everyone else chooses the same one. Fortunately, there is only one distinguished choice: zero. So I will try to make the average zero and I will hope that others are trying to do the same.
If we succeed in doing this, any winning entry will therefore be !!10!!. Not all !!n!! players can win because the average must be !!0!!. But !!n-1!! can win, if the one other player writes !!-10(n-1)!!. So my job is to decide whether I will be the loser. I should select a random integer between !!0!! and !!n-1!!. If it is zero, I have drawn a short straw, and will write !!-10(n-1)!!. otherwise I write !!10!!.
(The straw-drawing analogy is perhaps misleading. Normally, exactly one straw is short. Here, any or all of the straws might be short.)
If everyone follows this strategy, then I will win if exactly one person draws a short straw and if that one person isn't me. The former has a probability that rapidly approaches !!\frac1e\approx 36.8\%!! as !!n!! increases, and the latter is !!\frac{n-1}n!!. In an !!n!!-person class, the probability of my winning is $$\left(\frac{n-1}n\right)^n$$ which is already better than !!\frac13!! when !!n= 6!!, and it increases slowly toward !!36.8\%!! after that.
Some miscellaneous thoughts:
The whole thing depends on my idea that everyone will agree on !!0!! as a Schelling point. Is that even how Schelling points work? Maybe I don't understand Schelling points.
I like that the probability !!\frac1e!! appears. It's surprising how often this comes up, often when multiple agents try to coordinate without communicating. For example, in ALOHAnet a number of ground stations independently try to send packets to a single satellite transceiver, but if more than one tries to send a packet at a particular time, the packets are garbled and must be retransmitted. At most !!\frac1e!! of the available bandwidth can be used, the rest being lost to packet collisions.
The first strategy I thought of was plausible but worse: flip a coin, and write down !!10!! if it is heads and !!-10!! if it is tails. With this strategy I win if exactly !!\frac n2!! of the class flips heads and if I do too. The probability of this happening is only $$\frac{n\choose n/2}{2^n}\cdot \frac12 \approx \frac1{\sqrt{2\pi n}}.$$ Unlike the other strategy, this decreases to zero as !!n!! increases, and in no case is it better than the first strategy. It also fails badly if the class contains an odd number of people.
Thanks to Brian Lee for figuring out the asymptotic value of !!4^{-n}\binom{2n}{n}!! so I didn't have to.
Just because this was the best strategy I could think of in no way means that it is the best there is. There might have been something much smarter that I did not think of, and if there is then my strategy will sabotage everyone else.
Game theorists do think of all sorts of weird strategies that you wouldn't expect could exist. I wrote an article about one a few years back.
Going in the other direction, even if !!n-1!! of the smartest people all agree on the smartest possible strategy, if the !!n!!th person is Leeroy Jenkins, he is going to ruin it for everyone.
If I were grading this exam, I might give full marks to anyone who wrote down either !!10!! or !!-10(n-1)!!, even if the average came out to something else.
For a similar and also interesting but less slippery question, see Wikipedia's article on Guess ⅔ of the average. Much of the discussion there is directly relevant. For example, “For Nash equilibrium to be played, players would need to assume both that everyone else is rational and that there is common knowledge of rationality. However, this is a strong assumption.” LEEROY JENKINS!!
People sometimes suggest that the real Schelling point is for everyone to write !!\infty!!. (Or perhaps !!-\infty!!.)
Feh.
If the class knows ahead of time what the question will be, the strategy becomes a great deal more complicated! Say there are six students. At most five of them can win. So they get together and draw straws to see who will make a sacrifice for the common good. Vidkun gets the (unique) short straw, and agrees to write !!-50!!. The others accordingly write !!10!!, but they discover that instead of !!-50!!, Vidkun has written !!22!! and is the only person to have guessed correctly.
I would be interested to learn if there is a playable Nash equilibrium under these circumstances. It might be that the optimal strategy is for everyone to play as if they didn't know what the question was beforehand!
Suppose the players agree to follow the strategy I outlined, each rolling a die and writing !!-50!! with probability !!\frac16!!, and !!10!! otherwise. And suppose that although the others do this, Vidkun skips the die roll and unconditionally writes !!10!!. As before, !!n-1!! players (including Vidkun) win if exactly one of them rolls zero. Vidkun's chance of winning increases. Intuitively, the other players' chances of winning ought to decrease. But by how much? I think I keep messing up the calculation because I keep getting zero. If this were actually correct, it would be a fascinating paradox!
[Other articles in category /math] permanent link
Wed, 21 Aug 2024If you're an annoying know-it-all like me, I suggest that you try playing the following game when you attend a conference or a user group meetup or even a work meeting. The game is:
If someone asks you a question, and you say “I don't know”, you score a point.
That's it. That's the game. “I don't know” doesn't have to be perfectly truthful, only approximately truthful.
I forgot, there is one other rule:
If you follow up with something like “But if I had to guess…” you lose your point again.
[Other articles in category /brain] permanent link
Wed, 14 Aug 2024Benjamin Franklin wrote and published Poor Richard's Almanack annually from 1732 to 1758. Paper was expensive and printing difficult and time-consuming. The type would be inked, the sheet of paper laid on the press, the apprentices would press the sheet, by turning a big screw. Then the sheet was removed and hung up to dry. Then you can do another printing of the same page. Do this ten thousand times and you have ten thousand prints of a sheet. Do it ten thousand more to print a second sheet. Then print the second side of the first sheet ten thousand times and print the second side of the second sheet ten thousand times. Fold 20,000 sheets into eighths, cut and bind them into 10,000 thirty-two page pamphlets and you have your Almanacks.
As a youth, Franklin was apprenticed to his brother James, also a printer, in Boston. Franklin liked the work, but James drank and beat him, so he ran away to Philadelphia. When James died, Benjamin sent his widowed sister-in-law Ann five hundred copies of the Almanack to sell. When I first heard that I thought it was a mean present but I was being a twenty-first-century fool. The pressing of five hundred almanacks is no small feat of toil. Ann would have been able to sell those Almanacks in her print shop for fivepence each, or ₤10 8s. 4d. That was a lot of money in 1735.
In 1748 Franklin increased the size and the price. Here's a typical page from the 1748 Almanack:
Wow, there's a lot of stuff going on there. Here's a smaller excerpt, this time from November 1753:

The leftmost column is the day of the month, and then the next column is the day of the week, with 2–7 being Monday through Saturday. Sunday is denoted with a letter “G”. I thought this was G for God, but I see that in 1748 Franklin used “C” and in 1752 he used “A”, so I don't know.
The third column combines a weather forecast and a calendar. The weather forecast is in italic type, over toward the right: “Clouds and threatens cold rains and snow” in the early part of the month. Sounds like November in Philadelphia. The roman type gives important days. For example, November 1 is All Saints Day and November 5 is the anniversary of the Gunpowder Plot. November 10 is given as the birthday of King George II, then still the King of Great Britain.
The Sundays are marked with some description in the Christian liturgical calendar. For example, “20 past Trin.” means it's the start of the 20th week past Trinity Sunday.
This column also has notations like “Days dec. 4 32” and “Days dec. 5 h.” that I haven't been able to figure out. Something about the decreasing length of the day in November maybe? [ Addendum: Yes. See below. ] The notation on November 6 says “Day 10 10 long” which is consistent with the sunrise and sunset times Franklin gives for that day. The fourth and fifth columns, labeled “☉ ris” and “☉ set” are the times of sunrise and sunset, 6:55 (AM) and 5:05 (PM) respectively for November 6, ten hours and ten minutes apart as Franklin says.
“☽ pl.” is the position of the moon in the sky. (I guess “pl.” is short for “place”.) The sky is divided into twelve “houses” of 30 degrees each, and when it says that the “☽ pl.” on November 6 is “♓ 25” I think it means the moon is !!\frac{25}{30}!! of the way along in the house of Pisces on its way to the house of Aries ♈. If you look at the January 1748 page above you can see the moon making its way through the whole sky in 29 days, as it does.
The last column, “Aspects, &c.” contains more astronomy. “♂ rise 6 13” means that Mars will rise at 6:13 that day. (But in the morning or the evening?) ⚹♃♀ on the 12th says that Jupiter is in sextile aspect to Venus, which means that they are in the sky 60 degrees apart. Similarly □☉♃ means that the Sun and Jupiter are in Square aspect, 90 degrees apart in the sky.
Also mixed into that last column, taking up the otherwise empty space, are the famous wise sayings of Poor Richard. Here we see:
Serving God is Doing Good to Man,
but Praying is thought an easier Service,
and therefore more generally chosen.
Back on the January page you can see one of the more famous ones, Lost Time is never found again.
Franklin published an Almanack in 1752, the year that the British Calendar Act of 1751 updated the calendar from Julian to Gregorian reckoning. To bring the calendar into line with Gregorian, eleven days were dropped from September that year. I wondered what Franklin's calendar looked like that month. Here it is with the eleven days clearly missing:

The leftmost day-of-the-month column skips right from September 2 to September 14, as the law required. On this copy someone has added the old dates in the margin. Notice that St. Michael's Day, which would have been on Friday September 18th in the old calendar, has been moved up to September 29th. In most years Poor Richard's Almanack featured an essay by Poor Richard, little poems, and other reference material. The 1752 Almanack omitted most of this so that Franklin could use the space to instead reprint the entire text of the Calendar Act.
This page also commemorates the Great Fire of London, which began September 2, 1666.
Wikipedia tells me that Franklin may have gotten the King's birthday wrong. Franklin says November 10, but Wikipedia says November 9, and:
Over the course of George's life, two calendars were used: the Old Style Julian calendar and the New Style Gregorian calendar. Before 1700, the two calendars were 10 days apart. Hanover switched from the Julian to the Gregorian calendar on 19 February (O.S.) / 1 March (N.S.) 1700. Great Britain switched on 3/14 September 1752. George was born on 30 October Old Style, which was 9 November New Style, but because the calendar shifted forward a further day in 1700, the date is occasionally miscalculated as 10 November.
Ugh, calendars.
I got these scans from a web site called The Rare Book Room, but I found their user interface very troublesome, so I have scraped all the images they had. You may find them at https://pic.blog.plover.com/calendar/poor-richards-almanack/archive/. I'm pretty sure the copyright has expired, so share and enjoy.
Addenda
Several people have pointed out that the mysterious letters G, C, A on Sundays are the so-called dominical letters, used in remembering the correspondence between days of the month and days of the week, and important in the determination of the dates of Easter and other moveable feasts.
Why Franklin included them in the Almanack is not clear to me, as one of the main purposes of the almanac itself is so that you do not have to remember or calculate those things, you can just look them up in the almanac.
Mikkel Paulson explained the 'days dec.' and 'days inc.' notations: they describe the length of the day, but reported relative to the length of the most recent solstice. For example, the November 1753 excerpt for November 2 says "Days dec. 4 32". Going by the times of sunrise and sunset on that day, the day was 10 hours 18 minutes long. Adding the 4 hours 32 minutes from the notation we have 14 hours 50 minutes, which is indeed the length of the day on the summer solstice in Philadelphia, or close to it.
Similarly the notation on November 14 says "Days dec. 5 h" for a day that is 9 hours 50 minutes between sunrise and sunset, five hours shorter than on the summer solstice, and the January 3 entry says "Days inc. 18 m." for a 9h 28m day which is 18 minutes longer than the 9h 10m day one would have on the winter solstice.
[Other articles in category /calendar] permanent link
Wed, 07 Aug 2024
Stuff I wanted to say to the historic district people but didn't
[ Thanks to John Wiersba for noticing that I forgot to publish this. ]
A few weeks ago I wrote a letter to my neighbors about why I thought it was a bad idea to oppose building more housing in our neighborhood.
I didn't write this paragraph:
In the past it has often happened that a group of wealthy landowners conspired to hold onto what they had and keep anyone else from sharing it. I don't think anyone has ever looked back and said “Yep, those people had the right idea.”
But I wanted to.
Also, I omitted a long and detailed fantasy about how local landlords will have to lower rents and fix up their properties because of competition pressure from new apartment buildings.
“I wanted to raise rents this year, but I couldn't because all the rich Penn students moved into that new luxury apartment building. ”
“It was hard to find tenants this year, and I found out it was because Joe up the street fixed up all his bathrooms. If I wanna stay in business I'm gonna have to fix up all my bathrooms too!”
I left out any expression of my idea that if we really want to stick it to those greedy landlords, we should hit them where it really hurts, by expanding the supply of housing and breaking their monopoly.
And I didn't cite the literature that says that even building expensive apartment buildings tends to lower everyone else's rent:
The supply of new market rate units triggers moving chains that quickly reach middle- and low-income neighborhoods and individuals. Thus, new market-rate construction loosens the housing market in middle- and low-income areas even in the short run. Market-rate supply is likely to improve affordability outside the sub-markets where new construction occurs and to benefit low-income people.
(City-wide effects of new housing supply: Evidence from moving chains)
And I didn't vent my rage about Philadelphia's recent cash grants to people waiting for federal housing subsidies, which is an almost direct transfer of cash from the public purse into the pockets of landlords.
Ugh, housing policy is so messed up.
(I did later go to the public meeting about it, and what a fucking fuckhole of fucked-up fuckery that was. Fuck.)
[Other articles in category /politics] permanent link
Tue, 06 Aug 2024
Look at what they tried to take from us
When I was a kid, the Beatles’ seminal 1966 album Revolver was 20% shorter. The original release was not a long album: 14 tracks, totaling 34:45. But the version I grew up with had 11 tracks, totaling only 27:31.
Three tracks, all by Lennon, were omitted by Capitol from the North American release because they had previously been released on Yesterday and Today:

- “Taxman”
- “Eleanor Rigby”
-
“I'm Only Sleeping” - “Love You To”
- “Here, There and Everywhere”
- “Yellow Submarine”
- “She Said She Said”
- “Good Day Sunshine”
-
“And Your Bird Can Sing” - “For No One”
-
“Doctor Robert” - “I Want to Tell You”
- ”Got to Get You into My Life”
- “Tomorrow Never Knows”
In 1987, the album was rereleased, with the missing tracks restored. But until I was in college, I had not only never heard the three omitted tracks, I didn't even know they existed.
When I found out, I was apprehensive. I loved Revolver. What if I didn't like the ⸢new⸣ tracks? What if the new tracks changed the Revolver I loved into something else?
Nothing like this happened. The new tracks fit in seamlessly. Of course they did! The new Revolver was more Revolver than the old Revolver had been.
It took a little while before I was no longer startled when “For No One” wasn't followed by “I Want to Tell You”, but not too long. (It took me longer to get used to the absence of the horrible skip that was in our vinyl copy of “Strawberry Fields Forever”.) New Revolver was the same Revolver I had always loved, only 25% longer and considerably better.
Douglas Hofstadter once asked us to imagine that a previously unknown but certainly authentic Bach cantata has been discovered, hiding in a drawer or something, but that the eager concertgoers hearing it for the first time are horrified to discover that its main theme is identical with the first seven notes of “Rudolph the Red-Nosed Reindeer”. This was like that, without the horrid twist ending.
Revolver was released yesterday, August 5, in 1966.
[Other articles in category /music] permanent link
Mon, 05 Aug 2024
Everyday examples of morphisms with one-sided inverses
Like almost everyone except Alexander Grothendieck, I understand things better with examples. For instance, how do you explain that
$$(f\circ g)^{-1} = g^{-1} \circ f^{-1}?$$
Oh, that's easy. Let !!f!! be putting on your shoes and !!f^{-1}!! be taking off your shoes. And let !!g!! be putting on your socks and !!g^{-1}!! be taking off your socks.
Now !!f\circ g!! is putting on your socks and then your shoes. And !!g^{-1} \circ f^{-1}!! is taking off your shoes and then your socks. You can't !!f^{-1} \circ g^{-1}!!, that says to take your socks off before your shoes.
(I see a topologist jumping up and down in the back row, desperate to point out that the socks were never inside the shoes to begin with. Sit down please!)
Sometimes operations commute, but not in general. If you're teaching group theory to high school students and they find nonabelian operations strange, the shoes-and-socks example is an unrebuttable demonstration that not everything is abelian.
(Subtraction is not a good example here, because subtracting !!a!! and then !!b!! is the same as subtracting !!b!! and then !!a!!. When we say that subtraction isn't commutative, we're talking about something else.)
Anyway this weekend I was thinking about very very elementary category theory (the only kind I know) and about left and right inverses. An arrow !!f : A\to B!! has a left inverse !!g!! if
$$g\circ f = 1_A.$$
Example of this are easy. If !!f!! is putting on your shoes, then !!g!! is taking them off again. !!A!! is the state of shoelessness and !!B!! is the state of being shod. This !!f!! has a left inverse and no right inverse. You can't take the shoes off before you put them on.
But I wanted an example of an !!f!! with right inverse and no left inverse:
$$f\circ h = 1_B$$
and I was pretty pleased when I came up with one involving pouring the cream pitcher into your coffee, which has no left inverse that gets you back to black coffee. But you can ⸢unpour⸣ the cream if you do it before mixing it with the coffee: if you first put the cream back into the carton in the refrigerator, then the pouring does get you to black coffee.
But now I feel silly. There is a trivial theorem that if !!g!! is a left inverse of !!f!!, then !!f!! is a right inverse of !!g!!. So the shoe example will do for both. If !!f!! is putting on your shoes, then !!g!! is taking them off again. And just as !!f!! has a left inverse and no right inverse, because you can't take your shoes off before putting them on, !!g!! has a right inverse (!!f!!) and no left inverse, because you can't take your shoes off before putting them on.
This reminds me a little of the time I tried to construct an example to show that “is a blood relation of" is not a transitive relation. I had this very strange and elaborate example involving two sets of sisters-in-law. But the right example is that almost everyone is the blood relative of both of their parents, who nevertheless are not (usually) blood relations.
[Other articles in category /math] permanent link