Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| A message to the aliens, part 21/23 (the message) |
| A message to the aliens, part 22/23 (cosmology) |
| A message to the aliens, part 23/23 (wat) |
| Math SE report 2015-08 |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 21 Dec 2015
A message to the aliens, part 23/23 (wat)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth) Page 21 (the message) Page 22 (cosmology)
This is page 23 (the last) of the Cosmic Call message. An explanation follows.

This page is a series of questions for the recipients of the message.
It is labeled with the glyph  , which heretofore
appeared only on page 4 in the context
of solving of algebraic equations. So we might interpret it as
meaning a solution or a desire to solve or understand. I have chosen to translate
it as “wat”.
, which heretofore
appeared only on page 4 in the context
of solving of algebraic equations. So we might interpret it as
meaning a solution or a desire to solve or understand. I have chosen to translate
it as “wat”.
I find this page irritating in its vagueness and confusion. Its
layout is disorganized. Glyphs are used inconsistent with their uses
elsewhere on the page and elsewhere in the message.
For example, the mysterious glyph
 , which
has something to do with the recipients of the message, and which
appeared only on page 21 is used here to
ask about both the recipients themselves and also about their planet.
, which
has something to do with the recipients of the message, and which
appeared only on page 21 is used here to
ask about both the recipients themselves and also about their planet.
The questions are arranged in groups. For easy identification, I have color-coded the groups.
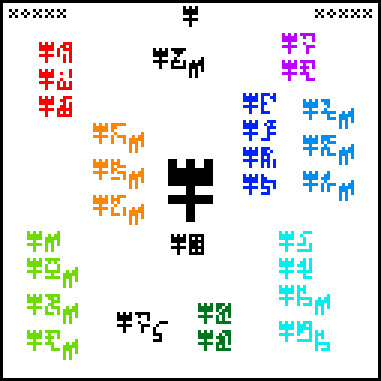
Starting from the upper-left corner, and proceeding counterclockwise, we have:
 Kilograms, meters, and seconds, wat. I would have used the glyphs for
abstract mass, distance, and time,
Kilograms, meters, and seconds, wat. I would have used the glyphs for
abstract mass, distance, and time,

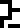 and
and 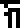 ,
since that seems to be closer to the intended meaning.
,
since that seems to be closer to the intended meaning.
 Alien mathematics, physics, and biology, wat. Note that this asks
specifically about the recipients’ version of the sciences.
None of these three glyphs has been subscripted before. Will the
meaning be clear to the recipients? One also wonders why the message
doesn't express a desire to understand human science, or science
generally. One might argue that it does not make sense to ask the
recipients about the human versions of mathematics and physics. But a
later group expresses a desire to understand males and females, and the
recipients don't know anything about that either.
Alien mathematics, physics, and biology, wat. Note that this asks
specifically about the recipients’ version of the sciences.
None of these three glyphs has been subscripted before. Will the
meaning be clear to the recipients? One also wonders why the message
doesn't express a desire to understand human science, or science
generally. One might argue that it does not make sense to ask the
recipients about the human versions of mathematics and physics. But a
later group expresses a desire to understand males and females, and the
recipients don't know anything about that either.
 Aliens wat. Alien [planet] mass, radius, acceleration wat.
The meaning of
Aliens wat. Alien [planet] mass, radius, acceleration wat.
The meaning of
 shifts here from meaning the recipients themselves to the recipients’
planet. “Acceleration”
shifts here from meaning the recipients themselves to the recipients’
planet. “Acceleration”
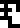 is intended to refer to the planet's gravitational acceleration as
on page 14. What if the recipients
don't live on a planet? I suppose they will be familiar with planets
generally and with the fact that we live on a planet, which explained
back on pages 11–13, and will get the idea.
is intended to refer to the planet's gravitational acceleration as
on page 14. What if the recipients
don't live on a planet? I suppose they will be familiar with planets
generally and with the fact that we live on a planet, which explained
back on pages 11–13, and will get the idea.
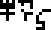 Fucking speed of light, how does it work?
Fucking speed of light, how does it work?
 Planck's constant, wat. Universal gravitation constant, wat?
Planck's constant, wat. Universal gravitation constant, wat?
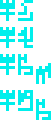 Males and females, wat. Alien people, wat. Age of people,
wat. This group seems to be about our desire to understand ourselves,
except that the third item relates to the aliens. I'm not quite sure
what is going on. Perhaps “males and females” is intended to refer to
the recipients? But the glyphs are not subscripted, and there is no
strong reason to believe that the aliens have the same sexuality.
Males and females, wat. Alien people, wat. Age of people,
wat. This group seems to be about our desire to understand ourselves,
except that the third item relates to the aliens. I'm not quite sure
what is going on. Perhaps “males and females” is intended to refer to
the recipients? But the glyphs are not subscripted, and there is no
strong reason to believe that the aliens have the same sexuality.
The glyph
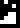 , already used
both to mean the age of the Earth and the typical human lifespan, is
even less clear here. Does it mean we want to understand the reasons
for human life expectancy? Or is it intended to continue the inquiry
from the previous line and is asking about the recipients’ history or
lifespan?
, already used
both to mean the age of the Earth and the typical human lifespan, is
even less clear here. Does it mean we want to understand the reasons
for human life expectancy? Or is it intended to continue the inquiry
from the previous line and is asking about the recipients’ history or
lifespan?
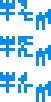 Land, water, and atmosphere of the recipients’ planet, wat.
Land, water, and atmosphere of the recipients’ planet, wat.
 Energy, force, pressure, power, wat. The usage here is
inconsistent from the first group, which asked not about mass,
distance, and time but about kilograms, meters, and seconds specifically.
Energy, force, pressure, power, wat. The usage here is
inconsistent from the first group, which asked not about mass,
distance, and time but about kilograms, meters, and seconds specifically.
 Velocity and acceleration, wat. I wonder why these are in a
separate group, instead of being clustered with the previous group or
the first group. I also worry about the equivocation in
Velocity and acceleration, wat. I wonder why these are in a
separate group, instead of being clustered with the previous group or
the first group. I also worry about the equivocation in
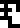 acceleration,
which is sometimes used to mean the Earth's gravitational acceleration
and sometimes acceleration generally. We already said we want to
understand
mass
acceleration,
which is sometimes used to mean the Earth's gravitational acceleration
and sometimes acceleration generally. We already said we want to
understand
mass 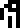 ,
!!G!!
,
!!G!! 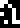 ,
and the size of the Earth. The Earth's surface gravity can be
straightforwardly calculated from these, so there's nothing else to
understand about that.
,
and the size of the Earth. The Earth's surface gravity can be
straightforwardly calculated from these, so there's nothing else to
understand about that.
 Alien planet, wat.
The glyph
Alien planet, wat.
The glyph
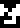 has
heretofore been used only to refer to the planet Earth. It does not mean planets
generally, because it was not used in connection with Jupiter
has
heretofore been used only to refer to the planet Earth. It does not mean planets
generally, because it was not used in connection with Jupiter
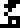 .
Here, however, it
seems to refer to the recipients’ planet.
.
Here, however, it
seems to refer to the recipients’ planet.
 The universe, wat. HUH???
The universe, wat. HUH???
That was the last page. Thanks for your kind attention.
[ Many thanks to Anna Gundlach, without whose timely email I might not have found the motivation to finish this series. ]
[Other articles in category /aliens/dd] permanent link
Fri, 18 Dec 2015I only posted three answers in August, but two of them were interesting.
In why this !!\sigma\pi\sigma^{-1}!! keeps apearing in my group theory book? (cycle decomposition) the querent asked about the “conjugation” operation that keeps cropping up in group theory. Why is it important? I sympathize with this; it wasn't adequately explained when I took group theory, and I had to figure it out a long time later. Unfortunately I don't think I picked the right example to explain it, so I am going to try again now.
Consider the eight symmetries of the square. They are of five types:
- Rotation clockwise or counterclockwise by 90°.
- Rotation by 180°.
- Horizontal or vertical reflection
- Diagonal reflection
- The trivial (identity) symmetry
What is meant when I say that a horizontal and a vertical reflection are of the same ‘type’? Informally, it is that the horizontal reflection looks just like the vertical reflection, if you turn your head ninety degrees. We can formalize this by observing that if we rotate the square 90°, then give it a horizontal flip, then rotate it back, the effect is exactly to give it a vertical flip. In notation, we might represent the horizontal flip by !!H!!, the vertical flip by !!V!!, the clockwise rotation by !!\rho!!, and the counterclockwise rotation by !!\rho^{-1}!!; then we have
$$ \rho H \rho^{-1} = V$$
and similarly
$$ \rho V \rho^{-1} = H.$$
Vertical flips do not look like diagonal flips—the diagonal flip leaves two of the corners in the same place, and the vertical flip does not—and indeed there is no analogous formula with !!H!! replaced with one of the diagonal flips. However, if !!D_1!! and !!D_2!! are the two diagonal flips, then we do have
$$ \rho D_1 \rho^{-1} = D_2.$$
In general, When !!a!! and !!b!! are two symmetries, and there is some symmetry !!x!! for which
$$xax^{-1} = b$$
we say that !!a!! is conjugate to !!b!!. One can show that conjugacy is an equivalence relation, which means that the symmetries of any object can be divided into separate “conjugacy classes” such that two symmetries are conjugate if and only if they are in the same class. For the square, the conjugacy classes are the five I listed earlier.
This conjugacy thing is important for telling when two symmetries are group-theoretically “the same”, and have the same group-theoretic properties. For example, the fact that the horizontal and vertical flips move all four vertices, while the diagonal flips do not. Another example is that a horizontal flip is self-inverse (if you do it again, it cancels itself out), but a 90° rotation is not (you have to do it four times before it cancels out.) But the horizontal flip shares all its properties with the vertical flip, because it is the same if you just turn your head.
Identifying this sameness makes certain kinds of arguments much simpler. For example, in counting squares, I wanted to count the number of ways of coloring the faces of a cube, and instead of dealing with the 24 symmetries of the cube, I only needed to deal with their 5 conjugacy classes.
The example I gave in my math.se answer was maybe less perspicuous. I considered the symmetries of a sphere, and talked about how two rotations of the sphere by 17° are conjugate, regardless of what axis one rotates around. I thought of the square at the end, and threw it in, but I wish I had started with it.
How to convert a decimal to a fraction easily? was the month's big winner. OP wanted to know how to take a decimal like !!0.3760683761!! and discover that it can be written as !!\frac{44}{117}!!. The right answer to this is of course to use continued fraction theory, but I did not want to write a long treatise on continued fractions, so I stripped down the theory to obtain an algorithm that is slower, but much easier to understand.
The algorithm is just binary search, but with a twist. If you are looking for a fraction for !!x!!, and you know !!\frac ab < x < \frac cd!!, then you construct the mediant !!\frac{a+c}{b+d}!! and compare it with !!x!!. This gives you a smaller interval in which to search for !!x!!, and the reason you use the mediant instead of using !!\frac12\left(\frac ab + \frac cd\right)!! as usual is that if you use the mediant you are guaranteed to exactly nail all the best rational approximations of !!x!!. This is the algorithm I described a few years ago in your age as a fraction, again; there the binary search proceeds down the branches of the Stern-Brocot tree to find a fraction close to !!0.368!!.
I did ask a question this month: I was looking for a simpler version of the dogbone space construction. The dogbone space is a very peculiar counterexample of general topology, originally constructed by R.H. Bing. I mentioned it here in 2007, and said, at the time:
[The paper] is on my desk, but I have not read this yet, and I may never.
I did try to read it, but I did not try very hard, and I did not understand it. So my question this month was if there was a simpler example of the same type. I did not receive an answer, just a followup comment that no, there is no such example.
[Other articles in category /math/se] permanent link
Sat, 12 Dec 2015
A message to the aliens, part 22/23 (cosmology)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth) Page 21 (the message)
This is page 22 of the Cosmic Call message. An explanation follows.

The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 |  9 |
This page discusses properties of the entire universe. It is labeled
with a new glyph,
 ,
which denotes the universe or the cosmos. On this page I am on
uncertain ground, because I know very little about cosmology. My
explanation here could be completely wrong without my realizing it.
,
which denotes the universe or the cosmos. On this page I am on
uncertain ground, because I know very little about cosmology. My
explanation here could be completely wrong without my realizing it.
The page contains only five lines of text. In order, they state:
The Friedmann equation which is the current model for the expansion of the universe. This expansion is believed to be uniform everywhere, but even if it isn't, the recipients are so close by that they will see exactly the same expansion we do. If they have noticed the expansion, they may well have come to the same theoretical conclusions about it. The equation is:
$$H^2 = \frac{8\pi G}3\rho + \frac{\Lambda c^2 }3$$
where !!H!! is the Hubble parameter (which describes how quickly the universe is expanding), !!G!! is the universal gravitation constant
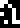 (introduced on page 9),
!!\rho!! is the density of the universe
(introduced on page 9),
!!\rho!! is the density of the universe
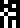
 (given on the next line),
and !!\Lambda c^2!! (
(given on the next line),
and !!\Lambda c^2!! ( )
is one of the forms of the
cosmological constant (given on the following line).
)
is one of the forms of the
cosmological constant (given on the following line).The average density
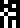 of the universe
of the universe  ,
given as !!2.76\times 10^{-27} \mathrm{kg}
~\mathrm{m}^{-3}!!. The “density” glyph would have been more at home
with the other physics definitions of page
9, but it wasn't needed until now, and
that page was full.
,
given as !!2.76\times 10^{-27} \mathrm{kg}
~\mathrm{m}^{-3}!!. The “density” glyph would have been more at home
with the other physics definitions of page
9, but it wasn't needed until now, and
that page was full.The cosmological constant !!\Lambda!! is about !!10^{-52} \mathrm{m}^{-2}!!. The related value given here, !!\Lambda c^2!!, is !!1.08\cdot 10^{-35} \mathrm{s}^{-2}!!.
The calculated value of the Hubble parameter !!H!!
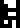 is given here in
the rather strange form !!\frac1{14000000000}\mathrm{year}^{-1}!!.
The reason it is phrased this way is that (assuming that !!H!! were
constant) !!\frac1H!! would be the age of the universe, approximately
14,000,000,000 years. So this line not only communicates our
estimate for the current value of the Hubble parameter, it
expresses it in units that may make clear our beliefs about the age
of the universe. It is regrettable that this wasn't stated more
explicitly, using the glyph
is given here in
the rather strange form !!\frac1{14000000000}\mathrm{year}^{-1}!!.
The reason it is phrased this way is that (assuming that !!H!! were
constant) !!\frac1H!! would be the age of the universe, approximately
14,000,000,000 years. So this line not only communicates our
estimate for the current value of the Hubble parameter, it
expresses it in units that may make clear our beliefs about the age
of the universe. It is regrettable that this wasn't stated more
explicitly, using the glyph 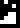 that was already used for the age of the Earth on page
13. There
was plenty of extra space, so perhaps the senders didn't think of it.
that was already used for the age of the Earth on page
13. There
was plenty of extra space, so perhaps the senders didn't think of it.The average temperature
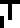 of the universe, about 2.736 kelvins. This is based on measurements of the cosmic microwave background radiation, which is the same in every direction, so if the recipients have noticed it at all, they have seen the same CMB that we have.
of the universe, about 2.736 kelvins. This is based on measurements of the cosmic microwave background radiation, which is the same in every direction, so if the recipients have noticed it at all, they have seen the same CMB that we have.
[Other articles in category /aliens/dd] permanent link
Sun, 06 Dec 2015
A message to the aliens, part 21/23 (the message)
Earlier articles: Introduction Common features Page 1 (numerals) Page 2 (arithmetic) Page 3 (exponents) Page 4 (algebra) Page 5 (geometry) Page 6 (chemistry) Page 7 (mass) Page 8 (time and space) Page 9 (physical units) Page 10 (temperature) Page 11 (solar system) Page 12 (Earth-Moon system) Page 13 (days, months, and years) Page 14 (terrain) Page 15 (human anatomy) Page 16 (vital statistics) Page 17 (DNA chemistry) Page 18 (cell respiration and division) Pages 19-20 (map of the Earth)
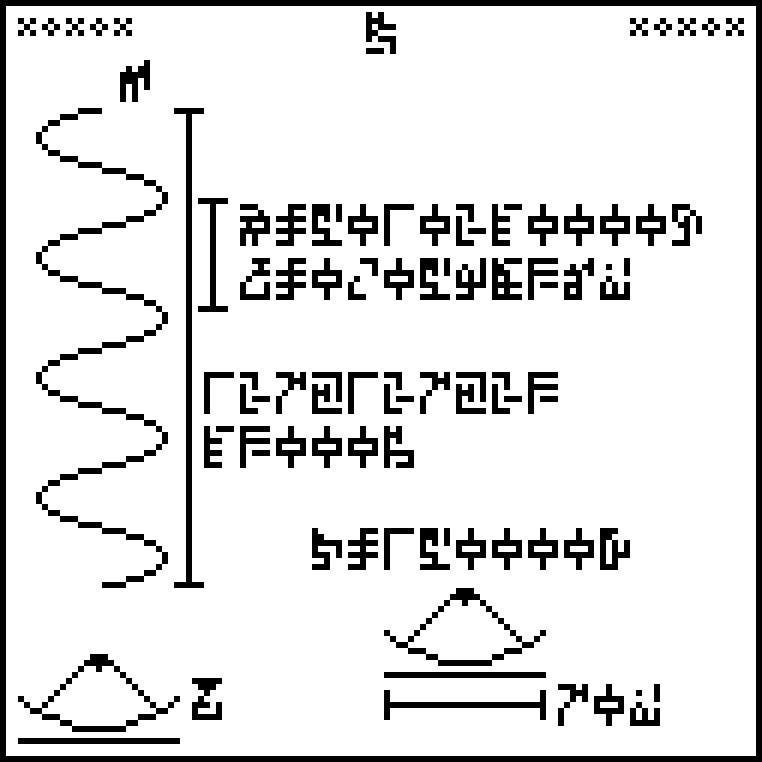
This is page 21 of the Cosmic Call message. An explanation follows.
The 10 digits are:
 0 |  1 |  2 |  3 |  4 |  5 |  6 |  7 |  8 |  9 |
This page discusses the message itself. It is headed with the glyph
for “physics” 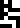 .
.
 The
leftmost part of the page has a cartoon of the Yevpatoria RT-70 radio
telescope
that was used to send the message, labeled “Earth”
The
leftmost part of the page has a cartoon of the Yevpatoria RT-70 radio
telescope
that was used to send the message, labeled “Earth” 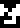 . Coming out the
the telescope is a stylized depiction of a radio wave. Two rulers
measure the radio wave. The smaller one measures a single wavelength,
and is labeled “frequency
. Coming out the
the telescope is a stylized depiction of a radio wave. Two rulers
measure the radio wave. The smaller one measures a single wavelength,
and is labeled “frequency 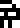 =
5,010,240,000 Hz
=
5,010,240,000 Hz 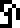 ” and “wavelength
” and “wavelength
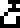 =
0.059836 meters
=
0.059836 meters 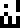 ”; these are the
frequency and the wavelength of the radio waves used to send the
message. The longer ruler has the notation “127×127×23”, describing
the format of the message itself, 23 pages of 127×127 bitmaps, and
also “43000 people
”; these are the
frequency and the wavelength of the radio waves used to send the
message. The longer ruler has the notation “127×127×23”, describing
the format of the message itself, 23 pages of 127×127 bitmaps, and
also “43000 people 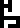 ”, which I do not
understand at all. Were 43,000 people somehow involved with sending
the message? That seems far too many. Were there 43,000 people in
Yevpatoria in 1999? That seems far too few; the current population is
over 100,000. I am mystified.
”, which I do not
understand at all. Were 43,000 people somehow involved with sending
the message? That seems far too many. Were there 43,000 people in
Yevpatoria in 1999? That seems far too few; the current population is
over 100,000. I am mystified.
At the other end of the radio wave is
the glyph  , which is
hard to decipher, because it appears only on this page and on the
unhelpful page 23. I guess it is intended to refer to the
recipients of the message.
, which is
hard to decipher, because it appears only on this page and on the
unhelpful page 23. I guess it is intended to refer to the
recipients of the message.
[ Addendum 20151219: Having reviewed page 23, I am still in the
dark.
References to the mass and radius of
 suggest that it refers to the recipients’ planet, but references to the mathematics, physics, and biology of
suggest that it refers to the recipients’ planet, but references to the mathematics, physics, and biology of
 suggests that it refers to the recipients themselves. ]
suggests that it refers to the recipients themselves. ]
In the lower-right corner of the page is another cartoon of the RT-70, this time with a ruler underneath showing its diameter, 70 meters. Above the cartoon is the power output of the telescope, 150 kilowatts.
The next article will discuss page 22, shown at right. (Click to enlarge.) Try to figure it out before then.[Other articles in category /aliens/dd] permanent link




