Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 13 Mar 2006
Why pi?
Simon Cozens wrote to me yesterday to ask what the heck was up with
π:
what property of a circle makes it . . . an irrational number. . . perhaps about as arbitrary a number as you can get.I thought about this pretty hard, and, to my amazement, I came up with a plausible answer. So here we are.
The one-paragraph summary: My theory is that the association of the very weird and complex number π with a geometric object as simple as a circle is a reflection of the underlying fundamental complexity of Euclidean geometry: specifically, that its metric is a nonlinear function.
First I'm going to spend some time arguing that π does require explanation. I expect that almost everyone will agree that π is weird; if you do agree, feel free to skip this section. Then I'll discuss Euclidean and non-Euclidean geometries. This is important, because the relation between π and circles appears to be a special property of Euclidean geometry, one which does not occur, for example, in spherical geometry. Finally, I'll look at the essential properties of Euclidean geometry, and why I think it is more complex than people usually realize.
π is complex and bizarre
In this section, I'm going to argue that the question is indeed worth asking. π is an extremely peculiar number, even by mathematical standards. You often hear π mentioned in the same breath with e, another constant of fundamental mathematical importance. But e is much more tractable than π is, and much better understood.In fact, the degree to which π is not understood is rather shocking when you consider its ubiquity.
If you don't need to be persuaded that π is unusually weird, even as transcendental numbers go, you may want to skip to the next section. Really, this section is here to address people who think they know more mathematics than they do, who want to argue that π is no more or less complicated than any other number. But I think it is.
It should be fairly clear that, as a representation of real numbers, decimal fractions are not very satisfactory. For example, you might like simple numbers to have simple representations. But the representation of 1/3 is 0.33333...., which isn't even finite. The fact that a complicated number like like 3674/31250 ("0.117568") has a simpler representation than a simple number like 1/3 just demonstrates that the system is defective. 3674/31250 gets a simple representation not because it is a simple number, but because 31250 happens to divide 106.
This being the case, it is perhaps not too surprising that nobody can make head or tail of the representation of π, which is 3.14159265358979... . As far as I know, the state of our current understanding of this representation of π can be summed up as:
None
But that might just be the fault of the representation. The representation is based on the number 10, and it is not clear that π has anything to do with 10, so our failure to find an answer here may just indicate that the question was not worth asking.There are better representations of real numbers; one such is the so-called "continued fraction representation". I don't want to explain this in detail in this article, but I can refer you to a talk I gave on the subject. But an itemization of this representation's desirable properties may be persuasive even if you don't know how it works:
- In
continued fraction notation, a number has a finite representation when,
and only when, it is rational.
- The representation is not inappropriately snuggly with the number
10, or with any other number.
- Simple rationals have simple
representations and more complicated rationals have more complicated
representations. For example, 1/3 is represented as [0; 3] and
3674/31250 is represented as [0; 8, 1, 1, 43, 4, 5].
- Some irrational numbers have simple (although infinite)
representations. For example, in the customary system, √2 is an
incomprehensible soup of digits starting 1.414213562... . In the continued
fraction system, it is [1; 2, 2, 2, 2, ...].
- If you turn an irrational number into a rational one by chopping
off the infinite tail of the continued fraction representation, you
get a very closely-related rational result, one that is numerically as
close as possible to the original number. This is not true of the
decimal fraction. If you chop off √2 after a couple of terms of
decimal fraction, you get 1.41, which is 141/100. If you chop off
√ after a couple of terms of continued fraction, you get [1; 2,
2], which is 7/5. This is slightly less accurate than 141/100, but
the denominator is twenty times smaller. If you chop a little later,
you get [1; 2, 2, 2], which is 17/12, which is a lot more accurate
than 141/100, even though the denominator is only 12.
But it doesn't work for π. The continued fraction representation of π is [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, ...], and as far as I know, the state of our current understanding of this representation of π can be summed up as:
None
So much for continued fractions.We might hope for some understanding about why π is irrational. The proof that √2 is irrational is elementary, and dates back to the Greeks; you can understand it as being related to the fact that 2 is not a perfect square. π was not shown to be irrational until 1761, and the proof is not simple, which means that nobody knows a simple argument about why it should be the complicated thing it is, rather than a simple fraction.
So π is complex and poorly-understood, even compared with other important transcendental numbers like e.
Euclidean geometry
M. Cozens asked:Is pi inherent in our definition of a circle, or our particular geometry, or our planet, or could the ratio be different in different worlds?I think this question is very insightful. π, at least as it relates to circles, is inherent in a particular geometry, namely, Euclidean geometry.
Euclidean geometry takes its name from Euclid, who wrote Elements, an extremely influential treatise on geometry, about 2300 years ago. Most of the Elements is concerned with plane geometry, which takes place in an infinite, flat two-dimensional space. π arises naturally in this kind of space as the perimeter of a circle.
Non-Euclidean geometry
In non-Euclidean spaces, π is geometrically much less important. For example, consider geometry done on a sphere. If we keep the definition of "line" as the path of shortest distance between two points, then our "lines" turn out to be great circles on the sphere—that is, circles whose centers are at the center of the sphere; the equator is an example. The 49th parallel is not a "line" because it's not a path of shortest distance; for any two points on the 49th parallel, there's a path between them over the surface of the sphere that is shorter than the one along the parallel. (This may seem strange, but it's true, and it's why direct flights from New York to Taipei often stop off in Anchorage, Alaska.) In addition to being a line, the equator is also an example of a circle. What's a circle? Circles look pretty much the way you expect them to. A circle is the set of all points that are some fixed distance from a center point. The equator is all the points that are a certain fixed distance from the north pole. The 49th parallel is also a circle; its center is also the north pole.
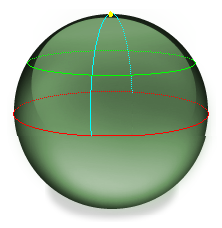 The "diameter" of a circle is the longest possible "line" you can draw
from one point on the circle to another. A diameter of a circle has
the property that it always goes through the center of the circle, as
you would hope and expect. For the equator, a diameter goes through
the north pole. The picture to the right shows the equator in red,
its center, the north pole, in yellow, and a diameter of the equator
in blue. The 49th parallel is in green.
The "diameter" of a circle is the longest possible "line" you can draw
from one point on the circle to another. A diameter of a circle has
the property that it always goes through the center of the circle, as
you would hope and expect. For the equator, a diameter goes through
the north pole. The picture to the right shows the equator in red,
its center, the north pole, in yellow, and a diameter of the equator
in blue. The 49th parallel is in green.
Let's say that the circumference of the equator, the red line, is 1. Then the length of the equator's diameter, the blue line, is 1/2. If we were expecting to divide the circumference by the diameter and get π, we are in for a surprise, because we just got 2 instead.
For the 49th parallel, the ratio of circumference to diameter is larger: I calculate about 2.88. For smaller circles, the ratio is larger still. For very small circles, the ratio is very close to π, because a small circle can't tell whether it's on a sphere or in a plane; up close the two things look the same.
So the relation between π and circles is actually a special property of Euclidean geometry. Circles in non-Euclidean spaces have a perimeter-to-diameter ratio that is different from π.
Euclidean metric
The single fundamental property of Euclidean geometry is that the distance between two points, say (x1, y1) and (x2, y2), is ((x2-x1)2 + (y2-y1)2)1/2. (Or, in higher-dimensional spaces, the obvious extension of this formula.) If you change the way you measure distance, you get a different kind of geometry with different kinds of circles that have different perimeter-to-diameter ratios. In an earlier article, I discussed an alternative distance function, called the Manhattan distance, which gives diamond-shaped circles whose perimeter-to-diameter ratio is always 4.The Euclidean distance function is nothing more than the familiar Pythagorean theorem. It is very difficult for me to imagine any reasonable way to do plane geometry without the Pythagorean theorem. It is just too simple. Even the proof is simple:
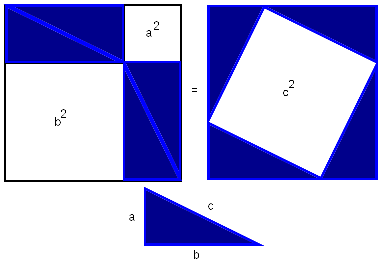
So the relationship of π (which is complicated) to circles (which appear to be simple) is grounded in the Euclidean distance formula. If you change the distance formula, π is no longer related to circles. So the weirdness must be due, at least in part, to some complexity in the Euclidean distance formula.
But what's complex about the Euclidean distance formula? How could it be simpler?
Actually, I think it only seems simple because it is so familiar. The Euclidean distance formula is, in some ways, deeply weird. I realized this a few months ago, but everyone I mentioned it to acted like I was insane. But now I'm pretty sure. I think the essence of the problem with π is that the Euclidean distance function is nonlinear in the two spatial coordinates x and y.
Nonlinearity of the Euclidean metric
Linear functions are very well-behaved. If F is a linear function, then F(a+b) = F(a) + F(b), which means that you can calculate the contributions of a and b independently of each other. To calculate F of some very complicated argument, you can break the argument into simple components and deal with them all separately. With quadratic functions like the Euclidean distance function, you cannot do this; complex problems are not easily decomposable into simple ones.For the Euclidean metric, it means that the horizontalness and verticalosity are not independent, but are tangled together and cannot be separated.
What do we really mean by the perimeter of a circle? The circle is the set of points (x, y) which are at distance 1 from the point (0,0). The only meaningful way I know to talk about the length of this set is to calculate it as a limit of an approximate polygonal path as the path gets more and more segments. So you are necessarily dragging in an infinite limiting process, and such processes are always complicated.
If the distance function were linear, it wouldn't matter, because then you could treat the horizontal and vertical components separately, and when you did that, you would be dealing with paths in one dimension, which, being straight lines, would be simple. You can see this if you consider the Manhattan distance function: It doesn't matter how you get from (x1, y1) to (x2, y2); whatever path you take, whether you take a lot of steps or only one, the distance is always |x2-x1| + |y2-y1|, because the distance function is linear, and thus there is no interaction between the x parts and the y parts. But with a nonlinear distance function like the Euclidean metric, it does matter what path you take.
I was thinking a few months ago about how peculiar this is. I cannot think of anything else that behaves this way. Suppose you have two jugs and you start filling them with milk. You find that to fill each jug separately requires one quart, but to fill both at once requires only 1.4142 quarts. Wouldn't that freak you out? But space does behave like that. To drive ten miles north takes a gallon of gas. To drive ten miles east takes a gallon of gas. North and east are perpendicular and should be completely independent of each other. To drive ten miles north and ten miles east should require two gallons of gas. But it requires only 1.4142 gallons. How the heck did that happen?
I believe that this strange entanglement between north and east, two things one might have supposed were independent, is the ultimate root of what makes the circumference of a circle such a peculiar number. I was very pleased to have this confirmation that the entanglement between horizontal and vertical is strange and complex, because, as I mentioned before, when I tried to explain to people what I found strange about it, they thought I was nuts.
One-dimensional circles
My theory is that the peculiar length of a circle's perimeter is a result of the peculiar interaction between the otherwise apparently independent spatial dimensions in Euclidean space. If this theory is correct, we should expect that the corresponding perimeter in a one-dimensional space will not be peculiar. A one-dimensional Euclidean space, having only one dimension, has no strange interactions between independent directions. And indeed, this is the case! The perimeter of a one-dimensional circle does not involve π. It's simply 2; the "area" (which is really length) is 2r. You only get difficult numbers in spaces of at least 2 dimensions.
Why 3?
M. Cozens also asked me why the number came out to be around 3, rather than around 5 or 57, and there I was on much shakier ground. I did not have any clever insights, and all I could do was itemize a bunch of stuff that seemed to bear on the issue. It will probably appear here in a future article.[ Addendum: Here it is. ]
[Other articles in category /math] permanent link


