Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 09 Jan 2006
Mixed fractions in Liber Abaci
Leonardo Pisano has an interesting notation for fractions. He often uses mixed-base systems. In general, he writes:
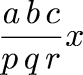
where a, b, c, p, q, r, x are integers. This represents the number:
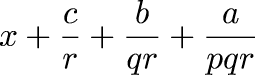
which may seem odd at first. But the notation is a good one, and here's why. Suppose your currency is pounds, and there are 20 soldi in a pound and 12 denari in a soldo. This is the ancient Roman system, used throughout Europe in the middle ages, and in England up through the 1970s. You have 6 pounds, 7 soldi, and 4 denari. To convert this to pounds requires no arithmetic whatsooever; the answer is simply
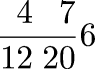
And in general, L pounds, S soldi and D denari can be written
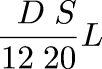
Now similarly you have a distance of 3 miles, 6 furlongs, 42 yards, 2 feet, and 7 inches. You want to calculate something having to do with miles, so you need to know how many miles that is. No problem; it's just
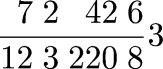
We tend to do this sort of thing either in decimals (which is inconvenient unless all the units are powers of 10) or else we reduce everything to a single denominator, in which case the numbers get quite large. If you have many mixed units, as medieval merchants did, Leonardo's notation is very convenient.
One operation that comes up all the time is as follows. Suppose you have
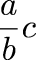
and you wish that the denominator were s instead of b. It is easy to convert. You calculate the quotient q and remainder r of dividing a·s by b. Then the equivalent fraction with denominator s is just:
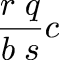
(Here we have replaced c + a/b with c + q/s + r/bs, which we can do since q and r were chosen so that qb + r = as.)
Why would you want to convert a denominator in this way? Here is a typical example. Suppose you have 24 pounds and you want to split it 11 ways. Well, clearly each share is worth
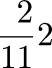
pounds; we can get that far without medieval arithmetic tricks. But how much is 2/11 pounds? Now you want to convert the 2/11 to soldi; there are 20 soldi in a pound. So you multiply 2/11 by 20 and get 40/11; the quotient is 3 and the remainder 7, so that each share is really worth
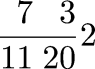
pounds. That is, each share is worth 2 pounds, plus 3 and 7/11 soldi.
But maybe you want to convert the 7/11 soldi to denari; there are 12 denari in a soldo. So you multiply 7/11 by 12 and get 84/11; the quotient is 7 and the remainder 7 also, so that each share is
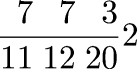
so each share is worth precisely 2 pounds, 3 soldi, and 7 7/11 denari.
Note that this system subsumes the usual decimal system, since you can always write something like
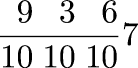
when you mean the number 7.639. And in fact Leanardo does do exactly this when it makes sense in problems concerning decimal currencies and other decimal matters. For example, in Chapter 12 of Liber Abaci, Leonardo says that there is a man with 100 bezants, who travels through 12 cities, giving away 1/10 of his money in each city. (A bezant was a medieval coin minted in Constantinople. Unlike the European money, it was a decimal currency, divided into 10 parts.) The problem is clearly to calculate (9/10)12 × 100, and Leonardo indeed gives the answer as
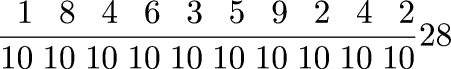
He then asks how much money was given away, subtracting the previous compound fraction from 100, getting
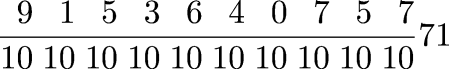
(Leonardo's extensive discussion of this problem appears on pp. 439–443 of L. E. Sigler Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation.)
The flexibility of the notation appears in many places. In a problem "On a Soldier Receiving Three Hundred Bezants for His Fief" (p. 392) Leonardo must consider the fraction
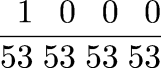
(That is, 1/534) which he multiplies by 2050601250 to get the final answer in beautiful base-53 decimals:
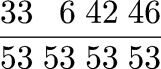
Post scriptum: The Roman names for pound, soldo, and denaro are librum ("pound"), solidus, and denarius. The names survived into Renaissance French (livre, sou, denier) and almost survived into modern English. Until the currency was decimalized, British money amounts were written in the form "£3 4s. 2d." even though the English names of the units are "pound", "shilling", "penny", because "£" stands for "libra", "s" for "solidi", and "d" for "denarii". In small amounts one would write simply "10/6" instead of "10s. 6d.", and thus the "/" symbol came to be known as a "solidus", and still is.
The Spanish word for money, dinero, means denarii. The Arabic word dinar, which is the name of the currency in Algeria, Bahrain, Iraq, Jordan, Kuwait, Libya, Sudan, and Tunisia, means denarii.
Soldiers are so called after the solidi with which they were paid.
[Other articles in category /math] permanent link


