Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Another example of a machine perception failure |
| How Shazam works |
| Miscellanea about 24 puzzles |
| Recognizing when two arithmetic expressions are essentially the same |
| That time I met Erdős |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sun, 27 Aug 2017
This is a collection of leftover miscellanea about twenty-four puzzles. In case you forgot what that is:
The puzzle «4 6 7 9 ⇒ 24» means that one should take the numbers 4, 6, 7, and 9, and combine them with the usual arithmetic operations of addition, subtraction, multiplication, and division, to make the number 24. In this case the unique solution is $$6\times\frac{7 + 9}{4}.$$ When the target number is 24, as it often is, we omit it and just write «4 6 7 9».
Prior articles on this topic:
- A simple but difficult arithmetic puzzle (July 2016)
- Solving twenty-four puzzles (March 2017)
- Recognizing when two arithmetic expressions are essentially the same (August 2017)
How many puzzles have solutions?
For each value of !!T!!, there are 715 puzzles «a b c d ⇒ T». (I discussed this digression in two more earlier articles: [1] [2].) When the target !!T = 24!!, 466 of the 715 puzzles have solutions. Is this typical? Many solutions of «a b c d» puzzles end with a multiplication of 6 and 4, or of 8 and 3, or sometimes of 12 and 2—so many that one quickly learns to look for these types of solutions right away. When !!T=23!!, there won't be any solutions of this type, and we might expect that relatively few puzzles with prime targets have solutions.
This turns out to be the case:
The x-axis is the target number !!T!!, with 0 at the left, 300 at right, and vertical guide lines every 25. The y axis is the number of solvable puzzles out of the maximum possible of 715, with 0 at the bottom, 715 at the top, and horizontal guide lines every 100.
Dots representing prime number targets are colored black. Dots for numbers with two prime factors (4, 6, 9, 10, 14, 15, 21, 22, etc.) are red; dots with three, four, five, six, and seven prime factors are orange, yellow, green, blue, and purple respectively.
Two countervailing trends are obvious: Puzzles with smaller targets have more solutions, and puzzles with highly-composite targets have more solutions. No target number larger than 24 has as many as 466 solvable puzzles.
These are only trends, not hard rules. For example, there are 156 solvable puzzles with the target 126 (4 prime factors) but only 93 with target 128 (7 prime factors). Why? (I don't know. Maybe because there is some correlation with the number of different prime factors? But 72, 144, and 216 have many solutions, and only two different prime factors.)
The smallest target you can't hit is 417. The following numbers 418 and 419 are also impossible. But there are 8 sets of four digits that can be used to make 416 and 23 sets that can be used to make 420. The largest target that can be hit is obviously !!6561 = 9⁴!!; the largest target with two solutions is !!2916 = 4·9·9·9 = 6·6·9·9!!.
(The raw data are available here).
There is a lot more to discover here. For example, from looking at the chart, it seems that the locally-best target numbers often have the form !!2^n3^m!!. What would we see if we colored the dots according to their largest prime factor instead of according to their number of prime factors? (I tried doing this, and it didn't look like much, but maybe it could have been done better.)
Making zero
As the chart shows, 705 of the 715 puzzles of the type «a b c d ⇒ 0», are solvable. This suggests an interesting inverse puzzle that Toph and I enjoyed: find four digits !!a,b,c, d!! that cannot be used to make zero. (The answers).
Identifying interesting or difficult problems
(Caution: this section contains spoilers for many of the most interesting puzzles.)
I spent quite a while trying to get the computer to rank puzzles by difficulty, with indifferent success.
Fractions
Seven puzzles require the use of fractions. One of these is the notorious «3 3 8 8» that I mentioned before. This is probably the single hardest of this type. The other six are:
«1 3 4 6»
«1 4 5 6»
«1 5 5 5»
«1 6 6 8»
«3 3 7 7»
«4 4 7 7»
(Solutions to these (formatted image); solutions to these (plain text))
«1 5 5 5» is somewhat easier than the others, but they all follow pretty much the same pattern. The last two are pleasantly symmetrical.
Negative numbers
No puzzles require the use of negative intermediate values. This surprised me at first, but it is not hard to see why. Subexpressions with negative intermediate values can always be rewritten to have positive intermediate values instead.
For instance, !!3 × (9 + (3 - 4))!! can be rewritten as !!3 × (9 - (4 - 3))!! and !!(5 - 8)×(1 -9)!! can be rewritten as !!(8 - 5)×(9 -1)!!.
A digression about tree shapes
In one of the earlier articles I asserted that there are only two possible shapes for the expression trees of a puzzle solution:
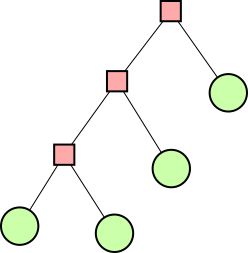
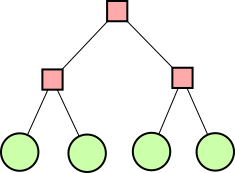
| 
|
| Form A | Form B |
(Pink square nodes contain operators and green round nodes contain numbers.)
Lindsey Kuper pointed out that there are five possible shapes, not two. Of course, I was aware of this (it is a Catalan number), so what did I mean when I said there were only two? It's because I had the idea that any tree that wasn't already in one of those two forms could be put into form A by using transformations like the ones in the previous section.
For example, the expression !!(4×((1+2)÷3))!! isn't in either form, but we can commute the × to get the equivalent !!((1+2)÷3)×4!!, which has form A. Sometimes one uses the associative laws, for example to turn !!a ÷ (b × c)!! into !!(a ÷ b) ÷ c!!.
But I was mistaken; not every expression can be put into either of these forms. The expression !!(8×(9-(2·3))!! is an example.
Unusual intermediate values
The most interesting thing I tried was to look for puzzles whose solutions require unusual intermediate numbers.
For example, the puzzle «3 4 4 4» looks easy (the other puzzles with just 3s and 4s are all pretty easy) but it is rather tricky because its only solution goes through the unusual intermediate number 28: !!4 × (3 + 4) - 4!!.
I ranked puzzles as follows: each possible intermediate number appears in a certain number of puzzle solutions; this is the score for that intermediate number. (Lower scores are better, because they represent rarer intermediate numbers.) The score for a single expression is the score of its rarest intermediate value. So for example !!4 × (3 + 4) - 4!! has the intermediate values 7 and 28. 7 is extremely common, and 28 is quite unusual, appearing in only 151 solution expressions, so !!4 × (3 + 4) - 4!! receives a fairly low score of 151 because of the intermediate 28.
Then each puzzle received a difficulty score which was the score of its easiest solution expression. For example, «2 2 3 8» has two solutions, one (!!(8+3)×2+2!!) involving the quite unusual intermediate value 22, which has a very good score of only 79. But this puzzle doesn't count as difficult because it also admits the obvious solution !!8·3·\frac22!! and this is the solution that gives it its extremely bad score of 1768.
Under this ranking, the best-scoring twenty-four puzzles, and their scores, were:
«1 2 7 7» 3
* «4 4 7 7» 12
* «1 4 5 6» 13
* «3 3 7 7» 14
* «1 5 5 5» 15
«5 6 6 9» 23
«2 5 7 9» 24
«2 2 5 8» 25
«2 5 8 8» 45
«5 8 8 8» 45
«2 2 2 9» 47
* «1 3 4 6» 59
* «1 6 6 8» 59
«2 4 4 9» 151
«3 4 4 4» 151
* «3 3 8 8» 152
«6 8 8 9» 152
«2 2 2 7» 155
«2 2 5 7» 155
«2 3 7 7» 155
«2 4 7 7» 155
«2 5 5 7» 155
«2 5 7 7» 156
«4 4 8 9» 162
(Something is not quite right here. I think «2 5 7 7» and «2 5 5 7» should have the same score, and I don't know why they don't. But I don't care enough to do it over.)
Most of these are at least a little bit interesting. The seven puzzles that require the use of fractions appear; I have marked them with stars. The top item is «1 2 7 7», whose only solution goes through the extremely rare intermediate number 49. The next items require fractions, and the one after that is «5 6 6 9», which I found difficult. So I think there's some value in this procedure.
But is there enough value? I'm not sure. The last item on the list, «4 4 8 9», goes through the unusual number 36. Nevertheless I don't think it is a hard puzzle.
(I can also imagine that someone might see the answer to «5 6 6 9» right off, but find «4 4 8 9» difficult. The whole exercise is subjective.)
Solutions with unusual tree shapes
I thought about looking for solutions that involved unusual sequences of operations. Division is much less common than the other three operations.
To get it right, one needs to normalize the form of expressions, so that the shapes !!(a + b) + (c + d)!! and !!a + (b + (c + d))!! aren't counted separately. The Ezpr library can help here. But I didn't go that far because the preliminary results weren't encouraging.
There are very few expressions totaling 24 that have the form !!(a÷b)÷(c÷d)!!. But if someone gives you a puzzle with a solution in that form, then !!(a×d)÷(b×c)!! and !!(a×d) ÷ (b÷c)!! are also solutions, and one or another is usually very easy to see. For example, the puzzle «1 3 8 9» has the solution !!(8÷1)÷(3÷9)!!, which has an unusual form. But this is an easy puzzle; someone with even a little experience will find the solution !!8 × \frac93 × 1!! immediately.
Similarly there are relatively few solutions of the form !!a÷((b-c)÷d)!!, but they can all be transformed into !!a×d÷(b-c)!! which is not usually hard to find. Consider $$\frac 8{\left(\frac{6 - 4}6\right)}.$$ This is pretty weird-looking, but when you're trying to solve it one of the first things you might notice is the 8, and then you would try to turn the rest of the digits into a 3 by solving «4 6 6 ⇒ 3», at which point it wouldn't take long to think of !!\frac6{6-4}!!. Or, coming at it from the other direction, you might see the sixes and start looking for a way to make «4 6 8 ⇒ 4», and it wouldn't take long to think of !!\frac8{6-4}!!.
Ezpr shape
Ezprs (see previous article) correspond more closely than abstract syntax trees do with our intuitive notion of how expressions ought to work, so looking at the shape of the Ezpr version of a solution might give better results than looking at the shape of the expression tree. For example, one might look at the number of nodes in the Ezpr or the depth of the Ezpr.
Ad-hockery
When trying to solve one of these puzzles, there are a few things I always try first. After adding up the four numbers, I then look for ways to make !!8·3, 6·4,!! or !!12·2!!; if that doesn't work I start branching out looking for something of the type !!ab\pm c!!.
Suppose we take a list of all solvable puzzles, and remove all the very easy ones: the puzzles where one of the inputs is zero, or where one of the inputs is 1 and there is a solution of the form !!E×1!!.
Then take the remainder and mark them as “easy” if they have solutions of the form !!a+b+c+d, 8·3, 6·4,!! or !!12·2!!. Also eliminate puzzles with solutions of the type !!E + (c - c)!! or !!E×\left(\frac cc\right)!!.
How many are eliminated in this way? Perhaps most? The remaining puzzles ought to have at least intermediate difficulty, and perhaps examining just those will suggest a way to separate them further into two or three ranks of difficulty.
I give up
But by this time I have solved so many twenty-four puzzles that I am no longer sure which ones are hard and which ones are easy. I suspect that I have seen and tried to solve most of the 466 solvable puzzles; certainly more than half. So my brain is no longer a reliable gauge of which puzzles are hard and which are easy.
Perhaps looking at puzzles with five inputs would work better for me now. These tend to be easy, because you have more to work with. But there are 2002 puzzles and probably some of them are hard.
Close, but no cigar
What's the closest you can get to 24 without hitting it exactly? The best I could do was !!5·5 - \frac89!!. Then I asked the computer, which confirmed that this is optimal, although I felt foolish when I saw the simpler solutions that are equally good: !!6·4 \pm\frac 19!!.
The paired solutions $$5 × \left(4 + \frac79\right) < 24 < 7 × \left(4 - \frac59\right)$$ are very handsome.
Phone app
The search program that tells us when a puzzle has solutions is only useful if we can take it with us in the car and ask it about license plates. A phone app is wanted. I built one with Code Studio.
Code Studio is great. It has a nice web interface, and beginners can write programs by dragging blocks around. It looks very much like MIT's scratch project, which is much better-known. But Code Studio is a much better tool than Scratch. In Scratch, once you reach the limits of what it can do, you are stuck, and there is no escape. In Code Studio when you drag around those blocks you are actually writing JavaScript underneath, and you can click a button and see and edit the underlying JavaScript code you have written.
Suppose you need to convert A to 1 and B to 2 and so on. Scratch
does not provide an ord function, so with Scratch you are pretty
much out of luck; your only choice is to write a 26-way if-else tree,
which means dragging around something like 104 stupid blocks. In Code
Studio, you can drop down to the JavaScript level and type in ord
to use the standard ord function. Then if you go back to blocks,
the ord will look like any other built-in function block.
In Scratch, if you want to use a data structure other than an array, you are out of luck, because that is all there is. In Code Studio, you can drop down to the JavaScript level and use or build any data structure available in JavaScript.
In Scratch, if you want to initialize the program with bulk data, say a precomputed table of the solutions of the 466 twenty-four puzzles, you are out of luck. In Code Studio, you can upload a CSV file with up to 1,000 records, which then becomes available to your program as a data structure.
In summary, you spend a lot of your time in Scratch working around the limitations of Scratch, and what you learn doing that is of very limited applicability. Code Studio is real programming and if it doesn't do exactly what you want out of the box, you can get what you want by learning a little more JavaScript, which is likely to be useful in other contexts for a long time to come.
Once you finish your Code Studio app, you can click a button to send the URL to someone via SMS. They can follow the link in their phone's web browser and then use the app.
Code Studio is what Scratch should have been. Check it out.
Thanks
Thanks to everyone who contributed to this article, including:
- my daughters Toph and Katara
- Shreevatsa R.
- Dr. Lindsey Kuper
- Darius Bacon
- everyone else who emailed me
[Other articles in category /math] permanent link
Sun, 20 Aug 2017
Recognizing when two arithmetic expressions are essentially the same
[ Warning: The math formatting in the RSS / Atom feed for this article is badly mutilated. I suggest you read the article on my blog. ]
In this article, I discuss “twenty-four puzzles”. The puzzle «4 6 7 9 ⇒ 24» means that one should take the numbers 4, 6, 7, and 9, and combine them with the usual arithmetic operations of addition, subtraction, multiplication, and division, to make the number 24. In this case the unique solution is !!6·\frac{7 + 9}{4}!!.
When the target number after the
⇒is 24, as it often is, we omit it and just write «4 6 7 9». Every example in this article has target number 24.This is a continuation of my previous articles on this topic:
- A simple but difficult arithmetic puzzle (July 2016)
- Solving twenty-four puzzles (March 2017)
My first cut at writing a solver for twenty-four puzzles was a straightforward search program. It had a couple of hacks in it to cut down the search space by recognizing that !!a+E!! and !!E+a!! are the same, but other than that there was nothing special about it and I've discussed it before.
It would quickly and accurately report whether any particular twenty-four
puzzle was solvable, but as it turned out that wasn't quite good
enough. The original motivation for the program was this: Toph and I
play this game in the car. Pennsylvania license plates have three
letters and four digits, and if we see a license plate FBV 2259 we
try to solve «2 2 5 9». Sometimes we can't find a solution and
then we wonder: it is because there isn't one, or is it because we
just didn't get it yet? So the searcher turned into a phone app,
which would tell us whether there was solution, so we'd know whether
to give up or keep searching.
But this wasn't quite good enough either, because after we would find that first solution, say !!2·(5 + 9 - 2)!!, we would wonder: are there any more? And here the program was useless: it would cheerfully report that there were three, so we would rack our brains to find another, fail, ask the program to tell us the answer, and discover to our disgust that the three solutions it had in mind were:
$$ 2 \cdot (5 + (9 - 2)) \\ 2 \cdot (9 + (5 - 2)) \\ 2 \cdot ((5 + 9) - 2) $$
The computer thinks these are different, because it uses different data structures to represent them. It represents them with an abstract syntax tree, which means that each expression is either a single constant, or is a structure comprising an operator and its two operand expressions—always exactly two. The computer understands the three expressions above as having these structures:

| 
| 
|
It's not hard to imagine that the computer could be taught to understand that the first two trees are equivalent. Getting it to recognize that the third one is also equivalent seems somewhat more difficult.
Commutativity and associativity
I would like the computer to understand that these three expressions should be considered “the same”. But what does “the same” mean? This problem is of a kind I particularly like: we want the computer to do something, but we're not exactly sure what that something is. Some questions are easy to ask but hard to answer, but this is the opposite: the real problem is to decide what question we want to ask. Fun!
Certainly some of the question should involve commutativity and associativity of addition and multiplication. If the only difference between two expressions is that one has !!a + b!! where the other has !!b + a!!, they should be considered the same; similarly !!a + (b + c)!! is the same expression as !!(a + b) + c!! and as !!(b + a) + c!! and !!b + (a + c)!! and so forth.
The «2 2 5 9» example above shows that commutativity and associativity are not limited to addition and multiplication. There are commutative and associative properties of subtraction also! For example, $$a+(b-c) = (a+b)-c$$ and $$(a+b)-c = (a-c)+b.$$ There ought to be names for these laws but as far as I know there aren't. (Sure, it's just commutativity and associativity of addition in disguise, but nobody explaining these laws to school kids ever seems to point out that subtraction can enter into it. They just observe that !!(a-b)-c ≠ a-(b-c)!!, say “subtraction isn't associative”, and leave it at that.)
Closely related to these identities are operator inversion identities like !!a-(b+c) = (a-b)-c!!, !!a-(b-c) = (a-b)+c!!, and their multiplicative analogues. I don't know names for these algebraic laws either.
One way to deal with all of this would to build a complicated comparison function for abstract syntax trees that tried to transform one tree into another by applying these identities. A better approach is to recognize that the data structure is over-specified. If we want the computer to understand that !!(a + b) + c!! and !!a + (b + c)!! are the same expression, we are swimming upstream by using a data structure that was specifically designed to capture the difference between these expressions.
Instead, I invented a data structure, called an Ezpr (“Ez-pur”), that can represent expressions, but in a somewhat more natural way than abstract syntax trees do, and in a way that makes commutativity and associativity transparent.
An Ezpr has a simplest form, called its “canonical” or “normal” form. Two Ezprs represent essentially the same mathematical expression if they have the same canonical form. To decide if two abstract syntax trees are the same, the computer converts them to Ezprs, simplifies them, and checks to see if resulting canonical forms are identical.
The Ezpr
Since associativity doesn't matter, we don't want to represent it. When we (humans) think about adding up a long column of numbers, we don't think about associativity because we don't add them pairwise. Instead we use an addition algorithm that adds them all at once in a big pile. We don't treat addition as a binary operation; we normally treat it as an operator that adds up the numbers in a list. The Ezpr makes this explicit: its addition operator is applied to a list of subexpressions, not to a pair. Both !!a + (b + c)!! and !!(a + b) + c!! are represented as the Ezpr
SUM [ a b c - ]
which just says that we are adding up !!a!!, !!b!!, and !!c!!. (The
- sign is just punctuation; ignore it for now.)
Similarly the Ezpr MUL [ a b c ÷ ] represents the product of !!a!!,
!!b!!, and !!c!!. (Please ignore the ÷ sign for the time being.)
To handle commutativity, we want those [ a b c ] lists to be bags.
Perl doesn't have a built-in bag object, so instead I used arrays and
required that the array elements be in sorted order. (Exactly which
sorted order doesn't really matter.)
Subtraction and division
This doesn't yet handle subtraction and division, and the way I chose
to handle them is the only part of this that I think is at all
clever. A SUM object has not one but two bags, one for the positive
and one for the negative part of the expression. An expression like
!!a - b + c - d!! is represented by the Ezpr:
SUM [ a c - b d ]
and this is also the representation of !!a + c - b - d!!, of !!c + a
- d - b!!, of !!c - d+ a-b!!, and of any other expression of the
idea that we are adding up !!a!! and !!c!! and then deducting !!b!!
and !!d!!. The - sign separates the terms that are added from those
that are subtracted.
Either of the two bags may be empty, so for example !!a + b!! is just
SUM [ a b - ].
Division is handled similarly. Here conventional mathematical
notation does a little bit better than in the sum case: MUL [ a c ÷ b
d ] is usually written as !!\frac{ac}{bd}!!.
Ezprs handle the associativity and commutativity of subtraction and division quite well. I pointed out earlier that subtraction has an associative law !!(a + b) - c = a + (b - c)!! even though it's not usually called that. No code is required to understand that those two expressions are equal if they are represented as Ezprs, because they are represented by completely identical structures:
SUM [ a b - c ]
Similarly there is a commutative law for subtraction: !!a + b - c = a - c + b!! and once again that same Ezpr does for both.
Ezpr laws
Ezprs are more flexible than binary trees. A binary tree can represent the expressions !!(a+b)+c!! and !!a+(b+c)!! but not the expression !!a+b+c!!. Ezprs can represent all three and it's easy to transform between them. Just as there are rules for building expressions out of simpler expressions, there are a few rules for combining and manipulating Ezprs.
Lifting and flattening
The most important transformation is lifting, which is the Ezpr
version of the associative law. In the canonical form of an Ezpr, a
SUM node may not have subexpressions that are also SUM nodes. If
you have
SUM [ a SUM [ b c - ] - … ]
you should lift the terms from the inner sum into the outer one:
SUM [ a b c - … ]
effectively transforming !!a+(b+c)!! into !!a+b+c!!. More generally, in
SUM [ a SUM [ b - c ]
- d SUM [ e - f ] ]
we lift the terms from the inner Ezprs into the outer one:
SUM [ a b f - c d e ]
This effectively transforms !!a + (b - c) - d - (e - f))!! to !!a + b + f - c - d - e!!.
Similarly, when a MUL node contains another MUL, we can flatten
the structure.
Say we are converting the expression !!7 ÷ (3 ÷ (6 × 4))!! to an Ezpr. The conversion function is recursive and the naïve version computes this Ezpr:
MUL [ 7 ÷ MUL [ 3 ÷ MUL [ 6 4 ÷ ] ] ]
But then at the bottom level we have a MUL inside a MUL, so the
4 and 6 in the innermost MUL are lifted upward:
MUL [ 7 ÷ MUL [ 3 ÷ 6 4 ] ]
which represents !!\frac7{\frac{3}{6\cdot 4}}!!.
Then again we have a MUL inside a MUL, and again the
subexpressions of the innermost MUL can be lifted:
MUL [ 7 6 4 ÷ 3 ]
which we can imagine as !!\frac{7·6·4}3!!.
The lifting only occurs when the sub-node has the same type as its
parent; we may not lift terms out of a MUL into a SUM or vice
versa.
Trivial nodes
The Ezpr SUM [ a - ] says we are adding up just one thing, !!a!!,
and so it can be eliminated and replaced with just !!a!!. Similarly
SUM [ - a ] can be replaced with the constant !!-a!!, if !!a!! is a
constant. MUL can be handled similarly.
An even simpler case is SUM [ - ] which can be replaced by the
constant 0; MUL [ ÷ ] can be replaced with 1. These sometimes arise
as a result of cancellation.
Cancellation
Consider the puzzle «3 3 4 6». My first solver found 49 solutions to this puzzle. One is !!(3 - 3) + (4 × 6)!!. Another is !!(4 + (3 - 3)) × 6!!. A third is !!4 × (6 + (3 - 3))!!.
I think these are all the same: the solution is to multiply the 4 by the 6, and to get rid of the threes by subtracting them to make a zero term. The zero term can be added onto the rest of expression or to any of its subexpressions—there are ten ways to do this—and it doesn't really matter where.
This is easily explained in terms of Ezprs: If the same subexpression appears in both of a node's bags, we can drop it. For example, the expression !!(4 + (3 -3)) × 6!! starts out as
MUL [ 6 SUM [ 3 4 - 3 ] ÷ ]
but the duplicate threes in SUM [ 3 4 - 3 ] can be canceled, to
leave
MUL [ 6 SUM [ 4 - ] ÷ ]
The sum is now trivial, as described in the previous section, so can be eliminated and replaced with just 4:
MUL [ 6 4 ÷ ]
This Ezpr records the essential feature of each of the three solutions to «3 3 4 6» that I mentioned: they all are multiplying the 6 by the 4, and then doing something else unimportant to get rid of the threes.
Another solution to the same puzzle is !!(6 ÷ 3) × (4 × 3)!!. Mathematically we would write this as !!\frac63·4·3!! and we can see this is just !!6×4!! again, with the threes gotten rid of by multiplication and division, instead of by addition and subtraction. When converted to an Ezpr, this expression becomes:
MUL [ 6 4 3 ÷ 3 ]
and the matching threes in the two bags are cancelled, again leaving
MUL [ 6 4 ÷ ]
In fact there aren't 49 solutions to this puzzle. There is only one, with 49 trivial variations.
Identity elements
In the preceding example, many of the trivial variations on the !!4×6!! solution involved multiplying some subexpression by !!\frac 33!!. When one of the input numbers in the puzzle is a 1, one can similarly obtain a lot of useless variations by choosing where to multiply the 1.
Consider «1 3 3 5»: We can make 24 from !!3 × (3 + 5)!!. We then have to get rid of the 1, but we can do that by multiplying it onto any of the five subexpressions of !!3 × (3 + 5)!!:
$$ 1 × (3 × (3 + 5)) \\ (1 × 3) × (3 + 5) \\ 3 × (1 × (3 + 5)) \\ 3 × ((1 × 3) + 5) \\ 3 × (3 + (1×5)) $$
These should not be considered different solutions.
Whenever we see any 1's in either of the bags of a MUL node,
we should eliminate them.
The first expression above, !!1 × (3 × (3 + 5))!!, is converted to the Ezpr
MUL [ 1 3 SUM [ 3 5 - ] ÷ ]
but then the 1 is eliminated from the MUL node leaving
MUL [ 3 SUM [ 3 5 - ] ÷ ]
The fourth expression, !!3 × ((1 × 3) + 5)!!, is initially converted to the Ezpr
MUL [ 3 SUM [ 5 MUL [ 1 3 ÷ ] - ] ÷ ]
When the 1 is eliminated from the inner MUL, this leaves a trivial
MUL [ 3 ÷ ] which is then replaced with just 3, leaving:
MUL [ 3 SUM [ 5 3 - ] ÷ ]
which is the same Ezpr as before.
Zero terms in the bags of a SUM node can similarly be dropped.
Multiplication by zero
One final case is that MUL [ 0 … ÷ … ] can just be simplified to 0.
The question about what to do when there is a zero in the denominator
is a bit of a puzzle.
In the presence of division by zero, some of our simplification rules
are questionable. For example, when we have MUL [ a ÷ MUL [ b ÷ c ]
], the lifting rule says we can simplify this to MUL [ a c ÷ b
]—that is, that !!\frac a{\frac bc} = \frac{ac}b!!. This is correct,
except that when !!b=0!! or !!c=0!! it may be nonsense, depending on what else is
going on. But since zero denominators never arise in the solution of
these puzzles, there is no issue in this application.
Results
The Ezpr module is around 200 lines of Perl code, including
everything: the function that converts abstract syntax trees to Ezprs,
functions to convert Ezprs to various notations (both MUL [ 4 ÷ SUM [
3 - 2 ] ] and 4 ÷ (3 - 2)), and the two versions of the
normalization process described in the previous section. The
normalizer itself is about 35 lines.
Associativity is taken care of by the Ezpr structure itself, and
commutativity is not too difficult; as I mentioned, it would have been
trivial if Perl had a built-in bag structure. I find it much easier
to reason about transformations of Ezprs than abstract syntax trees.
Many operations are much simpler; for example the negation of
SUM [ A - B ] is simply SUM [ B - A ]. Pretty-printing is also easier
because the Ezpr better captures the way we write and think about
expressions.
It took me a while to get the normalization tuned properly, but the results have been quite successful, at least for this problem domain. The current puzzle-solving program reports the number of distinct solutions to each puzzle. When it reports two different solutions, they are really different; when it fails to support the exact solution that Toph or I found, it reports one essentially the same. (There are some small exceptions, which I will discuss below.)
Since there is no specification for “essentially the same” there is no hope of automated testing. But we have been using the app for several months looking for mistakes, and we have not found any. If the normalizer failed to recognize that two expressions were essentially similar, we would be very likely to notice: we would be solving some puzzle, be unable to find the last of the solutions that the program claimed to exist, and then when we gave up and saw what it was we would realize that it was essentially the same as one of the solutions we had found. I am pretty confident that there are no errors of this type, but see “Arguable points” below.
A harder error to detect is whether the computer has erroneously conflated two essentially dissimilar expressions. To detect this we would have to notice that an expression was missing from the computer's solution list. I am less confident that nothing like this has occurred, but as the months have gone by I feel better and better about it.
I consider the problem of “how many solutions does this puzzle really have to have?” been satisfactorily solved. There are some edge cases, but I think we have identified them.
Code for my solver is on
Github. The Ezpr code
is in the Ezpr package in the Expr.pm
file.
This code is all in the public domain.
Some examples
The original program claims to find 35 different solutions to «4 6 6 6». The revised program recognizes that these are of only two types:
| !!4 × 6 × 6 ÷ 6!! | MUL [ 4 6 - ] |
| !!(6 - 4) × (6 + 6)!! | MUL [ SUM [ 6 - 4 ] SUM [ 6 6 - ] ÷ ] |
Some of the variant forms of the first of those include:
$$
6 × (4 + (6 - 6)) \\
6 + ((4 × 6) - 6) \\
(6 - 6) + (4 × 6) \\
(6 ÷ 6) × (4 × 6) \\
6 ÷ ((6 ÷ 4) ÷ 6) \\
6 ÷ (6 ÷ (4 × 6)) \\
6 × (6 × (4 ÷ 6)) \\
(6 × 6) ÷ (6 ÷ 4) \\
6 ÷ ((6 ÷ 6) ÷ 4) \\
6 × (6 - (6 - 4)) \\
6 × (6 ÷ (6 ÷ 4)) \\
\ldots
$$
In an even more extreme case, the original program finds 80 distinct expressions that solve «1 1 4 6», all of which are trivial variations on !!4·6!!.
Of the 715 puzzles, 466 (65%) have solutions; for 175 of these the solution is unique. There are 3 puzzles with 8 solutions each («2 2 4 8», «2 3 6 9», and «2 4 6 8»), one with 9 solutions («2 3 4 6»), and one with 10 solutions («2 4 4 8»).
The 10 solutions for «2 4 4 8» are as follows:
| !!4 × 8 - 2 × 4 !! | SUM [ MUL [ 4 8 ÷ ] - MUL [ 2 4 ÷ ] ] |
| !!4 × (2 + 8 - 4) !! | MUL [ 4 SUM [ 2 8 - 4 ] ÷ ] |
| !!(8 - 4) × (2 + 4) !! | MUL [ SUM [ 8 - 4 ] SUM [ 2 4 - ] ÷ ] |
| !!4 × (4 + 8) ÷ 2 !! | MUL [ 4 SUM [ 4 8 - ] ÷ 2 ] |
| !!(4 - 2) × (4 + 8) !! | MUL [ SUM [ 4 - 2 ] SUM [ 4 8 - ] ÷ ] |
| !!8 × (2 + 4/4) !! | MUL [ 8 SUM [ 1 2 - ] ÷ ] |
| !!2 × 4 × 4 - 8 !! | SUM [ MUL [ 2 4 4 ÷ ] - 8 ] |
| !!8 + 2 × (4 + 4) !! | SUM [ 8 MUL [ 2 SUM [ 4 4 - ] ÷ ] - ] |
| !!4 + 4 + 2 × 8 !! | SUM [ 4 4 MUL [ 2 8 ÷ ] - ] |
| !!4 × (8 - 4/2) !! | MUL [ 4 SUM [ 8 - MUL [ 4 ÷ 2 ] ] ÷ ] |
A complete listing of every essentially different solution to every «a b c d» puzzle is available here. There are 1,063 solutions in all.
Arguable points
There are a few places where we have not completely pinned down what it means for two solutions to be essentially the same; I think there is room for genuine disagreement.
Any solution involving !!2×2!! can be changed into a slightly different solution involving !!2+2!! instead. These expressions are arithmetically different but numerically equal. For example, I mentioned earlier that «2 2 4 8» has 8 solutions. But two of these are !! 8 + 4 × (2 + 2)!! and !! 8 + 4 × 2 × 2!!. I am willing to accept these as essentially different. Toph, however, disagrees.
A similar but more complex situation arises in connection with «1 2 3 7». Consider !!3×7+3!!, which equals 24. To get a solution to «1 2 3 7», we can replace either of the threes in !!3×7+3!! with !!(1+2)!!, obtaining !!((1 + 2) × 7) + 3!! or !! (3×7)+(1 +2)!!. My program considers these to be different solutions. Toph is unsure.
It would be pretty easy to adjust the normalization process to handle these the other way if the user wanted that.
Some interesting puzzles
«1 2 7 7» has only one solution, quite unusual. (Spoiler) «2 2 6 7» has two solutions, both somewhat unusual. (Spoiler)
Somewhat similar to «1 2 7 7» is «3 9 9 9» which also has an unusual solution. But it has two other solutions that are less surprising. (Spoiler)
«1 3 8 9» has an easy solution but also a quite tricky solution. (Spoiler)
One of my neighbors has the license plate JJZ 4631.
«4 6 3 1» is one of the more difficult puzzles.
What took so long?
I have enough material for at least three or four more articles about this that I hope to publish here in the coming weeks.
But the previous article on this subject ended similarly, saying
I hope to write a longer article about solvers in the next week or so.
and that was in July 2016, so don't hold your breath.
And here we are, five months later!
This article was a huge pain to write. Sometimes I sit down to write something and all that comes out is dreck. I sat down to write this one at least three or four times and it never worked. The tortured Git history bears witness. In the end I had to abandon all my earlier drafts and start over from scratch, writing a fresh outline in an empty file.
But perseverance paid off! WOOOOO.
[ Addendum 20170825: I completely forgot that Shreevatsa R. wrote a very interesting article on the same topic as this one, in July of last year soon after I published my first article in this series. ]
[ Addendum 20170829: A previous version of this article used the notations SUM [ … # … ]
and MUL [ … # … ], which I said I didn't like. Zellyn Hunter has
persuaded me to replace these with SUM [ … - … ] and MUL
[ … ÷ … ]. Thank you M. Hunter! ]
[Other articles in category /math] permanent link
Tue, 08 Aug 2017I should have written about this sooner, by now it has been so long that I have forgotten most of the details.
I first encountered Paul Erdős in the middle 1980s at a talk by János Pach about almost-universal graphs. Consider graphs with a countably infinite set of vertices. Is there a "universal" graph !!G!! such that, for any finite or countable graph !!H!!, there is a copy of !!H!! inside of !!G!!? (Formally, this means that there is an injection from the vertices of !!H!! to the vertices of !!G!! that preserves adjacency.) The answer is yes; it is quite easy to construct such a !!G!! and in fact nearly all random graphs have this property.
But then the questions become more interesting. Let !!K_\omega!! be the complete graph on a countably infinite set of vertices. Say that !!G!! is “almost universal” if it includes a copy of !!H!! for every finite or countable graph !!H!! except those that contain a copy of !!K_\omega!!. Is there an almost universal graph? Perhaps surprisingly, no! (Sketch of proof.)
I enjoyed the talk, and afterward in the lobby I got to meet Ron Graham and Joel Spencer and talk to them about their Ramsey theory book, which I had been reading, and about a problem I was working on. Graham encouraged me to write up my results on the problem and submit them to Mathematics Magazine, but I unfortunately never got around to this. Graham was there babysitting Erdős, who was one of Pách's collaborators, but I did not actually talk to Erdős at that time. I think I didn't recognize him. I don't know why I was able to recognize Graham.
I find the almost-universal graph thing very interesting. It is still an open research area. But none of this was what I was planning to talk about. I will return to the point. A couple of years later Erdős was to speak at the University of Pennsylvania. He had a stock speech for general audiences that I saw him give more than once. Most of the talk would be a description of a lot of interesting problems, the bounties he offered for their solutions, and the progress that had been made on them so far. He would intersperse the discussions with the sort of Erdősism that he was noted for: referring to the U.S. and the U.S.S.R. as “Sam” and “Joe” respectively; his ever-growing series of styles (Paul Erdős, P.G.O.M., A.D., etc.) and so on.
One remark I remember in particular concerned the $3000 bounty he offered for proving what is sometimes known as the Erdős-Túran conjecture: if !!S!! is a subset of the natural numbers, and if !!\sum_{n\in S}\frac 1n!! diverges, then !!S!! contains arbitrarily long arithmetic progressions. (A special case of this is that the primes contain arbitrarily long arithmetic progressions, which was proved in 2004 by Green and Tao, but which at the time was a long-standing conjecture.) Although the $3000 was at the time the largest bounty ever offered by Erdős, he said it was really a bad joke, because to solve the problem would require so much effort that the per-hour payment would be minuscule.
I made a special trip down to Philadelphia to attend the talk, with the intention of visiting my girlfriend at Bryn Mawr afterward. I arrived at the Penn math building early and wandered around the halls to kill time before the talk. And as I passed by an office with an open door, I saw Erdős sitting in the antechamber on a small sofa. So I sat down beside him and started telling him about my favorite graph theory problem.
Many people, preparing to give a talk to a large roomful of strangers, would have found this annoying and intrusive. Some people might not want to talk about graph theory with a passing stranger. But most people are not Paul Erdős, and I think what I did was probably just the right thing; what you don't do is sit next to Erdős and then ask how his flight was and what he thinks of recent politics. We talked about my problem, and to my great regret I don't remember any of the mathematical details of what he said. But he did not know the answer offhand, he was not able solve it instantly, and he did say it was interesting. So! I had a conversation with Erdős about graph theory that was not a waste of his time, and I think I can count that as one of my lifetime accomplishments.
After a little while it was time to go down to the auditorium for the the talk, and afterward one of the organizers saw me, perhaps recognized me from the sofa, and invited me to the guest dinner, which I eagerly accepted. At the dinner, I was thrilled because I secured a seat next to Erdős! But this was a beginner mistake: he fell asleep almost immediately and slept through dinner, which, I learned later, was completely typical.
[Other articles in category /math] permanent link
Sun, 06 Aug 2017Yesterday I discussed an interesting failure on the part of Shazam, a phone app that can recognize music by listening to it. I said I had no idea how it worked, but I did not let that stop me from pulling the following vague speculation out of my butt:
I imagine that it does some signal processing to remove background noise, accumulates digests of short sections of the audio data, and then matches these digests against a database of similar digests, compiled in advance from a corpus of recordings.
Julia Evans provided me with the following reference: “An Industrial-Strength Audio Search Algorithm” by Avery Li-Chun Wang of Shazam Entertainment, Ltd. Unfortunately the paper has no date, but on internal evidence it seems to be from around 2002–2006.
M. Evans summarizes the algorithm as follows:
- find the strongest frequencies in the music and times at which those frequencies happen
- look at pairs !!(freq_1, time_1, freq_2, time_2)!! and turn those into pairs into hashes (by subtracting !!time_1!! from !!time_2!!)
- look up those hashes in your database
She continues:
so basically Shazam will only recognize identical recordings of the same piece of music—if it's a different performance the timestamps the frequencies happen at will likely be different and so the hashes won't match
Thanks Julia!
Moving upwards from the link Julia gave me, I found a folder of papers maintained by Dan Ellis, formerly of the Columbia University Electrical Engineering department, founder of Columbia's LabROSA, the Laboratory for the Recognition and Organization of Speech and Audio, and now a Google research scientist.
In the previous article, I asked about research on machine identification of composers or musical genre. Some of M. Ellis’s LabROSA research is closely related to this. See for example:
There is a lot of interesting-looking material available there for free. Check it out.
(Is there a word for when someone gives you a URL like
http://host/a/b/c/d.html and you start prying into
http://host/a/b/c/ and http://host/a/b/ hoping for more goodies?
If not, does anyone have a suggestion?)
[Other articles in category /tech] permanent link
Sat, 05 Aug 2017
Another example of a machine perception failure
IEEE Spectrum has yet another article about fooling computer vision algorithms with subtle changes that humans don't even notice. For more details and references to the literature, see this excellent article by Andrej Karpathy. Here is a frequently-reprinted example:

The classifier is 57.7% confident that the left-hand image is a panda. When the image is perturbed—by less than one part in 140—with the seemingly-random pattern of colored dots to produce the seemingly identical image on the right, the classifier identifies it as a gibbon with 99.3% confidence.
(Illustration from Goodfellow, Shlens, and Szegedy, “Explaining and Harnessing Adversarial Examples”, International Conference on Learning Representations 2015.)
Here's an interesting complementary example that surprised me recently. I have the Shazam app on my phone. When activated, the app tries to listen for music, and then it tries to tell you what the music was. If I'm in the pharmacy and the background music is something I like but don't recognize, I can ask Shazam what it is, and it will tell me. Magic!
Earlier this year I was in the car listening to the radio and I tried this, and it failed. I ran it again, and it failed again. I pulled over to the side of the road, activated the app, and held the phone's microphone up to the car's speaker so that Shazam could hear clearly. Shazam was totally stumped.
So I resumed driving and paid careful attention when the piece ended so that I wouldn't miss when the announcer said what it was. It had been Mendelssohn's fourth symphony.
Shazam can easily identify Mendelssohn's fourth symphony, as I confirmed later. In fact, it can identify it much better than a human can—in some ways. When I tested it, it immediately recognized not only the piece, but the exact recording I used for the test: it was the 1985 recording by the London Symphony Orchestra, conducted by Claudio Abbado.
Why had Shazam failed to recognize the piece on the radio? Too much background noise? Poor Internet connectivity? Nope. It was because the piece was being performed live by the Detroit Symphony Orchestra and as far as Shazam was concerned, it had never heard it before. For a human familiar with Mendelssohn's fourth symphony, this would be of no import. This person would recognize Mendelssohn's fourth symphony whenever it was played by any halfway-competent orchestra.
But Shazam doesn't hear the way people do. I don't know what it does (really I have no idea), but I imagine that it does some signal processing to remove background noise, accumulates digests of short sections of the audio data, and then matches these digests against a database of similar digests, compiled in advance from a corpus of recordings. The Detroit Orchestra's live performance hadn't been in the corpus, so there was no match in the database.
Shazam's corpus has probably a couple of dozen recordings of Mendelssohn's fourth symphony, but it has no idea that all these recordings are of the same piece, or that they sound very similar, because to Shazam they don't sound similar at all. I imagine it doesn't even have a notion of whether two pieces in the corpus sound similar, because it knows them only as distillations of short snatches, and it never compares corpus recordings with one another. Whatever Shazam is doing is completely different from what people do. One might say it hears the sound but not the music, just as the classifier from the Goodfellow paper sees the image but not the panda.
I wonder about a different example. When I hear an unfamiliar piece on the radio, I can often guess who wrote it. “Aha,” I say. “This is obviously Dvořák.” And then more often than not I am right, and even when I am not right, I am usually very close. (For some reasonable meaning of “close” that might be impossible to explain to Shazam.) In one particularly surprising case, I did this with Daft Punk, at that time having heard exactly two Daft Punk songs in my life. Upon hearing this third one, I said to myself “Huh, this sounds just like those Daft Punk songs.” I not claiming a lot of credit for this; Daft Punk has a very distinctive sound. I bring it up just to suggest that whatever magic Shazam is using probably can't do this even a little bit.
Do any of my Gentle Readers know anything about research on the problem of getting a machine to identify the author or genre of music from listening to it?
[ Addendum 20170806: Julia Evans has provided a technical reference and a high-level summary of Shazam's algorithm. This also led me to a trove of related research. ]
[Other articles in category /tech] permanent link




