Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 15 Dec 2012
How I got four errors into a one-line program
At my current job, each task is assigned a ticket number of the form
e12345. The git history is extremely convoluted, and it's
been observed that it's easier to find things if you include the
ticket number at the front of the commit message. I got tired of
inserting it manually, and thought I would write a prepare-commit-message hook to insert
it automatically.
A prepare-commit-message hook is a program that you stick in the file .git/hooks/prepare-commit-hook. When you run git-commit, git first writes the commit message to a file, then invokes the prepare-commit-message program on file; the program can modify the contents of the message, or abort the commit if it wants to. Then git runs the editor on the message, if it was going to do that, and creates the commit with the edited message.
The hook I wrote was basically a one-liner, and the reason I am posting this note is because I found three significant programming errors in it in the first day of use.
Here's the first cut:
case $2 in
message)
perl -i -lpe "s/^(e\d+:\s+)?/$(cs -): /" $1
;;
esac
This is a shell script, but the main purpose is to run the perl
one-liner. The shell script gets two arguments: $1 is the
path to the file that contains the proposed commit message.
The $2 argument is a tag which describes the commit's
context; it's merge if the commit is a merge commit, for
example; it's template if the commit message is supplied from
a template via -t on the command line or the
commit.template configuration option. The default is the
empty string, and message, which I have here, means that the
message was supplied with the -m command-line option.The Perl script edits the commit message file, named in $1, in-place, looking for something like e12345: at the beginning of a line, and replacing it with the output of the cs - command, which is a little program I wrote to print the current ticket number.
(cs is run by the shell, and its output is inserted into the Perl script before perl is run, so that the program that Perl sees is something like s/^(e\d+:\s+)?/e12345: /.) Simple enough.
There is already an error here, although it's a design error, not an implementation error: the Perl one-liner is only invoked when $2 is message. For some reason I decided that I would want it only when I supplied git-commit with the -m message option. This belief lasted exactly until the first time I ran git-commit in default mode it popped up the editor to edit the commit message, and I had to insert the ticket number manually.
So the first change was to let the hook run in the default case as well as the message case:
case $2 in
""|message)
perl -i -lpe "s/^(e\d+:\s+)?/$(cs -): /" $1
;;
esac
This was wrong because it inserts the ticket number at the start of
each line; I wanted it only at the start of the first line. So that
was programming error number 1:
case $2 in
""|message)
perl -i -lpe "$. == 1 && s/^(e\d+:\s+)?/$(cs -): /" $1
;;
esac
So far, so good.Bug #2 appeared the first time I tried a rebase. The cs command infers the ticket number from the name of the current branch. If it fails, it issues a warning and emits the string eXXXXX instead. During a rebase, the head is detached and there is no current branch. So the four commits I rebased all had their formerly-correct ticket numbers replaced with the string eXXXXX.
There are several ways to fix this. The best way would be to make sure that the current ticket number was stashed somewhere that cs could always get it. Instead, I changed the Perl script to recognize when the commit message already began with a ticket number, and to leave it alone if so:
case $2 in
""|message)
perl -i -lpe "\$. == 1 && !/^e\d+:\s+/ && s/^/$(cs -): /" $1
;;
esac
It probably would have been a good idea to leave an escape hatch, and
have cs emit the value of $ENV{TICKET_NUMBER} if
that is set, to allow invocations like TICKET_NUMBER=e71828 git
commit -m …, but I didn't do it, yet.The third bug appeared when I did git commit --fixup for the first time. With --fixup you tell it which commit you are trying to fix up, and it writes the commit message in a special form that tells a subsequent git-rebase --interactive that this new commit should be handled specially. (It should be applied immediately after that other one, and should be marked as a "fixup", which means that it is squashed into the other one and that its log message is discarded in favor of the other one.) If you are fixing up a commit whose message was Frobulate the veeblefetzers, the fixup commit's message is automatically generated as fixup! Frobulate the veeblefetzers. Or it would have been, if you were not using my prepare-commit-message hook, which would rewrite it to e12345: fixup! Frobulate the veeblefetzers. This is not in the right form, so it's not recognized by git-rebase --interactive for special handling.
So the hook became:
case $2 in
""|message)
perl -i -lpe "\$. == 1 && !/^(squash|fixup)! / && !/^e\d+:\s+/ && s/^/$(cs -): /" $1
;;
esac
(The exception for squash is similar to the one for
fixup. I never use squash, but it seemed foolish not
to put it in while I was thinking of it.)This is starting to look a little gross, but in a program this small I can tolerate a little grossness.
I thought it was remarkable that such a small program broke in so many different ways. Much of that is because it must interact with git, which is very large and complicated, and partly it is that it must interact with git, which is in many places not very well designed. The first bug, where the ticket number was appended to each line instead of just the first, is not git's fault. It was fallout from my initial bad design decision to apply the script only to messages supplied with -m, which are typically one-liners, so that's what I was thinking of when I wrote the Perl script.
But the other two errors would have been avoided had the interface to the hook been more uniform. There seems to be no reason that rebasing (or cherry-picking) and git-commit --fixup contexts couldn't have been communicated to the hook via the same $2 argument that communicates other contexts. Had this been done in a more uniform way, my program would have worked more correctly. But it wasn't done, and it's probably too late to change it now, since such a change risks breaking many existing prepare-commit-message hooks. (“The enemy of software is software.”) A well-written hook will of course have a catchall:
case $2 in
""|message)
perl -i -lpe "\$. == 1 && !/^(squash|fixup)! / && !/^e\d+:\s+/ && s/^/$(cs -): /" $1
;;
merge|template|squash|commit)
# do nothing
;;
*) # wat
echo "prepare-message-hook: unknown context '$2'" 1>&2
exit 1;
;;
esac
But mine doesn't and I bet a lot of others don't either.
[Other articles in category /prog] permanent link
Sun, 26 Aug 2012
Rewriting published history in Git
My earlier article about my
habits using Git attracted some comment, most of which was
favorable. But one recurring comment was puzzlement about my seeming
willingness to rewrite published history. In practice, this was not
at all a problem, I think for three reasons:
- Rewriting published history is not nearly as confusing as people seem to think it will be.
- I worked in a very small shop with very talented developers, so the necessary communication was easy.
- Our repository setup and workflow were very well-designed and unusually effective, and made a lot of things easier, including this one.
If there are N developers, there are N+1 repositories.
There is a master repository to which only a few very responsible persons can push. It is understood that history in this repository should almost never be rewritten, only in the most exceptional circumstances. We usually call this master repository gitbox. It has only a couple of branches, typically master and deployed. You had better not push incomplete work to master, because if you do someone is likely to deploy it. When you deploy a new version from master, you advance deployed up to master to match.
In addition, each developer has their own semi-public repository, named after them, which everyone can read, but which nobody but them can write. Mine is mjd, and that's what we call it when discussing it, but my personal git configuration calls it origin. When I git push origin master I am pushing to this semi-public repo.
It is understood that this semi-public repository is my sandbox and I am free to rewrite whatever history I want in it. People building atop my branches in this repo, therefore, know that they should be prepared for me to rewrite the history they see there, or to contact me if they want me to desist for some reason.
When I get the changes in my own semi-public repository the way I want them, then I push the changes up to gitbox. Nothing is considered truly "published" until it is on the master repo.
When a junior programmer is ready to deploy to the master repository, they can't do it themselves, because they only have read access on the master. Instead, they publish to their own semi-private repository, and then notify a senior programmer to review the changes. The senior programmer will then push those changes to the master repository and deploy them.
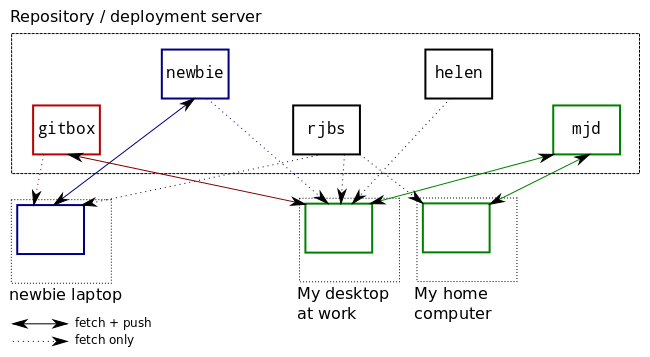
If I do work from three or four different machines, I can use the mjd repo to exchange commits between them. At the end of the day I will push my work-in-progress up to the mjd repo, and then if I want to look at it later that evening, I can fetch the work-in-progress to my laptop or another home computer.
I can create and abandon many topic branches without cluttering up the master repository's history. If I want to send a change or a new test file to a co-worker, I can push it to mjd and then point them at the branch there.
A related note: There is a lot of FUD around the rewriting of published history. For example, the "gitinfo" robot on the #git IRC channel has a canned message:
Rewriting public history is a very bad idea. Anyone else who may have pulled the old history will have to git pull --rebase and even worse things if they have tagged or branched, so you must publish your humiliation so they know what to do. You will need to git push -f to force the push. The server may not allow this. See receive.denyNonFastForwards (git-config)I think this grossly exaggerates the problems. Very bad! Humiliation! The server may deny you! But dealing with a rebased upstream branch is not very hard. It is at worst annoying: you have to rebase your subsequent work onto the rewritten branch and move any refs that pointed to that branch. If you don't have any subsequent work, you might still have to move refs, if you have any that point to it, but you might not have any.
[ Thanks to Rik Signes for helping me put this together. ]
[Other articles in category /prog] permanent link
Sat, 25 Aug 2012
On the consistency of PA
A monk asked Li Fu, "Master, how do we know that the Peano axioms are
consistent?"
Li Fu said, "The axioms are consistent because they have a model."
[Other articles in category /math] permanent link
Fri, 24 Aug 2012
More about ZF's asymmetry between union and intersection
In an article earlier this
week, I explored some oddities of defining a toplogy in terms of
closed sets rather than open sets, mostly as a result of analogous
asymmetry in the ZF
set theory axioms.
Let's review those briefly. The relevant axioms concern the operations by which sets can be constructed. There are two that are important. First is the axiom of union, which says that if !!{\mathcal F}!! is a family of sets, then we can form !!\bigcup {\mathcal F}!!, which is the union of all the sets in the family.
The other is actually a family of axioms, the specification axiom schema. It says that for any one-place predicate !!\phi(x)!! and any set !!X!! we can construct the subset of !!X!! for which !!\phi!! holds:
$$\{ x\in X \;|\; \phi(x) \}$$
Both of these are required. The axiom of union is for making bigger sets out of smaller ones, and the specification schema is for extracting smaller sets from bigger ones. (Also important is the axiom of pairing, which says that if !!x!! and !!y!! are sets, then so is the two-element set !!\{x, y\}!!; with pairing and union we can construct all the finite sets. But we won't need it in this article.)
Conspicuously absent is an axiom of intersection. If you have a family !!{\mathcal F}!! of sets, and you want a set of every element that is in some member of !!{\mathcal F}!!, that is easy; it is what the axiom of union gets you. But if you want a set of every element that is in every member of !!{\mathcal F}!!, you have to use specification.
Let's begin by defining this compact notation: $$\bigcap_{(X)} {\mathcal F}$$
for this longer formula: $$\{ x\in X \;|\; \forall f\in {\mathcal F} . x\in f \}$$
This is our intersection of the members of !!{\mathcal F}!!, taken "relative to !!X!!", as we say in the biz. It gives us all the elements of !!X!! that are in every member of !!{\mathcal F}!!. The !!X!! is mandatory in !!\bigcap_{(X)}!!, because ZF makes it mandatory when you construct a set by specification. If you leave it out, you get the Russell paradox.
Most of the time, though, the !!X!! is not very important. When !!{\mathcal F}!! is nonempty, we can choose some element !!f\in {\mathcal F}!!, and consider !!\bigcap_{(f)} {\mathcal F}!!, which is the "normal" intersection of !!{\mathcal F}!!. We can easily show that $$\bigcap_{(X)} {\mathcal F}\subseteq \bigcap_{(f)} {\mathcal F}$$ for any !!X!! whatever, and this immediately implies that $$\bigcap_{(f)} {\mathcal F} = \bigcap_{(f')}{\mathcal F}$$ for any two elements of !!{\mathcal F}!!, so when !!{\mathcal F}!! contains an element !!f!!, we can omit the subscript and just write $$\bigcap {\mathcal F}$$ for the usual intersection of members of !!{\mathcal F}!!.
Even the usually troublesome case of an empty family !!{\mathcal F}!! is no problem. In this case we have no !!f!! to use for !!\bigcap_{(f)} {\mathcal F}!!, but we can still take some other set !!X!! and talk about !!\bigcap_{(X)} \emptyset!!, which is just !!X!!.
Now, let's return to topology. I suggested that we should consider the following definition of a topology, in terms of closed sets, but without an a priori notion of the underlying space:
A co-topology is a family !!{\mathcal F}!! of sets, called "closed" sets, such that:
- The union of any two elements of !!{\mathcal F}!! is again in !!{\mathcal F}!!, and
- The intersection of any subfamily of !!{\mathcal F}!! is again in !!{\mathcal F}!!.
It now immediately follows that !!U!! itself is a closed set, since it is the intersection !!\bigcap_{(U)} \emptyset!! of the empty subfamily of !!{\mathcal F}!!.
If !!{\mathcal F}!! itself is empty, then so is !!U!!, and !!\bigcap_{(U)} {\mathcal F} = \emptyset!!, so that is all right. From here on we will assume that !!{\mathcal F}!! is nonempty, and therefore that !!\bigcap {\mathcal F}!!, with no relativization, is well-defined.
We still cannot prove that the empty set is closed; indeed, it might not be, because even !!M = \bigcap {\mathcal F}!! might not be empty. But as David Turner pointed out to me in email, the elements of !!M!! play a role dual to the extratoplogical points of a topological space that has been defined in terms of open sets. There might be points that are not in any open set anywhere, but we may as well ignore them, because they are topologically featureless, and just consider the space to be the union of the open sets. Analogously and dually, we can ignore the points of !!M!!, which are topologically featureless in the same way. Rather than considering !!{\mathcal F}!!, we should consider !!{\widehat{\mathcal F}}!!, whose members are the members of !!{\mathcal F}!!, but with !!M!! subtracted from each one:
$${\widehat{\mathcal F}} = \{\hat{f}\in 2^U \;|\; \exists f\in {\mathcal F} . \hat{f} = f\setminus M \}$$
So we may as well assume that this has been done behind the scenes and so that !!\bigcap {\mathcal F}!! is empty. If we have done this, then the empty set is closed.
Now we move on to open sets. An open set is defined to be the complement of a closed set, but we have to be a bit careful, because ZF does not have a global notion of the complement !!S^C!! of a set. Instead, it has only relative complements, or differences. !!X\setminus Y!! is defined as: $$X\setminus Y = \{ x\in X \;|\; x\notin Y\} $$
Here we say that the complement of !!Y!! is taken relative to !!X!!.
For the definition of open sets, we will say that the complement is taken relative to the universe of discourse !!U!!, and a set !!G!! is open if it has the form !!U\setminus f!! for some closed set !!f!!.
Anatoly Karp pointed out on Twitter that we know that the empty set is open, because it is the relative complement of !!U!!, which we already know is closed. And if we ensure that !!\bigcap {\mathcal F}!! is empty, as in the previous paragraph, then since the empty set is closed, !!U!! is open, and we have recovered all the original properties of a topology.
But gosh, what a pain it was; in contrast recovering the missing axioms from the corresponding open-set definition of a topology was painless. (John Armstrong said it was bizarre, and probably several other people were thinking that too. But I did not invent this bizarre idea; I got it from the opening paragraph of John L. Kelley's famous book General Topology, which has been in print since 1955.
Here Kelley deals with the empty set and the universe in two sentences, and never worries about them again. In contrast, doing the same thing for closed sets was fraught with technical difficulties, mostly arising from ZF. (The exception was the need to repair the nonemptiness of the minimal closed set !!M!!, which was not ZF's fault.)
On the other hand, perhaps this conclusion is knocking down a straw man. I think working mathematicians probably don't concern themselves much with whether their stuff works in ZF, much less with what silly contortions are required to make it work in ZF. I think day-to-day mathematical work, to the extent that it needs to deal with set theory at all, handles it in a fairly naïve way, depending on a sort of folk theory in which there is some reasonably but not absurdly big universe of discourse in which one can take complements and intersections, and without worrying about this sort of technical detail.
[ MathJax doesn't work in Atom or RSS syndication feeds, and can't be made to work, so if you are reading a syndicated version of this article, such as you would in Google Reader, or on Planet Haskell or PhillyLinux, you are seeing inlined images provided by the Google Charts API. The MathJax looks much better, and if you would like to compare, please visit my blog's home site. ]
[Other articles in category /math] permanent link
Tue, 21 Aug 2012
The non-duality of open and closed sets
I had long thought that it doesn't matter if we define a topology in
terms of open sets or in terms of closed sets, because the two
definitions are in every way dual and equivalent. This seems not to
be the case: the definition in terms of closed sets seems to be
slightly weaker than the definition in terms of open sets.
We can define a topology without reference to the underlying space as follows: A family !!{\mathfrak I}!! of sets is a topology if it is closed under pairwise intersections and arbitrary unions, and we call a set "open" if it is an element of !!{\mathfrak I}!!. From this we can recover the omitted axiom that says that !!\emptyset!! is open: it must be in !!{\mathfrak I}!! because it is the empty union !!\bigcup_{g\in\emptyset} g!!. We can also recover the underlying space of the topology, or at least some such space, because it is the unique maximal open set !!X=\bigcup_{g\in{\mathfrak I}} g!!. The space !!X!! might be embedded in some larger space, but we won't ever have to care, because that larger space is topologically featureless. From a topological point of view, !!X!! is our universe of discourse. We can then say that a set !!C!! is "closed" whenever !!X\setminus C!! is open, and prove all the usual theorems.
If we choose to work with closed sets instead, we run into problems. We can try starting out the same way: A family !!{\mathfrak I}!! of sets is a co-topology if it is closed under pairwise unions and arbitrary intersections, and we call a set "closed" if it is an element of !!{\mathfrak I}!!. But we can no longer prove that !!\emptyset\in{\mathfrak I}!!. We can still recover an underlying space !!X = \bigcup_{c\in{\mathfrak I}} c!!, but we cannot prove that !!X!! is closed, or identify any maximal closed set analogous to the maximal open set of the definition of the previous paragraph. We can construct a minimal closed set !!\bigcap_{c\in{\mathfrak I}} c!!, but we don't know anything useful about it, and in particular we don't know whether it is empty, whereas with the open-sets definition of a topology we can be sure that the empty set is the unique minimal open set.
We can repair part of this asymmetry by changing the "pairwise unions" axiom to "finite unions"; then the empty set is closed because it is a finite union of closed sets. But we still can't recover any maximal closed set. Given a topology, it is easy to identify the unique maximal closed set, but given a co-topology, one can't, and indeed there may not be one. The same thing goes wrong if one tries to define a topology in terms of a Kuratowski closure operator.
We might like to go on and say that complements of closed sets are open, but we can't, because we don't have a universe of discourse in which we can take complements.
None of this may make very much difference in practice, since we usually do have an a priori idea of the universe of discourse, and so we do not care much whether we can define a topology without reference to any underlying space. But it is at least conceivable that we might want to abstract away the underlying space, and if we do, it appears that open and closed sets are not as exactly symmetric as I thought they were.
Having thought about this some more, it seems to me that the ultimate source of the asymmetry here is in our model of set theory. The role of union and intersection in ZF is not as symmetric as one might like. There is an axiom of union, which asserts that the union of the members of some family of sets is again a set, but there is no corresponding axiom of intersection. To get the intersection of a family of sets !!\mathcal S!!, you use a specification axiom. Because of the way specification works, you cannot take an empty intersection, and there is no universal set. If topology were formulated in a set theory with a universal set, such as NF, I imagine the asymmetry would go away.
[ This is my first blog post using MathJax, which I hope will completely replace the ad-hoc patchwork of systems I had been using to insert mathematics. Please email me if you encounter any bugs. ]
[ Addendum 20120823: MathJax depends on executing Javascript, and so it won't render in an RSS or Atom feed or on any page where the blog content is syndicated. So my syndication feed is using the Google Charts service to render formulas for you. If the formulas look funny, try looking at http://blog.plover.com/ directly. ]
[ Addendum 20120824: There is a followup to this article. ]
[Other articles in category /math] permanent link
Wed, 15 Aug 2012
The weird ethics of life insurance
Many life insurance policies, including my own, include a clause that
says that they will not pay out in case of suicide. This not only
reduces the risk to the insurance company, it also removes an
important conflict of interest from the client. I own a life
insurance policy, and I am glad that I do not have this conflict of
interest, which, as I suffer from chronic depression, would only add
to my difficulties.
Without this clause, the insurance company might find itself in the business of enabling suicide, or even of encouraging people to commit suicide. Completely aside from any legal or financial problems this would cause for them, it is a totally immoral position to be in, and it is entirely creditable that they should try to avoid it.
But enforcement of suicide clauses raises some problems. The insurance company must investigate possible suicides, and enforce the suicide clauses, or else they have no value. So the company pays investigators to look into claims that might be suicides, and if their investigators determine that a death was due to suicide, the company must refuse to pay out. I will repeat that: the insurance company has a moral obligation to refuse to pay out if, in their best judgment, the death was due to suicide. Otherwise they are neglecting their duty and enabling suicide.
But the company's investigators will not always be correct. Even if their judgments are made entirely in good faith, they will still sometimes judge a death to be suicide when it wasn't. Then the decedent's grieving family will be denied the life insurance benefits to which they are actually entitled.
So here we have a situation in which even if everyone does exactly what they should be doing, and behaves in the most above-board and ethical manner possible, someone will inevitably end up getting horribly screwed.
[ Addendum 20120816: It has been brought to my attention that this post constains significant omissions and major factual errors. I will investigate further and try to post a correction. ]
Addendum 20220422: I never got around to the research, but the short summary is, the suicide determination is not made by the insurance company, but by the county coroner, who is independent of the insurer. This does point the way to a possible exploit, that the insurer could bribe or otherwise suborn the coroner. But this sort of exploit is present in all systems. My original point, that the hypothetical insurance company investigators would have a conflict of interest, has been completely addressed. ]
[Other articles in category /law] permanent link
Thu, 15 Mar 2012
My Git Habits
Miles Gould asked his Twitter followers whether they used git-add
-p or git-commit -a and how often. My reply was too
long for Twitter, so here it is.
First the short version: I use git-add -p frequently, and git-commit -a almost never. The exception is when I'm working on the repo that holds my blog, where I rarely commit changes to more than one or two files at a time. Then I'll usually just git-commit -a -m ....
But I use git-add -p all the time. Typically what will happen is that I will be developing some fairly complicated feature. It will necessitate a bunch of changes and reshuffling elsewhere in the system. I'll make commits on the topic branch as I go along without worrying too much about whether the commits are neatly packaged.
Often I'll be in the middle of something, with a dirty work tree, when it's time to leave for the day. Then I'll just commit everything with the subject WIP ("work-in-progress"). First thing the next morning I'll git-reset HEAD^ and continue where I left off.
So the model is that the current head is usually a terrible mess, accumulating changes as it moves forward in time. When I'm done, I will merge the topic into master and run the tests.
If they pass, I am not finished. The merge I just created is only a draft merge. The topic branch is often full of all sorts of garbage, commits where I tried one approach, found it didn't work later on, and then tried a different approach, places where I committed debugging code, and so on. So it is now time to clean up the topic branch. Only the cleaned-up topic branch gets published.
Cleaning up messy topic branches
The core of the cleanup procedure is to reset the head back to the last place that look good, possibly all the way back to the merge-base if that is not too long ago. This brings all the topic changes into the working directory. Then:
- Compose the commits: Repeat until the working tree is clean:
- Eyeball the output of git-diff
- Think of an idea for an intelligible commit
- Use git-add -p to stage the planned commit
- Use git diff --cached to make sure it makes sense
- Commit it
- Order the commits: Use git-rebase --interactive
By separating these tasks, I can proceed something like this: I eyeball the diff, and the first thing I see is something about the penguin feature. I can immediately say "Great, I'll make up a commit of all the stuff related to the penguin feature", and proceed to the git-add -p step without worrying that there might be other stuff that should precede the penguin feature in the commit sequence. I can focus on just getting the penguin commit right without needing to think about any of the other changes.
When the time comes to put the commits in order, I can do it well because by then I have abstracted away all the details, and reduced each group of changes to a single atomic unit with a one-line description.
For the most complicated cases, I will print out the diffs, read them over, and mark them up in six colors of highlighter: code to throw away gets marked in orange; code that I suspect is erroneous is pink. I make many notes in pen to remind me how I want to divide up the changes into commits. When a commit occurs to me I'll jot a numbered commit message, and then mark all the related parts of the diff with that number. Once I have the commits planned, I'll reset the topic ref and then run through the procedure above, using git-add -p repeatedly to construct the commits I planned on paper. Since I know ahead of time what they are I might do them in the right order, but more likely I'll just do them in the order I thought of them and then reorder them at the end, as usual.
For simple cases I'll just do a series of git-rebase --interactive passes, pausing at any leftover WIP commits to run the loop above, reordering the commits to squash related commits together, and so on.
The very simplest cases of all require no cleanup, of course.
For example, here's my current topic branch, called c-domain, with the oldest commits at the top:
055a2f7 correction to bulk consumer template
d9630bd DomainActivator half of Pobox Domain consumer
ebebb4a Add HasDomain role to provide ->domain reader for domain consumers
ade6ac6 stubbed domain test
e170e77 start templates for Pobox domain consumers
067ca81 stubbed Domain::ThumbTwiddler
685a3ee cost calculations for DomainActivator
ec8b1cc test fixes; trivial domain test passes now
845b1f2 rename InvoiceCharge::CreateDomain to ..::RegisterDomain
(e) 6083a97 add durations to Domain consumers and charges
c64fda0 tests for Domain::Activator consumer
41e4292 repeat activator tests for 1-year and 3-year durations
7d68065 tests for activator's replacement
(d) 87f3b09 move days_in_year to Moonpig::Util
3cd9f3b WIP
e5063d4 add test for sent invoice in domain.t
c8dbf41 WIP
9e6ffa4 add missing MakesReplacement stuff
fc13059 bring in Net::OpenSRS module
(c) 52c18fb OpenSRS interface
893f16f notes about why domain queries might fail
(b) f64361f rename "croak" method to "fail" to avoid conflicts
4e500ec Domain::Activator initial_invoice_charge_pairs
(a) 3c5cdd4 WIP
3c5cdd4 (a) was the end-of-day state for yesterday; I made it and
pushed it just before I dashed out the door to go home. Such commits
rarely survive beyond the following morning, but if I didn't make them,
I wouldn't be able to continue work from home if the mood took me to
do that.f64361f (b) is a prime candidate for later squashing. 5c218fb (c) introduced a module with a "croak" method. This turned out to be a stupid idea, because this conflicted with the croak function from Perl's Carp module, which we use everywhere. I needed to rename it. By then, the intervening commit already existed. I probably should have squashed these right away, but I didn't think of it at the time. No problem! Git means never having to say "If only I'd realized sooner."
Similarly, 6083a97 (e) added a days_in_year function that I later decided at 87f3b09 (d) should be in a utility module in a different repository. 87f3b09 will eventually be squashed into 6083a97 so that days_in_year never appears in this code at all.
I don't know what is in the WIP commits c8dbf41 or 3cd9f3b, for which I didn't invent commit messages. I don't know why those are left in the tree, but I can figure it out later.
An example cleanup
Now I'm going to clean up this branch. First I git-checkout -b cleanup c-domain so that if something goes awry I can start over completely fresh by doing git-reset --hard c-domain. That's probably superfluous in this case because origin/c-domain is also pointing to the same place, and origin is my private repo, but hey, branches are cheap.The first order of business is to get rid of those WIP commits. I'll git-reset HEAD^ to bring 3c5cdd4 into the working directory, then use git-status to see how many changes there are:
M lib/Pobox/Moonpig/Consumer/Domain/Activator.pm
M lib/Pobox/Moonpig/Role/HasDomain.pm
M lib/Pobox/Moonpig/TemplateSet.pm
?? bin/register_domains
M t/consumer/domain.t
?? t/lib/MockOpenSRS.pm
(This is the output from git-status --short, for which I have
an alias, git s. I use this probably 99 times as often as
plain git-status.)Not too bad, probably no need for a printout. The new bin/register-domains program can go in right away by itself:
% git add bin
% git commit -m 'new register_domains utility program'
Next I'll deal with that new mock object class in
t/lib/MockOpenSRS.pm. I'll add that, then use git-add
-p to add the related changes from the other files:
% git add t/lib
% git add -p
...
% git s
MM lib/Pobox/Moonpig/Consumer/Domain/Activator.pm
M lib/Pobox/Moonpig/Role/HasDomain.pm
M lib/Pobox/Moonpig/TemplateSet.pm
A t/lib/MockOpenSRS.pm
MM t/consumer/domain.t
% git ix
...
The git ix command at the end there is an alias for git diff
--cached: it displays what's staged in the index. The output
looks good, so I'll commit it:
% git commit -m 'mock OpenSRS object; add tests'
Now I want to see if those tests actually pass. Maybe I forgot
something!
% git stash
% make test
...
OK
% git stash pop
The git-stash command hides the unrelated changes from the
test suite so that I can see if the tests I just put into
t/consumer/domain.t work properly. They do, so I bring back
the stashed changes and continue. If they didn't, I'd probably amend
the last commit with git commit --amend and try again.Continuing:
% git diff
...
% git add -p lib/Pobox/Moonpig/Role/HasDomain.pm
...
% git commit -m 'Domains do not have explicit start dates'
% git diff
...
% git add -p
...
% git commit --fixup :/mock
That last bit should have been part of the "mock OpenSRS object"
commit, but I forgot it. So I make a fixup commit, which I'll merge
into the main commit later on. A fixup commit is one whose subject
begins with fixup!. Did you know that you can name a commit
by writing :/text, and it names the most recent commit
whose message contains that text?It goes on like that for a while:
% git diff
...
% git add -p ...
...
% git commit -m 'Activator consumer can generate special charges'
% git diff
...
% git checkout lib/Pobox/Moonpig/Role/HasDomain.pm
The only uncommitted change left in HasDomain.pm was a
superfluous line, so I just threw it away.
% git diff
...
% git add -u
% git commit -m 'separate templates for domain-registering and domain-renewing consumers'
By this time all the remaining changes belong in the same commit, so I
use git-add -u to add them all at once. The working tree is
now clean. The history is as I showed above, except that in place of
the final WIP commit, I have:
a3c0b92 new register_domains utility program
53d704d mock OpenSRS object; add tests
a24acd8 Domains do not have explicit start dates
17a915d fixup! mock OpenSRS object; add tests
86e472b Activator consumer can generate special charges
5b2ad2b separate templates for domain-registering and domain-renewing consumers
(Again the oldest commit is first.) Now I'll get rid of that
fixup!:
% git rebase -i --autosquash HEAD~6
Because of --autosquash, the git-rebase menu is
reordered so that the fixup commit is put just after
the commit it fixes up, and its default action is 'fixup' instead of
'pick'. So I don't need to edit the rebase instructions at all. But
I might as well take the opportunity to put the commits in the right
order. The result is:
a3c0b92 new register_domains utility program
ea8dacd Domains do not have explicit start dates
297366a separate templates for domain-registering and domain-renewing consumers
4ef0e28 mock OpenSRS object; add tests
c3ab1eb Activator consumer can generate special charges
I have two tools for dealing with cleaned-up
branches like this one. One is git-vee, which compares two branches. It's
just a wrapper around the command git log --decorate --cherry-mark
--oneline --graph --boundary A"..."B. Here's a comparison the original c-domain branch and my new cleanup version:
% git vee c-domain
* c3ab1eb (HEAD, cleanup) Activator consumer can generate special charges
* 4ef0e28 mock OpenSRS object; add tests
* 297366a separate templates for domain-registering and domain-renewing consumer
* ea8dacd Domains do not have explicit start dates
* a3c0b92 new register_domains utility program
| * 3c5cdd4 (origin/c-domain, c-domain) WIP
|/
o 4e500ec Domain::Activator initial_invoice_charge_pairs
This clearly shows where the original and cleaned up branches diverge,
and what the differences are. I also use git-vee to compare
pre- and post-rebase versions of branches (with git-vee
ORIG_HEAD) and local branches with their remote tracking branches
after fetching (with git-vee remote or just plain
git-vee).A cleaned-up branch should usually have the same final tree as the tree at the end of the original branch. I have another tool, git-treehash, which compares trees. By default it compares HEAD with ORIG_HEAD, so after I use git-rebase to squash or to split commits, I sometimes run "git treehash" to make sure that the tree hasn't changed. In this example, I do:
% git treehash c-domain HEAD
d360408d1afa90e0176aaa73bf8d3cae641a0850 HEAD
f0fd6ea0de7dbe60520e2a69fbec210260370d78 c-domain
which tells me that they are not the same. Most often this
happens because I threw away all the debugging code that I put in
earlier, but this time it was because of that line of superfluous code
I eliminated from HasDomain.pm. When the treehashes differ, I'll use
git-diff to make sure that the difference is innocuous:
% git diff c-domain
diff --git a/lib/Pobox/Moonpig/Role/HasDomain.pm b/lib/Pobox/Moonpig/Role/HasDomain.pm
index 3d8bb8c..21cb752 100644
--- a/lib/Pobox/Moonpig/Role/HasDomain.pm
+++ b/lib/Pobox/Moonpig/Role/HasDomain.pm
@@ -5,7 +5,6 @@ use Carp qw(croak confess);
use ICG::Handy qw(is_domain);
use Moonpig::Types qw(Factory Time);
use Moose::Util::TypeConstraints qw(duck_type enum subtype);
-use MooseX::SetOnce;
with (
'Moonpig::Role::StubBuild',
Okay then.The next task is probably to deal with the older WIP commits. This time I'll omit all the details. But the enclosing procedure looks like this:
% git checkout -b wip-cleanup c8dbf41
% git reset HEAD^
% ... (a lot of git-add -p as above) ...
...
% git vee c8dbf41
* 4c6ff45 (wip-cleanup) get rid of unused twiddler test
* b328de5 test full payment cycle
* 201a4f2 abstract out pay_invoice operation
* 55ae45e add upper limit (default 30d) to wait_until utility
| * c8dbf41 WIP
|/
o e5063d4 add test for sent invoice in domain.t
% git treehash c8dbf41 HEAD
7f52ba68923e2ede8fda407ffa9c06c5c48338ae
% git checkout cleanup
% git rebase wip-cleanup
The output of git-treehash says that the tree at the end of
the wip-cleanup branch is identical to the one in the WIP
commit it is supposed to replace, so it's perfectly safe to rebase the
rest of the cleanup branch onto it, replacing the one WIP
commit with the four new commits in wip-cleanup. Now the
cleaned up branch looks like this:
% git vee c-domain
* a425aa1 (HEAD, cleanup) Activator consumer can generate special charges
* 2bb0932 mock OpenSRS object; add tests
* a77bfcb separate templates for domain-registering and domain-renewing consumer
* 4c44db2 Domains do not have explicit start dates
* fab500f new register_domains utility program
= 38018b6 Domain::Activator initial_invoice_charge_pairs
= aebbae6 rename "croak" method to "fail" to avoid conflicts
= 45a224d notes about why domain queries might fail
= 80e4a90 OpenSRS interface
= 27f4562 bring in Net::OpenSRS module
= f5cb624 add missing MakesReplacement stuff
* 4c6ff45 (wip-cleanup) get rid of unused twiddler test
* b328de5 test full payment cycle
* 201a4f2 abstract out pay_invoice operation
* 55ae45e add upper limit (default 30d) to wait_until utility
| * 3c5cdd4 (origin/c-domain, c-domain) WIP
| = 4e500ec Domain::Activator initial_invoice_charge_pairs
| = f64361f rename "croak" method to "fail" to avoid conflicts
| = 893f16f notes about why domain queries might fail
| = 52c18fb OpenSRS interface
| = fc13059 bring in Net::OpenSRS module
| = 9e6ffa4 add missing MakesReplacement stuff
| * c8dbf41 WIP
|/
o e5063d4 add test for sent invoice in domain.t
git-vee marks a commit with an equal sign instead of a star
if it's equivalent to a commit in the other branch. The commits in
the middle marked with equals signs are the ones that weren't changed.
The upper WIP was replaced with five commits, and the lower one with
four.I've been planning for a long time to write a tool to help me with breaking up WIP commits like this, and with branch cleanup in general: It will write each changed hunk into a file, and then let me separate the hunk files into several subdirectories, each of which represents one commit, and then it will create the commits automatically from the directory contents. This is still only partly finished, but I think when it's done it will eliminate the six-color diff printouts.
[ Addendum 20120404: Further observation has revealed that I almost never use git-commit -a, even when it would be quicker to do so. Instead, I almost always use git-add -u and then git-commit the resulting index. This is just an observation, and not a claim that my practice is either better or worse than using git-commit -a. ]
[ Addendum 20120825: There is now a followup article about how to manage rewriting of published history. ]
[Other articles in category /prog] permanent link
Sun, 04 Mar 2012
Why can't Git resolve all conflicted merges?
I like to be prepared ahead of time for questions, and one such
question is why Git can't resolve all merge conflicts automatically.
People do show up on IRC asking this from time to time. If you're a
sophisticated user the answer is obvious, but I've made a pretty good
living teaching classes to people who don't find such things
obvious.
What we need is a nice example. In the past my example was sort of silly. You have a file that contains the instruction:
Pay potato tax every April 15
One branch adds an exception:
Pay potato tax every April 15
(Except in years of potato blight.)
While another branch broadens the original instruction:
Pay all tax due every April 15
What's the correct resolution here? It's easy to understand that
mashing together the two changes is a recipe for potential
catastrophe:
Pay all tax due every April 15
(Except in years of potato blight.)
You get fined for tax evasion after the next potato blight. And it's
similarly easy to construct scenarios in which the correct resolution
is to leave the whole thing in place including the modifier, change
the thing to something else completely, delete the whole thing, or to
refer the matter to Legal and shut down the whole system until you
hear back. Clearly it's outside Git's scope to recognize when to call
in the lawyers, much less to predict what their answer will be. But a few months ago I ran into a somewhat less silly example. At work we had two seprate projects, "Moonpig" and "Stick", each in its own repository. Moonpig contained a subsystem, "Collections", which we decided would make more sense as part of Stick. I did this work, removing the Collections code from the Moonpig project and integrating it into the Stick project. From the point of view of the Moonpig repository, the Collections system was deleted entirely.
Meanwhile, on a parallel branch of Moonpig, R.J.B. Signes made some changes that included bug fixes to the Collections. After I removed the collections, he tried to merge his changes into the master branch, and got a merge conflict, because some of the files to which he was making bug fixes were no longer there.
The correct resolution was to perform the rest of the merge without the bug fixes, which Git could conceivably have done. But then the unapplied bug fixes needed to be applied to the Collections module that was now in the completely separate Stick project, and there is no way Git could have done this, or even to have known it should be done. Human intervention was the only answer.
[Other articles in category /prog] permanent link
Fri, 17 Feb 2012
It came from... the HOLD SPACE
Since 2002, I've given a talk almost every December for the Philadelphia Linux Users'
Group. It seems like most of their talks are about the newest and
best developments in Linux applications, which is a topic I don't know
much about. So I've usually gone the other way, talking about the
oldest and worst stuff. I gave a couple of pretty good talks about
how files work, for example, and what's in the inode structure.
I recently posted about my work on Zach Holman's spark program, which culminated in a ridiculous workaround for the shell's lack of fractional arithmetic. That work inspired me to do a talk about all the awful crap we had to deal with before we had Perl. (And the other 'P' languages that occupy a similar solution space.) Complete materials are here. I hope you check them out, because i think they are fun. This post is a bunch of miscellaneous notes about the talk.
One example of awful crap we had to deal with before Perl etc. were invented was that some people used to write 'sed scripts', although I am really not sure how they did it. I tried once, without much success, and then for this talk I tried again, and again did not have much success.



 The little guy to the right is known
as hallucigenia. It is a creature so peculiar that when
the paleontologists first saw the fossils, they could not even agree
on which side was uppermost. It has nothing to do with Unix, but I
put it on the slide to illustrate "alien horrors from the dawn of
time".
The little guy to the right is known
as hallucigenia. It is a creature so peculiar that when
the paleontologists first saw the fossils, they could not even agree
on which side was uppermost. It has nothing to do with Unix, but I
put it on the slide to illustrate "alien horrors from the dawn of
time".
Between slides 9 and 10 (about the ed line editor) I did a
quick demo of editing with ed. You will just have to imagine
this. I first learned to program with a line editor like ed,
on a teletypewriter just like the one on slide 8.
Modern editors are much better. But it used to
be that Unix sysadmins were expected to know at least a little ed,
because if your system got into some horrible state where it couldn't
mount the /usr partition, you wouldn't be able to run
/usr/bin/vi or /usr/local/bin/emacs, but you would
still be able to use /bin/ed to fix /etc/fstab or
whatever else was broken. Knowing ed saved my bacon several
times.
 (Speaking of
teletypewriters, ours had an attachment for punching paper tape, which
you can see on the left side of the picture. The punched chads fell
into a plastic chad box (which is missing in the picture), and when I
was about three I spilled the chad box. Chad was everywhere, and it
was nearly impossible to pick up. There were still chads stuck
in the cracks in the floorboards when we moved out three years
later. That's why, when the contested election of 2000 came around, I
was one of the few people in North America who was not bemused to
learn that there was a name for the little punched-out bits.)
(Speaking of
teletypewriters, ours had an attachment for punching paper tape, which
you can see on the left side of the picture. The punched chads fell
into a plastic chad box (which is missing in the picture), and when I
was about three I spilled the chad box. Chad was everywhere, and it
was nearly impossible to pick up. There were still chads stuck
in the cracks in the floorboards when we moved out three years
later. That's why, when the contested election of 2000 came around, I
was one of the few people in North America who was not bemused to
learn that there was a name for the little punched-out bits.)
Anyway, back to ed. ed has one and only one diagnostic: if you do something it didn't like, it prints ?. This explains the ancient joke on slide 10, which first appeared circa 1982 in the 4.2BSD fortune program.
I really wanted to present a tour de force of sed mastery, but as slides 24–26 say, I was not clever enough. I tried really hard and just could not do it. If anyone wants to fix my not-quite-good-enough sed script, I will be quite grateful.
On slide 28 I called awk a monster. This was a slip-up; awk is not a monster and that is why it does not otherwise appear in this talk. There is nothing really wrong with awk, other than being a little old, a little tired, and a little underpowered.
If you are interested in the details of the classify program, described on slide 29, the sources are still available from the comp.sources.unix archive. People often say "Why don't you just use diff for that?" so I may as well answer that here: You use diff if you have two files and you want to see how they differ. You use classify if you have 59 files, of which 36 are identical, 17 more are also identical to each other but different from the first 36, and the remaining 6 are all weirdos, and you want to know which is which. These days you would probably just use md5sum FILES | accumulate, and in hindsight that's probably how I should have implemented classify. We didn't have md5sum but we had something like it, or I could have made a checksum program. The accumulate utility is trivial.
Several people have asked me to clarify my claim to have invented netcat. It seems that a similar program with the same name is attributed to someone called "Hobbit". Here is the clarification: In 1991 I wrote a program with the functionality I described and called it "netcat". You would run netcat hostname port and it would open a network socket to the indicated address, and transfer data from standard input into the socket, and data from the socket to standard output. I still have the source code; the copyright notice at the top says "21 October 1991". Wikipedia says that the same-named program by the other guy was released on 20 March 1996. I do not claim that the other guy stole it from me, got the idea from me, or ever heard of my version. I do not claim to be the first or only person to have invented this program. I only claim to have invented mine independently.
My own current version of the spark program is on GitHub, but I think Zach Holman's current version is probably simpler and better now.
[ Addendum 20170325: I have revised this talk a couple of times since this blog article was written. Links to particular slides go to the 2011 versions, but the current version is from 2017. There are only minor changes. For example, I removed `awk` from the list of “monsters”. ]
[Other articles in category /Unix] permanent link
Wed, 15 Feb 2012
Insane calculations in bash
A few weeks ago I wrote an
article about various methods of arithmetic calculation in shell
scripts and in bash in particular, but it was all leading
up to today's article, which I think is more interesting
technically.
A while back, Zach Holman (who I hadn't heard of before, but who is apparently a bigwig at GitHub) implemented a kind of cute little hack, called "spark". It's a little shell utility, spark, which gets a list of numbers as its input and uses Unicode block characters to print a little bar graph of the numbers on the output. For example, the invocation:
spark 2,4,6,8will print out something like:
▃▄▆▇To do this in one of the 'P' languages (Perl, Python, PHP, Puby, or maybe Pickle) takes something like four lines of code. But M. Holman decided to implement it in bash for maximum portability, so it took 72 lines, not counting comments, whitespace, etc.
Let's begin by discussing the (very simple) mathematics that underlies drawing bar graphs. Suppose you want to generate a set of bars for the numbers $1, $9, $20. And suppose you can actually generate bars of integer heights only, say integers from 0–7:
0 1 ▁ 2 ▂ 3 ▃ 4 ▄ 5 ▅ 6 ▆ 7 ▇(M. Holman 's original program did this, even though a height-8 bar █ is available. But the mathematics is the same either way.)
Absolute scaling
The first step is to scale the input numbers onto the range of the bars. To do this, we find a scale factor f that maps dollars onto bar heights, say that f bar units = $1.A reasonable thing to try is to say that since your largest number is $20, we will set 7 bar units = $20. Then 0.35 bar units = $1, and 3.45 bar units = $9. We'll call these the "natural heights" for the bars.
Unfortunately we can't render the bars at their natural heights; we can only render them at integer heights, so we have to round off. 0.35 bar units rounds off to 0, so we will represent $1 as no bar at all. 3.45 bar units rounds off, badly, to 3, but that's the way it goes; if you try to squeeze the numbers from 1 to 20 into the range 0 to 7, something has to give. Anyway, this gives
(1,9,20) → ( ▃▇)
The formula is: Let max be the largest input number (here,
20) and let n be the size of the largest possible bar (here, 7).
Then an input number x becomes a bar of size
n·x / max:
$$x\rightarrow {n\cdot x \over max } $$
Note that this maps max itself to n, and 0 to 0.I'll call this method "absolute scaling", because big numbers turn into big bars. (It fails for negative numbers, but we'll assume that the numbers are non-negative.)
(0…20) → ( ▁▁▁▂▂▂▃▃▄▄▄▅▅▅▆▆▆▇▇)There are a couple of variations we might want to apply. First, maybe we don't like that $1 mapped to no bar at all; it's too hard to see, depending on the context. Perhaps we would like to guarantee that only 0 maps to 0. One way to ensure that is to round everything up, instead of rounding to the nearest integer:
(0…20) → ( ▁▁▂▂▂▃▃▃▄▄▄▅▅▅▆▆▆▇▇▇)
(1,9,20) → (▁▄▇)
Another benefit of always rounding up is that it uses the bars
equally. Suppose we're mapping numbers in the range 1–100 to bars of
heights 1–7. If we round off to the nearest integer, each bar
represents 14 or 15 different numbers, except that the tallest bar
only represents the 8 numbers 93–100. This is a typical situation.
If we always round up, each bar corresponds to a nearly equal range of
numbers. (Another way to adjust this is to replace n with
n+½ in the formula.)
Relative scaling
Now consider the numbers $18, $19, $20. Under the absolute scaling method, we get:
(18,19,20) → (▆▇▇)or, if you're rounding up,
(18,19,20) → (▇▇▇)which obscures the difference between the numbers. There's only an 11% difference between the tallest and shortest bar, and that doesn't show up at this resolution. Depending on your application, this might be what you want, but we might also want to avail ourselves of the old trick of adjusting the baseline. Instead of the bottom of the bar being 0, we can say it represents 17. This effectively reduces every bar by 17 before scaling it, so that the number x is now represented by a bar with natural height n·(x−17) / (max−17). Then we get these bars:
(18,19,20) → (▃▅▇)Whether this "relative scaling" is a better representation than ▇▇▇ depends on the application. It emphasizes different properties of the data.
In general, if we put the baseline at b, the natural height for a bar representing number x is:
$$x\rightarrow {n\cdot (x-b) \over (max-b) } $$
That is the same formula as before, except that everything has been shifted down by b.A reasonable choice of b would be the minimum input value, or perhaps a bit less than the minimum input value.
The shell sucks
But anyway, what I really wanted to talk about was how to fix this program, because I think my solution was fun and interesting. There is a tricky problem, which is that you need to calculate values like (n-b)/(x-b), which so you might like to do some division, but as I wrote earlier, bash has no facilities for doing fractional arithmetic. The original program used $((…)) everywhere, which throws away fractions. You can work around that, because you don't actually the fractional part of (n-b)/(x-b); you only need the greatest integer part. But the inputs to the program might themselves be fractional numbers, like say 3.5, and $((…)) barfs if you try to operate on such a number:
$ x=3.5; echo $((x + 1)) bash: 3.5: syntax error: invalid arithmetic operator (error token is ".5")and you seemingly cannot work around that.
My first response to this was to replace all the uses of $((…)) with bc, which, as I explained in the previous article, does not share this problem. M. Holman rejected this, saying that calling out to bc all the time made the program too slow. And there is something to be said for this. M. Holman also said that bc is non-portable, which I find astounding, since it has been in Unix since 1974, but sadly plausible.
So supposing that you take this complaint seriously, what can you do? Are you just doomed? No, I found a solution to the problem that solves all the problems. It is portable, efficient, and correct. It is also slightly insane.
Portable fractions in bash
We cannot use decimal numbers:
$ x=3.5; echo $((x + 1)) bash: 3.5: syntax error: invalid arithmetic operator (error token is ".5")But we can use fractions:
$ x_n=7; x_d=2; echo $((x_n + x_d))/$((x_d))
9/2
And we can convert decimal inputs to fractions without arithmetic:
# given an input number which might be a decimal, convert it to
# a rational number; set n and d to its numerator and
# denominator. For example, 3.3 becomes n=33 and d=10;
# 17 becomes n=17 and d=1.
to_rational() {
# Crapulent bash can't handle decimal numbers, so we will convert
# the input number to a rational
if [[ $1 =~ (.*)\.(.*) ]] ; then
i_part=${BASH_REMATCH[1]}
f_part=${BASH_REMATCH[2]}
n="$i_part$f_part";
d=$(( 10 ** ${#f_part} ))
else
n=$1
d=1
fi
}
This processes a number like 35.17 in a purely lexical way, extracting
the 35 and the 17, and turning them into the numerator 3517 and the
denominator 100. If the input number contains no decimal point, our
task is trivial: 23 has a numerator of 23 and a denominator of 1.Now we can rewrite all the shell arithmetic in terms of rational numbers. If a_n and a_d are the numerator and denominator of a, and b_n and b_d are the numerator and denominator of b, then addition, subtraction, multiplication, and even division of a and b are fast, easy, and even portable:
# a + b
sum_n = $((a_n * b_d + a_d * b_n))
sum_d = $((a_d * b_d))
# a - b
diff_n = $((a_n * b_d - a_d * b_n))
diff_d = $((a_d * b_d))
# a * b
prod_n = $((a_n * b_n))
prod_d = $((a_d * b_d))
# a / b
quot_n = $((a_n * b_d))
quot_d = $((a_d * b_n))
We can easily truncate a number to produce an integer, because the
built-in division does this for us:
greatest_int = $((a_n / a_d))
And we can round to the nearest integer by adding 1/2 before
truncating:
nearest_int = $(( (a_n * 2 + a_d) / (a_d * 2) ))
(Since n/d + 1/2 = (2n+d)/2d.)For complicated calculations, you can work the thing out as several steps, or you can solve it on paper and then just embed a big rational expression. For example, suppose you want to calculate ((x-min)·number_of_tiers)/range, where number_of_tiers is known to be an integer. You could do each operation in a separate step, or you could use instead:
tick_index_n=$(( ( x_n * min_d - min_n * x_d ) * number_of_tiers * range_d )) tick_index_d=$(( range_n * x_d * min_d ))Should you need to convert to decimals for output, the following is a proof-of-concept converter:
function to_dec {
n=$1
d=$2
maxit=$(( 1 + ${3:-10} ))
while [ $n != 0 -a $maxit -gt -1 ]; do
next=$((n/d))
if [ "$r" = "" ]; then r="$next."; else r="$r$next"; fi
n=$(( (n - d * next) * 10 ))
maxit=$(( maxit - 1 ))
done
r=${r:-'0.'}
}
For example, to_dec 13 8 sets r to
1.625, and to_dec 13 7 sets r to
1.857142857. The optional third argument controls the
maximum number of digits after the decimal point, and defaults to
10. The principal defect is that it doesn't properly round off;
frac2dec 19 10 0 yields 1. instead of 2.,
but this could be fixed without much trouble. Extending it to
convert to arbitrary base output is quite easy as well.Coming next month, libraries in bash for computing with continued fractions using Gosper's algorithms. Ha ha, just kidding. The obvious next step is to implement base-10 floating-point numbers in bash like this:
prod_mantissa=$((a_mantissa * b_mantissa)) prod_exponent=$((a_exponent + b_exponent))[ Addendum 20120306: David Jones corrects a number of portability problems in my implementation. ]
[ Addendum 20180101: Shane Hansen did something similar to calculate Euler's number (2.71818…) in Bash a while back. It might be fun to compare our implementations. ]
[Other articles in category /prog] permanent link
Fri, 10 Feb 2012
I abandon my abusive relationship with Facebook
I have just deactivated my Facebook account, I hope for good.
This interview with Eben Moglen provides many of the reasons, and was probably as responsible as anything for my decision.
But the straw that broke the camel's back was a tiny one. What finally pushed me over the edge was this: "People who can see your info can bring it with them when they use apps.". This time, that meant that when women posted reviews of men they had dated on a dating review site, the review site was able to copy the men's pictures from Facebook to insert into the reviews. Which probably was not what the men had in mind when they first posted those pictures to Facebook.
This was, for me, just a little thing. But it was the last straw because when I read Facebook's explanation of why this was, or wasn't, counter to their policy, I realized that with Facebook, you cannot tell the difference.
For any particular appalling breach of personal privacy you can never guess whether it was something that they will defend (and then do again), or something that they will apologize for (and then do again anyway). The repeated fuckups for which they are constantly apologizing are indistinguishable from their business model.
So I went to abandon my account, and there was a form they wanted me to fill out to explain why: "Reason for leaving (Required)": One choice was "I have a privacy concern.":
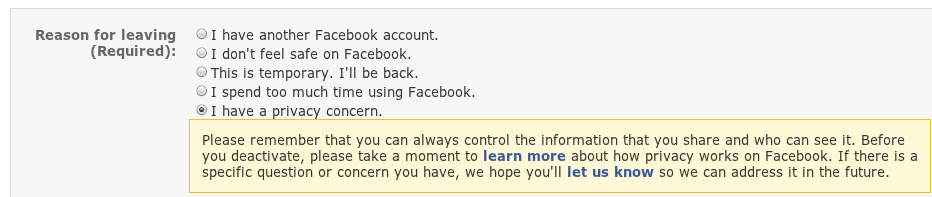
Please remember that you can always control the information that you share and who can see it. Before you deactivate, please take a moment to learn more about how privacy works on Facebook. If there is a specific question or concern you have, we hope you'll let us know so we can address it in the future.It was really nice of Facebook to provide this helpful reminder that their corporation is a sociopath: "Please remember that you can always control the information that you share and who can see it. You, and my wife, Morgan Fairchild."
Facebook makes this insane claim in full innocence, expecting you to believe it, because they believe it themselves. They make this claim even after the times they have silently changed their privacy policies, the times they have silently violated their own privacy policies, the times they have silently opted their users into sharing of private information, the times they have buried the opt-out controls three pages deep under a mountain of confusing verbiage and a sign that said "Beware of The Leopard".
There's no point arguing with a person who makes a claim like that. Never mind that I was in the process of deactivating my account. I was deactivating my account, and not destroying it, because they refuse to destroy it. They refuse to relinquish the personal information they have collected about me, because after all it is their information, not mine, and they will never, ever give it up, never. That is why they allow you only to deactivate your account, while they keep and continue to use everything, forever.
But please remember that you can always control the information that you share and who can see it. Thanks, Facebook! Please destroy it all and never let anyone see it again. "Er, no, we didn't mean that you could have that much control."
This was an abusive relationship, and I'm glad I decided to walk away.
[ Addendum 20120210: Ricardo Signes points out that these is indeed an option that they claim will permanently delete your account, although it is hard to find. ]
[ Addendum 20220704: Looking back on this from ten years out, I am struck by two things. First, there many many times in the intervening decade that Facebook did horrible, awful things to its users, and I shrugged because I wasn't involved. And second, there were not any times when I regretted not being on Facebook. Leaving was a pure win. Come join me, it's not too late. ]
[Other articles in category /misc] permanent link
Thu, 09 Feb 2012
Testing for exceptions
The Test::Fatal
module makes it very easy to test code that is supposed to throw
an exception. It provides an exception function that takes a
code block. If the code completes normally, exception {
code } returns undefined; if the code throws an exception,
exception { code } returns the exception value that
was thrown. So for example, if you want to make sure that some
erroneous call is detected and throws an exception, you can use
this:
isnt( exception { do_something( how_many_times => "W" ) },
undef,
"how_many_times argument requires a number" );
which will succeed if do_something(…) throws an exception,
and fail if it does not. You can also write a stricter test, to look
for the particular exception you expect:
like( exception { do_something( how_many_times => "W" ) },
qr/how_many_times is not numeric/,
"how_many_times argument requires a number" );
which will succeed if do_something(…) throws an exception
that contains how_many_times is not numeric, and fail
otherwise.Today I almost made the terrible mistake of using the first form instead of the second. The manual suggests that you use the first form, but it's a bad suggestion. The problem is that if you completely screw up the test and write a broken code block that dies, the first test will cheerfully succeed anyway. For example, suppose you make a typo in the test code:
isnt( exception { do_something( how_many_tims => "W" ) },
undef,
"how_many_times argument requires a number" );
Here the do_something(…) call throws some totally different
exception that we are not interested in, something like unknown
argument 'how_many_tims' or mandatory 'how_many_times'
argument missing, but the exception is swallowed and the test
reports success, even though we know nothing at all about the feature
we were trying to test. But the test looks like it passed.In my example today, the code looked like this:
isnt( exception {
my $invoice = gen_invoice();
$invoice->abandon;
}, undef,
"Can't abandon invoice with no abandoned charges");
});
The abandon call was supposed to fail, for reasons you don't
care about. But in fact, the execution never got that far, because
there was a totally dumb bug in gen_invoice() (a missing
required constructor argument) that caused it to die with a completely
different exception.I would never have noticed this error if I hadn't spontaneously decided to make the test stricter:
like( exception {
my $invoice = gen_invoice();
$invoice->abandon;
}, qr/Can't.*with no abandoned charges/,
"Can't abandon invoice with no abandoned charges");
});
This test failed, and the failure made clear that
gen_invoice(), a piece of otherwise unimportant test
apparatus, was completely broken, and that several other tests I had
written in the same style appeared to be passing but weren't actually
running the code I thought they were.So the rule of thumb is: even though the Test::Fatal manual suggests that you use isnt( exception { … }, undef, …), do not.
I mentioned this to Ricardo Signes, the author of the module, and he released a new version with revised documentation before I managed to get this blog post published.
[Other articles in category /prog/perl] permanent link
Wed, 11 Jan 2012
Where should usage messages go?
Last week John Speno complained about Unix commands which, when
used incorrectly, print usage messages to standard error instead of to
standard output. The problem here is that if the usage message is
long, it might scroll off the screen, and it's a pain when you try to
pipe it through a pager with command | pager and discover
that the usage output has gone to stderr, missed the pager, and
scrolled off the screen anyway.
Countervailing against this, though, is the usual argument for stderr: if you had run the command in a pipeline, and it wrote its error output to stdout instead of to stderr, then the error message would have gotten lost, and would possibly have caused havoc further down the pipeline. I considered this argument to be the controlling one, but I ran a quick and informal survey to see if I was in the minority.
After 15 people had answered the survey, Ron Echeverri pointed out that although it makes sense for the usage message to go to stderr when the command is used erroneously, it also makes sense for it to go to stdout if the message is specifically requested, say by the addition of a --help flag, since in that case the message is not erroneous. So I added a second question to the survey to ask about where the message should go in such a case.
83 people answered the first question, "When a command is misused, should it deliver its usage message to standard output or to standard error?". 62 (75%) agreed that the message should go to stderr; 11 (13%) said it should go to stdout. 10 indicated that they preferred a more complicated policy, of which 4 were essentially (or exactly) what M. Echeverri suggested; this brings the total in favor of stderr to 66 (80%). The others were:
- stdout, if it is a tty; stderr otherwise
- stdout, if it is a pipe; stderr otherwise
- A very long response that suggested syslog.
- stderr, unless an empty stdout would cause problems
- It depends, but the survey omitted the option of printing directly on the console
- It depends
68 people answered the second question, "Where should the command send the output when the user specifically requests usage information?". (15 people took the survey before I added this question.) 50 (74%) said the output should go to stdout, 12 (18%) to the user's default pager and then to stdout, and 5 (7%) to stderr. One person (The same as #5 above) said "it depends".
Thanks to everyone who participated.
[Other articles in category /Unix] permanent link
Tue, 10 Jan 2012
Elaborations of Russell's paradox
When Katara was five or six, I told her about Russell's paradox in the
following form: in a certain library, some books are catalogs that
contain lists of other books. For example, there is a catalog of all
the books on the second floor, and a catalog of all the books about
birds. Some catalogs might include themselves. For example, the
catalog of all the books in the library certainly includes itself.
Such catalogs have red covers; the other catalogs, which do not
include themselves, such as the catalog of all the plays of
Shakespeare, have blue covers. Now is there a catalog of all the
catalogs with blue covers?
I wasn't sure she would get this, but it succeeded much better than I expected. After I prompted her to consider what color cover it would have, she thought it out, first ruling out one color, and then, when she got to the second color, she just started laughing.
A couple of days ago she asked me if I could think of anything that was like that but with three different colors. Put on the spot, I suggested she consider what would happen if there could be green catalogs that might or might not include themselves. This is somewhat interesting, because you now can have a catalog of all the blue catalogs; it can have a green cover. But I soon thought of a much better extension.
I gave it to Katara like this: say you have a catalog, let's call it X. If X mentions a catalog that mentions X, it has a gold stripe on the spine. Otherwise, it has a silver stripe. Now:
- Could there be a red catalog with a gold stripe?
- Could there be a red catalog with a silver stripe?
- Could there be a blue catalog with a gold stripe?
- Could there be a blue catalog with a silver stripe?
- Is there a catalog of all the catalogs with gold stripes?
- Is there a catalog of all the catalogs with silver stripes?
Translating this into barber language is left as an exercise for the reader.
[ Addendum 20231128: More about uncountable sets for seven-year-olds. ]
[Other articles in category /math] permanent link
Wed, 04 Jan 2012
Mental astronomical calculations
As you can see from the following graph, the daylight length starts
increasing after the winter solstice (last week) but it does so quite
slowly at first, picking up speed, and reaching a maximum rate of
increase at the vernal equinox.
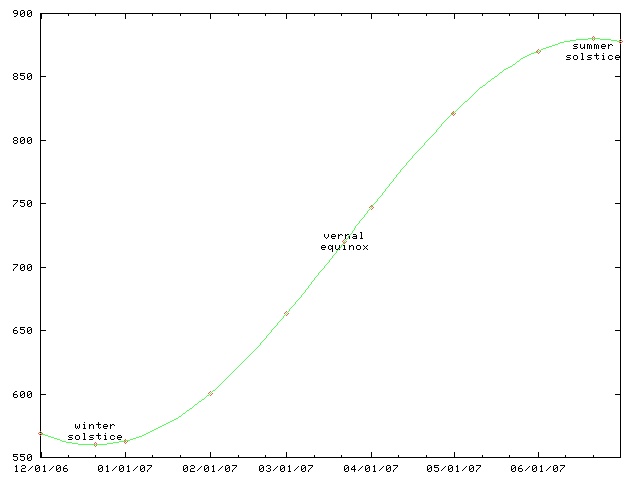
The day length is given by a sinusoid with amplitude that depends on your latitude (and also on the axial tilt of the Earth, which is a constant that we can disregard for this problem.) That is, it is a function of the form a + k sin 2πt/p, where a is the average day length (12 hours), k is the amplitude, p is the period, which is exactly one year, and t is amount of time since the vernal equinox. For Philadelphia, where I live, k is pretty close to 3 hours because the shortest day is about 3 hours shorter than average, and the longest day is about 3 hours longer than average. So we have:
day length = 12 hours + 3 hours · sin(2πt / 1 year)Now let's compute the rate of change on the equinox. The derivative of the day length function is:
rate of change = 3h · (2π / 1y) · cos(2πt / 1y)At the vernal equinox, t=0, and cos(…) = 1, so we have simply:
rate of change = 6πh / 1 year = 18.9 h / 365.25 daysThe numerator and the denominator match pretty well. If you're in a hurry, you might say "Well, 360 = 18·20, so 365.25 / 18.9 is probably about 20," and you would be right. If you're in slightly less of a hurry, you might say "Well, 361 = 192, so 365.25 / 18.9 is pretty close to 19, maybe around 19.2." Then you'd be even righter.
So the change in day length around the equinox (in Philadelphia) is around 1/20 or 1/19 of an hour per day—three minutes, in other words.
The exact answer, which I just looked up, is 2m38s. Not too bad. Most of the error came from my estimation of k as 3h. I guessed that the sun had been going down around 4:30, as indeed it had—it had been going down around 4:40, so the correct value is not 3h but only 2h40m. Had I used the correct k, my final result would have been within a couple of seconds of the right answer.
Exercise: The full moon appears about the same size as a U.S. quarter (1 inch diameter circle) held nine feet away (!) and also the same size as the sun, as demonstrated by solar eclipses. The moon is a quarter million miles away and the sun is 93 million miles away. What is the actual diameter of the sun?
[ Addendum 20120104: An earlier version of this article falsely claimed that the full moon appears the same size as a quarter held at arm's length. This was a momentary brain fart, not a calculational error. Thanks to Eric Roode for pointing out this mistake. ]
[Other articles in category /calendar] permanent link
Tue, 03 Jan 2012
Eta-reduction in Haskell and English
The other day Katara and I were putting together a model, and she asked
what a certain small green part was for. I said "It's a thing for
connecting a thing to another thing."
Katara objected that this was a completely unhelpful explanation, but I disagreed. I would have agreed that it was an excessively verbose explanation, but she didn't argue that point.
Later, it occurred to me that Haskell has a syntax for eliding unnecessary variables in cases like this. In Haskell, one can abbreviate the expression
λx → λy → x + y
to just (+). (Perl users may find it helpful to know that
the Perl equivalent of the expression above is sub { my ($x) = @_;
return sub { my ($y) = @_; return $x + $y } }.) This is an
example of a general transformation called η-reduction. In general, for
any function f, λx → f x is a
function that takes an argument x and returns f x. But
that's exactly what f does. So we can replace the longer
version with the shorter version, and that's η-reduction, or we can go the
other way, which is η-expansion.Anyway, once I thought of this it occurred to me that, just like the longer expression could be reduced to (+), my original explanation that the small green part was "a thing for connecting a thing to another thing" could be η-reduced to "a connector".
Perhaps if I had said that in the first place Katara would not have complained.
Happy new year, all readers.
[Other articles in category /lang] permanent link




