Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Adventures in systems administration |
| Arithmetic expressions in shell scripts |
| Concerts |
| Longshot bets by time travelers |
| Watch out for the Calendar Geeks |
| Why use a digital stadiometer? |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 16 Nov 2011
Arithmetic expressions in shell scripts
This spring will be the 25th anniversary of my involvement with Unix,
and I have spent way too much of that time writing shell scripts.
Back before we had Perl and the other 'P' languages (Python, PHP,
Puby, and Pickle) you programmed in C or you programmed in shell.
Bourne shell, to be specific. (It was named for its author, Steven
Bourne. There was a time before there was a Bourne shell, when there
was only "the shell", written by Ken Thompson, but that predates even
my experience.) People did sometimes try to program the C shell,
but only the very foolish tried it more than once. (Tom Christiansen
once wrote a very
detailed article explaining why, if you are interested.)
C is still used, but it is still C, and, as they say, C is a language that combines the power of raw assembly with the expressiveness of raw assembly. If you wanted to do systems programming, you wrote in C, because that was what there was, but if you wanted to do almost anything else, you wrote in Bourne shell, because otherwise you spent a lot of time counting bytes and groveling over core dumps. If you knew what you were doing, you wrote as much as possible in Bourne shell, and for the parts where your shell script needed to do something interesting, you had it invoke some small utility program that you or someone else had written in C.
"Interesting" in this case had an extremely low threshhold. You called out to a C utility to sort data. You called out to a C utility to remove or rename a file. You called out to a C utility to test for the existence of a file. You called out to a C utility to compare two strings. In early versions of the shell, you called out to a C utility to perform file globbing—that is, to expand something like dir?/*.c to a list of files—although this function had been absorbed into the shell itself by 1979, several years before I arrived. You called out to a C utility to print a string to the terminal. And you called out to a C utility if you wanted to do arithmetic.
Even including languages that nobody is expected to actually use, Bourne shell is probably the only programming language I have ever used that does not have any built-in operators for performing arithmetic. Instead, there is a C utility program called expr which interprets its command-line arguments as an arithmetic expression, evaluates the expression, and prints the result on the standard output. So for example, if your script has variables x and y and you want to add these and store the result into z, you write:
z=`expr $x + $y`
This will fork a subprocess, which will execute the command expr
3 + 4 (or whatever). The command will emit the string
7 into a pipe, and the shell will read the string out of the
pipe and store it into z. Astounding!The expr program is a real piece of crap. The following reasonable-seeming invocations of expr all fail:
z=`expr $x + 1.5`
z=`expr $x+$y`
z=`expr $x * $y`
The first fails because the craptastic yacc parser in expr has a value stack
that is integer-only, so the program was not written to handle
fractional values, and will instantly abort with the message
non-numeric argument upon encountering the string 1.5 in
the input. The second fails because the craptastrophic lexer (a whole 12
lines of C code) assumes that
each command argument will be a single token, and makes no effort to
actually do any, you know, lexing. The third fails because
expr is a command run in a subshell, and since the * character is special
in the shell it expands to a list of the files in the current
directory, so although you thought you were going to run expr 3 * 4
you actually ran expr 3 hostid sys3 sys3.tar.gz v5root
v5root.tar.gz v6doc v6doc.tar.gz v6root v6root.tar.gz v6src
v6src.tar.gz v7 v7.tar.gz 4. The whole thing is a craptaclysm of craptitude.A better way to do arithmetic in a shell script was to invoke a different utility program, bc, the "basic calculator". You sent your arithmetic expression to bc on the standard input (which avoided the craptysmal shell expansion of *) and got the answer on the standard output, typically something like this:
z=`echo "$x + $y" | bc -l`
You needed the -l flag to enable floating-point calculations;
it also enabled certain higher functions such as square roots and
trigonometry. [ Addendum 20200108: The effect of -l is rather more complicated than I said; bc actually does base-10 floating-point arithmetic by default. ]
I had assumed that bc was a later development than expr, but it appeared in Unix version 6, while expr did not appear until version 7. So then I thought perhaps expr had been thrown in as a demonstration of yacc, but no, yacc was already present in version 5, and anyway, bc was written with yacc. So I no longer have any workable theory about who perpetrated expr, or why. (I have emailed Brian Kernighan to ask, and if he says anything interesting I will post an addendum.)
Anyway, about ten years after all this, the GNU project was in full swing and was reimplementing all the standard Unix tools, including the shell. Since they wanted their implementations to displace the standard implementations, they added all sorts of bells and whistles to them. So their shell, bash, contained all sorts of stuff. Among other things, it had built-in arithmetic. In bash, if you want to add x and y and put the result into z you can write:
z=$(( x + y ))
or even:
z=$((x+y))
The nifty $(( punctuation was necessary because the syntax had
to be backward compatible with the Bourne shell, and every clean
syntax was already used for something else. The $((…)) feature was a great
improvement over expr, and in some ways, it was even an
improvement over bc. It is much faster, for one thing. And
since it does not invoke a subshell, you don't have to worry about
* doing something weird.But in other ways it was a step backwards. It does not have any of bc's higher mathematical functions. It doesn't do radix conversion. And it does all its calculation in machine integers, so not only does it fall short of bc's arbitrary-precision arithmetic, it can't even handle fractions:
x=3; y=4.5 echo $((x+y)) bash: 4.5: syntax error: invalid arithmetic operator (error token is ".5")Why? Why why why??? Who ordered that? I mean, I hate floating-point arithmetic as much as the next guy—probably more—but even I recognize that people need to do it sometimes.
Well, here we are, eleven hundred words into this article and I have still not come to the point. That is typical for me, but I think that contrary to my usual practice, I will cut the scroll here and get to the real point in a day or two.
[ Addendum 20120215: At last, I got to the real point. ]
[Other articles in category /prog] permanent link
Mon, 13 Jun 2011
Longshot bets by time travelers
 Back in February 2007, I started a blog article that was to begin as
follows:
Back in February 2007, I started a blog article that was to begin as
follows:
If you're a time traveller, one way to make money is by placing bets on events that you already know the outcomes of. The stock market is only the most obvious example of this; who wouldn't have liked to have invested in IBM in 1916?I never finished this article, and I no longer remember where I planned to take it from there. I think I probably abandoned it because I realized that nothing else I could say would be as interesting as the Bosom Buddies thing. I don't think I could think of any examples that were less likely-seeming.But if making money is only your secondary goal, and your real object is to amaze your friends and confound your enemies, there may be more effective bets to place. I forget who it was who suggested to me how much fun it would be to go back to 1980 and bet that the cross-dressing star of Bosom Buddies would win back-to-back "Best Actor" Oscars within twenty years. But it's a fine idea.
Until today. I wonder what sort of odds you could have gotten in 1995 betting that within twenty years, the creators of "What Would Brian Boitano Do" ("Dude! Don't say 'pigfucker' in front of Jesus!") would win the Tony Award for "Best Musical".
[ Addendum 2017-03-17: This article is now obsolete, as something happened late last year that leaves both of my suggestions completely in the dust. ]
[Other articles in category /misc] permanent link
Sat, 11 Jun 2011 At a book sale I recently picked up Terence Tao's little book on problem solving for 50¢. One of the exercises (pp. 85–86) is the following little charmer: There are six musicians who will play a series of concerts. At each concert, some of the musicians will be on stage and some will be in the audience. What is the fewest number of concerts that can be played to that each musician gets to see the each of the others play?Obviously, no more than six concerts are required. (I have a new contribution to the long-debated meaning of the mathematical jargon term "obviously": if my six-year-old daughter Katara could figure out the answer, so can you.) And an easy argument shows that four are necessary: let's say that when a musician views another, that is a "viewing event"; we need to arrange at least 5×6 = 30 viewing events. A concert that has p performers and 6-p in the audience arranges p(6 - p) events, which must be 5, 8, or 9. Three concerts yield no more than 27 events, which is insufficient. So there must be at least 4 concerts, and we may as well suppose that each concert has three musicians in the audience and three onstage, to maximize the number of events at 9·4 = 36. (It turns out there there is no solution otherwise, but that is a digression.)
Each musician must attend at least 2 concerts, or else they would see only 3 other musicians onstage. But 6 musicians attending 2 concerts each takes up all 12 audience spots, so every musician is at exactly 2 concerts. Each musician thus sees exactly six musicians onstage, and since five of them must be different, one is a repeat, and the viewing event is wasted. We knew there would be some waste, since there are 36 viewing avents available and only 30 can be useful, but now we know that each spectator wastes exactly one event.
A happy side effect of splitting the musicians evenly between the stage and the audience in every concert is that we can exploit the symmetry: if we have a solution to the problem, then we can obtain a dual solution by exchanging the performers and the audience in each concert. The conclusion of the previous paragraph is that in any solution, each spectator wastes exactly one event; the duality tells us that each performer is the subject of exactly one wasted event.
Now suppose the same two musicians, say A and B, perform together twice. We know that some spectator must see A twice; this spectator sees B twice also, this wasting two events. But each spectator wastes only one event. So no two musicians can share the stage twice; each two musicians share the stage exactly once. By duality, each two spectators are in the same audience together exactly once.
So we need to find four 3-sets of the elements { A, B, C, D, E, F }, with each element appearing in precisely two sets, and such that each two sets have exactly one element in common.
Or equivalently, we need to find four triangles in K4, none of which share an edge.
The solution is not hard to find:
| 1 | 2 | 3 | 4 | |
| On stage | A B C | C D E | E F A | B D F |
| In audience | D E F | A B F | B C D | A C E |
If you generalize these arguments to 2m musicians, you find that there is a lower bound of $$\left\lceil{4m^2 - 2m \over m^2 }\right\rceil$$ concerts, which is 4. And indeed, even with as few as 4 musicians, you still need four concerts. So it's tempting to wonder if 4 concerts is really sufficient for all even numbers of musicians. Consider 8 musicians, for example. You need 56 viewing events, but a concert with half the musicians onstage and half in the audience provides 16 events, so you might only need as few as 4 concerts to provide the necessary events.
The geometric formulation is that you want to find four disjoint K4s in a K8; or alternatively, you want to find four 4-element subsets of { 1,2,3,4,5,6,7,8 }, such that each element appears in exactly two sets and no two elements are in the same. There seemed to be no immediately obvious reason that this wouldn't work, and I spent a while tinkering around looking for a way to do it and didn't find one. Eventually I did an exhaustive search and discovered that it was impossible.
But the tinkering and the exhaustive search were a waste of time, because there is an obvious reason why it's impossible. As before, each musician must be in exactly two audiences, and can share audiences with each other musician at most once. But there are only 6 ways to be in two audiences, and 8 musicians, so some pair of musicians must be in precisely the same pair of audiences, this wastes too many viewing events, and so there's no solution. Whoops!
It's easy to find solutions for 8 musicians with 5 concerts, though. There is plenty of room to maneuver and you can just write one down off the top of your head. For example:
| 1 | 2 | 3 | 4 | 5 | |
| On stage | E F G H | B C D H | A C D F G | A B D E G | A B C E F H |
| In audience | A B C D | A E F G | B E H | C F H | D G |
[ Addendum: For n = 1…10 musicians, the least number of concerts required is 0, 2, 3, 4, 4, 4, 5, 5, 5, 5; beyond this, I only have bounds. ]
[Other articles in category /math] permanent link
Fri, 27 May 2011
Watch out for the Calendar Geeks
Yesterday on the private IRC server run by my employer, one of my
co-workers said:
<MHO> [My wife] just informed me that this year, July has five Fridays, five Saturdays and five Sundays. This only happens every 800 or so years.He made the mistake of invoking the Calendar Geeks, so here I am, ready to assist!<MHO> Calendar geeks, rejoice!
First, I note that any weird calendar event that occurs, will recur in no more than 400 years, because the Gregorian calendar repeats in a 400-year cycle and 400 Gregorian years is also an exact multiple of 7 days. (It is 400·365 days + (100 - 4 + 1) leap days = 146,097 days, which is exactly 20,871 weeks.) So it is impossible that the event could be as rare as once every 800 or so years. If it happens in 2011, then it happened in 1611 (in Catholic countries) and it will happen in 2411 also.
Now in the particular case cited by MHO, it's clear that since the length of July doesn't vary, the number of Fridays, Saturdays or Sundays depends only on the day of the week on which July 1 falls. You get five Fridays, Saturdays, and Sundays whenever July 1 falls on a Friday. Common sense suggests that this should happen about 1/7 of the time, and so around every 7 years, not every 800, or even every 400 years. And in fact it last occurred in 2005, and will occur next in 2016.
[ Addendum 20110527: It turns out this is actually a Thing; there is even a Snopes page about it. People will tweet almost anything, it seems. ]
[ Addendum 20110701: Matt Parker posted an extensive article about why he found this particular non-fact so dismaying. ]
[Other articles in category /calendar] permanent link
Wed, 25 May 2011
Why use a digital stadiometer?

The article periodically shows up on places like Reddit and Hacker News, and someone often asks why the stadiometer is so complex. Most recently, for example:
How is this an advance on looking at a conventionally numbered ruler (with a similar bracket to touch the top of the head) and writing down the number? It's technological and presumably expensive, but it isn't delivering any discernible benefit that I can see.Not long after I wrote the original article, I was back at the office, so I asked one of the senior doctors about it. She said that the manual stadiometers were always giving inaccurate readings and that they constantly had to have the service guys in to recalibrate them. The electronic stadiometer, she said, is much more reliable.
"But it's a really expensive stadiometer," I said.
"The service calls on the manual stadiometers were costing us a fortune."
This stadiometer transmits its reading via radio to a portable digital display. For this doctors' office, the portable display is a red herring. They had the display mounted on the wall right next to the stadiometer. I asked if they ever took it down and moved it around; the doctor said they never did.
At the time I observed that the answer was mundane and reasonable, but not something that one would be able to deduce. In the several discussions of the topic, none of the people speculating have guessed the correct answer.
When I was working on Red Flags talks, people would send me code, and I would then fix it up to be better code. Often you see code written in what seems to be the worst possible way, and the obvious conclusion is that the author is a complete idiot, or maybe just mentally ill. Perhaps this is sometimes the case, but when I took the time to write back and ask why the author had done it the way they did, there was usually a reasonable answer.
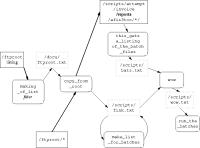
Here's an example that stands out in my memory. A novice once sent me a program he had written that did some sort of tedious file-munging job in Perl, selecting files and copying some of them around in the filesystem. It was a bad program in many ways, but what was most striking about it was that there were many functions to perform operations on lists of filenames, and whenever one of these functions called another, it passed the list of data by writing it to a temporary file, which the called function would then read back.The diagram at right shows the structure of the program. Rectangles with rounded corners indicate subroutines; dotted rectangles are the temporary files they use for argument passing.
I suggested to the author that it would have been easier to have passed the data using the regular argument passing techniques, and his reply astounded me, because it was so reasonable: he said he had used the temporary files as a debugging measure, because that way he could inspect the files and see if the contents were correct.
I was thunderstruck. I had been assuming that the programmer was either a complete beginner, who didn't even know how to pass arguments to a function, or else a complete blockhead. But I was utterly wrong. He was just someone who needed to be introduced to the debugger. Or perhaps the right suggestion for him would be to call something like this from inside the functions that needed debugging:
sub dump_arguments {
my ($file) = (caller)[4];
open my($f), ">", $file or die "$file: $!";
print $f join("\n", @_, "");
}
But either way, this was clearly a person who was an order of
magnitude less incompetent than I initially imagined from seeing the
ridiculous code he had written. He had had a specific problem and had
chosen a straightforward and reasonably effective way to address it.
But until I got the correct explanation, the only explanation I could
think of was unlimited incompetence.This is only one of many such examples. Time and time again people would send me perfectly idiotic code, and when I asked why they had done it that way the answer was not that they were idiots, but that there was some issue I had not appreciated, some problem they were trying to solve that was not apparent. Not to say that the solutions were not inept, or badly engineered, or just plain wrong. But there is a difference between a solution that is inept and one that is utterly insane. These appeared at first to be insane, but on investigation turned out to be sane but clumsy.
I said a while back that it is a good idea to get in the habit of assuming that everything is more complex than you imagine. I think there is parallel advice here: assume that bad technical decisions are made rationally, for reasons that are not apparent.
### Addendum 20240327 A fascinating example of a bad technical outcome that I couldn't imagine could have been caused by anything other than massive incompetence — until a very plausible explanation was suggested: [Software horror show: SAP Concur](BLOGREF/prog/crap-warning-signs-2.html).
[Other articles in category /tech] permanent link
Wed, 04 May 2011
Adventures in systems administration
The toilet snake costs ten dollars. It is a three-foot long steel spring with a pointy corkscrew on the end. You work it down the toilet pipe while twisting it. It either breaks up the blockage, pokes the blockage far enough down the pipe that it can be flushed away, or else the corkscrew tangles in the blockage and you can pull it out. Professional plumbers use a much larger, motorized version to unclog sewer pipes.
People on the train stare at you if you are carrying around a toilet snake, I learned.
When I got home from work I snaked the toilet, and lo and behold, it disgorged a plastic comb. Mission accomplished, most likely.
Later on, Toph, who is three now and fascinated with all things poop, asked me for the umpteenth time why the toilet was clogged. This time I had an answer. "It clogged because someone flushed a comb down it. Do you have any idea who might have done that?"
Toph considered. "I don't know..." she said, thoughtfully. Then her face brightened. "Maybe Katara did it!"
[Other articles in category /misc] permanent link