Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 31 Dec 2007
Harriet Tubman
Katara and I had a pretty heavy conversation in the car on the way home
from school last week. I should begin by saying that Philadelphia has a lot of murals.
More murals than any other city in the world, in fact. The mural arts
people like to put up murals on large, otherwise ugly party walls.
That is, when you have two buildings that share a wall, and one of
them is torn down, leaving a vacant lot with a giant blank wall, the
mural arts people see it as a prime location and put a mural there.
On the way back from Katara's school we drive through Mantua, which is
not one of the rosier Philadelphia neighborhoods, and has a lot of
vacant lots, and so a lot of murals. We sometimes count the murals on
the way home, and usually pass four or five.
Katara pointed out a mural she liked, and I observed that there was construction on the adjacent vacant lot, which is likely to mean that the mural will be covered up soon by the new building. I mentioned that my favorite Philadelphia mural of all had been on the side of a building that was torn down in 2002.
Katara asked me to tell her about it, so I did. It was the giant mural of Harriet Tubman that used to be on the side of the I. Goldberg building at 9th and Chestnut Streets. It was awesome. There was 40-foot-high painting of Harriet Tubman raising her lantern at night, leading a crowd of people through a dark tunnel (Underground Railroad, obviously) into a beautiful green land beyond, and giant chains that had once barred the tunnel, but which were now shattered.
It's hard to photograph a mural well. The scale and the space do not translate to photographs. It looked something like this:

Here's a detail:

Anyway, I said that my favorite mural had been the Harriet Tubman one, and that it had been torn down before she was born. (As you can see from the picture, the building was located next to a parking lot. The owners of the building ripped it down to expand the parking lot.)
But then Katara asked me to tell her about Harriet Tubman, and that was something of a puzzle, because Katara is only three and a half. But the subject is not intrinsically hard to understand; it's just unpleasant. And I don't believe that it's my job to shield her from the unpleasantness of the world, but it is my job to try to answer her questions, if I can. So I tried.
"Okay, you know how you own stuff, and you can do what you want, because it's yours?"
Sure, she understands that. We have always been very clear in distinguishing between her stuff and our stuff, and in defending her property rights against everyone, including ourselves.
"But you know that you can't own other people, right?"
This was confusing, so I tried an example. "Emily is your friend, and sometimes you ask her to do things, and maybe she does them. But you can't make her do things she doesn't want to do, because she gets to decide for herself what she does."
Sure, of course. Now we're back on track. "Well, a long time ago, some people decided that they owned some other people, called slaves, and that the slaves would have to do whatever their owners said, even if they didn't want to."
Katara was very indignant. I believe she said "That's not nice!" I agreed; I said it was terrible, one of the most terrible things that had ever happened in this country. And then we were over the hump. I said that slaves sometimes tried to run away from the owners, and get away to a place where they could do whatever they wanted, and that Harriet Tubman helped slaves escape.
There you have Harriet Tubman in a nutshell for a three-and-a-half year-old. It was a lot easier than the time she asked me why ships in 1580 had no women aboard.
I did not touch the racial issue at all. When you are explaining something complicated, it is important to keep it in bite-sized chunks, and to deal with them one at a time, and I thought slavery was already a big enough chunk. Katara is going to meet this issue head-on anyway, probably sooner than I would like, because she is biracial.
I explained about the Underground Railroad, and we discussed what a terrible thing slavery must have been. Katara wanted to know what the owners made the slaves do, and there my nerve failed me. I told her that I didn't want to tell her about it because it was so awful and frightening. I had pictures in my head of beatings, and of slaves with their teeth knocked out so that they could be forced to eat, to break hunger strikes, and of rape, and families broken up, and I just couldn't go there. Well, I suppose it is my job to shield her from some the unpleasantness of the world, for a while.
I realize now I could have talked about slaves forced to do farm work, fed bad food, and so on, but I don't think that would really have gotten the point across. And I do think I got the point across: the terrible thing about being a slave is that you have to do what you are told, whether you want to or not. All preschoolers understand that very clearly, whereas for Katara, toil and neglect are rather vague abstractions. So I'm glad I left it where I did.
But then a little later Katara asked some questions about family relations among the slaves, and if slaves had families, and I said yes, that if a mother had a child, then her child belonged to the same owner, and sometimes the owner would take the child away from its mother and sell it to someone else and they would never see each other again. Katara, of course, was appalled by this.
I'm not sure I had a point here, except that Katara is a thoughtful kid, who can be trusted with grown-up issues even at three and a half years old, and I am very proud of her.
That seems like a good place to end the year. Thanks for reading.
[ Addendum 20080201: The mural was repainted in a new location, at 2950 Germantown Avenue! ]
[ Addendum 20160420: The Germantown Avenue mural is by the same artist, Sam Donovan, but is not the same design. The model was Kat Lindsey. Donovan’s web site provides a better picture. ]
[Other articles in category /kids] permanent link
Sun, 30 Dec 2007
Welcome to my ~/bin
In the previous article I
mentioned "a conference tutorial about the contents of my
~/bin directory". Usually I have a web page about each
tutorial, with a description, and some sample slides, and I wanted to
link to the page about this tutorial. But I found to my surprise that
I had forgotten to make the page about this one.
So I went to fix that, and then I couldn't decide which sample slides to show. And I haven't given the tutorial for a couple of years, and I have an upcoming project that will prevent me from giving it for another couple of years. Eh, figuring out what to put online is more trouble than it's worth. I decided it would be a lot less toil to just put the whole thing online.
The materials are copyright © 2004 Mark Jason Dominus, and are not under any sort of free license.
But please enjoy them anyway.
I think the title is an accidental ripoff of an earlier class by Damian Conway. I totally forgot that he had done a class on the same subject, and I think he used the same title. But that just makes us even, because for the past few years he has been making money going around giving talks on "Conference Presentation Aikido", which is a blatant (and deliberate) ripoff of my 2002 Perl conference talk on Conference Presentation Judo. So I don't feel as bad as I might have.
Welcome to my ~/bin complete slides and other materials.
I hereby wish you a happy new year, unless you don't want one, in which case I wish you a crappy new year instead.
[Other articles in category /prog/perl] permanent link
Thu, 20 Dec 2007
Another trivial utility: accumulate
As usual, whenever I write one of these things, I wonder why it took
me so long to get off my butt and put in the five minutes of work that
were actually required. I've wanted something like this for
years. It's called accumulate. It reads an input of
this form:
k1 v1
k1 v2
k2 v3
k1 v4
k2 v5
k3 v6
and writes it out in this format:
k1 v1 v2 v4
k2 v3 v5
k3 v6
I wanted it this time because I had a bunch of files that included some
duplicates, and wanted to get rid of the duplicates. So:
md5sum * | accumulate | perl -lane 'unlink @F[2..$#F]'
(Incidentally, people sometimes argue that Perl's .. operator
should count backwards when the left operand exceeds the right one.
These people are wrong. There is only one argument that needs to be
made to refute this idea; maybe it is the only argument that
can be made. And examples of it abound. The code above is one
such example.)I'm afraid of insulting you by showing the source code for accumulate, because of course it is so very trivial, and you could write it in five minutes, as I did. But who knows; maybe seeing the source has some value:
#!/usr/bin/perl
use Getopt::Std;
my %opt = (k => 1, v => 2);
getopts('k:v:', \%opt) or usage();
for (qw(k v)) {
$opt{$_} -= 1 if $opt{$_} > 0;
}
while (<>) {
chomp;
my @F = split;
push @{$K{$F[$opt{k}]}}, $F[$opt{v}];
}
for my $k (keys %K) {
print "$k @{$K{$k}}\n";
}
It's tempting to add a -F option to tell it that the input is
not delimited by white space, or an option to change the output
format, or blah blah blah, but I managed to restrain myself, mostly.Several years ago I wrote a conference tutorial about the contents of my ~/bin directory. The clearest conclusion that transpired from my analysis was that the utilities I write have too many features that I don't use. The second-clearest was that I waste too much time writing custom argument-parsing code instead of using Getopt::Std. I've tried to learn from this. One thing I found later is that a good way to sublimate the urge to put in some feature is to put in the option to enable it, and to document it, but to leave the feature itself unimplemented. This might work for you too if you have the same problem.
I did put in -k and -v options to control which input columns are accumulated. These default to the first and second columns, naturally. Maybe this was a waste of time, since it occurs to me now that accumulate -k k -v v could be replaced by cut -fk,v | accumulate, if only cut didn't suck quite so badly. Of course one could use awk {print "$k $v" } | accumulate to escape cut's suckage. And some solution of this type obviates the need for accumulate's putative -F option also. Well, I digress.
The accumulate program itself reminds me of a much more ambitious project I worked on for a while between 1998 and 2001, as does the yucky line:
push @{$K{$F[$opt{k}]}}, $F[$opt{v}];
The ambitious project was tentatively named "twingler".Beginning Perl programmers often have trouble with compound data structures because Perl's syntax for the nested structures is so horrendous. Suppose, for example, that you have a reference to a two-dimensional array $aref, and you want to produce a hash, such that each value in the array appears as a key in the hash, associated with a list of strings in the form "m,n" indicating where in the array that value appeared. Well, of course it is obviously nothing more than:
for my $a1 (0 .. $#$aref) {
for my $a2 (0 .. $#{$aref->[$a1]}) {
push @{$hash{$aref->[$a1][$a2]}}, "$a1,$a2";
}
}
Obviously. <sarcasm>Geez, a child could see
that.</sarcasm>The idea of twingler was that you would specify the transformation you wanted declaratively, and it would then write the appropriate Perl code to perform the transformation. The interesting part of this project is figuring out the language for specifying the transformation. It must be complex enough to be able to express most of the interesting transformations that people commonly want, but if it isn't at the same time much simpler than Perl itself, it isn't worth using. Nobody will see any point in learning a new declarative language for expressing Perl data transformations unless it is itself simpler to use than just writing the Perl would have been.
[ Addendum 20150508: I dumped all my Twingler notes on the blog last year. ]
There are some hard problems here: What do people need? What subset of this can be expressed simply? How can we design a simple, limited language that people can use to express their needs? Can the language actually be compiled to Perl?
I had to face similar sorts of problems when I was writing linogram, but in the case of linogram I was more successful. I tinkered with twingler for some time and made several pages of (typed) notes but never came up with anything I was really happy with.
[ Addendum 20150508: I dumped all my Twingler notes on the blog last year. ]
At one point I abandoned the idea of a declarative language, in favor of just having the program take a sample input and a corresponding sample output, and deduce the appropriate transformation from there. For example, you would put in:
[ [ A, B ],
[ C, B ],
[ D, E ] ]
and
{ B => [A, C],
E => [D],
}
and it would generate:
for my $a1 (@$input) {
my ($e1, $e2) = @$a1;
push @{$output{$e2}}, $e1;
}
And then presumably you could eyeball this, and if what you really
wanted was @{$a1}[0, -1] instead of @$a1 you could
tinker it into the form you needed without too much extra trouble.
This is much nicer from a user-experience point of view, but at the
same time it seems more difficult to implement. I had some ideas. One idea was to have it generate a bunch of expressions for mapping single elements from the input to the output, and then to try to unify those expressions. But as I said, I never did figure it out.
It's a shame, because it would have been pretty cool if I had gotten it to work.
The MIT CS grad students' handbook used to say something about how you always need to have several projects going on at once, because two-thirds of all research projects end in failure. The people you see who seem to have one success after another actually have three projects going on all the time, and you only see the successes. This is a nice example of that.
[Other articles in category /prog] permanent link
Tue, 18 Dec 2007
Happy birthday Perl!
In case you hadn't yet heard, today is the 20th anniversary of the
first release of Perl.
[Other articles in category /anniversary] permanent link
Mon, 17 Dec 2007
Strangest Asian knockoff yet
A few years ago Lorrie and I had brunch at the very trendy
Philadelphia restaurant "Striped Bass". I guess it wasn't too
impressive, because usually if the food is really good I will remember
what I ate, even years later, and I do not. But the plates
were awesome. They were round, with an octagonal depression in the
center, a rainbow-colored pattern around the edge, garnished with
pictures of ivy leaves.
Good plates have the name of the maker on the back. These were made by Villeroy & Boch. Some time later, we visited the Villeroy & Boch outlet in Woodbury, New York, and I found the pattern I wanted, "Pasadena". The cool circular plates from Striped Bass were only for sale to restaurants, but the standard ones were octagonal, which is also pretty cool. So I bought a set. (57% off list price! Whee!)
(The picture gets much bigger when you click it.)
They no longer make these plates. If you broke one, and wanted a replacement, you could buy one online for $43.99. Ouch! But there is another option, if you are not too fussy.
Many years after I bought my dishes, I was shopping in one of the big Asian grocery stores on Washington Avenue. They have a kitchenware aisle. I found this plate:
The real VB plate is made of porcelain. The Washington Avenue knockoff is made of plastic.
Of course I bought it. It is hilarious! And it only cost two dollars.
[ Addendum 20170131: A challenger appears! ]
[Other articles in category /food] permanent link
Tue, 11 Dec 2007
More notes on power series
It seems I wasn't done thinking about this. I pointed out in yesterday's article that,
having defined the cosine function as:
coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])
one has the choice to define the sine function analogously:
sins = zipWith (*) (cycle [0,1,0,-1]) (map ((1/) . fact) [0..])
or in a totally different way, by reference to cosine:
sins = (srt . (add one) . neg . sqr) coss
Here is a third way. Sine and cosine are solutions of the
differential equation f = -f''. Since I now have enough
infrastructure to get Haskell to solve differential equations, I can
use this to define sine and cosine:
solution_of_equation f0 f1 = func
where func = int f0 (int f1 (neg func))
sins = solution_of_equation 0 1
coss = solution_of_equation 1 0
The constants f0 and f1 specify the initial
conditions of the differential equation, values for f(0) and
f'(0), respectively.Well, that was fun.
One problem with the power series approach is that the answer you get is not usually in a recognizable form. If what you get out is
[1.0,0.0,-0.5,0.0,0.0416666666666667,0.0,-0.00138888888888889,0.0,2.48015873015873e-05,0.0,...]
then you might recognize it as the cosine function. But last night I
couldn't sleep because I was wondering about the equation
f·f' = 1, so I got up and put it in, and out
came:
[1.0,1.0,-0.5,0.5,-0.625,0.875,-1.3125,2.0625,-3.3515625,5.5859375,-9.49609375,16.40234375,...]
Okay, now what? Is this something familiar? I'm wasn't sure. One
thing that might help a bit is to get the program to disgorge rational
numbers rather than floating-point numbers. But even that won't
completely solve the problem. One thing I was thinking about in the shower is doing Fourier analysis; this should at least identify the functions that are sinusoidal. Suppose that we know (or believe, or hope) that some power series a1x + a3x3 + ... actually has the form c1 sin x + c2 sin 2x + c3 sin 3x + ... . Then we can guess the values of the ci by solving a system of n equations of the form:
$$\sum_{i=1}^n i^kc_i = k!a_k\qquad{\hbox{($k$ from 1 to $n$)}}$$
And one ought to be able to do something analogous, and more general, by including the cosine terms as well. I haven't tried it, but it seems like it might work.But what about more general cases? I have no idea. If you have the happy inspiration to square the mystery power series above, you get [1, 2, 0, 0, 0, ...], so it is √(2x+1), but what if you're not so lucky? I wasn't; I solved it by a variation of Gareth McCaughan's method of a few days ago: f·f' is the derivative of f2/2, so integrate both sides of f·f' = 1, getting f2/2 = x + C, and so f = √(2x + C). Only after I had solved the equation this way did I try squaring the power series, and see that it was simple.
I'll keep thinking.
[Other articles in category /math] permanent link
Mon, 10 Dec 2007
Lazy square roots of power series return
In an earlier article I
talked about wanting to use lazy streams to calculate the power series
expansion of the solution of this differential equation:
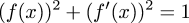
At least one person wrote to ask me for the Haskell code for the power series calculations, so here's that first off.
A power series a0 + a1x + a2x2 + a3x3 + ... is represented as a (probably infinite) list of numbers [a0, a1, a2, ...]. If the list is finite, the missing terms are assumed to be all 0.
The following operators perform arithmetic on functions:
-- add functions a and b
add [] b = b
add a [] = a
add (a:a') (b:b') = (a+b) : add a' b'
-- multiply functions a and b
mul [] _ = []
mul _ [] = []
mul (a:a') (b:b') = (a*b) : add (add (scale a b')
(scale b a'))
(0 : mul a' b')
-- termwise multiplication of two series
mul2 = zipWith (*)
-- multiply constant a by function b
scale a b = mul2 (cycle [a]) b
neg a = scale (-1) a
And there are a bunch of other useful utilities:
-- 0, 1, 2, 3, ... iota = 0 : zipWith (+) (cycle [1]) iota -- 1, 1/2, 1/3, 1/4, ... iotaR = map (1/) (tail iota) -- derivative of function a deriv a = tail (mul2 iota a) -- integral of function a -- c is the constant of integration int c a = c : (mul2 iotaR a) -- square of function f sqr f = mul f f -- constant function con c = c : cycle [0] one = con 1
| Buy Structure and Interpretation of Computer Programs from Bookshop.org (with kickback) (without kickback) |
-- reciprocal of argument function inv (s0:st) = r where r = r0 : scale (negate r0) (mul r st) r0 = 1/s0 -- divide function a by function b squot a b = mul a (inv b) -- square root of argument function srt (s0:s) = r where r = r0 : (squot s (add [r0] r)) r0 = sqrt(s0)We can define the cosine function as follows:
coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])We could define the sine function analogously, or we can say that sin(x) = √(1 - cos2(x)):
sins = (srt . (add one) . neg . sqr) cossThis works fine.
Okay, so as usual that is not what I wanted to talk about; I wanted to show how to solve the differential equation. I found I was getting myself confused, so I decided to try to solve a simpler differential equation first. (Pólya says: "Can you solve a simpler problem of the same type?" Pólya is a smart guy. When the voice talking in your head is Pólya's, you better pay attention.) The simplest relevant differential equation seemed to be f = f'. The first thing I tried was observing that for all f, f = f0 : mul2 iotaR f'. This yields the code:
f = f0 : mul2 iotaR (deriv f)
This holds for any function, and so it's unsolvable. But if you
combine it with the differential equation, which says that f =
f', you get:
f = f0 : mul2 iotaR f
where f0 = 1 -- or whatever the initial conditions dictate
and in fact this works just fine. And then you can observe that this
is just the definition of int; replacing the definition with
the name, we have:
f = int f0 f
where f0 = 1 -- or whatever
This runs too, and calculates the power series for the
exponential function, as it should. It's also transparently obvious,
and makes me wonder why it took me so long to find. But I was looking
for solutions of the form:
f = deriv f
which Haskell can't figure out. It's funny that it only handles
differential equations when they're expressed as integral equations. I
need to meditate on that some more.It occurs to me just now that the f = f0 : mul2 iotaR (deriv f) identity above just says that the integral and derivative operators are inverses. These things are always so simple in hindsight.
Anyway, moving along, back to the original problem, instead of f = f', I want f2 + (f')2 = 1, or equivalently f' = √(1 - f2). So I take the derivative-integral identity as before:
f = int f0 (deriv f)
and put in √(1 - f2) for deriv f:
f = int f0 ((srt . (add one) . neg . sqr) f)
where f0 = sqrt 0.5 -- or whatever
And now I am done; Haskell cheerfully generates the power series
expansion for f for any given initial condition. (The
parameter f0 is precisely the desired value of f(0).)
For example, when f(0) = √(1/2), as above, the calculated
terms show the function to be exactly
√(1/2)·(sin(x) + cos(x)); when f(0)
= 0, the output terms are exactly those of sin(x). When
f(0) = 1, the output blows up and comes out as [1, 0, NaN, NaN,
...]. I'm not quite sure why yet, but I suspect it has something to
do with there being two different solutions that both have f(0) = 1. All of this also works just fine in Perl, if you build a suitable lazy-list library; see chapter 6 of HOP for complete details. Sample code is here. For a Scheme implementation, see SICP. For a Java, Common Lisp, Python, Ruby, or SML implementation, do the obvious thing.
But anyway, it does work, and I thought it might be nice to blog about something I actually pursued to completion for a change. Also I was afraid that after my week of posts about Perl syntax, differential equations, electromagnetism, Unix kernel internals, and paint chips in the shape of Austria, the readers of Planet Haskell, where my blog has recently been syndicated, were going to storm my house with torches and pitchforks. This article should mollify them for a time, I hope.
[ Addendum 20071211: Some additional notes about this. ]
[Other articles in category /math] permanent link
Sun, 09 Dec 2007
Four ways to solve a nonlinear differential equation
In a recent article I
mentioned the differential equation:
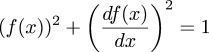
I got interested in this a few weeks ago when I was sitting in on a freshman physics lecture at Penn. I took pretty much the same class when I was a freshman, but I've never felt like I really understood physics. Sitting in freshman physics class again confirms this. Every time I go to a class, I come out with bigger questions than I went in.
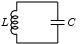 The instructor was
talking about LC circuits, which are simple circuits with a capacitor
(that's the "C") and an inductor (that's the "L", although I don't
know why). The physics people claim that in such a circuit the
capacitor charges up, and then discharges again, repeatedly. When one
plate of the capacitor is full of electrons, the electrons want to
come out, and equalize the charge on the plates, and so they make a
current flowing from the negative to the positive plate. Without the inductor, the current
would fall off exponentially, as the charge on the plates equalized.
Eventually the two plates would be equally charged and nothing more
would happen.
The instructor was
talking about LC circuits, which are simple circuits with a capacitor
(that's the "C") and an inductor (that's the "L", although I don't
know why). The physics people claim that in such a circuit the
capacitor charges up, and then discharges again, repeatedly. When one
plate of the capacitor is full of electrons, the electrons want to
come out, and equalize the charge on the plates, and so they make a
current flowing from the negative to the positive plate. Without the inductor, the current
would fall off exponentially, as the charge on the plates equalized.
Eventually the two plates would be equally charged and nothing more
would happen.
But the inductor generates an electromotive force that tends to resist any change in the current through it, so the decreasing current in the inductor creates a force that tends to keep the electrons moving anyway, and this means that the (formerly) positive plate of the capacitor gets extra electrons stuffed into it. As the charge on this plate becomes increasingly negative, it tends to oppose the incoming current even more, and the current does eventually come to a halt. But by that time a whole lot of electrons have moved from the negative to the positive plate, so that the positive plate has become negative and the negative plate positive. Then the electrons come out of the newly-negative plate and the whole thing starts over again in reverse.
In practice, of course, all the components offer some resistance to the current, so some of the energy is dissipated as heat, and eventually the electrons stop moving back and forth.
Anyway, the current is nothing more nor less than the motion of the electrons, and so it is proportional to the derivative of the charge in the capacitor. Because to say that current is flowing is exactly the same as saying that the charge in the capacitor is changing. And the magnetic flux in the inductor is proportional to rate of change of the current flowing through it, by Maxwell's laws or something.
The amount of energy in the whole system is the sum of the energy stored in the capacitor and the energy stored in the magnetic field of the inductor. The former turns out to be proportional to the square of the charge in the capacitor, and the latter to the square of the current. The law of conservation of energy says that this sum must be constant. Letting f(t) be the charge at time t, then df/dt is the current, and (adopting suitable units) one has:
$$(f(x))^2 + \left(df(x)\over dx\right)^2 = 1$$
which is the equation I was considering.Anyway, the reason for this article is mainly that I wanted to talk about the different methods of solution, which were all quite different from each other. Michael Lugo went ahead with the power series approach I was using. Say that:
$$ \halign{\hfil $\displaystyle #$&$\displaystyle= #$\hfil\cr f & \sum_{i=0}^\infty a_{i}x^{i} \cr f' & \sum_{i=0}^\infty (i+1)a_{i+1}x^{i} \cr } $$
Then:
$$ \halign{\hfil $\displaystyle #$&$\displaystyle= #$\hfil\cr f^2 & \sum_{i=0}^\infty \sum_{j=0}^{i} a_{i-j} a_j x^{i} \cr (f')^2 & \sum_{i=0}^\infty \sum_{j=0}^{i} (i-j+1)a_{i-j+1}(j+1)a_{j+1} x^{i} \cr } $$
And we want the sum of these two to be equal to 1.Equating coefficients on both sides of the equation gives us the following equations:
| !!a_0^2 + a_1^2!! | = | 1 |
| !!2a_0a_1 + 4a_1a_2!! | = | 0 |
| !!2a_0a_2 + a_1^2 + 6a_1a_3 + 4a_2^2!! | = | 0 |
| !!2a_0a_3 + 2a_1a_2 + 8a_1a_4 + 12a_2a_3!! | = | 0 |
| !!2a_0a_4 + 2a_1a_3 + a_2^2 + 10a_1a_5 + 16a_2a_4 + 9a_3^2!! | = | 0 |
| ... | ||
Now take the next line from the table, 2a0a2 + a12 + 6a1a3 + 4a22. This can be separated into the form 2a2(a0 + 2a2) + a1(a1 + 6a3). The left-hand term is zero, by the previous paragraph, and since the whole thing equals zero, we have a3 = -a1/6.
Continuing in this way, we can conclude that a0 = -2!a2 = 4!a4 = -6!a6 = ..., and that a1 = -3!a3 = 5!a5 = ... . These should look familiar from first-year calculus, and together they imply that f(x) = a0 cos(x) + a1 sin(x), where (according to the first line of the table) a02 + a12 = 1. And that is the complete solution of the equation, except for the case we omitted, when either a0 or a1 is zero; these give the trivial solutions f(x) = ±1.
Okay, that was a lot of algebra grinding, and if you're not as clever as M. Lugo, you might not notice that the even terms of the series depend only on a0 and the odd terms only on a1; I didn't. I thought they were all mixed together, which is why I alluded to "a bunch of not-so-obvious solutions" in the earlier article. Is there a simpler way to get the answer?
Gareth McCaughan wrote to me to point out a really clever trick that solves the equation right off. Take the derivative of both sides of the equation; you immediately get 2ff' + 2f'f'' = 0, or, factoring out f', f'(f + f'') = 0. So there are two solutions: either f'=0 and f is a constant function, or f + f'' = 0, which even the electrical engineers know how to solve.
David Speyer showed a third solution that seems midway between the two in the amount of clever trickery required. He rewrote the equation as:
$${df\over dx} = \sqrt{1 - f^2}$$
$${df\over\sqrt{1 - f^2} } = dx$$
The left side is an old standby of calculus I classes; it's the derivative of the arcsine function. On integrating both sides, we have:$$\arcsin f = x + C$$
so f = sin(x + C). This is equivalent to the a0 cos(x) + a1 sin(x) form that we got before, by an application of the sum-of-angles formula for the sine function. I think M. McCaughan's solution is slicker, but M. Speyer's is the only one that I feel like I should have noticed myself.Finally, Walt Mankowski wrote to tell me that he had put the question to Maple, which disgorged the following solution after a few seconds:
f(x) = 1, f(x) = -1, f(x) = sin(x - _C1), f(x) = -sin(x - _C1).This is correct, except that the appearance of both sin(x + C) and -sin(x + C) is a bit odd, since -sin(x + C) = sin(x + (C + π)). It seems that Maple wasn't clever enough to notice that. Walt says he will ask around and see if he can find someone who knows what Maple did to get the solution here.
I would like to add a pithy and insightful conclusion to this article, but I've been working on it for more than a week now, and also it's almost lunch time, so I think I'll have to settle for observing that sometimes there are a lot of ways to solve math problems.
Thanks again to everyone who wrote in about this.
[Other articles in category /math] permanent link
Sat, 08 Dec 2007
Corrections about sync(2)
I made some errors in today's post
about sync and fsync.
Most important, I said that "the sync() system call marks all the kernel buffers as dirty". This is totally wrong, and doesn't even make sense. Dirty buffers are those with data that needs to be written out. Marking a non-dirty buffer as dirty is a waste of time, since nothing has changed in the buffer, but it will now be rewritten anyway. What sync() does is schedule all the dirty buffers to be written as soon as possible.
On some recent systems, sync() actually waits for all the dirty buffers to be written, and a bunch of people tried to correct me about this. But my original article was right: historically, it was not so, and even today it's not universally true. In former times, sync() would schedule the buffers for writing, and then return before the data was actually written.
I said that one of the duties of init was to call sync() every thirty seconds, but this was mistaken. That duty actually fell to a separate program, known as update. While discussing this with one of the readers who wrote to correct me, I looked up the source for Version 7 Unix, to make sure I was right, and it's so short I thought I might as well show it here:
/*
* Update the file system every 30 seconds.
* For cache benefit, open certain system directories.
*/
#include <signal.h>
char *fillst[] = {
"/bin",
"/usr",
"/usr/bin",
0,
};
main()
{
char **f;
if(fork())
exit(0);
close(0);
close(1);
close(2);
for(f = fillst; *f; f++)
open(*f, 0);
dosync();
for(;;)
pause();
}
dosync()
{
sync();
signal(SIGALRM, dosync);
alarm(30);
}
The program is so simple I don't have much more to say about it. It
initially invokes dosync(), which calls sync() and
then schedules another call to dosync() in 30 seconds. Note
that the 0 in the second argument to open had not
yet been changed to O_RDONLY. The pause() call is
equivalent to sleep(0): it causes the process to relinquish
its time slice whenever it is active.In various systems more recent than V7, the program was known by various names, but it was update for a very long time.
Several people wrote to correct me about the:
# sync
# sync
# sync
# halt
thing, some saying that I had the reason wrong, or that it did not make
sense, or that only two syncs were used, rather than three.
But I had it right. People did use three, and they did it for the
reason I said, whether that makes sense or not. (Some of the people
who miscorrected me were unaware that sync() would finish and
exit before the data was actually written.) But for example, see this
old Usenet thread for a discussion of the topic that confirms what
I said.Nobody disputed my contention that Linus was suffering from the promptings of the Evil One when he tried to change the semantics of fsync(), and nobody seems to know the proper name of the false god of false efficiency. I'll give this some thought and see what I can come up with.
Thanks to Tony Finch, Dmitry Kim, and Stefan O'Rear for discussion of these points.
[Other articles in category /Unix] permanent link
Dirty, dirty buffers!
One side issue that arose during my talk on Monday about
inodes was the write-buffering normally done by Unix kernels. I
wrote a pretty long note to the PLUG mailing list about it, and
I thought I'd repost it here.
When your process asks the kernel to write data:
int bytes_written = write(file_descriptor,
buffer,
n_bytes);
the kernel normally copies the data from your buffer into a kernel
buffer, and then, instead of writing out the data to disk, it marks
its buffer as "dirty" (that is, as needing to be written eventually),
and reports success back to the process immediately, even though the
dirty buffer has not yet been written, and the data is not yet on the disk.Normally, the kernel writes out the dirty buffer in due time, and the data makes it to the disk, and you are happy because your process got to go ahead and do some more work without having to wait for the disk, which could take milliseconds. ("A long time", as I so quaintly called it in the talk.) If some other process reads the data before it is written, that is okay, because the kernel can give it the updated data out of the buffer.
But if there is a catastrophe, say a power failure, then you see the bad side of this asynchronous writing technique, because the data, which your process thought had been written, and which the kernel reported as having been written, has actually been lost.
There are a number of mechanisms in place to deal with this. The oldest is the sync() system call, which marks all the kernel buffers as dirty. All Unix systems run a program called init, and one of init's principal duties is to call sync() every thirty seconds or so, to make sure that the kernel buffers get flushed to disk at least every thirty seconds, and so that no crash will lose more than about thirty seconds' worth of data.
(There is also a command-line program sync which just does a sync() call and then exits, and old-time Unix sysadmins are in the habit of halting the system with:
# sync
# sync
# sync
# halt
because the second and third syncs give the kernel time to actually
write out the
buffers that were marked dirty by the first sync. Although I
suspect that few of them know why they do this. I swear I am not
making this up.)But for really crucial data, sync() is not enough, because, although it marks the kernel buffers as dirty, it still does not actually write the data to the disk.
So there is also an fsync() call; I forget when this was introduced. The process gives fsync() a file descriptor, and the call demands that the kernel actually write the associated dirty buffers to disk, and does not return until they have been. And since, unlike write(), it actually waits for the data to go to the disk, a successful return from fsync() indicates that the data is truly safe.
The mail delivery agent will use this when it is writing your email to your mailbox, to make sure that no mail is lost.
Some systems have an O_SYNC flag than the process can supply when it opens the file for writing:
int fd = open("blookus", O_WRONLY | O_SYNC);
This sets the O_SYNC flag in the kernel file pointer
structure, which means that whenever data is
written to this file pointer, the kernel, contrary to its usual
practice, will implicitly fsync() the descriptor.Well, that's not what I wanted to write about here. What I meant to discuss was...
No, wait. That is what I wanted to write about. How about that?
Anyway, there's an interesting question that arises in connection with fsync(): suppose you fsync() a file. That guarantees that the data will be written. But does it also guarantee that the mtime and the file extent of the file will be updated? That is, does it guarantee that the file's inode will be written?
On most systems, yes. But on some versions of Linux's ext2 filesystem, no. Linus himself broke this as a sacrifice to the false god of efficiency, a very bad decision in my opinion, for reasons that should be obvious to everyone but those in the thrall of Mammon. (Mammon's not right here. What is the proper name of the false god of efficiency?)
Sanity eventually prevailed. Recent versions of Linux have an fsync() call, which updates both the data and the inode, and a fdatasync() call, which only guarantees to update the data.
[ Addendum 20071208: Some of this is wrong. I posted corrections. ]
[Other articles in category /Unix] permanent link
Fri, 07 Dec 2007
Freshman electromagnetism questions
As I haven't quite managed to mention here before, I have occasionally
been sitting in on one of Penn's first-year physics classes, about
electricity and magnetism. I took pretty much the same class myself
during my freshman year of college, so all the material is quite
familiar to me.
But, as I keep saying here, I do not understand physics very well, and I don't know much about it. And every time I go to a freshman physics lecture I come out feeling like I understand it less than I went in.
I've started writing down my questions in class, even though I don't really have anyone to ask them to. (I don't want to take up the professor's time, since she presumably has her hands full taking care of the paying customers.) When I ask people I know who claim to understand physics, they usually can't give me plausible answers.
Maybe I should mutter something here under my breath about how mathematicians and mathematics students are expected to have a better grasp on fundamental matters.
The last time this came up for me I was trying to understand the phenomenon of dissolving. Specifically, why does it usually happen that substances usually dissolve faster and more thoroughly in warmer solutions than in cooler solutions? I asked a whole bunch of people about this, up to and including a full professor of physical chemistry, and never got a decent answer.
The most common answer, in fact, was incredibly crappy: "the warm solution has higher entropy". This is a virtus dormitiva if ever there was one. There's a scene in a play by Molière in which a candidate for a medical degree is asked by the examiners why opium puts people to sleep. His answer, which is applauded by the examiners, is that it puts people to sleep because it has a virtus dormitiva. That is, a sleep-producing power. Saying that warm solutions dissolve things better than cold ones because they have more entropy is not much better than saying that it is because they have a virtus dormitiva.
The entropy is not a real thing; it is a reification of the power that warmer substances have to (among other things) dissolve solutes more effectively than cooler ones. Whether you ascribe a higher entropy to the warm solution, or a virtus dissolva to it, comes to the same thing, and explains nothing. I was somewhat disgusted that I kept getting this non-answer. (See my explanation of why we put salt on sidewalks when it snows to see what sort of answer I would have preferred. Probably there is some equally useless answer one could have given to that question in terms of entropy.)
(Perhaps my position will seem less crackpottish if I a make an analogy with the concept of "center of gravity". In mechanics, many physical properties can be most easily understood in terms of the center of gravity of some object. For example, the gravitational effect of small objects far apart from one another can be conveniently approximated by supposing that all the mass of each object is concentrated at its center of gravity. A force on an object can be conveniently treated mathematically as a component acting toward the center of gravity, which tends to change the object's linear velocity, and a component acting perpendicular to that, which tends to change its angular velocity. But nobody ever makes the mistake of supposing that the center of gravity has any objective reality in the physical universe. Everyone understands that it is merely a mathematical fiction. I am considering the possibility that energy should be understood to be a mathematical fiction in the same sort of way. From the little I know about physics and physicists, it seems to me that physicists do not think of energy in this way. But I am really not sure.)
Anyway, none of this philosophizing is what I was hoping to discuss in this article. Today I wrote up some of the questions I jotted down in freshman physics class.
- What are the physical interpretations of μ0 and ε0,
the magnetic permeability and electric permittivity of vacuum?
Can these be directly measured? How?
- Consider a simple circuit with a battery, a switch, and a
capacitor. When the switch is closed, the battery will suck
electrons out of one plate of the capacitor and pump them into the
other plate, so the capacitor will charge up.
When we open the switch, the current will stop flowing, and the capacitor will stop charging up.
But why? Suppose the switch is between the capacitor and the positive terminal of the battery. Then the negative terminal is still connected to the capacitor even when the switch is open. Why doesn't the negative terminal of the battery continue to pump electrons into the capacitor, continuing to charge it up, although perhaps less than it would be if the switch were closed?
- Any beam of light has a time-varying electric field, perpendicular
to the direction that the light is travelling. If I shine a light
on an electron, why doesn't the electron vibrate up and down in the
varying electric field? Or does it?
[ Addendum 20080629: I figured out the answer to this one. ]
- Suppose I take a beam of polarized light whose electric field is in
the x direction. I split it in two, delay one of the beams by
exactly half a wavelength, and merge it with the other beam. The
electric fields are exactly out of phase and exactly cancel out.
What happens? Where did the light go? What about conservation of
energy?
- Suppose I have two beams of light whose wavelengths are close but
not exactly the same, say λ and (λ+dλ). I superimpose these. The
electric fields will interfere, and sometimes will be in phase and
sometimes out of phase. There will be regions where the electric
field varies rapidly from the maximum to almost zero, of length on the order of dλ. If I look at the
beam of light only over one of these brief intervals, it should
look just like very high frequency light of wavelength dλ. But
it doesn't. Or does it?
- An electron in a varying magnetic field experiences an
electromotive force. In particular, an electron near a wire that
carries a varying current will move around as the current in the
wire varies.
Now suppose we have one electron A in space near a wire. We will put a very small current into the wire for a moment; this causes electron A to move a little bit.
Let's suppose that the current in the wire is as small as it can be. In fact, let's imagine that the wire is carrying precisely one electron, which we'll call B. We can calculate the amount of current we can attribute to the wire just from B. (Current in amperes is just coulombs per second, and the charge on electron B is some number of coulombs.) Then we can calculate the force on A as a result of this minimal current, and the motion of A that results.
But we could also do the calculation another way ,by forgetting about the wire, and just saying that electron B is travelling through space, and exerts an electrostatic force on A, according to Coulomb's law. We could calculate the motion of A that results from this electrostatic force.
We ought to get the same answer both ways. But do we?
- Suppose we have a beam of light that is travelling along the
x axis, and the electric field is perpendicular to the
x axis, say in the y direction. We learned in
freshman physics how to calculate the vector quantity that
represents the intensity of the electric field at every point on
the x axis; that is, at every point of the form (x,
0, 0). But what is the electric field at (x, 1, 0)? How
does the electric field vary throughout space? Presumably a beam
of light of wavelength λ has a minimum diameter on the order
of λ, but how how does the electric field vary as you move
away from the core? Can you take two such minimum-diameter beams
and overlap them partially?
[ Addendum 20090204: I eventually remembered that Noether's theorem has something to say about the necessity of the energy concept. ]
[Other articles in category /physics] permanent link
Thu, 06 Dec 2007
What's a File?
Almost every December since 2001 I have given a talk to the
local Linux users' group on some aspect of Unix internals. My
first talk was on the
internals of the ext2 filesystem. This year I was under
a lot of deadline pressure at work, so I decided I would give the 2001
talk again, maybe with a few revisions.
Actually I was under so much deadline pressure that I did not have time to revise the talk. I arrived at the user group meeting without a certain idea of what talk I was going to give.
Fortunately, the meeting structure is to have a Q&A and discussion period before the invited speaker gives his talk. The Q&A period always lasts about an hour. In that hour before I had to speak, I wrote a new talk called What's a File?. It mostly concerns the Unix "inode" structure, and what the kernel uses it for. It uses the output of the well-known ls -l command as a jumping-off point, since most of the ls -l information comes from the inode.
Then I talk about how files are opened and permissions are checked, how the filesystem is organized, how the kernel reads and writes data, how directories are structured, how it's possible to have one file with two names, how symbolic links work, and what that mysterious field is in the ls -l output between the permissions and the owner.
The talk was quite successful, much more so than I would have expected, given how quickly I wrote it and my complete inability to edit or revise it. Of course, it does help that I know this material backwards and forwards and standing on my head, and also that I could reuse all the diagrams and illustrations from the 2001 version of the talk.
I would not, however, recommend this technique.
As my talks have gotten better over the years, I find that less and less of the talk material is captured in the slides, and so the slides become less and less representative of the talk itself. But I put them online anyway, and here they are.
Here's a .tgz file in case you want to download it all at once.
[Other articles in category /Unix] permanent link
Tue, 04 Dec 2007
An Austrian coincidence
Only one of these depicts a location in my obstetrician's
waiting room where the paint is chipped.

[Other articles in category /misc] permanent link
Sat, 01 Dec 2007
19th-century elementary arithmetic
In grade school I read a delightful story, by C. A.
Stephens, called The Jonah. In the story, which
takes place in 1867, Grandma and Grandpa are away for the weekend,
leaving the kids alone on the farm. The girls make fried pies for
lunch.
They have a tradition that one or two of the pies are "Jonahs": they look the same on the outside, but instead of being filled with fruit, they are filled with something you don't want to eat, in this case a mixture of bran and cayenne pepper. If you get the Jonah pie, you must either eat the whole thing, or crawl under the table to be a footstool for the rest of the meal.
Just as they are about to serve, a stranger knocks at the door. He is an old friend of Grandpa's. They invite him to lunch, of course removing the Jonahs from the platter. But he insists that they be put back, and he gets the Jonah, and crawls under the table, marching it around the dining room on his back. The ice is broken, and the rest of the afternoon is filled with laughter and stories.
Later on, when the grandparents return, the kids learn that the elderly visitor was none other than Hannibal Hamlin, formerly Vice-President of the United States.
A few years ago I tried to track this down, and thanks to the Wonders of the Internet, I was successful. Then this month I had the library get me some other C. A. Stephens stories, and they were equally delightful and amusing.
In one of these, the narrator leaves the pump full of water overnight, and the pipe freezes solid. He then has to carry water for forty head of cattle, in buckets from the kitchen, in sub-freezing weather. He does eventually manage to thaw the pipe. But why did he forget in the first place? Because of fractions:
I had been in a kind of haze all day over two hard examples in complex fractions at school. One of them I still remember distinctly:At that point I had to stop reading and calculate the answer, and I recommend that you do the same.
$${7\over8} \; {\rm of} \; {60 {5\over10} \over 10 {3\over8}} \; {\rm of} \; {8\over 5} \; \div \; 8{68\over 415} = {\rm What?}$$
I got the answer wrong, by the way. I got 25/64 or 64/25 or something of the sort, which suggests that I flipped over an 8/5 somewhere, because the correct answer is exactly 1. At first I hoped perhaps there was some 19th-century precedence convention I was getting wrong, but no, it was nothing like that. The precedence in this problem is unambiguous. I just screwed up.
Entirely coincidentally (I was investigating the spelling of the word "canceling") I also recently downloaded (from Google Books) an arithmetic text from the same period, The National Arithmetic, on the Inductive System, by Benjamin Greenleaf, 1866. Here are a few typical examples:
Some of these are rather easy, but others are a long slog. For example, #1 and #3 here (actually #1 and #25 in the book) can be solved right off, without paper. But probably very few people have enough skill at mental arithmetic to carry off $612/(83 3/7) * (14 7/10) in their heads.
- If 7/8 of a bushel of corn cost 63 cents, what cost a bushel? What cost 15 bushels?
- When 14 7/8 tons of copperas are sold for $500, what is the value of 1 ton? what is the value of 9 11/12 tons?
- If a man by laboring 15 hours a day, in 6 days can perform a certain piece of work, how many days would it require to do the same work by laboring 10 hours a day?
- Bought 87 3/7 yards of broadcloth for $612; what was the value for 14 7/10 yards?
- If a horse eat 19 3/7 bushels of oats in 87 3/7 days, how many will 7 horses eat in 60 days?
The "complex fractions" section, which the original problem would have fallen under, had it been from the same book, includes problems like this: "Add 1/9, 2 5/8, 45/(94 7/11), and (47 5/9)/(314 3/5) together." Such exercises have gone out of style, I think.
In addition to the complicated mechanical examples, there is some good theory in the book. For example, pages 227–229 concern continued fraction expansions of rational numbers, as a tool for calculating simple rational approximations of rationals. Pages 417–423 concern radix-n numerals, with special attention given to the duodecimal system. A typical problem is "How many square feet in a floor 48 feet 6 inches long, and 24 feet 3 inches broad?" The remarkable thing here is that the answer is given in the form 1176 sq. feet. 1' 6'', where the 1' 6'' actually means 1/12 + 6/144 square feet— that is, it is a base-12 "decimal".
I often hear people bemoaning the dumbing-down of the primary and secondary school mathematics curricula, and usually I laugh at those people, because (for example) I have read a whole stack of "College Algebra" books from the early 20th century, which deal in material that is usually taken care of in 10th and 11th grades now. But I think these 19th-century arithmetics must form some part of an argument in the other direction.
On the other hand, those same people often complain that students' time is wasted by a lot of "new math" nonsense like base-12 arithmetic, and that we should go back to the tried and true methods of the good old days. I did not have an example in mind when I wrote this paragraph, but two minutes of Google searching turned up the following excellent example:
Most forms of life develop random growths which are best pruned off. In plants they are boles and suckerwood. In humans they are warts and tumors. In the educational system they are fashionable and transient theories of education created by a variety of human called, for example, "Professor Of The Teaching Of Mathematics."(Smart Machines, by Lawrence J. Kamm; chapter 11, "Smart Machines in Education".)When the Russians launched Sputnik these people came to the rescue of our nation; they leapfrogged the Russians by creating and imposing on our children the "New Math."
They had heard something about digital computers using base 2 arithmetic. They didn't know why, but clearly base 10 was old fashioned and base 2 was in. So they converted a large fraction of children's arithmetic education to learning how to calculate with any base number and to switch from base to base. But why, teacher? Because that is the modern way. No one knows how many potential engineers and scientists were permanently turned away by this inanity.
Fortunately this lunacy has now petered out.
Pages 417–423 of The National Arithmetic, with their problems on the conversion from base-6 to base-11 numerals, suggest that those people may not know what they are talking about.
[Other articles in category /math] permanent link





