Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 15 Apr 2023
I liked this simple calculus exercise
A recent Math SE question asked for help computing the value of $$\int_0^{2000} e^{x/2-\left\lfloor x/2\right\rfloor}\; dx.\tag{$\star$}$$
(!!\left\lfloor \frac x2 \right\rfloor!! means !!\frac x2!! rounded down to the nearest integer.)
Often when I see someone's homework problems I exclaim “what blockhead TA assigned this?” But I think this is a really good exercise. Here's why.
In a calculus class, some people will have learned to integrate common functions by rote manipulatation of the expressions. They have learned a set of rules for converting $$\int_a^b x^k\; dx$$ to $$\left.\frac{x^{k+1}}{k+1}\right\rvert_a^b$$ and then to $$\frac{b^{k+1}}{k+1}- \frac{a^{k+1}}{k+1}$$ and such like, and they grind through the algebra. If this is all someone knows how to do, they are going to have a lot of trouble with !!(\star)!!. They might say “But nobody ever taught us how to integrate functions with !!\left\lfloor \frac x2\right\rfloor!!”.
A calculus tyro trying to deal with this analytically might also try rewriting $$e^{x/2-\left\lfloor x/2\right\rfloor}$$ as $$\frac{e^{x/2}}{e^{\left\lfloor x/2\right\rfloor}}$$ but that makes the problem harder, not easier.
To solve this, the student has to actually understand what the integral is computing, and if they don't they will have to learn something about it. The integral is computing the area under a curve. if you graph the function $$\frac x2-\left\lfloor \frac x2\right\rfloor$$
you find that it looks like this:
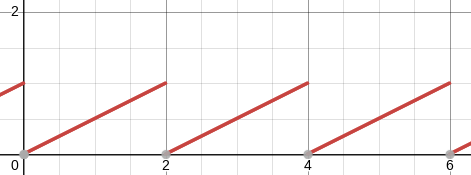
If the interval of integration in !!(\star)!! were only !!(0,2)!! instead of !!(0, 2000)!!, the problem would be very easy because, on this interval, the complicated exponent is identically equal to !!\frac x2!!:
$$\begin{align} \int_0^2 e^{x/2-\left\lfloor x/2\right\rfloor}\; dx & = \int_0^2 e^{x/2}\; dx \\ & = \left. 2e^{x/2} \right\rvert_0^2 \\ & = 2e-2 \end{align} $$
Since the function is completely periodic, integrating over any of the !!1000!! intervals of length !!2!! will produce the same value, so the final answer is simply $$1000\cdot (2e-2).$$
But just pushing around the symbols won't get you there, to solve this problem you have to actually know something about calculus.
The student who overcomes this problem might learn the following useful techniques:
If some expression looks complicated, try graphing it and see if you get any insight into how it behaves.
Some complicated functions can be understood by breaking them into simple parts and dealing with the parts separately.
Piecewise-continuous functions can be integrated by breaking them into continuous intervals and integrating the intervals separately.
You can exploit symmetry to reduce the amount of calculation required.
None of this is deep stuff, but it's all valuable technique. Also they might make the valuable observation that not every problem should be solved by pushing around the symbols.
[Other articles in category /math/se] permanent link


