Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 01 Oct 2008
The Lake Wobegon Distribution
Michael
Lugo mentioned a while back that most distributions are normal. He
does not, of course, believe any such silly thing, so please do not
rush to correct him (or me). But the remark reminded me of how many
people do seem to believe that most distributions are normal.
More than once on internet mailing lists I have encountered people who
ridiculed others for asserting that "nearly all x are above [or
below] average". This is a recurring joke on Prairie Home
Companion, broadcast from the fictional town of Lake Wobegon,
where "all the women are strong, all the men are good looking, and all
the children are above average." And indeed, they can't all be above
average. But they could nearly all be above average. And this
is actually an extremely common situation.
To take my favorite example: nearly everyone has an above-average number of legs. I wish I could remember who first brought this to my attention. James Kushner, perhaps?
But the world abounds with less droll examples. Consider a typical corporation. Probably most of the employees make a below-average salary. Or, more concretely, consider a small company with ten employees. Nine of them are paid $40,000 each, and one is the owner, who is paid $400,000. The average salary is $76,000, and 90% of the employees' salaries are below average.
The situation is familiar to people interested in baseball statistics because, for example, most baseball players are below average. Using Sean Lahman's database, I find that 588 players received at least one at-bat in the 2006 National League. These 588 players collected a total of 23,501 hits in 88,844 at-bats, for a collective batting average of .265. Of these 588, only 182 had an individual batting average higher than 265. 69% of the baseball players in the 2006 National League were below-average hitters. If you throw out the players with fewer than 10 at-bats, you are left with 432 players of whom 279, or 65%, hit worse than their collective average of 23430/88325 = .265. Other statistics, such as earned-run averages, are similarly skewed.
The reason for this is not hard to see. Baseball-hitting talent in the general population is normally distributed, like this:
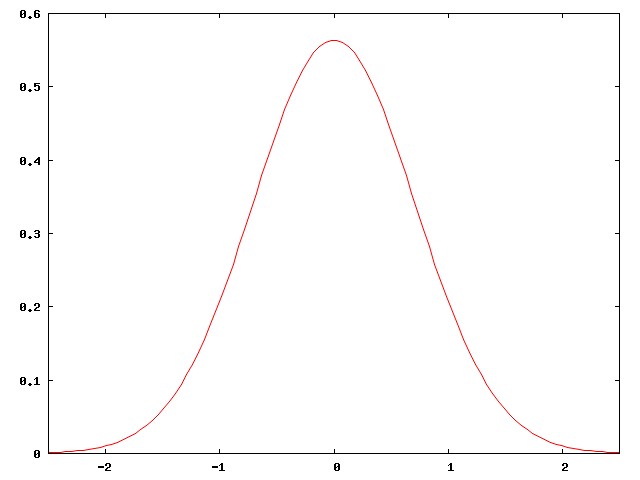
But major-league baseball players are not the general population. They are carefully selected, among the best of the best. They are all chosen from the right-hand edge of the normal curve. The people in the middle of the normal curve, people like me, play baseball in Clark Park, not in Quankee Stadium.
Here's the right-hand corner of the curve above, highly magnified:
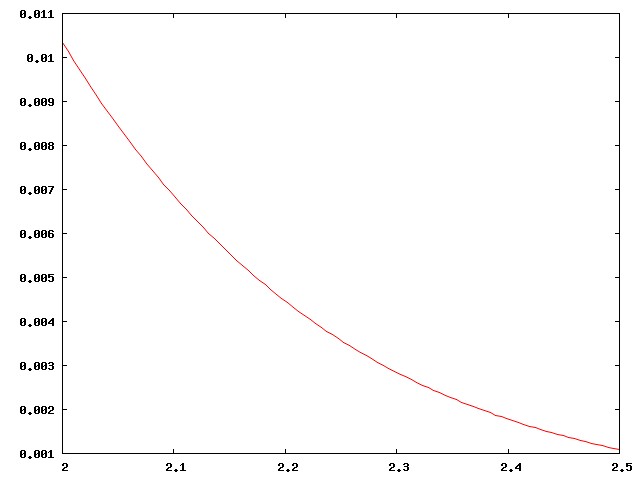
Actually I didn't present the case strongly enough. There are around 800 regular major-league ballplayers in the USA, drawn from a population of around 300 million, a ratio of one per 375,000. Well, no, the ratio is smaller, since the U.S. leagues also draw the best players from Mexico, Venezuela, Canada, the Dominican Republic, Japan, and elsewhere. The curve above is much too inclusive. The real curve for major-league ballplayers looks more like this:
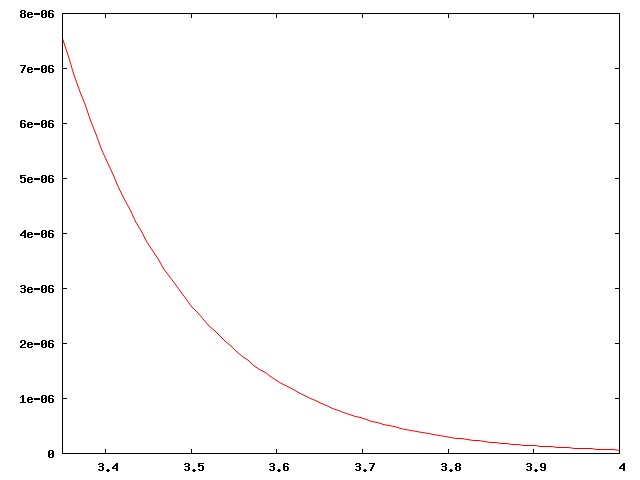
This has important implications for the analysis of baseball. A player who is "merely" above average is a rare and precious resource, to be cherished; far more players are below average. Skilled analysts know that comparisons with the "average" player are misleading, because baseball is full of useful, effective players who are below average. Instead, analysts compare players to a hypothetical "replacement level", which is effectively the leftmost edge of the curve, the level at which a player can be easily replaced by one of those kids from triple-A ball.
In the Historical Baseball Abstract, Bill James describes some great team, I think one of the Cincinnati Big Red Machine teams of the mid-1970s, as "possibly the only team in history that was above average at every position". That's an important thing to know about the sport, and about team sports in general: you don't need great players to completely clobber the opposition; it suffices to have players that are merely above average. But if you're the coach, you'd better learn to make do with a bunch of players who are below average, because that's what you have, and that's what the other team will beat you with.
The right-skewedness of the right side of a normal distribution has implications that are important outside of baseball. Stephen Jay Gould wrote an essay about how he was diagnosed with cancer and given six months to live. This sounds awful, and it is awful. But six months was the expected lifetime for patients with his type of cancer—the average remaining lifetime, in other words—and in fact, nearly everyone with that sort of cancer lived less than six months, usually much less. The average was only skewed up as high as six months because of a few people who took years to die. Gould realized this, and then set about trying to find out how the few long-lived outliers survived and what he could do to turn himself into one of the long-lived freaks. And he succeeded, and lived for twenty years, dying eventually at age 60.
My heavens, I just realized that what I've written is an article about the "long tail". I had no idea I was being so trendy. Sorry, everyone.
[Other articles in category /math] permanent link


