The Universe of Discourse : Lazy square roots of power series return

12 recent entries
Monad terminology problem / A short bibliography of probability monads / A monad for probability and provenance / Monads are like burritos / Another short explanation of Gödel's theorem / World's shortest explanation of Gödel's theorem / On failing open / You think you're All That, but you're not! / Dijkstra was not insane / Gray code at the pediatrician's office / Haskell logo fail / A child is bitten by a dog every 0.07 seconds...

Archive:

2010: JFMAMJ
JA
2009: J F MAM J
JASOND
2008: J F M A M J
JAS O ND
2007: J F M A M J
J A S O N D
2006: J F M A M J
JAS O N D
2005: O N D

Comments disabled

Mon, 10 Dec 2007

Lazy square roots of power series return
In an earlier article I talked about wanting to use lazy streams to calculate the power series expansion of the solution of this differential equation:

$(f(x))^2 + (f'(x))^2 = 1$

To do that I decided I would need a function to calculate the square root of a power series, which I did figure out; it's in the earlier article. But then I got distracted with other issues, and then folks wrote to me with several ways to solve the differential equation, and I spent a lot of time writing that up, and I didn't get back to the original problem until today, when I had to attend the weekly staff meeting. I get a lot of math work done during that meeting.

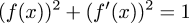
At least one person wrote to ask me for the Haskell code for the power series calculations, so here's that first off.

A power series a₀ + a₁x + a₂x² + a₃x³ + ... is represented as a (probably infinite) list of numbers [a₀, a₁, a₂, ...]. If the list is finite, the missing terms are assumed to be all 0.

The following operators perform arithmetic on functions:

	-- add functions a and b
	add [] b = b
	add a [] = a
	add (a:a') (b:b') = (a+b) : add a' b'

	-- multiply functions a and b
	mul [] _ = []
	mul _ [] = []
	mul (a:a') (b:b') = (a*b) : add (add (scale a b')
					     (scale b a'))
					(0 : mul a' b')

	-- termwise multiplication of two series
        mul2 = zipWith (*)

        -- multiply constant a by function b
    	scale a b = mul2 (cycle [a]) b
	neg a = scale (-1) a

And there are a bunch of other useful utilities:

	-- 0, 1, 2, 3, ...
	iota = 0 : zipWith (+) (cycle [1]) iota
	-- 1, 1/2, 1/3, 1/4, ...
	iotaR = map (1/) (tail iota)

	-- derivative of function a
	deriv a = tail (mul2 iota a)

	-- integral of function a
	-- c is the constant of integration
	int c a = c : (mul2 iotaR a)

	-- square of function f
	sqr f = mul f f

	-- constant function
	con c = c : cycle [0]
	one = con 1

Order
Structure and Interpretation of Computer Programs

with kickback
no kickback

The really interesting operators perform division and evolve square roots of functions. I discussed how these work in the earlier article. The reciprocal operation is well-known; it appears in Structure and Interpretation of Computer Programs, Higher-Order Perl, and I presume elsewhere. I haven't seen the square root extractor anywhere else, but I'm sure that's just because I haven't looked.

	-- reciprocal of argument function
	inv (s0:st) = r
	  where r = r0 : scale (negate r0) (mul r st)
		r0 = 1/s0

	-- divide function a by function b
	squot a b = mul a (inv b)

	-- square root of argument function
	srt (s0:s) = r 
	   where r = r0 : (squot s (add [r0] r))
		 r0 = sqrt(s0)

We can define the cosine function as follows:

	coss = zipWith (*) (cycle [1,0,-1,0]) (map ((1/) . fact) [0..])

We could define the sine function analogously, or we can say that sin(x) = √(1 - cos²(x)):

	sins = (srt . (add one) . neg . sqr) coss

This works fine.

Order
How to Solve It

with kickback
no kickback

Okay, so as usual that is not what I wanted to talk about; I wanted to show how to solve the differential equation. I found I was getting myself confused, so I decided to try to solve a simpler differential equation first. (Pólya says: "Can you solve a simpler problem of the same type?" Pólya is a smart guy. When the voice talking in your head is Pólya's, you better pay attention.) The simplest relevant differential equation seemed to be f = f'. The first thing I tried was observing that for all f, f = f₀ : mul2 iotaR f'. This yields the code:

     f = f0 : mul2 iotaR (deriv f)

This holds for any function, and so it's unsolvable. But if you combine it with the differential equation, which says that f = f', you get:

     f = f0 : mul2 iotaR f
       where f0 = 1   -- or whatever the initial conditions dictate

and in fact this works just fine. And then you can observe that this is just the definition of int; replacing the definition with the name, we have:

     f = int f0 f
       where f0 = 1   -- or whatever

This runs too, and calculates the power series for the exponential function, as it should. It's also transparently obvious, and makes me wonder why it took me so long to find. But I was looking for solutions of the form:

     f = deriv f

which Haskell can't figure out. It's funny that it only handles differential equations when they're expressed as integral equations. I need to meditate on that some more.

It occurs to me just now that the f = f0 : mul2 iotaR (deriv f) identity above just says that the integral and derivative operators are inverses. These things are always so simple in hindsight.

Anyway, moving along, back to the original problem, instead of f = f', I want f² + (f')² = 1, or equivalently f' = √(1 - f²). So I take the derivative-integral identity as before:

     f = int f0 (deriv f)

and put in √(1 - f²) for deriv f:

     f = int f0 ((srt . (add one) . neg . sqr) f)
       where f0 = sqrt 0.5   -- or whatever

And now I am done; Haskell cheerfully generates the power series expansion for f for any given initial condition. (The parameter f0 is precisely the desired value of f(0).) For example, when f(0) = √(1/2), as above, the calculated terms show the function to be exactly √(1/2)·(sin(x) + cos(x)); when f(0) = 0, the output terms are exactly those of sin(x). When f(0) = 1, the output blows up and comes out as [1, 0, NaN, NaN, ...]. I'm not quite sure why yet, but I suspect it has something to do with there being two different solutions that both have f(0) = 1.

Order
Higher-Order Perl

with kickback
no kickback

All of this also works just fine in Perl, if you build a suitable lazy-list library; see chapter 6 of HOP for complete details. Sample code is here. For a Scheme implementation, see SICP. For a Java, Common Lisp, Python, Ruby, or SML implementation, do the obvious thing.

But anyway, it does work, and I thought it might be nice to blog about something I actually pursued to completion for a change. Also I was afraid that after my week of posts about Perl syntax, differential equations, electromagnetism, Unix kernel internals, and paint chips in the shape of Austria, the readers of Planet Haskell, where my blog has recently been syndicated, were going to storm my house with torches and pitchforks. This article should mollify them for a time, I hope.

[ Addendum 20071211: Some additional notes about this. ]

[Other articles in category /math] permanent link