Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 01 Mar 2006
What is topology?
Popular descriptions of topology tell you that it's like geometry, but
bending and stretching are allowed, so that a sphere is considered the
same as a cube, or a doughnut is the same as a coffee cup. There's
some truth in that, but it really doesn't get across the idea of what
topology is really like or really about.
Over the years I've spent a lot of time thinking about how to briefly explain topology to someone with only an ordinary math background, say one year of college calculus. Usually when I try hard to find good short explanations of things like this, I'm successful. So far, I haven't found any such explanation of topology. I haven't given up, though.
The difficulty is that topology was invented to give mathematicians a better understanding of analysis and the structure of the real numbers. Analysis was invented to give mathematicians a better understanding of calculus and limit processes. Calculus was invented to solve physics problems. So topology is three degrees removed from anything real. Contrast this with, say, graph theory, where the central object of study, the graph, is only one degree removed from something real. If you understand the vertices of a graph as computers and the edges as network connections, you can immediately see the point of graph theory. To understand the point of topology, you need to understand the point of analysis, and to understand the point of analysis, you need to understand the point of calculus. That's a lot of stuff to pack into a short explanation.
On top of that, you have the difficulty that topology has become a field of study in itself, with sub-branches that have nothing to do with the original goal of better understanding of the reals. The structure of the Tychonoff corkscrew (a particularly bizarre and counterintuitive topological object) may illuminate certain facts in set theory, but it has nothing to do with better understanding of the real numbers.
I think I can explain topology clearly, just not briefly. This is the first in what I hope will be a series of articles in which I'll try to do that.
The first thing to know is that mathematicians think of the real numbers as being points in an infinite line, with zero in the middle, and the positive numbers stretching away to the right and negative numbers to the left. Real numbers are points on this line, with a number n to the right of m if n > m . So mathematicians have a visual and spatial conception of numbers as well as a quantitative conception.

One consequence of this view is that a set of numbers is not merely an arithmetic object. It also has geometric properties, such as a length (find the smallest and largest numbers in the set, and subtract the smaller from the larger) and whether the set is a single connected piece or the union of smaller, disconnected components. Another consequence of this view of numbers as points on a line is that mathematicians refer to the numbers as "points" and to the set of numbers as a "space".
One idea that appears over and over again in analysis, and which is the source of the single driving idea of topology, is the notion of an open interval.
An open interval is very simple: it's just the set of all numbers in between two points. The notation (a, b) represents the set of all numbers greater than a and less than b. In the mathematician's mental picture of the real numbers, the interval (1, 5/2) looks like this:
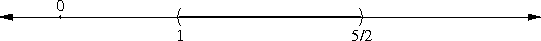
There is a different notation for an interval that does include the endpoints, a so-called closed interval; [a, b] represents the set of all points greater than or equal to a and less than or equal to b. So [a, b] includes all the points of (a, b), and, additionally, a and b themselves:
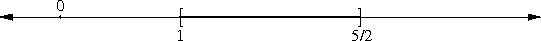
This matter of the endpoints is crucial. Open and closed intervals have very different behaviors, stemming from the fact that a closed interval contains its boundary points and an open interval does not. A point inside an open interval can be close to the edge, but not at the edge, because the open interval omits the edge. But a closed interval does include the edge.
In a closed interval, the points a and b are clearly special, and quite different from the other points in the interval, in a way that I will make more precise in a moment. But in an open interval, there is a certain sense in which all the points behave the same.
Here's the essential property of an open interval, as identified by topologists. If you choose any point p in the open interval, you can draw a little circle around p so that all the points inside the circle are also in the interval. For example, consider the open interval (1, 5/2) and the point 2, which is inside the interval:

We can do this for any point at all that is in the interval, as long as we make the circle sufficiently small:
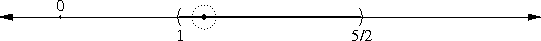
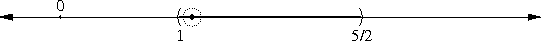
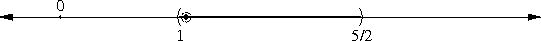
This is not true of closed intervals. A circle around the point 1 will include some points outside of the closed interval [1, 5/2], no matter how small we make the circle:
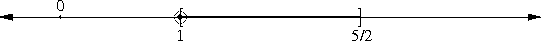
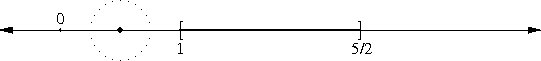
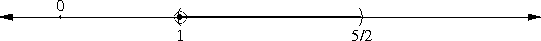
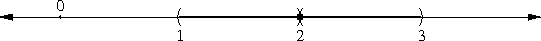
Mathematicians sum up all these properties by saying that a closed interval contains all the points of its boundary, whereas an open interval contains none of them.
This business of the small circle drawn around a particular point p is clearly important, so it's good to have a name for it. The idea is that we're trying to look at what happens "close to" p. But to pin that down, we need a notion of what "close to" means, so we need a way of measuring distances.
In the real numbers, measuring distances is easy. The distance between a and b is just |a - b|. |x| denotes the absolute value of x, which means that if x is negative, you make it positive instead. For |a - b|, it simply means that you should subtract the smaller one from the larger, and not the other way around. This is because you don't want to have negative distances, and you want the distance between 4 and 3 to be the same as the distance between 3 and 4.
Then mathematicians formalize those little circles this way: they say that the "ball" of radius ε around some point p, symbolized as Bε(p), is just the set of all points whose distance from p is less than ε. The use of the odd word "ball" here should tip you off that we're soon going to generalize this from one to three dimensions. In one dimension, balls are actually open intervals, and Bε(p) is precisely the interval (p - ε, p + ε). In two dimensions, the balls are discs, and in three dimensions they are actually ball-shaped.
The balls capture a flexible notion of "closeness": two points are "close" if they are inside the same ball. By making the balls small enough, we can make the notion of "close" as restrictive as we want. In this sense, we can see that no matter how restrictive we make the notion of closeness, there are always some points in an open interval that are close to the end of the interval—but no point is "close" for all possible notions of closeness; there is always some sufficiently restrictive definition under which a particular point is far from the end. Closed sets are different, and contain points that are close to the end for any definition of "close".
Similarly, the sets (1, 2) and (2, 3) are close together, for any definition of "close", although they don't actually intersect, or even touch, since you can't get from one to the other without leaving the sets entirely.
The essential property of open intervals that I mentioned before can be phrased in terms of the balls in this way: a set G is said to be open if, for any point p of G, there is some positive number ε such that Bε(p) is entirely contained in G.
Open intervals are open, but they are are not the only open sets. Let S be set of all points in either (1, 2) or (3, 4). S is open, but it's not an interval. But open sets all look pretty much the same; all open sets are unions of non-overlapping intervals, for example. There are some unbounded open sets, such as the set of all positive numbers, but we can think of that as the interval (0, ∞). Similarly (-∞, 3), the set of all numbers less than 3, is open. And the set of all real numbers is open, since it contains every ball whatsoever, but we can think of that set as (-∞, ∞).
Other concepts can be defined in terms of the balls. For example, a "limit point" of a set S is a point p for which any ball around p must contain some point of S other than p. 5/2 is a limit point of both the open interval (1, 5/2) and the closed interval [1, 5/2] because every ball Bε(5/2) contains points of both intervals other than 5/2 itself. The open interval omits 5/2, but the closed set includes it. One can define a closed set as a set that includes all of its limit points.
With these definitions, plenty of useful stuff follows, such as: Every open set is a union of non-overlapping open intervals. For every closed set C, there is some open set G such that every real number is in either C or in G but not both. The union or intersection of any two open sets is another open set. The union or intersection of any two closed sets is another closed set. Every ball is an open set. Every finite set is closed.
Other geometric notions come out of this too. For example, an "interior point" of a set S is a point p for which there's some Bε(p) is completely contained in S. Then an open set is precisely a set whose points are all interior points. Every point in [1, 5/2] is an interior point except the boundary points 1 and 5/2. We can define the "interior" of a set as the set of all its interior points, a "boundary point" as a point in a set that isn't an interior point, and the "boundary" of a set as the set of all its boundary points.
To generalize these notions to more complex spaces, we can generalize the idea of distance. Consider points in the plane, for example. These points have a well-known distance function, the so-called Pythagorean distance, which says that the distance between (a, b) and (c, d) is, as usual, √((c-a)2 + (d-b)2). If we use this as our definition of distance, and defined balls as before, we find that Bε(p) is just a disc of radius ε centered at p.
The definitions still make sense. Consider the set of points in the plane that are on or inside the circle of radius 1 centered at a particular point p. The boundary of this set, even under the very abstract definitions above, is just what you would expect: the boundary is the circle itself. The interior is the disc that lies inside the circle, including the center but not the edge. Once again, open sets are sets in the plane that omit their boundaries, and closed sets are those sets that include their boundaries. Most theorems still work; for example, the intersection of two open sets is still an open set, and balls are still examples of open sets.
We've started with a very thin, weak-looking base, which was simply the idea of measuring distances. From the simple idea of measurement, we get the balls, and from the balls we get ways to understand geometric notions like boundaries and interiors, and analytic notions like limits.
A metric space is a generalization of the idea of measuring distance. The "space" is now a set of things, which could be anything at all: points, or numbers, or train stations, or whatever. The things are customarily called "points". The "metric" describes how you are planning to measure the distance between two points.
To be a sensible distance function, the metric needs to have a few simple properties. It must never be negative, must be zero when measuring the distance from a point to itself, and must be positive when measuring the distance between two different points. It must be symmetric, which means that the distance from a to b must be the same as the distance from b to a in all cases. And the metric must satisfy the triangle inequality, which just means that the length of a route from a to b that stops off at c in between must be at least as long as the one that goes directly from a to b.
In mathematical notation, we write d(a, b) to represent the distance from a to b. We then want d to have the following properties:
- d(a, b) ≥ 0
- d(a, b) = 0 if and only if a = b
- d(a, b) = d(b, a)
- d(a, b) ≤ d(a, c) + d(c, b)
Once you have the metric, you can define the balls: the ball Bε(p) is still the set of all points q for which d(p, q) < ε. (This ball is sometimes written as Bd,ε(p), because it depends on the metric.) And once you have defined the balls, you can define the open and closed sets.
One thing this gets you is that you can talk about notions of closeness and nearness and limits in spaces that are much less tractable than lines and planes. For example, if you want to do analysis on the surface of a torus (a doughnut shape) this gives you a theoretical basis for treating it as a subset of ordinary three-dimensional space, and helps you understand which theorems of analysis will work on the torus and which ones won't.
Another thing it gets you is the opportunity to consider analogous notions in spaces that are nothing at all like lines or planes. Sometimes this might lead to insights that are useful in analysis. Sometimes it might not. But it does keep mathematicians employed.
Here's one example—I'm not sure whether it's genuinely useful or whether it serves primarily to keep mathematicians employed. Let's consider a plane, but instead of using the usual Pythagorean distance formula, let's say that the distance between (a, b) and (c, d) is |a-c| + |b-d|. This corresponds to a world in which you can only travel due north, south, east, and west; for this reason it is sometimes called the "Manhattan distance". In Manhattan, when you want to go from (a, b) to (c, d), you first walk east or west on b street, for a distance of |a-c|, until you get to c avenue. You then turn ninety degrees and walk north (or south) on c avenue, for a distance of |b-d|, until you reach the intersection with d street. The path is shown below:
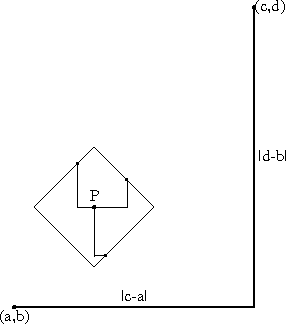
But one interesting thing about the Manhattan metric is that it doesn't affect which sets are open or closed. So in a certain way, it doesn't matter whether you measure distance according to the usual function or according to the Manhattan metric.
A metric that is different is the "discrete" metric. In this metric, the distance between points p and q is 1, unless they are the same point, in which case it is 0. You may want to check to make sure that this metric has the requisite properties.
Balls in the discrete metric are even weirder than the diamond-shaped balls of the Manhattan metric. A ball around p either includes p and nothing else (if its radius is less than or equal to 1) or else it includes the entire universe (if its radius is bigger than 1). In a space measured with the discrete metric, nothing is close to anything else. Our typical example of closeness was the interval (1, 5/2) and the point 1, which was not inside the interval, but was close to it, because any Bε(1) overlapped the interval, no matter how small ε was. But in the discrete metric, the point is not close to the interval, because the ball B1/2(1) does not overlap the interval—it contains only the point 1, and nothing else!
In this article, I've tried to give a motivated and historical account of some of the basic notions of topology, and how they are generalizations of ideas of analysis, for the purpose of better understanding analysis. But I should break the news now that topology, when studied on its own, starts from a somewhat more abstract place. Instead of starting with a metric, and getting the balls from the metric, and the open sets from the balls, it starts with the open sets, and formulates the properties directly in terms of the open sets. This allows you to clean away a lot of unnecessary complication involving arithmetic and questions about Pythagorean vs. Manhattan distances and so on. The usual properties, like "interior" and "boundary" and "connected" can be formulated entirely in terms of the open sets.
Now suppose you have two sets, A and B, with two different definitions of open sets. And suppose you know some way to transform A into B and back again, say by rotating it or something, so that open sets in A are transformed into open sets in B, and vice versa on the way back. Then in a certain sense the open sets of A and B are the same, and anything that will be true of A's open sets will be true of B's as well. Since all the properties of interest are defined solely in terms of the open sets, any of these properties possessed by A will also be possessed by B and vice versa, so in terms of topological properties, A and B are the same.
The transformations that preserve the open sets are easy to understand intuitively: You can bend, stretch, or twist the sets any way you want. But you can't add or subtract material, or poke holes in them, or close up holes that were there before, and you can't tear the sets apart unless you glue them back together afterwards. You can crumple the sets, but you can't crush or explode them; points that were different before the transformation must remain different, and vice versa. A circle can be transformed into a square, by straightening out the sides; I hinted at this before when I mentioned that the Pythagorean and the Manhattan metrics yield the same open sets. But the circle can't be transformed into a line (you'd have to rip it apart) or a figure-eight (two formerly different points would have to fuse together at the waist of the 8). Spheres and cubes are topologically the same, but spheres are not the same as discs, or planes, or balls, or coffee cups.
I hope to develop this explanation further in future articles. My plans are to go backwards a little, and write an article about the structure of the real numbers, explaining why the open intervals are so important for calculus and analysis. And I hope to go forward and write an article about point-set topology, which abandons the metrics entirely in favor of dealing directly with the open sets.
[Other articles in category /math] permanent link


