The Universe of Discourse : How to calculate binomial coefficients, again

Wed, 13 Jun 2007

How to calculate binomial coefficients, again
Yesterday's article about how to calculate binomial coefficients was well-received. It was posted on Reddit, and to my surprise and gratification, the comments were reasonably intelligent. Usually when a math article of mine shows up on Reddit, all the megacretins come out of the woodwork to say what an idiot I am, and why don't I go back to school and learn basic logic.

A couple of people pointed out that, contrary to what I asserted, the algorithm I described can in fact overflow even when the final result is small enough to fit in a machine word. Consider 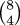$8\choose 4$ for example. The algorithm, as I wrote it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and 70 is the final answer. If your computer has 7-bit machine integers, the answer (70) will fit, but the calculation will overflow along the way at the 168 and 280 steps.

Perhaps more concretely, $35\choose11$ is 417,225,900, which is small enough to fit in a 32-bit unsigned integer, but the algorithm I wrote wants to calculate this as $35{34\choose10}\over11$ , and the numerator here is 4,589,484,900, which does not fit.

One Reddit user suggested that you can get around this as follows: To multiply r by a/b, first check if b divides r. If so, calculate (r/b)·a; otherwise calculate r·(a/b). This should avoid both overflow and fractions.

Unfortunately, it does not. A simple example is ${14\choose4} = {11\over1}{12\over2}{13\over3}{14\over4}$ . After the first three multiplications one has 286. One then wants to multiply by 14/4. 4 does not divide 286, so the suggestion calls for multiplying 286 by 14/4. But 14/4 is 3.5, a non-integer, and the goal was to use integer arithmetic throughout.

Order
The Art of Computer Programming: Volume 2, Seminumerical Algorithms

with kickback
no kickback

Fortunately, this is not hard to fix. Say we want to multiply r by a/b without overflow or fractions. First let g be the greatest common divisor of r and b. Then calculate (r/g) · (a/(b/g)). In the example above, g is 2, and we calculate (286/2) · (14/2) = 143 · 7; this is the best we can do.

I haven't looked, but it is hard to imagine that Volume II of Knuth doesn't discuss this in exhaustive detail, including all the stuff I just said, plus a bunch of considerations that hadn't occurred to any of us.

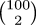A few people also pointed out that you can save time when n > m/2 by calculating $m\choose m-n$ instead of $m \choose n$ . For example, instead of calculating $100\choose98$ , calculate $100\choose 2$ . I didn't mention this in the original article because it was irrelevant to the main point, and because I thought it was obvious.

[Other articles in category /math] permanent link