Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sat, 20 Jan 2007
Linogram development: 20070120 Update
The array feature is working, pending some bug fixes. I have not yet
found all the bugs, I think. But the feature has definitely moved
from the does-not-work-at-all phase into the mostly-works phase. That
is, I am spending most of my time tracking down bugs, rather than
writing large amount of code. The test suite is expanding rapidly.
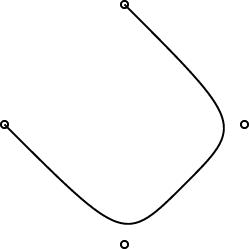
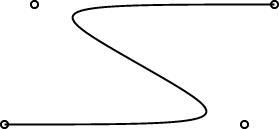
The regular polygons are working pretty well, and the curves are working pretty well. Here are some simple examples:
| 
|
One interesting design problem turned up that I had not foreseen. I had planned for the curve object to be specified by 2 or more control points. (The control points are marked by little circles in the demo pictures above.) The first and last controlpoints would be endpoints, and the curve would start at point 0, then head toward point 1, veer off toward point 2, then veer off toward point 3, etc., until it finally ended at point N. You can see this in the pictures.
This is like the behavior of pic, which has good-looking curves. You don't want to require that the curve pass through all the control points, because that does not give it enough freedom to be curvy. And this behavior is easy to get just by using a degree-N Bézier curve, which was what I planned to do.
However, PostScript surprised me. I had thought that it had degree-N Bézier curves, but it does not. It has only degree-3 ("cubic") Bézier curves. So then I was left with the puzzle of how to use PostScript's Bézier curves to get what I wanted. Or should I just change the definition of curve in linogram to be more like what PostScript wanted? Well, I didn't want to do that, because linogram is supposed to be generic, not a front-end to PostScript. Or, at least, not a front-end only to PostScript.
I did figure out a compromise. The curves generated by the PostScript drawer are made of PostScript's piecewise-cubic curves, but, as you can see from the demo pictures, they still have the behavior I want. The four control points in the small demos above actually turn into two PostScript cubic Bézier curves, with a total of seven control points. If you give linogram the points A, B, C, and D, the PostScript engine draws two cubic Bézier curves, with control points {A, B, B, (B + C)/2} and {(B + C)/2, C, C, D}, respectively. Maybe I'll write a blog article about why I chose to do it this way.
One drawback of this approach is that the curves turn rather sharply near the control points. I may tinker with the formula later to smooth out the curves a bit, but I think for now this part is good enough for beta testing.
[Other articles in category /linogram] permanent link


