Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Wed, 01 Mar 2006
Google query roundup
My blog continues to attract interesting Google queries. I had fun
looking over the queries and writing about them last month, so I
thought I'd try it again.
Sometimes the queries are for very specific information that I can't provide:
1 the four type of flowers by aristotle 1 c-source code for earth revolving sun 1 colleges christian goldbach went to 1 moon sky rhode island position feb 01-feb 14 1 what is robert hooke' s middle name? 1 scientific definition on why fingers get pruney 1 source code of unrestricted simplex protocol in cI thought the reason that the fingers get pruney is that the skin has absorbed water, which makes it get bigger, and since it has nowhere to go, it bunches up. I haven't a clue where Christian Goldbach went to college, and I don't even have a clue why anyone would care, since Goldbach is a nobody. I don't know Robert Hooke's middle name, although there I can see why you might want to know, since Hooke was one of the foremost scientists of the 17th century. Did he even have a middle name?
| Buy An Essay Towards a Real Character and a Philosophical Language from Bookshop.org (with kickback) (without kickback) |
In the "you're asking the wrong question, so all you'll get is the wrong answer" department:
1 books typical copies soldThe only remotely reasonable answer I can imagine here is "zero". There were some related questions that were more sensical:
1 "typical royalties" 1 total o'reilly books sold 1 typical royaltiesI don't know how many O'Reilly books have sold, but I bet if you wrote to ask them, they would tell you.
In the "damn, I wish I had the foggiest idea" department:
1 what happens inside the chrysalisDamn, I wish I had the foggiest idea.
Sometimes, the page to which the user is referred is just perfect for their query:
1 every natural number is either a fibonacci number or it can be written as a sum of nonconsecutive fibonacci numbersThis is my favorite of that type:
6 how many people can use an armonica properlyThis query came up last month; apparently the author is trying it over and over. (The 6 indicates that the query was placed six times.) Last month when I saw it, it inspired me to discuss the armonica in some detail; I can only assume that the original author came back and saw my discussion, in which I answered the question.
Contrary to this, however, is this recurring query:
1 linear math system eliminate debtI didn't know what the author was after last month, and I still don't.
Some of the queries are even more depressing. For example:
1 which expression represents the number 96 written as a
product of primes?
This is depressing because, first, it's obviously a case of some kid
typing in his homework questions verbatim, and second, because the
problem is so very easy. It's not as though he was asked for
the expression that represents the number 6,951,541,603 as a product
of primes. Here's another one like that:
1 greatest common factor of 36 and 63The depressing thing here is that the author hasn't figured out that the way to answer this question is to search for greatest common factor and then read and understand the documents you find. Searching for this one specific arithmetic fact is just silly. It's like trying to multiply 17 and 7 by searching for product of 17 and 7, which also doesn't work.
But sometimes searching for the exact question you want answered does work:
1 a rope lying over the top of a fence is the same length on each side. it weighs one third of a pound per foot. on one end hangs a monkey holding a banana, and on the other end a weight equal to the weight of the monkey. the banana weighs two ounces per inch. the rope is as long (in feet) as the age of the monkey (in years), and the weight of the monkey (in ounces) is the same as the age of the monkey's mother. the combined age of the monkey and its mother is thirty years. one half of the weight of the monkey, plus the weight of the banana, is one forth as much as the weight of the weight and the weight of the rope. the monkey's mother is half as old as the monkey will be when it is three times as old as its mother was when she she was half as old as the monkey will be when when it is as old as its mother will be when she is four times as old as the monkey was when it was twice as its mother was when she was one third as old as the monkey was when it was old as is mother was when she was three times as old as the monkey was when it was one fourth as old as it is now. how long is the banana?And behold, the answer is here. The question comes from Games for the Superintelligent, by Jim Fixx, although it isn't all that difficult. When it was first posed to me, probably around 1980, I was stumped by the long final statement about the monkey's mother's age. I could turn the rest of the information into algebra, but I couldn't understand that final statement. It didn't occur to me at the time to try looking at simpler versions of the same thing, such as "the monkey's mother is half as old as the monkey is now" or "the monkey's mother is half as old as the monkey will be when it is three times as old as its mother is now". These are pretty clear, and demonstrate the pattern for the rest of the sentence, which is a lot simpler than it first appears.
Speaking of problems that are simpler than they first appear, Jeff Abrahamson told me a good one a few months ago: One-tenth of a sphere is painted red, the rest blue. Show that there must exist eight blue points that lie at the vertices of a cube.
1 how did they invent the chinese symbolsNow this is an interesting question. My recollection from my 1991 visit to the National Palace Museum in Taipei is that the earliest known Chinese writing appears on the so-called "oracle bones". The ancient Chinese would foretell the future by heating the shoulder blades of oxen until the bones cracked. (The oxen were dead and the bones cleaned before this process was employed.) The cracks were then annotated with marks indicating their interpretations.
As for the symbols themselves, there are a number of explanations. Some, such as the symbols for "sun"
 , "moon"
, "moon"
 , and "tree"
, and "tree" 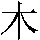 are clearly pictographic. That is, they are stylized pictures of the
sun, the moon, and a tree. Others are compounds; for example, the
character for "man"
are clearly pictographic. That is, they are stylized pictures of the
sun, the moon, and a tree. Others are compounds; for example, the
character for "man"  is a compound of the
characters for "power"
is a compound of the
characters for "power" 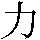 and "field"
and "field"  ; the character for "east"
; the character for "east" 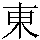 , the direction of the rising sun, depicts the
sun rising behind a tree; the character for "grove"
, the direction of the rising sun, depicts the
sun rising behind a tree; the character for "grove" 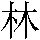 is two trees, and "forest"
is two trees, and "forest" 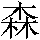 is three trees.
is three trees.
Others are phonetically motivated. For example, the word for
"ridgepole"  is a compound of
"wood"
is a compound of
"wood"  and "east"
and "east"  . The tree makes sense, because ridgepoles are
made of wood, but why "east"? It's because the word for
"ridgepole" is pronounced dòng, exactly the same as the word for
"east". Lots of words are dòng, but this is the
wooden dòng. The "east" component tells you how to
pronounce it, and the "wood" component hints at the meaning.
. The tree makes sense, because ridgepoles are
made of wood, but why "east"? It's because the word for
"ridgepole" is pronounced dòng, exactly the same as the word for
"east". Lots of words are dòng, but this is the
wooden dòng. The "east" component tells you how to
pronounce it, and the "wood" component hints at the meaning.
Writing Systems, by Geoffrey Sampson, has a chapter about this; I recommend both the chapter and the rest of the book.
1 fundamental theorem of phyllotaxisPhyllotaxis is the tendency of plants to put out leaves in certain directions; I probably mentioned them in connection with Fibonacci numbers. I had no idea there was a fundamental theorem of phyllotaxis. But, amazingly, there is. I think it relates the angle at which successive leaves appear on the stem with the resulting periodic pattern of leaves overall. I may do some further research on this later this month.
Other fundamental theorems include: the fundamental theorem of arithmetic, which says that every positive integer has a unique factorization into primes; the fundamental theorem of algebra, which says that every nth degree polynomial has n roots over the complex numbers; and the fundamental theorem of calculus, which relates the integral and differential calculus by saying that if f' is the derivative function of f, then:
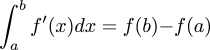
1 doctor dolittle racism 1 dr dolittle prince bumpo racism 1 dr doolittle racismWhen I posted my Doctor Dolittle article, I was hoping that it would become The Place to Go for information on that particular topic, since I seem to have done a lot more analysis than anyone else I could find. Now it's Google listing #6.
I think a lot could be said about the presence or absence of racism in the Dolittle books, although I wouldn't expect much agreement on such a hot-button topic. But I imagine there would be more agreement that the changes that were made to the book in the name of greater racial sensitivity are rather weird.
[Other articles in category /google-roundup] permanent link


