Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sun, 30 Nov 2008
License plate sabotage
A number of years ago I was opening a new bank account, and the bank
clerk asked me what style of checks I wanted, with pictures clowns or
balloons or whatever. I said I wanted them to be pale blue, possibly
with wavy lines. I reasoned that there was no circumstance under
which it would be a benefit to me to have my checks be memorable or
easily-recognized.
So it is too with car license plates, and for a number of years I have toyed with the idea of getting a personalized plate with II11I11I or 0OO0OO00 or some such, on the theory that there is no possible drawback to having the least legible plate number permitted by law. (If you are reading this post in a font that renders 0 and O the same, take my word for it that 0OO0OO00 contains four letters and four digits.)
A plate number like O0OO000O increases the chance that your traffic tickets (or convictions!) will be thrown out because your vehicle has not been positively identified, or that some trivial clerical error will invalidate them.
Recently a car has appeared in my neighborhood that seems to be owned by someone with the same idea:

Other Pennsylvanians should take note. Consider selecting OO0O0O, 00O00, and other plate numbers easily confused with this one. The more people with easily-confused license numbers, the better the protection.
[Other articles in category /misc] permanent link
Mon, 24 Nov 2008
Variations on the Goldbach conjecture
- Every prime number is the sum of two even numbers.
- Every odd number is the sum of two primes.
- Every even number is the product of two primes.

[Other articles in category /math] permanent link
Wed, 12 Nov 2008
Flag variables in Bourne shell programs
Who the heck still programs in Bourne shell? Old farts like me,
occasionally. Of course, almost every time I do I ask myself why I
didn't write it in Perl. Well, maybe this will be of some value
to some fart even older than me..
Suppose you want to set a flag variable, and then later you want to test it. You probably do something like this:
if some condition; then
IS_NAKED=1
fi
...
if [ "$IS_NAKED" == "1" ]; then
flag is set
else
flag is not set
fi
Or maybe you use ${IS_NAKED:-0} or some such
instead of "$IN_NAKED". Whatever.Today I invented a different technique. Try this on instead:
IS_NAKED=false
if some condition; then
IS_NAKED=true
fi
...
if $IS_NAKED; then
flag is set
else
flag is not set
fi
The arguments both for and against it seem to be obvious, so I won't
make them.I have never seen this done before, but, as I concluded and R.J.B. Signes independently agreed, it is obvious once you see it.
[ Addendum 20090107: some followup notes ]
[Other articles in category /prog] permanent link
Tue, 11 Nov 2008
Another note about Gabriel's Horn
 I forgot to mention in the
original article that I think referring to Gabriel's Horn as
"paradoxical" is straining at a gnat and swallowing a camel.
I forgot to mention in the
original article that I think referring to Gabriel's Horn as
"paradoxical" is straining at a gnat and swallowing a camel.
Presumably people think it's paradoxical that the thing should have a finite volume but an infinite surface area. But since the horn is infinite in extent, the infinite surface area should be no surprise.
The surprise, if there is one, should be that an infinite object might contain a merely finite volume. But we swallowed that gnat a long time ago, when we noticed that the infinitely wide series of bars below covers only a finite area when they are stacked up as on the right.

[ Addendum 2014-07-03: I have just learned that this same analogy was
also described in this
math.stackexchange post of 2010. ]
[Other articles in category /math]
permanent link
Gabriel's Horn is not so puzzling
The calculations themselves do not lend much insight into what is
going on here. But I recently read a crystal-clear explanation that I
think should be more widely known.
Take out some Play-Doh and roll out a snake. The surface area of the
snake (neglecting the two ends, which are small) is the product of the
length and the circumference; the circumference is proportional to the
diameter. The volume is the product of the length and the
cross-sectional area, which is proportional to the square of the
diameter.
As you continue to roll the snake thinner and thinner, the volume
stays the same, but the surface area goes to infinity.
Gabriel's Horn does exactly the same thing, except without the rolling, because
the parts of the Horn that are far from the origin look exactly the
same as very long snakes.
There's nothing going on in the Gabriel's Horn example that isn't also happening
in the snake example, except that in the explanation of Gabriel's Horn, the
situation is obfuscated by calculus.
I read this explanation in H. Jerome Keisler's caclulus textbook.
Keisler's book is an ordinary undergraduate calculus text, except that
instead of basing everything on limits and on limiting processes, it
is based on nonstandard analysis and explicit infinitesimal
quantities. Check it out; it is
available online for free. (The discussion of Gabriel's Horn is in chapter 6,
page 356.)
[ Addendum 20081110: A bit
more about this. ]
[Other articles in category /math]
permanent link
Addenda to recent articles 200810
Several people helpfully pointed out that the notion I was looking for
here is the "cofinality" of the ordinal, which I had not heard of
before. Cofinality is fairly simple. Consider some ordered set S. Say
that an element b is an "upper bound" for an element a
if a ≤ b. A subset of S is
cofinal if it contains an upper bound for every element of
S. The cofinality of S is the minimum
cardinality of its cofinal subsets, or, what is pretty much the
same thing, the minimum order type of its cofinal subsets.
So, for example, the cofinality of ω is ℵ0, or, in the language
of order types, ω. But the cofinality of ω + 1 is only 1
(because the subset {ω} is cofinal), as is the cofinality of
any successor ordinal. My question, phrased in terms of cofinality,
is simply whether any ordinal has uncountable cofinality. As we saw,
Ω certainly does.
But some uncountable ordinals have countable cofinality. For example,
let ωn be the smallest ordinal with
cardinality ℵn for each n. In
particular, ω0 = ω, and ω1 =
Ω. Then ωω is uncountable, but has
cofinality ω, since it contains a countable cofinal subset
{ω0, ω1, ω2, ...}.
This is the kind of bullshit that set theorists use to occupy their
time.
A couple of readers brought up George Boolos, who is disturbed by
extremely large sets in something of the same way I am. Robin Houston
asked me to consider the ordinal number which is the least fixed point
of the ℵ operation, that is, the smallest ordinal number
κ such that |κ| = ℵκ. Another
way to define this is as the limit of the sequence 0, ℵ0
ℵℵ0, ... . M. Houston describes κ as
"large enough to be utterly mind-boggling, but not so huge as to defy
comprehension altogether". I agree with the "utterly mind-boggling"
part, anyway. And yet it has countable cofinality, as witnessed by
the limiting sequence I just gave.
M. Houston says that Boolos uses κ as an example of a set
that is so big that he cannot agree that it really exists. Set theory
says that it does exist, but somewhere at or before that point, Boolos
and set theory part ways. M. Houston says that a relevant essay,
"Must we believe in set theory?" appears in Logic, Logic, and
Logic. I'll have to check it out.
My own discomfort with uncountable sets is probably less nuanced, and
certainly less well thought through. This is why I presented it as a
fantasy, rather than as a claim or an argument. Just the sort of
thing for a future blog post, although I suspect that I don't have
anything to say about it that hasn't been said before, more than once.
Finally, a pseudonymous Reddit user brought up a paper of
Coquand, Hancock, and Setzer that discusses just which ordinals
are representable by the type defined above. The answer turns
out to be all the ordinals less than ωω. But
in Martin-Löf's type theory (about which more this month, I hope)
you can actually represent up to ε0. The paper is
Ordinals
in Type Theory and is linked from here.
Thanks to Charles Stewart, Robin Houston, Luke Palmer, Simon Tatham,
Tim McKenzie, János Krámar, Vedran Čačić,
and Reddit user "apfelmus" for discussing this with me.
[ Meta-addendum 20081130: My summary of Coquand, Hancock, and Setzer's
results was utterly wrong. Thanks to Charles Stewart and Peter
Hancock (one of the authors) for pointing this out to me. ]
One reader wondered what should be done about homophones of
"infinity", while another observed that a start has already been
made on "googol". These are just the sort of issues my proposed
Institute is needed to investigate.
One clever reader pointed out that "half" has the homophone "have". Except
that it's not really a homophone. Which is just right!
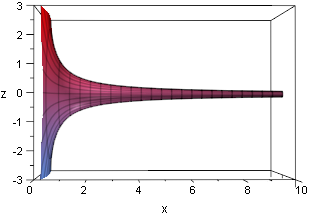
Take the curve y = 1/x for x ≥ 1.
Revolve it around the x-axis, generating a trumpet-shaped
surface, "Gabriel's Horn".
Buy
Elementary Calculus: An Infinitesimal Approach
from Bookshop.org
(with kickback)
(without kickback)
data Nat = Z | S Nat
data Ordinal = Zero
| Succ Ordinal
| Lim (Nat → Ordinal)
In particular, I asked
"What about Ω, the first uncountable ordinal?" Several readers
pointed out that the answer to this is quite obvious: Suppose
S is some countable sequence of (countable) ordinals. Then the
limit of the sequence is a countable union of countable sets, and so
is countable, and so is not Ω. Whoops! At least my intuition
was in the right direction.
[Other articles in category /addenda] permanent link
Election results
Regardless of how you felt about the individual candidates in the
recent American presidential election, and regardless of whether you
live in the United States of America, I hope you can
appreciate the deeply-felt sentiment that pervades this program:
#!/usr/bin/perl
my $remain = 1232470800 - time();
$remain > 0 or print("It's finally over.\n"), exit;
my @dur;
for (60, 60, 24, 100000) {
unshift @dur, $remain % $_;
$remain -= $dur[0];
$remain /= $_;
}
my @time = qw(day days hour hours minute minutes second seconds);
my @s;
for (0 .. $#dur) {
my $n = $dur[$_] or next;
my $unit = $time[$_*2 + ($n != 1)];
$s[$_] = "$n $unit";
}
@s = grep defined, @s;
$s[-1] = "and $s[-1]" if @s > 2;
print join ", ", @s;
print "\n";
[Other articles in category /politics] permanent link
Mon, 03 Nov 2008
Atypical Typing
I just got back from Nashville, Tennessee, where I delivered a talk at
OOPSLA 2008, my first
talk as an "invited
speaker". This post is a bunch of highly miscellaneous notes
about the talk.
If you want to skip the notes and just read the talk, here it is.
Talk abstract
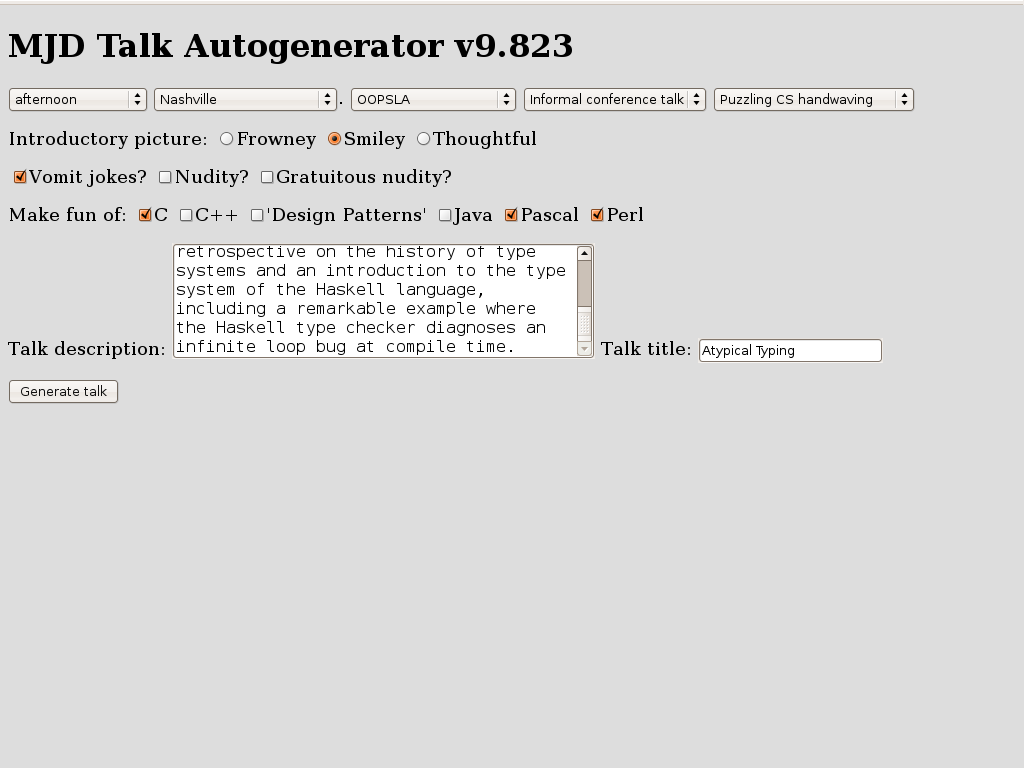
Many of the shortcomings of Java's type system were addressed by the addition of generics to Java 5.0. Java's generic types are a direct outgrowth of research into strong type systems in languages like SML and Haskell. But the powerful, expressive type systems of research languages like Haskell are capable of feats that exceed the dreams of programmers familiar only with mainstream languages.I did not say in the abstract that the talk was a retread of a talk I gave for the Perl mongers in 1999 titled "Strong Typing Doesn't Have to Suck. Nobody wants to hear that. Still, the talk underwent a major rewrite, for all the obvious reasons.In this talk I'll give a brief retrospective on the history of type systems and an introduction to the type system of the Haskell language, including a remarkable example where the Haskell type checker diagnoses an infinite loop bug at compile time.
In 1999, the claim that strong typing does not have to suck was surprising news, and particularly so to Perl Mongers. In 2008, however, this argument has been settled by Java 5, whose type system demonstrates pretty conclusively that strong typing doesn't have to suck. I am not saying that you must like it, and I am not saying that there is no room for improvement. Indeed, it's obvious that the Java 5 type system has room for improvement: if you take the SML type system of 15 years ago, and whack on it with a hammer until it's chipped and dinged all over, you get the Java 5 type system; the SML type system of the early 1990s is ipso facto an improvement. But that type system didn't suck, and neither does Java's.
So I took out the arguments about how static typing didn't have to suck, figuring that most of the OOPSLA audience was already sold on this point, and took a rather different theme: "Look, this ivory-tower geekery turned out to be important and useful, and its current incarnation may turn out to be important and useful in the same way and for the same reasons."
In 1999, I talked about Hindley-Milner type systems, and although it was far from clear at the time that mainstream languages would follow the path blazed by the HM languages, that was exactly what happened. So the HM languages, and Haskell in particular, contained some features of interest, and, had you known then how things would turn out, would have been worth looking at. But Haskell has continued to evolve, and perhaps it still is worth looking at.
Or maybe another way to put it: If the adoption of functional programming ideas into the mainstream took you by surprise, fair enough, because sometimes these things work out and sometimes they don't, and sometimes they get adopted and sometimes they don't. But if it happens again and takes you by surprise again, you're going to look like a dumbass. So start paying attention!
Haskell types are hard to explain
I spent most of the talk time running through some simple examples of Haskell's type inference algorithm, and finished with a really spectacular example that I first saw in a talk by Andrew R. Koenig at San Antonio USENIX where the type checker detects an infinite-loop bug in a sorting function at compile time. The goal of the 1999 talk was to explain enough of the ML type system that the audience would appreciate this spectacular example. The goal of the 2008 talk was the same, except I wanted to do the examples in Haskell, because Haskell is up-and-coming but ML is down-and-going.It is a lot easier to explain ML's type system than it is to explain Haskell's. Partly it's because ML is simpler to begin with, but also it's because Haskell is so general and powerful that there are very few simple examples! For example, in SML one can demonstrate:
(* SML *)
val 3 : int;
val 3.5 : real;
which everyone can understand.But in Haskell, 3 has the type (Num t) ⇒ t, and 3.5 has the type (Fractional t) ⇒ t. So you can't explain the types of literal numeric constants without first getting into type classes.
The benefit of this, of course, is that you can write 3 + 3.5 in Haskell, and it does the right thing, whereas in ML you get a type error. But it sure does make it a devil to explain.
Similarly, in SML you can demonstrate some simple monomorphic functions:
not : bool → bool real : int → real sqrt : real → real floor : real → intOf these, only not is simple in Haskell:
not :: Bool → Bool
fromInteger :: (Num a) ⇒ Integer → a -- analogous to 'real'
sqrt :: (Floating a) ⇒ a → a
floor :: (RealFrac a, Integral b) ⇒ a → b
There are very few monomorphic functions in the Haskell standard
prelude.
Slides
I'm still using the same slide-generation software I used in 1999, which makes me happy. It's a giant pile of horrible hacks, possibly the worst piece of software I've ever written. I'd like to hold it up as an example of "worse is better", but actually I think it only qualifies for "bad is good enough". I should write a blog article about this pile of hacks, just to document it for future generations.
Conference plenary sessions
This was the first "keynote session" I had been to at a conference in several years. One of the keynote speakers at a conference I attended was such a tedious, bloviating windbag that I walked out and swore I would never attend another conference plenary session. And I kept that promise until last week, when I had to attend, because now I was not only the bloviating windbag behind the lectern, but an oath-breaker to boot. This is the "shameful confession" alluded to on slide 3.
On the other hand...
One of the highest compliments I've ever received. It says "John McCarthy will be there. Mark Jason Dominus, too." Wow, I'm almost in the same paragraph with John McCarthy.McCarthy didn't actually make it, unfortunately. But I did get to meet Richard Gabriel and Gregor Kiczales. And Daniel Weinreb, although I didn't know who he was before I met him. But now I'm glad I met Daniel Weinreb. During my talk I digressed to say that anyone who is appalled by Perl's regular expression syntax should take a look at Common Lisp's format feature, which is even more appalling, in much the same way. And Weinreb, who had been sitting in the front row and taking copious notes, announced "I wrote format!".
More explaining of jokes
As I get better at giving conference talks, the online slides communicate less and less of the amusing part of the content. You might find it interesting to compare the 1999 version of this talk with the 2008 version.One joke, however, is too amusing to leave out. At the start of the talk, I pretended to have forgotten my slides. "No problem," I said. "All my talks these days are generated automatically by the computer anyway. I'll just rebuild it from scratch." I then displayed this form, which initialliy looked like this:
Wadler's anecdote
I had the chance to talk to Philip Wadler, one of the designers of Haskell and of the Java generics system, before the talk. I asked him about the history of the generics feature, and he told me the following story: At this point in the talk I repeated an anecdote that Wadler told me. After he and Odersky had done the work on generics in their gj and "Pizza" projects, Odersky was hired by Sun to write the new Java compiler. Odersky thought the generics were a good idea, so he put them into the compiler. At first the Sun folks always ran the compiler with the generics turned off. But they couldn't rip out the generics support completely, because they needed it in the compiler in order to get it to compile its own source code, which Odersky had written with generics. So Sun had to leave the feature in, and eventually they started using it, and eventually they decided they liked it. I related this story in the talk, but it didn't make it onto the slides, so I'm repeating it here.I had never been to OOPSLA, so I also asked Wadler what the OOPSLA people would want to hear about. He mentioned STM, but since I don't know anything about STM I didn't say anything about it.
View it online
The slides are online.[ Addendum 20081031: Thanks to a Max Rabkin for pointing out that Haskell's analogue of real is fromInteger. I don't know why this didn't occur to me, since I mentioned it in the talk. Oh well. ]
[Other articles in category /talk] permanent link


