Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Fri, 24 Feb 2006
Blog Post Escapes from Lab
My blog pages get regenerated when I run Blosxom. Also, I have a cron
job that runs it every night at 12:10.
Files named something.blog turn into blog posts. While posts are under construction, I name them something.notyet. Then when they're done, I rename them to something.blog and either rerun Blosxom or wait until 12:10.
Sometimes I get a little cocky, and I figure that I'm going to finish the post quickly. Then I name the file something.blog right from the start.
Sometimes I'm mistaken about finishing the post quickly. Then I have to fix the name before 12:10 so that the unfinished post doesn't show up on the blog.
Because if it does show up, I can't really retract it. I can remove it from the main blog pages at plover.com. But bloglines.com won't remove it until another twelve posts have come in, no matter what I do with the syndication files.
And that's why there's a semi-finished post about Simplified Poker on bloglines.com today.
[Other articles in category /oops] permanent link
Mon, 20 Feb 2006 I am browsing through the Right Reverend John Wilkins' book Mercury: The Secret and Swift Messenger, published in 1641, which is a compendium of techniques for cryptography and steganography. (I had supposed that the word "steganography" was of recent coinage, but it turns out it dates back to the year 1500, when Johannes Trithemius wrote a book titled Steganographia. (You can find it online, but it is in Latin.)The following passage appears on page 3:
How strange a thing this art of writing did seem at its first invention, we may guess by the late discovered Americans, who were amazed to see men converse with books, and could scarce make themselves believe that a paper could speak; especially, when after all their attention and listening to any writing . . . they could never perceive any words or sound to proceed from it.I find this plausible, since as far as I know none of the aboriginal peoples in the part of the world colonized by the English had writing, and because writing does seem strange and astonishing to me. Also, it seems that many other people found it so. For example, in The Origin of Consciousness in the Breakdown of the Bicameral Mind (which I am sure will turn up here again) Jaynes quotes examples of letters written by the Assyrians. The standard form of such letters was to address the messenger who delivered them, like this:
To Babu-aha-iddina, governor of Eridu, say thus:This form arose originally because the recipient was unable to read, and the messages were sent orally. A messenger would memorize the message at the source, and recite it from memory at the destination. So the message is written as an instruction to the messenger who would deliver it: "To Babu-aha-iddina, say thus..." and ends with a closing statement, also to be made by the messenger, that "so says Tukulti-Ninurta." But in later times, the form was still followed even when both sender and recipient were literate, and then it becomes an instruction to the letter itself to "say thus".You have not sent me the blueberry pie recipe you promised; why haven't you sent it? . . .
So says Tukulti-Ninurta, high king.
The idea that it is the letter itself that speaks seems to be a natural one. Wilkins tells a story of an Indian who is sent to deliver a letter and a basket of figs to a man in the next village. The messenger ate half the figs on the way, and was surprised to be found out upon his arrival when the quantity of figs he delivered did not match the quantity described in the letter. He responded by cursing the letter as a false and lying witness. On the next trip, he was careful to bury the letter under a rock while he ate the figs, so that it would not be able to accuse him when it was delivered.
Written and spoken language are only a little bit separate. Nearly all written language is a written representation of spoken language. Uninformed people call Chinese characters "ideographs", but this is a misnomer, because it suggests that the characters represent ideas. But they don't; they represent the words of whatever particular variety of spoken Chinese the writer uses. (Examples may be found on p. 149 of Geoffrey Sampson's excellent book Writing Systems, which may appear here in more detail in the future.) Very little writing is actually ideographic. One example is the symbol 3, which does not represent the word three or the sound "three" (nor does it represent the words or sounds "drei" or "sam" or "tres") but rather the abstract notion of three. Many mathematical symbols are similarly ideographic.
Children first learn to read by pronouncing the words aloud and hearing them; when they hear, they understand. Hearing is much easier than reading, and I think this is one reason why people like to attend lecture classes instead of just reading the book. People who "move their lips when they read" are widely ridiculed. But reading aloud is a good strategy for anyone faced with difficult material. When I can't make sense of a difficult paragraph, especially a long and confused one, I always back up and try reading it aloud, and this often resolves the difficulty. Even when I have forgotten the words at the beginning by the time I get to the end, I find that I still retain the sense of them. Reading aloud is also a good exercise for writers. If you read aloud what you wrote, you are much more likely to notice when it doesn't make sense. If you are too self-conscious to read aloud, or if the sign says QUIET PLEASE, try subvocalizing; it is still a big help.
Some kinds of literature should always be read aloud. Poetry, of course. If it is good poetry, it loses a lot of its value when read silently. I find that humor also loses its savor for me when I read it non-orally. When I first read Fear and Loathing in Las Vegas myself, I thought it was just stupid. When I heard James Woodyatt read it aloud, it was riotously funny. Lorrie and I found that Louise Erdrich's stories and novels, which can seem unrelievedly depressing when you read them alone, when read aloud became rich, complex, funny, sometimes bitter, sometimes joyful, and often sad—but never depressing.
Someone once told me that some famous scholar, I think perhaps Thomas Aquinas [ addendum: it was Ambrose; see below ] was the only one of his contemporaries to read non-orally, that they were astonished at how the information would just fly from the book into his mind without his having to read it. Their failure to understand non-oral reading may be surprising today, when everyone is expected to do it. But I can remember making the same mistake myself. I was sitting on the floor, reading (aloud) the Sunday comics pages one evening, and I remarked that grown-ups did not actually read; they only looked at the pictures. My mother told me that they did read, but they did so silently. This was the first time I had encountered this idea, which I immediately adopted. I can't remember a time before I could read, but I do remember that occasion of my first silent reading.
[ Addendum 20120611: It turns out that there is a story collected by the Brothers Grimm, but unpublished, which recounts the lying letter story. It is "The Poor Boy in the Grave": "As he again was so extremely hungry and thirsty, he could not help it, and again ate two grapes. But first he took the letter out of the basket, put it under a stone and seated himself thereon in order that the letter might not see and betray him." ]
[ Addendum 20141202: The story about the famous scholar who astounded his contemporaries by reading silently was not Thomas Aquinas, as I said above, but Ambrose. Augustine, in his Confessions, says:
But when he was reading, his eye glided over the pages, and his heart searched out the sense, but his voice and tongue were at rest.I missed by eight hundred years! ]
[ Addendum 2010406: Keshav Kini directed my attention to chapter 2 of Alberto Manguel's A History of Reading, “The Silent Readers”, which discusses the history of silent reading in some detail, and notes that silent reading greatly facilitated the spread of heresy. The chapter is available online, probably without the appropriate permissions. ]
[Other articles in category /IT] permanent link
Sat, 18 Feb 2006
On the prolixity of Baroque authors
As readers of my blog know, I have lately been reading scientific and
philosophical works of Robert Hooke, the diary of Samuel Pepys,
and various
essays by John Wilkins, all written during the 17th century. I've
also been reading various works of Sir Thomas Browne, also from around
the same time; I'm not sure how I've avoided mentioning him so far.
(Had I been writing the blog back in December, Browne would have been
all over it. I'm sure he will appear here sooner or later.)
As any reader of Gulliver's Travels (another contemporaneous book) will know, the literary style of the time was verbose. The writers had plenty to say, and they said it, with plenty of subordinate clauses, itemization of examples, parallel constructions, allusions to and quotations (sometimes in Latin and Greek) from previous authors, digression, intermediate discussion, parenthetical remarks, and other such. For example, here is a sentence I chose at random from Wilkins' essay That the Earth May Be a Planet:
The reason why that motion which is caused by the earth does appear as if it were in the heavens, is, because the sensus communit in judging of it, does conceive the eye to be itself immoveable (as was said before) there being no sense that does discern the effects of any motion in the body; and therefore it does conclude every thing to move, which it does perceive to change its distance from it: so that the clouds do not seem to move sometimes, when as notwithstanding they are everywhere carried about with our earth, by such a swift revolution; yet this can be no hindrance at all, why we may not judge aright of their other particular motions, for which there is not the same reason.There is a reason why this style is called "Baroque".
Baroque writing suits me just fine. The sentences are long, but always clear, if read with care and attention, and I like being required to read with care and attention. I'm good at it, and most modern writing does not offer the reader much repayment for that talent.
The long discussions full of allusion and quotation make me feel as though I'm part of a community of learned scholars, engaged in a careful and centuries-long analysis of the universe and Man's place in it. That's something I've always wanted, something I think we don't have much of today. In these authors I've at last begun to find it. When Wilkins mentions something that Vossius said on some topic, it doesn't bother me that I've never heard of Vossius. I feel that Wilkins is paying me a compliment by assuming that I will know who he's talking about, and that I might even recognize the quotation, or that even if I don't I will want to find out.
These authors do not patronize the reader or try to amuse him with cheap tricks. They assume that the reader wants to think, and that to be instructed is to be entertained.
But as usual I have wandered from the main point, which is to present a couple of contrasts to the usual 17th-century verbosity.
One is from Robert Hooke, in a review he wrote about John Dee's Book of Spirits. Dee was a mathematician, scholar, and occultist of the previous century. Hooke starts by saying:
Having lately met a book, which . . . I never had the Curiosity to examine further into, than upon opening here and there to read some few Lines, which seeming for the most very extravagant, I neglected any further Inquiry into it. . .Hooke says he eventually decided to read it and see how it was:
Nor was I frighted from this my Purpose, either by the six pretended Conjurers prefixt to the Title. . .; nor by the Title, viz. A true and full Relation of what passed for many Years between Dr. John Dee (a Mathematician of great Fame in Queen Elizabeth and King James, their Reigns) and some spirits, tending (had it succeeded) to a General Alteration of most States and Kingdoms in the World, &c. . . . No, nor thirdly the long and frighting Preface of the Publisher. . .Even Hooke was put off by the long and extravagant title and the "long and frighting Preface". That must have been some preface!
Another contrast is provided by Wilkins again. He is discussing the same point as the sentence I quoted above: what would be the observable effects of the rotation of the earth. In particular, the current point is whether a spinning earth would cause tall buildings to fall down, I suppose because their bottoms would be swept away by the earth while the tops stayed in place. (Yes, Wilkins provides a reference to someone who thinks this.) Wilkins answers at some length:
The motion of the earth is always equal and like itself; not by starts and fits. If a glass of beer may stand firmly enough in a ship, when it moves swiftly upon a smooth stream, much less then will the motion of the earth, which is more natural, an so consequently more equal, cause any danger unto those buildings that are erected upon it.But then he quotes another writer's dissenting view:
But supposing (saith Rosse) that this motion were natural to the earth, yet it is not natural to towns and buildings, for these are artificial.Wilkins' response to this is not at all what I expected. Here it is, complete:
To which I answer: ha, ha, he.Finally, I'm going to add that of all the books I've ever read, the one with the longest and most baroque title was a work on extremal graph theory, published in 1985:
Graphical evolution: An introduction to the theory of random graphs, wherein the most relevant probability models for graphs are described together with certain threshold functions which facilitate the careful study of the structure of a graph as it grows and specifically reveal the mysterious circumstances surrounding the abrupt appearance of the unique giant component which systematically absorbs its neighbors, devouring the larger first and ruthlessly continuing until the last isolated vertices have been swallowed up, whereupon the giant is suddenly brought under control by a spanning cycle. The text is laced with challenging exercises especially designed to instruct, and its accompanied by an appendix stuffed with useful formulas that everyone should know.The rest of the book is similarly eccentric, including, for example, a footnote pointing out that fish do not obey the Poisson distribution.
[Other articles in category /book] permanent link
Fri, 17 Feb 2006
More on the frequency of vibrations in 1666 and other matters
In a series of earlier posts (1
2
3) I
discussed Robert Hooke's measurement of the frequency of G above
middle C: he determined that it was 272 beats per second. There are
two questions here: first, how did he do that, and second, why is his
answer so badly wrong? (Modern definitions make it about 384 hertz;
17th-century definitions differ, and vary among themselves, but not by
so much as that.)
The article Mr. Birchensha's Ear, by Benjamin Wardhaugh, provides the answers. In 1664, Hooke and the Royal Society set up a vibrating brass wire 136 feet long. It could be seen to vibrate once per second. Hooke divided it in half, and it vibrated twice per second. He truncated it to one foot, and the assembled musicians pronounced the sound to be a G below middle C. Since a wire one foot long vibrates 136 times as fast as one 136 feet long, we have the answer.
And the error? Partly just slop in the dividing and the estimation of the original frequency. Wardhaugh says:
In fact, the frequency is badly wrong (G has a frequency of 196 Hz), probably because Hooke was careless about the length of the pendulum that measured the time. In private he is meticulously precise, but maybe the details don't matter so much for Society showpieces.Pepys wasn't there, which is why he had to learn about it from Hooke in 1666.
The rest of the article is well worth reading:
Passers-by jeer at the useless toy: the pointlessness of the Royal Society's activities is already threatening to become proverbial. (Shadwell later wrote a comedy in which 'the Virtuoso' weighed air, swam on dry land and read by the light of a decaying fish. Poor Hooke went to see it and 'people almost pointed'.)The Royal Society is well-known to be the inspiration for the Grand Academy of Laputa in Gulliver's Travels, one of whose members "had been eight years upon a project for extracting sunbeams out of cucumbers...".
Reading the contents of Derham's 1726 collection of Hooke's papers on Wednesday, I was struck by the title "Hooke's Experiments on Floating of Lead". I was gearing up to write a blog post about how no real scientific paper has ever reminded me quite so much of the Grand Academy. But I abandoned the idea when I remembered that there is nothing unusual or surprising about being reminded of the grand Academy by a Royal Society paper. Also, the title only sounds silly until you learn that the paper itself is about the manner in which solid lead floats on molten lead.
 Final note: while searching for the title of the floating-lead paper
(which I left at home today) I learned something else interesting. In
South Philadelphia there is a playground attached to an antique "shot
tower". I had had no idea what a shot tower was, and I had supposed
it was a place for storing shot and gunpowder. But why build a
tower? It turns out it is the place where lead shot is manufactured.
You melt up a cauldron of lead at the top, then dump it through a
copper sieve and let it fall into a tub of water at the bottom. On
the way down, the molten lead turns into round shot. You sort it for
size and roundness, re-melt the ones that aren't round, and you have
your shot.
Final note: while searching for the title of the floating-lead paper
(which I left at home today) I learned something else interesting. In
South Philadelphia there is a playground attached to an antique "shot
tower". I had had no idea what a shot tower was, and I had supposed
it was a place for storing shot and gunpowder. But why build a
tower? It turns out it is the place where lead shot is manufactured.
You melt up a cauldron of lead at the top, then dump it through a
copper sieve and let it fall into a tub of water at the bottom. On
the way down, the molten lead turns into round shot. You sort it for
size and roundness, re-melt the ones that aren't round, and you have
your shot.
[ Addendum: More about this: [1] [2] [3] ]
[Other articles in category /physics] permanent link
Thu, 16 Feb 2006
The rate of a vibrating string in 1666
In an earlier post, I discussed a report by Samuel Pepys, from 1666,
that Robert
Hooke claimed to be able to tell how often a fly beat its wings,
by comparing the pitch of the sound with that of a known source such
as a vibrating string. But I didn't know how he had determined the
rate at which the string vibrated. I guessed a couple of ways of
measuring this with 17th-century technology.
Clinton Pierce wrote to me with a clever and highly plausible suggestion: build a "buzzer". Take a spoked wheel, and spin it at a known rate, and hold some flexible object against the spokes. If the wheel spins, say, four times per second, and has 64 spokes, the buzzing will be a middle C. It should be possible to space the spokes evenly, and to spin the wheel uniformly at the correct speed.
My own idea involved attaching a bristle to the string, and letting it draw a sinusoid on a smoked glass plate that was drawn past it. The more I thought about the bristle, the more I was sure I had really read about it somewhere. This morning as I made breakfast, I asked myself "What is this 'bristle', anyway? Where do you get one?" and the answer came immediately "You pull it out of a hog." I'm sure I am recalling this and not just making it up. But I liked M. Pierce's suggestion much better than the bristle and smoked glass idea, because it seemed to me much more likely to work. What Hooke actually did, I still have no idea.
I did a little research today, and I have not yet been able to find out how Hooke measured the frequency of a vibrating string. But I have been able to get some information.
Hooke died in 1703. Many of his papers were given to Richard Waller, and in 1705 Waller published Posthumous Works of Dr. Robert Hooke. As an introduction, Waller wrote "The Life of Dr. Robert Hooke", an itemization of every important research or contribution made by Hooke. Two of the entries are as follows:
In July 1664. he produc'd an Experement to shew the number of Vibrations of an extended String, made in a determinate time, requisite to make a certain Tone or Note, by which it was found that a Wire making two hundred seventy two vibrations in one Second of Time, founded G Sol Re Ut in the Scale of all Musick.(We would make it 384 vibrations; 272 is only C#. Whether this is due to a change in the definition of G, or experimental error, or both, I do not know. But it does resolve my question of whether Hooke did have a specific number for the rate at which a fly beat its wings, or whether he just identified it as low D and left it at that.)
[ Addendum 20060216: I realized this morning that it might also be caused by a change in the length of the second. ]
[ Addendum 20070917: I realized sometime later that this was a dumb suggestion. One second is 1/86400 of a day, then as it is now, and the length of the day has not changed significantly since 1664. ]
In July [1680] he shew'd a way of making Musical and other Sounds, by the striking of the Teeth of several Brass Wheels, proportionaly cut as to their numbers, and turned very fast round, in which it was observable, that the equal or proprtional stroaks of the Teeth, that is, 2 to 1, 4 to 3, &c. made the Musical Notes, but the unequal stroaks of the Teeth more answer'd the sound of the Voice in speaking.There we have it: He didn't think of the buzzing rotating wheel until 1680, so he must have been doing something else in 1664. What, I do not yet know.
[ Addendum: More about this: [1] [3] [4] ]
[Other articles in category /physics] permanent link
More low-tech sound recording
In an
earlier post, I wondered how Robert Hooke could have discovered
the frequency of a vibrating string in 1664. I suggested a device
involving a bristle that traced a sinusoid on a smoked glass plate. I
was sure that I head heard about this somewhere before, and wasn't
making it up.
With the Wonders of the Internet, such things are easy to look up. Google for "bristle" and "smoked glass" and there you have it. The device is called a "phonautograph", and was invented in 1857 by Leon Scott. So the idea does work, but was probably not what Hooke used. My search continues.
The phonautograph was one of Alexander Graham Bell's inspirations for the telephone. Bell, whose principal research area was to improve education of deaf persons, built a phonautograph of his own, using—get this—an actual human ear. The bristle was attached to the ossicles. He cut away the stapes bone, and attached a wheat straw to the incus. I wonder whose ear he used?
I've read that a phonautograph recording survives from around 1860 and is the oldest known sound recording, although there was no way to play it back until recently, when the tracing was digitized and given to a computer to synthesize.
There was some talk a few years ago about the possibility that clay pots might retain recordings of the ambient sounds from the time they were created: they are thrown on potters' wheels that revolve at a uniform speed; they have high recording resolution, and are frequently worked with sharp tools that would have left grooves in them much like the grooves of phonograph records. I saw an exhibit of this in a science museum somewhere, but I could not make anything of the sound that they recovered from the pot, even though it had been specially constructed for the purpose. There are obvious, major problems with the idea, but it's nice to think that we might someday be able to listen to sound recordings of Sumerians chatting in the potter's workshop.
Come to think of it, conventional phonography was pretty low-tech itself, until the introduction of magnetic and later digital media.
[ Addendum: More about this: [1] [2] [4] ]
[Other articles in category /physics] permanent link
Wed, 15 Feb 2006
Biblical infallibility and pi
Two recent minor themes of the blog have been the value
purportedly given for π in the Bible, and the
value of serendipity and random browsing in the library. Here's a
story about the Library Gods and how they sometimes shower you with
blessings, if you let them.
I went to the Penn library today to see what I could turn up about Robert Hooke's measurement of the vibrational rate of strings. (Incidentally, Clinton Pierce had an excellent suggestion about this, which I will relate sooner or later.) I checked the electronic catalog for collections of essays by Hooke, and found several; I picked a likely one and wrote down its call number. Or so I thought; I actually wrote down the call number of the previous entry by mistake. Upon arriving at the appropriate place in the stacks, or so I thought, I realized my mistake when I found the wrong book instead of the right one.
| Buy Mathematical and Philosophical Works of John Wilkins from Bookshop.org (with kickback) (without kickback) |
(I don't have an example handy, so I will make one up. All words that begin with "p" are animals. Words beginning with "pa" are birds, those with "pe" are fish, and so forth. Words beginning with "pel" are fish with fins and scales. Words for fin-fish that live in rivers and streams all begin with "pela". "pelam" is a salmon.)
| Buy An Essay Towards a Real Character and a Philosophical Language from Bookshop.org (with kickback) (without kickback) |
This discussion appears in Wilkins' book The Discovery of a New World, or, a discourse tending to prove that (it is probable) there may be another habitable world in the moon. This book is divided into two parts, the second of which is on the question of whether the Earth is a planet. There is, as you would expect from a book on the subject written in 1638, an extensive discussion of the Biblical evidence on this question.
Wilkins comes down very strongly against the Bible on this matter. The entire third chapter is devoted to arguing:
That the Holy Ghost, in many places of scripture, does plainly conform his expressions unto the errors of our conceits; and does not speak of divers things as they are in themselves, but as they appear to us.The chapter begins:
There is not any particular by which philosophy hath been more endamaged, than the ignorant superstition of such men: who in stating the controversies of it, do so closely adhere unto the mere words of scripture.(By "philosophy", here and elsewhere, Wilkins means what we would now call "natural science".) Wilkins then quotes an earlier author on the same topic:
"I for my part am persuaded, that these divine treatises were not written by the holy and inspired penmen, for the interpretation of philosophy, because God left such things to be found out by men's labour and industry."And he quotes John Calvin similarly:
It was not the purpose of the Holy Ghost to teach us astronomy: but being to propound a doctrine that concerns the most rude and simple people, he does (both by Moses and the prophets) conform himself unto their phrases and conceits. . .For example, Wilkins cites Psalms 19:6 ("the ends of heaven") and 22:27 ("the ends of the world"), Job 38:4 ("the foundations of the earth"), and says "all of which phrases do plainly allude unto the error of vulgar capacities, which hereby is better instructed, than it would be by more proper expressions."
After much discussion and many examples, Wilkins finally concludes:
From all these scriptures it is clearly manifest that it is a frequent custom of the Holy Ghost to speak of natural things, rather according to their appearance and common opinion, than the truth itself.So much for Biblical inerrancy. The following chapter is devoted to the demonstration "That divers learned men have fallen into great absurdities, whiles they have looked for the sects of philosophy from the words of scripture."
In the course of my (limited and cursory) research into the analysis of the Biblical value of π given in Kings and Chronicles, I learned something that I found shocking: to wit, that this is still considered a serious argument, at least to the extent that the world is filled with knuckleheaded assholes arguing about it. I don't think I can remember encountering any other topic that seemed to attract as many knuckleheaded assholes. The knuckleheaded assholes are on both sides of the argument, too. On the one hand you have the biblical inerrancy idiots, for whom words fail to express my contempt, and on the other hand you have the smug and intellectually lazy atheists, who ought to know better, but who are only too happy to grab any opportunity to ridicule the Bible.
If John Wilkins, who became a bishop, was able to understand in 1638 that it is a stupid argument, and that all the arguing on both sides is pointless and ill-conceived, why haven't we moved on by now? We have the Wonders of the Internet; why are we filling it up with the same old crap? Can't we do any better? Will we ever lay this one to rest? Isn't there something else to argue about yet?
But no, we still have knuckleheaded assholes trying to get special creation and 4,004 B.C. into school curricula. It's almost as though the Enlightenment never happened. It's obvious, of course, that these losers have missed out on the mainstream of twentieth-century thought. But next time you bump into them, remember that they've also missed out on the mainstream of seventeenth-century thought.
And atheists, please try to remember that just because stupid people flock to stupid religions, that it doesn't have to be that way, and remember the example of Bishop John Wilkins, who wrote a whole book to argue that when the Bible conflicts with common sense and physical evidence, you have to keep the evidence and ignore the scripture.
[Other articles in category /math] permanent link
Saguaros
In a
recent post, I discussed an uninteresting travel book I had read
recently, and compared it with Kon-Tiki, which is
an interesting travel book. I'm sure I'll write more about travel
books later; I have at least one post coming up about
Kon-Tiki, and at least one about William Bligh's book
about the mutiny on the H.M.S. Bounty. This latter one may not
sound much like a travel book, but it is, and it's a corker.
But today I realized I'd forgotten to mention one of my favorite travel books of all, Blue Highways, by William Least Heat Moon. Heat Moon lost his job and his wife, and decided that it was time to take a long trip. He got in his van and drove around the United States, staying away from big cities and big highways, driving on the little roads, the ones that are marked in blue on the maps. (My grandmother had a Bud Blake cartoon hanging in her kitchen for my whole life. It depicted an annoyed husband, driving a small, 1940's-style car, being crowded almost out of his seat by the large folding roadmap his wife was consulting. The caption said "And then, in about half an inch, you turn onto a tiny blue road...".)
Everywhere he went, Heat Moon stopped and talked to people: men refurbishing an 18th-century log cabin in Kentucky; a monk in Georgia; hang-gliders in Washington; farmers in New York and fishermen in Maine; old folks and young folks. All of them have interesting things to say, and Heat Moon has interesting things to say about all of them. You can open up the book anywhere and strike gold.
For example, on page 11, Heat Moon stops in Shelbyville, Kentucky, for dinner:
Just outside of town and surrounded by cattle and pastures was Claudia Sanders Dinner House, a low building attached to an old brick farmhouse with red roof. I didn't make the connection in names until I was inside and saw a mantel full of coffee mugs of a smiling Harlan Sanders. Claudia was his wife, and the Colonel once worked out of the farmhouse before the great buckets-in-the-sky poured down their golden bounty of extra crispy. The Dinner House specialized in Kentucky ham and country-style vegetables.One of my favorite passages is right at the beginning:
She came back with grape jelly. In a land of quince jelly, apple butter, apricot jam, blueberry preserves, pear conserves, and lemon marmalade, you always get grape jelly.Another is right at the end:
Order Point, Long Island, was a few houses and a collapsed four-story inn built in 1810, so I went to Greenport for gas. At an old-style station, the owner himself came out and pumped the no-lead and actually wiped the windshield. I happened to refer to him as a New Yorker.I really would like to know what would have happened if the East River had been ten miles wide instead of the stream of piss it is. No Brooklyn, for one thing; and that would be a shame."Don't call me a New Yorker. This is Long Island."
"I meant the state, not the city."
"Manhattan's a hundred miles from here. We're closer to Boston than the city. Long Island hangs under Connecticut. Look at the houses here, the old ones. They're New England-style because the people that built them came from Connecticut. Towns out here look like Connecticut. I don't give a damn if the city's turned half the island into a suburb—we should rightfully be Connecticut Yankees. Or we should be the seventh New England state. This island's bigger than Rhode Island any way you measure it. The whole business gets my dander up. We used to berth part of the New England whaling fleet here, and that was a pure Yankee business. They called this part of the island 'the flikes' because Long Island even looks like a whale. But you go down to the wharf now and you'll see city boats and a big windjammer that sells rides to people from Mamaroneck and Scarsdale."
He got himself so exercised he overfilled the tank, but he didn't pipe down. "If the East River had've been ten miles wide, we'da been all right." He jerked the nozzle out and clanked it into the pump. "We needed a bay and we got a bastard river no wider than a stream of piss."
But as usual, what I planned to write about was a completely different passage:
That's pretty interesting all by itself. I wonder if he's right? The arms do need an explanation, not just because they are weird-looking, but also because they would seem to be survival-negative. The big problem that desert plants have is the same one that desert animals have: how to stay out of the sun. Unlike animals, they can't hide in underground burrows during the day, or move to shady spots. So most of them do their best to be as narrow and vertical as possible; hence the barrel cactus and the saguaro. Deviating from this pattern, as the saguaro does, exposes more of the plant to the burning rays of the sun, so the plant wouldn't do it without good reason.The saguaro is ninety percent water, and a big, two-hundred-year-old cactus may hold a ton of it—a two-year supply. With this weight, a plant that begins to lean is soon on the ground; one theory now says that the arms, which begin sprouting only after forty or fifty years when the cactus has some height, are counterweights to keep the plant erect.
I wonder how you'd test something like that? You can't just tip a saguaro over a bit and see where the arms grow out, because those arms can take years and years to grow. (Also, it's not good for the plant, which is an endangered species. There's a reason that biologists like to study fruit flies.) Well, there's another thing on my list of things to look up after I'm granted immortality.
The Monday I drove northeast out of Phoenix, saguaros were in bloom—comparatively small, greenish-white blossoms perched on top of the trunks like undersized Easter bonnets; at night, long-nosed bats came to pollinate them. But by day, cactus wrens, birds of daring aerial skill, put on the show as they made kamikaze dives between toothpick-sized thorns into nest cavities, where they were safe from everything except the incredible ascents over the spines by black racers in search of eggs the snakes would swallow whole.Climbing snakes, wow! One of the legends of my house comes from a nature show that Lorrie and I once saw about alligators. The show depicted a woodpecker that lives in pitchy pine trees and pecks the trees to encourage a flow of the irritating sap down the outside. This deters the corn snakes from climbing the trees to eat the woodpeckers' eggs. This show followed the slow and careful ascent of a corn snake up one of the trees. As it was almost at the nest, it lost its grip and fell twenty feet to the ground. Stunned, it gathered its snaky wits and slithered away, apparently embarrassed, into the water nearby--where it was immediately devoured by a huge gator. A corn snake having the worst day of its life.
But the cosmic balance was preserved, because the cameraman was having the best day of his life.
I can just imagine how Mirza Abu Taleb Khan would have related this same journey:
We saw some large and remarkable plants as we left Phoenix. Mr. Charles Hightower informed me that they are called "cactus". These plants grew in many surprising and diverse shapes.
[Other articles in category /book] permanent link
Tue, 14 Feb 2006
More approximations to pi
In an earlier
post I discussed the purported Biblical approximation to π, and
the verses that supposedly equate it to 3.
Eli Bar-Yahalom wrote in to tell me of a really fascinating related matter. He says that the word for "perimeter" is normally written "QW", but in the original, canonical text of the book of Kings, it is written "QWH", which is a peculiar (mis-)spelling. (M. Bar-Yahalom sent me the Hebrew text itself, in addition to the Romanizations I have shown, but I don't have either a Hebrew terminal or web browser handy, and in any event I don't know how to type these characters. Q here is qoph, W is vav, and H is hay.) M. Bar-Yahalom says that the canonical text also contains a footnote, which explains the peculiar "QWH" by saying that it represents "QW".
The reason this is worth mentioning is that the Hebrews, like the Greeks, made their alphabet do double duty for both words and numerals. The two systems were quite similar. The Greek one went something like this:
| Α | 1 | Κ | 10 | Τ | 100 |
| Β | 2 | Λ | 20 | Υ | 200 |
| Γ | 3 | Μ | 30 | Φ | 300 |
| Δ | 4 | Ν | 40 | Χ | 400 |
| Ε | 5 | Ξ | 50 | Ψ | 500 |
| Ζ | 6 | Ο | 60 | Ω | 600 |
| Η | 7 | Π | 70 | ||
| Θ | 8 | Ρ | 80 | ||
| Ι | 9 | Σ | 90 |
Anyway, the Hebrew system was similar, only using the Hebrew alphabet. So here's the point: "QW" means "circumference", but it also represents the number 106. (Qoph is 100; vav is 6.) And the odd spelling, "QWH", also represents the number 111. (Hay is 5.) So the footnote could be interpreted as saying that the 106 is represented by 111, or something of the sort.
Now it so happens that 111/106 is a highly accurate approximation of π/3. π/3 is 1.04719755 and 111/106 is 1.04716981. And the value cited for the perimeter, 30, is in fact accurate, if you put 111 in place of 106, by multiplying it by 111/106.
It's really hard to know for sure. But if true, I wonder where the Hebrews got hold of such an accurate approximation? Archimedes pushed it as far as he could, by calculating the perimeters of 96-sided polygons that were respectively inscribed within and circumscribed around a unit circle, and so calculated that 223/71 < π < 22/7. Neither of these fractions is as good an approximation as 333/106.
Thanks very much, M. Bar-Yaholom.
[Other articles in category /math] permanent link
I was leafing through The Diary of Samuel Pepys recently. Pepys, in case you hadn't heard, was an official of the Royal Navy in England in the 17th century. He kept a meticulous diary, in which he recorded all sorts of trivia about what he did, who he saw, what he liked and didn't, what he ate and drank, and so on. It gives a wonderfully clear picture of life in London at the time. (The diary is available online; the version linked to the right is selections only. If you want to buy a paper copy of the complete diary, get it used, or it will be absurdly expensive. I got my copy at a library sale.)The diary is a good book for browsing. Someday I'd like to read a long stretch of it and try to get a sense of the history and continuity of what's going on. But in the meantime, it's still good for browsing. Every few pages you run into something fascinating. Here's what I ran into today:
August 8th, 1666. Discoursed with Mr. Hooke, whom I met in the streete, about the nature of sounds, and he did make me understand the nature of musicall sounds made by strings, mighty prettily; and told me that having come to a certain number of vibrations proper to make any tone, he is able to tell how many strokes a fly makes with her wings (those flies that hum in their flying) by the note that it answers to in musique, during their flying.Mr. Hooke, I hardly need tell you, is Robert Hooke, a groundbreaking scientist, and secretary of the (then newly-formed) Royal Society. (Pepys was later a member of the Society, and, still later, its president.) Hooke is responsible for Hooke's law, which states that the force exerted by a spring is proportional to the distance by which it has been extended or compressed from its natural length. He is also responsible for the use of the word "cell" to describe living cells.
This passage struck me first because it seemed so simple and clever to determine the rate at which a fly's wings beat by comparing the sound with that of a vibrating string. But as I thought about it more, it grew more puzzling. How do you know that a certain string, a middle C, say, is vibrating 256 times per second? How can you measure that with only 17th-century technology?
My first thought was that you can attach a bristle to the string, and then draw a piece of smoked glass under the bristle as the string vibrates; the bristle will leave a track on the glass. I seem to recall having heard of this being done at some time, but I can't remember the details. I'm also not sure that it could be done accurately enough. If you can pull a foot of glass past the bristle in one second, and the string is a middle C, then the bristle will trace a sinusoid whose peaks are about 1/21 inch apart, which is enough to measure. It seems plausible that something like this might be made to work with 17th-century technology. I think the sticking point would be moving the glass at a uniform speed. I don't think they had accurately machined screws yet.
So far the only other thing I have been able to think of is that since the relationship between the mass, tension, length, and pitch of a vibrating string was already known, Hooke measured some slow, massive vibrating rope, and then measured the tension, mass, and length of the string and extrapolated the vibrational rate from that. Perhaps there was a more direct method, but I don't know what it was.
These days you would just hold up a microphone that was plugged into an oscilliscope, or shine an adjustable strobe light on the fly. But you had to be pretty clever to carry out useful physics experiments in 1666.
That's one of the things that always amazes me about historical physics. The equipment was so crappy, it seems almost miraculous that they figured out anything at all. Consider the Greeks, who figured out that the moon shines by the reflected light of the sun. Presumably this idea originated in the observation that the lit side of the moon always faces the sun. But that's not all they did. They observed that the shape of the illuminated area was consistent with the shape you would see if part of a sphere was illuminated from without. Who the heck noticed that? They could presumably make spheres out of clay, but they didn't have any reliable, steady, directed light source. Candles flicker. So who got the idea to look at partially illuminated spherical wads of clay, and then went to the trouble of setting up the light source so they could examine the shape of the illuminated area?
[ Addendum: More about this: [2] [3] [4] ]
[Other articles in category /physics] permanent link
Mon, 13 Feb 2006
Accidental Features
Last week I was away in Chicago as part of my Red Flags world
tour, about which more in an upcoming entry. I mentioned before that
I always learn something surprising from giving these classes, and
this time was no exception. I was reviewing a medium-sized piece of
code for a client and I encountered the following astonishing
construction:
for $i qw(foo bar baz) {
# do something with $i
}
If you're not familiar with Perl, you aren't going to see what is
wrong with this. You may not see it for a while even if you
are familiar with Perl.Normally, the syntax for this sort of construction is:
for $VAR (LIST) {
...
}
where the parentheses around the LIST are not
optional. And the qw(...) construction generates a list. So
it should be:
for $i (qw(foo bar baz)) {
# do something with $i
}
Leave off the outer parentheses, and you should get a syntax error.
So when I saw this code, I said, "Oh, that's a syntax error."Except, of course, it wasn't. The code I was reviewing was in production on the client's web site, and was processing millions of dollars of orders. If it had bee a syntax error, they would have known right away. And indeed, it worked when I tried it.
But it's not documented anywhere, and I have never seen it before. It is certainly little-known. I believe it is an accidental feature.
This is not the first time that someone has discovered an unintended but useful feature in Perl. Another example that comes to mind is the s/.../.../ee trick. Normally, you give s/.../.../ a pattern and a replacement string, and it performs a substitution, locating some string that matches the pattern and replacing it with the replacement. For example, s/\d+/carrots/ locates a a numeral (a sequence of digits) and replaces it with carrots. But you might want to do something tricky; say you want to replace each numeral with its double. Then you can use s/(\d+)/$1 * 2/e. The $1 is replaced with the digits, so that if the digits are 123, you get 123 * 2, and the trailing e means that this is a Perl expression, rather than a literal string, and should be evaluated. Without the e, 123 becomes 123 * 2; with e, it becomes 246. (Other modifiers were permitted: for example, i made the pattern match case-insensitive.)
The implemenation was to scan the modifiers left-to-right, and to call Perl's expression evaluator if an e was seen. The accidental feature was that the implementation therefore allowed one to put two es to force two evaluations. The typical use of this was to write something like s/(\$\w+)/$1/ee, which finds $foo and replaces it with the value of the variable $foo. The first e evaluates $1 to $foo, and the second evaluates $foo to its value. I believe this was discovered by Tom Christiansen. It's rarely used now, since there are more straightforward ways to accomplish the same thing, but it still appears in three different places in the documentation.
I don't think it says anything good about Perl that this sort of accidental feature shows up in the language. I can't think of anything comparable in any other language. (Except APL.) C has the 4[ptr] syntax, but that's not a feature; it's just a joke. The for $i qw(...) { ... } syntax in Perl seems genuinely valuable.
Accordingly, I dropped a note to the Perl development mailing list, asking if anyone had ever noticed this before, and whether people thought we should commit to supporting it in the future. (It works in all versions of Perl that support qw().) I was surprised that there was no reply. So I suppose that the next step is to prepare a documentation patch describing it and some tests in the test suite for it. If everyone is still asleep when I post those, they may go in without comment, and once a feature is put in, it is very difficult to remove it.
[Other articles in category /prs] permanent link
Wed, 08 Feb 2006
Generating strings of balanced parentheses
About a year and a half ago, the Perl Quiz of the Week question was to
write a program which, given an argument n, printed out all the
strings containing n balanced pairs of parentheses. For
example, if the argument was 3, the output was to contain the
lines:
()()()
(())()
(()())
()(())
((()))
in some order.Enumerating parentheses is important because the parentheses obviously correspond to all the forms that an infix expression can take, so any attempt to enumerate all possible expressions of some form can be built atop a parenthesis-enumerator. But also, there's a straightforward correspondence between parentheses and tree structures, so by enumerating parentheses you are also enumerating all possible tree structures.
There were quite a few correct solutions posted to the list, and also some wrong ones. The commonest mistake to make was to assume that any string of n+1 pairs of balanced parentheses must have the form S(), ()S, or (S), where S is a string of n pairs of balanced parentheses. But this isn't so; (())(()) doesn't have this form. The commonest strategy that worked correctly was to generate all the strings of the right length of the form (S)S, where S is a shorter balanced string. This can be done recursively as follows:
sub parens {
my ($N) = @_;
return ("") if $N == 0;
my @result;
for my $i (0 .. $N-1) {
for $a (parens($i)) {
for $b (parens($N-$i-1)) {
push @result, "($a)$b";
}
}
}
return @result;
}
print join "\n", parens(shift()), "";
Or you can organize the logic differently:
sub parens {
my $N = shift;
$pattern = @_ ? shift : "S";
if ($N == 0) {
$pattern =~ tr/S//d;
return $pattern;
}
return unless $pattern =~ /S/;
my $new_pattern_a = my $new_pattern_b = $pattern;
$new_pattern_a =~ s/S/S(S)/;
$new_pattern_b =~ s/S//;
return parens($N-1, $new_pattern_a), parens($N, $new_pattern_b);
}
print join "\n", parens(shift()), "";
A somewhat different approach was to build up the string from left to
right. Here $s tracks the string built so far, $N
counts the number of )'s that are still required, and
$unclosed counts the number of ('s that have been
added without a corresponding ). The function may append a
( to the string, increasing the number of unclosed open
parentheses, if there are fewer than $N such unclosed pairs
total, and it may append a ), decreasing both the number of
required close parentheses and the number of unmatched open
parentheses, as long as at least one open parenthesis remains
unclosed.
sub parens {
my ($N, $unclosed, $s) = @_;
$unclosed ||= 0;
$s ||= "";
return $s if $N == 0;
my @result;
push @result, parens($N, $unclosed+1, "$s(") if $unclosed < $N;
push @result, parens($N-1, $unclosed-1, "$s)") if $unclosed > 0 ;
return @result;
}
print join "\n", parens(shift()), "";
I had originally planned to do something like the first of these. But
a couple of days of intermittent tinkering revealed a completely
different and unexpected algorithm:
#!/usr/bin/perl -l
print $_ = "()" x shift();
print while s{^ ( \(+ ) ( \)+ ) \( }
{"()" x (length($2) - 1)
. "(" x (length($1) - length($2) + 2)
. ")"
}xe;
This is understandably mystifying, since in tidying it up (and getting
it to run as fast as possible) I also erased all the clues as to how I
got here to begin with. Folks on the mailing list asked how I came up
with this. What follows is a somewhat edited version of my reply. I
said at the time:
I can explain how I thought it up, although I'm not sure whether the explanation will be helpful or whether it will sound like "I just counted the legs and divided by four."By this I meant that the explanation might leave people even more mystified than the algorithm itself. I'm still not sure it won't sound like that, so I'm going to include the following one-paragraph summary that omits the details:
One of the other list members suggested an alternative representation for the strings that seemed promising, so I tried out some examples. Close examination of those examples reminded me of a technique I had used to solve some other problems, so I tried to apply it in this case with the necesary variations. It worked well enough to continue the investigation, but the alternative representation was getting in the way. So I took what I had learned from applying the technique to the alternative representation and tried to write an algorithm to do the same thing directly to the strings of parentheses. Then I optimized the result for speed and code compactness.The details follow.
I had originally planned to write a recursive solution, but before I started I thought it would be smart to investigate alternative representations. (Someday I'm going to write a long essay about this. I mentioned to Kurt Starsinic last week that the one sure sign of a program written by a novice programmer is that it will represent the data internally in the same format in which it needs to be output, typically as strings.)
One of the representations I looked at was one that had earlier been mentioned by Roger Burton West on the list. In this representation, a string of one "(" followed by n ")"'s becomes the number n, thus:
()()()() 1111
()()(()) 1102
()(())() 1021
()(()()) 1012
()((())) 1003
(())()() 0211
(())(()) 0202
(()())() 0121
(()()()) 0112
(()(())) 0103
((()))() 0031
((())()) 0022
((()())) 0013
(((()))) 0004
Now if you look at the right-hand column, and at the way the numbers,
change, it will seem awfully familiar. Or at least, it felt familiar
to me. It reminded me very strongly of a counting process. The essence of a counting process is that you find the rightmost column that has a certain property, and then you do a little transformation on it so that it gets a little less of that property and the columns to the right get reset to have more of it.
I realize that if you've never thought of it that way that is going to sound totally bizarre, so here's an example. Let's count base-10 numerals. The magic property in this case is the property of being less than 9. 0 has the largest possible amount of this property, since it is as much less than 9 as any digit can be. 8 has very little of this property, since it is just a little less than 9. 9 itself does not have any of this property, since it is not less than 9.
When you count, you find the rightmost column that is less than 9 and then you do a little transformation on it so that it has a little less of that property, so that it a little closer to 9:
387
388
389
After you have done that a few times, you get to a point where the
rightmost column's less-than-9-ness has been entirely depleted and you
can't change it any more. So you move to the next column to the left
and deplete that one instead, and you reset the rightmost column so
that it is full of less-than-9-ness again:
390
Then you continue:
391
392
...
399
and now you have to deplete the less-than-9-ness of the third column,
and reset the two to its right:
400
This may be a weird way to look at counting, but it describes all
sorts of useful processes. To count in base 2, you allow the columns
to hold 0's and 1's, and the property of interest is the property of
being a 0; you find the rightmost column that is a 0, and change it to
a 1, and change the columns to its right back to 0's.Probably the next simplest example is when the property of interest is that the n'th column contains a number less than or equal to n:
0000
0010
0100
0110
0200
0210
1000
1010
1100
1110
1200
1210
2000
2010
...
3210
This turns out to be useful if you are trying to
enumerate permutations; I wrote about it on pages 128–135 of
Higher-Order Perl, where I called it the "odometer
method". It's used again in the following section to enumerate DNA
sequences. So it's a pretty fundamental technique, and turns out to
be useful in a wide variety of settings.Another example I was already familiar with is like the base-2 counting example, but with the added restriction that you are not allowed to have two adjacent 1's:
0000000
0000001
0000010
0000100
0000101
0001000
0001001
0001010
0010000
0010001
0010010
0010100
0010101
0100000
...
We can generate these strings by repeatedly doing this:
s/00((10)*1?)$/"01" . "0" x length $1/e;
(This pattern has close relations to the Fibonacci sequence. For
example, the nth string contains a single 1 exactly
when n is a Fibonacci number. Moreover, every positive integer
has a unique representation as a sum of distinct nonconsecutive
Fibonacci numbers, the so-called "Zeckendorff representation", and
this counting thing tells you what it is. This is analogous to the
way that every positive integer has a unique representation as a sum
of distinct powers of 2, and the binary expansion tells you what it
is.)So anyway, I was already familiar with this idea, and when I saw the parenthesis numbers, it reminded me strongly of one of these counting processes. Here they are again:
1111
1102
1021
1012
1003
0211
0202
0121
0112
0103
0031
0022
0013
0004
Here the rule seems to be that you always decrement the rightmost
nonzero digit that isn't in the last column and increment the
following digit—I imagine that the digits are little heaps of
1's, and you are allowed to transfer a 1 from its
heap to the heap on its right. But there are some additional
constraints.Since a number n here represents the string ()))...), with n close parentheses, we have the constraints that the leftmost column may not exceed 1; the sum of the two leftmost columns may not exceed 2, and so on. Under these constraints, 1111 is clearly an extreme case, and no string has the 1's any farther to the left. To go from 1111 to 1102, the rightmost moveable 1, which is in the third column, moves to the right, into the fourth column, which I now imagine contains a heap of two 1's.
Now the rightmost 1 is in the second column. So I reset the columns to the right of that (getting back 1111) and then move the 1 from the second to the third column, yielding 1021. Again, I imagine that the 2 here represents a heap of two 1's. These 1's can move to the right, yielding 1012 and then 1003.
Now I'll need to move the 1 from the first to the second column, so I reset the columns to the right of that (getting back 1111 again) and move the 1 from the first to the second column, yielding 0211. Then the 1 in the third column moves, yielding 0202, and then I reset the third and fourth columns back to 0211 so that I can move a 1 from the second to the third column, yielding 0121.
My first cut at implementing this actually manipulated these digit strings directly, like this:
output while s/([1-9])(0*)([1-9])$/($1-1).($3-length($2)+1).1x length($2)/e;
As a result, it wouldn't work for n > 9. But after I
thought about it some more, I realized I didn't need to deal with the
digit strings; I could directly manipulate the parentheses in the
corresponding way. This was faster, simpler, and got rid of the
n < 10 restriction.Translated back into parentheses, the algorithm might even be simpler to understand. The property we are trying to reduce is appearances of )(, in which ( appears to the right of ). In ()()()...(), the open parentheses are as far to the right as they can be, so this represents the maximal configuration. At each step, we're going to find the rightmost moveable open parenthesis, and we're going to move it one step to the left. That is, we're going to find the rightmost )( and change it to (). If there are other parentheses to the right of the ones that moved, we'll reset them into their minimal configuration. In what follows, the )( that just changed to () is in red, and the parentheses to its right that were reset are in blue. The )( that is about to change to () in the next step is in boldface.
In the initial configuration, the rightmost )( is in positions 6-7:
()()()() 1111
We replace it with ():
()()(()) 1102
Now the rightmost )( is in positions 4 and 5. We replace it
with () and reset the following
parentheses to the minimal configuration:
()(())() 1021
The rightmost )( is on the right again, so we get:
()(()()) 1012
Now the rightmost )( is at positions 5 and 6, so the string
changes to:
()((())) 1003
Now the only )( is far to the left, at positions 2–3, so
when we change it, we need to reset the parentheses to its right:
(())()() 0211
And it continues in the same way:
(())(()) 0202
(()())() 0121
(()()()) 0112
(()(())) 0103
((()))() 0031
((())()) 0022
((()())) 0013
(((()))) 0004
After I had implemented that, I realized there was nothing stopping me
from writing all the strings backward, and doing the substitutions at
the left end of the string instead of at the right end. This is
always much cheaper in perl's regex engine because it doesn't have to
guess where to start matching in the target string. So I reversed the
whole thing. It no longer produced the parentheses in lexicographic
order (unless you read right to left) but it was substantially
faster. Another solution to the problem is "consult Knuth". Volume IV of The Art of Computer Programming will contain an entire section devoted to this problem, and includes the algorithm I described. Volume IV isn't published yet, but the relevant section is. As of this writing, it is also still available from Knuth's web site.
[Other articles in category /CS] permanent link
Mon, 06 Feb 2006 I continue to read Martin Chuzzlewit. I have reached the point in the book at which Dickens realized that sales were poorer than he had hoped, and threw in a plot twist to raise interest: Martin has decamped for America. Dickens is now insulting the Americans as hard as he can. I find that the book has suddenly become substantially less interesting and that Dickens's keen observation and superior characterization are becoming sloppy. Or perhaps I'm just taking it too personally.(On the bright side, we are getting to see more of Mark Tapley. Mark is kind, astute, thrifty, and above all, cheerful. Born with a naturally jolly disposition, he has chosen it as his life goal to remain jolly under even the most trying circumstances. In pursuit of this goal, he seeks out the most trying circumstances possible, the better to do himself credit by his unfailing jollity. When we first meet him, he is working at the Blue Dragon pub, but is planning to quit:
`What's the use of my stopping at the Dragon? It an't at all the sort of place for me. When I left London (I'm a Kentish man by birth, though), and took that situation here, I quite made up my mind that it was the dullest little out-of-the-way corner in England, and that there would be some credit in being jolly under such circumstances. But, Lord, there's no dullness at the Dragon! Skittles, cricket, quoits, nine-pins, comic songs, choruses, company round the chimney corner every winter's evening. Any man could be jolly at the Dragon. There's no credit in that.'Anyway, that is the end of my digression about Mark Tapley. I started this note not to discuss the delightfully insane Mark Tapley, but to bring up the following passage:`But if common report be true for once, Mark, as I think it is, being able to confirm it by what I know myself,' said Mr. Pinch, `you are the cause of half this merriment, and set it going.'
`There may be something in that, too, sir,' answered Mark. `But that's no consolation.'
Martin thought this an uncomfortable custom, but he kept his opinion to himself for the present, being anxious to hear, and inform himself by, the conversation of the busy gentlemen . . . .This reminded me of something, and it took me a while to dredge it up from my memory. But at last I did, and I present it to you:It was rather barren of interest, to say the truth; and the greater part of it may be summed up in one word. Dollars. All their cares, hopes, joys, affections, virtues, and associations, seemed to be melted down into dollars. Whatever the chance contributions that fell into the slow cauldron of their talk, they made the gruel thick and slab with dollars. Men were weighed by their dollars, measures gauged by their dollars; life was auctioneered, appraised, put up, and knocked down for its dollars. The next respectable thing to dollars was any venture having their attainment for its end. The more of that worthless ballast, honour and fair-dealing, which any man cast overboard from the ship of his Good Name and Good Intent, the more ample stowage-room he had for dollars. Make commerce one huge lie and mighty theft. Deface the banner of the nation for an idle rag; pollute it star by star; and cut out stripe by stripe as from the arm of a degraded soldier. Do anything for dollars! What is a flag to them!
I heard an Englishman, who had been long resident in America, declare that in following, in meeting, or in overtaking, in the street, on the road, or in the field, at the theatre, the coffee-house, or at home, he had never overheard Americans conversing without the word DOLLAR being pronounced between them. Such unity of purpose, such sympathy of feeling, can, I believe, be found nowhere else, except, perhaps, in an ants' nest. The result is exactly what might be anticipated. This sordid object, for ever before their eyes, must inevitably produce a sordid tone of mind, and, worse still, it produces a seared and blunted conscience on all questions of probity.That's from Domestic Manners of the Americans, by Frances Trollope, published 1832. (Thanks to the Wonders of the Internet, it is available online. I have not read this myself; I remembered the quotation from The Book of Insults, edited by Nancy McPhee, and thanks to more Wonders, was able to track down the source for the first time.)
Martin Chuzzlewit was written in 1843-1844. Dickens had travelled in America for the first time in 1842. I wonder how much of what he saw and thought was colored by Trollope's account, which I imagine he had read.
[ Addendum 20160206: I did later read some of the Trollope book. ]
[Other articles in category /book] permanent link
Sat, 04 Feb 2006
Approximations to pi
In an earlier
post I mentioned G.H. Hardy's astonishment when he first
encountered Ramanujan's approximation to π:
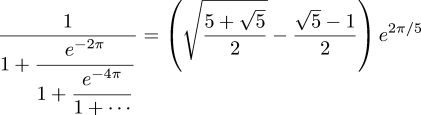
I'm planning to write a blog article about Gaussian integers, and in the course of my research I picked up my old, battered copy of G.H. Hardy's Pure Mathematics. I haven't spent as much time reading this book as I should have; it's full of good stuff. There didn't seem to be anything in there about the Gaussian integers (digression: What's next in the sequence 1, 2, 4, 6, 10, 14, 16, 24, 26?) but while scanning the index I noticed there was an entry for Ramanujan, so I checked it out.
The entry concerns approximations to π, and in particular π ≅ (13/25)√146. Hardy says "If R is the earth's radius, the error in supposing AM to be its circumference is less than 11 yards."
Hardy continues, mentioning the well-known approximations 22/7 and 355/113, about which I am sure I will have something to say in the future, in connection with continued fractions. He then says:
A large number of curious approximations will be found in Ramanujan's Collected papers, pp. 23-39. Among the simplest areAll of which, in my usual digressive style, is only an introduction to the main point of this note, which is that Hardy finishes the section by saying:
these are correct to 3, 3, 8, and 9 places respectively.
;
It is stated in the Bible (1 Kings vii. 23, 2 Chron. iv. 2) that π = 3.Let's look at what the Bible actually says:
1 Kings 7:23 And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about.I think there are two arguments that must be made here in defense of the Bible. First, one can infer the supposed value of π only if one assumes that the molten sea was a geometrically exact circle. But the sea is not described as circular; it is described only as "round". It could have been an approximate circle; or it could have been a mathematically exact ellipse; or it could have had many other shapes. Veterans' Stadium in Philadelphia was often described as "round" also, and it was not a circle, but an octorad. Watermelons are round, but are not circular, or spherical.2 Chronicles 4:2 Also he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about.
The other argument I would make is that it is not at all clear that any attempt was being made to state the sizes with mathematical exactitude. The use of round numbers throughout (no pun intended) supports this. If the Bible had said that the molten sea was thirteen cubits across and thirty-nine cubits around, I might agree that Hardy was right to complain. But if we suppose that the measurements are only being reported to one significant figure, we cannot conclude whether the value of π that was used was 3 or 3.1416—or 2.7 for that matter. If you say that your house is forty feet tall, you would be rightly annoyed to have G.H. Hardy to come and ridicule you for being unable to distinguish between the numbers 40 and 41.37.
Hardy was an atheist, and was very strongly anti-religious. (C.P. Snow says, in the preface to A Mathematician's Apology, that "On a quiet and lovely May evening at Fenner's, round about the same period, the chimes of six o'clock fell across the ground. 'It's rather unfortunate', said Hardy simply, 'that some of the happiest hours of my life should have been spent within sound of a Roman Catholic church.'") He was only too glad to take little potshots at the Bible at any opportunity, even in his pure mathematics textbook—or especially so, since he could get in an additional dig through the implied comparison with Ramanujan. It's certainly true that the ancient Hebrews were not mathematically sophisticated. But this particular potshot, which Hardy is far from the only person to take, seems to me to be unearned.
[Other articles in category /math] permanent link
The Kansas state quarter
In the 1986 Baseball Abstract, sportswriter Bill James, a
Kansas native, included an article titled A History of Being a
Kansas City Baseball Fan. The article begins:
I am, and have been for as long as it is possible to remember, a fan of the Kansas City baseball teams. In my youth this required that I support the Kansas City Athletics, the only team in modern history which has never had a .500 or better season.It goes on from there for about thirty pages, and ends with a detailed account of the Kansas City Royals' victory in the World Series the previous season. My old friend James Kushner once described this article to me as the best piece of sports writing he had ever read. I have not read anywhere near as much sports writing as my friend, but I would also rank it as number one. Like all my favorite writing, it drags in all sorts of fascinating peripheral matters, such as the negative depictions of Kansas in popular culture, and Kansas City's inferiority complex when it compares itself to other cities:
At every insurgence of the national media, Kansas City press packets were handed out repeating a number of overworked boasts about the place. "Kansas City has more fountains than Rome." . . . "Kansas City has more miles of boulevards than Paris." This one always conjures up images of the International Board of Boulevard Certification, walking along saying "No, I'm afraid this one is just an 'Avenue' unless you widen the curb space by four more inches and plant six more trees per half mile." . . . The city's image would improve a lot of they would just accept themselves for what they are, and stop handing out malarkey about how many miles of boulevard they have.Anyway, the Kansas state quarter was minted last year, and it's my favorite state quarter so far.
 It's attractive and clean, and clearly
represents the state. It features sunflowers and a bison. They're
good-looking sunflowers and it's a good-looking bison.
It's attractive and clean, and clearly
represents the state. It features sunflowers and a bison. They're
good-looking sunflowers and it's a good-looking bison.And, unlike most of the other state quarters, it has no extraneous text. No patronizing caption. No vapid mottoes. No "Land of Lincoln" or "Pioneers of Aviation". No cutesy state nickname. No malarkey about how many miles of boulevard. Just "Kansas 1861". The designers let the picture speak for itself. That takes confidence, and I think it paid off.
Good job, Kansans.
[Other articles in category ] permanent link
Thu, 02 Feb 2006
Preventing multiple SMTP connections
As I believe I said somewhere else, I have a lot of ideas, and only
about one in ten turns out really well in the end. About seven-tenths
get abandoned before the development stage, and then of the three that
survive to development, two don't work.
The MIT CS graduate student handbook used to have a piece of advice in it that I think is very wise. It said that two-thirds of all research projects are failures. The people that you (as a grad student at MIT) see at MIT who seem to have one success after another are not actually successful all the time. It's just that they always have at least three projects going on at once, and you don't hear about the ones that are flops. So the secret of success is to always be working on several projects at once. (I wish I could find this document again. It used to be online.)
Anyway, this note is about one of those projects that I carried through to completion, but that was a failure.
The project was based in the observation that spam computers often make multiple simultaneous connections to my SMTP server and use all the connections to send spam at once. It's very rare to get multiple legitimate simultaneous connections from the same place. So rejecting or delaying simultaneous connections may reduce incoming spam and load on the SMTP server.
My present SMTP architecture spawns a separate process for each incoming SMTP connection. So an IPC mechanism is required for the separate processes to communicate with each other to determine that several of them are servicing the same remote IP address. Then all but one of the processes can commit suicide. If the incoming email is legitimate, the remote server will try the other messages later.
The IPC mechanism I chose was this: Whenever an SMTP server starts up, servicing a connection from address a.b.c.d, it creates an empty file named smtplock/a/b/c/d and gets an exclusive file lock on it. It's OK if the file already exists. But if the file is already locked, the server should conclude that some other server is already servicing that address, and commit suicide.
This worked really well for a few weeks. Then one day I came home from work and found my system all tied into knots. The symptoms were similar to those that occurred the time I used up all the space on the root partition, so I checked the disk usage right away. But none of the disks were full. A minute later, I realized what the problem was: creating a file for each unique IP address that sent mail had used up all the inodes, and no new files could be created.
The IPC strategy I had chosen gobbled up about twenty thousand inodes a day. At the time I had implemented it, I had had a few hundred thousand inodes free on the root partition. Whoops.
Compounding this mistake, I had made another. I didn't provide any easy way to shut off the feature! It would have been trivial to do so. All I had to do was predicate its use on the existence of the smtplock directory. Then I could have moved the directory aside and the servers would have instantly stopped consuming inodes. I would then have been able to remove the directory at my convenience. Instead, the servers "gracefully" handle the non-existence of smtplock by reporting a temporary failure back to the remote system and aborting the transmission. To shut off the feature, I had to modify, recompile, and re-install the server software.
Duh.
[ Addendum 20060202: There is a brief followup to this article. ]
[Other articles in category /oops] permanent link
More on multiple SMTP connections
[ The previous
article is here. ]
Two people so far have written in to ask why I didn't just have the SMTP server delete the lock files when it was done with them. Well, more accurately, one person wrote in to ask that, one other person just said that it would solve my problem to do it.
But I thought of that, and I didn't do it; here's why. The lock directory contains up to 16,843,009 directories that cannot, typically, be deleted. Thus deleting the lock files does not solve the problem; at best it postpones it.
John Macdonald had a better suggestion: To lock address a.b.c.d, open file a/b and lock byte 256·c+d. This might work.
But at this point my thinking on the project is that if a thing's not worth doing at all, it's not worth doing well.
[Other articles in category /oops] permanent link
Petard corrections
Eric Cholet has written in to mention that he is familiar with the fried choux
pastry that I mentioned yesterday, but under the name pets de
nonne, not pets de soeurs, as I said. (Nonne, of
course, is "nun". The word soeur is literally "sister", but in
this context means "nun". ) I had cited On Food and
Cooking as mentioning pets de soeurs, but it agrees with
Eric, not with me.
It appears, though, that many people do use the name pets de soeurs to refer to these fritters, and some people also use it to refer to a kind of soda-raised cinnamon roll. Citations to various cookbooks are available through the usual searches.
Eric also points out that petard is the current word for a firecracker, and also now refers to a doobie. I was already aware of this because pictures of those things appeared when I did Google image seach for petard. Thank you, Eric.
[Other articles in category /lang/etym] permanent link
Wed, 01 Feb 2006
The 3n+1 domain
In an earlier
post, I said:
The second proof depends on the (unproved) fact that lowest-term fractions are unique. This is actually a very strong theorem. It is true in the integers, but not in general domains.To fully address this, I need to discuss one of the most fundamental ideas of number theory, the prime factorization. Every positive integer is either a product of two smaller integers, or else is a prime. Primes include 2, 3, 5, and 7. 4 is not prime because it is the product of 2 and 2; 6 is not prime because it is the product of 2 and 3. 221 is the product of 13 and 17; 222 is the product of 6 and 37; 223 is prime. (1 is a special case, and is not considered prime.) This much you probably already know.
The primes were recognized by mathematicians thousands of years ago. Euclid's Elements, written around 2300 years ago, includes a proof that there is no largest prime number. The most important theorem about the positive integers, also known to the Greeks, is that every positive integer has a unique representation as a product of primes. This theorem, fittingly, is known as the "fundamental theorem of arithmetic".
It's quite easy to show that every positive integer can be represented as a product of primes. Suppose that this were not so. Then there would have to be a smallest positive integer n that was not so representable. The number n is either 1, or is prime, or is a product of smaller numbers. If it is 1, it is representable as the "empty product", another special case. If n itself is prime, then it is trivially represented as the product of the single prime n. (Mathematicians customarily allow such things.) Otherwise, n is the product of two smaller numbers, say p and q. But these two numbers are representable as the products of primes, since they are smaller than n, and n is the smallest number not so representable. And then n's representation would be the concatenation of the representations of p and q.
But showing that the representation is unique is trickier. If it seems obvious, you probably haven't thought about it enough. For example, consider the number 24. We can decompose 24 into the product of smaller numbers as 4×6. Then 4 decomposes to 2×2 and 6 to 2×3, so 24 = 2×2×2×3. But what if we had decomposed 24 differently, say as 3×8? Then we decompose 8 as 2×4, and 4 as 2×2, yielding 24 = 3×2×2×2. The two decompositions end up in the same place. But was that guaranteed? What about for a really big number, like 3,628,800? There are a lot of ways to decompose this. Can we be sure that all paths will end at the same place?
For the integers, the answer is yes, they do. But this is a special property of the integers. One can find simple structures, analogous to the integers, where two paths might not end at the same factorization.
The usual example of this is the so-called 3n+1 domain. In this world, we consider only the integers of the form 3n+1. That is, the only numbers of interest are 1, 4, 7, 10, 13, 16, and so on. It's quite easy to show that the product of any collection of these numbers is another one of the form 3n+1. (Briefly, because (3n+1) × (3m+1) = 9mn+3m+3n+1 = 3·(3mn+m+n) + 1. But if you're not convinced by this, just try some examples.)
The 3n+1 domain has its own idea of what is prime and what isn't. 1, as usual, is a special case. 4 is prime, because it is not a product of smaller numbers. (2×2 doesn't work, because the 3n+1 domain has no 2.) 7 is prime, as usual. 10 is prime. (Again, because the 3n+1 domain has neither 2 nor 5.) 13 is prime, as usual. 16 is not prime; it is 4×4, as usual.
The proof that every number has a prime factorization goes through in the 3n+1 domain just as in the regular integers. But the proof that the factorization is unique does not go through, because in fact the 3n+1 domain does not have this property. The smallest example for which it fails is 100, which has not one but two factorizations into primes: 100 = 4 × 25 = 10 × 10.
The failure of the fundamental theorem of arithmetic in the 3n+1 domain triggers the failure of a long series of related results, like the first domino in a series knocking over the others. For example, in the regular integers, if p is prime, and ab is a multiple of p, then either a or b (or both) is a multiple of p. In particular, if the product of two integers is even, then at least one of the two integers must have been even. This does not hold true in the 3n+1 domain. A counterexample is that neither 4 nor 25 is a multiple of the prime 10, but their product is.
Yet another failure is the one with which I opened the article. We say that two integers have a common factor d if they are both multiples of d. (d = 1 is conventionally excluded, since all integers are multiples of 1.) For example, 28 and 18 have a common factor of 2 since they are both multiples of 2; 36 and 63 have a common factor of 9. 14 and 15 have no common factor. When we write fractions, we customarily forbid the numerator and denominator to have a common factor, since the fraction can then be written more simply by canceling the common factor. For example, we never write 36/90; we always cancel the common factor of 18 and write 2/5 instead. When the numerator and denominator have no common factor, we say that the fraction is "in lowest terms".
Each rational number has a unique representation as a lowest-terms fraction, as the quotient of two integers that have no common factor. There is no way to write 2/5 as the quotient of two numbers other than 2 and 5, except by multiplying them by some constant factor, to get something uninteresting like 200/500.
This property also fails in the 3n+1 domain. Some rational numbers have more than one representation. 4/10 = 10/25, but neither 4 and 10 nor 10 and 25 have common factors to cancel, since the 3n+1 domain omits both 2 and 5.
Exercise: Does the analogous 4n+1 domain have unique prime factorizations?
Coming eventually: Gaussian integers and Eisenstein integers.
[Other articles in category /math] permanent link