Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 23 Apr 2024
Well, I guess I believe everything now!
The principle of explosion is that in an inconsistent system everything is provable: if you prove both !!P!! and not-!!P!! for any !!P!!, you can then conclude !!Q!! for any !!Q!!:
$$(P \land \lnot P) \to Q.$$
This is, to put it briefly, not intuitive. But it is awfully hard to get rid of because it appears to follow immediately from two principles that are intuitive:
If we can prove that !!A!! is true, then we can prove that at least one of !!A!! or !!B!! is true. (In symbols, !!A\to(A\lor B)!!.)
If we can prove that at least one of !!A!! or !!B!! is true, and we can prove that !!A!! is false, then we may conclude that that !!B!! is true. (Symbolically, !!(A\lor B) \to (\lnot A\to B)!!.).
Then suppose that we have proved that !!P!! is both true and false. Since we have proved !!P!! true, we have proved that at least one of !!P!! or !!Q!! is true. But because we have also proved that !!P!! is false, we may conclude that !!Q!! is true. Q.E.D.
This proof is as simple as can be. If you want to get rid of this, you have a hard road ahead of you. You have to follow Graham Priest into the wilderness of paraconsistent logic.
Raymond Smullyan observes that although logic is supposed to model ordinary reasoning, it really falls down here. Nobody, on discovering the fact that they hold contradictory beliefs, or even a false one, concludes that therefore they must believe everything. In fact, says Smullyan, almost everyone does hold contradictory beliefs. His argument goes like this:
Consider all the things I believe individually, !!B_1, B_2, \ldots!!. I believe each of these, considered separately, is true.
However, I also believe that I'm not infallible, and that at least one of !!B_1, B_2, \ldots!! is false, although I don't know which ones.
Therefore I believe both !!\bigwedge B_i!! (because I believe each of the !!B_i!! separately) and !!\lnot\bigwedge B_i!! (because I believe that not all the !!B_i!! are true).
And therefore, by the principle of explosion, I ought to believe that I believe absolutely everything.
Well anyway, none of that was exactly what I planned to write about. I was pleased because I noticed a very simple, specific example of something I believed that was clearly inconsistent. Today I learned that K2, the second-highest mountain in the world, is in Asia, near the border of Pakistan and westernmost China. I was surprised by this, because I had thought that K2 was in Kenya somewhere.
But I also knew that the highest mountain in Africa was Kilimanjaro. So my simultaneous beliefs were flatly contradictory:
- K2 is the second-highest mountain in the world.
- Kilimanjaro is not the highest mountain in the world, but it is the highest mountain in Africa
- K2 is in Africa
Well, I guess until this morning I must have believed everything!
[Other articles in category /math/logic] permanent link
Mon, 04 Sep 2023
Gantō's axe does have computational content
A while back I was thinking about this theorem of intuitionistic logic:
$$((P\to Q)\land ((P\to \bot) \to Q)) \to {(Q\to\bot)\to \bot} \tag{$\color{darkred}{\heartsuit}$}$$
Since it's intuitionistically valid, its proof can be converted into a program with the corresponding type. But the function that you get seemed to be computationally vacuous, since it could only be called with arguments that were impossible to obtain, or else with arguments that render the whole thing silly. For the former, you can make it work in general if you have at hand a function of type !!(P\to\bot)\to Q!! — but how could you? And for the latter, you can make it work if !!Q=\mathtt{int}!!, in which case you don't really need the program at all since !!(Q\to\bot)\to\bot!! is trivially true.
Several people replied to me about this, but the most interesting response I got was from Simon Tatham, who observed that !!\color{darkred}{\heartsuit}!! is still intuitionistically valid if you replace !!\bot!! with arbitrary !!R!!:
$$((P\to Q)\land ((P\to R) \to Q)) \to {(Q\to R)\to R} \tag{$\color{purple}{\spadesuit}$}$$
The proof is essentially the same:
- Suppose you have: !!f : P\to Q!! and !!g:(P\to R) \to Q!!
- then if you also have !!h: Q\to R!!, you can compose it with !!f!! to get !!h\circ f : P\to R!!
- which you can feed to !!g!! to get !!g(h\circ f) : Q!!
- and then feed that to !!h!! to get !!h(g(h\circ f)) : R!!.
But unlike !!\color{darkred}{\heartsuit}!!, this is computationally interesting.
M. Tatham gives this example: Take !!R!! to be !!\mathtt{bool}!!. We can understand a function !!X \to R!! as a subset of !!X!!, represented by its characteristic function. Say that !!Q!! is the type of subsets of !!P!!, perhaps in some representation that is more concrete than characteristic functions. If you'd like a more specific example, take !!P!! to be the natural numbers, and !!Q!! to be (recursive) sets of natural numbers as represented by (possibly infinite) lists in strictly increasing order.
Then:
!!f!! is some arbitrary function that assigns, to each element of !!P!!, a related subset of !!P!!. Say for example that !!f(p)!! is the semispatulated closure of !!p!!.
!!g!! could be the isomorphism that converts a subset of !!P!!, represented as a characteristic function, into one represented as a !!Q!!.
!!h : Q\to \mathtt{bool}!! is a single subset of !!Q!!, represented as a characteristic function on !!Q!!. Say, !!h(q)!! is true if and only the set !!q\subset P!! has the Cosell property.
With these interpretations, !!(h\circ f)(p) : P\to \mathtt{bool}!! tells you whether !!p!!'s semispatulated closure has the Cosell property, and !!g(h\circ f)!! is the element of !!Q!! that represents, !!Q!!-style, the set of all such !!p!!.
Then !!h(g(h\circ f)) : R!! computes whether this set itself also has the Cosell property: true if so, false if not.
This is certainly nontrivial, and if the made-up properties were replaced by real ones, it could even be interesting.
One could also replace !!R=\mathtt{bool}!! with some other set, and then instead of a characteristic function, !!X\to R!! would be some sort of valuation function.
I had asked:
Is the whole thing just trivial because there is no interesting way to instantiate data objects with the right types? Or is there some real computational content here?
I think M. Tatham's example shows that there is, and that the apparent vacuity of the theorem !!\color{darkred}{\heartsuit}!! arose only because !!R!! had been replaced with the empty set.
[Other articles in category /math/logic] permanent link
Tue, 01 Aug 2023
Computational content of Gantō's axe
Lately I have been thinking about the formula
$$((P\to Q)\land (\lnot P \to Q)) \to Q \tag{$\color{darkgreen}{\heartsuit}$}$$
which is a theorem of classical logic, but not of intuitionistic logic. This shouldn't be surprising. In CL you know that one of !!P!! and !!\lnot P!! is true (although perhaps not which), and whichever it is, it implies !!Q!!. In IL you don't know that one of !!P!! and !!\lnot P!! is provable, so you can't conclude anything.
Except you almost can. There is a family of transformations !!T!! where, if !!C!! is classically valid !!T(C)!! is intuitionistically valid even if !!C!! itself isn't.
For example, if !!C!! is classically valid, then !!\lnot\lnot C!! is intuitionistically valid whether or not !!C!! is. IL won't prove that !!(\color{darkgreen}{\heartsuit})!! is true, but it will prove that it isn't false.
I woke up in the middle of the night last month with the idea that even though I can't prove !!(\color{darkgreen}{\heartsuit})!!, I should be able to prove !!(\color{darkred}{\heartsuit})!!:
$$((P\to Q)\land (\lnot P \to Q)) \to \color{darkred}{\lnot\lnot Q} \tag{$\color{darkred}{\heartsuit}$}$$
This is correct; !!(\color{darkred}{\heartsuit})!! is intuitionistically valid. Understanding !!\lnot X!! as an abbreviation for !!X\to\bot!! (as is usual in IL), and assuming $$ \begin{array}{rlc} P\to Q & & (1) \\ \lnot P\to Q & & (2) \\ \lnot Q & (≡ Q\to\bot) & (3) \end{array} $$
we can combine !!P\to Q!! and !!Q\to\bot!! to get !!P\to\bot!! which is the definition of !!\lnot P!!. Then detach !!Q!! from !!(2)!!. Then from !!Q!! and !!(3)!! we get !!\bot!!, and discharging the three assumptions we conclude:
$$ \begin{align} \color{darkblue}{(P\to Q)\to (\lnot P \to Q)} & \to \color{darkgreen}{\lnot Q \to \bot} \\ ≡ \color{darkblue}{((P\to Q)\land (\lnot P \to Q))} & \to \color{darkgreen}{\lnot\lnot Q} \tag{$\color{darkred}{\heartsuit}$} \end{align}$$
But what is going on here? It makes sense to me that !!(P\to Q)\land (\lnot P \to Q)!! doesn't prove !!Q!!. That wasn't the part that puzzled me. The puzzling part was that it would prove anything more than zero. And if !!(P\to Q)\land (\lnot P\to Q)!! can prove !!\lnot\lnot Q!!, then why can't it prove anything else?
This isn't a question about the formal logical system. It's a question about the deeper meaning: how are we to understand this? Does it make sense?
I think the answer is that !!Q\to\bot!! is an extremely strong assumption, in fact the strongest possible statement you can make about !!Q!!. So it's easist possible thing you can disprove about !!Q!!. Even though !!(P\to Q)\land(\lnot P\to Q)!! is not enough to prove anything positive, it is enough, just barely, to disprove the strongest possible statement about !!Q!!.
When you assume !!Q\to \bot!!, you are restricting your attention to a possible world where !!Q!! is actually false. When you find yourself in such a world, you discover that both !!P\to Q!! and !!\lnot P\to Q!! are much stronger than you suspected.
My high school friends and I used to joke about “very strong theorems”: “I'm trying to prove that a product of Lindelöf spaces is also a Lindelöf space” one of us would say, and someone would reply “I think that is a very strong theorem,” meaning, facetiously or perhaps sarcastically, that it was false. But facetious or sarcastic, it's funny because it's correct. False theorems are really strong, that's why they are so hard to prove! We've been trying for thousands of years to prove a false theorem, but every time we think we have done it, there turns out to be a mistake in the proof.
My puzzlement about why !!(P\to Q)\land (\lnot P\to Q)!! can prove anything, translated into computational language, looks like this: I have a function !!P\to Q!! (but I don't have any !!P!!) and a function !!\lnot P\to Q!! (but I don't have any !!\lnot P!!). The intutionistic logic says that I can't use these functions to to actually get any !!Q!!, which is not at all surprising, because I don't have anything to use as arguments. But IL says that I can get !!\lnot\lnot Q!!. The question is, how can I get anything from these functions when I don't have anything to use as arguments?
Translating the proof of the theorem into computations, the answer one gets is quite unsatisfying. The proof observes that if I also had a !!Q\to\bot!! function, I could compose it with the first function to make a !!P\to\bot\equiv \lnot P!! which I could then feed to the second function and get !!Q!! from nowhere. Which is very strange, since operationally, where does that !!Q!! actually come from? It's manufactured by the !!\lnot P\to Q!! function, which was rather suspicious to begin with. What does such a function actually look like? What functions of this type can actually be implemented? It all seems rather unlikely: how on earth would you turn a !!P \to \bot!! value into a !!Q!! value?
One reasonable answer is that if !!Q = \lnot P!!, then it's easy to write that suspicious !!\lnot P\to Q!! function. But if !!Q=\lnot P!! then the claim that I also have a !!P\to Q!! function looks extremely dubious.
An answer that looks good at first but flops is that if !!Q=\mathtt{int}!! or something, then it's quite easy to produce the required functions, both !!P\to Q!! and !!\lnot P\to Q!!. The constant function that always returns !!23!! will do for either or both. But this approach does not answer the question, because in such a case we can deduce not only !!\lnot\lnot Q!! but !!Q!! itself (the !!23!! again), so we didn't need the functions in the first place.
Is the whole thing just trivial because there is no interesting way to instantiate data objects with the right types? Or is there some real computational content here? And if there is, what is it, and how does that translate into the logic? Does this argument ever allow us to conclude something actually interesting? Or is it always just reasoning about vacuities?
Note
As far as I know the formula !!(\color{darkgreen}{\heartsuit})!! was first referred to as “Gantō's Axe” by Douglas Hofstadter. This is a facetious reference to a certain Zen koan, which says, in part:
Ganto picked up an axe and went to the hut where the two monks were meditating. He raised the axe, saying, “If you say a word I will cut off your heads. If you do not say anything, I will also behead you.”
(See Kubose, Gyomay M. Zen Koans, p.178.)
Addendum 20230904
Simon Tatham observed that this is a special case of the theorem:
$$((P\to Q)\land ((P\to R) \to Q)) \to {(Q\to R)\to R}$$
which definitely has nontrivial computational content, and that the vacuity or !!\color{darkred}{\heartsuit}!! arises because !!R!! has been replaced by the empty set. Full details are here.
[Other articles in category /math/logic] permanent link
Thu, 13 Feb 2020
Gentzen's rules for natural deduction
Here is Gerhard Gentzen's original statement of the rules of Natural Deduction (“ein Kalkül für ‘natürliche’, intuitionistische Herleitungen”):
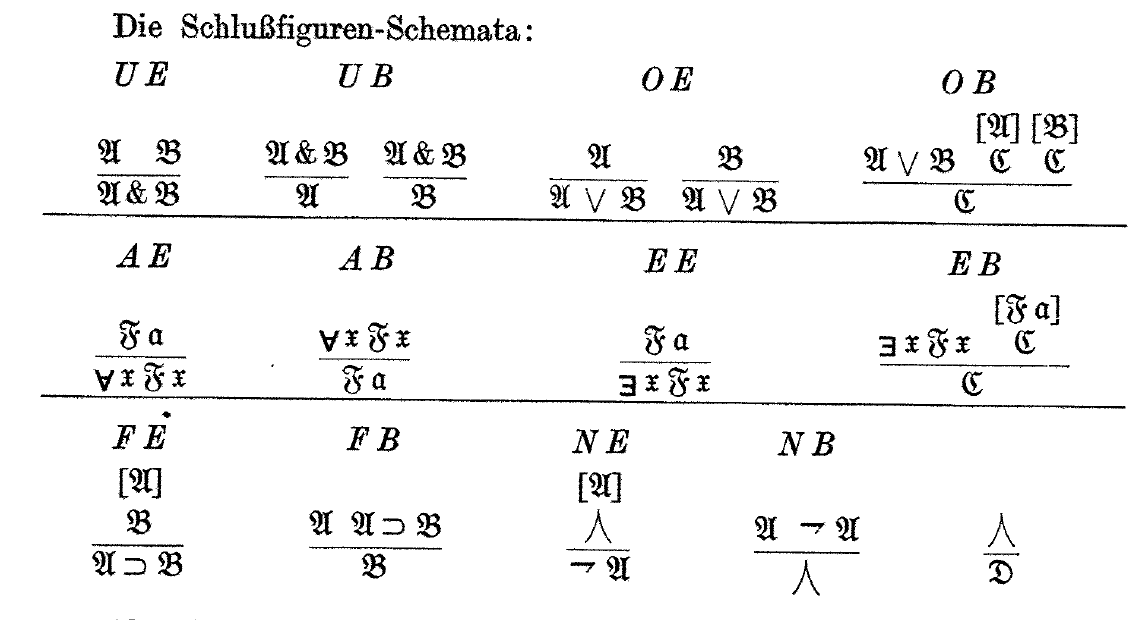
Natural deduction looks pretty much exactly the same as it does today, although the symbols are a little different. But only a little! Gentzen has not yet invented !!\land!! for logical and, and is still using !!\&!!. But he has invented !!\forall!!. The style of the !!\lnot!! symbol is a little different from what we use now, and he has that tent thingy !!⋏!! where we would now use !!\bot!!. I suppose !!⋏!! didn't catch on because it looks too much like !!\land!!. (He similarly used !!⋎!! to mean !!\top!!, but as usual, that doesn't appear in the deduction rules.)
We still use Gentzen's system for naming the rules. The notations “UE” and “OB” for example, stand for “und-Einführung” and “oder-Beseitigung”, which mean “and-introduction” and “or-elimination”.
Gentzen says (footnote 4, page 178) that he got the !!\lor, \supset, \exists!! signs from Russell, but he didn't want to use Russell's signs !!\cdot, \equiv, \sim, ()!! because they already had other meanings in mathematics. He took the !!\&!! from Hilbert, but Gentzen disliked his other symbols. Gentzen objected especially to the “uncomfortable” overbar that Hilbert used to indicate negation (“[Es] stellt eine Abweichung von der linearen Anordnung der Zeichen dar”). He attributes his symbols for logical equivalence (!!\supset\subset!!) and negation to Heyting, and explains that his new !!\forall!! symbol is analogous to !!\exists!!. I find it remarkable how quickly this caught on. Gentzen also later replaced !!\&!! with !!\land!!. Of the rest, the only one that didn't stick was !!\supset\subset!! in place of !!\equiv!!. But !!\equiv!! is much less important than the others, being merely an abbreviation.
Gentzen died at age 35, a casualty of the World War.
Source: Gerhard Gentzen, “Untersuchungen über das logische Schließen I”, pp. 176–210 Mathematische Zeitschrift v. 39, Springer, 1935. The display above appears on page 186.
[ Addendum 20200214: Thanks to Andreas Fuchs for correcting my German grammar. ]
[Other articles in category /math/logic] permanent link
Mon, 29 Jan 2018
The rubber duck explains coherence spaces
I've spent a chunk of the past week, at least, trying to understand the idea of a coherence space (or coherent space). This appears in Jean-Yves Girard's Proofs and Types, and it's a model of a data type. For example, the type of integers and the type of booleans can be modeled as coherence spaces.
The definition is one of those simple but bafflingly abstract ones that you often meet in mathematics: There is a set !!\lvert \mathcal{A}\rvert!! of tokens, and the points of the coherence space !!\mathcal{A}!! (“cliques”) are sets of tokens. The cliques are required to satisfy two properties:
- If !!a!! is a clique, and !!a'\subset a!!, then !!a'!! is also a clique.
- Suppose !!\mathcal M!! is some family of cliques such that !!a\cup a'!! is a clique for each !!a, a'\in \mathcal M!!. Then !!\bigcup {\mathcal M}!! is also a clique.
To beginning math students it often seems like these sorts of definitions are generated at random. Okay, today we're going to study Eulerian preorders with no maximum element that are closed under finite unions; tomorrow we're going to study semispatulated coalgebras with countably infinite signatures and the weak Cosell property. Whatever, man.
I have a long article about this in progress, but I'll summarize: they are never generated at random. The properties are carefully chosen because we have something in mind that we are trying to model, and until you understand what that thing is, and why someone thinks those properties are the important ones, you are not going to get anywhere.
So when I see something like this I must stop immediately and ask ‘wat’. I can try to come up with the explanation myself, or I can read on hoping for an explanation, or I can do some of each, but I am not going to progress very far until I understand what it is about. And I'm not sure anyone short of Alexander Grothendieck would have any more success trying to move on with the definition itself and nothing else.
Girard explains shortly after:
The aim is to interpret a type by a coherence space !!\mathcal{A}!!, and a term of this type as a point [clique] of !!\mathcal{A}!!, infinite in general…
Okay, fine. I understand the point of the project, although not why the definition is what it is. I know a fair amount about types. And Girard has given two examples: booleans and integers. But these examples are unusually simple, because none of the cliques has more than one element, and so the examples are not as illuminating as they might be.
Some of the ways I tried to press onward were:
Read ahead and see if there is more explanation. I tried this but I still wasn't getting it. The next section seemed clear: the cliques define a “coherence” relation on the tokens, from which the cliques can be recovered. Consider a graph, where the vertices are tokens and there is an edge !!a—b!! exactly when !!\{a, b\}!! is a clique; we say that !!a!! and !!b!! are coherent. Then the cliques of the coherence space are exactly the cliques of the graph; hence the name. The graph is called the web of the space, and from the web one can recover the original space.
But after that part came stable functions, which I couldn't figure out, and I got stuck again.
Read ahead and see if there is a more complicated specific example. There wasn't.
Read ahead and see if any of the derived concepts are familiar, and if so then work backward. For instance, if I had been able to recognize that I already knew what stable functions were, I might have been able to leverage that into an understanding of what was going on with the coherence spaces. But for me they were just another problem of the same sort: what is a stable function supposed to be modeling?
Read someone else's explanation instead. I tried several without much success. They all seemed to be written for someone who already had a clue what was going on. (That is a large part of the reason I have written up this long and clueless explanation.)
Try to construct some examples and see if they make sense in the context of what comes later. For example, I know what the coherence space of booleans looks like because Girard showed me. Can I figure out the structure of the coherence space for the type of “wrapped booleans”?
-- (Haskell) data WrappedBoolean = W BoolCan I figure it out for the type of pairs of booleans?
-- (Haskell) type BooleanPair = (Bool, Bool)
None of this was working. I had several different ideas about what the coherence spaces might look like for other types, but none of them seemed to fit with what Girard was doing. I couldn't come up with any consistent story.
So I prepared to ask on StackExchange, and I spent about an hour writing up my question, explaining all the things I had tried and what the problems were with each one. And as I drew near to the end of this, the clouds parted! I never had to post the question. I was in the middle of composing this paragraph:
In section 8.4 Girard defines a direct product of coherence spaces, but it doesn't look like the direct product I need to get a product type; it looks more like a disjoint union type. If the coherence space for
Pairboolis the square of the coherence space for !!{{\mathcal B}ool}!!, how? It has 4 2-cliques, but if those are the total elements of !!{{\mathcal B}ool}^2!!, then what are do the 1-cliques mean?
I decided I hadn't made enough of an effort to understand the direct product. So even though I couldn't see how it could possibly give me anything like what I wanted, I followed its definition for !!{{\mathcal B}ool}^2!! — and the light came on.
Here's the puzzling coproduct-like definition of the product of two coherence spaces, from page 61:
If !!{\mathcal A}!! and !!{\mathcal B}!! are two coherence spaces, we define !!{\mathcal A}\&{\mathcal B}!! by:
!!|{\mathcal A}\&{\mathcal B}| = |{\mathcal A}| + |{\mathcal B}| = \{1\}×|{\mathcal A}| \cup \{2\}×|{\mathcal B}|!!
That is, the tokens in the product space are literally the disjoint union of the tokens in the component spaces.
And the edges in the product's web are whatever they were in !!{\mathcal A}!!'s web (except lifted from !!|{\mathcal A}|!! to !!\{1\}×|{\mathcal A}|!!), whatever they were in !!{\mathcal B}!!'s web (similarly), and also there is an edge between every !!\langle1, {\mathcal A}\rangle!! and each !!\langle2, {\mathcal B}\rangle!!. For !!{{\mathcal B}ool}^2!! the web looks like this:
There is no edge between !!\langle 1, \text{True}\rangle!! and !!\langle 1, \text{False}\rangle!! because in !!{{\mathcal B}ool}!! there is no edge between !!\text{True}!! and !!\text{False}!!.
This graph has nine cliques. Here they are ordered by set inclusion:
(In this second diagram I have abbreviated the pair !!\langle1, \text{True}\rangle!! to just !!1T!!. The top nodes in the diagram are each labeled with a set of two ordered pairs.)
What does this mean? The ordered pairs of booleans are being represented by functions. The boolean pair !!\langle x, y\rangle!! is represented by the function that takes as its argument a number, either 1 or 2, and then returns the corresponding component of the pair: the first component !!x!! if the argument was 1, and the second component !!y!! if the argument was 2.
The nodes in the bottom diagram represent functions. The top row are fully-defined functions. For example, !!\{1F, 2T\}!! is the function with !!f(1) = \text{False}!! and !!f(2) = \text{True}!!, representing the boolean pair !!\langle\text{False}, \text{True}\rangle!!. Similarly if we were looking at a space of infinite lists, we could consider it a function from !!\Bbb N!! to whatever the type of the lists elements was. Then the top row of nodes in the coherence space would be infinite sets of pairs of the form !!\langle n, \text{(list element)}\rangle!!.
The lower nodes are still functions, but they are functions about which we have only incomplete information. The node !!\{2T\}!! is a function for which !!f(2) = \text{True}!!. But we don't yet know what !!f(1)!! is because we haven't yet tried to compute it. And the bottommost node !!\varnothing!! is a function where we don't know anything at all — yet. As we test the function on various arguments, we move up the graph, always following the edges. The lower nodes are approximations to the upper ones, made on the basis of incomplete information about what is higher up.
Now the importance of finite approximants on page 56 becomes clearer. !!{{\mathcal B}ool}^2!! is already finite. But in general the space is infinite because the type is functions on an infinite domain, or infinite lists, or something of that sort. In such a space we can't get all the way to the top row of nodes because to do that we would have to call the function on all its possible arguments, or examine every element of the list, which is impossible. Girard says “Above all, there are enough finite approximants to a.” I didn't understand what he meant by “enough”. But what he means is that each clique !!a!! is the union of its finite approximants: each bit of information in the function !!a!! is obtainable from some finite approximation of !!a!!. The “stable functions” of section 8.3 start to become less nebulous also.
I had been thinking that the !!\varnothing!! node was somehow like the
!!\bot!! element in a Scott domain, and then I struggled to
identify anything like !!\langle \text{False}, \bot\rangle!!.
It looks at first
like you can do it somehow, because there are the right number of
nodes at the middle level.
Trouble arises in other coherence
spaces.
For the WrappedBoolean type, for example, the type has
four elements: !!
W\ \text{True},
W\ \text{False},
W\ \bot,!! and !!\bot!!. I think the coherence space for WrappedBoolean is just like the one
for !!{{\mathcal B}ool}!!:
Presented with a value from WrappedBoolean, you don't initially know
what it is. Then you examine it, and you know whether it is
!!W\ \text{True}!! or !!W\ \text{False}!!. You are now done.
I think there isn't anything like !!\bot!! or !!W\ \bot!! in the coherence space. Or maybe they they are there but sharing the !!\varnothing!! node. But I think more likely partial objects will appear in some other way.
Whew! Now I can move along.
(If you don't understand why “rubber duck”, Wikipedia explains:
Many programmers have had the experience of explaining a problem to someone else, possibly even to someone who knows nothing about programming, and then hitting upon the solution in the process of explaining the problem.
[“Rubber duck”] is a reference to a story in the book The Pragmatic Programmer in which a programmer would carry around a rubber duck and debug their code by forcing themselves to explain it, line-by-line, to the duck.
I spent a week on this but didn't figure it out until I tried formulating my question for StackExchange. The draft question, never completed, is here if for some reason you want to see what it looked like.)
[Other articles in category /math/logic] permanent link
Tue, 31 Oct 2017
The Blind Spot and the cut rule
[ The Atom and RSS feeds have done an unusually poor job of preserving the mathematical symbols in this article. It will be much more legible if you read it on my blog. ]
Lately I've been enjoying The Blind Spot by Jean-Yves Girard, a very famous logician. (It is translated from French; the original title is Le Point Aveugle.) This is an unusual book. It is solidly full of deep thought and technical detail about logic, but it is also opinionated, idiosyncratic and polemical. Chapter 2 (“Incompleteness”) begins:
It is out of question to enter into the technical arcana of Gödel’s theorem, this for several reasons:
(i) This result, indeed very easy, can be perceived, like the late paintings of Claude Monet, but from a certain distance. A close look only reveals fastidious details that one perhaps does not want to know.
(ii) There is no need either, since this theorem is a scientific cul-de-sac : in fact it exposes a way without exit. Since it is without exit, nothing to seek there, and it is of no use to be expert in Gödel’s theorem.
(The Blind Spot, p. 29)
He continues a little later:
Rather than insisting on those tedious details which «hide the forest», we shall spend time on objections, from the most ridiculous to the less stupid (none of them being eventually respectable).
As you can see, it is not written in the usual dry mathematical-text style, presenting the material as a perfect and aseptic distillation of absolute truth. Instead, one sees the history of logic, the rise and fall of different theories over time, the interaction and relation of many mathematical and philosophical ideas, and Girard's reflections about it all. It is a transcription of a lecture series, and reads like one, including all of the speaker's incidental remarks and offhand musings, but written down so that each can be weighed and pondered at length. Instead of wondering in the moment what he meant by some intriguing remark, then having to abandon the thought to keep up with the lecture, I can pause and ponder the significance. Girard is really, really smart, and knows way more about logic than I ever will, and his offhand remarks reward this pondering. The book is profound in a way that mathematics books often aren't. I wanted to provide an illustrative quotation, but to briefly excerpt a profound thought is to destroy its profundity, so I will have to refrain.[1])
The book really gets going with its discussion of Gentzen's sequent calculus in chapter 3.
Between around 1890 (when Peano and Frege began to liberate logic from its medieval encrustations) and 1935 when the sequent calculus was invented, logical proofs were mainly in the “Hilbert style”. Typically there were some axioms, and some rules of deduction by which the axioms could be transformed into other formulas. A typical example consists of the axioms $$A\to(B\to A)\\ (A \to (B \to C)) \to ((A \to B) \to (A \to C)) $$ (where !!A, B, C!! are understood to be placeholders that can be replaced by any well-formed formulas) and the deduction rule modus ponens: having proved !!A\to B!! and !!A!!, we can deduce !!B!!.
In contrast, sequent calculus has few axioms and many deduction rules. It deals with sequents which are claims of implication. For example: $$p, q \vdash r, s$$ means that if we can prove all of the formulas on the left of the ⊢ sign, then we can conclude some of the formulas on the right. (Perhaps only one, but at least one.)
A typical deductive rule in sequent calculus is:
$$ \begin{array}{c} Γ ⊢ A, Δ \qquad Γ ⊢ B, Δ \\ \hline Γ ⊢ A ∧ B, Δ \end{array} $$
Here !!Γ!! and !!Δ!! represent any lists of formulas, possibly empty. The premises of the rule are:
!!Γ ⊢ A, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!A!! or some of the formulas in !!Δ!!.
!!Γ ⊢ B, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!B!! or some of the formulas in !!Δ!!.
From these premises, the rule allows us to deduce:
!!Γ ⊢ A ∧ B, Δ!!: If we can prove all of the formulas in !!Γ!!, then we can conclude either the formula !!A \land B!! or some of the formulas in !!Δ!!.
The only axioms of sequent calculus are utterly trivial:
$$ \begin{array}{c} \phantom{A} \\ \hline A ⊢ A \end{array} $$
There are no premises; we get this deduction for free: If can prove !!A!!, we can prove !!A!!. (!!A!! here is a metavariable that can be replaced with any well-formed formula.)
One important point that Girard brings up, which I had never realized despite long familiarity with sequent calculus, is the symmetry between the left and right sides of the turnstile ⊢. As I mentioned, the interpretation of !!Γ ⊢ Δ!! I had been taught was that it means that if every formula in !!Γ!! is provable, then some formula in !!Δ!! is provable. But instead let's focus on just one of the formulas !!A!! on the right-hand side, hiding in the list !!Δ!!. The sequent !!Γ ⊢ Δ, A!! can be understood to mean that to prove !!A!!, it suffices to prove all of the formulas in !!Γ!!, and to disprove all the formulas in !!Δ!!. And now let's focus on just one of the formulas on the left side: !!Γ, A ⊢ Δ!! says that to disprove !!A!!, it suffices to prove all the formulas in !!Γ!! and disprove all the formulas in !!Δ!!.
The all-some correspondence, which had previously caused me to wonder why it was that way and not something else, perhaps the other way around, has turned into a simple relationship about logical negation: the formulas on the left are positive, and the ones on the right are negative.[2]) With this insight, the sequent calculus negation laws become not merely simple but trivial:
$$ \begin{array}{cc} \begin{array}{c} Γ, A ⊢ Δ \\ \hline Γ ⊢ \lnot A, Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A, Δ \\ \hline Γ, \lnot A ⊢ Δ \end{array} \end{array} $$
For example, in the right-hand deduction: what is sufficient to prove !!A!! is also sufficient to disprove !!¬A!!.
(Compare also the rule I showed above for ∧: It now says that if proving everything in !!Γ!! and disproving everything in !!Δ!! is sufficient for proving !!A!!, and likewise sufficient for proving !!B!!, then it is also sufficient for proving !!A\land B!!.)
But none of that was what I planned to discuss; this article is (intended to be) about sequent calculus's “cut rule”.
I never really appreciated the cut rule before. Most of the deductive rules in the sequent calculus are intuitively plausible and so simple and obvious that it is easy to imagine coming up with them oneself.
But the cut rule is more complicated than the rules I have already shown. I don't think I would have thought of it easily:
$$ \begin{array}{c} Γ ⊢ A, Δ \qquad Λ, A ⊢ Π \\ \hline Γ, Λ ⊢ Δ, Π \end{array} $$
(Here !!A!! is a formula and !!Γ, Δ, Λ, Π!! are lists of formulas, possibly empty lists.)
Girard points out that the cut rule is a generalization of modus ponens: taking !!Γ, Δ, Λ!! to be empty and !!Π = \{B\}!! we obtain:
$$ \begin{array}{c} ⊢ A \qquad A ⊢ B \\ \hline ⊢ B \end{array} $$
The cut rule is also a generalization of the transitivity of implication:
$$ \begin{array}{c} X ⊢ A \qquad A ⊢ Y \\ \hline X ⊢ Y \end{array} $$
Here we took !!Γ = \{X\}, Π = \{Y\}!!, and !!Δ!! and !!Λ!! empty.
This all has given me a much better idea of where the cut rule came from and why we have it.
In sequent calculus, the deduction rules all come in pairs. There is a rule about introducing ∧, which I showed before. It allows us to construct a sequent involving a formula with an ∧, where perhaps we had no ∧ before. (In fact, it is the only way to do this.) There is a corresponding rule (actually two rules) for getting rid of ∧ when we have it and we don't want it:
$$ \begin{array}{cc} \begin{array}{c} Γ ⊢ A\land B, Δ \\ \hline Γ ⊢ A, Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A\land B, Δ \\ \hline Γ ⊢ B, Δ \end{array} \end{array} $$
Similarly there is a rule (actually two rules) about introducing !!\lor!! and a corresponding rule about eliminating it.
The cut rule seems to lie outside this classification. It is not paired.
But Girard showed me that it is part of a pair. The axiom
$$ \begin{array}{c} \phantom{A} \\ \hline A ⊢ A \end{array} $$
can be seen as an introduction rule for a pair of !!A!!s, one on each side of the turnstile. The cut rule is the corresponding rule for eliminating !!A!! from both sides.
Sequent calculus proofs are much easier to construct than Hilbert-style proofs. Suppose one wants to prove !!B!!. In a Hilbert system the only deduction rule is modus ponens, which requires that we first prove !!A\to B!! and !!A!! for some !!A!!. But what !!A!! should we choose? It could be anything, and we have no idea where to start or how big it could be. (If you enjoy suffering, try to prove the simple theorem !!A\to A!! in the Hilbert system I described at the beginning of the article. (Solution)
In sequent calculus, there is only one way to prove each kind of thing, and the premises in each rule are simply related to the consequent we want. Constructing the proof is mostly a matter of pushing the symbols around by following the rules to their conclusions. (Or, if this is impossible, one can conclude that there is no proof, and why.[3]) Construction of proofs can now be done entirely mechanically!
Except! The cut rule does require one to guess a formula: If one wants to prove !!Γ, Λ ⊢ Δ, Π!!, one must guess what !!A!! should appear in the premises !!Γ, A ⊢ Δ!! and !!Λ ⊢ A, Π!!. And there is no constraint at all on !!A!!; it could be anything, and we have no idea where to start or how big it could be.
The good news is that Gentzen, the inventor of sequent calculus, showed that one can dispense with the cut rule: it is unnecessary:
In Hilbert-style systems, based on common sense, the only rule is (more or less) the Modus Ponens : one reasons by linking together lemmas and consequences. We just say that one can get rid of that : it is like crossing the English Channel with fists and feet bound !
(The Blind Spot, p. 61)
Gentzen's demonstration of this shows how one can take any proof that involves the cut rule, and algorithmically eliminate the cut rule from it to obtain a proof of the same result that does not use cut. Gentzen called this the “Hauptsatz” (“principal theorem”) and rightly so, because it reduces construction of logical proofs to an algorithm and is therefore the ultimate basis for algorithmic proof theory.
The bad news is that the cut-elimination process can super-exponentially increase the size of the proof, so it does not lead to a practical algorithm for deciding provability. Girard analyzed why, and what he discovered amazed me. The only problem is in the contraction rules, which had seemed so trivial and innocuous—uninteresting, even—that I had never given them any thought:
$$ \begin{array}{cc} \begin{array}{c} Γ, A, A ⊢ Δ \\ \hline Γ, A ⊢ Δ \end{array} & \qquad \begin{array}{c} Γ ⊢ A, A, Δ \\ \hline Γ ⊢ A, Δ \end{array} \end{array} $$
And suddenly Girard's invention of linear logic made sense to me. In linear logic, contraction is forbidden; one must use each formula in one and only one deduction.
Previously it had seemed to me that this was a pointless restriction. Now I realized that it was no more of a useless hair shirt than the intuitionistic rejection of the law of the proof by contradiction: not a stubborn refusal to use an obvious tool of reasoning, but a restriction of proofs to produce better reasoning. With the rejection of contraction, cut-elimination no longer explodes proof size, and automated theorem proving becomes practical:
This is why its study is, implicitly, at the very heart of these lectures.
(The Blind Spot, p. 63)
The book is going to get into linear logic later in the next chapter. I have read descriptions of linear logic before, but never understood what it was up to. (It has two logical and operators, and two logical or operators; why?) But I am sure Girard will explain it marvelously.
- In place of a profound excerpt, I will present the following, which isn't especially profound but struck a chord for me: “By the way, nothing is more arbitrary than a modal logic « I am done with this logic, may I have another one ? » seems to be the motto of these guys.” (p. 24)
- Compare my alternative representation of arithmetic expressions that collapses addition and subtraction, and multiplication and division.
- A typically Girardian remark is that analytic tableaux are “the poor man's sequents”.
A brief but interesting discussion of The Blind Spot on Hacker News.
[Other articles in category /math/logic] permanent link
Fri, 03 Jul 2015
The annoying boxes puzzle: solution
I presented this logic puzzle on Wednesday:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."It's not too late to try to solve this before reading on. If you want, you can submit your answer here:Can you figure out which box contains the treasure?
Results
There were 506 total responses up to Fri Jul 3 11:09:52 2015 UTC; I kept only the first response from each IP address, leaving 451. I read all the "something else" submissions and where it seemed clear I recoded them as votes for "red", for "not enough information", or as spam. (Several people had the right answer but submitted "other" so they could explain themselves.) There was also one post attempted to attack my (nonexistent) SQL database. Sorry, Charlie; I'm not as stupid as I look.
66.52% 300 red 25.72 116 not-enough-info 3.55 16 green 2.00 9 other 1.55 7 spam 0.44 2 red-with-qualification 0.22 1 attack 100.00 451 TOTAL
What?
Let me show you. I stated:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."
The labels are as I said. Everything I told you was literally true.
The treasure is definitely not in the red box.
No, it is actually in the green box.
(It's hard to see, but one of the items in the green box is the gold and diamond ring made in Vienna by my great-grandfather, which is unquestionably a real treasure.)
So if you said the treasure must be in the red box, you were simply mistaken. If you had a logical argument why the treasure had to be in the red box, your argument was fallacious, and you should pause and try to figure out what was wrong with it.
I will discuss it in detail below.
Solution
The treasure is undeniably in the green box. However, correct answer to the puzzle is "no, you cannot figure out which box contains the treasure". There is not enough information given. (Notice that the question was not “Where is the treasure?” but “Can you figure out…?”)
(Fallacious) Argument A
Many people erroneously conclude that the treasure is in the red box, using reasoning something like the following:
- Suppose the red label is true. Then exactly one label is true, and since the red label is true, the green label is false. Since it says that the treasure is in the green box, the treasure must really be in the red box.
- Now suppose that the red label is false. Then the green label must also be false. So again, the treasure is in the red box.
- Since both cases lead to the conclusion that the treasure is in the red box, that must be where it is.
What's wrong with argument A?
Here are some responses people commonly have when I tell them that argument A is fallacious:
"If the treasure is in the green box, the red label is lying."
Not quite, but argument A explicitly considers the possibility that the red label was false, so what's the problem?
"If the treasure is in the green box, the red label is inconsistent."
It could be. Nothing in the puzzle statement ruled this out. But actually it's not inconsistent, it's just irrelevant.
"If the treasure is in the green box, the red label is meaningless."
Nonsense. The meaning is plain: it says “exactly one of these labels is true”, and the meaning is that exactly one of the labels is true. Anyone presenting argument A must have understood the label to mean that, and it is incoherent to understand it that way and then to turn around and say that it is meaningless! (I discussed this point in more detail in 2007.)
"But the treasure could have been in the red box."
True! But it is not, as you can see in the pictures. The puzzle does not give enough information to solve the problem. If you said that there was not enough information, then congratulations, you have the right answer. The answer produced by argument A is incontestably wrong, since it asserts that the treasure is in the red box, when it is not.
"The conditions supplied by the puzzle statement are inconsistent."
They certainly are not. Inconsistent systems do not have models, and in particular cannot exist in the real world. The photographs above demonstrate a real-world model that satisfies every condition posed by the puzzle, and so proves that it is consistent.
"But that's not fair! You could have made up any random garbage at all, and then told me afterwards that you had been lying."
Had I done that, it would have been an unfair puzzle. For example, suppose I opened the boxes at the end to reveal that there was no treasure at all. That would have directly contradicted my assertion that "One [box] contains a treasure". That would have been cheating, and I would deserve a kick in the ass.But I did not do that. As the photograph shows, the boxes, their colors, their labels, and the disposition of the treasure are all exactly as I said. I did not make up a lie to trick you; I described a real situation, and asked whether people they could diagnose the location of the treasure.
(Two respondents accused me of making up lies. One said:
There is no treasure. Both labels are lying. Look at those boxes. Do you really think someone put a treasure in one of them just for this logic puzzle?What can I say? I did put a treasure in a box just for this logic puzzle. Some of us just have higher standards.)
"But what about the labels?"
Indeed! What about the labels?
The labels are worthless
The labels are red herrings; the provide no information. Consider the following version of the puzzle:
There are two boxes on a table, one red and one green. One contains a treasure.Obviously, the problem cannot be solved from the information given.Which box contains the treasure?
Now consider this version:
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "gcoadd atniy fnck z fbi c rirpx hrfyrom". The green box is labelled "ofurb rz bzbsgtuuocxl ckddwdfiwzjwe ydtd."One is similarly at a loss here.Which box contains the treasure?
(By the way, people who said one label was meaningless: this is what a meaningless label looks like.)
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."The point being that in the absence of additional information, there is no reason to believe that the labels give any information about the contents of the boxes, or about labels, or about anything at all. This should not come as a surprise to anyone. It is true not just in annoying puzzles, but in the world in general. A box labeled “fresh figs” might contain fresh figs, or spoiled figs, or angry hornets, or nothing at all.But then the janitor happens by. "Don't be confused by those labels," he says. "They were stuck on there by the previous owner of the boxes, who was an illiterate shoemaker who only spoke Serbian. I think he cut them out of a magazine because he liked the frilly borders."
Which box contains the treasure?
Why doesn't every logic puzzle fall afoul of this problem?
I said as part of the puzzle conditions that there was a treasure in one box. For a fair puzzle, I am required to tell the truth about the puzzle conditions. Otherwise I'm just being a jerk.Typically the truth or falsity of the labels is part of the puzzle conditions. Here's a typical example, which I took from Raymond Smullyan's What is the name of this book? (problem 67a):
… She had the following inscriptions put on the caskets:Notice that the problem condition gives the suitor a certification about the truth of the labels, on which he may rely. In the quotation above, the certification is in boldface.Portia explained to the suitor that of the three statements, at most one was true.
Gold Silver Lead THE PORTRAIT IS IN THIS CASKET THE PORTRAIT IS NOT IN THIS CASKET THE PORTRAIT IS NOT IN THE GOLD CASKET Which casket should the suitor choose [to find the portrait]?
A well-constructed puzzle will always contain such a certification, something like “one label is true and one is false” or “on this island, each person always lies, or always tells the truth”. I went to What is the Name of this Book? to get the example above, and found more than I had bargained for: problem 70 is exactly the annoying boxes problem! Smullyan says:
Good heavens, I can take any number of caskets that I please and put an object in one of them and then write any inscriptions at all on the lids; these sentences won't convey any information whatsoever.(Page 65)
Had I known ahead of time that Smullyan had treated the exact same topic with the exact same example, I doubt I would have written this post at all.
But why is this so surprising?
I don't know.
Final notes
16 people correctly said that the treasure was in the green box. This has to be counted as a lucky guess, unacceptable as a solution to a logic puzzle.One respondent referred me to a similar post on lesswrong.
I did warn you all that the puzzle was annoying.
I started writing this post in October 2007, and then it sat on the shelf until I got around to finding and photographing the boxes. A triumph of procrastination!
Addendum 2015091
Steven Mazie has written a blog article about this topic, A Logic Puzzle That Teaches a Life Lesson.
Addendum 20240628
It seems that the Lesswrongers call this The Parable of the Dagger. Here's their version of the payoff:
The jester opened the second box, and found a dagger.“How?!” cried the jester in horror, as he was dragged away. “It’s logically impossible!”
“It is entirely possible,” replied the king. “I merely wrote those inscriptions on two boxes, and then I put the dagger in the second one.”
[Other articles in category /math/logic] permanent link
Wed, 01 Jul 2015
The annoying boxes puzzle
Here is a logic puzzle. I will present the solution on Friday.
There are two boxes on a table, one red and one green. One contains a treasure. The red box is labelled "exactly one of the labels is true". The green box is labelled "the treasure is in this box."Starting on 2015-07-03, the solution will be here.Can you figure out which box contains the treasure?
[Other articles in category /math/logic] permanent link
Fri, 09 Feb 2007What to make of this?
- Sentence 2 is false.
- Sentence 1 is true.
Many answers are possible. The point of this note is to refute one particular common answer, which is that the whole thing is just meaningless.
This view is espoused by many people who, it seems, ought to know better. There are two problems with this view.
The first problem is that it involves a theory of meaning that appears to have nothing whatsoever to do with pragmatics. You can certainly say that something is meaningless, but that doesn't make it so. I can claim all I want to that "jqgc ihzu kenwgeihjmbyfvnlufoxvjc sndaye" is a meaningful utterance, but that does not avail me much, since nobody can understand it. And conversely, I can say as loudly and as often as I want to that the utterance "Snow is white" is meaningless, but that doesn't make it so; the utterance still means that snow is white, at least to some people in some contexts.
Similarly, asserting that the sentences are meaningless is all very well, but the evidence is against this assertion. The meaning of the utterance "sentence 2 is false" seems quite plain, and so does the meaning of the utterance "sentence 1 is true". A theory of meaning in which these simple and plain-seeming sentences are actually meaningless would seem to be at odds with the evidence: People do believe they understand them, do ascribe meaning to them, and, for the most part, agree on what the meaning is. Saying that "snow is white" is meaningless, contrary to the fact that many people agree that it means that snow is white, is foolish; saying that the example sentences above are meaningless is similarly foolish.
I have heard people argue that although the sentences are individually meaningful, they are meaningless in conjunction. This position is even more problematic. Let us refer to a person who holds this position as P. Suppose sentence 1 is presented to you in isolation. You think you understand its meaning, and since P agrees that it is meaningful, he presumably would agree that you do. But then, a week later, someone presents you with sentence 2; according to P's theory, sentence 1 now becomes meaningless. It was meaningful on February 1, but not on February 8, even though the speaker and the listener both think it is meaningful and both have the same idea of what it means. But according to P, as midnight of February 8, they are suddenly mistaken.
The second problem with the notion that the sentences are meaningless comes when you ask what makes them meaningless, and how one can distinguish meaningful sentences from sentences like these that are apparently meaningful but (according to the theory) actually meaningless.
The answer is usually something along the lines that sentences that
contain self-reference are meaningless. This answer is totally
inadequate, as has been demonstrated many times by many people,
notably W.V.O. Quine. In the example above, the self-reference
objection is refuted simply by observing that neither sentence is
self-referent. One might try to construct an argument about
reference loops, or something of the sort, but none of this will
avail, because of Quine's example:
But all of this is peripheral to the main problem with the argument
that sentences that contain self-reference are meaningless. The main
problem with this argument is that it cannot be true. The
sentence "sentences that contain self-reference are meaningless" is
itself a sentence, and therefore refers to itself, and is therefore
meaningless under its own theory. If the assertion is true, then the
sentence asserting it is meaningless under the assertion itself; the
theory deconstructs itself. So anyone espousing this theory has
clearly not thought through the consequences. (Graham Priest says that
people advancing this theory are subject to a devastating ad
hominem attack. He doesn't give it specifically, but many such
come to mind.)
In fact, the self-reference-implies-meaninglessness theory obliterates
not only itself, but almost all useful statements of logic. Consider
for example "The negation of a true sentence is false and the negation
of a false sentence is true." This sentence, or a variation of it, is
probably found in every logic textbook ever written. Such a sentence
refers to itself, and so, in the
self-reference-implies-meaninglessness theory, is meaningless. So too
with most of the other substantive assertions of our logic textbooks,
which are principally composed of such self-referent sentences about
properties of sentences; so much for logic.
The problems with ascribing meaninglessness to self-referent sentences
run deeper still. If a sentence is meaningless, it cannot be
self-referent, because, being meaningless, it cannot refer to anything
at all. Is "jqgc ihzu kenwgeihjmbyfvnlufoxvjc sndaye" self-referent?
No, because it is meaningless. In order to conclude that it was
self-referent, we would have to understand it well enough to ascribe a
meaning to it, and this would prove that it was meaningful.
So the position that the example sentences 1 and 2 are "meaningless"
has no logical or pragmatic validity at all; it is totally
indefensible. It is the philosophical equivalent of putting one's
fingers in one's ears and shouting "LA LA LA I CAN'T HEAR YOU!"
[Other articles in category /math/logic]
permanent link
"snow is white" is false when you change "is" to "is not".
Or similarly:
If a sentence is false, then its negation is true.
Nevertheless, Quine's sentence is an antinomy of the same sort as the
example sentences at the top of the article.








