Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAM |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 15 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 29 May 2020
Infinite zeroes with one on the end
I recently complained about people who claim:
you can't have a 1 after an infinite sequence of zeroes, because an infinite sequence of zeroes goes on forever.
When I read something like this, the first thing that usually comes to mind is the ordinal number !!\omega+1!!, which is a canonical representative of this type of ordering. But I think in the future I'll bring up this much more elementary example:
$$ S = \biggl\{-1, -\frac12, -\frac13, -\frac14, \ldots, 0\biggr\} $$
Even a middle school student can understand this, and I doubt they'd be able to argue seriously that it doesn't have an infinite sequence of elements that is followed by yet another final element.
Then we could define the supposedly problematic !!0, 0, 0, \ldots, 1!! thingy as a map from !!S!!, just as an ordinary sequence is defined as a map from !!\Bbb N!!.
[ Related: A familiar set with an unexpected order type. ]
[Other articles in category /math] permanent link
A couple of years ago I wrote an article about a topological counterexample, which included this illustration:
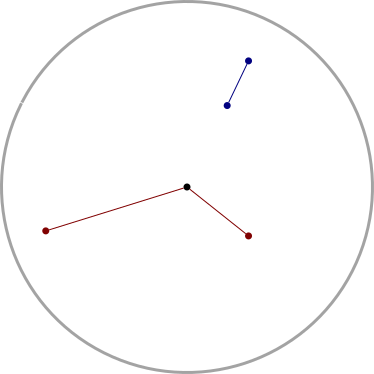
Since then, every time I have looked at this illustration, I have noticed that the blue segment is drawn wrong. It is intended to be a portion of a radius, so if I extend it toward the center of the circle it ought to intersect the center point. But clearly, the slope is too high and the extension passes significantly below the center.
Or so it appears. I have checked the original SVG, using Inkscape to extend the blue segment: the extension passes through the center of the circle. I have also checked the rendered version of the illustration, by holding a straightedge up to the screen. The segment is pointing in the correct direction.
So I know it's right, but still I'm jarred every time I see it, because to me it looks so clearly wrong.
[ Addendum 20200530: John Gleeson has pointed out the similarity to the Poggendorff illusion. ]
[Other articles in category /brain] permanent link


