Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Breaking pills |
| Southern Strategy |
| The straight man comes first |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Tue, 17 Sep 2019
Suppose you have a bottle that contains !!N!! whole pills. Each day you select a pill at random from the bottle. If it is a whole pill you eat half and put the other half back in the bottle. If it is a half pill, you eat it. How many half-pills can you expect to have in the bottle the day after you break the last whole pill?
Let's write !!H(N)!! for the expected number of half-pills left, if you start with !!N!!. It's easily seen that !!H(N) = 0, 1, \frac32!! for !!N=0,1,2!!, and it's not hard to calculate that !!H(3) = \frac{11}{6}!!.
For larger !!N!! it's easy to use Monte Carlo simulation, and find that !!H(30)!! is almost exactly !!4!!. But it's also easy to use dynamic programming and compute that $$H(30) = \frac{9304682830147}{2329089562800}$$ exactly, which is a bit less than 4, only !!3.994987!!. Similarly, the dynamic programming approach tells us that $$H(100) = \frac{14466636279520351160221518043104131447711}{2788815009188499086581352357412492142272}$$ which is about !!5.187!!.
(I hate the term “dynamic programming”. It sounds so cool, but then you find out that all it means is “I memoized the results in a table”. Ho hum.)
As you'd expect for a distribution with a small mean, you're much more likely to end with a small number of half-pills than a large number. In this graph, the red line shows the probability of ending with various numbers of half-pills for an initial bottle of 100 whole pills; the blue line for an initial bottle of 30 whole pills, and the orange line for an initial bottle of 5 whole pills. The data were generated by this program.
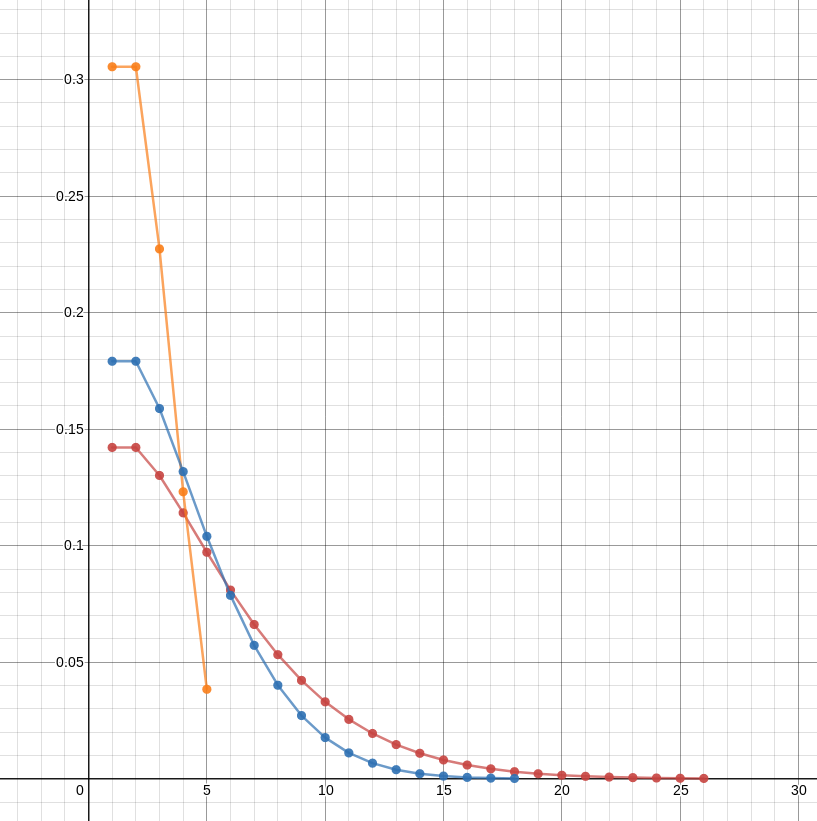
The !!E!! function appears to increase approximately logarithmically. It first exceeds !!2!! at !!N=4!!, !!3!! at !!N=11!!, !!4!! at !!N=31!!, and !!5!! at !!N=83!!. The successive ratios of these !!N!!-values are !!2.75, 2.81,!! and !!2.68!!. So we might guess that !!H(N)!! first exceeds 6 around !!N=228!! or so, and indeed !!H(226) < 6 < H(227)!!. So based on purely empirical considerations, we might guess that $$H(N) \approx \frac{\log{\frac{15}{22}N}}{\log 2.75}.$$
(The !!\frac{15}{22}!! is a fudge factor to get the curves to line up properly.)
I don't have any theoretical justification for this, but I think it might be possible to get a bound.
I don't think modeling this as a Markov process would work well. There are too many states, and it is not ergodic.
[ Addendum 20190919: Ben Handley informs me that !!H(n)!! is simply the harmonic numbers, !!H(n) = \sum_1^n \frac1n!!. I feel a little foolish that I did not notice that the first four terms matched. The appearance of !!H(3)=\frac{11}6!! should have tipped me off. Thank you, M. Handley. ]
[ Addendum 20190920: I was so fried when I wrote this that I also didn't notice that the denominator I guessed, !!2.75!!, is almost exactly !!e!!. (The correct value is !!e!!.) I also suspect that the !!\frac{15}{22}!! is just plain wrong, and ought to be !!e^\gamma!! or something like that, but I need to take a closer look. ]
[ Addendum 20191004: More about this ]
[Other articles in category /math] permanent link
Today it occurred to me that in the many comedy duos that feature a “straight man” and a “comedian”, the straight man is invariably named first. The central example, of course, is Abbott and Costello. But we also have:
- Laurel and Hardy
- Burns and Allen
- Rowan and Martin
- Martin and Lewis
- Bert and Ernie
and this even extends to entirely fictitious pairs such as Jeeves and Wooster, Harold and Kumar, or Sam and Max, Freelance Police. Also, if you are a mathematician, Smothers and Smothers. This is why people hate mathematicians.
I did Google search for "Kermit and Fozzie" (hits outnumber "Fozzie and Kermit" by around three-to-one) and "Kermit and Miss Piggy" (hits outnumber "Miss Piggy and Kermit", although only by about 60%.)
Wikipedia says this is no accident!
In vaudeville, effective straight men were much less common than comedians. The straight man's name usually appeared first and he usually received 60% of the take.
But my co-worker Jeff Culverhouse found a counterexample: Silent Bob is certainly the straight man of Jay and Silent Bob.
Wikipedia also has a list of American Comedy Duos. Not all of them follow the straight man / comedian pattern, and I don't recognize many of those that do. More research is needed.
Addenda
I wanted to find a gender-neutral term for "straight man", but failed.
20220623
I thought of another counterexample: Wallace and Gromit.
20230221
Google search hits for “Tom and Dick Smothers” outnumber those for “Dick and Tom Smothers” to more than 7 to 1. (20600 to 2670.) Dick was the straight man.
20250508
Michel Dingler points out that R2-D2 and C-3PO are another counterexample:
Popular consensus in my Mastodon timeline seems to agree.
I haven't seen it, but I suppose that in the action comedy series B.J. and the Bear, B.J. (played by Greg Evigan) is the straight man to the Bear (played by some monkey).
[Other articles in category /misc] permanent link
According to the New York Times of 10 March 1982:
In 1970, for example, President Nixon and Vice President Agnew did a piano duet built around their so-called ''Southern Strategy.'' No matter what song Mr. Nixon played, Mr. Agnew cut in with ''Dixie.'' The audience found it uproariously funny, as they did the spectacle of the Vice President clicking his heels, saluting and telling Mr. Nixon, ''Yes suh, Mr. President, ah agree with you completely on yoah Southern strategy.''
And yet the cruel earth refused to open and swallow everyone involved.
[Other articles in category /politics] permanent link



