Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | JFM |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 246 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 36 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 23 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 24 Sep 2018
A long time ago, I wrote up a blog article about how to derive the linear regression formulas from first principles. Then I decided it was not of general interest, so I didn't publish it. (Sometime later I posted it to math stack exchange, so the effort wasn't wasted.)
The basic idea is, you have some points !!(x_i, y_i)!!, and you assume that they can be approximated by a line !!y=mx+b!!. You let the error be a function of !!m!! and !!b!!: $$\varepsilon(m, b) = \sum (mx_i + b - y_i)^2$$ and you use basic calculus to find !!m!! and !!b!! for which !!\varepsilon!! is minimal. Bing bang boom.
I knew this for a long time but it didn't occur to me until a few months ago that you could use basically the same technique to fit any other sort of curve. For example, suppose you think your data is not a line but a parabola of the type !!y=ax^2+bx+c!!. Then let the error be a function of !!a, b, !! and !!c!!:
$$\varepsilon(a,b,c) = \sum (ax_i^2 + bx_i + c - y_i)^2$$
and again minimize !!\varepsilon!!. You can even get a closed form as you can with ordinary linear regression.
I especially wanted to try fitting hyperbolas to data that I expected to have a Zipfian distribution. For example, take the hundred most popular names for girl babies in Illinois in 2017. Is there a simple formula which, given an ordinal number like 27, tells us approximately how many girls were given the 27th most popular name that year? (“Scarlett”? Seriously?)
I first tried fitting a hyperbola of the form !!y = c + \frac ax!!. We could, of course, take !!y_i' = \frac 1{y_i}!! and then try to fit a line to the points !!\langle x_i, y_i'\rangle!! instead. But this will distort the measurement of the error. It will tolerate gross errors in the points with large !!y!!-coordinates, and it will be extremely intolerant of errors in points close to the !!x!!-axis. This may not be what we want, and it wasn't what I wanted. So I went ahead and figured out the Zipfian regression formulas:
$$ \begin{align} a & = \frac{HY-NQ}D \\ c & = \frac{HQ-JY}D \end{align} $$
Where:
$$\begin{align} H & = \sum x_i^{-1} \\ J & = \sum x_i^{-2} \\ N & = \sum 1\\ Q & = \sum y_ix_i^{-1} \\ Y & = \sum y_i \\ D & = H^2 - NJ \end{align} $$
When I tried to fit this to some known hyperbolic data, it worked just fine. For example, given the four points !!\langle1, 1\rangle, \langle2, 0.5\rangle, \langle3, 0.333\rangle, \langle4, 0.25\rangle!!, it produces the hyperbola $$y = \frac{1.00018461538462}{x} - 0.000179487179486797.$$ This is close enough to !!y=\frac1x!! to confirm that the formulas work; the slight error in the coefficients is because we used !!\bigl\langle3, \frac{333}{1000}\bigr\rangle!! rather than !!\bigl\langle3, \frac13\bigr\rangle!!.
Unfortunately these formulas don't work for the Illinois baby data. Or rather, the hyperbola fits very badly. The regression produces !!y = \frac{892.765272442475}{x} + 182.128894972025:!!
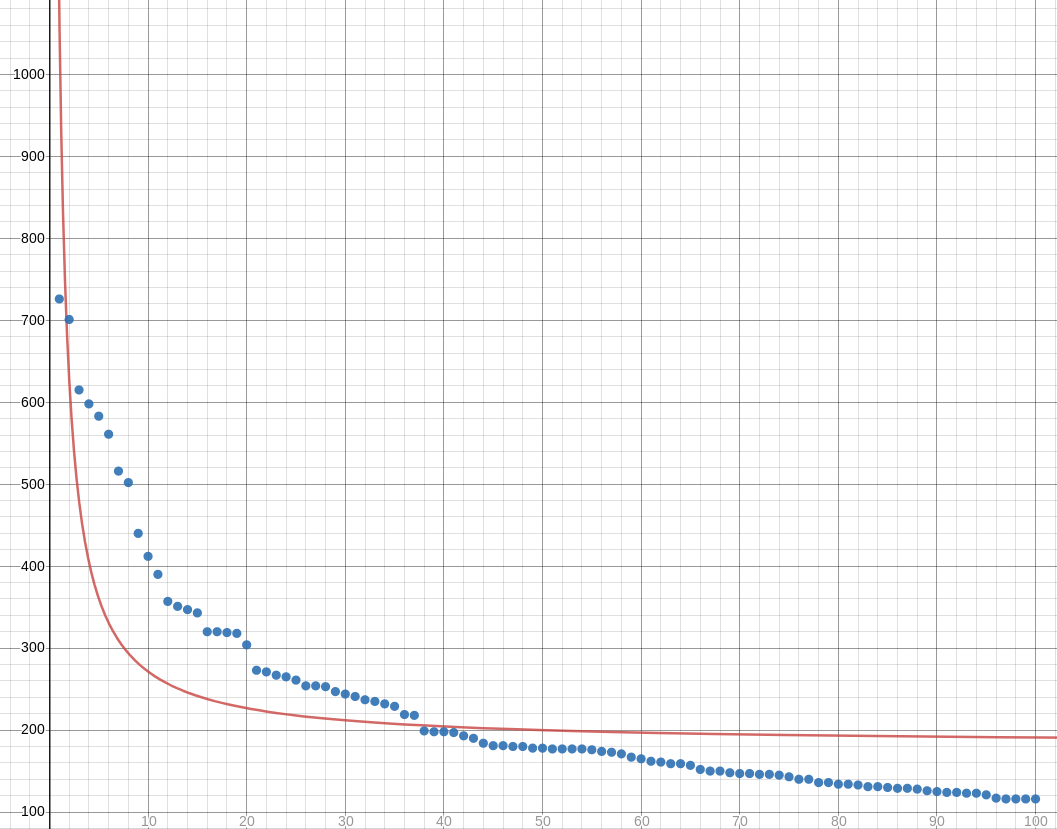
I think maybe I need to be using some hyperbola with more parameters, maybe something like !!y = \frac a{x-b} + c!!.
In the meantime, here's a trivial script for fitting !!y = \frac ax + c!! hyperbolas to your data:
while (<>) {
chomp;
my ($x, $y) = split;
($x, $y) = ($., $x) if not defined $y;
$H += 1/$x;
$J += 1/($x*$x);
$N += 1;
$Q += $y/$x;
$Y += $y;
}
my $D = $H*$H - $J*$N;
my $c = ($Q*$H - $J*$Y)/$D;
my $a = ($Y*$H - $Q*$N)/$D;
print "y = $a / x + $c\n";
[ Addendum 20180925: Shreevatsa R. asked a related question on StackOverflow and summarized the answers. The problem is more complex than it might first appear. Check it out. ]
[Other articles in category /math] permanent link
Fri, 14 Sep 2018
How not to remember the prime numbers under 1,000
A while back I said I wanted to memorize all the prime numbers under 1,000, because I am tired of getting some number like 851 or 857, or even 307, and then not knowing whether it is prime.
The straightforward way to deal with this is: just memorize the list. There are only 168 of them, and I have the first 25 or so memorized anyway.
But I had a different idea also. Say that a set of numbers from !!10n!! to !!10n+9!! is a “decade”. Each decade contains at most 4 primes, so 4 bits are enough to describe the primes in a single decade. Assign a consonant to each of the 16 possible patterns, say “b” when none of the four numbers is a prime, “d” when only !!10n+1!! is prime, “f” when only !!10n+3!! is, and so on.
Now memorizing the primes in the 90 decades is reduced to memorizing 90 consonants. Inserting vowels wherever convenient, we have now turned the problem into one of memorizing around 45 words. A word like “potato” would encode the constellation of primes in three consecutive decades. 45 words is only a few sentences, so perhaps we could reduce the list of primes to a short and easily-remembered paragraph. If so, memorizing a few sentences should be much easier than memorizing the original list of primes.
The method has several clear drawbacks. We would have to memorize the mapping from consonants to bit patterns, but this is short and maybe not too difficult.
More significant is that if we're trying to decide if, say, 637 is prime, we have to remember which consonant in which word represents the 63rd decade. This can be fixed, maybe, by selecting words and sentences of standard length. Say there are three sentences and each contains 30 consonants. Maybe we can arrange that words always appear in patterns, say four words with 1 or 2 consonants each that together total 7 consonants, followed by a single long word with three consonants. Then each sentence can contain three of these five-word groups and it will be relatively easy to locate the 23rd consonant in a sentence: it is early in the third group.
Katara and I tried this, with not much success. But I'm not ready to give up on the idea quite yet. A problem we encountered early on is that we remember consonants not be how words are spelled but by how they sound. So we don't want a word like “hammer” to represent the consonant pattern h-m-m but rather just h-m.
Another problem is that some constellations of primes are much more common than others. We initially assigned consonants to constellations in order. This assigned letter “b” to the decades that contain no primes. But this is the most common situation, so the letter “b” tended to predominate in the words we needed for our mnemonic. We need to be careful to assign the most common constellations to the best letters.
Some consonants in English like to appear in clusters, and it's not trivial to match these up with the common constellations. The mapping from prime constellations to consonants must be carefully chosen to work with English. We initially assigned “s” to the constellation “☆•☆☆” (where !!10n+1, 10n+7,!! and !!10n+9!! are prime but !!10n+3!! is not) and “t” to the constellation “☆☆••” (where !!10n+1!! and !!10n+3!! are prime but !!10n+7!! and !!10n+9!! are not) but these constellations cannot appear consecutively, since at least one of !!10n+7, 10n+9, 10n+11!! is composite. So any word with “s” and “t” with no intervening consonants was out of play. This eliminated a significant fraction of the entire dictionary!
I still think it could be made to work, maybe. If you're interested
in playing around with this, the programs I wrote are available on
Github. The mapping
from decade constellations to consonant clusters is in
select_words.py.
[Other articles in category /math] permanent link
Wed, 12 Sep 2018
Perils of hacking on mature software
Yesterday I wrote up an interesting bug in git-log --follow's
handling of empty files. Afterward
I thought I'd see if I could fix it.
People complain that the trouble of working on mature software like Git is to understand the way the code is structured, its conventions, the accumulated layers of cruft, and where everything is. I think this is a relatively minor difficulty. The hard part is no so much doing what you want, as knowing what you want to do.
My original idea for the fix was this: I can give git log a new
option, say --follow-size-threshhold=n. This would disable all
copy and rename detection for any files of size less than n bytes.
If not specified or configured, n would default to 1, so that the
default behavior would disable copy and rename detection of empty
files but not of anything else. I was concerned that an integer
option was unnecessarily delicate. It might have been sufficient to
have a boolean --follow-empty-files flag. But either way the
programming would be almost the same and it would be easy to simplify
the option later if the Git maintainers wanted it that way
I excavated the code and found where the change needed to go. It's
not actually in git-log itself. Git has an internal system for
diffing pairs of files, and git-log --follow uses this to decide
when two blobs are similar enough for it to switch from following one
to the other. So the flag actually needed to be added to git-diff,
where I called it --rename-size-threshhold. Then git-log would
set that option internally before using the Git diff system to detect
renames.
But then I ran into a roadblock. Diff already has an undocumented
flag called --rename-empty that tells it to report on renames of
empty files in certain contexts — not the context I was interested in
unfortunately. The flag is set by default, but it is cleared internally
when git-merge is resolving conflicts. The issue it addresses is
this: Suppose the merge base has some empty file X. Somewhere along
the line X has been removed. In one branch, an unrelated empty file
Y has been created, and in the other branch a different unrelated
empty file Z has been created. When merging these two branches, Git
will detect a merge conflict: was file X moved to location Y or to
location Z? This ⸢conflict⸣ is almost certainly spurious, and is is
very unlikely that the user will thank us for demanding that they
resolve it manually. So git-merge sets --no-rename-empty
internally and Git resolves the ⸢conflict⸣ automatically.
(See this commit for further details.)
The roadblock is: how does --rename-empty fit together with my
proposed --rename-size-threshhold flag? Should they be the same
thing? Or should they be separate options? There appear to be at
least three subsystems in Git that try to decide if two similar or
identical files (which might have different names, or the same name in
different directories) are “the same file” for various purposes. Do
we want to control the behavior of these subsystems separately or in
unison?
If they should be controlled in unison, should
--rename-size-threshhold be demoted to a boolean, or should
--rename-empty be promoted to an integer? And if they should be the
same, what are the implications for backward compatibility? Should
the existing --rename-empty be documented?
If we add new options, how do they interact with the existing and
already non-orthogonal flags that do something like this? They
include at least the following options of git-diff, git-log, and
git-show:
--follow
--find-renames=n
--find-copies
--find-copies-harder
-l
Only git-log has --follow and my new feature was conceived as a
modification of it, which is why I named it
--follow-size-threshhold. But git-log wouldn't be implementing
this itself, except to pass the flag into the diff system. Calling it
--follow-size-threshhold in git-diff didn't make sense because
git-diff doesn't have a --follow option. It needs a different
name. But if I do that, then we have git-diff and git-log options
with different names that nevertheless do exactly the same thing.
Confusing!
Now suppose you would like to configure a default for this option in
your .gitconfig. Does it make sense to have both
diff.renameSizeThreshhold and log.followSizeThreshhold options?
Not really. It would never be useful to set one but not the other.
So eliminate log.followSizeThreshhold. But now someone like me who
wants to change the behavior of git-log --follow will not know to
look in the right place for the option they need.
The thing to do at this point is to come up with some
reasonable-seeming proposal and send it to Jeff King, who created the
undocumented --rename-empty feature, and who is also a good person
to work with. But coming up with a good solution entirely on my own
is unlikely.
Doing any particular thing would not be too hard. The hard part is deciding what particular thing to do.
[Other articles in category /prog] permanent link
Language fluency in speech and print
Long ago I worked among the graduate students at the University of Pennsylvania department of Computer and Information Sciences. Among other things, I did system and software support for them, and being about the same age and with many common interests, I socialized with them also.
There was one Chinese-Malaysian graduate student who I thought of as having poor English. But one day, reading one of his emailed support requests, I was struck by how clear and well-composed it was. I suddenly realized I had been wrong. His English was excellent. It was his pronunciation that was not so good. When speaking to him in person, this was all I had perceived. In email, his accent vanished and he spoke English like a well-educated native. When I next met him in person I paid more careful attention and I realized that, indeed, I had not seen past the surface: he spoke the way he wrote, but his accent had blinded me to his excellent grammar and diction.
Once I picked up on this, I started to notice better. There were many examples of the same phenomenon, and also the opposite phenomenon, where someone spoke poorly but I hadn't noticed because their pronunciation was good. But then they would send email and the veil would be lifted. This was even true of native speakers, who can get away with all sorts of mistakes because their pronunciation is so perfect. (I don't mean perfect in the sense of pronouncing things the way the book says you should; I mean in the sense of pronouncing things the way a native speaker does.) I didn't notice this unless I was making an effort to look for it.
I'm not sure I have anything else to say about this, except that it seems to me that when learning a foreign language, one ought to consider whether one will be using it primarily for speech or primarily for writing, and optimize one's study time accordingly. For speech, concentrate on good pronunciation; for writing, focus on grammar and diction.
Hmm, put that way it seems obvious. Also, the sky is sometimes blue.
[Other articles in category /lang] permanent link
Mon, 10 Sep 2018
Why hooks and forks in the J language?
I don't know why [Ken] Iverson thought the hook was the thing to embed in the [J] language.
And I think I now recall that the name of the language itself, J, is intended to showcase the hook, so he must have thought it was pretty wonderful.
A helpful Hacker News
comment pointed me to
the explanation. Here Iverson explains why the “hook”
feature: it is actually the
S combinator in disguise. Recall that
$${\bf S} x y z = x z (y z).$$ This is exactly what J's hook computes
when you write (x y) z. For instance, if I understand correctly, in
J (+ !) means the one-place operation that takes an argument !!z!!
to !!z + z! !!.
As McBride and Paterson point
out, S
is also the same as the <*> operator in the Reader instance of
Applicative.
Since in J the only possible inputs to a hook are functions, it is
operating in the Reader idiom and in that context its hook is doing
the same thing as Haskell's <*>. Similarly, J's “fork” feature can
be understood as essentially the same as the Reader insance of
Haskell's liftA2.
[Other articles in category /prog] permanent link
git log --follow enthusiastically tracks empty files
This bug I just found in git log --follow is impressively massive.
Until I worked out what was going on I was really perplexed, and even
considered that my repository might have become corrupted.
I knew I'd written a draft of a blog article about the Watchmen movie, and I went to find out how long it had been sitting around:
% git log -- movie/Watchmen.blog
commit 934961428feff98fa3cb085e04a0d594b083f597
Author: Mark Dominus <mjd@plover.com>
Date: Fri Feb 3 16:32:25 2012 -0500
link to Mad Watchmen parody
also recategorize under movie instead of under book
The log stopped there, and the commit message says clearly that the
article was moved from elsewhere, so I used git-log --follow --stat
to find out how old it really was. The result was spectacularly
weird. It began in the right place:
commit 934961428feff98fa3cb085e04a0d594b083f597
Author: Mark Dominus <mjd@plover.com>
Date: Fri Feb 3 16:32:25 2012 -0500
link to Mad Watchmen parody
also recategorize under movie instead of under book
{book => movie}/Watchmen.blog | 8 +++++++-
1 file changed, 7 insertions(+), 1 deletion(-)
Okay, it was moved, with slight modifications, from book to movie,
as the message says.
commit 5bf6e946f66e290fc6abf044aa26b9f7cfaaedc4
Author: Mark Jason Dominus (陶敏修) <mjd@plover.com>
Date: Tue Jan 17 20:36:27 2012 -0500
finally started article about Watchment movie
book/Watchmen.blog | 40 ++++++++++++++++++++++++++++++++++++++++
1 file changed, 40 insertions(+)
Okay, the previous month I added some text to it.
Then I skipped to the bottom to see when it first appeared, and the bottom was completely weird, mentioning a series of completely unrelated articles:
commit e6779efdc9510374510705b4beb0b4c4b5853a93
Author: mjd <mjd>
Date: Thu May 4 15:21:57 2006 +0000
First chunk of linear regression article
prog/maxims/paste-code.notyet => math/linear-regression.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
tech/mercury.notyet => prog/maxims/paste-code.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
commit 1273c618ed6efa4df75ce97255204251678d04d3
Author: mjd <mjd>
Date: Tue Apr 4 15:32:00 2006 +0000
Thingy about propagation delay and mercury delay lines
tech/mercury.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
(The complete output is available for your perusal.)
The log is showing unrelated files being moved to totally unrelated
places. And also, the log messages do not seem to match up. “First
chunk of linear regression article” should be on some commit that adds
text to math/linear-regression.notyet or
math/linear-regression.blog. But according to the output above,
that file is still empty after that commit. Maybe I added the text in
a later commit? “Maxims directory reorganization” suggests that I
reorganized the contents of prog/maxims, but the stat says
otherwise.
My first thought was: when I imported my blog from CVS to Git, many years ago, I made a series of mistakes, and mismatched the log messages to the commits, or worse, and I might have to do it over again. Despair!
But no, it turns out that git-log is just intensely confused.
Let's look at one of the puzzling commits. Here it is as reported by
git log --follow --stat:
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
tech/mercury.notyet => prog/maxims/paste-code.notyet | 0
1 file changed, 0 insertions(+), 0 deletions(-)
But if I do git show --stat 9d9038a3, I get a very different
picture, one that makes sense:
% git show --stat 9d9038a3
commit 9d9038a3358a82616a159493c6bdc91dd03d03f4
Author: mjd <mjd>
Date: Tue May 2 14:16:24 2006 +0000
maxims directory reorganization
prog/maxims.notyet | 226 -------------------------------------------
prog/maxims/maxims.notyet | 95 ++++++++++++++++++
prog/maxims/paste-code.blog | 134 +++++++++++++++++++++++++
prog/maxims/paste-code.notyet | 0
4 files changed, 229 insertions(+), 226 deletions(-)
This is easy to understand. The commit message was correct: the
maxims are being reorganized. But git-log --stat, in conjunction
with --follow, has produced a stat that has only a tenuous
connection with reality.
I believe what happened here is this: In 2012 I “finally started article”. But I didn't create the file at that time. Rather, I had created the file in 2009 with the intention of putting something into it later:
% git show --stat 5c8c5e66
commit 5c8c5e66bcd1b5485576348cb5bbca20c37bd330
Author: mjd <mjd>
Date: Tue Jun 23 18:42:31 2009 +0000
empty file
book/Watchmen.blog | 0
book/Watchmen.notyet | 0
2 files changed, 0 insertions(+), 0 deletions(-)
This commit does appear in the git-log --follow output, but it
looks like this:
commit 5c8c5e66bcd1b5485576348cb5bbca20c37bd330
Author: mjd <mjd>
Date: Tue Jun 23 18:42:31 2009 +0000
empty file
wikipedia/mega.notyet => book/Watchmen.blog | 0
1 file changed, 0 insertions(+), 0 deletions(-)
It appears that Git, having detected that book/Watchmen.blog was
moved to movie/Watchmen.blog in Febraury 2012, is now following
book/Watchmen.blog backward in time. It sees that in January 2012
the file was modified, and was formerly empty, and after that it sees
that in June 2009 the empty file was created. At that time there was
another empty file, wikipedia/mega.notyet. And git-log decides that the
empty file book/Watchmen.blog was copied from the other empty
file.
At this point it has gone completely off the rails, because it is now
following the unrelated empty file wikipedia/mega.notyet. It then
makes more mistakes of the same type. At one point there was an empty
wikipedia/mega.blog file, but commit ff0d744d5 added some text to it
and also created an empty wikipedia/mega.notyet alongside it. The
git-log --follow command has interpreted this as the empty
wikipedia/mega.blog being moved to wikipedia/mega.notyet and a
new wikipedia/mega.blog being created alongside it. It is now following
wikipedia/mega.blog.
Commit ff398402 created the empty file wikipedia/mega.blog fresh,
but git-log --follow interprets the commit as copying
wikipedia/mega.blog from the already-existing empty file
tech/mercury.notyet. Commit 1273c618 created tech/mercury.notyet,
and after that the trail comes to an end, because that was shortly
after I started keeping my blog in revision control; there were no
empty files before that. I suppose that attempting to follow the
history of any file that started out empty is going to lead to the
same place, tech/mercury.notyet.
On a different machine with a different copy of the repository, the
git-log --follow on this file threads its way through ten
irrelvant files before winding up at tech/mercury.notyet.
There is a --find-renames=... flag to tell Git how conservative to
be when guessing that a file might have been renamed and modified at
the same time. The default is 50%. But even turning it up to 100%
doesn't help with this problem, because in this case the false
positives are files that are actually identical.
As far as I can tell there is no option to set an absolute threshhold
on when two files are considered the same by --follow. Perhaps it
would be enough to tell Git that it should simply not try to follow
files whose size is less than !!n!! bytes, for some small !!n!!, perhaps
even !!n=1!!.
The part I don't fully understand is how git-log --follow is
generating its stat outputs. Certainly it's not doing it in the
same way that git show is. Instead it is trying to do something
clever, to highlight the copies and renames it thinks it has found,
and in this case it goes badly wrong.
The problem appears in Git 1.7.11, 2.7.4, and 2.13.0.
[ Addendum 20180912: A followup about my work on a fix for this. ]
[Other articles in category /prog] permanent link
Sun, 09 Sep 2018I very recently suggested a mathematical operation that does this:
$$\begin{align} \left((\sqrt\bullet) \cdot x + \left(\frac1\bullet\right) \cdot 1 \right) ⊛ (9x+4) & = \sqrt9 x^2 + \sqrt4 x + \frac19 x + \frac14 \\ & = 3x^2 + \frac{19}{9} x + \frac 14 \end{align}$$
Here the left-hand argument is like a polynomial, except that the coefficients are functions. The right-hand argument is an ordinary polynomial.
It occurs to me that the APL progamming lanaguage (invented around 1966) actually has something almost like this, in its generalized matrix product.
In APL, if ? and ! are any binary operators, you can write ?.!
to combine them into a matrix operator. Like ordinary matrix
multiplication, the new operator combines an !!m×n!! and an !!n×r!! matrix
into an !!m×r!! matrix. Ordinary matrix multiplication is defined like
this:
$$c_{ij} = a_{i1} \cdot b_{1j} +
a_{i2} \cdot b_{2j} + \ldots +
a_{in} \cdot b_{nj} $$
The APL ?.! operator replaces the addition with ? and the
multiplication with !, so that +.× is exactly the standard matrix
multiplication. Several other combined operations of this type are,
if not common, at least idiomatic. For example, I have seen, and
perhaps used, ∨.∧, +.∧, and ⌈.⌊. (⌈ and ⌊ are APL's
two-argument minimum and maximum operators.)
With this feature, the ⊛ operator I proposed above would be something
like +.∘, where ∘ means function composition. To make it work you
need to interpret the coefficients of an ordinary polynomial as
constant functions, but that is not much of a stretch. APL doesn't
actually have a function composition operator.
APL does have a ∘ symbol, but it doesn't mean function composition,
and also the !.? notation is special cased, in typically APL style,
so that ∘.? does something sort of related but rather different.
Observe also that if !!a!! and !!b!! are !!1×n!! and !!n×1!! matrices,
respectively, then !!a +.× b!! ought to be dot product of !!a!! and !!b!!:
it is a !!1×1!! matrix whose sole entry is:
$$c_{11} = a_{11} \cdot b_{11} +
a_{12} \cdot b_{21} + \ldots +
a_{1n} \cdot b_{n1} $$
and similarly if !!a!! is !!n×1!! and !!b!! is !!1×m!! then !!a +.× b!! is the
outer product, the !!n×m!! matrix whose !!c_{ij} = a_i × b_j!!. But I
think APL doesn't distinguish between a !!1×n!! matrix and a vector,
though, and always considers them to be vectors, so that in such cases
!!a +.× b!! always gets you the dot product, if !!a!! and !!b!! are the same
length, and an error otherwise. If you want the outer product of two
vectors you use a ∘.× b instead. a ∘.+ b would be the outer
product matrix with !!c_{ij} = a_i + b_j!!. APL is really strange.
I applied for an APL job once; I went to a job fair (late 1980s maybe?) and some Delaware bank was looking for APL programmers to help maintain their legacy APL software. I was quite excited at the idea of programming APL professionally, but I had no professional APL experience so they passed me over. I think they made a mistake, because there are not that many people with professional APL experience anyway, and how many twenty-year-olds are there who know APL and come knocking on your door looking for a job? But whatever, it's probably better that I didn't take that route.
The +.× thing exemplifies my biggest complaint about APL semantics:
it was groping toward the idea of functional programming without quite
getting there, never quite general enough. You could use !/, where
! was any built-in binary operator, and this was quite like a fold.
But you couldn't fold a user-defined function of two arguments! And
you couldn't write a higher-order fold function either.
I was pleased to find out that Iverson had designed a successor language, J, and then quickly disappointed when I saw how little it added. For example, it has an implicit “hook” construction, which is a special case in the language for handling one special case of function composition. In Haskell it would be:
hook f g x = x `f` (g x)
but in J the hook itself is implicit. If you would rather use (g x) `f` x
instead, you are out of luck because that is not built-in. I don't
know why Iverson thought the hook was the thing to embed in the
language. (J also has an implicit “fork” which is fork f g h x =
(f x) `g` (h x).)
[ Addendum 20180910: The explanation. ]
Meanwhile the awful APL notation has gotten much more awful in J, and
you get little in return. You even lose all the fun of the little
squiggles. Haskell is a much better J than J ever was. Haskell's
notation can be pretty awful too ((.) . (.)?), but at least you are
are getting your money's worth.
I thought I'd see about implementing APL's !.? thing in Haskell to
see what it would look like. I decided to do it by implementing a
regular matrix product and then generalizing. Let's do the simplest
thing that could possibly work and represent a matrix as a list of
rows, each of which is a list of entries.
For a regular matrix product, !!C = AB!! means that !!c_{ij}!! is the dot product of the !!i!!th row of !!A!! and the !!j!!th column of !!B!!, so I implemented a dot product function:
dot_product :: Num b => [b] -> [b] -> b
dot_product a b = foldr (+) 0 $ zipWith (*) a b
OK, that was straightforward.
The rows of !!A!! are right there, but we also need the columns from !!B!!, so here's a function to get those:
transpose ([]:_) = []
transpose x = (map head x) : transpose (map tail x)
Also straightforward.
After that I toiled for a very long time over the matrix product itself. My first idea was to turn !!A!! into a list of functions, each of which would dot-product one of the rows of !!A!! by a given vector. Then I would map each of these functions over the columns of !!B!!.
Turning !!A!! into a list of functions was easy:
map dot_product a :: [ [x] -> x ]
and getting the columns of !!B!! I had already done:
transpose b :: [[x]]
and now I just need to apply each row of functions in the first part to each column in the second part and collect the results:
??? (map dot_product a) (transpose b)
I don't know why this turned out to be so damn hard. This is the sort of thing that ought to be really, really easy in Haskell. But I had many difficulties.
First I wasted a bunch of time trying to get <*> to work, because it
does do something like that.
But the thing
I wanted has signature
??? :: [a -> b] -> [a] -> [[b]]
whereas <*> flattens the result:
<*> :: [a -> b] -> [a] -> [b]
and I needed to keep that extra structure. I tried all sorts of
tinkering with <*> and <$> but never found what I wanted.
Another part of the problem was I didn't know any primitive for “map a list of functions over a single argument”. Although it's not hard to write, I had some trouble thinking about it after I wrote it:
pamf fs b = fmap ($ b) fs
Then the “map each function over each list of arguments” is map . pamf, so I got
(map . pamf) (map dot_product a) (transpose b)
and this almost works, except it produces the columns of the results
instead of the rows. There is an easy fix and a better fix. The easy
fix is to just transpose the final result. I never did find the
better fix. I thought I'd be able to replace map . pamf with pamf
. map but the latter doesn't even type check.
Anyway this did work:
matrix_product a b =
transpose $ (map . pamf) (map dot_product a) (transpose b)
but that transpose on the front kept bothering me and I couldn't
leave it alone.
So then I went down a rabbit hole and wrote nine more versions of
???:
fs `op` as = do
f <- fs
return $ fmap f as
fs `op2` as = fs >>= (\f -> return $ fmap f as)
fs `op3` as = fs >>= (return . flip fmap as )
fs `op4` as = fmap ( flip fmap as ) fs
op5 as = fmap ( flip fmap as )
op6 :: [a -> b] -> [a] -> [[b]]
op6 = flip $ fmap . (flip fmap)
fs `op7` as = map (\f -> [ f a | a <- as ]) fs
fs `op8` as = map (\f -> (map f as)) fs
fs `op9` as = map (flip map as) fs
I finally settled on op6, except it takes the arguments in the
“wrong” order, with the list of functions second and their arguments
first. But I used it anyway:
matrix_product a b = (map . flip map) (transpose b) (map dot_product a)
The result was okay, but it took me so long to get there.
Now I have matrix_product and I can generalize it to uses two
arbitrary operations instead of addition and multiplication. And
hey, I don't have to touch matrix_product! I only need to change
dot_product because that's where the arithmetic is. Instead of
dot_product a b = foldr (+) 0 $ zipWith (*) a b
just use:
inner_product u v = foldr add 0 $ zipWith mul u v
Except uh oh, that 0 is wrong. It might not be the identity for
whatever weird operation add is; it might be min and then we need
the 0 to be minus infinity.
I tinkered a bit with requiring a Monoid instance for the matrix
entries, which seemed interesting at least, but to do that I would
need to switch monoids in the middle of the computation and I didn't
want to think about how to do that. So instead I wrote a version of
foldr that doesn't need an identity element:
foldr' f (a:as) = foldr f a as
This fails on empty lists, which is just fine, since I wasn't planning on multiplying any empty matrices.
Then I have the final answer:
general_matrix_product add mul a b =
(map . flip map) (transpose b) (map inner_product a) where
inner_product u v = foldr' add $ zipWith mul u v
It's nice and short, but on the other hand it has that mysterious map
. flip map in there. If I hadn't written that myself I would see it
and ask what on earth it was doing. In fact I did write it myself
and I although I do know what it is doing I don't really understand
why.
As for the shortness, let's see what it looks like in a more conventional language:
def transpose(m):
return list(zip(*m))
Wow, that was amazingly easy.
def matrix_product(a, b):
def dot_product(u, v):
total = 0
for pair in zip(u, v):
total += pair[0] * pair[1]
return total
bT = transpose(b)
c = []
for i in range(len(a)):
c.append([])
for j in range(len(bT)):
c[-1].append(None)
c[i][j] = dot_product(a[i], bT[j])
return c
Okay, that was kind of a mess. The dot_product should be shorter
because Python has a nice built-in sum function but how do I build
the list of products I want to sum? It doesn't have map because it
doesn't have lambdas. I know, I know, someone is going to insist that
Python has lambdas. It does, sort of, but they suck.
I think the standard Python answer to this is that you don't need
map because you're supposed to use list comprehension instead:
def dot_product(u, v):
return sum([ x*y for (x, y) in zip(u, v) ])
I don't know how I feel about that argument in general but in this case the result was lovely. I have no complaints.
While I was writing the Python program I got a weird bug that turned
out to be related to mutability: I had initialized c with
c = [[None] * len(bT)] * len(a)
But this makes the rows of c the same mutable object, and then
installing values in each row overwrites the entries we stored in the
previous rows. So definitely score one point for Haskell there.
A lot of the mess in the code is because Python is so obstinate about extending lists when you need them extended, you have to say pretty please every time. Maybe I can get rid of that by using more list comprehensions?
def matrix_product2(a, b):
def dot_product(u, v):
return sum([ x*y for (x, y) in zip(u, v) ])
return [ [ dot_product(u, v) for v in transpose(b) ] for u in a ]
Python's list comprehensions usually make me long for Haskell's, which are so much nicer, but this time they were fine. Python totally wins here. No wait, that's not fair: maybe I should have been using list comprehensions in Haskell also?
matrix_product = [ [ dot_product row col | col <- transpose b ] | row <- a ]
Yeah, okay. All that map . flip map stuff was for the birds. Guido
thinks that map is a bad idea, and I thought he was being silly, but
maybe he has a point. If I did want the ??? thing that applies a
list of functions to a list of arguments, the list comprehension
solves that too:
[ f x | f <- fs, x <- xs ]
Well, lesson learned.
I really wish I could write Haskell faster. In the mid-1990s I wrote thousands of lines of SML code and despite (or perhaps because of) SML's limitations I was usually able to get my programs to do what I wanted. But when I try to write programs in Haskell it takes me a really long time to get anywhere.
Apropos of nothing, today is the 77th birthday of Dennis M. Ritchie.
[ Addendum: It took me until now to realize that, after all that, the operation I wanted for polynomials is not matrix multiplication. Not at all! It is actually a convolution:
$$ c_k = \sum_{i+j=k} a_ib_j $$
or, for my weird functional version, replace the multiplication !!a_ib_j!! with function composition !!a_i ∘ b_j!!. I may implement this later, for practice. And it's also tempting to try to do it in APL, even though that would most likely be a terrible waste of time… ]
[ Addendum 20180909: Vaibhav Sagar points out that my foldr' is the
standard Prelude function
foldr1.
But as I said in the previous
article, one of the
problems I have is that faced with a need for something like foldr1,
instead of taking one minute to write it, I will waste fifteen minutes
looking for it in Hoogle. This time I opted to not do that. In
hindsight it was a mistake, perhaps, but I don't regret the choice.
It is not easy to predict what is worth looking for. To see the
downside risk, consider pamf. A Hoogle search for
pamf
produces nothing like what I want, and, indeed, it doesn't seem to
exist. ]
[Other articles in category /prog] permanent link
Sat, 08 Sep 2018
Why I never finish my Haskell programs (part 2 of ∞)
Here's something else that often goes wrong when I am writing a Haskell program. It's related to the problem in the previous article but not the same.
Let's say I'm building a module for managing polynomials. Say
Polynomial a is the type of (univariate) polynomials over some
number-like set of coefficients a.
Now clearly this is going to be a functor, so I define the Functor instance, which is totally straightforward:
instance Functor Polynomial where
fmap f (Poly a) = Poly $ map f a
Then I ask myself if it is also going to be an Applicative.
Certainly the pure function makes sense; it just lifts a number to
be a constant polynomial:
pure a = Poly [a]
But what about <*>? This would have the
type:
(Polynomial (a -> b)) -> Polynomial a -> Polynomial b
The first argument there is a polynomial whose coefficients are functions. This is not something we normally deal with. That ought to be the end of the matter.
But instead I pursue it just a little farther. Suppose we did have such an object. What would it mean to apply a functional polynomial and an ordinary polynomial? Do we apply the functions on the left to the coefficients on the right and then collect like terms? Say for example
$$\begin{align} \left((\sqrt\bullet) \cdot x + \left(\frac1\bullet\right) \cdot 1 \right) ⊛ (9x+4) & = \sqrt9 x^2 + \sqrt4 x + \frac19 x + \frac14 \\ & = 3x^2 + \frac{19}{9} x + \frac 14 \end{align}$$
Well, this is kinda interesting. And it would mean that the pure
definition wouldn't be what I said; instead it would lift a number to
a constant function:
pure a = Poly [λ_ -> a]
Then the ⊛ can be understood to be just like polynomial
multiplication, except that coefficients are combined with function
composition instead of with multiplication. The operation is
associative, as one would hope and expect, and even though the ⊛
operation is not commutative, it has a two-sided identity element,
which is Poly [id]. Then I start to wonder if it's useful for anything, and
how ⊛ interacts with ordinary multiplication, and so forth.
This is different from the failure mode of the previous article because in that example I was going down a Haskell rabbit hole of more and more unnecessary programming. This time the programming is all trivial. Instead, I've discovered a new kind of mathematical operation and I abandon the programming entirely and go off chasing a mathematical wild goose.
[ Addendum 20181109: Another one of these. ]
[Other articles in category /prog/haskell] permanent link
Mon, 03 Sep 2018
Why I never finish my Haskell programs (part 1 of ∞)
Whenever I try to program in Haskell, the same thing always goes wrong. Here is an example.
I am writing a module to operate on polynomials. The polynomial !!x^3 - 3x + 1!! is represented as
Poly [1, -3, 0, 1]
[ Addendum 20180904: This is not an error. The !!x^3!! term is last, not first. Much easier that way. Fun fact: two separate people on Reddit both commented that I was a dummy for not doing it the easy way, which is the way I did do it. Fuckin' Reddit, man. ]
I want to add two polynomials. To do this I just add the corresponding coefficients, so it's just
(Poly a) + (Poly b) = Poly $ zipWith (+) a b
Except no, that's wrong, because it stops too soon. When the lists
are different lengths, zipWith discards the extra, so for example it
says that !!(x^2 + x + 1) + (2x + 2) = 3x + 3!!, because it has
discarded the extra !!x^2!! term. But I want it to keep the extra, as
if the short list was extended with enough zeroes. This would be a
correct implementation:
(Poly a) + (Poly b) = Poly $ addup a b where
addup [] b = b
addup a [] = a
addup (a:as) (b:bs) = (a+b):(addup as bs)
and I can write this off the top of my head.
But do I? No, this is where things go off the rails. “I ought to be
able to generalize this,” I say. “I can define a function like
zipWith that is defined over any Monoid, it will combine the
elements pairwise with mplus, and when one of the lists
runs out, it will pretend that that one has some memptys stuck on the
end.” Here I am thinking of something like ffff :: Monoid a => [a] ->
[a] -> [a], and then the (+) above would just be
(Poly a) + (Poly b) = Poly (ffff a b)
as long as there is a suitable Monoid instance for the as and bs.
I could write ffff in two minutes, but instead I spend fifteen
minutes looking around in Hoogle to see if there is already an ffff,
and I find mzip, and waste time being confused by mzip, until I
notice that I was only confused because mzip is for Monad, not
for Monoid, and is not what I wanted at all.
So do I write ffff and get on with my life? No, I'm still not done.
It gets worse. “I ought to be able to generalize this,” I say. “It
makes sense not just for lists, but for any Traversable… Hmm, or
does it?” Then I start thinking about trees and how it should decide
when to recurse and when to give up and use mempty, and then I start
thinking about the Maybe version of it.
Then I open a new file and start writing
mzip :: (Traversable f, Monoid a) => f a -> f a -> f a
mzip as bs = …
And I go father and farther down the rabbit hole and I never come back
to what I was actually working on. Maybe the next step in this
descent into madness is that I start thinking about how to perform
unification of arbitrary algebraic data structures, I abandon mzip
and open a new file for defining class Unifiable…
Actually when I try to program in Haskell there a lot of things that go wrong and this is only one of them, but it seems like this one might be more amenable to a quick fix than some of the other things.
[ Addendum 20180904: A lobste.rs
user
points out that I don't need Monoid, but only Semigroup, since
I don't need mempty. True that! I didn't know there was a
Semigroup class. ]
[ Addendum 20181109: More articles in this series: [2] [3] ]
[Other articles in category /prog/haskell] permanent link


