Mark Dominus (陶敏修)
mjd@pobox.com

Historical backlog:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Backtalk plugin shut off
Sun, 29 Apr 2018
In August 2011, on a particular famous discussion forum (brought up on this blog again and again) an individual A, notorious for such acts, posts a quasi-philosophical inquiry, incurring unpopularity, antagonism, and many bad marks, although also a surprising quantity of rational discussion, including a thoughtful solution or two.
Many months forward, a distinct party B puts up a substantial bounty on this inquiry, saying:
I would like a complete answer to this question which does not use the letter "e" at any point.
(My apology for any anguish you may go through at this point in my story on account of this quotation and its obvious and blatant faults. My wrongdoing was involuntary, but I had no way to avoid it and still maintain full accuracy.)
By and by, a valiant third individual constructs a brilliant disquisition satisfying this surprising condition and thus obtains B's award.
Now, this month, in our group's accompanying policy board, a fourth collaborator, a guy (or gal, for all I know) I shall call D, and who I think may lack a minimal inclination for fun, finds fault with A's original post and particularly with C's bounty, and complains as follows:
Should we discourage bounties that encourage “clever” but unclear answers?
(Again, I must ask you for absolution. This is a word-for-word quotation.)
A thorough dismissal of OP's complaint, from a fifth author, adds a fully satisfactory finish to our affair.
[Additional posts on topic /lang] immortal link
Fri, 20 Apr 2018Here is a list of March's shitposts. I don't recall what my excuse was for there being only 22, but in my defense, I will add that they were almost all terrible. There was one decent math post I maybe should have promoted.
(And also Nancy and Squid, which was awesome, and also 100% Grade A shitpost. I thought when I posted it a crowd of people would burst into the room and carry me off on their shoulders. Instead, nobody seems to have noticed.)
April will be better; I'm on pace to break the previous volume record, and I've also been doing a good job of promoting better posts to the major leagues.
- Today I learned…
- Soot
- Seedless fruit
- I'm so old…
- Whether to get donations via Patreon
- Nancy and Squid
- Today I learned…
- Poor phrasing of the day…
- W and V
- Executive departments
- Stuff my brain came up with this morning
- Browning
- The opposite of vegan soup
- Cantonese style non-vegan soup
- Israeli chicken sandwich
- Names that begin with an 'X', and don't
- Ear care tips
- Icelandic butt
- Peddler's Pantry
- Chaise LONGUE
- Hotel ritual
- Things English fails to distinguish
[Additional posts on topic /meta/shitpost] immortal link
Thu, 19 Apr 2018
Soldier fly protein: why so expensive?

There have been recurring news stories about the use of dried maggots as protein supplement in animal feed. For example Insects could feed the animals of tomorrow’s meat industry (maggots fed on slaughterhouse waste, particularly blood) or Insect farms gear up to feed soaring global protein demand (maggots fed on rotten fruit). Then they dry the larvae and either use them whole or grind them into meal. In particular the fly meal can be used as a replacement for fish meal, which is ground dried fish that is used as feed for fish in fish farms. (Yep, we grind up fish we don't like, to feed to other, better fish.)
I was referred to that second article by Metafilter and The Google, in its infinite wisdom, decided to show me an advertisement for dried fly larvae. The ad was for NaturesPeck, which sells bagged fly larvae and fly meal for use as poultry feed or wild bird feed. They have a special “value pack” that contains 16 pounds of dried larvae for $88. That is $5.50 a pound! Holy cow, WTF? How can that even be possible when my local grocery store is selling boneless center cut pork chops for $2.50 per pound?
Okay, I thought maybe NaturesPeck was some sort of boutique operation, charging a high markup for small quantities, maybe they claim to have sustainably-harvested fly meal from free-range organically-fed flies or something. So I went looking for an industrial wholesaler of bulk fly meal and quickly found Haocheng Mealworms Inc. in Xiangtan, China. This is definitely what I was looking for; they will be glad to sell you a standard 40-foot shipping container full of dried maggots or other larvae. The quoted price for dried mealworm larvae is $8400 per metric tonne, plus shipping ($170–200 per tonne).
Prices, converted to U.S. dollars per pound, are as follows:
| Dried soldier fly maggots | $2.49 |
| Powdered soldier fly maggots | 2.81 |
| Dried mealworms | 3.81 |
| Powdered mealworms | 4.22 |
| Live mealworms | 5.67 |
| Canned fresh mealworms | 7.08 |
| Dried superworms | 4.76 |
| Live superworms | 8.30 |
| Canned fresh superworms | 7.71 |
So it wasn't just that NaturesPeck was marking them up. Even the least expensive product costs as much as retail pork chops.
I don't get it. There must be some important aspect of this that I am missing, because a market failure of this magnitude is impossible.
BTW, Haocheng recommends that:
As a source of high protein additive, put [mealworms] into the bread, flour, instant noodle, pastry, biscuit, candy, condiment, and direct into the dishes on the dining table like the foodstuff, and process into the health care nourishment to improve the human body immunity ability.
Not at those prices, buddy.
[ Addendum 20180502: Some possible explanations ]
[Additional posts on topic /food] immortal link
Wed, 18 Apr 2018
Lower mathematics solves an easy problem
[ Warning: this article is mathematically uninteresting. ]
I woke up in the middle of the night last night and while I was waiting to go back to sleep, I browsed math Stack Exchange. At four in the morning I am not at my best, but sometimes I can learn something and sometimes I can even contribute.
The question that grabbed my attention this time was Arithmetic sequence where every term is prime?. OP wants to know if the arithmetic sequence $$d\mapsto a+d b$$ contains composite elements for every fixed positive integers !!a,b!!.
Now of course the answer is yes, or the counterexample would give us a quick and simple method for constructing prime numbers, and finding such has been an open problem for thousands of years. OP was certainly aware of this, but had not been able to find a simple proof. Their searching was confounded by more advanced matters relating to the Green-Tao theorem and such like, which, being more interesting, are much more widely discussed.
There are a couple of remarkable things about the answers that were given. First, even though the problem is easy, the first two answers posted were actually wrong, and another (quickly deleted) was so complicated that I couldn't tell if it was right or not.
One user immediately commented:
What happens if !!d=a!!?
which is very much to the point; when !!d=a!! then the element of the sequence is !!a+ab!! which is necessarily composite…
…unless !!a=1!!. So the comment does not quite take care of the whole question. A second user posted an answer with this same omission, and had to correct it later.
I might not have picked up on this case either, during the daytime. But at 4 AM I was not immediately certain that !!a+ab!! was composite and I had to think about it. I factored it to get !!a(1+b)!! and then I saw that if !!a=1!! or !!1+b=1!! then we lose. (!!1+b=1!! is impossible. !!a+ab!! might of course be composite even if !!a=1!!, but further argumentation is needed.)
So I did pick up on this, and gave a complete answer, of which the important part is:
Just take !!d=kb+k+a!! for any !!k!! whatever. Then the element is $$kb^2+(k+a)b+a = (kb+a)(b+a)$$ which is composite.
Okay, fine. But OP asked how I came up with that and if it was pure “insight”, so I thought I'd try to reconstruct how I got there at 4 AM. The problem is simple enough that I think I can remember most of how I got to the answer.
As I've mentioned before, I am not a pure insight kind of person. While better mathematicians are flitting swiftly from peak to peak, I plod along in the dark and gloomy valleys. I did not get !!d=kb+k+a!! in a brilliant flash of inspiration.
Instead, my thought process, as well as I can remember it, went like this:
“That doesn't work when !!a=1!!. But there must be composite numbers in sequences of the form !!d b+1!!. I wonder what they look like?”
“I guess I'll try an example. How about !!4d+1!!?”
“Hmm, it starts at 5, 5 is composite… No it isn't.”
“But it's increasing by 4 each time so it must hit each mod-5 residue class in some order.”
I should cut in at this point to add that my thinking was nowhere near this articulate or even verbal. The thing about the sequence hitting all the residue classes was more like a feeling in my body, like when I am recognizing a familiar place. When !!a!! and !!b!! are relatively prime, that means that when you are taking steps of size !!b!!, you hit all the !!a!!'s and don't skip any; that's what relatively prime is all about.
So maybe that counts as “insight”? Or “intuition about relative primality”? I think that description makes it sound much more impressive than it really is. I do not want a lot of credit for this. Maybe a better way to describe it is that I had been in this familiar place many times before, and I recognized it again.
Anyway I continued something like this:
- “If it hits every residue class over and over in sequence it must hit residue class !!0!! infinitely often. How does that go? It hits !!5!!, so it hits !!5+4·5 = 25!! also.”
That was good enough for me; I did not even consider the next hit, !!45!!, perhaps because that number was too big for me to calculate at that moment.
I didn't use the phrase “residue class” either. That's just my verbal translation of my 4AM nonverbal thinking. At the time it was more like: there are some good things to hit and some bad ones, and the good ones are evenly spaced out, so if we hit each position in the even spacing-ness we must periodically hit some of the good things.
- “Okay, then the first element of !!1+d b!! is !!1+b!!, and then every !!1+b!! steps after that it hits another multiple of !!1+b!!, so we want every !!1+b!! elements, so take !!d = 1 + k(1+b)!!.”
Then I posted the answer, saying that when !!a=1!! you take !!d=1+k(1+b)!! and the sequence element is !!1+b+kb+kb^2 = (1+b)(1+kb)!!.
Then I realized that I had the same feeling in my body even when !!a≠1!!, because it only depended on the way the residue classes repeated, and changing !!a!! doesn't affect that, it just slides everything left or right by a constant amount. So I went back to edit the !!1+k(1+b)!! to be !!a+k(1+b)!! instead.
I have no particular conclusion to draw about this.
[Additional posts on topic /math] immortal link
Mon, 16 Apr 2018
A familiar set with an unexpected order type
I dreamed this one up in high school and I recommend it as an exercise for kids at an appropriate level.
Consider the set of all Roman numerals
$${ \text{I}, \text{II}, \text{III}, \text{IV}, \text{V}, \ldots, \text{XIII}, \text{XIV}, \text{XV}, \text{XVI}, \ldots, \\ \text{XXXVIII}, \text{XXXIX}, \text{XL}, \text{XLI}, \ldots, \text{XLIX}, \text{L},\ldots,\\ \text{C}, \ldots , \text{D}, \ldots, \text{M}, \ldots, \text{MM}, \ldots, \text{MMM}, \ldots, \text{MMMM}, \ldots, \text{MMMMM}, \ldots }$$
where we allow an arbitrarily large number of M's on the front, so that every number has a unique representation. For example the number 10,067 is represented by !!\text{MMMMMMMMMMLXVII}!!.
Now sort the list into alphabetical order.
It is easy to show that it begins with !!\text{C}, \text{CC}, \text{CCC}, \text{CCCI}, \ldots!! and ends !!\text{XXXVII}, \text{XXXVIII}!!. But it's still an infinite list! Instead of being infinite at one end or the other, or even both, like most infinite lists, it's infinite in the middle.
Of course once you have the idea it's easy to think of more examples (!!\left\{ \frac1n\mid n\in\Bbb Z, n\ne 0\right\}!! for instance) but I hadn't seen anything like this before and I was quite pleased.
[Additional posts on topic /math] immortal link
Sun, 15 Apr 2018
On the smallest natural number
The earliest known mathematics book printed in Europe is an untitled arithmetic text published in Treviso in 1478, Originally written in Venetian dialect.
The Treviso Arithmetic states unequivocally:
Number is a multitude brought together or assembled from several units, and always from two at least, as in the case of 2, which is the first and the smallest number.
And a little later:
Of [the digits] the first figure, 1, is not called a number but the source of number.
(English translations are from David Eugene Smith, A Source Book in Mathematics (1959). A complete translation appears in Frank J. Swetz, Capitalism and Arithmetic The New Math of the Fifteenth Century (1987).)
By the way, today is the 311th birthday of Leonhard Euler.
[Additional posts on topic /math] immortal link
Sat, 14 Apr 2018
Colored blobs on electric wires
The high-voltage power lines run along the New Jersey Turnpike for a long way, and there is this one short stretch of road where the wires have red, white, and yellow blobs on them. Google's Street View shot shows them quite clearly.
A thousand feet or so farther down the road, no more blobs.
I did Internet searches to find out what the blobs were about, and everyone seemed to agree that they were to make the wires more visible to low-flying aircraft. Which seemed reasonable, but puzzling, because as far as I knew there was no airport in the vicinity. And anyway, why blobs only on that one short stretch of wire?
Last week I drove Katara up to New York and when I saw the blobs coming I asked her to photograph them and email me the pictures. She did, and as I hoped, there in the EXIF data in the images was the exact location at which the pictures had been taken: !!(40.2106, -74.57726675)!!. I handed the coordinates to Google and it gave me the answer to my question:
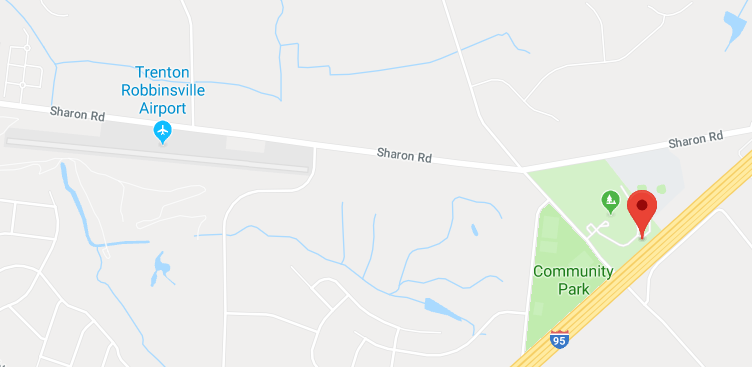
The wires with blobs are exactly in line with the runway of nearby Trenton-Robbinsville Airport. Mystery solved!
(It is not surprising that I didn't guess this. I had no idea there was a nearby airport. Trenton itself is about ten miles west of there, and its main airport, Trenton-Mercer Airport, is another five miles beyond that.)
I have been wondering for years why those blobs were in that exact place, and I am really glad to have it cleared up. Thank you, Google!
Dear vision-impaired readers: I wanted to add a description of the
view in the iframed Google Street View picture above. Iframes do not
support an alt attribute, and MDN says that longdesc is “not
helpful for non-visual
browsers”.
I was not sure what to do.
In the future, is there a better place to put a description of an iframed image? Thanks.
[Additional posts on topic /tech] immortal link
Fri, 13 Apr 2018As an undergraduate I wondered and wondered about how manifolds and things are classified in algebraic topology, but I couldn't find any way into the subject. All the presentations I found were too abstract and I never came out of it with any concrete idea of how you would actually calculate any specific fundamental groups. I knew that the fundamental group of the circle was !!\Bbb Z!! and the group of the torus was !!\Bbb Z^2!! and I understood basically why, but I didn't know how you would figure this out without geometric intuition.
This was fixed for me in the very last undergrad math class I took, at Columbia University with Johan Tysk. That was the lowest point of my adult life, but the algebraic topology was the one bright spot in it. I don't know what might have happened to me if I hadn't had that class to sustain my spirit. And I learned how to calculate homotopy groups!
(We used Professor Tysk's course notes, supplemented by William Massey's introduction to algebraic topology. I didn't buy a copy of Massey and I haven't read it all, but I think I can recommend it for this purpose. The parts I have read seemed clear and direct.)
Anyway there things stood for a long time. Over the next few decades I made a couple of superficial attempts to find out about homology groups, but again the presentations were too abstract. I had been told that the homology approach was preferred to the homotopy approach because the groups were easier to actually calculate. But none of the sources I found seemed to tell me how to actually calculate anything concrete.
Then a few days ago I was in the coffee shop working on a geometry problem involving an icosi-dodecahedron, and the woman next to me asked me what I was doing. Usually when someone asks me this in a coffee shop, they do not want to hear the answer, and I do not want to give it, because if I do their eyes will glaze over and then they will make some comment that I have heard before and do not want to hear again. But it transpired that this woman was a math postdoc at Penn, and an algebraic topologist, so I could launch into an explanation of what I was doing, comfortable in the knowledge that if I said something she didn't understand she would just stop me and ask a question. Yay, fun!
Her research is in “persistent homology”, which I had never heard of. So I looked that up and didn't get very far, also because I still didn't know anything about homology. (Also, as she says, the Wikipedia article is kinda crappy.) But I ran into her again a couple of days later and she explained the persistent part, and I know enough about what homology is that the explanation made sense.
Her research involves actually calculating actual homology groups of actual manifolds on an actual computer, so I was inspired to take another crack at understanding homology groups. I did a couple of web searches and when I searched for “betti number tutorial” I hit paydirt: these notes titled “persistent homology tutorial” by Xiaojin Zhu of the University of Wisconsin at Madison. They're only 37 slides long, and I could skip the first 15. Then slide 23 gives the magic key. Okay! I have not yet calculated any actual homology groups, so this post might be premature, but I expect I'll finish the slides in a couple of days and try my hand at the calculations and be more or less successful. And the instructions seem clear enough that I can imagine implementing a computer algorithm to calculate the homology groups for a big ugly complex, as this math postdoc does.
I had heard before that the advantage of the homology approach over the homotopy approach is that the homologies are easier to actually calculate with, and now I see why. I could have programmed a computer to do homotopy group calculations, but the output would in general have been some quotient of a free group given by a group presentation, and this is basically useless as far as further computation goes. For example the question of whether two differently-presented groups are isomorphic is undecidable, and I think similar sorts of questions, such as whether the group is abelian, or whether it is infinite, are similarly undecidable.
Sometimes you get a nice group, but usually you don't. For example the homotopy group of the Klein bottle is the quotient of the free group on two generators under the smallest equivalence relation in which !!aba = b!!; that is:
$$\langle a, b\mid abab^{-1}\rangle$$
which is not anything I have seen in any other context. Even the question of whether two given group elements are equal is in general undecidable. So you get an answer, but then you can't actually do anything with it once you have it. (“You're in a balloon!”) The homology approach throws away a lot of information, enough to render the results comprehensible, but it also leaves enough to do something with.
[Additional posts on topic /math] immortal link
Tue, 10 Apr 2018
Inconceivable things and non-contingent facts
Philosophy makes a distinguish between necessary and contingent facts, but I'm not exactly sure what it is. I think they would say that the election of Al Gore in 2000 is contingent because it's easy to imagine a universe in which it went the other way and the other guy won. But that seems to depend on our powers of imagination, which doesn't seem very rigorous. Is the mass of the electron necessary or contingent? What about the fine-structure constant?
What facts are necessary? Often in this context people fall back on mathematical truths, for example !!1+1=2!!, which does seem hard to assail. But I recently thought of something even farther down the scale, which seems to me even harder to argue.
Mathematics deals with many sorts of objects which are more or less like the ordinary numbers. Some are more complicated, and ordinary numbers are special cases, for example functions and matrices. Some are simpler, and are special cases themselves. Mathematicians can and do define !!2!! in many different ways. There are mathematical systems with !!1!! and !!+!! in which there is no !!2!!, and instead of !!1+1=2!! we have !!1+1=0!!. Well, not quite; there is !!2!!, but !!2=0!!. So one can say that !!1+1=2!! still, but the !!2!! is not very much like the !!2!! that we usually mean when we say !!1+1=2!!. Anyway certainly there is such a system, and I can certainly conceive of it, so there might be a philosophical argument that could be made that !!1+1=2!! is a contingent fact about how numbers happen to work in the universe in which we happen to find ourselves: we are not living in a universe where numbers form a field of characteristic 2.
But here's a fact that I think is unassailably necessary: rubies are red. Why? By definition! A ruby is a kind of gemstone, a type of aluminum oxide called a corundum, that has a deep red color. There are non-red corundums, but they are sapphires, not rubies, because a ruby is a red corundum. There is no such thing as a blue or a green ruby; a blue or green ruby is not a ruby at all, but a sapphire.
How about over in Narnia, where rubies are blue? Well, maybe the Narnians people call hats “avocadoes”, but whether those things are hats or avocadoes depends not on what the Narnians call them but on their properties. If those things are made of felt and the Narnians wear them on their heads, they are hats, regardless of what the Narnians call them; they are avocadoes only if they are globular and can be eaten on toast. Narnians might put actual avocadoes on their heads and then there might be an argument that these things were hats, but if the avocado is a hat it is only because it is customarily worn on the head.
And so too the Narnians can call !!2!! an avocado and say that !!1+1=\text{avocado}!! but that doesn't mean that !!1+1!! is an avocado, even in Narnia. Maybe the Narnians call avocadoes “rubies”, but they're still avocadoes, not rubies. And maybe the Narnians call blue corundums “rubies”, but they're still sapphires, not rubies, because rubies are red.
So I think it might be conceivable that !!1+1=2!! is contingent, and it's certainly easy to conceive of a universe with no rubies at all, but I can't conceive of any way that a ruby could be other than red.
[Additional posts on topic /misc/philosophy] immortal link
Wed, 04 Apr 2018
Genealogy of the Saudi royal family
[ Note: None of this is a joke, nothing here is intended humorously, and certainly none of it should be taken as mockery or disparagement. The naming conventions of Saudi royalty are not for me to judge or criticize, and if they cause problems for me, the problems are my own. It is, however, a serious lament. ]
The following innocuous claim appears in Wikipedia's article on Abdullah bin Abdul-Rahman:
He was the seventh son of the Emir of the Second Saudi State, Abdul Rahman bin Faisal.
Yesterday I tried to verify this claim and I was not able to do it.
Somewhere there must be a complete and authoritative pedigree of the entire Saudi royal family, but I could not find it online, perhaps because it is very big. There is a Saudi royal family official web site, and when I found that it does have a page about the family tree, I rejoiced, thinking my search was over. But the tree only lists the descendants of King Abdulaziz Ibn Saud, founder of the modern Saudi state. Abdullah was his half-brother and does not appear there.
Well, no problem, just Google the name, right? Ha!
Problem 1: These princes all have at least twenty kids each. No, seriously. The Wikipedia article on Ibn Saud himself lists twenty-one wives and then gives up, ending with an exhausted “Possibly other wives”. There is a separate article on his descendants that lists 72 children of various sexes, and the following section on grandchildren begins:
Due to the Islamic traditions of polygyny and easy divorce (on the male side), King Abdul Aziz [Ibn Saud] has approximately a thousand grandchildren.
Problem 2: They reuse many of the names. Because of course they do; if wife #12 wants to name her first son the same as the sixth son of wife #2, why not? They don't live in the same house. So among the children of Ibn Saud there are two Abdullahs (“servant of God”), two Badrs (“full moon”), two Fahds (“leopard”), two each of Majid (“majestic”), Mishari (I dunno), Talal (dunno), and Turki (“handsome”). There are three sons named Khalid (“eternal”). There is a Sa'ad and a Saad, which I think are the exact same name (“success”) as spelled by two different Wikipedia editors.
And then they reuse the names intergenerationally. Among Ibn Saud's numerous patrilineal grandsons there are at least six more Fahds, the sons respectively of Mohammed, Badr (the second one), Sultan, Turki (also the second one), Muqrin, and Salman. Abdulaziz Ibn Saud has a grandson also named Abdulaziz, whose name is therefore Abdulaziz bin Talal bin Abdulaziz Al Saud. (The “bin” means “son of”; the feminine form is “bint”.) It appears that the House of Saud does not name sons after their fathers, for which I am grateful.
Ibn Saud's father was Abdul Rahman (this is the Abdul Rahman of Abdullah bin Abdul-Rahman, who is the subject of this article. Remember him?) One of Ibn Saud's sons is also Abdul Rahman, I think probably the first one to be born after the death of his grandfather, and at least two of his patrilineal grandsons are also.
Problem 3: Romanization of Arabic names is done very inconsistently. I mentioned “Saad” and “Sa'ad” before. I find the name Abdul Rahman spelled variously “Abdul Rahman”, “Abdulrahman”, “Abdul-Rahman”, and “Abd al-Rahman”. This makes text searches difficult and unreliable. (The name, by the way, means "Servant of the gracious one”, referring to God.)
Problem 4: None of these people has a surname. Instead they are all patronymics. Ibn Saud has six grandsons named Fahd; how do you tell them apart? No problem, their fathers all have different names, so they are Fahd bin Mohammed, Fahd bin Badr, Fahd bin Sultan, Fahd bin Turki, Fahd bin Muqrin, and Fahd bin Salman. But again this confuses text searches terribly.
You can search for “Abdullah bin Abdul-Rahman” but many of the results will be about his descendants Fahd bin Abdullah bin Abdul Rahman, Fahd bin Khalid bin Abdullah bin Abdul Rahman, Fahd bin Muhammad bin Abdullah bin Abdul Rahman, Abdullah bin Bandar bin Abdullah bin Abdul Rahman, Faisal bin Abdullah bin Abdul Rahman, Faisal bin Abdul Rahman bin Abdullah bin Abdul Rahman, etc.
In combination with the reuse of the same few names, the result is even more confusing. There is Bandar bin Khalid, and Khalid bin Bandar; Fahad bin Khalid and Khalid bin Fahd.
There is Mohammed al Saud (Mohammed of (the house of) Saud) and Mohammed bin Saud (Mohammed the son of Saud).
There are grandsons named Saad bin Faisal, Faisal bin Bandar, Bandar bin Sultan, Sultan bin Fahd, Fahd bin Turki, Turki bin Talal, Talal bin Mansour, Mansour bin Mutaib, Mutaib bin Abdullah, and Abdullah bin Saad. I swear I am not making this up.
Perhaps Abdullah was the seventh son of Abdul Rahman.
Perhaps not.
I surrender.
Addendum 20250211
Today I became aware of a comparably confusing European tradition. Since the 13th century, every male in the House of Reuss has been named “Heinrich”.
[Additional posts on topic /lang] immortal link


