Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Sat, 24 Mar 2018
Today I went to see The Death of Stalin. If someone is going to go to the trouble of making a comedy about the death of Stalin, that seems like a worthy attempt, and I will do them the courtesy of going to watch it. At least I can be sure it will not be the same old shit.
I was interested to see if it was possible to make a comedy about the death of Stalin, and if so, would it would be funny? I got my answer: no, you can't, and it isn't.
It was worth a shot, I guess, and I give the writers and director top marks for audacity. The cast was great. The acting was great. I thought Jason Isaacs as Marshal Zhukov stole every scene he was in. But yeah, it's hard to be funny when Lavrenty Beria is raping a bunch of fourteen-year-old girls, and the movie didn't work for me.
There's a long and solid tradition of comedy about completely loathsome people, but I think most of it follows pretty much the same pattern: terrible stuff happens to the loathsome people and it is funny because the people are so loathsome and because they so richly deserve all the terrible stuff that happens to them. It can be fun to see a horrible person sabotage themselves with their own horribleness.
(Examples off the top of my head: Fawlty Towers. Otto in A Fish Called Wanda. Jack Vance's Cugel books. Married With Children. I think this might have been the main attraction of Seinfeld, although if it is I didn't get the joke until after the series was over.)
Unfortunately this movie, being historical fiction, has to stick to the history: Malenkov gets swept under a rug. Khrushchev seizes power. Molotov keeps on doing what he does. Beria is murdered, but there is nothing funny about it, and I found it unsatisfying. Indeed, all of these horrible people are suffering because of the horrible world they have created for themselves, but I found no fun in it because there were another 170 million people suffering much worse from the same horrible crap. The coyote's look of dismay as he falls of the cliff loses all its savor if he has the road runner's broken body in his jaws when it happens.
So, eh. Sorry, Iannucci. I wanted to like your movie.
[ Odd trivium: I started writing articles in the “movies” section of this blog back in 2007, but this is the first one that has seen publication. ]
[Other articles in category /movie] permanent link
Addenda to recent articles 201803
It's been a while since we had one of these. But gosh, people have sent me quite a lot of really interesting mail lately.
I related my childhood disappointment at the limited number of cool coordinate systems. Norman Yarvin directed me to prolate spheroidal coordinates which are themselves a three-dimensional version of elliptic coordinates which are a system of exactly the sort I escribed in the article, this time parametrized by a family of ellipses and a family of hyperbolas, all of which share the same two foci; this article links in turn to parabolic coordinates in which the two families are curves are up-facing and down-facing parabolas that all share a focus. (Hmm, this seems like a special case of the ellipses, where one focus goes to infinity.)
Walt Mankowski also referred me to the Smith chart, shown at right, which is definitely relevant. It is a sort of nomogram, and parametrizes certain points by their position on circles from two families
$$\begin{align} F_1(c): && (x- c)^2 & + y^2 & =c^2 \\ F_2(c): && x^2 & + (y- c)^2 & =c^2 \\ \end{align} $$
Electrical engineers use this for some sort of electrical engineer calculation. They use the letter !!j!! instead of !!i!! for the imaginary unit because they had already used !!i!! to stand for electrical current, which is totally reasonable because “electrical current” does after all start with the letter !!i!!. (In French! The French word is courant. Now do you understand? Stop asking questions!)
Regarding what part of the body Skaði was looking at when the Norse text says fótr, which is probably something like the foot, Alexander Gurney and Brent Yorgey reminded me that Biblical Hebrew often uses the foot as a euphemism for the genitals. One example that comes immediately to mind is important in the book of Ruth:
And when Boaz had eaten and drunk, and his heart was merry, he went to lie down at the end of the heap of corn: and she came softly, and uncovered his feet, and laid her down. (Ruth 3:7)
M. Gurney suggested Isaiah 6:2. (“Above him were seraphim, each with six wings: With two wings they covered their faces, with two they covered their feet, and with two they were flying.”) I think Ezekiel 16:25 is also of this type.
I mentioned to Brent that I don't think Skaði was looking at the Æsir's genitals, because it wouldn't fit the tone of the story.
Alexander Gurney sent me a lot of other interesting material. I had translated the Old Icelandic hreðjar as “scrotum”, following Zoëga. But M. Gurney pointed out that the modern Icelandic for “radish” is hreðka. Coincidence? Or was hreðjar a euphemism even then? Zoëga doesn't mention it, but he doesn't say what word was used for “radish”, so I don't know.
He also pointed me to Parts of the body in older Germanic and Scandinavian by Torild Washington Arnoldson. As in English, there are many words for the scrotum and testicles; some related to bags, some to balls, etc. Arnoldson does mention hreðjar in the section about words that are bag-derived but doesn't say why. Still if Arnoldson is right it is not about radishes.
I should add that the Skáldskaparmál itself has a section about parts of the body listing suitable words and phrases for use by skálds:
Hönd, fótr.
… Á fæti heitir lær, kné, kálfi, bein, leggr, rist, jarki, il, tá. …
(… The parts of the legs are called thigh, knee, calf, lower leg, upper leg, instep, arch, sole, toe … [ Brodeur ])
I think Brodeur's phrase “of the legs” here is an interpolation. Then he glosses lær as “thigh”, kné as “knee”, kálfi as “calf”, and so on. This passage is what I was thinking of when I said
Many of the words seem to match, which is sometimes helpful but also can be misleading, because many don't.
I could disappear down this rabbit hole for a long time.
Regarding mental estimation of the number of primes less than 1,000, which the Prime Number Theorem says is approximately !!\frac{1000}{\ln 1000}!!, several people pointed out that if I had memorized !!\ln 10\approx 2.3!! then I would have had that there are around !!\frac{1000}{3·2.3}!! primes under 1,000.
Now it happens that I do have memorized !!\ln 10\approx 2.3!! and although I didn't happen come up with it while driving that day, I did come up with it a couple of days later in the parking lot of a Wawa where I stopped to get coffee before my piano lesson. The next step, if you are in a parking lot, is to approximate the division as !!\frac{1000}{6.9} \approx \frac{1000}7 = 142.857\ldots!! (because you have !!\frac17=0.\overline{142857}!! memorized, don't you?) and that gives you an estimate of around 145 primes.
Which, perhaps surprisingly, is worse than what I did the first time around; it is 14% too low instead of 8% too high. (The right answer is 168 and my original estimate was 182.)
The explanation is that for small !!n!!, the approximation !!\pi(N)\sim\frac{N}{\ln N}!! is not actually very good, and I think the interpolation I did, using actual low-value counts, takes better account of the low-value error.
[Other articles in category /addenda] permanent link
Fri, 23 Mar 2018Here is a list of February's shitposts, later than usual, but who cares? Boldface indicates the articles that may (may) be of more general interest (ha). I think that I did a better job of noticing when a post wasn't shitty enough and promoting it, pre-publication, to this blog, so you will have seen all the better stuff already.
I'm pleased, volume over January is slightly up, and quality is definitely down, especially in the last half of the month. But I posted on only 21 of 28 days; I'll have to work on that.
- Gitignore patterns
- Grook
- English orthography
- Uncountable tilings of the line
- Cork flakes
- Non compote mentis
- Oaken tokens
- The sinister bag strap
- Puzzle Zapper Blog
- CNS
- Andy Lee's higgledy-piggledy
- The fickle gods of math Stackexchange
- Woo Philadelphia Eagles 2018 Super Bowl champs!!1!
- The remainder of a square root
- Ear piercing
- Eagles-related property damage
- Mathematicians with the same name
- Only
- My current favorite puncutation mark
- Qihui
- Qen
- Best practices for cache management
- “Obvious” in mathematics
- SVG images rendered at different scales
- Tom Waits
- Weighted reservoir sampling
- More reservoir sampling [1] [2] [3]
- People who are only photographed in black and white
- Reservoids
- Dumbest math.se question this week
- The duties of John von Neumann's assistant
- Calculate the Taylor expansion… OR DIE
- I'm so old… [4] [5]
- Pizza delivery failure
- Scorpion and Felix
- Google flubs a spelling correction
- Thus!
- Public service announcement about spamming
- The Platonic thing
- A peculiar genre of joke
- Michael Jordan and Charles Barkley
- Historical followup
- Another joke in this peculiar genre
- Calculus
- Imbricated
- French is verbose
- Stuff I wanted to say but didn't
- Today I learned…
[Other articles in category /meta/shitpost] permanent link
Thu, 22 Mar 2018
Does Skaði choose the husband with the best butt?
(Warning: I do not know anything about Old Norse, so everything I say about it should be understood as ill-informed speculation. I welcome corrections.)
In one of my favorite episodes from Norse mythology, the Æsir owe a payment to the Jötunn Skaði in compensation for killing her father. But they know she is very wealthy, and offer her an alternative compensation: one of their men in marriage.
Skaði wants to marry Baldr, because he is extremely handsome. But Baldr is already married. Odin proposes a compromise: the Æsir will line up behind a short curtain, and Skaði will choose her husband. She will marry whomever she picks; if she can pick out Baldr by his legs, she can have him. Skaði agrees, assuming that the beautiful Baldr will have the best legs.
(She chooses wrong. Njörðr has the best legs.)
Thinking on this as an adult, I said to myself “Aha, this is like that horn full of milk that was actually mead. I bet this was also cleaned up in the version I read, and that in the original material, Skaði was actually choosing the husband with the best butt.”
I went to check, and I was wrong. The sources say she was looking only at their feet.
I was going to just quote this:
she should choose for herself a husband from among the Æsir and choose by the feet only, seeing no more of him.
But then I got worried. This is of course not the original source but an English translation; what if it is inaccurate?
Well, there was nothing else to do but ask Snorri about it. He says:
En æsir buðu henni sætt ok yfirbætr ok it fyrsta, at hon skal kjósa sér mann af ásum ok kjósa at fótum ok sjá ekki fleira af.
(Sætt is recompense or settlement; yfirbætr similarly. (Bætr is a cure, as in “I was sick, but I got better”.) The first (fyrsta) part of the settlement is that she “shall choose a man for herself” (skal kjósa sér mann) but choose by the feet (kjósa at fótum) seeing nothing else (sjá ekki fleira af).)
The crucial word here is fótum, which certainly looks like “foot”. (It is the dative form of fótr.) Could it possibly mean the buttocks? I don't think so. It's hard to be 100% certain, because it could be a euphemism — anything could be a euphemism for the buttocks if you paused before saying it and raised one eyebrow. (Did the Norse bards ever do this?) Also the Norse seem to have divided up the leg differently than we do. Many of the words seem to match, which is sometimes helpful but also can be misleading, because many don't. For example, I think leggr, despite its appearance, means just the shank. And I think fótum may not be just the foot itself, but some part of the leg that includes the foot.
But I'm pretty sure fótum is not the butt, at least not canonically. To do this right I would look at all the other instances of fótr to see what I could glean from the usage, but I have other work to do today. So anyway, Skaði probably was looking at their feet, and not at their butts. Oh well.
However! the other part of Skaði's settlement is that the Æsir must make her laugh. In the version I first read, Loki achieves this by tying his beard to a goat's. Nope!
Þá gerði Loki þat, at hann batt um skegg geitar nökkurrar ok öðrum enda um hreðjar sér, ok létu þau ýmsi eftir ok skrækði hvárt tveggja hátt.
Skegg geitar nökkurar is indeed some goat's beard. But hann batt … ok öðrum enda um hreðjar sér is “he tied … the other end to his own scrotum”.
Useful resources:
- Skáldskaparmál, English translation of Arthur Gilchrist Brodeur (1916)
- Skáldskaparmál, original Old Icelandic (1220-ish)
- Zoëga's Concise Dictionary of Old Icelandic (1910)
Addendum 20240712
Toph has asked an excellent question about this.
[Other articles in category /lang] permanent link
Wed, 21 Mar 2018A couple of years ago I was reading Wikipedia's article about the the 1943 Bengal famine, and I was startled by the following claim:
"If food is so scarce, why hasn’t Gandhi died yet?"
Winston Churchill's response to an urgent request to release food stocks for India.
It was cited, but also marked with the “not in citation” tag, which is supposed to mean that someone checked the reference and found that it did not actually support the claim.
It sounded like it might be the sort of scurrilous lie that is widely repeated but not actually supportable, so I went to follow it up. It turned out that although the quotation was not quite exact, it was not misleadingly altered, and not a scurrilous lie at all. The attributed source (Tharoor, Shashi "The Ugly Briton". Time, (29 November 2010).) claimed:
Churchill's only response to a telegram from the government in Delhi about people perishing in the famine was to ask why Gandhi hadn't died yet.
I removed the “not in citation” tag, which I felt was very misleading.
Still, I felt that anything this shocking should be as well-supported as possible. It cited Tharoor, but Tharoor could have been mistaken. So I put in some effort and dug up the original source. It is from the journal entry of Archibald Wavell, then Viceroy of India, of 5 July 1944:
Winston sent me a peevish telegram to ask why Gandhi hadn't died yet! He has never answered my telegram about food.
This appears in the published version of Lord Wavell's journals. (Wavell, Archibald Percival. Wavell: The Viceroy's journal, p. 78. Moon, Penderel, ed. Oxford University Press, 1973.) This is the most reliable testimony one could hope for. The 1973 edition is available from the Internet Archive.
A few months later, the entire article was massively overhauled by a group of anglophiles and Churchill-rehabilitators. Having failed to remove the quotation for being uncited, and then having failed to mendaciously discredit the cited source, they removed the quotation in a typical episode of Wikipedia chicanery. In a 5,000-word article, one sentence quoting the views of the then-current British Prime Minister was deemed “undue weight”, and a failure to “fairly represent all significant viewpoints that have been published by reliable sources”.
Further reading: In Winston Churchill, Hollywood rewards a mass murderer. (Tharoor again, in last week's Washington Post.)
[Other articles in category /wikipedia] permanent link
Mon, 19 Mar 2018In English we can sometimes turn an adjective into a verb by suffixing “-en”. For example:
black → blacken
red → redden
white → whiten
wide → widen
But not
blue → bluen*
green → greenen*
yellow → yellowen*
long → longen*
(Note that I am only looking at -en verbs that are adjective-derived present tenses. This post is not concerned with the many -en verbs that are past participles, such as “smitten” (past participle of “smite”), “spoken” (“speak”), “molten” (“melt”), “sodden” (“seethe”), etc.)
I asked some linguist about this once and they were sure it was purely morphological, something like: black, red, and white end in stop consonants, and blue, green, and yellow don't.
Well, let's see:
| Morphology | Good | Bad |
|---|---|---|
| Stop |
Blacken Brighten Broaden Cheapen Darken Deaden Embolden Fatten Flatten Gladden Golden Harden Hearten Heighten Louden Madden Open (?) Quicken Quieten Redden Ripen Sadden Sharpen Shorten Sicken Slacken Smarten Straighten Straiten Sweeten Thicken Tighten Weaken Whiten Widen |
Biggen |
| Fricative |
Coarsen Deafen Enlargen Enliven Fasten Freshen Hasten Leaven Lengthen Lessen Loosen Moisten Roughen Soften Stiffen Strengthen Toughen Worsen |
Largen Smoothen |
| Nasal |
Cleanen Dimmen Dumben Finen Greenen Longen Slimmen Strongen Thinnen | |
| Vowel |
Angrien Bluen Dirtien Dryen Grayen Highen Lowen Narrowen Noisien Saltien Slowen Yellowen | |
| Nasalized stop |
Dampen Pinken | Blunten |
| Glide |
Betteren Bitteren Dullen Faren Greateren Moren Nearen Smallen Souren Stalen |
There are some fine points:
- “Biggen” used to exist but has fallen out of use
- Perhaps I should have ommitted “strengthen” and “hasten”, which are derived from nouns, not from adjectives
- I'm not sure whether “closen”, “hotten” and “wetten” are good or bad so I left them off
- “moisten” and “soften” might belong with the stops instead of the fricatives
- etc.
but clearly the morphological explanation wins. I'm convinced.
[ Addendum: Wiktionary discusses this suffix, distinguishing it from the etymologically distinct participial “-en”, and says “it is not currently very productive in forming new words, being mostly restricted to monosyllabic bases which end in an obstruent”. ]
[Other articles in category /lang] permanent link
I had a fun idea this morning. As a kid I was really interested in polar coordinates and kind of disappointed that there didn't seem to be any other coordinate systems to tinker with. But this morning I realized there were a lot.
Let !!F(c)!! be some parametrized family of curves that partition the plane, or almost all of the plane, say except for a finite number of exceptions. If you have two such families !!F_1(c)!! and !!F_2(c)!!, and if each curve in !!F_1!! intersects each curve in !!F_2!! in exactly one point (again with maybe a few exceptions) then you have a coordinate system: almost every point !!P!! lies on !!F_1(a)!! and !!F_2(b)!! for some unique choice of !!\langle a, b\rangle!!, and these are its coordinates in the !!F_1–F_2!! system.
For example, when !!F_1(c)!! is the family of lines !!x=c!! and !!F_2(c)!! is the family of lines !!y=c!! then you get ordinary Cartesian coordinates, and when !!F_1(c)!! is the family of circles !!x^2+y^2=c!! and !!F_2(c)!! is the family !!y=cx!! (plus also !!x=0!!) you get standard polar coordinates, which don't quite work because the origin is in every member of !!F_2!!, but it's the only weird exception.
But there are many other families that work. To take a particularly simple example you can pick some constant !!k!! and then take
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && y & =kx+c. \end{align} $$
This is like Cartesian coordinates except the axes are skewed. I did know about this when I was a kid but I considered it not sufficiently interesting.
For a more interesting example, try
$$\begin{align} F_1(c): && x^2-y^2 & =c \\ F_2(c): && xy & =c \end{align} $$
which looks like this:
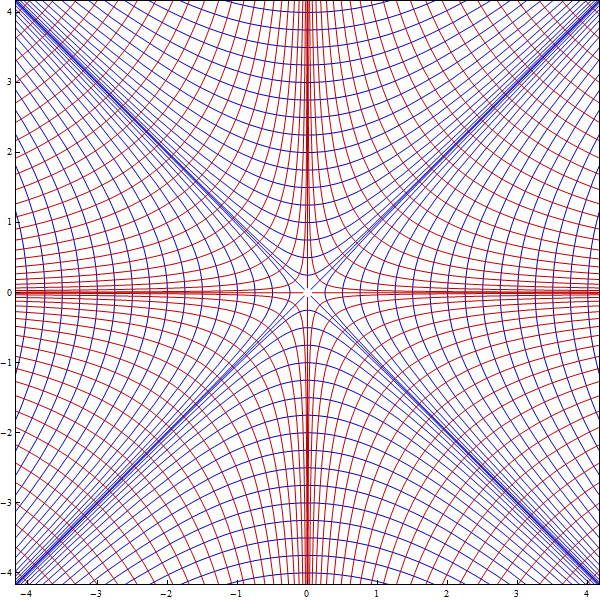 The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
The hyperbolas
!!x^2-y^2 = c!! (in blue) and !!xy=c!! (in red)
I've seen that illustration before but I don't think I thought of using it as a coordinate system. Well, okay, every pair of hyperbolas intersects in two points, not one. So it's a parametrization of the boundary of real projective space or something, fine. Still fun!
In the very nice cases (such as the hyperbolas) each pair of curves is orthogonal at their point of intersection, but that's not a requirement, as with the skew Cartesian system. I'm pretty sure that if you have one family !!F!! you can construct a dual family !!F'!! that is orthogonal to it everywhere by letting !!F'!! be the paths of gradient descent or something. I'm not sure what the orthogonality is going to be important for but I bet it's sometimes useful.
You can also mix and match families, so for example take:
$$\begin{align} F_1(c): && x & =c \\ F_2(c): && xy & =c \end{align} $$
Some examples work better than others. The !!xy=c!! hyperbolas are kind of a mess when !!c=0!!, and they don't go together with the !!x^2+y^2=c!! circles in the right way at all: each circle intersects each hyperbola in four points. But it occurs to me that as with the projective plane thingy, we don't have to let that be a problem. Take !!S!! to be the quotient space of the plane where two points are identified if their !!F_1–F_2!!-coordinates are the same and then investigate !!S!!. Or maybe go more directly and take !!S = F_1 \times F_2!! (literally the Cartesian product), and then topologize !!S!! in some reasonably natural way. Maybe just give it the product topology. I dunno, I have to think about it.
(I was a bit worried about how to draw the hyperbola picture, but I tried Google Image search for “families of orthogonal hyperbolas”, and got just what I needed. Truly, we live in an age of marvels!)
[Other articles in category /math] permanent link
Sun, 11 Mar 2018
Quick and dirty prime counting
I've been thinking for a while that I probably ought to get around to memorizing all the prime numbers under 1,000, so that I don't have to wonder about things like 893 all the time, and last night in the car I started thinking about it again, and wondered how hard it would be. There are 25 primes under 100, so presumably fewer than 250 under 1,000, which is not excessive. But I wondered if I could get a better estimate.
The prime number theorem tells us that the number of primes less than !!n!! is !!O(\frac n{\log n})!! and I think the logarithm is a natural one, but maybe there is some constant factor in there or something, I forget and I did not want to think about it too hard because I was driving. Anyway I cannot do natural logarithms in my head.
Be we don't need to do any actual logarithms. Let's estimate the fraction of primes up to !!n!! as !!\frac 1{c\log n}!! where !!c!! is unknown and the base of the logarithm is then unimportant. The denominator scales linearly with the power of !!n!!, so the difference between the denominators for !!n=10!! and !!n=100!! is the same as the difference between the denominators for !!n=100!! and !!n=1000!!.
There are 4 primes less than 10, or !!\frac25!!, so the denominator is 2.5. And there are 25 primes less than 100, so the denominator here is 4. The difference is 1.5, so the denominator for !!n=1000!! ought to be around 5.5, and that means that about !!\frac2{11}!! of the numbers up to 1000 are prime. This yields an estimate of 182.
I found out later that the correct number is 186, so I felt pretty good about that.
[ Addendum: The correct number is 168, not 186, so I wasn't as close as I thought. ]
[Other articles in category /math] permanent link



