Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Addenda to recent articles 200604 |
| Creeping featurism and the ratchet effect |
| Egyptian Fractions |
| Google query roundup |
| Google query roundup |
| Irreducible polynomials |
| My favorite math problem |
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 29 May 2006
A puzzle for high school math students
Factor x4 + 1.
Solution
As I mentioned in yesterday's very long article about GF(2n), there is only one interesting polynomial over the reals that is irreducible, namely x2 + 1. Once you make up a zero for this irreducible polynomial, name it i, and insert it into the reals, you have the complex numbers, and you are done, because the fundmental theorem of algebra says that every polynomial has a zero in the complex numbers, and therefore no polynomials are irreducible. Once you've inserted i, there is nothing else you need to insert.This implies, however, that there are no irreducible real polynomials of degree higher than 2. Every real polynomial of degree 3 or higher factors into simpler factors.
For odd-degree polynomials, this is not surprising, since every such polynomial has a real zero. But I remember the day, surprisingly late in my life, when I realized that it also implies that x4 + 1 must be factorable. I was so used to x2 + 1 being irreducible, and I had imagined that x4 + 1 must be irreducible also. x2 + bx + 1 factors if and only if |b| ≥ 2, and I had imagined that something similar would hold for x4 + 1—But no, I was completely wrong.
x4 + 1 has four zeroes, which are the fourth roots of -1, or, if you prefer, the two square roots of each of i and -i. When I was in elementary school I used to puzzle about the square root of i; I hadn't figured out yet that it was ±(1 + i)/√2; let's call these two numbers j and -j. The square roots of -i are the conjugates of j and -j: ±(1 - i)/√2, which we can call k and -k because my typewriter doesn't have an overbar.
So x4 + 1 factors as (x + j)(x - j)(x + k)(x - k). But this doesn't count because j and k are complex. We get the real factorization by remembering that j and k are conjugate, so that (x - j)(x - k) is completely real; it equals x2 - √2x + 1. And similarly (x + j)(x + k) = x2 + √2x + 1.
So x4 + 1 factors into (x2 - √2x + 1)(x2 + √2x + 1). Isn't that nice?
[ Addendum 20220221: I accidentally wrote the same article a second time. ]
[Other articles in category /math] permanent link
Sat, 27 May 2006Introduction
According to legend, the imaginary unit i = √-1 was invented by mathematicians because the equation x2 + 1 = 0 had no solution. So they introduced a new number i, defined so that i2 + 1 = 0, and investigated the consequences. Like most legends, this one has very little to do with the real history of the thing it purports to describe. But let's pretend that it's true for a while.
Descartes' theorem
If P(x) is some polynomial, and z is some number such that P(z) = 0, then we say that z is a zero of P or a root of P. Descartes' theorem (yes, that Descartes) says that if z is a zero of P, then P can be factored into P = (x-z)P', where P' is a polynomial of lower degree, and has all the same roots as P, except without z. For example, consider P = x3 - 6x2 + 11x - 6. One of the zeroes of P is 1, so Descartes theorem says that we can write P in the form (x-1)P' for some second-degree polynomial P', and if there are any other zeroes of P, they will also be zeroes of P'. And in fact we can; x3 - 6x2 + 11x - 6 = (x-1)(x2 - 5x + 6). The other zeroes of the original polynomial P are 2 and 3, and both of these (but not 1) are also zeroes of x2 - 5x + 6.We can repeat this process. If a1, a2, ... an are the zeroes of some nth-degree polynomial P, we can factor P as (x-a1)(x-a2)...(x-an).
The only possibly tricky thing here is that some of the ai might be the same. x2 - 2x + 1 has a zero of 1, but twice, so it factors as (x-1)(x-1). x3 - 4x2 + 5x - 2 has a zero of 1, but twice, so it factors as (x-1)(x2 - 3x + 2), where (x2 - 3x + 2) also has a zero of 1, but this time only once.
Descartes' theorem has a number of important corollaries: an nth-degree polynomial has no more than n zeroes. A polynomial that has a zero can be factored. When coupled with the so-called fundamental theorem of algebra, which says that every polynomial has a zero over the complex numbers, it implies that every nth-degree polynomial can be factored into a product of n factors of the form (x-z) where z is complex, or into a product of first- and second-degree polynomials with real coefficients.
The square roots of -1
Suppose we want to know what the square roots of 1 are. We want numbers x such that x2 = 1, or, equivalently, such that x2 - 1 = 0. x2 - 1 factors into (x-1)(x+1), so the zeroes are ±1, and these are the square roots of 1. On the other hand, if we want the square roots of 0, we need the solutions of x2 = 0, and the corresponding calculation calls for us to factor x2, which is just (x-0)(x-0), So 0 has the same square root twice; it is the only number without two distinct square roots.If we want to find the square roots of -1, we need to factor x2 + 1. There are no real numbers that do this, so we call the polynomial irreducible. Instead, we make up some square roots for it, which we will call i and j. We want (x - i)(x - j) = x2 + 1. Multiplying through gives x2 - (i + j)x + ij = x2 + 1. So we have some additional relationships between i and j: ij = 1, and i + j = 0.
Because i + j = 0, we always dispense with j and just call it -i. But it's essential to realize that neither one is more important than the other. The two square roots are identical twins, different individuals that are completely indistinguishable from each other. Our choice about which one was primary was completely arbitrary. That doesn't even do justice to the arbitrariness of the choice: i and j are so indistinguishable that we still don't know which one got the primary notation. Every property enjoyed by i is also enjoyed by j. i3 = j, but j3 = i. eiπ = -1, but so too ejπ = -1. And so on.
In fact, I once saw the branch of mathematics known as Galois theory described as being essentially the observation that i and -i were indistinguishable, plus the observation that there are no other indistinguishable pairs of complex numbers.
Anyway, all this is to set up the main point of the article, which is to describe my favorite math problem of all time. I call it the "train problem" because I work on it every time I'm stuck on a long train trip.
We are going to investigate irreducible polynomials; that is, polynomials that do not factor into products of simpler polynomials. Descartes' theorem implies that irreducible polynomials are zeroless, so we are going to start by looking for polynomials without zeroes. But we are not going to do it in the usual world of the real numbers. The answer in that world is simple: x2 + 1 is irreducible, and once you make up a zero for this polynomial and insert it into the universe, you are done; the fundamental theorem of algebra guarantees that there are no more irreducible polynomials. So instead of the reals, we're going to do this in a system known as Z2.
Z2
Z2 is much simpler than the real numbers. Instead of lots and lots of numbers, Z2 has only two. (Hence the name: The 2 means 2 and the Z means "numbers". Z is short for Zahlen, which is German.) Z2 has only 0 and 1. Addition and multiplication are as you expect, except that instead of 1 + 1 = 2, we have 1 + 1 = 0.
|
|
The 1+1=0 oddity is the one and only difference between Z2 and ordinary algebra. All the other laws remain the same. To be explicit, I will list them below:
- a + 0 = a
- a + b = b + a
- (a + b) + c = a + (b + c)
- a × 0 = 0
- a × 1 = a
- a × b = b × a
- (a × b) × c = a × (b × c)
- a × (b + c) = a × c + b × c
Algebra in Z2
But the 1+1=0 oddity does have some consequences. For example, a + a = a·(1 + 1) = a·0 = 0 for all a. This will continue to be true for all a, even if we extend Z2 to include more elements than just 0 and 1, just as x + x = 2x is true not only in the real numbers but also in their extension, the complex numbers.Because a + a = 0, we have a = -a for all a, and this means that in Z2, addition and subtraction are the same thing. If you don't like subtraction—and really, who does?—then Z2 is the place for you.
As a consequence of this, there are some convenient algebraic manipulations. For example, suppose we have a + b = c and we want to solve for a. Normally, we would subtract b from both sides. But in Z2, we can add b to both sides, getting a + b + b = c + b. Then the b + b on the left cancels (because b + b = 0) leaving a = c + b. From now on, I'll call this the addition law.
If you suffered in high school algebra because you wanted (a + b)2 to be equal to a2 + b2, then suffer no more, because in Z2 they are equal. Here's the proof:
| (a + b)2 | = | |
| (a + b)(a + b) | = | |
| a(a + b) + b(a + b) | = | |
| (a2 + ab) + (ba + b2) | = | |
| a2 + ab + ab + b2 | = | |
| a2 + b2 |
Because the ab + ab cancels in the last step.
This happy fact, which I'll call the square law, also holds true for sums of more than two terms: (a + b + ... + z)2 = a2 + b2 + ... + z2. But it does not hold true for cubes; (a + b)3 is a3 + a2b + ab2 + b3, not a3 + b3.
Irreducible polynomials in Z2
Now let's try to find a polynomial that is irreducible in Z2. The first degree polynomials are x and x+1, and both of these have zeroes: 0 and 1, respectively.There are four second-degree polynomials:
- x2
- x2 + 1
- x2 + x
- x2 + x + 1
| Polynomial | Zeroes | Factorization |
|---|---|---|
| x2 | 0 (twice) | x2 |
| x2 + 1 | 1 (twice) | (x+1)2 |
| x2 + x | 0, 1 | x(x+1) |
| x2 + x + 1 | none |
Note in particular that, unlike in the real numbers, x2 + 1 is not irreducible in Z2. 1 is a zero of this polynomial, which, because of the square law, factors as (x+1)(x+1). But we have found an irreducible polynomial, x2 + x + 1. The other three second-degree polynomials all can be factored, but x2 + x + 1 cannot.
Like the fictitious mathematicians who invented i, we will rectify this problem, by introducing into Z2 a new number, called b, which has the property that b2 + b + 1 = 0. What are the consequences of this?
The first thing to notice is that we haven't added only one new number to Z2. When we add i to the real numbers, we also get a lot of other stuff like i+1 and 3i-17 coming along for the ride. Here we can't add just b. We must also add b+1.
The next thing we need to do is figure out how to add and multiply with b. The addition and multiplication tables are extended as follows:
|
|
The only items here that might require explanation are the entries in the lower-right-hand corner of the multiplication table. Why is b×b = b+1? Well, b2 + b + 1 = 0, by definition, so b2 = b + 1 by the addition law. Why is b × (b+1) = 1? Well, b × (b+1) = b2 + b = (b + 1) + b = 1 because the two b's cancel. Perhaps you can work out (b+1) × (b+1) for yourself.
From here there are a number of different things we could investigate. But what I think is most crucial is to discover the value of b3. Let's calculate that. b3 = b·b2. b2, we know, is b+1. So b3 = b(b+1) = 1. Thus b is a cube root of 1.
People with some experience with this sort of study will not be surprised by this. The cube roots of 1 are precisely the zeroes of the polynomial x3 + 1 = 0. 1 is obviously a cube root of 1, and so Descartes' theorem says that x3 + 1 must factor into (x+1)P, where P is some second-degree polynomial whose zeroes are the other two cube roots. P can't be divisible by x, because 0 is not a cube root of 1, so it must be either (x+1)(x+1), or something else. If it were the former, then we would have x3 + 1 = (x+1)3, but as I pointed out before, we don't. So it must be something else. The only candidate is x2 + x + 1. Thus the other two cube roots of 1 must be zeroes of x2 + x + 1.
The next question we must answer without delay is: b is one of the zeroes of x2 + x + 1; what is the other? There is really only one possibility: it must be b+1, because that is the only other number we have. But another way to see this is to observe that if p is a cube root of 1, then p2 must also be a cube root of 1:
| b3 | = | 1 |
| (b3)2 | = | 12 |
| b6 | = | 1 |
| (b2)3 | = | 1 |
So we now know the three zeroes of x3 + 1: they are 1, b, and b2. Since x3 + 1 factors into (x+1)(x2+x+1), the two zeroes of x2+x+1 are b and b2. As we noted before, b2 = b+1.
This means that x2 + x + 1 should factor into (x+b)(x+b+1). Multiplying through we get x2 + bx + (b+1)x + b(b+1) = x2 + x + 1, as hoped.
Actually, the fact that both b and b2 are zeroes of x2+x+1 is not a coincidence. Z2 has the delightful property that if z is a zero of any polynomial whose coefficients are all 0's and 1's, then z2 is also a zero of that polynomial. I'll call this Theorem 1. Theorem 1 is not hard to prove; it follows from the square law. Feel free to skip the demonstration which follows in the rest of the paragraph. Suppose the polynomial is P(x) = anxn + an-1xn-1 + ... + a1x + a0, and z is a zero of P, so that P(z) = 0. Then (P(z))2 = 0 also, so (anzn + an-1zn-1 + ... + a1z + a0)2 = 0. By the square law, we have an2(zn)2 + an-12(zn-1)2 + ... + a12z2 + a02 = 0. Since all the ai are either 0 or 1, we have ai2 = ai, so an(zn)2 + an-1(zn-1)2 + ... + a1z2 + a0 = 0. And finally, (zk)2 = (z2)k, so we get an(z2)n + an-1(z2)n-1 + ... + a1z2 + a0 = P(z2) = 0, which is what we wanted to prove.
Now you might be worried about something: the fact that b is a zero of x2 + x + 1 implies that b2 is also a zero; doesn't the fact that b2 is a zero imply that b4 is also a zero? And then also b8 and b16 and so forth? Then we would be in trouble, because x2 + x + 1 is a second-degree polynomial, and, by Descartes' theorem, cannot have more than two zeroes. But no, there is no problem, because b3 = 1, so b4 = b·b3 = b·1 = b, and similarly b8 = b2, so we are getting the same two zeroes over and over.
Symmetry again
Just as i and -i are completely indistinguishable from the point of view of the real numbers, so too are b and b+1 indistinguishable from the point of view of Z2. One of them has been given a simpler notation than the other, but there is no way to tell which one we gave the simpler notation to! The one and only defining property of b is that b2 + b + 1 = 0; since b+1 also shares this property, it also shares every other property of b. b and b+1 are both cube roots of 1. Each, added to the other gives 1; each, added to 1 gives the other. Each, when multiplied by itself gives the other; each when multiplied by the other gives 1.
Third-degree polynomials
We have pretty much exhausted the interesting properties of b and its identical twin b2, so let's move on to irreducible third-degree polynomials. If a third-degree polynomial is reducible, then it is either a product of three linear factors, or of a linear factor and an irreducible second-degree polynomial. If the former, it must be one of the four products x3, x2(x+1), x(x+1)2, or (x+1)3. If the latter, it must be one of x(x2+x+1) or (x+1)(x2+x+1). This makes 6 reducible polynomials. Since there are 8 third-degree polynomials in all, the other two must be irreducible:
| Polynomial | Zeroes | Factorization | |||
|---|---|---|---|---|---|
| x3 | 0, 0, 0 | x3 | |||
| x3 | + 1 | 1, b, b+1 | (x+1)(x2+x+1) | ||
| x3 | + x | 0, 1, 1 | x(x+1)2 | ||
| x3 | + x | + 1 | none | ||
| x3 | + x2 | 0, 0, 1 | x2(x+1) | ||
| x3 | + x2 | + 1 | none | ||
| x3 | + x2 | + x | 0, b, b+1 | x(x2+x+1) | |
| x3 | + x2 | + x | + 1 | 1, 1, 1 | (x+1)3 |
There are two irreducible third-degree polynomials. Let's focus on x3 + x + 1, since it seems a little simpler. As before, we will introduce a new number, c, which has the property c3 + c + 1 = 0. By the addition law, this implies that c3 = c + 1. Using this, we can make a table of powers of c, which will be useful later:
| c1 | = | c | ||
| c2 | = | c2 | ||
| c3 | = | c + | 1 | |
| c4 | = | c2 + | c | |
| c5 | = | c2 + | c + | 1 |
| c6 | = | c2 + | 1 | |
| c7 | = | 1 |
To calculate the entries in this table, just multiply each line by c to get the line below. For example, once we know that c5 = c2 + c + 1, we multiply by c to get c6 = c3 + c2 + c. But c3 = c + 1 by definition, so c6 = (c + 1) + c2 + c = c2 + 1. Once we get as far as c7, we find that c is a 7th root of 1. Analogous to the way b and b2 were both cube roots of 1, the other 7th roots of 1 are c2, c3, c4, c5, c6, and 1. For example, c5 is a 7th root of 1 because (c5)7 = c35 = (c7)5 = 15 = 1.
We've decided that c is a zero of x3 + x + 1. What are the other two zeroes? By theorem 1, they must be c2 and (c2)2 = c4. Wait, what about c8? Isn't that a zero also, by the same theorem? Oh, but c8 = c·c7 = c, so it's really the same zero again.
What about c3, c5, and c6? Those are the zeroes of the other irreducible third-degree polynomial, x3 + x2 + 1. For example, (c3)3 + (c3)2 + 1 = c9 + c6 + 1 = c2 + (c2+1) + 1 = 0.
So when we take Z2 and adjoin a new number that is a solution of the previously unsolvable equation x3 + x + 1 = 0, we're actually forced to add six new numbers; the resulting system has 8, and includes three different solutions to both irreducible third-degree polynomials, and a full complement of 7th roots of 1. Since the zeroes of x3 + x + 1 and x3 + x2 + 1 are all 7th roots of 1, this tells us that x7 + 1 factors as (x+1)(x3 + x + 1)(x3 + x2 + 1), which might not have been obvious.
Onward
I said this was my favorite math problem, but I didn't say what the question was. But by this time we have dozens of questions. For example:
- We've seen cube roots and seventh roots of 1. Where did the fifth
roots go?
(The square theorem ensures that even-order roots are uninteresting. The fourth roots of 1, for example, are just 1, 1, 1, and 1. The sixth roots are the same as the cube roots, but repeated: 1, 1, b, b, b2, and b2.)
The fifth roots, it turns out, appear later, as the four zeroes of the polynomial x4 + x3 + x2 + x + 1. These four, and 1, are five of the 15 fifteenth roots of 1. Eight others appear as the zeroes of the other two irreducible fourth-degree polynomials, and the other two fifteenth roots are b and b2. If we let d be a zero of one of the other irreducible fourth-degree polynomials, say x4 + x + 1, then the zeroes of this polynomial are d, d2, d4, and d8, and the zeroes of the other are d7, d11, d13, and d14. So we have an interesting situation. We can extend Z2 by adjoining the zeroes of x3 + 1, to get a larger system with 4 elements instead of only 2. And we can extend Z2 by adjoining the zeroes of x7 + 1, to get a larger system with 8 elements instead of only 2. But we can't do the corresponding thing with x5 + 1, because the fifth roots of 1 don't form a closed system. The sum of any two of the seventh roots of 1 was another seventh root of 1; for example, c3 + c4 = c6 and c + c2 = c4. But the corresponding fact about fifth roots is false. Suppose, for example, that y5 = 1. We'd like for y + y2 to be another fifth root of 1, but it isn't; it actually turns out that (y + y2)5 = b. For which n do the nth roots of 1 form a closed system?
- What do we get if we extend Z2 with both
b and c? What's bc? What's b + c?
(Spoiler: b + c turns out to be zero of
x6 + x5 + x3 +
x2 + 1, and is a 63rd root of 1, so we may as well
call it f. bc = f48.)
The degree of a number is the degree of the simplest polynomial of which it is a zero. What's the degree of b + c? In general, if p and q have degrees d(p) and d(q), respectively, what can we say about the degrees of pq and p + q?
- Since there is an nth root of 1 for every odd n,
that implies that for all odd n, there is some k such
that n divides 2k - 1. How are n and
k related?
- For n = 2, 3, and 4, the polynomial
xn + x + 1 was irreducible. Is this
true in general? (No: x5 + x + 1 =
(x3 + x2 + 1)(x2
+ x + 1).) When is it true? Is there a good way to find
irreducible polynomials? How many irreducible polynomials are there
of degree n? (The sequence starts out 0, 0, 1, 2, 3, 6, 9,
18, 30, 56, 99,...)
- The Galois theorem says that any finite field that contains
Z2 must have 2n elements, and its
addition component must be
isomorphic to a direct product of n copies of
Z2. Extending Z2 with c,
for example, gives us the field
GF(8),
obtained as the direct product of {0,
1}, {0, c}, and {0, c2}. The addition is
very simple, but the multiplication, viewed in this light, is rather
difficult, since it depends on knowing the secret identity c
· c2 = c + 1.
Identify the element a0 + a1c + a2c2 with the number a0 + 2a1 + 4a2, and let the addition operation be exclusive-or. What happens to the multiplication operation?
- Consider a linear-feedback shift register:
# Arguments: N, a positive integer # 0 <= K <= 2**N-1 MAXBIT = 2**N c = 2 until c == 1: c *= 2 if (c => MAXBIT): c &= ~MAXBIT c ^= K print c(Except that this function runs backward relative to the way that LFSRs usually work.)Does this terminate for all choices of N and K? (Yes.) For any given N, the maximum number of iterations of the until loop is 2N - 1. For which choices of K is this maximum achieved?
- Consider irreducible sixth-degree polynomials. We should expect
that adjoining a zero of one of these, say f, will expand
Z2 to contain 64 elements: 0, 1, f,
f2, ..., f62, and
f63 = 1. In fact, this is the case.
But of these 62 new elements, some are familiar. Specifically, f9 = c, and f21 = b. Of the 62 powers of f, 8 are numbers we have seen before, leaving only 54 new numbers. Each irreducible 6th-degree polynomial has 6 of these 54 as its zeroes, so there are 9 such polynomials. What does this calculation look like in general?
- c1,
c2,
and c4 are zeroes of
x3 + x + 1,
one of the two irreducible
third-degree polynomials. This means that
x3 + x + 1 =
(x + c1)(x +
c2)(x + c4). Multiplying
out the right-hand side, we get:
x3 + (c + c2 +
c4)x2 + (c3 +
c5 + c6)x +
1. Equating coefficients, we have
c + c2 +
c4 = 0 and
c3 +
c5 + c6 = 1.
c3, c5, and c6
are the zeroes of the other irreducible third-degree
polynomial. Coincidence? (No.)
- The irreducible polynomials appear to come in symmetric pairs:
if
anxn +
an-1xn-1 + ... +
a1x + a0
is irreducible, then so is
a0xn +
a1xn-1 + ... +
an-1x + an.
Why?
- c1, c2, and
c4 are the zeroes of one of the irreducible
third-degree polynomials. 1, 2, and 4 are all the three-bit binary
numbers that have exactly one 1 bit.
c3, c5, and
c6 are the zeroes the other irreducible
third-degree polynomial. 3, 5, and 6 are all the three-bit binary
numbers that have exactly one 0 bit. Coincidence? (No; theorem 1 is
closely related here.)
Now consider the analogous case for fourth-degree polynomials. The 4-bit numbers that have one 1 bit are 0001, 0010, 0100, and 1000 (1, 2, 4, and 8) which are all zeroes of one of the irreducible 4th-degree polynomials. The 4-bit numbers that have one 0 bit are 1110, 1101, 1011, and 0111 (7, 11, 13, and 14) which are all zeroes of another of the irreducible 4th-degree polynomials.
The 4-bit numbers with two 1 bits and two 0 bits fall into two groups. In one group we have the numbers where similar bits are adjacent: 0011, 0110, 1100, and 1001, or 3, 6, 9, and 12. These are the zeroes of the third irreducible 4th-degree polynomial. The remaining 4-bit numbers are 0101 and 1010, which correspond to b and b2.
There is, therefore, a close relationship between the structure an extension of Z2 and the so-called "necklace patterns" of bits, which are patterns that imagine that the bits are joined into a circle with no distinguishable starting point.The exceptional values (b and b2) corresponded to necklace patterns that did not possess the full n-fold symmetry. This occurs for composite values of n. But we might also expect to find exceptions at n = 11, since then 2n-1 = 2047 is composite. However, 2047 is exceptional in another way: 2047 = 23 · 89, and neither 23 nor 89 is a divisor of 2n-1 for any smaller value of n. Can we prove from this that when p is prime and 2p-1 is not, the divisors of 2p-1 do not divide 2q-1 for any q < p?
- Since ci are the seventh roots of 1, we
have x7 + 1 = (x + 1)(x +
c)(x + c2)...(x +
c6). After dividing out the trivial factor of
x+1, we are left with:
x6 + x5 + ... + 1 = (x + c)(x + c2)...(x + c6)
Multiplying through on the right side and equating coefficients gives:c + c2 + ... + c6 = 1 cc2 + cc3 + ... + c5c6 = 1 cc2c3 + cc2c4 + ... + c4c5c6 = 1 ... = ... cc2c3c4c5c6 = 1 What, if anything, can one make of this?
And then, when I get tired of Z2, I can start all over with Z3.
[Other articles in category /math] permanent link
Mon, 15 May 2006
Creeping featurism and the ratchet effect
"Creeping featurism" is a well-known phenomenon in the software
world. It refers to the tendency of software to acquire more and more
features, to the ultimate detriment of its usability. Software with
more and more features is harder to learn to use; it's harder to
document effectively. Perhaps most important, it is harder to
maintain; the more complicated software is, the more likely it is to
have bugs. Partly this is because the different features interact
with one another in unanticipated ways; partly it is just that there
is more stuff to spend the maintenance budget on.
But the concept of "creeping featurism" his wider applicability than just to program features. We can recognize it in other contexts.
For example, someone is reading the Perl manual. They read the section on the unpack function and they find it confusing. So they propose a documentation patch to add a couple of sentences, explicating the confusing point in more detail.
It seems like a good idea at the time. But if you do it over and over—and we have—you end up with a 2,000 page manual—and we did.
The real problem is that it's easy to see the benefit of any proposed addition. But it is much harder to see the cost of the proposed addition, that the manual is now 0.002% larger.
The benefit has a poster child, an obvious beneficiary. You can imagine a confused person in your head, someone who happens to be confused in exactly the right way, and who is miraculously helped out by the presence of the right two sentences in the exact right place.
The cost has no poster child. Or rather, the poster child is much harder to imagine. This is the person who is looking for something unrelated to the two-sentence addition. They are going to spend a certain amount of time looking for it. If the two-sentence addition hadn't been in there, they would have found what they were looking for. But the addition slowed them down just enough that they gave up without finding what they needed. Although you can grant that such a person might exist, they really aren't as compelling as the confused person who is magically assisted by timely advice.
Even harder to imagine is the person who's kinda confused, and for whom the extra two sentences, clarifying some obscure point about some feature he wasn't planning to use in the first place, are just more confusion. It's really hard to understand the cost of that.
But the benefit, such as it is, comes in one big lump, whereas the cost is distributed in tiny increments over a very large population. The benefit is clear, and the cost is obscure. It's easy to make a specific argument in favor of any particular addition ("people might be confused by X, so I'm going to explain it in more detail") and it's hard to make such an argument against the addition. And conversely: it's easy to make the argument that any particular bit of text should stay in, hard to argue that it should be removed.
As a result, there's what I call a "ratchet effect": you can make the manual bigger, one tiny notch at a time, and people do. But having done so, you can't make it smaller again; someone will object to almost any proposed deletion. The manual gets bigger and bigger, worse and worse organized, more and more unusable, until finally it collapses under its own weight and all you can do is start over again.
You see the same thing happen in software, of course. I maintain the Text::Template Perl module, and I frequently get messages from people saying that it should have some feature or other. And these people sometimes get quite angry when I tell them I'm not going to put in the feature they want. They're angry because it's easy to see the benefit of adding another feature, but hard to see the cost. "If other people don't like it," goes the argument, "they don't have to use it." True, but even if they don't use it, they still pay the costs of slightly longer download times, slightly longer compile times, a slightly longer and more confusing manual, slightly less frequent maintenance updates, slightly less prompt bug fix deliveries, and so on. It is so hard to make this argument, because the cost to any one person is so very small! But we all know where the software will end up if I don't make this argument every step of the way: on the slag heap.
This has been on my mind on and off for years. But I just ran into it in a new context.
Lately I've been working on a book about code style and refactoring in Perl. One thing you see a lot in Perl programs written by beginners is superfluous parentheses. For example:
next if ($file =~ /^\./);
next if !($file =~ (/[0-9]/));
next if !($file =~ (/txt/));
Or:
die $usage if ($#ARGV < 0);
There are a number of points I want to make about this. First, I'd
like to express my sympathy for Perl programmers, because Perl has
something like 95 different operators at something like 17 different
levels of precedence, and so nobody knows what all the precedences are
and whether parentheses are required in all circumstances. Does the
** operator have higher or lower precedence than the
<<= operator? I really have no idea.So the situation is impossible, at least in principle, and yet people have to deal with it somehow. But the advice you often hear is "if you're not sure of the precedence, just put in the parentheses." I think that's really bad advice. I think better advice would be "if you're not sure of the precedence, look it up."
Because Perl's Byzantine operator table is not responsible for all the problems. Notice in the examples above, which are real examples, taken from real code written by other people: Many of the parentheses there are entirely superfluous, and are not disambiguating the precedence of any operators. In particular, notice the inner parentheses in:
next if !($file =~ (/txt/));
Inside the inner parentheses, there are no operators! So they cannot
be disambiguating any precedence, and they are completely unnecessary:
next if !($file =~ /txt/);
People sometimes say "well, I like to put them in anyway, just to be
sure." This is pure superstition, and we should not tolerate it in
people who purport to be engineers. Engineers should be capable of
making informed choices, based on technical realities, not on some
creepy feeling in their guts that perhaps a failure to sprinkle enough
parentheses over their program will invite the wrath the Moon God.By saying "if you're not sure, just avoid the problem" we are encouraging this kind of fearful, superstitious approach to the issue. That approach would be appropriate if it were the only way to deal with the issue, but fortunately it is not. There is a more rational approach: you can look it up, or even try an experiment, and then you will know whether the parentheses are required in a particular case. Then you can make an informed decision about whether to put them in.
But when I teach classes on this topic, people sometimes want to take the argument even further: they want to argue that even if you know the precedence, and even if you know that the parentheses are not required, you should put them in anyway, because the next person to see the code might not know that.
And there we see the creeping featurism argument again. It's easy to see the potential benefit of the superfluous parentheses: some hapless novice maintenance programmer might misunderstand the expression if I don't put them in. It's much harder to see the cost: The code is fractionally harder for everyone to read and understand, novice or not. And again, the cost of the extra parentheses to any particular person is so small, so very small, that it is really hard to make the argument against it convincingly. But I think the argument must be made, or else the code will end up on the slag heap much faster than it would have otherwise.
Programming cannot be run on the convoy system, with the program code written to address the most ignorant, uneducated programmer. I think you have to assume that the next maintenance programmer will be competent, and that if they do not know what the expression means, they will look up the operator precedence in the manual. That assumption may be false, of course; the world is full of incompetent programmers. But no amount of parentheses are really going to help this person anyway. And even if they were, you do not have to give in, you do not have to cater to incompetence. If an incompetent programmer has trouble understanding your code, that is not your fault; it is their fault for being incompetent. You do not have to take special steps to make your code understandable even by incompetents, and you certainly should not do so at the expense of making it harder for competent programmers to read and understand, no, not to the tiniest degree.
The advice that one should always put in the parentheses seems to me to be going in the wrong direction. We should be struggling for higher standards, both for ourselves and for our associates. The conventional advice, it seems to me, is to give up.
[Other articles in category /prog] permanent link
Thu, 11 May 2006
Egyptian Fractions
The Ahmes papyrus is one of the very oldest extant mathematical
documents. It was written around 3800 years ago. As I mentioned
recently, a large part of it is a table of the values of fractions of
the form !!\frac 2n!! for odd integers !!n!!. The Egyptians, at
least at that time, did not have a generalized fraction notation.
They would write fractions of the form \frac 1n, and they could
write sums of these. But convention dictated that they could not use
the same unit fraction more than once. So to express !!\frac 35!! they would
have needed to write something like !!\frac 12 + \frac{1}{10}!!, which from now on I
will abbreviate as !![2, 10]!!. (They also had a special notation for
!!\frac 23!!, but I will ignore that for a while.) Expressing arbitrary
fractions in this form can be done, but it is non-trivial.
A simple algorithm for calculating this so-called "Egyptian fraction representation" is the greedy algorithm: To represent !!\frac nd!!, find the largest unit fraction !!\frac 1a!! that is less than !!\frac nd!!. Calculate a representation for !!\frac nd -\frac 1a!!, and append !!\frac 1a!!. This always works, but it doesn't always work well. For example, let's use the greedy algorithm to find a representation for !!\frac 29!!. The largest unit fraction less than !!\frac 29!! is !!\frac 15!!, and !!\frac 29 - \frac 15 = \frac{1}{45}!!, so we get !!\frac 29 = \frac 15 + \frac{1}{45} = [5, 45]!!. But it also happens that !!\frac 29 = [6, 18]!!, which is much more convenient to calculate with because the numbers are smaller. Similarly, for !!\frac{19}{20}!! the greedy algorithm produces $$\begin{align} \frac{19}{20} & = [2] + \frac{9}{20}\\\\ & = [2, 3] + \frac{7}{60} \\\\ & = [2, 3, 9, 180]. \end{align}$$ But even !!\frac{7}{60}!! can be more simply written than as !![9, 180]!!; it's also !![10, 60], [12, 30]!!, and, best of all, !![15, 20]!!.
So similarly, for !!\frac 37!! this time, the greedy methods gives us !!\frac 37 = \frac 13 + \frac{2}{21}!!, and that !!\frac{2}{21}!! can be expanded by the greedy method as !![11, 231]!!, so !!\frac 37 = [3, 11, 231]!!. But even !!\frac{2}{21}!! has better expansions: it's also !![12, 84], [14, 42],!! and, best of all, !![15, 35],!! so !!\frac 37 = [3, 15, 35]!!. But better than all of these is !!\frac 37 = [4, 7, 28]!!, which is optimal.
Anyway, while I was tinkering with all this, I got an answer to a question I had been wondering about for years, which is: why did Ahmes come up with a table of representations of fractions of the form !!\frac 2n!!, rather than the representations of all possible quotients? Was there a table somewhere else, now lost, of representations of fractions of the form !!\frac 3n!!?
The answer, I think, is "probably not"; here's why I think so.
Suppose you want !!\frac 37!!. But !!\frac 37 = \frac 27 + \frac 17!!. You look up !!\frac 27!! in the table and find that !!\frac 27 = [4, 28]!!. So !!\frac 37 = [4, 7, 28]!!. Done.
OK, suppose you want !!\frac 47!!. You look up !!\frac 27!! in the table and find that !!\frac 27 = [4, 28]!!. So !!\frac 47 = [4, 4, 28, 28] = [2, 14]!!. Done.
Similarly, !!\frac 57 = [2, 7, 14]!!. Done.
To calculate !!\frac 67!!, you first calculate !!\frac 37!!, which is !![4, 7, 28]!!. Then you double !!\frac 37!!, and get !!\frac 67 = \frac 12 + \frac 27 + \frac{1}{14}!!. Now you look up !!\frac 27!! in the table and get !!\frac 27 = [4, 28]!!, so !!\frac 67 = [2, 4, 14, 28]!!. Whether this is optimal or not is open to argument. It's longer than !![2, 3, 42]!!, but on the other hand the denominators are smaller.
Anyway, the table of !!\frac 2n!! is all you need to produce Egyptian representations of arbitrary rational numbers. The algorithm in general is:
- To sum up two Egyptian fractions, just concatenate their
representations. There may now be unit fractions that appear twice,
which is illegal.
If a pair of such fractions have an even denominator, they can be
eliminated using the rule that !!\frac 1{2n} + \frac 1{2n} =
\frac 1n!!. Otherwise, the denominator is odd, and you can look the
numbers up in the !!\frac 2n!! table and replace the matched pair with
the result from the table lookup. Repeat until no pairs remain.
- To double an Egyptian fraction, add it to itself as per the
previous.
- To calculate !!\frac ab!!, when !!a = 2k!!, first
calculate !!\frac kb!! and then double it as per the previous.
- To calculate !!\frac ab!! when !!a!! is odd, first
calculate !!\frac{a-1}{b}!! as per the previous; then add !!\frac 1b!!.
- !!\frac{19}{20} = \frac{18}{20} + \frac{1}{20}!!
- !!\frac{19}{20} = \frac{9}{10} + \frac{1}{20}!!
- !!\frac{9}{10} = \frac{8}{10} + \frac{1}{10}!!
- !!\frac{9}{10} = \frac 45 + \frac{1}{10}!!
- !!\frac 45 = \frac 25 + \frac 25!!
- !!\frac 25 = [3, 15]!! (from the table)
- !!\frac 45 = [3, 3, 15, 15]!!
- !!\frac 45 = \frac 23 + \frac{2}{15}!!
- !!\frac 23 = [2, 6]!! (from the table)
- !!\frac{2}{15} = [12, 20]!! (from the table)
- !!\frac 45 = [2, 6, 12, 20]!!
- !!\frac 45 = \frac 25 + \frac 25!!
- !!\frac{9}{10} = [2, 6, 10, 12, 20] !!
- !!\frac{19}{20} = [2, 6, 10, 12, 20, 20] !!
- !!\frac{19}{20} = [2, 6, 10, 10, 12] !!
- !!\frac{19}{20} = [2, 5, 6, 12] !!
An alternative algorithm is to expand the numerator as a sum of powers of !!2!!, which the Egyptians certainly knew how to do. For !!\frac{19}{20}!! this gives us $$\frac{19}{20} = \frac{16}{20} + \frac{2}{20} + \frac{1}{20} = \frac 45 + [10, 20].$$ Now we need to figure out !!\frac 45!!, which we do as above, getting !!\frac 45 = [2, 6, 12, 20]!!, or !!\frac 45 = \frac 23 + [12, 20]!! if we are Egyptian, or !!\frac 45 = [2, 4, 20]!! if we are clever. Supposing we are neither, we have $$\begin{align} \frac{19}{20} & = [2, 6, 12, 20, 10, 20] \\\\ & = [2, 6, 12, 10, 10] \\\\ &= [2, 6, 12, 5] \\\\ \end{align}$$ as before.
(It is not clear to me, by the way, that either of these algorithms is guaranteed to terminate. I need to think about it some more.)
Getting the table of good-quality representations of !!\frac 2n!! is not trivial, and requires searching, number theory, and some trial and error. It's not at all clear that !!\frac{2}{105} = [90, 126]!!.
Once you have the table of !!\frac 2n!!, however, you can grind out the answer to any division problem. This might be time-consuming, but it's nevertheless trivial. So Ahmes needed a table of !!\frac 2n!!, but once he had it, he didn't need any other tables.
[Other articles in category /math] permanent link
Tue, 02 May 2006
Addenda to recent articles 200604
Here are some notes on posts from the last
month that I couldn't find better places for.
- Stan Yen points out that I missed an important aspect of the
convenience of instant mac & cheese: it has a long shelf life, so
it is possible to keep a couple of boxes on hand for when you want
them, and then when you do want macaroni and cheese you don't have to
go shopping for cheese and pasta. M. Yen has a good point. I
completely overlooked this, because my eating habits are such that I
nearly always have the ingredients for macaroni and cheese on hand.
M. Yen also points out that some of the attraction of Kraft Macaroni and Cheese Dinner is its specific taste and texture. We all have occasional longings for the comfort foods of childhood, and for many people, me included, Kraft dinner is one of these. When you are trying to recreate the memory of a beloved food from years past, the quality of the ingredients is not the issue. I can sympathize with this: I would continue to eat Kraft dinner if it tasted the way I remember it having tasted twenty years ago. I still occasionally buy horrible processed American cheese slices not because it's a good deal, or because I like the cheese, but because I want to put it into grilled cheese sandwiches to eat with Campbell's condensed tomato soup on rainy days.
- Regarding the invention of
the = sign, R. Koch sent me two papers by Florian Cajori, a
famous historian of mathematics. One paper, Note on our sign
of Equality, presented evidence that a certain Pompeo
Bolognetti independently invented the sign, perhaps even before Robert
Recorde did. The = sign appears in some notes that Bolognetti made,
possibly before 1557, when Recorde's book The Whetstone of
Witte was published, and certainly before 1568, when Bolognetti
died. Cajori suggests that Bolognetti used the sign because the dash
----- was being used for both equality and subtraction, so perhaps
Bolognetti chose to double the dash when he used it to denote
equality. Cajori says "We have here the extraordinary spectacle of
the same arbitrary sign having been chosen by independent workers
guided in their selection by different considerations."
The other paper M. Koch sent is Mathematical Signs of Equality, and traces the many many symbols that have been used for equality, and the gradual universal adoption of Recorde's sign. Introduced in England in 1557, the Recorde sign was first widely adopted in England. Cajori: "In the seventeenth century Recorde's ===== gained complete ascendancy in England." But at that time, mathematicians in continental Europe were using a different sign , introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.
, introduced by René Descartes.
Cajori believes that the universal adoption of Recorde's = sign in
Europe was due to its later use by Leibniz. Much of this material
reappears in Volume I of Cajori's book A History of Mathematical
Notations. Thank you, M. Koch.Ian Jones at the University of Warwick has a good summary of Cajori's discussion of this matter.
- Regarding Rayleigh
scattering in the atmosphere, I asserted:
The sun itself looks slightly redder ... this effect is quite pronounced ... when there are particles of soot in the air ... .
Neil Kandalgaonkar wrote to inform me that there is a web page at the site of the National Oceanic and Atmospheric Administration that appears at first to dispute this. I said that I could not believe that the NOAA was actually disputing this. I was in San Diego in October 2003, and when I went outside at lunchtime, the sun was red. At the time, the whole county was on fire, and anyone who wants to persuade me that these two events were entirely unrelated will have an uphill battle.
Fortunately, M. Kandalgaonkar and I determined that the NOAA web page not asserting any such silly thing as that smoke does not make the sun look red. Rather, it is actually asserting that smoke does not contribute to good sunsets. And M. Kandalgaonkar then referred me to an amazing book, M. G. Minnaert's Light and Color in the Outdoors.This book explains every usual and unusual phenomenon of light and color in the outdoors that you have ever observed, and dozens that you may have observed but didn't notice until they were pointed out. (Random example: "This explains why the smoke of a cigar or cigarette is blue when blown immediately into the air, but becomes white if it is been kept in the mouth first. The particles of smoke in the latter case are covered by a coat of water and become much larger.") I may report on this book in more detail in the future. In the meantime, Minnaert says that the redness of the sun when seen through smoke is due primarily to absorption of light, not to Rayleigh scattering:
The absorption of carbon increases rapidly from the red to the violet of the spectrum; this characteristic is exemplified in the blood-red color of the sun when seen through the smoke of a house on fire.
- A couple of people have written to suggest that perhaps the one
science question any high school graduate ought to be able to answer
is "What is the scientific method?" Yes, I quite agree.
Nathan G. Senthil has also pointed out Richard P. Feynman's suggestion on this topic. In one of the first few of his freshman physics lectures, Feynman said that if nearly all scientific knowledge were to be destroyed, and he were able to transmit only one piece of scientific information to future generations, it would be that matter is composed of atoms, because a tremendous amount of knowledge can be inferred from this one fact. So we might turn this around and suggest that every high school graduate should be able to give an account of the atomic theory of matter.
- I said that Pick's theorem
Implies that every lattice polygon has an area that is an integer
multiple of 1/2, "which I would not have thought was obvious." Dan
Schmidt pointed out that it is in fact obvious. As I pointed out in
the Pick's theorem article, every such polygon can be built up from
right triangles whose short sides are vertical
and horizontal; each such triangle is half of a rectangle, and
rectangles have integer areas. Oops.
- Seth David Schoen brought to my attention the fascinating
phenomenon of tetrachromacy. It is believed that some (or all) humans
may have a color sensation apparatus that supports a four-dimensional
color space, rather than the three-dimensional space that it is
believed most humans have.
As is usual with color perception, the complete story is very complicated and not entirely understood. In my brief research, I discovered references to at least three different sorts of tetrachromacy.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
So it's at least conceivable that the brain could make use of rod cell response to distinguish more colors than would be possible without it. Impediments to this are that rods are poorly represented on the fovea (the central part of the retina where the receptors are densest) and they have a slow response. Also, because of the way the higher neural layers are wired up, rod vision has poorer resolution than cone vision.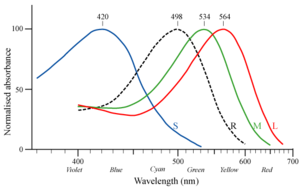
I did not find any scientific papers that discussed rod tetrachromacy, but I didn't look very hard.
- The most common form of color blindness is deuteranomaly,
in which the pigment in the "green" cones is "redder" than it should
be. The result is that the subject has difficulty distinguishing
green and red. (Also common is protanomaly, which is just the
reverse: the "red" pigment is "greener" than it should be, with the
same result. What follows holds for protanomaly as well as
deuteranomaly.)
Genes for the red and green cone pigments are all carried on the X chromosomes, never on the Y chromosomes. Men have only one X chromosome, and so have only one gene each for the red and green pigments. About 6-8% of all men carry an anomalous green pigment gene on their X chromosome instead of a normal one and suffer from deuteranomaly.
Each of these men inherited his X chromosome from his mother, who must also therefore carry the anomalous gene on one of her two X chromosomes. The other X chromosome of such a woman typically carries the normal version of the gene. Since such a woman has genes for both the normal and the "redder" version of the green pigment, she might have both normal and anomalous cone cells. That is, she might have the normal "green" cones and also the "redder" version of the "green" cones. If so, she will have four different kinds of cones with four different color responses: the usual "red", "green" and "blue" cones, and the anomalous "green" cone, which we might call "yellow".
The big paper on this seems to be A study of women heterozygous for colour deficiencies, by G. Jordan and J. D. Mollon, appeared in Vision Research, Volume 33, Issue 11, July 1993, Pages 1495-1508. I haven't finished reading it yet. Here's my summary of the abstract: They took 31 of women who were known to be carriers of the anomalous gene and had them perform color-matching tasks. Over a certain range of wavelengths, a tetrachromat who is trying to mix light of wavelengths a and b to get as close as possible to perceived color c should do it the same way every time, whereas a trichromat would see many different mixtures as equivalent. And Jordan and Mollon did in fact find a person who made the same color match every time.
Another relevant paper with similar content is Richer color experience in observers with multiple photopigment opsin genes, by Kimberly A. Jameson, Susan M. Highnote, and Linda M. Wasserman, appeared in Psychonomic Bulletin & Review 2001, 8 (2), 244-261. Happily, this is available online for free.
My own description is highly condensed. Ryan's Sutherland's article Aliens among us: Preliminary evidence of superhuman tetrachromats is clear and readable, much more so than my explanation above. Please do not be put off by the silly title; it is an excellent article.
- The website Processes in
Biological Vision claims that the human eye normally contains a
color receptor that responds to very short-wavelength violet and even
ultraviolet light, but that previous studies have missed this because
the lens tends to filter out such light and because indoor light
sources tend not to produce it. The site discusses the color
perception of persons who had their lenses removed. I have not yet
evaluated these claims, and the web site has a strong stink of
crackpotism, so beware.
- In addition to three types of cone cells, humans also have rod
cells in their retinas. The rod cells have a peak response to photons
of about 500 nm wavelength, which is quite different from the peak
responses of any of the cones. In the figure below, the dotted black
line is the response of the
rods; the colored lines are the responses of the three types of cones.
- In discussing Hero's
formula, I derived the formula
(2a2b2 + 2a2c2 +
2b2c2 - a4 - b4-
c4)/16 for the square of the area of a triangle with sides of lengths
a, b, and c, and then wondered how to get from
that mess to Hero's formula itself, which is nice and simple:
p(p-a)(p-b)(p-c),
where p is half the perimeter.
François Glineur wrote in to show me how easy it is. First, my earlier calculations had given me the simpler expression 16A2 = 4a2b2 - (a2+b2-c2)2, which, as he says, is unfortunately not symmetric in a, b and c. We know that it must be expressible in a symmetric form somehow, because the triangle's area does not know or care which side we have decided to designate as side a.
But the formula above is a difference of squares, so we can factor it to obtain (2ab + a2 + b2 - c2)(2ab + c2 - a2 - b2), and then simplify the a2 ±2ab + b2 parts to get ((a+b)2 - c2)(c2 - (a-b)2). But now each factor is itself a difference of squares and can be factored, obtaining (a+b+c)(a+b-c)(c+a-b)(c-a+b). From here to Hero's formula is just a little step. As M. Glineur says, there are no lucky guesses or complicated steps needed. Thank you, M. Glineur.
M. Glineur ended his note by saying:
In my opinion, an even "better" proof would not break the symmetry between a, b and c at all, but I don't have convincing one at hand.
Gareth McCaughan wrote to me with just such a proof; I hope to present it sometime in the next few weeks. It is nicely symmetric, and its only defect is that it depends on trigonometry. - Carl Witty pointed out that my equation of the risk of Russian
roulette with the risk of driving an automobile was an
oversimplification. For example, he said, someone playing Russian
roulette, even at extremely favorable odds, appears to be courting
suicide in a way that someone driving a car does not; a person with
strong ethical or religious beliefs against suicide might then reject
Russian roulette even if it is less risky than driving a car. I
hadn't appreciated this before; thank you, M. Witty.
I am reminded of the story of the philosopher Ramon Llull (1235–1315). Llull was beatified, but not canonized, and my recollection was that this was because of the circumstances of his death: he had a habit of going to visit the infidels to preach loudly and insistently about Christianity. Several narrow escapes did not break him of this habit, and he was eventually he was torn apart by an angry mob. Although it wasn't exactly suicide, it wasn't exactly not suicide either, and the Church was too uncomfortable with it to let him be canonized.
Then again, Wikipedia says he died "at home in Palma", so perhaps it's all nonsense.
- Three people have written in to contest my assertion that I did not know
anyone who had used a gas chromatograph. By which I mean that
three people I know have asserted that they have used gas
chromatographs.
It also occurred to me that my cousin Alex Scheeline is a professor of chemistry at UIUC, and my wife's mother's younger brother's daughter's husband's older brother's wife's twin sister is Laurie J. Butler, a professor of physical chemistry at the University of Chicago. Both of these have surely used gas chromatographs, so they bring the total to five.
So it was a pretty dumb thing to say.
- In yesterday's
Google query roundup, I brought up the following search query,
which terminated at my blog:
a collection of 2 billion points is completely enclosed by a circle. does there exist a straight line having exactly 1 billion of these points on each sideThis has the appearance of someone's homework problem that they plugged into Google verbatim. What struck me about it on rereading is that the thing about the circle is a tautology. The rest of the problem does not refer to the circle, and every collection of 2 billion points is completely enclosed by a circle, so the clause about the circle is entirely unnecessary. So what is it doing there?All of my speculations about this are uncharitable (and, of course, speculative), so I will suppress them. I did the query myself, and was not enlightened.
If this query came from a high school student, as I imagine it did, then following question probably has at least as much educational value:
Show that for any collection of 2 billion points, there is a circle that completely encloses them.It seems to me that to answer that question, you must get to the heart of what it means for something to be a mathematical proof. At a higher educational level, this theorem might well be dismissed as "obvious", or passed over momentarily on the way to something more interesting with the phrase "since X is a finite set, it is bounded." But for a high school student, it is worth careful consideration. I worry that the teacher who asked the question does not know that finite sets are bounded. Oops, one of my uncharitable speculations leaked out.
[Other articles in category /addenda] permanent link
Mon, 01 May 2006
Google query roundup
A highly incomplete version of this month's Google query roundup
appeared on the blog on Saturday by mistake. It's fixed now, but if
you are reading this through an aggregator, the aggregator may not
give you the chance to see the complete version.
The complete article is available here.
[Other articles in category /google-roundup] permanent link
Google query roundup
Once again I am going to write up the interesting Google queries that
my blog has attracted this month.
Probably the one I found most interesting was:
1 if n + 1 are put inside n boxes, then at least one box
will contain more than one ball. prove this principle by
induction.
But I found this so interesting that I wrote a 1,000 word
article about it, which is not finished. Briefly: I believe that
nearly all
questions of the form "solve the problem using/without using technique
X" are pedagogically bogus and represent a failure of
instructor or curriculum. Well, it will have to wait for another
time. Another mathematical question that came up was:
1 a collection of 2 billion points is completely enclosed
by a circle. does there exist a straight line having
exactly 1 billion of these points on each side
This one is rather interesting. The basic idea is that you take a
line, any line, and put it way off to one side of the points; all the
points are now on one side of the line. Then you move the line
smoothly across the points to the other side. As you do this, the
number of points on one side decreases and the number of points on the
other side increases until all the points are on the other side.
Unless something funny happens in the middle, then somewhere along the
way, half the points will be on one side and half on the other. For
concreteness, let's say that the line is moving from left to right,
and that the points start out to the right of the line.What might happen in the middle is that you might have one billion minus n points on the left, and then suddenly the line intersects more than n points at once, so that the number of points on the left jumps up by a whole bunch, skipping right past one billion, instead of ticking up by one at a time. So what we really need is to ensure that this never happens. But that's no trouble. Taking the points two at a time, we can find the slope of the line that will pass through the two points. There are at most 499,999,999,500,000,000 such slopes. If we pick a line that has a slope different from one of these, then no matter where we put it, it cannot possibly intersect more than one of the points. Then as we slide the line from one side to the other, as above, the count of the number of points on the left never goes up by more than 1 at a time, and we win.
Another math query that did not come from Google is:
Why can't there be a Heron's formula for an arbitrary quadrilateral
Heron's formula, you will
recall, gives the area of a triangle in terms of the lengths of
its sides. The following example shows that there can be no such
formula for the area of a quadrilateral:
 |
 |
 |
The following query is a little puzzling:
1 undecidable problems not in np
It's puzzling because no undecidable problem is in NP. NP is
the class of problems for which proposed solutions can be checked in
polynomial time. Problems in NP can therefore be solved by the simple
algorithm of: generate everything that could possibly be a solution,
and check each one to see if it is a solution. Undecidable
problems, on the other hand, cannot be solved at all, by any method.
So if you want an example of an undecidable problem that is not in NP,
you start by choosing an undecidable problem, and then you are
done.It might be that the querent was looking for decidable problems that are not in NP. Here the answer is more interesting. There are many possibilities, but surprisingly few known examples. The problem of determining whether there is any string that is matched by a given regex is known to require exponential time, if regular expressions are extended with a {2} notation so that a{2} is synonymous with aa. Normally, if someone asks you if there is any string that matches a regex, you can answer just by presenting such a string, and then the querent can check the answer by running the regex engine and checking (in polynomial time) that the string you have provided does indeed match.
But for regexes with the {2} notation, the string you would provide might have to be gigantic, so gigantic that it could not be checked efficiently. This is because one can build a relatively short regex that matches only enormous strings: a{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2} is only 61 characters long, and it does indeed match one string, but the string it matches is 1,048,576 characters long.
Many problems involving finding the good moves in certain games are known to be decidable and believed to not be in NP, but it isn't known for sure.
Many problems that involve counting things are known to be decidable but are believed to not be in NP. For example, consider the NP-complete problem discussed here, called X3C. X3C is in NP. If Sesame Workshop presents you with a list of episodes and a list of approved topics for dividing the episodes into groups of 3, and you come up with a purported solution, Sesame Workshop can quickly check whether you did it right, whether each segment of Elmo's World is on exactly one video, and whether all the videos are on the approved list.
But consider the related problem in which Sesame Workshop comes to you with the same episodes and the same list of approved combinations, and asks, not for a distribution of episodes onto videotapes, but a count of the number of possible distributions. You might come back with an answer, say 23,487, but Sesame Workshop has no way to check that this is in fact the right number. Nobody has been able to think of a way that they might do this, anyhow.
Such a problem is clearly decidable: enumerate all possible distributions of episodes onto videos, check each one to see if it satisfies Sesame Workshop's criteria, and increment a counter if so. It is clearly at least as hard as the NP-complete problem of determining whether there is any legal distribution, because if you can count the number of legal distributions, there is a legal distribution if and only if the count of legal distributions is not 0. But it may well be outside of NP, because seems quite plausible that there is no quick way to verify a purported count of solutions, short of generating, checking, and recounting all possible distributions.
This is on my mind anyway, because this month I got email from two separate people both asking me for examples of problems that were outside of NP but still decidable, one on March 18:
I was hoping to get some information on a problem that is considered np-hard but not in NP (other than halting problem).And then one on March 31:
I was visiting your website in search of problems that are NP-Hard but not NP-Complete which are decision problems, but not the halting problem.It turned out that they were both in the same class at Brock University in Canada.
Here's one that was surprising:
1 wife site:plover.com
My first thought was that this might have been posted by my wife, looking
to see if I was talking about her on my blog. But that is really not
her style. She would be much more likely just to ask me rather than
to do something sneaky. That is why I married her, instead of a sneaky
person. And indeed, the query came from Australia. I still wonder
what it was about, though.
1 mathematical solution for eliminating debt
Something like this has come up month after month:
[18/Jan/2006:09:10:46 -0500] eliminate debt using linear math
[08/Feb/2006:13:48:13 -0500] linear math system eliminate debt
[08/Feb/2006:13:53:28 -0500] linear math system eliminate debt
[25/Feb/2006:15:12:01 -0500] how to get out of debt using linear math
[23/Apr/2006:10:32:18 -0400] Mathematical solution for eliminating debt
[23/Apr/2006:10:33:43 -0400] Mathematical solution for eliminating debt
At first I assumed that it was the same person. But analysis of the
logs suggests it's not. I tried the query myself and found that many
community colleges and continuing education programs offer courses on
using linear math to eliminate debt. I don't know what it's about. I
don't even know what "linear" means in this context. I am unlikely to
shell out $90 to learn the big secret, so a secret it will have to
remain.
1 which 2 fraction did archimedes add together to write 3/4
I don't know what this was about, but it reminded me of Egyptian
fractions. Apparently, the Egyptians had no general notation for
fractions. They did, however, have notations for numbers of the form
1/n, and they could write sums of these. They also had a
special notation for 2/3. So they could in fact write all fractions,
although it wasn't always easy.There are several algorithms for writing any fraction as a sum of fractions of the form 1/n. The greedy algorithm suffices. Say you want to write 2/5. This is bigger than 1/3 and smaller than 1/2, so write 2/5 = 1/3 + x. x is now 1/15 and we are done. Had x had a numerator larger than 1, we would have repeated the process.
The greedy algorithm produces an Egyptian fraction representation of any number, but does not always do so conveniently. For example, consider 19/20. The greedy algorithm finds 19/20 = 1/2 + 1/3 + 1/9 + 1/180. But 19/20 = 1/2 + 1/4 + 1/5, which is much more convenient. So the problem of finding good representations for various numbers was of some interest, and the Ahmes papyrus, one of the very oldest mathematical manuscripts known, devotes a large amount of space to the representations of various numbers of the form 2/n.
1 why does pi appear in both circle area and circumference?
This is not a coincidence. I have a mostly-written article about
this; I will post it here when I finish it.
1 the only two things in our universe starting with m & e
I hope the high school science teacher who asked this idiotic question burns
in hell.It does, however, remind me of the opening episode of The Cyberiad, by Stanislaw Lem, in which Trurl the inventor builds a machine that can manufacture anything that begins with the letter N. Trurl orders his machine to manufacture "needles, then nankeens and negligees, which it did, then nail the lot to narghiles filled with nepenthe and numerous other narcotics." The story goes on from there, with the machine refusing to manufacture natrium:
"Never heard of it," said the machine.I have a minor reading disorder: I hardly ever think books are funny, except when they are read out loud. When I tell people this, they always start incredulously enumerating funny books: "You didn't think that the Hitchhiker's Guide books were funny?" No, I didn't. I thought Fear and Loathing in Las Vegas was the dumbest thing I'd ever read, until I heard James Woodyatt reading it aloud in the back of the car on the way to a party in Las Vegas (New Mexico, not Nevada) and then I laughed my head off. I did not think Evelyn Waugh's humorous novel Scoop was funny. I did not think Daniel Pinkwater's books were funny. I do not think Christopher Moore's books are funny. Louise Erdrich's books are sometimes funny, but I only know this because Lorrie and I read them aloud to each other. Had I read them myself, I would have thought them unrelievedly depressing."What? But it's only sodium. You know, the metal, the element..."
"Sodium starts with an s, and I work only in n."
"But in Latin it's natrium."
"Look, old boy," said the machine, "if I could do everything starting with n in every possible language, I'd be a Machine That Could Do Everything in the Whole Alphabet, since any item you care to mention undoubtedly starts with n in one foreign language or another. It's not that easy. I can't go beyond what you programmed. So no Sodium."
I think The Cyberiad is uproarious. It is easily the funniest book I have ever read. I laugh out out every time I read it.
The most amazing thing about it is that it was originally written in Polish. The translator, Michael Kandel, is a genius. I would not have dared to translate a Polish story about a machine that can make anything that begins with n. It is an obvious death trap. Eventually, the story is going to call for the machine to manufacture something like napad rabunkowy ("stickup") that begins with n in Polish but not in English. Perhaps the translator will get lucky and find a synonym that begins with n in English, but sooner or later his luck will run out.
I once met M. Kandel, and I asked him if it had been n in the original, or if it had been some other letter that was easy in Polish but impossible in English, like z, or even ł. No, he said it had indeed been n. He said that the only real difficulty he had was that Trurl asks the machine to make nauka ("science") and he had to settle for "nature".
(Incidentally, I put the word napad rabunkowy into the dictionary lookup at poltran.com and it told me angrily "PLEASE TYPE POLISH WORDS USING CAPITAL LETTERS ONLY!" Yeah, that's a good advertisement for your software.)
In addition to being funny, The Cyberiad is philosophically serious. In the final chapter, Trurl is contracted by a wicked, violent despot to manufacture a new kingdom to replace the one that overthrew and exiled him. Trurl does so, and then he and his friend Klapaucius debate the ethics of this matter. Trurl argues that the miniature subjects in the replacement kingdom are not actually suffering under the oppressive rule of the despot, because they are only mechanical, and programmed to give the appearance of suffering and misery. Klapaucius persuades him otherwise, and me also. Perhaps someday I will write a blog article comparing Klapaucius's arguments with the similar arguments against zombies in Dennett's book Consciousness Explained.
By the way, narghiles are like hookahs, and nankeens are trousers made of a certain kind of cotton cloth, also called nankeen.
The most intriguing query I got was:
1 consciousness torus photon core
Wow, isn't that something? I have no idea what this person was
looking for. So I did the search myself, to see what would come up.
I found a lot of amazingly nutty theories about physics. As I
threatened a while back, I may do an article about crackpotism; if so,
I will certainly make this query again, to gather material.My favorite result from this query is unfortunately offline, available only from the Google cache:
The photon is actually composed of two tetrahedrons that are joined together, as we see in figure 4.6, and they then pass together through a cube that is only big enough to measure one of them at a time.Wow! The photon is actually composed of two tetrahedrons! Who knew? But before you get too excited about this, I should point out that the sentence preceding this one asserted that the volume of a regular tetrahedron is one-third the volume of the smallest sphere containing it. (Exercise: without knowing very much about the volumes of tetrahedra and their circumscribed spheres, how can you quickly guess that this is false?)
Also, I got 26 queries from people looking for the Indiana Pacers' cheerleaders, and 31 queries from people looking for examples of NP-complete problems.
This is article #100 on my blog.
[Other articles in category /google-roundup] permanent link


