Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Fri, 07 Apr 2006
Robert Recorde invents the equals sign
I mentioned recently that
the integral sign 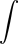 is actually a letter
"S", chosen by Leibnitz because it was the first letter of the word
"sum". Seth David Schoen suggested that Leibnitz probably wrote in
Latin, so that it is actually the first letter of the word "summa",
which means "sum" in Latin. I do not know, but I will see if I can
track down the original paper.
is actually a letter
"S", chosen by Leibnitz because it was the first letter of the word
"sum". Seth David Schoen suggested that Leibnitz probably wrote in
Latin, so that it is actually the first letter of the word "summa",
which means "sum" in Latin. I do not know, but I will see if I can
track down the original paper.
I once gave a conference talk about how it was a good idea to go dig up original materials, and why. Someday I may write a blog article about this. One of the best reasons is that these materials are the original materials because they are the ones that are so brilliant and penetrating and incisive that they inspired other people to follow them. So I thought it might be fun to read Leibnitz's original papers and see what I might find out that I did not already know. Also, there is an element of touristry in it: I would like to gaze upon the world's first use of the integral sign with my own eyes, in the same way that I would like to gaze on the Grand Canyon with my own eyes. The trip to the library is a lot more convenient, this month.
Anyway, this sparked a discussion with M. Schoen about original mathematic manuscripts, and he mentioned to me that he had seen the page of Robert Recorde's The Whetstone of Witte that contains the world's first use, in 1557, of the equals sign. He had a scan of this handy; I have extracted the relevant portion of the page, and here it is:

Howbeit, for easie alteration of equations. I will propounde a fewe exanples, bicause the extraction of their rootes, maie the more aptly bee wroughte. And to avoide the tediouse repetition of these woordes : is equalle to : I will sette as I doe often in woorke use, a pair of paralleles, or Gemowe lines of one lengthe, thus: =====, bicause noe .2. thynges, can be moare equalle.If you are still having trouble reading this, try reading it aloud. The only tricky things are the spelling and the word "Gemowe". Reading aloud will solve the spelling problem. "Gemowe" means "twin", like in the astrological sign of Gemini. (I had to look this up in the big dictionary.) Reading 16th-century books takes a little time to get used to, but once you know the tricks, it is surprisingly easy, given how uncouth they appear at first look.
I must say, compared with the writing of the Baroque period, which just goes on and on and on, this is extremely concise and to the point. It does not read all that differently from modern technical material.
One reason I like to visit original documents is that I never know what I am going to find. If you visit someone else's account of the documents, you can only learn a subset of whatever that person happened to notice and think was important. This time I learned something surprising.
I knew that the German "umlaut" symbol was originally a small letter "e". A word like schön ("beautiful") was originally spelled schoen, and then was written as schon with a tiny "e" over the "o", and eventually the tiny "e" dwindled away to nothing but two dots. I have a German book printed around 1800 in which the little "e"s are quite distinct.
And I had recently learned that the twiddle in the Spanish ñ character was similarly a letter "n". A word like "año" was originally "anno" (as it is in Latin) and the second "n" was later abbreviated to a diacritic over the first "n". (This makes a nice counterpoint to the fact that the mathematical logical negation symbol $$\sim$$ was selected because of its resemblance to the letter "N".) But I had no idea that anything of the sort was ever done in English.
Recorde's book shows clearly that it was, at least for a time. The short passage illustrated above contains two examples. One is the word "examples" itself, which is written "exãples", with a tilde over the "a". The other is "alteration", which is written "alteratiõ", with a tilde over the "o". More examples abound: "cõpendiousnesse", "nõbers", "denominatiõ", and, I think, "reme~ber". (The print is unclear.)
I had never seen this done before in English. I will investigate further and see what I can find out.
Would I have learned about this if I hadn't returned to the original document? Unlikely.
Here's another interesting fact about this book: It coined the bizarre word "zenzizenzizenzike", which, of all the words in the big dictionary, is the one with the most "z"s. Recorde uses the word "zenzike" to refer to the square of a number, or to a term in an expression with a square power. "Zenzizenzike" is similarly a fourth power, and "zenzizenzizenzike" an eighth power. I uploaded a scan of the relevant pages to Wikipedia, where you can see them; the word appears at the very top of the right-hand page. That page also contains the delightful phrase "zzzz Betokeneth a Square of squares, squaredly squared." Squares, squares, squares, squares, squares, squares, squares, baked beans, squares, squares, squares, and squares!
Addendum 20240524
The entire book is now online at the Internet Archive. The extract above appears on page 238.[Other articles in category /math] permanent link


