Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2025: | JFMAMJ |
| JAS | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 99 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Mon, 10 Nov 2008
Gabriel's Horn is not so puzzling
Take the curve y = 1/x for x ≥ 1.
Revolve it around the x-axis, generating a trumpet-shaped
surface, "Gabriel's Horn".
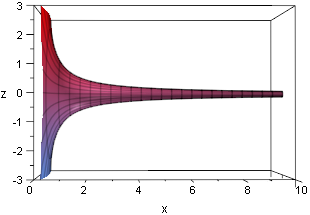
The calculations themselves do not lend much insight into what is going on here. But I recently read a crystal-clear explanation that I think should be more widely known.
Take out some Play-Doh and roll out a snake. The surface area of the snake (neglecting the two ends, which are small) is the product of the length and the circumference; the circumference is proportional to the diameter. The volume is the product of the length and the cross-sectional area, which is proportional to the square of the diameter.
| Buy Elementary Calculus: An Infinitesimal Approach  from Bookshop.org (with kickback) (without kickback) |
As you continue to roll the snake thinner and thinner, the volume stays the same, but the surface area goes to infinity.
Gabriel's Horn does exactly the same thing, except without the rolling, because the parts of the Horn that are far from the origin look exactly the same as very long snakes.
There's nothing going on in the Gabriel's Horn example that isn't also happening in the snake example, except that in the explanation of Gabriel's Horn, the situation is obfuscated by calculus.
I read this explanation in H. Jerome Keisler's caclulus textbook. Keisler's book is an ordinary undergraduate calculus text, except that instead of basing everything on limits and on limiting processes, it is based on nonstandard analysis and explicit infinitesimal quantities. Check it out; it is available online for free. (The discussion of Gabriel's Horn is in chapter 6, page 356.)
[ Addendum 20081110: A bit more about this. ]
[Other articles in category /math] permanent link


