Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| Elaborations of Russell's paradox |
| Eta-reduction in Haskell and English |
| Mental astronomical calculations |
| Where should usage messages go? |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Wed, 11 Jan 2012
Where should usage messages go?
Last week John Speno complained about Unix commands which, when
used incorrectly, print usage messages to standard error instead of to
standard output. The problem here is that if the usage message is
long, it might scroll off the screen, and it's a pain when you try to
pipe it through a pager with command | pager and discover
that the usage output has gone to stderr, missed the pager, and
scrolled off the screen anyway.
Countervailing against this, though, is the usual argument for stderr: if you had run the command in a pipeline, and it wrote its error output to stdout instead of to stderr, then the error message would have gotten lost, and would possibly have caused havoc further down the pipeline. I considered this argument to be the controlling one, but I ran a quick and informal survey to see if I was in the minority.
After 15 people had answered the survey, Ron Echeverri pointed out that although it makes sense for the usage message to go to stderr when the command is used erroneously, it also makes sense for it to go to stdout if the message is specifically requested, say by the addition of a --help flag, since in that case the message is not erroneous. So I added a second question to the survey to ask about where the message should go in such a case.
83 people answered the first question, "When a command is misused, should it deliver its usage message to standard output or to standard error?". 62 (75%) agreed that the message should go to stderr; 11 (13%) said it should go to stdout. 10 indicated that they preferred a more complicated policy, of which 4 were essentially (or exactly) what M. Echeverri suggested; this brings the total in favor of stderr to 66 (80%). The others were:
- stdout, if it is a tty; stderr otherwise
- stdout, if it is a pipe; stderr otherwise
- A very long response that suggested syslog.
- stderr, unless an empty stdout would cause problems
- It depends, but the survey omitted the option of printing directly on the console
- It depends
68 people answered the second question, "Where should the command send the output when the user specifically requests usage information?". (15 people took the survey before I added this question.) 50 (74%) said the output should go to stdout, 12 (18%) to the user's default pager and then to stdout, and 5 (7%) to stderr. One person (The same as #5 above) said "it depends".
Thanks to everyone who participated.
[Other articles in category /Unix] permanent link
Tue, 10 Jan 2012
Elaborations of Russell's paradox
When Katara was five or six, I told her about Russell's paradox in the
following form: in a certain library, some books are catalogs that
contain lists of other books. For example, there is a catalog of all
the books on the second floor, and a catalog of all the books about
birds. Some catalogs might include themselves. For example, the
catalog of all the books in the library certainly includes itself.
Such catalogs have red covers; the other catalogs, which do not
include themselves, such as the catalog of all the plays of
Shakespeare, have blue covers. Now is there a catalog of all the
catalogs with blue covers?
I wasn't sure she would get this, but it succeeded much better than I expected. After I prompted her to consider what color cover it would have, she thought it out, first ruling out one color, and then, when she got to the second color, she just started laughing.
A couple of days ago she asked me if I could think of anything that was like that but with three different colors. Put on the spot, I suggested she consider what would happen if there could be green catalogs that might or might not include themselves. This is somewhat interesting, because you now can have a catalog of all the blue catalogs; it can have a green cover. But I soon thought of a much better extension.
I gave it to Katara like this: say you have a catalog, let's call it X. If X mentions a catalog that mentions X, it has a gold stripe on the spine. Otherwise, it has a silver stripe. Now:
- Could there be a red catalog with a gold stripe?
- Could there be a red catalog with a silver stripe?
- Could there be a blue catalog with a gold stripe?
- Could there be a blue catalog with a silver stripe?
- Is there a catalog of all the catalogs with gold stripes?
- Is there a catalog of all the catalogs with silver stripes?
Translating this into barber language is left as an exercise for the reader.
[ Addendum 20231128: More about uncountable sets for seven-year-olds. ]
[Other articles in category /math] permanent link
Wed, 04 Jan 2012
Mental astronomical calculations
As you can see from the following graph, the daylight length starts
increasing after the winter solstice (last week) but it does so quite
slowly at first, picking up speed, and reaching a maximum rate of
increase at the vernal equinox.
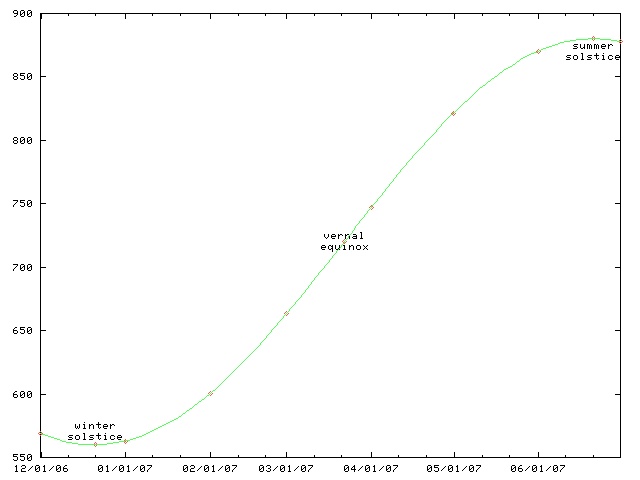
The day length is given by a sinusoid with amplitude that depends on your latitude (and also on the axial tilt of the Earth, which is a constant that we can disregard for this problem.) That is, it is a function of the form a + k sin 2πt/p, where a is the average day length (12 hours), k is the amplitude, p is the period, which is exactly one year, and t is amount of time since the vernal equinox. For Philadelphia, where I live, k is pretty close to 3 hours because the shortest day is about 3 hours shorter than average, and the longest day is about 3 hours longer than average. So we have:
day length = 12 hours + 3 hours · sin(2πt / 1 year)Now let's compute the rate of change on the equinox. The derivative of the day length function is:
rate of change = 3h · (2π / 1y) · cos(2πt / 1y)At the vernal equinox, t=0, and cos(…) = 1, so we have simply:
rate of change = 6πh / 1 year = 18.9 h / 365.25 daysThe numerator and the denominator match pretty well. If you're in a hurry, you might say "Well, 360 = 18·20, so 365.25 / 18.9 is probably about 20," and you would be right. If you're in slightly less of a hurry, you might say "Well, 361 = 192, so 365.25 / 18.9 is pretty close to 19, maybe around 19.2." Then you'd be even righter.
So the change in day length around the equinox (in Philadelphia) is around 1/20 or 1/19 of an hour per day—three minutes, in other words.
The exact answer, which I just looked up, is 2m38s. Not too bad. Most of the error came from my estimation of k as 3h. I guessed that the sun had been going down around 4:30, as indeed it had—it had been going down around 4:40, so the correct value is not 3h but only 2h40m. Had I used the correct k, my final result would have been within a couple of seconds of the right answer.
Exercise: The full moon appears about the same size as a U.S. quarter (1 inch diameter circle) held nine feet away (!) and also the same size as the sun, as demonstrated by solar eclipses. The moon is a quarter million miles away and the sun is 93 million miles away. What is the actual diameter of the sun?
[ Addendum 20120104: An earlier version of this article falsely claimed that the full moon appears the same size as a quarter held at arm's length. This was a momentary brain fart, not a calculational error. Thanks to Eric Roode for pointing out this mistake. ]
[Other articles in category /calendar] permanent link
Tue, 03 Jan 2012
Eta-reduction in Haskell and English
The other day Katara and I were putting together a model, and she asked
what a certain small green part was for. I said "It's a thing for
connecting a thing to another thing."
Katara objected that this was a completely unhelpful explanation, but I disagreed. I would have agreed that it was an excessively verbose explanation, but she didn't argue that point.
Later, it occurred to me that Haskell has a syntax for eliding unnecessary variables in cases like this. In Haskell, one can abbreviate the expression
λx → λy → x + y
to just (+). (Perl users may find it helpful to know that
the Perl equivalent of the expression above is sub { my ($x) = @_;
return sub { my ($y) = @_; return $x + $y } }.) This is an
example of a general transformation called η-reduction. In general, for
any function f, λx → f x is a
function that takes an argument x and returns f x. But
that's exactly what f does. So we can replace the longer
version with the shorter version, and that's η-reduction, or we can go the
other way, which is η-expansion.Anyway, once I thought of this it occurred to me that, just like the longer expression could be reduced to (+), my original explanation that the small green part was "a thing for connecting a thing to another thing" could be η-reduced to "a connector".
Perhaps if I had said that in the first place Katara would not have complained.
Happy new year, all readers.
[Other articles in category /lang] permanent link


