Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 68 |
| Book | 50 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 24 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 29 Apr 2024
Hawat! Hawat! Hawat! A million deaths are not enough for Hawat!
[ Content warning: Spoilers for Frank Herbert's novel Dune. Conversely none of this will make sense if you haven't read it. ]
Summary: Thufir Hawat is the real traitor. He set up Yueh to take the fall.
This blog post began when I wondered:
Hawat knows that Wellington Yueh has, or had a wife, Wanna. She isn't around. Hasn't he asked where she is?
In fact she is (or was) a prisoner of the Harkonnens and the key to Yueh's betrayal. If Hawat had asked the obvious question, he might have unraveled the whole plot.
But Hawat is a Mentat, and the Master of Assassins for a Great House. He doesn't make dumbass mistakes like forgetting to ask “what are the whereabouts of the long-absent wife of my boss's personal physician?”
The Harkonnens nearly succeed in killing Paul, by immuring an agent in the Atreides residence six weeks before Paul even moves in. Hawat is so humiliated by his failure to detect the agent hidden in the wall that he offers the Duke his resignation on the spot. This is not a guy who would have forgotten to investigate Yueh's family connections.
And that wall murder thing wasn't even the Harkonnens' real plan! It was just a distraction:
"We've arranged diversions at the Residency," Piter said. "There'll be an attempt on the life of the Atreides heir — an attempt which could succeed."
"Piter," the Baron rumbled, "you indicated —"
"I indicated accidents can happen," Piter said. "And the attempt must appear valid."
Piter de Vries was so sure that Hawat would find the agent in the wall, he was willing to risk spoiling everything just to try to distract Hawat from the real plan!
If Hawat was what he appeared to be, he would never have left open the question of Wanna's whereabouts. Where is she? Yueh claimed that she had been killed by the Harkonnens, and Jessica offers that as a reason that Yueh can be trusted.
But the Bene Gesserit have a saying: “Do not count a human dead until you've seen his body. And even then you can make a mistake.” The Mentats must have a similar saying. Wanna herself was Bene Gesserit, who are certainly human and notoriously difficult to kill. She was last known to be in the custody of the Harkonnens. Why didn't Hawat consider the possibility that Wanna might not be dead, but held hostage, perhaps to manipulate Duke Leto's physician and his heir's tutor — as in fact she was? Of course he did.
"Not to mention that his wife was a Bene Gesserit slain by the Harkonnens," Jessica said.
"So that’s what happened to her," Hawat said.
There's Hawat, pretending to be dumb.
Supposedly Hawat also trusted Yueh because he had received Imperial Conditioning, and as Piter says, “it's assumed that ultimate conditioning cannot be removed without killing the subject”. Hawat even says to Jessica: “He's conditioned by the High College. That I know for certain.”
Okay, and? Could it be that Thufir Hawat, Master of Assassins, didn't consider the possibility that the Imperial Conditioning could be broken or bent? Because Piter de Vries certainly did consider it, and he was correct. If Piter had plotted to subvert Imperial Conditioning to gain an advantage for his employer, surely Hawat would have considered the same.
Notice, also, what Hawat doesn't say to Jessica. He doesn't say that Yueh's Imperial Conditioning can be depended on, or that Yueh is trustworthy. Jessica does not have the gift of the full Truthsay, but it is safest to use the truth with her whenever possible. So Hawat misdirects Jessica by saying merely that he knows that Yueh has the Conditioning.
Yueh gave away many indications of his impending betrayal, which would have been apparent to Hawat. For example:
Paul read: […]
"Stop it!" Yueh barked.
Paul broke off, stared at him.
Yueh closed his eyes, fought to regain composure. […]
"Is something wrong?" Paul asked.
"I'm sorry," Yueh said. "That was … my … dead wife's favorite passage."
This is not subtle. Even Paul, partly trained, might well have detected Yueh's momentary hesitation before his lie about Wanna's death. Paul detects many more subtle signs in Yueh as well as in others:
"Will there be something on the Fremen?" Paul asked.
"The Fremen?" Yueh drummed his fingers on the table, caught Paul staring at the nervous motion, withdrew his hand.
Hawat the Mentat, trained for a lifetime in observing the minutiae of other people's behavior, and who saw Yueh daily, would surely have suspected something.
So, Hawat knew the Harkonnens’ plot: Wanna was their hostage, and they were hoping to subvert Yueh and turn him to treason. Hawat might already have known that the Imperial Conditioning was not a certain guarantee, but at the very least he could certainly see that the Harkonnens’ plan depended on subverting it. But he lets the betrayal go ahead. Why? What is Hawat's plan?
Look what he does after the attack on the Atreides. Is he killed in the attack, as so many others are? No, he survives and immediately runs off to work for House Harkonnen.
Hawat might have had difficulty finding a new job — “Say aren't you the Master of Assassins whose whole house was destroyed by their ancient enemies? Great, we'll be in touch if we need anyone fitting that description.” But Vladimir Harkonnen will be glad to have him, because he was planning to get rid of Piter and would soon need a new Mentat, as Hawat presumably knoew or guessed. And also, the Baron would enjoy having someone around to remind him of his victory over the Atreides, which Hawat also knows.
Here's another question: Where did Yueh get the tooth with the poison gas? The one that somehow wasn't detected by the Baron's poison snooper? The one that conveniently took Piter out of the picture? We aren't told. But surely this wasn't the sort of thing was left lying around the Ducal Residence for anyone to find. It is, however, just the sort of thing that the Master of Assassins of a Great House might be able to procure.
However he thought he came by the poison in the tooth, Yueh probably never guessed that its ultimate source was Hawat, who could have arranged that it was available at the right time.
This is how I think it went down:
The Emperor announces that House Atreides will be taking over the Arrakis fief from House Harkonnen. Everyone, including Hawat, sees that this is a trap. Hawat also foresees that the trap is likely to work: the Duke is too weak and Paul too young to escape it. Hawat must choose a side. He picks the side he thinks will win: the Harkonnens. With his assistance, their victory will be all but assured. He just has to arrange to be in the right place when the dust settles.
Piter wants Hawat to think that Jessica will betray the Duke. Very well, Hawat will pretend to be fooled. He tells the Atreides nothing, and does his best to turn the suspicions of Halleck and the others toward Jessica.
At the same time he turns the Harkonnens' plot to his advantage. Seeing it coming, he can avoid dying in the massacre. He provides Yueh with the chance to strike at the Baron and his close advisors. If Piter dies in the poison gas attack, as he does, his position will be ready for Hawat to fill; if not the position was going to be open soon anyway. Either way the Baron or his successor would be only too happy to have a replacement at hand.
(Hawat would probably have preferred that the Baron also be killed by the tooth, so that he could go to work for the impatient and naïve Feyd-Rautha instead of the devious old Baron. But it doesn't quite go his way.)
Having successfully made Yueh his patsy and set himself up to join the employ of the new masters of Arrakis and the spice, Hawat has some loose ends to tie up. Gurney Halleck has survived, and Jessica may also have survived. (“Do not count a human dead until you've seen his body.”) But Hawat is ready for this. Right from the beginning he has been assisting Piter in throwing suspicion on Jessica, with the idea that it will tend to prevent survivors of the massacre from reuniting under her leadership or Paul's. If Hawat is fortunate Gurney will kill Jessica, or vice versa, wrapping up another loose end.
Where Thufir Hawat goes, death and deceit follow.
Addendum
Maybe I should have mentioned that I have not read any of the sequels to Dune, so perhaps this is authoritatively contradicted — or confirmed in detail — in one of the many following books. I wouldn't know.
[Other articles in category /book] permanent link
Sun, 28 Apr 2024
Rod R. Blagojevich will you please go now?
I'm strangely fascinated and often amused by crooked politicians, and Rod Blagojevich was one of the most amusing.
In 2007 Barack Obama, then a senator of Illinois, resigned his office to run for United States President. Under Illinois law, the governor of Illinois was responsible for appointing Obama's replacement until the next election was held. The governor at the time was Rod Blagojevich, and Blagojevich had a fine idea: he would sell the Senate seat to the highest bidder. Yes, really.
Zina Saunders did this wonderful painting of Blago and has kindly given me permission to share it with you.

When the governor's innovation came to light, the Illinois state legislature ungratefully but nearly unanimously impeached him (the vote was 117–1) and removed him from office (59–0). He was later charged criminally, convicted, and sentenced to 168 months years in federal prison for this and other schemes. He served about 8 years before Donald Trump, no doubt admiring the initiative of a fellow entrepreneur, commuted his sentence.
Blagojevich was in the news again recently. When the legislature gave him the boot they also permanently disqualified him from holding any state office. But Blagojevich felt that the people of Illinois had been deprived for too long of his wise counsel. He filed suit in Federal District Court, seeking not only vindication of his own civil rights, but for the sake of the good citizens of Illinois:
Preventing the Plaintiff from running for state or local public office outweighs any harm that could be caused by denying to the voters their right to vote for or against him in a free election.
Allowing voters decide who to vote for or not to vote for is not adverse to the public interest. It is in the public interest.
…
The Plaintiff is seeking a declaratory judgement rendering the State Senate's disqualifying provision as null and void because it violates the First Amendment rights of the voters of Illinois.
This kind of thing is why I can't help but be amused by crooked politicians. They're so joyful and so shameless, like innocent little children playing in a garden.
Blagojevich's lawsuit was never going to go anywhere, for so many reasons. Just the first three that come to mind:
Federal courts don't have a say over Illinois' state affairs. They deal in federal law, not in matters of who is or isn't qualified to hold state office in Illinois.
Blagojevich complained that his impeachment violated his Sixth Amendment right to Due Process. But the Sixth Amendment applies to criminal prosecutions and impeachments aren't criminal prosecutions.
You can't sue to enforce someone else's civil rights. They have to bring the suit themselves. Suing on behalf of the people of a state is not a thing.
Well anyway, the judge, Steven C. Seeger, was even less impressed than I was. Federal judges do not normally write “you are a stupid asshole, shut the fuck up,” in their opinions, and Judge Seeger did not either. But he did write:
He’s back.
and
[Blagojevich] adds that the “people’s right to vote is a fundamental right.” And by that, Blagojevich apparently means the fundamental right to vote for him.
and
The complaint is riddled with problems. If the problems are fish in a barrel, the complaint contains an entire school of tuna. It is a target-rich environment.
and
In its 205-year history, the Illinois General Assembly has impeached, convicted, and removed one public official: Blagojevich.
and
The impeachment and removal by the Illinois General Assembly is not the only barrier keeping Blagojevich off the ballot. Under Illinois law, a convicted felon cannot hold public office.
Federal judges don't get to write “sit down and shut up”. But Judge Seeger came as close as I have ever seen when he quoted from Marvin K. Mooney Will you Please Go Now!:
“The time has come. The time has come. The time is now. Just Go. Go. GO! I don’t care how. You can go by foot. You can go by cow. Marvin K. Mooney, will you please go now!”

[Other articles in category /politics] permanent link
Tue, 23 Apr 2024
Well, I guess I believe everything now!
The principle of explosion is that in an inconsistent system everything is provable: if you prove both !!P!! and not-!!P!! for any !!P!!, you can then conclude !!Q!! for any !!Q!!:
$$(P \land \lnot P) \to Q.$$
This is, to put it briefly, not intuitive. But it is awfully hard to get rid of because it appears to follow immediately from two principles that are intuitive:
If we can prove that !!A!! is true, then we can prove that at least one of !!A!! or !!B!! is true. (In symbols, !!A\to(A\lor B)!!.)
If we can prove that at least one of !!A!! or !!B!! is true, and we can prove that !!A!! is false, then we may conclude that that !!B!! is true. (Symbolically, !!(A\lor B) \to (\lnot A\to B)!!.).
Then suppose that we have proved that !!P!! is both true and false. Since we have proved !!P!! true, we have proved that at least one of !!P!! or !!Q!! is true. But because we have also proved that !!P!! is false, we may conclude that !!Q!! is true. Q.E.D.
This proof is as simple as can be. If you want to get rid of this, you have a hard road ahead of you. You have to follow Graham Priest into the wilderness of paraconsistent logic.
Raymond Smullyan observes that although logic is supposed to model ordinary reasoning, it really falls down here. Nobody, on discovering the fact that they hold contradictory beliefs, or even a false one, concludes that therefore they must believe everything. In fact, says Smullyan, almost everyone does hold contradictory beliefs. His argument goes like this:
Consider all the things I believe individually, !!B_1, B_2, \ldots!!. I believe each of these, considered separately, is true.
However, I also believe that I'm not infallible, and that at least one of !!B_1, B_2, \ldots!! is false, although I don't know which ones.
Therefore I believe both !!\bigwedge B_i!! (because I believe each of the !!B_i!! separately) and !!\lnot\bigwedge B_i!! (because I believe that not all the !!B_i!! are true).
And therefore, by the principle of explosion, I ought to believe that I believe absolutely everything.
Well anyway, none of that was exactly what I planned to write about. I was pleased because I noticed a very simple, specific example of something I believed that was clearly inconsistent. Today I learned that K2, the second-highest mountain in the world, is in Asia, near the border of Pakistan and westernmost China. I was surprised by this, because I had thought that K2 was in Kenya somewhere.
But I also knew that the highest mountain in Africa was Kilimanjaro. So my simultaneous beliefs were flatly contradictory:
- K2 is the second-highest mountain in the world.
- Kilimanjaro is not the highest mountain in the world, but it is the highest mountain in Africa
- K2 is in Africa
Well, I guess until this morning I must have believed everything!
[Other articles in category /math/logic] permanent link
I've just learned that Oddbins, a British chain of discount wine and liquor stores, went out of business last year. I was in an Oddbins exactly once, but I feel warmly toward them and I was sorry to hear of their passing.
In February of 2001 I went into the Oddbins on Canary Wharf and asked for bourbon. I wasn't sure whether they would even sell it. But they did, and the counter guy recommended I buy Woodford Reserve. I had not heard of Woodford before but I took his advice, and it immediately became my favorite bourbon. It still is.
I don't know why I was trying to buy bourbon in London. Possibly it was pure jingoism. If so, the Oddbins guy showed me up.
Thank you, Oddbins guy.
[Other articles in category /food] permanent link
Mon, 22 Apr 2024
Talking Dog > Stochastic Parrot
I've recently needed to explain to nontechnical people, such as my chiropractor, why the recent ⸢AI⸣ hype is mostly hype and not actual intelligence. I think I've found the magic phrase that communicates the most understanding in the fewest words: talking dog.
These systems are like a talking dog. It's amazing that anyone could train a dog to talk, and even more amazing that it can talk so well. But you mustn't believe anything it says about chiropractics, because it's just a dog and it doesn't know anything about medicine, or anatomy, or anything else.
For example, the lawyers in Mata v. Avianca got in a lot of trouble when they took ChatGPT's legal analysis, including its citations to fictitious precendents, and submitted them to the court.
“Is Varghese a real case,” he typed, according to a copy of the exchange that he submitted to the judge.
“Yes,” the chatbot replied, offering a citation and adding that it “is a real case.”
Mr. Schwartz dug deeper.
“What is your source,” he wrote, according to the filing.
“I apologize for the confusion earlier,” ChatGPT responded, offering a legal citation.
“Are the other cases you provided fake,” Mr. Schwartz asked.
ChatGPT responded, “No, the other cases I provided are real and can be found in reputable legal databases.”
It might have saved this guy some suffering if someone had explained to him that he was talking to a dog.
The phrase “stochastic parrot” has been offered in the past. This is completely useless, not least because of the ostentatious word “stochastic”. I'm not averse to using obscure words, but as far as I can tell there's never any reason to prefer “stochastic” to “random”.
I do kinda wonder: is there a topic on which GPT can be trusted, a non-canine analog of butthole sniffing?
Addendum
I did not make up the talking dog idea myself; I got it from someone else. I don't remember who.
[Other articles in category /tech/gpt] permanent link
Mon, 15 Apr 2024I thought about this because of yesterday's article about the person who needed to count the 3-colorings of an icosahedron, but didn't try constructing any to see what they were like.
Around 2015 Katara, then age 11, saw me writing up my long series of articles about the Cosmic Call message and asked me to explain what the mysterious symbols meant. (It's intended to be a message that space aliens can figure out even though they haven't met us.)

I said “I bet you could figure it out if you tried.” She didn't believe me and she didn't want to try. It seemed insurmountable.
“Okay,” I said, handing her a printed copy of page 1. “Sit on the chaise there and just look at it for five minutes without talking or asking any questions, while I work on this. Then I promise I'll explain everything.”
She figured it out in way less than five minutes. She was thrilled to discover that she could do it.
I think she learned something important that day: A person can accomplish a lot with a few minutes of uninterrupted silent thinking, perhaps more than they imagine, and certainly a lot more than if they don't try.
I think there's a passage somewhere in Zen and the Art of Motorcycle Maintenance about how, when you don't know what to do next, you should just sit with your mouth shut for a couple of minutes and see if any ideas come nibbling. Sometimes they don't. But if there are any swimming around, you won't catch them unless you're waiting for them.
[Other articles in category /misc] permanent link
Sun, 14 Apr 2024
Stuff that is and isn't backwards in Australia
I recently wrote about things that are backwards in Australia. I made this controversial claim:
The sun in the Southern Hemisphere moves counterclockwise across the sky over the course of the day, rather than clockwise. Instead of coming up on the left and going down on the right, as it does in the Northern Hemisphere, it comes up on the right and goes down on the left.
Many people found this confusing and I'm not sure our minds met on this. I am going to try to explain and see if I can clear up the puzzles.
“Which way are you facing?” was a frequent question. “If you're facing north, it comes up on the right, not the left.”
(To prevent endless parenthetical “(in the Northern Hemisphere)” qualifications, the rest of this article will describe how things look where I live, in the northern temperate zones. I understand that things will be reversed in the Southern Hemisphere, and quite different near the equator and the poles.)
Here's what I think the sky looks like most of the day on most of the days of the year:
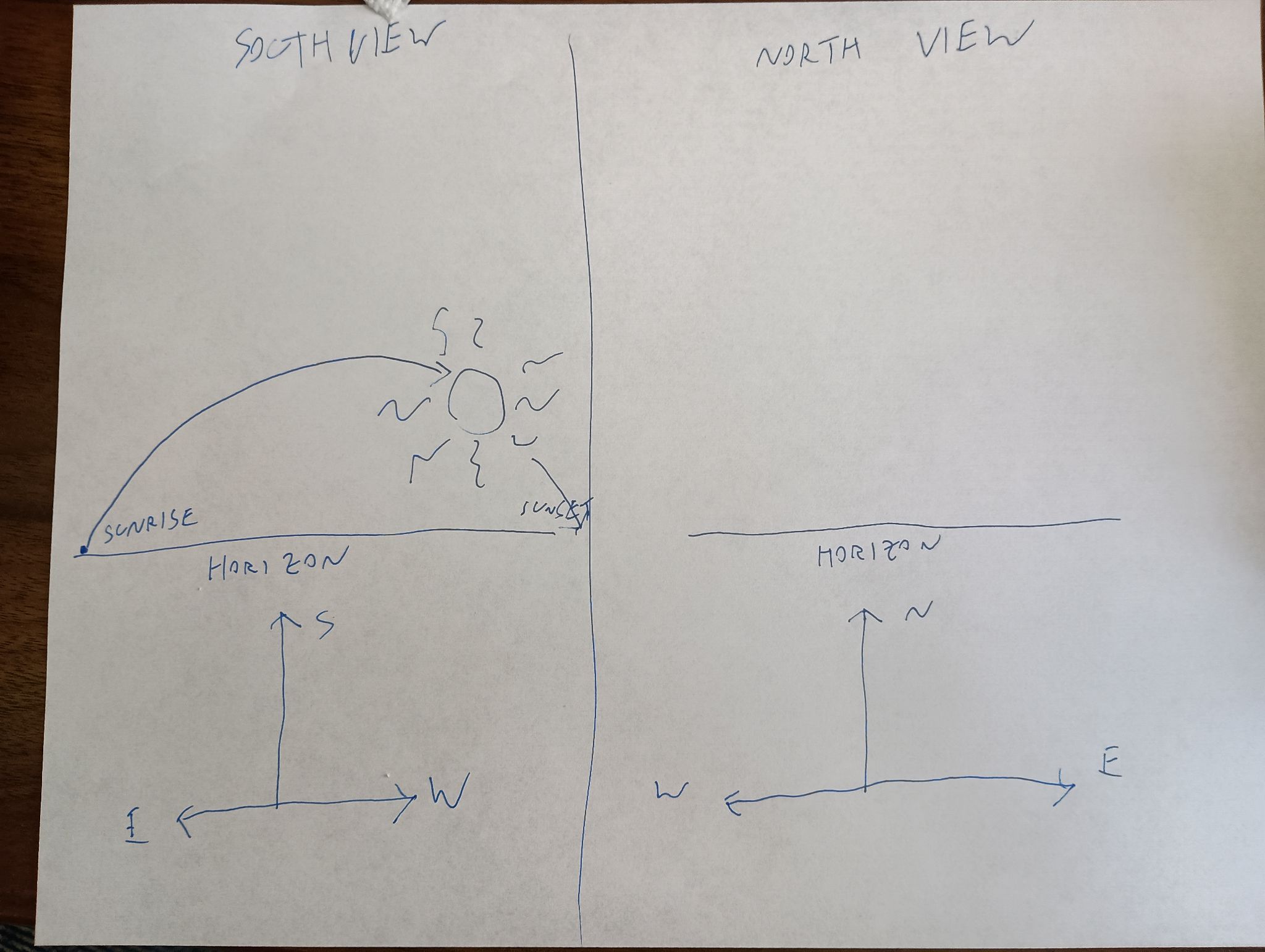
The sun is in the southern sky through the entire autumn, winter, and spring. In summer it is sometimes north of the celestial equator, for up to a couple of hours after sunrise and before sunset, but it is still in the southern sky most of the time. If you are watching the sun's path through the sky, you are looking south, not north, because if you are looking north you do not see the sun, it is behind you.
Some people even tried to argue that if you face north, the sun's path is a counterclockwise circle, rather than a clockwise one. This is risible. Here's my grandfather's old grandfather clock. Notice that the hands go counterclockwise! You study the clock and disagree. They don't go counterclockwise, you say, they go clockwise, just like on every other clock. Aha, but no, I say! If you were standing behind the clock, looking into it with the back door open, then you would clearly see the hands go counterclockwise! Then you kick me in the shin, as I deserve.
Yes, if you were to face away from the sun, its path could be said to be counterclockwise, if you could see it. But that is not how we describe things. If I say that a train passed left to right, you would not normally expect me to add “but it would have been right to left, had I been facing the tracks”.
At least one person said they had imagined the sun rising directly ahead, then passing overhead, and going down in back. Okay, fair enough. You don't say that the train passed left to right if you were standing on the tracks and it ran you down.
Except that the sun does not pass directly overhead. It only does that in the tropics. If this person were really facing the sun as it rose, and stayed facing that way, the sun would go up toward their right side. If it were a train, the train tracks would go in a big curve around their right (south) side, from left to right:
Mixed gauge track (950 and 1435mm) at Sassari station, Sardinia, 1996 by user Afterbrunel, CC BY-SA 3.0 DEED, via Wikimedia Commons. I added the big green arrows.
After the train passed, it would go back the other way, but they wouldn't be able see it, because it would be behind them. If they turned around to watch it go, it would still go left to right:
And if they were to turn to follow it over the course of the day, they would be turning left to right the whole time, and the sun would be moving from left to right the whole time, going up on the left and coming down on the right, like the hands of a clock — “clockwise”, as it were.
One correspondent suggested that perhaps many people in technologically advanced countries are not actually familiar with how the sun and moon move, and this was the cause of some of the confusion. Perhaps so, it's certainly tempting to dismiss my critics as not knowing how the sun behaves. The other possibility is that I am utterly confused. I took Observational Astronomy in college twice, and failed both times.
Anyway, I will maybe admit that “left to right” was unclear. But I will not recant my claim that the sun moves clockwise. E pur si muove in senso orario.
Sundials
Here I was just dead wrong. I said:
In the Northern Hemisphere, the shadow of a sundial proceeds clockwise, from left to right.
Absolutely not, none of this is correct. First, “left to right”. Here's a diagram of a typical sundial:
It has a sticky-up thing called a ‘gnomon’ that casts a shadow across the numbers, and the shadow moves from left to right over the course of the day. But obviously the sundial will work just as well if you walk around and look at it from the other side:
It still goes clockwise, but now clockwise is right to left instead of left to right.
It's hard to read because the numerals are upside down? Fine, whatever:
Here, unlike with the sun, “go around to the other side” is perfectly reasonable.
Talking with Joe Ardent, I realized that not even “clockwise” is required for sundials. Imagine the south-facing wall of a building, with the gnomon sticking out of it perpendicular. When the sun passes overhead, the gnomon will cast a shadow downwards on the wall, and the downward-pointing shadow will move from left to right — counterclockwise — as the sun makes its way from east to west. It's not even far-fetched. Indeed, a search for “vertical sundials” produced numerous examples:

Sundial on the Moot Hall by David Dixon, CC BY 2.0 https://creativecommons.org/licenses/by/2.0, via Wikimedia Commons and Geograph.
Winter weather on July 4
Finally, it was reported that there were complaints on Hacker News that Australians do not celebrate July 4th. Ridiculous! All patriotic Americans celebrate July 4th.
[Other articles in category /geo] permanent link
Sat, 13 Apr 2024
3-coloring the vertices of an icosahedron
I don't know that I have a point about this, other than that it makes me sad.
A recent Math SE post (since deleted) asked:
How many different ways are there to color the vertices of the icosahedron with 3 colors such that no two adjacent vertices have the same color?
I would love to know what was going on here. Is this homework? Just someone idly wondering?
Because the interesting thing about this question is (assuming that the person knows what an icosahedron is, etc.) it should be solvable in sixty seconds by anyone who makes the least effort. If you don't already see it, you should try. Try what? Just take an icosahedron, color the vertices a little, see what happens. Here, I'll help you out, here's a view of part of the end of an icosahedron, although I left out most of it. Try to color it with 3 colors so that no two adjacent vertices have the same color, surely that will be no harder than coloring the whole icosahedron.
The explanation below is a little belabored, it's what OP would have discovered in seconds if they had actually tried the exercise.
Let's color the middle vertex, say blue.
The five vertices around the edge can't be blue, they must be the other two colors, say red and green, and the two colors must alternate:
Ooops, there's no color left for the fifth vertex.
The phrasing of the question, “how many” makes the problem sound harder than it is: the answer is zero because we can't even color half the icosahedron.
If OP had even tried, even a little bit, they could have discovered this. They didn't need to have had the bright idea of looking at a a partial icosahedron. They could have grabbed one of the pictures from Wikipedia and started coloring the vertices. They would have gotten stuck the same way. They didn't have to try starting in the middle of my diagram, starting at the edge works too: if the top vertex is blue, the three below it must be green-red-green, and then the bottom two are forced to be blue, which isn't allowed. If you just try it, you win immediately. The only way to lose is not to play.
Before the post was deleted I suggested in a comment “Give it a try, see what happens”. I genuinely hoped this might be helpful. I'll probably never know if it was.
Like I said, I would love to know what was going on here. I think maybe this person could have used a dose of Lower Mathematics.
Just now I wondered for the first time: what would it look like if I were to try to list the principles of Lower Mathematics? “Try it and see” is definitely in the list.
Then I thought: How To Solve It has that sort of list and something like “try it and see” is probably on it. So I took it off the shelf and found: “Draw a figure”, “If you cannot solve the proposed problem”, “Is it possible to satisfy the condition?”. I didn't find anything called “fuck around with it and see what you learn” but it is probably in there under a different name, I haven't read the book in a long time. To this important principle I would like to add “fuck around with it and maybe you will stumble across the answer by accident” as happened here.
Mathematics education is too much method, not enough heuristic.
[Other articles in category /math] permanent link
Sun, 31 Mar 2024
Stuff that is backwards in Australia
I thought at first was going to be kind of a dumb article, because it was just going to be a list of banal stuff like:
- When it's day here, it's night there, and vice versa
but a couple of years back I was rather startled to realize that in the Southern Hemisphere the sun comes up on the right and goes counterclockwise through the sky instead of coming up on the left and going clockwise as I have seen it do all my life, and that was pretty interesting.
Then more recently I was thinking about it more carefully and I was stunned when I realized that the phases of the moon go the other way. So I thought I'd should actually make the list, because a good deal of it is not at all obvious. Or at least it wasn't to me!
When it's day here, it's night there, and vice versa. (This isn't a Southern Hemisphere thing, it's an Eastern Hemisphere thing.)
When it's summer here, it's winter there, and vice versa. Australians celebrate Christmas by going to the beach, and July 4th with sledding and patriotic snowball fights.
Australia's warmer zones are in the north, not the south. Their birds fly north for the winter. But winter is in July, so the reversals cancel out and birds everywhere fly south in September and October, and north in March and April, even though birds can't read.
The sun in the Southern Hemisphere moves counterclockwise across the sky over the course of the day, rather than clockwise. Instead of coming up on the left and going down on the right, as it does in the Northern Hemisphere, it comes up on the right and goes down on the left.
In the Northern Hemisphere, the shadow of a sundial proceeds clockwise, from left to right. (This is the reason clock hands also go clockwise: for backward compatibility with sundials.) But in the Southern Hemisphere, the shadow on a sundial goes counterclockwise.
In the Southern Hemisphere, the designs on the moon appear upside-down compared with how they look in the Northern Hemisphere. Here's a picture of the full moon as seen from the Northern Hemisphere. The big crater with the bright rays that is prominent in the bottom half of the picture is Tycho.

In the Southern Hemisphere the moon looks like this, with Tycho on top:

Australians see the moon upside-down because their heads are literally pointing in the opposite direction.
For the same reason, the Moon's phases in the Southern Hemisphere sweep from left to right instead of from right to left. In the Northern Hemisphere they go like this as the month passes from new to full:





And then in the same direction from full back to new:





But in the Southern Hemisphere the moon changes from left to right instead:




And then:





Unicode U+263D and U+263E are called
FIRST QUARTER MOON☽ andLAST QUARTER MOON☾ , respectively, and are depicted Northern Hemisphere style. (In the Southern Hemisphere, ☽ appears during the last quarter of the month, not the first.) Similarly the emoji U+1F311 through U+1F318, 🌑🌒🌓🌔🌕🌖🌗🌘 are depicted in Northern Hemisphere order, and have Northern Hemisphere descriptions like “🌒 waxing crescent moon”. In the Southern Hemisphere, 🌒 is actually a waning crescent.In the Northern Hemisphere a Foucault pendulum will knock down the pins in clockwise order, as shown in the picture. (This one happens to be in Barcelona.) A Southern Hemisphere Foucault pendulum will knock them down in counterclockwise order, because the Earth is turning the other way, as viewed from the fulcrum of the pendulum.

Northern Hemisphere tornadoes always rotate counterclockwise. Southern Hemisphere tornadoes always rotate clockwise.
Dishonorable mention
As far as I know the thing about water going down the drain in one direction or the other is not actually true.
Addendum 20240414
Several people took issue with some of the claims in this article, and the part about sundials was completely wrong. I wrote a followup.
[Other articles in category /geo] permanent link
Fri, 08 Mar 2024This week I read on Tumblr somewhere this intriguing observation:
how come whenever someone gets a silver bullet to kill a werewolf or whatever the shell is silver too. Do they know that part gets ejected or is it some kind of scam
Quite so! Unless you're hunting werewolves with a muzzle-loaded rifle or a blunderbuss or something like that. Which sounds like a very bad idea.
Once you have the silver bullets, presumably you would then make them into cartidge ammunition using a standard ammunition press. And I'd think you would use standard brass casings. Silver would be expensive and pointless, and where would you get them? The silver bullets themselves are much easier. You can make them with an ordinary bullet mold, also available at Wal-Mart.
Anyway it seems to me that a much better approach, if you had enough silver, would be to use a shotgun and manufacture your own shotgun shells with silver shot. When you're attacked by a werewolf you don't want to be fussing around trying to aim for the head. You'd need more silver, but not too much more.
I think people who make their own shotgun shells usually buy their shot in bags instead of making it themselves. A while back I mentioned a low-tech way of making shot:
But why build a tower? … You melt up a cauldron of lead at the top, then dump it through a copper sieve and let it fall into a tub of water at the bottom. On the way down, the molten lead turns into round shot.
That's for 18th-century round bullets or maybe small cannonballs. For shotgun shot it seems very feasible. You wouldn't need a tower, you could do it in your garage. (Pause while I do some Internet research…) It seems the current technique is a little different: you let the molten lead drip through a die with a small hole.
Wikipedia has an article on silver bullets but no mention of silver shotgun pellets.
Addendum
I googled the original Tumblr post and found that it goes on very amusingly:
catch me in the woods the next morning with a metal detector gathering up casings to melt down and sell to more dumb fuck city shits next month
[Other articles in category /tech] permanent link
Wed, 06 Mar 2024
Optimal boxes with and without lids
Sometime around 1986 or so I considered the question of the dimensions that a closed cuboidal box must have to enclose a given volume but use as little material as possible. (That is, if its surface area should be minimized.) It is an elementary calculus exercise and it is unsurprising that the optimal shape is a cube.
Then I wondered: what if the box is open at the top, so that it has only five faces instead of six? What are the optimal dimensions then?
I did the calculus, and it turned out that the optimal lidless box has a square base like the cube, but it should be exactly half as tall.
For example the optimal box-with-lid enclosing a cubic meter is a 1×1×1 cube with a surface area of !!6!!.
Obviously if you just cut off the lid of the cubical box and throw it away you have a one-cubic-meter lidless box with a surface area of !!5!!. But the optimal box-without-lid enclosing a cubic meter is shorter, with a larger base. It has dimensions $$2^{1/3} \cdot 2^{1/3} \cdot \frac{2^{1/3}}2$$
and a total surface area of only !!3\cdot2^{2/3} \approx 4.76!!. It is what you would get if you took an optimal complete box, a cube, that enclosed two cubic meters, cut it in half, and threw the top half away.
I found it striking that the optimal lidless box was the same proportions as the optimal complete box, except half as tall. I asked Joe Keane if he could think of any reason why that should be obviously true, without requiring any calculus or computation. “Yes,” he said. I left it at that, imagining that at some point I would consider it at greater length and find the quick argument myself.
Then I forgot about it for a while.
Last week I remembered again and decided it was time to consider it at greater length and find the quick argument myself. Here's the explanation.
Take the cube and saw it into two equal halves. Each of these is a lidless five-sided box like the one we are trying to construct. The original cube enclosed a certain volume with the minimum possible material. The two half-cubes each enclose half the volume with half the material.
If there were a way to do better than that, you would be able to make a lidless box enclose half the volume with less than half the material. Then you could take two of those and glue them back together to get a complete box that enclosed the original volume with less than the original amount of material. But we already knew that the cube was optimal, so that is impossible.
[Other articles in category /math] permanent link
Mon, 04 Mar 2024
Children and adults see in very different ways
I was often struck with this thought when my kids were smaller. We would be looking at some object, let's say a bollard.
The kid sees the actual bollard, as it actually appears, and in detail! She sees its shape and texture, how the paint is chipped and mildewed, whether it is straight or crooked.
I don't usually see any of those things. I see the bollard abstractly, more as an idea of a “bollard” than as an actual physical object. But instead I see what it is for, and what it is made of, and how it was made and why, and by whom, all sorts of things that are completely invisible to the child.
The kid might mention that someone was standing by the crooked bollard, and I'd be mystified. I wouldn't have realized there was a crooked bollard. If I imagined the bollards in my head, I would have imagined them all straight and identical. But kids notice stuff like that.
Instead, I might have mentioned that someone was standing by the new bollard, because I remembered a couple of years back when one of them was falling apart and Rich demolished it and put in a new one. The kid can't see any of that stuff.
[Other articles in category /kids] permanent link












