Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2026: | J |
| 2025: | JFMAMJ |
| JASOND | |
| 2024: | JFMAMJ |
| JASOND | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 245 |
| Programming | 100 |
| Language | 95 |
| Miscellaneous | 75 |
| Book | 50 |
| Tech | 49 |
| Etymology | 35 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 25 |
| Law | 22 |
| Physics | 21 |
| Perl | 17 |
| Biology | 16 |
| Brain | 15 |
| Calendar | 15 |
| Food | 15 |
Comments disabled
Wed, 13 Sep 2006
More about automorphisms
In a recent article, I asserted
that "there aren't even any reasonable [automorphisms of R]
that preserve addition.". This is patently untrue.
My proof started by referring to a previous result that any such automorphism f must have f(1) = 1. But actually, I had only proved this for automorphisms that must preserve multiplication. For automorphisms that preserve addition only, f(1) need not be 1; it can be anything. In fact, x → kx is an automorphism of R for all k except zero. It is not hard to show, following the technique in the earlier article, that every continuous automorphism has this form.
In hopes of salvaging something from my embarrassing error, I thought I'd spend a little time talking about the other automorphisms of R, the ones that aren't "reasonable". They are unreasonable in at least two ways: they are everywhere discontinuous, and they cannot be exhibited explicitly.
To manufacture the function, we first need a mathematical horror called a Hamel basis. A Hamel basis is a set of real numbers Hα such that every real number r has a unique representation in the form:
$$r = \sum_{i=1}^n q_i H_{\alpha_i}$$
where all the qi are rational. (It is called a Hamel basis because it makes the real numbers into a vector space over the rationals. If this explanation makes no sense to you, please ignore it.)The sum here is finite, so only a finite number of the uncountably many Hα are involved for any particular r; this is what characterizes it as a Hamel basis.
Leaving aside the proof that the Hamel basis exists at all, if we suppose we have one, we can easily construct an automorphism of R. Just pick some rational numbers mα, one for each Hα. Then if as above, we have:
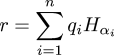
$$f(r) = \sum_{i=1}^n q_i H_{\alpha_i}m_{\alpha_i}$$
At this point I should probably prove that this is an automorphism. But it seems unwise, because I think that in the unlikely case that you have understood everything so far, you will find the statement that this is an automorphism both clear and obvious, and will be able to imagine the proof yourself, and for me to spell it out will only confuse the issue. And I think that if you have not understood everything so far, the proof will not help. So I should probably just say "clearly, this is an automorphism" and move on.
But against my better judgement, I'll give it a try. Let r and s be real numbers. We want to show that f(s) + f(r) = f(s + r). Represent r and s using the Hamel basis. For each element H of the Hamel basis, let's say that cH(r) is the (rational) coefficient of H in the representation of r. That is, it's the qi in the definition above.
By a simple argument involving commutativity and associativity of addition, cH(r+s) = cH(r) + cH(s) for all r, s, and H.
Also, cH(f(r)) = m·cH(r), for all r and H, where m is the multiplier we chose for H back when we were making up the automorphism, because that's how we defined f.
Then cH(f(r+s)) = m·cH(r+s) = m·(cH(r) + cH(s)) = m·cH(r) + m·cH(s) = cH(f(r)) + cH(f(s)) = cH(f(r) + f(s)), for all H.
This means that f(r+s) and f(r) + f(s) have the same Hamel basis representation. They are therefore the same number. This is what we wanted to show.
If anyone actually found that in the least enlightening, I would be really interested to hear about it.
One property of a Hamel basis is that exactly one of its uncountably many elements is rational. Say it's H0. Then every rational number q is represented as q = (q/H0)·H0. Then f(q) = (q/H0)·H0m0 = m0q for all rational numbers q. But in general, an irrational number x will not have f(x) = m0x, so the automorphism is discontinuous everywhere, unless all the mα are equal, in which case it's just x → mx again.
The problem with this construction is that it is completely abstract. Nobody can exhibit an example of a Hamel basis, being, as it is, an uncountably infinite set of mainly irrational numbers. So the discontinuous automorphisms constructed here are among the most utterly useless of all mathematical examples.
I think that is the full story about additive automorphisms of R. I hope I got everything right this time.
I should add, by the way, that there seems to be some disagreement about what is called a Hamel basis. Some people say it is what I said: a basis for the reals over the rationals, with the properties I outlined above. However, some people, when you say this, will sniff, adjust their pocket protectors, and and correct you, saying that that a Hamel basis is any basis for any vector space, as long as it has the analogous property that each vector is representable as a combination of a finite subset of the basis elements. Some say one, some the other. I have taken the definition that was convenient for the exposition of this article.
[ Thanks to James Wetterau for pointing out the error in the earlier article. ]
[ Previous articles in this series: Part 1 Part 2 Part 3 Part 4 ]
[Other articles in category /math] permanent link


