Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Thu, 23 Feb 2017
Miscellaneous notes on anagram scoring
My article on finding the best anagram in English was well-received, and I got a number of interesting comments about it.
A couple of people pointed out that this does nothing to address the issue of multiple-word anagrams. For example it will not discover “I, rearrangement servant / Internet anagram server” True, that is a different problem entirely.
Markian Gooley informed me that “megachiropteran / cinematographer” has been long known to Scrabble players, and Ben Zimmer pointed out that A. Ross Eckler, unimpressed by “cholecystoduodenostomy / duodenocholecystostomy”, proposed a method almost identical to mine for scoring anagrams in an article in Word Ways in 1976. M. Eckler also mentioned that the “remarkable” “megachiropteran / cinematographer” had been published in 1927 and that “enumeration / mountaineer” (which I also selected as a good example) appeared in the Saturday Evening Post in 1879!
The Hacker News comments were unusually pleasant and interesting. Several people asked “why didn't you just use the Levenshtein distance”? I don't remember that it ever occured to me, but if it had I would have rejected it right away as being obviously the wrong thing. Remember that my original chunking idea was motivated by the observation that “cholecystoduodenostomy / duodenocholecystostomy” was long but of low quality. Levenshtein distance measures how far every letter has to travel to get to its new place and it seems clear that this would give “cholecystoduodenostomy / duodenocholecystostomy” a high score because most of the letters move a long way.
Hacker News user
tyingqtried it anyway, and reported that it produced a poor outcome. The top-scoring pair by Levenshtein distance is “anatomicophysiologic physiologicoanatomic”, which under the chunking method gets a score of 3. Repeat offender “cholecystoduodenostomy / duodenocholecystostomy” only drops to fourth place.A better idea seems to be Levenshtein score per unit of length, suggested by lobste.rs user
cooler_ranch.A couple of people complained about my “notaries / senorita” example, rightly observing that “senorita” is properly spelled “señorita”. This bothered me also while I was writing the article. I eventually decided although “notaries” and “señorita” are certainly not anagrams in Spanish (even supposing that “notaries” was a Spanish word, which it isn't) that the spelling of “senorita” without the tilde is a correct alternative in English. (Although I found out later that both the Big Dictionary and American Heritage seem to require the tilde.)
Hacker News user
ggambettaobserved that while ‘é’ and ‘e’, and ‘ó’ and ‘o’ feel interchangeable in Spanish, ‘ñ’ and ‘n’ do not. I think this is right. The ‘é’ is an ‘e’, but with a mark on it to show you where the stress is in the word. An ‘ñ’ is not like this. It was originally an abbreviation for ‘nn’, introduced in the 18th century. So I thought it might make sense to allow ‘ñ’ to be exchanged for ‘nn’, at least in some cases.(An analogous situation in German, which may be more familiar, is that it might be reasonable to treat ‘ö’ and ‘ü’ as if they were ‘oe’ and ‘ue’. Also note that in former times, “w” and “uu” were considered interchangeable in English anagrams.)
Unfortunately my Spanish dictionary is small (7,000 words) and of poor quality and I did not find any anagrams of “señorita”. I wish I had something better for you. Also, “señorita” is not one of the cases where it is appropriate to replace “ñ” with “nn”, since it was never spelled “sennorita”.
I wonder why sometimes this sort of complaint seems to me like useless nitpicking, and other times it seems like a serious problem worthy of serious consideration. I will try to think about this.
Mike Morton, who goes by the anagrammatic nickname of “Mr. Machine Tool”, referred me to his Higgledy-piggledy about megachiropteran / cinematographer, which is worth reading.
Regarding the maximum independent set algorithm I described yesterday, Shreevatsa R. suggested that it might be conceptually simpler to find the maximum clique in the complement graph. I'm not sure this helps, because the complement graph has a lot more edges than the original. Below right is the complement graph for “acrididae / cidaridae”. I don't think I can pick out the 4-cliques in that graph any more than the independent sets in the graph on the lower-left, and this is an unusually favorable example case for the clique version, because the original graph has an unusually large number of edges.
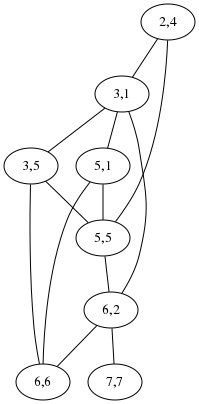
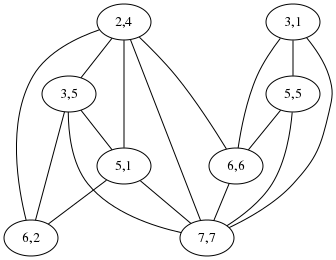
But perhaps the cliques might be easier to see if you know what to look for: in the right-hand diagram the four nodes on the left are one clique, and the four on the right are the other, whereas in the left-hand diagram the two independent sets are all mixed together.
An earlier version of the original article mentioned the putative 11-pointer “endometritria / intermediator”. The word “endometritria” seemed pretty strange, and I did look into it before I published the article, but not carefully enough. When Philip Cohen wrote to me to question it, I investigated more carefully, and discovered that it had been an error in an early WordNet release, corrected (to “endometria”) in version 1.6. I didn't remember that I had used WordNet's word lists, but I am not surprised to discover that I did.
A rare printing of Webster's 2¾th American International Lexican includes the word “endometritriostomoscopiotomous” but I suspect that it may be a misprint.
Philippe Bruhat wrote to inform me of Alain Chevrier’s book notes / sténo, a collection of thematically related anagrams in French. The full text is available online.
Alexandre Muñiz, who has a really delightful blog, and who makes and sells attractive and clever puzzles of his own invention. pointed out that soapstone teaspoons are available. The perfect gift for the anagram-lover in your life! They are not even expensive.
Thanks also to Clinton Weir, Simon Tatham, Jon Reeves, Wei-Hwa Huang, and Philip Cohen for their emails about this.
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
Tue, 21 Feb 2017
Moore's law beats a better algorithm
Yesterday I wrote about the project I did in the early 1990s to find the best anagrams. The idea is to give pair of anagram words a score, which is the number of chunks into which you have to divide one word in order to rearrange the chunks to form the other word. This was motivated by the observation that while “cholecysto-duodeno-stomy” and “duodeno-cholecysto-stomy” are very long words that are anagrams of one another, they are not interesting because they require so few chunks that the anagram is obvious. A shorter but much more interesting example is “aspired / diapers”, where the letters get all mixed up.
I wrote:
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search.
I wrote about the brute-force search yesterday. Today I am going to discuss the clever algorithm. (The paper is Avraham Goldstein, Petr Kolman, Jie Zheng “Minimum Common String Partition Problem: Hardness and Approximations”, The Electronic Journal of Combinatorics, 12 (2005).)
The plan is to convert a pair of anagrams into a graph that expresses
the constraints on how the letters can move around when one turns into
the other. Shown below is the graph for comparing
acrididae (grasshoppers)
with cidaridae (sea
urchins):
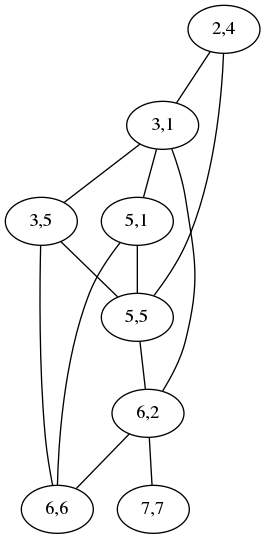
The “2,4” node at the top means that the letters ri at position
2 in acrididae match the letters ri at position 4 in cidaridae;
the “3,1” node is for the match between the first id and the first
id. The two nodes are connected by an edge to show that the two
matchings are incompatible: if you map the ri to the ri, you
cannot also map the first id to the first id; instead you have to
map the first id to the second one, represented by the node “3,5”,
which is not connected to “2,4”. A maximum independent set in this
graph is a maximum selection of compatible matchings in the words,
which corresponds to a division into the minimum number of chunks.
Usually the graph is much less complicated than this. For simple cases it is empty and the maximum independent set is trivial. This one has two maximum independent sets, one (3,1; 5,5; 6,6; 7,7) corresponding to the obvious minimum splitting:

and the other (2,4; 3,5; 5,1; 6,2) to this other equally-good splitting:
[ Addendum 20170511: It actually has three maximum independent sets. ]
In an earlier draft of yesterday's post, I wrote:
I should probably do this over again, because my listing seems to be incomplete. For example, it omits “spectrum / crumpets” which would have scored 5, because the Webster's Second list contains crumpet but not crumpets.
I was going to leave it at that, but then I did do it over again, and this time around I implemented the “good” algorithm. It was not that hard. The code is on GitHub if you would like to see it.
To solve the maximum independent set instances, I used a guided brute-force search. Maximum independent set is NP-complete, and so the best known algorithm for it runs in exponential time. But the instances in which we are interested here are small enough that this doesn't matter. The example graph above has 8 nodes, so one needs to check at most 256 possible sets to see which is the maximum independent set.
I collated together all the dictionaries I had handy. (I didn't know yet about SCOWL.) These totaled 275,954 words, which is somewhat more than Webster's Second by itself. One of the new dictionaries did contain crumpets so the result does include “spectrum / crumpets”.
The old scored anagram list that I made in the 1990s contained 23,521 pairs. The new one contains 38,333. Unfortunately most of the new stuff is of poor quality, as one would expect. Most of the new words that were missing from my dictionary the first time around are obscure. Perhaps some people would enjoy discovering that that “basiparachromatin” and “Marsipobranchiata” are anagrams, but I find it of very limited appeal.
But the new stuff is not all junk. It includes:
10 antiparticles paternalistic
10 nectarines transience
10 obscurantist subtractions11 colonialists oscillations
11 derailments streamlined
which I think are pretty good.
I wasn't sure how long the old program had taken to run back in the early nineties, but I was sure it had been at least a couple of hours. The new program processes the 275,954 inputs in about 3.5 seconds. I wished I knew how much of this was due to Moore's law and how much to the improved algorithm, but as I said, the old code was long lost.
But then just as I was finishing up the article, I found the old brute-force code that I thought I had lost! I ran it on the same input, and instead of 3.5 seconds it took just over 4 seconds. So almost all of the gain since the 1990s was from Moore's law, and hardly any was from the “improved” algorithm.
I had written in the earlier article:
In 2016 [ the brute force algorithm ] would probably still [ run ] quicker than implementing the maximum independent set algorithm.
which turned out to be completely true, since implementing the maximum independent set algorithm took me a couple of hours. (Although most of that was building out a graph library because I didn't want to look for one on CPAN.)
But hey, at least the new program is only twice as much code!
[ Addendum: The program had a minor bug: it would disregard
capitalization when deciding if two words were anagrams, but then
compute the scores with capitals and lowercase letters distinct. So
for example Chaenolobus was considered an anagram of unchoosable,
but then the Ch in Chaenolobus would not be matched to the ch in
unchoosable, resulting in a score of 11 instead of 10. I have
corrected the program and the output. Thanks to Philip Cohen for
pointing this out. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
I found the best anagram in English
I planned to publish this last week sometime but then I wrote a line of code with three errors and that took over the blog.
A few years ago I mentioned in passing that in the 1990s I had constructed a listing of all the anagrams in Webster's Second International dictionary. (The Webster's headword list was available online.)
This was easy to do, even at the time, when the word list itself, at 2.5 megabytes, was a file of significant size. Perl and its cousins were not yet common; in those days I used Awk. But the task is not very different in any reasonable language:
# Process word list
while (my $word = <>) {
chomp $word;
my $sorted = join "", sort split //, $word; # normal form
push @{$anagrams{$sorted}}, $word;
}
for my $words (values %anagrams) {
print "@$words\n" if @$words > 1;
}
The key technique is to reduce each word to a normal form so that
two words have the same normal form if and only if they are anagrams
of one another. In this case we do this by sorting the letters into
alphabetical order, so that both megalodon and moonglade become
adeglmnoo.
Then we insert the words into a (hash | associative array | dictionary), keyed by their normal forms, and two or more words are anagrams if they fall into the same hash bucket. (There is some discussion of this technique in Higher-Order Perl pages 218–219 and elsewhere.)
(The thing you do not want to do is to compute every permutation of the letters of each word, looking for permutations that appear in the word list. That is akin to sorting a list by computing every permutation of the list and looking for the one that is sorted. I wouldn't have mentioned this, but someone on StackExchange actually asked this question.)
Anyway, I digress. This article is about how I was unhappy with the results of the simple procedure above. From the Webster's Second list, which contains about 234,000 words, it finds about 14,000 anagram sets (some with more than two words), consisting of 46,351 pairs of anagrams. The list starts with
aal ala
and ends with
zolotink zolotnik
which exemplify the problems with this simple approach: many of the 46,351 anagrams are obvious, uninteresting or even trivial. There must be good ones in the list, but how to find them?
I looked in the list to find the longest anagrams, but they were also disappointing:
cholecystoduodenostomy duodenocholecystostomy
(Webster's Second contains a large amount of scientific and medical jargon. A cholecystoduodenostomy is a surgical operation to create a channel between the gall bladder (cholecysto-) and the duodenum (duodeno-). A duodenocholecystostomy is the same thing.)
This example made clear at least one of the problems with boring anagrams: it's not that they are too short, it's that they are too simple. Cholecystoduodenostomy and duodenocholecystostomy are 22 letters long, but the anagrammatic relation between them is obvious: chop cholecystoduodenostomy into three parts:
cholecysto duodeno stomy
and rearrange the first two:
duodeno cholecysto stomy
and there you have it.
This gave me the idea to score a pair of anagrams according to how many chunks one had to be cut into in order to rearrange it to make the other one. On this plan, the “cholecystoduodenostomy / duodenocholecystostomy” pair would score 3, just barely above the minimum possible score of 2. Something even a tiny bit more interesting, say “abler / blare” would score higher, in this case 4. Even if this strategy didn't lead me directly to the most interesting anagrams, it would be a big step in the right direction, allowing me to eliminate the least interesting.
This rule would judge both “aal / ala” and “zolotink / zolotnik” as being uninteresting (scores 2 and 4 respectively), which is a good outcome. Note that some other boring-anagram problems can be seen as special cases of this one. For example, short anagrams never need to be cut into many parts: no four-letter anagrams can score higher than 4. The trivial anagramming of a word to itself always scores 1, and nontrivial anagrams always score more than this.
So what we need to do is: for each anagram pair, say
acrididae (grasshoppers)
and cidaridae (sea
urchins), find the smallest number of chunks into which we can chop
acrididae so that the chunks can be rearranged into cidaridae.
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. (More about this tomorrow.) I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search. Or rather, I used a very small amount of cleverness to reduce the search space, and then used brute-force search to search the reduced space.
Let's consider a example, scoring the anagram “abscise / scabies”.
You do not have to consider every possible permutation of
abscise. Rather, there are only two possible mappings from the
letters of abscise to the letters of scabies. You know that the
C must map to the C, the A must map to the A, and so
forth. The only question is whether the first S of abscise maps to
the first or to the second S of scabies. The first mapping gives
us:
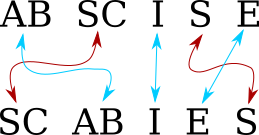
and the second gives us

because the S and the C no longer go to adjoining positions. So
the minimum number of chunks is 5, and this anagram pair gets a score
of 5.
To fully analyze cholecystoduodenostomy by this method required considering 7680
mappings. (120 ways to map the five O's × 2 ways to map the two
C's × 2 ways to map the two D's, etc.) In the 1990s this took a
while, but not prohibitively long, and it worked well enough that I
did not bother to try to find a better algorithm. In 2016 it would
probably still run quicker than implementing the maximum independent
set algorithm. Unfortunately I have lost the code that I wrote then
so I can't compare.
Assigning scores in this way produced a scored anagram list which began
2 aal ala
and ended
4 zolotink zolotnik
and somewhere in the middle was
3 cholecystoduodenostomy duodenocholecystostomy
all poor scores. But sorted by score, there were treasures at the end, and the clear winner was
I declare this the single best anagram in English. It is 15 letters
long, and the only letters that stay together are the E and the R.
“Cinematographer” is as familiar as a 15-letter word can be, and
“megachiropteran” means a giant bat. GIANT BAT! DEATH FROM
ABOVE!!!
And there is no serious competition. There was another 14-pointer, but both its words are Webster's Second jargon that nobody knows:
14 rotundifoliate titanofluoride
There are no score 13 pairs, and the score 12 pairs are all obscure. So this is the winner, and a deserving winner it is.
I think there is something in the list to make everyone happy. If you are the type of person who enjoys anagrams, the list rewards casual browsing. A few examples:
7 admirer married
7 admires sidearm8 negativism timesaving
8 peripatetic precipitate
8 scepters respects
8 shortened threnodes
8 soapstone teaspoons9 earringed grenadier
9 excitation intoxicate
9 integrals triangles
9 ivoriness revisions
9 masculine calumnies10 coprophagist topographics
10 chuprassie haruspices
10 citronella interlocal11 clitoridean directional
11 dispensable piebaldness
“Clitoridean / directional” has been one of my favorites for years. But my favorite of all, although it scores only 6, is
6 yttrious touristy
I think I might love it just because the word yttrious is so delightful. (What a debt we owe to Ytterby, Sweden!)
I also rather like
5 notaries senorita
which shows that even some of the low-scorers can be worth looking at. Clearly my chunk score is not the end of the story, because “notaries / senorita” should score better than “abets / baste” (which is boring) or “Acephali / Phacelia” (whatever those are), also 5-pointers. The length of the words should be worth something, and the familiarity of the words should be worth even more.
Here are the results:
In former times there was a restaurant in Philadelphia named “Soupmaster”. My best unassisted anagram discovery was noticing that this is an anagram of “mousetraps”.
[ Addendum 20170222: There is a followup article comparing the two algorithms I wrote for computing scores. ]
[ Addendum 20170222: An earlier version of this article mentioned the putative 11-pointer “endometritria / intermediator”. The word “endometritria” seemed pretty strange, and I did look into it before I published the article, but not carefully enough. When Philip Cohen wrote to me to question it, I investigated more carefully, and discovered that it had been an error in an early WordNet release, corrected (to “endometria”) in version 1.6. I didn't remember that I had used WordNet's word lists, but I am not surprised to discover that I did. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
Thu, 16 Feb 2017
Automatically checking for syntax errors with Git's pre-commit hook
Previous related article
Earlier related article
Over the past couple of days I've written about how I committed a syntax error on a cron script, and a co-worker had to fix it on Saturday morning. I observed that I should have remembered to check the script for syntax errors before committing it, and several people wrote to point out to me that this is the sort of thing one should automate.
(By the way, please don't try to contact me on Twitter. It won't work. I have been on Twitter Vacation for months and have no current plans to return.)
Git has a “pre-commit hook” feature, which means that you can set up a program that will be run every time you attempt a commit, and which can abort the commit if it doesn't like what it sees. This is the natural place to put an automatic syntax check. Some people suggested that it should be part of the CI system, or even the deployment system, but I don't control those, and anyway it is much better to catch this sort of thing as early as possible. I decided to try to implement a pre-commit hook to check syntax.
Unlike some of the git hooks, the pre-commit hook is very simple to use. It gets run when you try to make a commit, and the commit is aborted if the hook exits with a nonzero status.
I made one mistake right off the bat: I wrote the hook in Bourne shell, even though I swore years ago to stop writing shell scripts. Everything that I want to write in shell should be written in Perl instead or in some equivalently good language like Python. But the sample pre-commit hook was written in shell and when I saw it I went into automatic shell scripting mode and now I have yet another shell script that will have to be replaced with Perl when it gets bigger. I wish I would stop doing this.
Here is the hook, which, I should say up front, I have not yet tried in day-to-day use. The complete and current version is on github.
#!/bin/bash
function typeof () {
filename=$1
case $filename in
*.pl | *.pm) echo perl; exit ;;
esac
line1=$(head -1 $1)
case $line1 in '#!'*perl )
echo perl; exit ;;
esac
}
Some of the sample programs people showed me decided which files
needed to be checked based only on the filename. This is not good
enough. My most important Perl programs have filenames with no
extension. This typeof function decides which set of checks to
apply to each file, and the minimal demonstration version here can do
that based on filename or by looking for the #!...perl line in the
first line of the file contents. I expect that this function will
expand to include other file types; for example
*.py ) echo python; exit ;;
is an obvious next step.
if [ ! -z $COMMIT_OK ]; then
exit 0;
fi
This block is an escape hatch. One day I will want to bypass the hook
and make a commit without performing the checks, and then I can
COMMIT_OK=1 git commit …. There is actually a --no-verify flag to
git-commit that will skip the hook entirely, but I am unlikely to
remember it.
(I am also unlikely to remember COMMIT_OK=1. But I know from
experience that I will guess that I might have put an escape hatch
into the hook. I will also guess that there might be a flag to
git-commit that does what I want, but that will seem less likely to
be true, so I will look in the hook program first. This will be a
good move because my hook is much shorter than the git-commit man
page. So I will want the escape hatch, I will look for it in the best place,
and I will find it. That is worth two lines of code. Sometimes I feel
like the guy in Memento. I have not yet resorted to tattooing
COMMIT_OK=1 on my chest.)
exec 1>&2
This redirects the standard output of all subsequent commands to go to
standard error instead. It makes it more convenient to issue error
messages with echo and such like. All the output this hook produces
is diagnostic, so it is appropriate for it to go to standard error.
allOK=true
badFiles=
for file in $(git diff --cached --name-only | sort) ; do
allOK is true if every file so far has passed its checks.
badFiles is a list of files that failed their checks. the
git diff --cached --name-only function interrogates the Git index
for a list of the files that have been staged for commit.
type=$(typeof "$file")
This invokes the typeof function from above to decide the type of
the current file.
BAD=false
When a check discovers that the current file is bad, it will signal
this by setting BAD to true.
echo
echo "## Checking file $file (type $type)"
case $type in
perl )
perl -cw $file || BAD=true
[ -x $file ] || { echo "File is not executable"; BAD=true; }
;;
* )
echo "Unknown file type: $file; no checks"
;;
esac
This is the actual checking. To check Python files, we would add a
python) … ;; block here. The * ) case is a catchall. The perl
checks run perl -cw, which does syntax checking without executing
the program. It then checks to make sure the file is executable, which
I am sure is a mistake, because these checks are run for .pm files,
which are not normally supposed to be executable. But I wanted to
test it with more than one kind of check.
if $BAD; then
allOK=false;
badFiles="$badFiles;$file"
fi
done
If the current file was bad, the allOK flag is set false, and the
commit will be aborted. The current filename is appended to badFiles
for a later report. Bash has array variables but I don't remember how
they work and the manual made it sound gross. Already I regret not
writing this in a real language.
After the modified files have been checked, the hook exits successfully if they were all okay, and prints a summary if not:
if $allOK; then
exit 0;
else
echo ''
echo '## Aborting commit. Failed checks:'
for file in $(echo $badFiles | tr ';' ' '); do
echo " $file"
done
exit 1;
fi
This hook might be useful, but I don't know yet; as I said, I haven't
really tried it. But I can see ahead of time that it has a couple of
drawbacks. Of course it needs to be built out with more checks. A
minor bug is that I'd like to apply that is-executable check to Perl
files that do not end in .pm, but that will be an easy fix.
But it does have one serious problem I don't know how to fix yet. The hook checks the versions of the files that are in the working tree, but not the versions that are actually staged for the commit!
The most obvious problem this might cause is that I might try to commit some files, and then the hook properly fails because the files are broken. Then I fix the files, but forget to add the fixes to the index. But because the hook is looking at the fixed versions in the working tree, the checks pass, and the broken files are committed!
A similar sort of problem, but going the other way, is that I might
make several changes to some file, use git add -p to add the part I
am ready to commit, but then the commit hook fails, even though the
commit would be correct, because the incomplete changes are still in
the working tree.
I did a little tinkering with git stash save -k to try to stash the
unstaged changes before running the checks, something like this:
git stash save -k "pre-commit stash" || exit 2
trap "git stash pop" EXIT
but I wasn't able to get anything to work reliably. Stashing a modified index has never worked properly for me, perhaps because there is something I don't understand. Maybe I will get it to work in the future. Or maybe I will try a different method; I can think of several offhand:
The hook could copy each file to a temporary file and then run the check on the temporary file. But then the diagnostics emitted by the checks would contain the wrong filenames.
It could move each file out of the way, check out the currently-staged version of the file, check that, and then restore the working tree version. (It can skip this process for files where the staged and working versions are identical.) This is not too complicated, but if it messes up it could catastrophically destroy the unstaged changes in the working tree.
Check out the entire repository and modified index into a fresh working tree and check that, then discard the temporary working tree. This is probably too expensive.
This one is kind of weird. It could temporarily commit the current index (using
--no-verify), stash the working tree changes, and check the files. When the checks are finished, it would unstash the working tree changes, usegit-reset --softto undo the temporary commit, and proceed with the real commit if appropriate.Come to think of it, this last one suggests a much better version of the same thing: instead of a pre-commit hook, use a post-commit hook. The post-commit hook will stash any leftover working tree changes, check the committed versions of the files, unstash the changes, and, if the checks failed, undo the commit with
git-reset --soft.
Right now the last one looks much the best but perhaps there's something straightforward that I didn't think of yet.
[ Thanks to Adam Sjøgren, Jeffrey McClelland, and Jack Vickeridge for discussing this with me. Jeffrey McClelland also suggested that syntax checks could be profitably incorporated as a post-receive hook, which is run on the remote side when new commits are pushed to a remote. I said above that running the checks in the CI process seems too late, but the post-receive hook is earlier and might be just the thing. ]
[ Addendum: Daniel Holz wrote to tell me that the Yelp pre-commit frameworkhandles the worrisome case of unstaged working tree changes. The strategy is different from the ones I suggested above. If I'm reading this correctly, it records the unstaged changes in a patch file, which it sticks somewhere, and then checks out the index. If all the checks succeed, it completes the commit and then tries to apply the patch to restore the working tree changes. The checks in Yelp's framework might modify the staged files, and if they do, the patch might not apply; in this case it rolls back the whole commit. Thank you M. Holtz! ]
[Other articles in category /prog] permanent link
Tue, 14 Feb 2017
More thoughts on a line of code with three errors
Yesterday I wrote, in great irritation, about a line of code I had written that contained three errors.
I said:
What can I learn from this? Most obviously, that I should have tested my code before I checked it in.
Afterward, I felt that this was inane, and that the matter required a little more reflection. We do not test every single line of every program we write; in most applications that would be prohibitively expensive, and in this case it would have been excessive.
The change I was making was in the format of the diagnostic that the program emitted as it finished to report how long it had taken to run. This is not an essential feature. If the program does its job properly, it is of no real concern if it incorrectly reports how long it took to run. Two of my errors were in the construction of the message. The third, however, was a syntax error that prevented the program from running at all.
Having reflected on it a little more, I have decided that I am only really upset about the last one, which necessitated an emergency Saturday-morning repair by a co-worker. It was quite acceptable not to notice ahead of time that the report would be wrong, to notice it the following day, and to fix it then. I would have said “oops” and quietly corrected the code without feeling like an ass.
The third problem, however, was serious. And I could have prevented it with a truly minimal amount of effort, just by running:
perl -cw the-script
This would have diagnosed the syntax error, and avoided the main problem at hardly any cost. I think I usually remember to do something like this. Had I done it this time, the modified script would have gone into production, would have run correctly, and then I could have fixed the broken timing calculation on Monday.
In the previous article I showed the test program that I wrote to test the time calculation after the program produced the wrong output. I think it was reasonable to postpone writing this until after program ran and produced the wrong output. (The program's behavior in all other respects was correct and unmodified; it was only its report about its running time that was incorrect.) To have written the test ahead of time might be an excess of caution.
There has to be a tradeoff between cautious preparation and risk. Here I put everything on the side of risk, even though a tiny amount of caution would have eliminated most of the risk. In my haste, I made a bad trade.
[ Addendum 20170216: I am looking into automating the perl -cw check. ]
[Other articles in category /prog] permanent link
Mon, 13 Feb 2017
How I got three errors into one line of code
At work we had this script that was trying to report how long it had
taken to run, and it was using DateTime::Duration:
my $duration = $end_time->subtract_datetime($start_time);
my ( $hours, $minutes, $seconds ) =
$duration->in_units( 'hours', 'minutes', 'seconds' );
log_info "it took $hours hours $minutes minutes and $seconds seconds to run"
This looks plausible, but because
DateTime::Duration is shit,
it didn't work. Typical output:
it took 0 hours 263 minutes and 19 seconds to run
I could explain to you why it does this, but it's not worth your time.
I got tired of seeing 0 hours 263 minutes show up in my cron email
every morning, so I went to fix it. Here's what I changed it to:
my $duration = $end_time->subtract_datetime_absolute($start_time)->seconds;
my ( $hours, $minutes, $minutes ) = (int(duration/3600), int($duration/60)%60, $duration%3600);
I was at some pains to get that first line right, because getting
DateTime to produce a useful time interval value is a tricky
proposition. I did get the first line right. But the second line is
just simple arithmetic, I have written it several times before, so I
dashed it off, and it contains a syntax error, that duration/3600 is
missing its dollar sign, which caused the cron job to crash the next
day.
A co-worker got there before I did and fixed it for me. While he was
there he also fixed the $hours, $minutes, $minutes that should have
been $hours, $minutes, $seconds.
I came in this morning and looked at the cron mail and it said
it took 4 hours 23 minutes and 1399 seconds to run
so I went back to fix the third error, which is that $duration%3600
should have been $duration%60. The thrice-corrected line has
my ( $hours, $minutes, $seconds ) = (int($duration/3600), int($duration/60)%60, $duration%60);
What can I learn from this? Most obviously, that I should have tested my code before I checked it in. Back in 2013 I wrote:
Usually I like to draw some larger lesson from this sort of thing. … “Just write the tests, fool!”
This was a “just write the tests, fool!” moment if ever there was one. Madame Experience runs an expensive school, but fools will learn in no other.
I am not completely incorrigible. I did at least test the fixed code before I checked that in. The test program looks like this:
sub dur {
my $duration = shift;
my ($hours, $minutes, $seconds ) = (int($duration/3600), int($duration/60)%60, $duration%60);
sprintf "%d:%02d:%02d", $hours, $minutes, $seconds;
}
use Test::More;
is(dur(0), "0:00:00");
is(dur(1), "0:00:01");
is(dur(59), "0:00:59");
is(dur(60), "0:01:00");
is(dur(62), "0:01:02");
is(dur(122), "0:02:02");
is(dur(3599), "0:59:59");
is(dur(3600), "1:00:00");
is(dur(10000), "2:46:40");
done_testing();
It was not necessary to commit the test program, but it was necessary to write it and to run it. By the way, the test program failed the first two times I ran it.
Three errors in one line isn't even a personal worst. In 2012 I posted here about getting four errors into a one-line program.
[ Addendum 20170215: I have some further thoughts on this. ]
[Other articles in category /oops] permanent link
Tue, 07 Feb 2017
How many 24 puzzles are there?
[ Note: The tables in this article are important, and look unusually crappy if you read this blog through an aggregator. The properly-formatted version on my blog may be easier to follow. ]
A few months ago I wrote about puzzles of the following type: take four digits, say 1, 2, 7, 7, and, using only +, -, ×, and ÷, combine them to make the number 24. Since then I have been accumulating more and more material about these puzzles, which will eventually appear here. But meantime here is a delightful tangent.
In the course of investigating this I wrote programs to enumerate the solutions of all possible puzzles, and these programs were always much faster than I expected at first. It appears as if there are 10,000 possible puzzles, from «0,0,0,0» through «9,9,9,9». But a moment's thought shows that there are considerably fewer, because, for example, the puzzles «7,2,7,1», «1,2,7,7», «7,7,2,1», and «2,7,7,1» are all the same puzzle. How many puzzles are there really?
A back-of-the-envelope estimate is that only about 1 in 24 puzzles is really distinct (because there are typically 24 ways to rearrange the elements of a puzzle) and so there ought to be around !!\frac{10000}{24} \approx 417!! puzzles. This is an undercount, because there are fewer duplicates of many puzzles; for example there are not 24 variations of «1,2,7,7», but only 12. The actual number of puzzles turns out to be 715, which I think is not an obvious thing to guess.
Let's write !!S(d,n)!! for the set of sequences of length !!n!! containing up to !!d!! different symbols, with the duplicates removed: when two sequences are the same except for the order of their symbols, we will consider them the same sequence.
Or more concretely, we may imagine that the symbols are sorted into nondecreasing order, so that !!S(d,n)!! is the set of nondecreasing sequences of length !!n!! of !!d!! different symbols.
Let's also write !!C(d,n)!! for the number of elements of !!S(d,n)!!.
Then !!S(10, 4)!! is the set of puzzles where input is four digits. The claim that there are !!715!! such puzzles is just that !!C(10,4) = 715!!. A tabulation of !!C(\cdot,\cdot)!! reveals that it is closely related to binomial coefficients, and indeed that $$C(d,n)=\binom{n+d-1}{d-1}.\tag{$\heartsuit$}$$
so that the surprising !!715!! is actually !!\binom{13}{9}!!. This is not hard to prove by induction, because !!C(\cdot,\cdot)!! is easily shown to obey the same recurrence as !!\binom\cdot\cdot!!: $$C(d,n) = C(d-1,n) + C(d,n-1).\tag{$\spadesuit$}$$
To see this, observe that an element of !!C(d,n)!! either begins with a zero or with some other symbol. If it begins with a zero, there are !!C(d,n-1)!! ways to choose the remaining !!n-1!! symbols in the sequence. But if it begins with one of the other !!d-1!! symbols it cannot contain any zeroes, and what we really have is a length-!!n!! sequence of the symbols !!1\ldots (d-1)!!, of which there are !!C(d-1, n)!!.
| 0 0 0 0 | 1 1 1 |
| 0 0 0 1 | 1 1 2 |
| 0 0 0 2 | 1 1 3 |
| 0 0 0 3 | 1 1 4 |
| 0 0 1 1 | 1 2 2 |
| 0 0 1 2 | 1 2 3 |
| 0 0 1 3 | 1 2 4 |
| 0 0 2 2 | 1 3 3 |
| 0 0 2 3 | 1 3 4 |
| 0 0 3 3 | 1 4 4 |
| 0 1 1 1 | 2 2 2 |
| 0 1 1 2 | 2 2 3 |
| 0 1 1 3 | 2 2 4 |
| 0 1 2 2 | 2 3 3 |
| 0 1 2 3 | 2 3 4 |
| 0 1 3 3 | 2 4 4 |
| 0 2 2 2 | 3 3 3 |
| 0 2 2 3 | 3 3 4 |
| 0 2 3 3 | 3 4 4 |
| 0 3 3 3 | 4 4 4 |
Now we can observe that !!\binom74=\binom73!! (they are both 35) so that !!C(5,3) = C(4,4)!!. We might ask if there is a combinatorial proof of this fact, consisting of a natural bijection between !!S(5,3)!! and !!S(4,4)!!. Using the relation !!(\spadesuit)!! we have:
$$ \begin{eqnarray} C(4,4) & = & C(3, 4) + & C(4,3) \\ C(5,3) & = & & C(4,3) + C(5,2) \\ \end{eqnarray}$$
so part of the bijection, at least, is clear: There are !!C(4,3)!! elements of !!S(4,4)!! that begin with a zero, and also !!C(4,3)!! elements of !!S(5, 3)!! that do not begin with a zero, so whatever the bijection is, it ought to match up these two subsets of size 20. This is perfectly straightforward; simply match up !!«0, a, b, c»!! (blue) with !!«a+1, b+1, c+1»!! (pink), as shown at right.
But finding the other half of the bijection, between !!S(3,4)!! and !!S(5,2)!!, is not so straightforward. (Both have 15 elements, but we are looking for not just any bijection but for one that respects the structure of the elements.) We could apply the recurrence again, to obtain:
$$ \begin{eqnarray} C(3,4) & = \color{darkred}{C(2, 4)} + \color{darkblue}{C(3,3)} \\ C(5,2) & = \color{darkblue}{C(4,2)} + \color{darkred}{C(5,1)} \end{eqnarray}$$
and since $$ \begin{eqnarray} \color{darkred}{C(2, 4)} & = \color{darkred}{C(5,1)} \\ \color{darkblue}{C(3,3)} & = \color{darkblue}{C(4,2)} \end{eqnarray}$$
we might expect the bijection to continue in that way, mapping !!\color{darkred}{S(2,4) \leftrightarrow S(5,1)}!! and !!\color{darkblue}{S(3,3) \leftrightarrow S(4,2)}!!. Indeed there is such a bijection, and it is very nice.
To find the bijection we will take a detour through bitstrings. There is a natural bijection between !!S(d, n)!! and the bit strings that contain !!d-1!! zeroes and !!n!! ones. Rather than explain it with pseudocode, I will give some examples, which I think will make the point clear. Consider the sequence !!«1, 1, 3, 4»!!. Suppose you are trying to communicate this sequence to a computer. It will ask you the following questions, and you should give the corresponding answers:
- “Is the first symbol 0?” (“No”)
- “Is the first symbol 1?” (“Yes”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“No”)
- “Is the third symbol 2?” (“No”)
- “Is the third symbol 3?” (“Yes”)
- “Is the fourth symbol 3?” (“No”)
- “Is the fourth symbol 4?” (“Yes”)
At each stage the
computer asks about the identity of the next symbol. If the answer is
“yes” the computer has learned another symbol and moves on to the next
element of the sequence. If it is “no” the computer tries guessing a
different symbol. The “yes” answers become ones and “no”
answers become zeroes, so that the resulting bit string is 0 1 1 0 0 1 0 1.
It sometimes happens that the computer figures out all the elements of the sequence before using up its !!n+d-1!! questions; in this case we pad out the bit string with zeroes, or we can imagine that the computer asks some pointless questions to which the answer is “no”. For example, suppose the sequence is !!«0, 1, 1, 1»!!:
- “Is the first symbol 0?” (“Yes”)
- “Is the second symbol 0?” (“No”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“Yes”)
- “Is the fourth symbol 1?” (“Yes”)
The bit string is 1 0 1 1 1 0 0 0, where the final three 0 bits are
the padding.
We can reverse the process, simply taking over the role of the
computer. To find the sequence that corresponds to the bit string
0 1 1 0 1 0 0 1, we ask the questions ourselves and use the bits as the
answers:
- “Is the first symbol 0?” (“No”)
- “Is the first symbol 1?” (“Yes”)
- “Is the second symbol 1?” (“Yes”)
- “Is the third symbol 1?” (“No”)
- “Is the third symbol 2?” (“Yes”)
- “Is the fourth symbol 2?” (“No”)
- “Is the fourth symbol 3?” (“No”)
- “Is the fourth symbol 4?” (“Yes”)
We have recovered the sequence !!«1, 1, 2, 4»!! from the
bit string 0 1 1 0 1 0 0 1.
This correspondence establishes relation !!(\heartsuit)!! in a different way from before: since there is a natural bijection between !!S(d, n)!! and the bit strings with !!d-1!! zeroes and !!n!! ones, there are certainly !!\binom{n+d-1}{d-1}!! of them as !!(\heartsuit)!! says because there are !!n+d-1!! bits and we may choose any !!d-1!! to be the zeroes.
We wanted to see why !!C(5,3) = C(4,4)!!. The detour above shows that there is a simple bijection between
!!S(5,3)!! and the bit strings with 4 zeroes and 3 ones
on one hand, and between
!!S(4,4)!! and the bit strings with 3 zeroes and 4 ones
on the other hand. And of course the bijection between the two sets of bit strings is completely obvious: just exchange the zeroes and the ones.
The table below shows the complete bijection between !!S(4,4)!! and its descriptive bit strings (on the left in blue) and between !!S(5, 3)!! and its descriptive bit strings (on the right in pink) and that the two sets of bit strings are complementary. Furthermore the top portion of the table shows that the !!S(4,3)!! subsets of the two families correspond, as they should—although the correct correspondence is the reverse of the one that was displayed earlier in the article, not the suggested !!«0, a, b, c» \leftrightarrow «a+1, b+1, c+1»!! at all. Instead, in the correct table, the initial digit of the !!S(4,4)!! entry says how many zeroes appear in the !!S(5,3)!! entry, and vice versa; then the increment to the next digit says how many ones, and so forth.
| !!S(4,4)!! | (bits) | (complement bits) | !!S(5,3)!! |
|---|---|---|---|
| 0 0 0 0 | 1 1 1 1 0 0 0 | 0 0 0 0 1 1 1 | 4 4 4 |
| 0 0 0 1 | 1 1 1 0 1 0 0 | 0 0 0 1 0 1 1 | 3 4 4 |
| 0 0 0 2 | 1 1 1 0 0 1 0 | 0 0 0 1 1 0 1 | 3 3 4 |
| 0 0 0 3 | 1 1 1 0 0 0 1 | 0 0 0 1 1 1 0 | 3 3 3 |
| 0 0 1 1 | 1 1 0 1 1 0 0 | 0 0 1 0 0 1 1 | 2 4 4 |
| 0 0 1 2 | 1 1 0 1 0 1 0 | 0 0 1 0 1 0 1 | 2 3 4 |
| 0 0 1 3 | 1 1 0 1 0 0 1 | 0 0 1 0 1 1 0 | 2 3 3 |
| 0 0 2 2 | 1 1 0 0 1 1 0 | 0 0 1 1 0 0 1 | 2 2 4 |
| 0 0 2 3 | 1 1 0 0 1 0 1 | 0 0 1 1 0 1 0 | 2 2 3 |
| 0 0 3 3 | 1 1 0 0 0 1 1 | 0 0 1 1 1 0 0 | 2 2 2 |
| 0 1 1 1 | 1 0 1 1 1 0 0 | 0 1 0 0 0 1 1 | 1 4 4 |
| 0 1 1 2 | 1 0 1 1 0 1 0 | 0 1 0 0 1 0 1 | 1 3 4 |
| 0 1 1 3 | 1 0 1 1 0 0 1 | 0 1 0 0 1 1 0 | 1 3 3 |
| 0 1 2 2 | 1 0 1 0 1 1 0 | 0 1 0 1 0 0 1 | 1 2 4 |
| 0 1 2 3 | 1 0 1 0 1 0 1 | 0 1 0 1 0 1 0 | 1 2 3 |
| 0 1 3 3 | 1 0 1 0 0 1 1 | 0 1 0 1 1 0 0 | 1 2 2 |
| 0 2 2 2 | 1 0 0 1 1 1 0 | 0 1 1 0 0 0 1 | 1 1 4 |
| 0 2 2 3 | 1 0 0 1 1 0 1 | 0 1 1 0 0 1 0 | 1 1 3 |
| 0 2 3 3 | 1 0 0 1 0 1 1 | 0 1 1 0 1 0 0 | 1 1 2 |
| 0 3 3 3 | 1 0 0 0 1 1 1 | 0 1 1 1 0 0 0 | 1 1 1 |
| 1 1 1 1 | 0 1 1 1 1 0 0 | 1 0 0 0 0 1 1 | 0 4 4 |
| 1 1 1 2 | 0 1 1 1 0 1 0 | 1 0 0 0 1 0 1 | 0 3 4 |
| 1 1 1 3 | 0 1 1 1 0 0 1 | 1 0 0 0 1 1 0 | 0 3 3 |
| 1 1 2 2 | 0 1 1 0 1 1 0 | 1 0 0 1 0 0 1 | 0 2 4 |
| 1 1 2 3 | 0 1 1 0 1 0 1 | 1 0 0 1 0 1 0 | 0 2 3 |
| 1 1 3 3 | 0 1 1 0 0 1 1 | 1 0 0 1 1 0 0 | 0 2 2 |
| 1 2 2 2 | 0 1 0 1 1 1 0 | 1 0 1 0 0 0 1 | 0 1 4 |
| 1 2 2 3 | 0 1 0 1 1 0 1 | 1 0 1 0 0 1 0 | 0 1 3 |
| 1 2 3 3 | 0 1 0 1 0 1 1 | 1 0 1 0 1 0 0 | 0 1 2 |
| 1 3 3 3 | 0 1 0 0 1 1 1 | 1 0 1 1 0 0 0 | 0 1 1 |
| 2 2 2 2 | 0 0 1 1 1 1 0 | 1 1 0 0 0 0 1 | 0 0 4 |
| 2 2 2 3 | 0 0 1 1 1 0 1 | 1 1 0 0 0 1 0 | 0 0 3 |
| 2 2 3 3 | 0 0 1 1 0 1 1 | 1 1 0 0 1 0 0 | 0 0 2 |
| 2 3 3 3 | 0 0 1 0 1 1 1 | 1 1 0 1 0 0 0 | 0 0 1 |
| 3 3 3 3 | 0 0 0 1 1 1 1 | 1 1 1 0 0 0 0 | 0 0 0 |
Observe that since !!C(d,n) = \binom{n+d-1}{d-1} = \binom{n+d-1}{n} = C(n+1, d-1)!! we have in general that !!C(d,n) = C(n+1, d-1)!!, which may be surprising. One might have guessed that since !!C(5,3) = C(4,4)!!, the relation was !!C(d,n) = C(d+1, n-1)!! and that !!S(d,n)!! would have the same structure as !!S(d+1, n-1)!!, but it isn't so. The two arguments exchange roles. Following the same path, we can identify many similar ‘coincidences’. For example, there is a simple bijection between the original set of 715 puzzles, which was !!S(10,4)!!, and !!S(5,9)!!, the set of nondecreasing sequences of !!0\ldots 4!! of length !!9!!.
[ Thanks to Bence Kodaj for a correction. ]
[ Addendum 20170829: Conway and Guy, in The Book of Numbers, describe the same bijection, but a little differently; see their discussion of the Sweet Seventeen deck on pages 70–71. ]
[ Addendum 20171015: More about this, using Burnside's lemma. ]
[Other articles in category /math] permanent link




