Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| An ounce of theory is worth a pound of search |
| A public service announcement about contracts |
| Examples of contracts you should not sign |
| Rectangles with equal area and perimeter |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sat, 21 Mar 2015
Examples of contracts you should not sign
Shortly after I posted A public service announcement about contracts Steve Bogart asked me on on Twitter for examples of dealbreaker clauses. Some general types I thought of immediately were:
Any nonspecific non-disclosure agreement with a horizon more than three years off, because after three years you are not going to remember what it was that you were not supposed to disclose.
Any contract in which you give up your right to sue the other party if they were to cheat you.
Most contracts in which you permanently relinquish your right to disparage or publicly criticize the other party.
Any contract that leaves you on the hook for the other party's losses if the project is unsuccessful.
Any contract that would require you to do something immoral or unethical.
Addendum 20150401: Chas. Owens suggests, and I agree, that you not sign a contract that gives the other party ownership of everything you produce, even including things you created on your own time with your own equipment.
A couple of recent specific examples:
Comcast is negotiating a contract with our homeowner's association to bring cable Internet to our village; the proposed agreement included a clause in which we promised not to buy Internet service from any other company for the next ten years. I refused to sign. The guy on our side who was negotiating the agreement was annoyed with me. If too many people refuse to sign, maybe Comcast will back out. “Do you think you're going to get FIOS in here in the next ten years?” he asked sarcastically. “No,” I said. “But I might move.”
Or, you know, I might get sick of Comcast and want to go back to whatever I was using before. Or my satellite TV provider might start delivering satellite Internet. Or the municipal wireless might suddenly improve. Or Google might park a crazy Internet Balloon over my house. Or some company that doesn't exist yet might do something we can't even imagine. Google itself is barely ten years old! The iPhone is only eight!
In 2013 I was on a job interview at company X and was asked to sign an NDA that enjoined me from disclosing anything I learned that day for the next ten years. I explained that I could not sign such an agreement because I would not be able to honor it. I insisted on changing it to three years, which is also too long, but I am not completely unwilling to compromise. It's now two years later and I have completely forgotten what we discussed that day; I might be violating the NDA right now for all I know. Had they insisted on ten years, would I have walked out? You bet I would. You don't let your mouth write checks that your ass can't cash.
[ Addendum 20191107: Our FIOS was installed in January of 2018. Lucky I hadn't signed that ten-year contract, huh? ]
[ Addendum 20220420: More about why it's important to push back ]
[Other articles in category /law] permanent link
Fri, 20 Mar 2015
A public service announcement about contracts
Every so often, when I am called upon to sign some contract or other, I have a conversation that goes like this:
Me: I can't sign this contract; clause 14(a) gives you the right to chop off my hand.
Them: Oh, the lawyers made us put that in. Don't worry about it; of course we would never exercise that clause.
There is only one response you should make to this line of argument:
Well, my lawyer says I can't agree to that, and since you say that you would never exercise that clause, I'm sure you will have no problem removing it from the contract.
Because if the lawyers made them put in there, that is for a reason. And there is only one possible reason, which is that the lawyers do, in fact, envision that they might one day exercise that clause and chop off your hand.
The other party may proceed further with the same argument: “Look, I have been in this business twenty years, and I swear to you that we have never chopped off anyone's hand.” You must remember the one response, and repeat it:
Great! Since you say that you have never chopped off anyone's hand, then you will have no problem removing that clause from the contract.
You must repeat this over and over until it works. The other party is lazy. They just want the contract signed. They don't want to deal with their lawyers. They may sincerely believe that they would never chop off anyone's hand. They are just looking for the easiest way forward. You must make them understand that there is no easier way forward than to remove the hand-chopping clause.
They will say “The deadline is looming! If we don't get this contract executed soon it will be TOO LATE!” They are trying to blame you for the blown deadline. You should put the blame back where it belongs:
As I've made quite clear, I can't sign this contract with the hand-chopping clause. If you want to get this executed soon, you must strike out that clause before it is TOO LATE.
And if the other party would prefer to walk away from the deal rather than abandon their hand-chopping rights, what does that tell you about the value they put on the hand-chopping clause? They claim that they don't care about it and they have never exercised it, but they would prefer to give up on the whole project, rather than abandon hand-chopping? That is a situation that is well worth walking away from, and you can congratulate yourself on your clean escape.
[ Addendum: Steve Bogart asked on Twitter for examples of unacceptable contract demands; I thought of so many that I put them in a separate article. ]
[ Addendum 20150401: Chas. Owens points out that you don't have to argue about it; you can just cross out the hand-chopping clause, add your initials and date in the margin. I do this also, but then I bring the modification it to the other party's attention, because that is the honest and just thing to do. ]
[ Addendum 20220420: More and more, contracts are moving online and getting electronic signatures. This removes the option to modify the contract before signing: you can sign it intact, or not at all. Don't ever forget that the Man is always trying to get his foot on your neck. ]
[ Addendum 20220420: More about why it's important to push back ]
[Other articles in category /law] permanent link
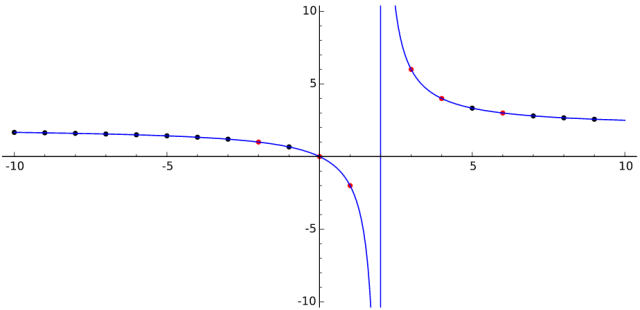
Rectangles with equal area and perimeter
Wednesday while my 10-year-old daughter Katara was doing her math homework, she observed with pleasure that a !!6×3!! rectangle has a perimeter of 18 units and also an area of 18 square units. I mentioned that there was an infinite family of such rectangles, and, after a small amount of tinkering, that the only other such rectangle with integer sides is a !!4×4!! square, so in a sense she had found the single interesting example. She was very interested in how I knew this, and I promised to show her how to figure it out once she finished her homework. She didn't finish before bedtime, so we came back to it the following evening.
This is just one of many examples of how she has way too much homework, and how it interferes with her education.
She had already remarked that she knew how to write an equation expressing the condition she wanted, so I asked her to do that; she wrote $$(L×W) = ([L+W]×2).$$ I remember being her age and using all different shapes of parentheses too. I suggested that she should solve the equation for !!W!!, getting !!W!! on one side and a bunch of stuff involving !!L!! on the other, but she wasn't sure how to do it, so I offered suggestions while she moved the symbols around, eventually obtaining $$W = 2L\div (L-2).$$ I would have written it as a fraction, but getting the right answer is important, and using the same notation I would use is much less so, so I didn't say anything.
I asked her to plug in !!L=3!! and observe that !!W=6!! popped right out, and then similarly that !!L=6!! yields !!W=3!!, and then I asked her to try the other example she knew. Then I suggested that she see what !!L=5!! did: it gives !!W=\frac{10}3!!, This was new, so she checked it by calculating the area and the perimeter, both !!\frac{50}3!!. She was very excited by this time. As I have mentioned earlier, algebra is magical in its ability to mechanically yield answers to all sorts of questions. Even after thirty years I find it astonishing and delightful. You set up the equations, push the symbols around, and all sorts of stuff pops out like magic. Calculus is somehow much less astonishing; the machinery is all explicit. But how does algebra work? I've been thinking about this on and off for a long time and I'm still not sure.
At that point I took over because I didn't think I would be able to guide her through the next part of the problem without a demonstration; I wanted to graph the function !!W=2L\div(L-2)!! and she does not have much experience with that. She put in the five points we already knew, which already lie on a nice little curve, and then she asked an incisive question: does it level off, or does it keep going down, or what? We discussed what happens when !!L!! gets close to 2; then !!W!! shoots up to infinity. And when !!L!! gets big, say a million, you can see from the algebra that !!W!! is a hair more than 2. So I drew in the asymptotes on the hyperbola.
Katara is not yet familiar with hyperbolas. (She has known about parabolas since she was tiny. I have a very fond memory of visiting Portland with her when she was almost two, and we entered Holladay park, which has fountains that squirt out of the ground. Seeing the water arching up before her, she cried delightedly “parabolas!”)
Once you know how the graph behaves, it is a simple matter to see that there are no integer solutions other than !!\langle 3,6\rangle, \langle 4,4\rangle,!! and !!\langle6,3\rangle!!. We know that !!L=5!! does not work. For !!L>6!! the value of !!W!! is always strictly between !!2!! and !!3!!. For !!L=2!! there is no value of !!W!! that works at all. For !!0\lt L\lt 2!! the formula says that !!W!! is negative, on the other branch of the hyperbola, which is a perfectly good numerical solution (for example, !!L=1, W=-2!!) but makes no sense as the width of a rectangle. So it was a good lesson about how mathematical modeling sometimes introduces solutions that are wrong, and how you have to translate the solutions back to the original problem to see if they make sense.
[ Addendum 20150330: Thanks to Steve Hastings for his plot of the hyperbola, which is in the public domain. ]
[Other articles in category /math] permanent link
Thu, 19 Mar 2015
An ounce of theory is worth a pound of search
The computer is really awesome at doing quick searches for numbers with weird properties, and people with an amateur interest in recreational mathematics would do well to learn some simple programming. People appear on math.stackexchange quite often with questions about tic-tac-toe, but there are only 5,478 total positions, so any question you want to ask can be instantaneously answered by an exhaustive search. An amateur showed up last fall asking “Is it true that no prime larger than 241 can be made by either adding or subtracting 2 coprime numbers made up out of the prime factors 2,3, and 5?” and, once you dig through the jargon, the question is easily answered by the computer, which quickly finds many counterexamples, such as !!162+625=787!! and !!2^{19}+3^4=524369!!.
But sometimes the search appears too large to be practical, and then you need to apply theory. Sometimes you can deploy a lot of theory and solve the problem completely, avoiding the search. But theory is expensive, and not always available. A hybrid approach often works, which uses a tiny amount of theory to restrict the search space to the point where the search is easy.
One of these I wrote up on this blog back in 2006:
A number !!n!! is excellent if it has an even number of digits, and if when you chop it into a front half !!a!! and a back half !!b!!, you have !!b^2 - a^2 = n!!. For example, !!48!! is excellent, because !!8^2 - 4^2 = 48!!, and !!3468!! is excellent, because !!68^2 - 34^2 = 4624 - 1156 = 3468!!.
The programmer who gave me thie problem had tried a brute-force search over all numbers, but to find all 10-digit excellent numbers, this required an infeasible search of 9,000,000,000 candidates. With the application of a tiny amount of algebra, one finds that !!a(10^k+a) = b^2+b!! and it's not hard to quickly test candidates for !!a!! to see if !!a(10^k+a)!! has this form and if so to find the corresponding value of !!b!!. (Details are in the other post.) This reduces the search space for 10-digit excellent numbers from 9,000,000,000 candidates to 90,000, which could be done in under a minute even with last-century technology, and is pretty nearly instantaneous on modern equipment.
But anyway, the real point of this note is to discuss a different problem entirely. A recreational mathematician on stackexchange wanted to find distinct integers !!a,b,c,d!! for which !!a^2+b^2, b^2+c^2, c^2+d^2, !! and !!d^2+a^2!! were all perfect squares. You can search over all possible quadruples of numbers, but this takes a long time. The querent indicated later that he had tried such a search but lost patience before it yielded anything.
Instead, observe that if !!a^2+b^2!! is a perfect square then !!a!! and !!b!! are the legs of a right triangle with integer sides; they are terms in what is known as a Pythagorean triple. The prototypical example is !!3^2 + 4^2 = 5^2!!, and !!\langle 3,4,5\rangle!! is the Pythagorean triple. (The querent was quite aware that he was asking for Pythagorean triples, and mentioned them specifically.)
Here's the key point: It has been known since ancient times that if !!\langle a,b,c\rangle!! is a Pythagorean triple, then there exist integers !!m!! and !!n!! such that: $$\begin{align} \require{align} a & = n^2-m^2 \\ b & = 2mn \\ c & = n^2 + m^2 \end{align}$$
So you don't have to search for Pythagorean triples; you can just generate them with no searching:
for my $m (1 .. 200) {
for my $n ($m+1 .. 200) {
my $a = $n*$n-$m*$m;
my $b = 2 * $n * $m;
$trip{$a}{$b} = 1;
$trip{$b}{$a} = 1;
}
}
This builds a hash table, %trip, with two important properties:
$trip{$a}is a sub-table whose keys are all the numbers that can form a triple with !!a!!. For example,$trip{20}is a hash with three keys: 21, 48, and 99, because !!20^2+21^2 = 29^2, 20^2+48^2= 52^2, !! and !!20^2 + 99^2 = 101^2!!, but 20 is not a participant in any other triples.$trip{$a}{$b}is true if and only if !!a^2+b^2!! is a perfect square, and false otherwise.
The table has only around 40,000 entries. Having constructed it, we now search it:
for my $a (keys %trip) {
for my $b (keys %{$trip{$a}}) {
for my $c (keys %{$trip{$b}}) {
next if $c == $a;
for my $d (keys %{$trip{$c}}) {
next if $d == $b;
print "$a $b $c $d\n" if $trip{$d}{$a};
}
}
}
}
The outer loop runs over each !!a!! that is known to be a member of a Pythagorean triple. (Actually the !!m,n!! formulas show that every number bigger than 2 is a member of some triple, but we may as well skip the ones that are only in triples we didn't tabulate.) Then the next loop runs over every !!b!! that can possibly form a triple with !!a!!; that is, every !!b!! for which !!a^2+b^2!! is a perfect square. We don't have to search for them; we have them tabulated ahead of time. Then for each such !!b!! (and there aren't very many) we run over every !!c!! that forms a triple with !!b!!, and again there is no searching and very few candidates. Then then similarly !!d!!, and if the !!d!! we try forms a triple with !!a!!, we have a winner.
The next if $c == $a and next if $d == $b tests are to rule out
trivial solutions like !!a=c=3, b=d=4!!, which the querent wasn't
interested in anyway. We don't have to test for equality of any of
ther other pairs because no number can form a Pythagorean triple with
itself (because !!\sqrt2!! is irrational).
This runs in less than a second on so-so hardware and produces 11 solutions:
3472 7296 10400 2175
4312 23520 12008 465
6512 9984 800 6375
12312 666 1288 8415
14592 6944 4350 20800
16830 2576 1332 24624
19968 13024 12750 1600
25500 26048 39936 3200
30192 6175 2400 9856
41600 29184 13888 8700
47040 8624 930 24016
Only five of these are really different. For example, the last one is the same as the second, with every element multiplied by 2; the third, seventh, and eighth are similarly the same. In general if !!\langle a,b,c,d\rangle!! is a solution, so is !!\langle ka, kb,kc,kd\rangle!! for any !!k!!. A slightly improved version would require that the four numbers not have any common factor greater than 1; there are few enough solutions that the cost of this test would be completely negligible.
The only other thing wrong with the program is that it produces each solution 8 times; if !!\langle a,b,c,d\rangle!! is a solution, then so are !!\langle b,c,d,a\rangle, \langle d,c,b,a\rangle,!! and so on. This is easily fixed with a little post-filtering; pipe the output through
perl -nle '$k = join " ", sort { $a <=> $b } split; print unless $seen{$k}++ '
or something of that sort.
The corresponding run with !!m!! and !!n!! up to 2,000 instead of only 200 takes 5 minutes and finds 445 solutions, of which 101 are distinct, including !!\langle 3614220, 618192, 2080820, 574461\rangle!!. It would take a very long time to find this with a naïve search.
[ For a much larger and more complex example of the same sort of thing, see When do !!n!! and !!2n!! have the same digits?. I took a seemingly-intractable problem and analyzed it mathematically. I used considerably more than an ounce of theory in this case, and while the theory was not enough to solve the problem, it was enough to reduce the pool of candates to the point that a computer search was feasible. ]
[ Addendum 20150728: Another example ]
[Other articles in category /math] permanent link