Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| I abandon my abusive relationship with Facebook |
| Insane calculations in bash |
| It came from... the HOLD SPACE |
| Testing for exceptions |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Fri, 17 Feb 2012
It came from... the HOLD SPACE
Since 2002, I've given a talk almost every December for the Philadelphia Linux Users'
Group. It seems like most of their talks are about the newest and
best developments in Linux applications, which is a topic I don't know
much about. So I've usually gone the other way, talking about the
oldest and worst stuff. I gave a couple of pretty good talks about
how files work, for example, and what's in the inode structure.
I recently posted about my work on Zach Holman's spark program, which culminated in a ridiculous workaround for the shell's lack of fractional arithmetic. That work inspired me to do a talk about all the awful crap we had to deal with before we had Perl. (And the other 'P' languages that occupy a similar solution space.) Complete materials are here. I hope you check them out, because i think they are fun. This post is a bunch of miscellaneous notes about the talk.
One example of awful crap we had to deal with before Perl etc. were invented was that some people used to write 'sed scripts', although I am really not sure how they did it. I tried once, without much success, and then for this talk I tried again, and again did not have much success.



 The little guy to the right is known
as hallucigenia. It is a creature so peculiar that when
the paleontologists first saw the fossils, they could not even agree
on which side was uppermost. It has nothing to do with Unix, but I
put it on the slide to illustrate "alien horrors from the dawn of
time".
The little guy to the right is known
as hallucigenia. It is a creature so peculiar that when
the paleontologists first saw the fossils, they could not even agree
on which side was uppermost. It has nothing to do with Unix, but I
put it on the slide to illustrate "alien horrors from the dawn of
time".
Between slides 9 and 10 (about the ed line editor) I did a
quick demo of editing with ed. You will just have to imagine
this. I first learned to program with a line editor like ed,
on a teletypewriter just like the one on slide 8.
Modern editors are much better. But it used to
be that Unix sysadmins were expected to know at least a little ed,
because if your system got into some horrible state where it couldn't
mount the /usr partition, you wouldn't be able to run
/usr/bin/vi or /usr/local/bin/emacs, but you would
still be able to use /bin/ed to fix /etc/fstab or
whatever else was broken. Knowing ed saved my bacon several
times.
 (Speaking of
teletypewriters, ours had an attachment for punching paper tape, which
you can see on the left side of the picture. The punched chads fell
into a plastic chad box (which is missing in the picture), and when I
was about three I spilled the chad box. Chad was everywhere, and it
was nearly impossible to pick up. There were still chads stuck
in the cracks in the floorboards when we moved out three years
later. That's why, when the contested election of 2000 came around, I
was one of the few people in North America who was not bemused to
learn that there was a name for the little punched-out bits.)
(Speaking of
teletypewriters, ours had an attachment for punching paper tape, which
you can see on the left side of the picture. The punched chads fell
into a plastic chad box (which is missing in the picture), and when I
was about three I spilled the chad box. Chad was everywhere, and it
was nearly impossible to pick up. There were still chads stuck
in the cracks in the floorboards when we moved out three years
later. That's why, when the contested election of 2000 came around, I
was one of the few people in North America who was not bemused to
learn that there was a name for the little punched-out bits.)
Anyway, back to ed. ed has one and only one diagnostic: if you do something it didn't like, it prints ?. This explains the ancient joke on slide 10, which first appeared circa 1982 in the 4.2BSD fortune program.
I really wanted to present a tour de force of sed mastery, but as slides 24–26 say, I was not clever enough. I tried really hard and just could not do it. If anyone wants to fix my not-quite-good-enough sed script, I will be quite grateful.
On slide 28 I called awk a monster. This was a slip-up; awk is not a monster and that is why it does not otherwise appear in this talk. There is nothing really wrong with awk, other than being a little old, a little tired, and a little underpowered.
If you are interested in the details of the classify program, described on slide 29, the sources are still available from the comp.sources.unix archive. People often say "Why don't you just use diff for that?" so I may as well answer that here: You use diff if you have two files and you want to see how they differ. You use classify if you have 59 files, of which 36 are identical, 17 more are also identical to each other but different from the first 36, and the remaining 6 are all weirdos, and you want to know which is which. These days you would probably just use md5sum FILES | accumulate, and in hindsight that's probably how I should have implemented classify. We didn't have md5sum but we had something like it, or I could have made a checksum program. The accumulate utility is trivial.
Several people have asked me to clarify my claim to have invented netcat. It seems that a similar program with the same name is attributed to someone called "Hobbit". Here is the clarification: In 1991 I wrote a program with the functionality I described and called it "netcat". You would run netcat hostname port and it would open a network socket to the indicated address, and transfer data from standard input into the socket, and data from the socket to standard output. I still have the source code; the copyright notice at the top says "21 October 1991". Wikipedia says that the same-named program by the other guy was released on 20 March 1996. I do not claim that the other guy stole it from me, got the idea from me, or ever heard of my version. I do not claim to be the first or only person to have invented this program. I only claim to have invented mine independently.
My own current version of the spark program is on GitHub, but I think Zach Holman's current version is probably simpler and better now.
[ Addendum 20170325: I have revised this talk a couple of times since this blog article was written. Links to particular slides go to the 2011 versions, but the current version is from 2017. There are only minor changes. For example, I removed `awk` from the list of “monsters”. ]
[Other articles in category /Unix] permanent link
Wed, 15 Feb 2012
Insane calculations in bash
A few weeks ago I wrote an
article about various methods of arithmetic calculation in shell
scripts and in bash in particular, but it was all leading
up to today's article, which I think is more interesting
technically.
A while back, Zach Holman (who I hadn't heard of before, but who is apparently a bigwig at GitHub) implemented a kind of cute little hack, called "spark". It's a little shell utility, spark, which gets a list of numbers as its input and uses Unicode block characters to print a little bar graph of the numbers on the output. For example, the invocation:
spark 2,4,6,8will print out something like:
▃▄▆▇To do this in one of the 'P' languages (Perl, Python, PHP, Puby, or maybe Pickle) takes something like four lines of code. But M. Holman decided to implement it in bash for maximum portability, so it took 72 lines, not counting comments, whitespace, etc.
Let's begin by discussing the (very simple) mathematics that underlies drawing bar graphs. Suppose you want to generate a set of bars for the numbers $1, $9, $20. And suppose you can actually generate bars of integer heights only, say integers from 0–7:
0 1 ▁ 2 ▂ 3 ▃ 4 ▄ 5 ▅ 6 ▆ 7 ▇(M. Holman 's original program did this, even though a height-8 bar █ is available. But the mathematics is the same either way.)
Absolute scaling
The first step is to scale the input numbers onto the range of the bars. To do this, we find a scale factor f that maps dollars onto bar heights, say that f bar units = $1.A reasonable thing to try is to say that since your largest number is $20, we will set 7 bar units = $20. Then 0.35 bar units = $1, and 3.45 bar units = $9. We'll call these the "natural heights" for the bars.
Unfortunately we can't render the bars at their natural heights; we can only render them at integer heights, so we have to round off. 0.35 bar units rounds off to 0, so we will represent $1 as no bar at all. 3.45 bar units rounds off, badly, to 3, but that's the way it goes; if you try to squeeze the numbers from 1 to 20 into the range 0 to 7, something has to give. Anyway, this gives
(1,9,20) → ( ▃▇)
The formula is: Let max be the largest input number (here,
20) and let n be the size of the largest possible bar (here, 7).
Then an input number x becomes a bar of size
n·x / max:
$$x\rightarrow {n\cdot x \over max } $$
Note that this maps max itself to n, and 0 to 0.I'll call this method "absolute scaling", because big numbers turn into big bars. (It fails for negative numbers, but we'll assume that the numbers are non-negative.)
(0…20) → ( ▁▁▁▂▂▂▃▃▄▄▄▅▅▅▆▆▆▇▇)There are a couple of variations we might want to apply. First, maybe we don't like that $1 mapped to no bar at all; it's too hard to see, depending on the context. Perhaps we would like to guarantee that only 0 maps to 0. One way to ensure that is to round everything up, instead of rounding to the nearest integer:
(0…20) → ( ▁▁▂▂▂▃▃▃▄▄▄▅▅▅▆▆▆▇▇▇)
(1,9,20) → (▁▄▇)
Another benefit of always rounding up is that it uses the bars
equally. Suppose we're mapping numbers in the range 1–100 to bars of
heights 1–7. If we round off to the nearest integer, each bar
represents 14 or 15 different numbers, except that the tallest bar
only represents the 8 numbers 93–100. This is a typical situation.
If we always round up, each bar corresponds to a nearly equal range of
numbers. (Another way to adjust this is to replace n with
n+½ in the formula.)
Relative scaling
Now consider the numbers $18, $19, $20. Under the absolute scaling method, we get:
(18,19,20) → (▆▇▇)or, if you're rounding up,
(18,19,20) → (▇▇▇)which obscures the difference between the numbers. There's only an 11% difference between the tallest and shortest bar, and that doesn't show up at this resolution. Depending on your application, this might be what you want, but we might also want to avail ourselves of the old trick of adjusting the baseline. Instead of the bottom of the bar being 0, we can say it represents 17. This effectively reduces every bar by 17 before scaling it, so that the number x is now represented by a bar with natural height n·(x−17) / (max−17). Then we get these bars:
(18,19,20) → (▃▅▇)Whether this "relative scaling" is a better representation than ▇▇▇ depends on the application. It emphasizes different properties of the data.
In general, if we put the baseline at b, the natural height for a bar representing number x is:
$$x\rightarrow {n\cdot (x-b) \over (max-b) } $$
That is the same formula as before, except that everything has been shifted down by b.A reasonable choice of b would be the minimum input value, or perhaps a bit less than the minimum input value.
The shell sucks
But anyway, what I really wanted to talk about was how to fix this program, because I think my solution was fun and interesting. There is a tricky problem, which is that you need to calculate values like (n-b)/(x-b), which so you might like to do some division, but as I wrote earlier, bash has no facilities for doing fractional arithmetic. The original program used $((…)) everywhere, which throws away fractions. You can work around that, because you don't actually the fractional part of (n-b)/(x-b); you only need the greatest integer part. But the inputs to the program might themselves be fractional numbers, like say 3.5, and $((…)) barfs if you try to operate on such a number:
$ x=3.5; echo $((x + 1)) bash: 3.5: syntax error: invalid arithmetic operator (error token is ".5")and you seemingly cannot work around that.
My first response to this was to replace all the uses of $((…)) with bc, which, as I explained in the previous article, does not share this problem. M. Holman rejected this, saying that calling out to bc all the time made the program too slow. And there is something to be said for this. M. Holman also said that bc is non-portable, which I find astounding, since it has been in Unix since 1974, but sadly plausible.
So supposing that you take this complaint seriously, what can you do? Are you just doomed? No, I found a solution to the problem that solves all the problems. It is portable, efficient, and correct. It is also slightly insane.
Portable fractions in bash
We cannot use decimal numbers:
$ x=3.5; echo $((x + 1)) bash: 3.5: syntax error: invalid arithmetic operator (error token is ".5")But we can use fractions:
$ x_n=7; x_d=2; echo $((x_n + x_d))/$((x_d))
9/2
And we can convert decimal inputs to fractions without arithmetic:
# given an input number which might be a decimal, convert it to
# a rational number; set n and d to its numerator and
# denominator. For example, 3.3 becomes n=33 and d=10;
# 17 becomes n=17 and d=1.
to_rational() {
# Crapulent bash can't handle decimal numbers, so we will convert
# the input number to a rational
if [[ $1 =~ (.*)\.(.*) ]] ; then
i_part=${BASH_REMATCH[1]}
f_part=${BASH_REMATCH[2]}
n="$i_part$f_part";
d=$(( 10 ** ${#f_part} ))
else
n=$1
d=1
fi
}
This processes a number like 35.17 in a purely lexical way, extracting
the 35 and the 17, and turning them into the numerator 3517 and the
denominator 100. If the input number contains no decimal point, our
task is trivial: 23 has a numerator of 23 and a denominator of 1.Now we can rewrite all the shell arithmetic in terms of rational numbers. If a_n and a_d are the numerator and denominator of a, and b_n and b_d are the numerator and denominator of b, then addition, subtraction, multiplication, and even division of a and b are fast, easy, and even portable:
# a + b
sum_n = $((a_n * b_d + a_d * b_n))
sum_d = $((a_d * b_d))
# a - b
diff_n = $((a_n * b_d - a_d * b_n))
diff_d = $((a_d * b_d))
# a * b
prod_n = $((a_n * b_n))
prod_d = $((a_d * b_d))
# a / b
quot_n = $((a_n * b_d))
quot_d = $((a_d * b_n))
We can easily truncate a number to produce an integer, because the
built-in division does this for us:
greatest_int = $((a_n / a_d))
And we can round to the nearest integer by adding 1/2 before
truncating:
nearest_int = $(( (a_n * 2 + a_d) / (a_d * 2) ))
(Since n/d + 1/2 = (2n+d)/2d.)For complicated calculations, you can work the thing out as several steps, or you can solve it on paper and then just embed a big rational expression. For example, suppose you want to calculate ((x-min)·number_of_tiers)/range, where number_of_tiers is known to be an integer. You could do each operation in a separate step, or you could use instead:
tick_index_n=$(( ( x_n * min_d - min_n * x_d ) * number_of_tiers * range_d )) tick_index_d=$(( range_n * x_d * min_d ))Should you need to convert to decimals for output, the following is a proof-of-concept converter:
function to_dec {
n=$1
d=$2
maxit=$(( 1 + ${3:-10} ))
while [ $n != 0 -a $maxit -gt -1 ]; do
next=$((n/d))
if [ "$r" = "" ]; then r="$next."; else r="$r$next"; fi
n=$(( (n - d * next) * 10 ))
maxit=$(( maxit - 1 ))
done
r=${r:-'0.'}
}
For example, to_dec 13 8 sets r to
1.625, and to_dec 13 7 sets r to
1.857142857. The optional third argument controls the
maximum number of digits after the decimal point, and defaults to
10. The principal defect is that it doesn't properly round off;
frac2dec 19 10 0 yields 1. instead of 2.,
but this could be fixed without much trouble. Extending it to
convert to arbitrary base output is quite easy as well.Coming next month, libraries in bash for computing with continued fractions using Gosper's algorithms. Ha ha, just kidding. The obvious next step is to implement base-10 floating-point numbers in bash like this:
prod_mantissa=$((a_mantissa * b_mantissa)) prod_exponent=$((a_exponent + b_exponent))[ Addendum 20120306: David Jones corrects a number of portability problems in my implementation. ]
[ Addendum 20180101: Shane Hansen did something similar to calculate Euler's number (2.71818…) in Bash a while back. It might be fun to compare our implementations. ]
[Other articles in category /prog] permanent link
Fri, 10 Feb 2012
I abandon my abusive relationship with Facebook
I have just deactivated my Facebook account, I hope for good.
This interview with Eben Moglen provides many of the reasons, and was probably as responsible as anything for my decision.
But the straw that broke the camel's back was a tiny one. What finally pushed me over the edge was this: "People who can see your info can bring it with them when they use apps.". This time, that meant that when women posted reviews of men they had dated on a dating review site, the review site was able to copy the men's pictures from Facebook to insert into the reviews. Which probably was not what the men had in mind when they first posted those pictures to Facebook.
This was, for me, just a little thing. But it was the last straw because when I read Facebook's explanation of why this was, or wasn't, counter to their policy, I realized that with Facebook, you cannot tell the difference.
For any particular appalling breach of personal privacy you can never guess whether it was something that they will defend (and then do again), or something that they will apologize for (and then do again anyway). The repeated fuckups for which they are constantly apologizing are indistinguishable from their business model.
So I went to abandon my account, and there was a form they wanted me to fill out to explain why: "Reason for leaving (Required)": One choice was "I have a privacy concern.":
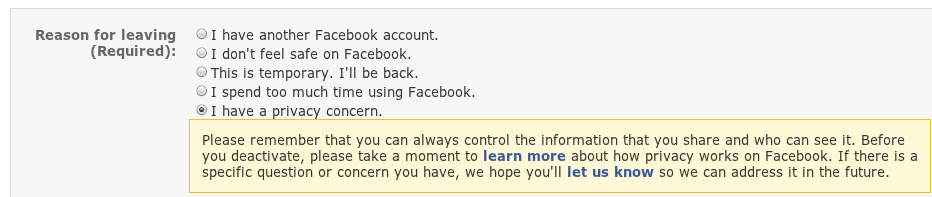
Please remember that you can always control the information that you share and who can see it. Before you deactivate, please take a moment to learn more about how privacy works on Facebook. If there is a specific question or concern you have, we hope you'll let us know so we can address it in the future.It was really nice of Facebook to provide this helpful reminder that their corporation is a sociopath: "Please remember that you can always control the information that you share and who can see it. You, and my wife, Morgan Fairchild."
Facebook makes this insane claim in full innocence, expecting you to believe it, because they believe it themselves. They make this claim even after the times they have silently changed their privacy policies, the times they have silently violated their own privacy policies, the times they have silently opted their users into sharing of private information, the times they have buried the opt-out controls three pages deep under a mountain of confusing verbiage and a sign that said "Beware of The Leopard".
There's no point arguing with a person who makes a claim like that. Never mind that I was in the process of deactivating my account. I was deactivating my account, and not destroying it, because they refuse to destroy it. They refuse to relinquish the personal information they have collected about me, because after all it is their information, not mine, and they will never, ever give it up, never. That is why they allow you only to deactivate your account, while they keep and continue to use everything, forever.
But please remember that you can always control the information that you share and who can see it. Thanks, Facebook! Please destroy it all and never let anyone see it again. "Er, no, we didn't mean that you could have that much control."
This was an abusive relationship, and I'm glad I decided to walk away.
[ Addendum 20120210: Ricardo Signes points out that these is indeed an option that they claim will permanently delete your account, although it is hard to find. ]
[ Addendum 20220704: Looking back on this from ten years out, I am struck by two things. First, there many many times in the intervening decade that Facebook did horrible, awful things to its users, and I shrugged because I wasn't involved. And second, there were not any times when I regretted not being on Facebook. Leaving was a pure win. Come join me, it's not too late. ]
[Other articles in category /misc] permanent link
Thu, 09 Feb 2012
Testing for exceptions
The Test::Fatal
module makes it very easy to test code that is supposed to throw
an exception. It provides an exception function that takes a
code block. If the code completes normally, exception {
code } returns undefined; if the code throws an exception,
exception { code } returns the exception value that
was thrown. So for example, if you want to make sure that some
erroneous call is detected and throws an exception, you can use
this:
isnt( exception { do_something( how_many_times => "W" ) },
undef,
"how_many_times argument requires a number" );
which will succeed if do_something(…) throws an exception,
and fail if it does not. You can also write a stricter test, to look
for the particular exception you expect:
like( exception { do_something( how_many_times => "W" ) },
qr/how_many_times is not numeric/,
"how_many_times argument requires a number" );
which will succeed if do_something(…) throws an exception
that contains how_many_times is not numeric, and fail
otherwise.Today I almost made the terrible mistake of using the first form instead of the second. The manual suggests that you use the first form, but it's a bad suggestion. The problem is that if you completely screw up the test and write a broken code block that dies, the first test will cheerfully succeed anyway. For example, suppose you make a typo in the test code:
isnt( exception { do_something( how_many_tims => "W" ) },
undef,
"how_many_times argument requires a number" );
Here the do_something(…) call throws some totally different
exception that we are not interested in, something like unknown
argument 'how_many_tims' or mandatory 'how_many_times'
argument missing, but the exception is swallowed and the test
reports success, even though we know nothing at all about the feature
we were trying to test. But the test looks like it passed.In my example today, the code looked like this:
isnt( exception {
my $invoice = gen_invoice();
$invoice->abandon;
}, undef,
"Can't abandon invoice with no abandoned charges");
});
The abandon call was supposed to fail, for reasons you don't
care about. But in fact, the execution never got that far, because
there was a totally dumb bug in gen_invoice() (a missing
required constructor argument) that caused it to die with a completely
different exception.I would never have noticed this error if I hadn't spontaneously decided to make the test stricter:
like( exception {
my $invoice = gen_invoice();
$invoice->abandon;
}, qr/Can't.*with no abandoned charges/,
"Can't abandon invoice with no abandoned charges");
});
This test failed, and the failure made clear that
gen_invoice(), a piece of otherwise unimportant test
apparatus, was completely broken, and that several other tests I had
written in the same style appeared to be passing but weren't actually
running the code I thought they were.So the rule of thumb is: even though the Test::Fatal manual suggests that you use isnt( exception { … }, undef, …), do not.
I mentioned this to Ricardo Signes, the author of the module, and he released a new version with revised documentation before I managed to get this blog post published.
[Other articles in category /prog/perl] permanent link


