Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sat, 30 Jun 2007
How to calculate the square root of 2
A few weeks ago I
mentioned the following recurrence:
| p0 = 1 | q0 = 1 |
| pi+1 = pi + 2qi | qi+1 = pi + qi |
I said that this formula comes from consideration of continued fractions. But I was thinking about it a little more, and I realized that there is a way to get such a recurrence for pretty much any algebraic constant you want.
Consider for a while the squaring function s : x → x2. This function has two obvious fixed points, namely 0 and 1, by which I mean that s(0) = 0 and s(1) = 1. Actually it has a third fixed point, ∞.
If you consider the behavior on some x in the interval (0, 1), you see that s(x) is also in the same interval. But also, s(x) < x on this interval. Now consider what happens when you iterate s on this interval, calculating the sequence s(x), s(s(x)), and so on. The values must stay in (0, 1), but must always decrease, so that no matter what x you start with, the sequence converges to 0. We say that 0 is an "attracting" fixed point of s, because any starting value x, no matter how far from 0 it is (as long as it's still in (0, 1)), will eventually be attracted to 0. Similarly, 1 is a "repelling" fixed point, because any starting value of x, no matter how close to 1, will be repelled to 0.
Consideration of the interval (1, ∞) is similar. 1 is a repeller and ∞ is an attractor.
Fixed points are not always attractors or repellers. The function x → 1/x has fixed points at ±1, but these points are neither attractors nor repellers.
Also, a fixed point might attract from one side and repel from the other. Consider x → x/(x+1). This has a fixed point at 0. It maps the interval (0, ∞) onto (0, 1), which is a contraction, so that 0 attracts values on the right. On the other hand, 0 repels values on the left, because 1/-n goes to 1/(-n+1). -1/4 goes to -1/3 goes to -1/2 goes to -1, at which point the whole thing blows up and goes to -∞.
The idea about the fixed point attractors is suggestive. Suppose we were to pick a function f that had √2 as a fixed point. Then √2 might be an attractor, in which case iterating f will get us increasingly accurate approximations to √2.
So we want to find some function f such that f(√2) = √2. Such functions are very easy to find! For example, take √2. square it, and divide by 2, and add 1, and take the square root, and you have √2 again. So x → √(1+x2/2) is such a function. Or take √2. Take the reciprocal, double it, and you have √2 again. So x → 2/x is another such function. Or take √2. Add 1 and take the reciprocal. Then add 1 again, and you are back to √2. So x → 1 + 1/(x+1) is a function with √2 as a fixed point.
Or we could look for functions of the form ax2 + bx + c. Suppose √2 were a fixed point of this function. Then we would have 2a + b√2 + c = √2. We would like a, b, and c to be simple, since the whole point of this exercise is to calculate √2 easily. So let's take a=b=1, c=-2. The function is now x → x2 + x - 2.
Which one to pick? It's an embarrasment of riches.
Let's start with the polynomial, x → x2 + x - 2. Well, unfortunately this is the wrong choice. √2 is a fixed point of this function, but repels on both sides: √2 ± ε → √2 ± ε(1 + 2√2), which is getting farther away.
The inverse function of x → x2 + x - 2 will have √2 as an attractor on both sides, but it is not so convenient to deal with because it involves taking square roots. Still, it does work; if you iterate ½(-1 + √(9 + 4x)) you do get √2.
Of the example functions I came up with, x → 2/x is pretty simple too, but again the fixed points are not attractors. Iterating the function for any initial value other than the fixed points just gets you in a cycle of length 2, bouncing from one side of √2 to the other forever, and not getting any closer.
But the next function, x → 1 + 1/(x+1), is a winner. (0, ∞) is crushed into (1, 2), with √2 as the fixed point, so √2 attracts from both sides.
Writing x as a/b, the function becomes a/b → 1 + 1/(a/b+1), or, simplifying, a/b → (a + 2b) / (a + b). This is exactly the recurrence I gave at the beginning of the article.
We did get a little lucky, since the fixed point of interest, √2, was the attractor, and the other one, -√2, was the repeller. ((-∞, -1) is mapped onto (-∞, 1), with -√2 as the fixed point; -√2 repels on both sides.) But had it been the other way around we could have exchanged the behaviors of the two fixed points by considering -f(-x) instead. Another way to fix it is to change the attractive behavior into repelling behavior and vice versa by running the function backwards. When we tried this for x → x2 + x - 2 it was a pain because of the square roots. But the inverse of x → 1 + 1/(x+1) is simply x → (-x + 2) / (x - 1), which is no harder to deal with.
The continued fraction stuff can come out of the recurrence, instead of the other way around. Let's iterate the function x → 1 + 1/(1+x) formally, repeatedly replacing x with 1 + 1/(1+x). We get:
1 + 1/(1+x)So we might expect the fixed point, if there is one, to be 1 + 1/(2 + 1/(2 + 1/(2 + ...))), if this makes sense. Not all such expressions do make sense, but this one is a continued fraction, and continued fractions always make sense. This one is eventually periodic, and a theorem says that such continued fractions always have values that are quadratic surds. The value of this one happens to be √2. I hope you are not too surprised.
1 + 1/(1+1 + 1/(1+x))
1 + 1/(1+1 + 1/(1+1 + 1/(1+x)))
...
In the course of figuring all this out over the last two weeks or so, I investigated many fascinating sidetracks. The x → 1 + 1/(x+1) function is an example of a "Möbius transformation", which has a number of interesing properties that I will probably write about next month. Here's a foretaste: a Möbius transformation is simply a function x → (ax + b) / (cx + d) for some constants a, b, c, and d. If we agree to abbreviate this function as !!{ a\, b \choose c\,d}!!, then the inverse function is also a Möbius transformation, and is in fact !!{a\, b\choose c\,d}^{-1}!!.
[ Addendum 20070719: There is a followup article to this one. ] [ Addendum 20201018: Another followup article. ]
[Other articles in category /math] permanent link
Sun, 24 Jun 2007
Do you dream in color?
People have occasionally asked me whether I dreamt in color or on
black-and-white, by which I suppose they meant grayscale. This
question was strange to me the first time I heard it, because up to
then it had not occurred to me that anyone did not dream in color. I
still find it strange, and I had to do a Google search to verify that
there really are people who claim not to dream in color.
One time, when I replied that I did dream in color, my interlocutor asked me if I was sure: perhaps I dreamt in black and white, but only remembered it as being in color later.
I am sure I dream in color, because on more than one occasion I have had discussions in dreams about colors of objects. I can't remember any examples right now, but it was something like this: "Give me the red apple." "Okay, here." "That is not the red apple, that is the green apple!" And then I looked and saw that the apple I had thought was red was really green.
One could still argue that I wasn't really dreaming in color, that it only seemed like that, or something. It's a delicate philosophical point. One could also argue that I didn't have any dream at all, I only thought I did after I woke up. I suppose the only refutations of such an argument either appeal to neurology or involve a swift kick in the pants.
And then suppose I have a dream in which I take LSD and have marvelous hallucinations. Did I really have hallucinations? Or did I only dream them? If I dream that I kill someone, we agree that it wasn't real, that a dream murder is not a real murder; it is only in your head. But hallucinations, by definition, are only in your head even when they are real, so don't dream hallucinations have as much claim to reality as waking hallucinations?
One might argue that dreamt LSD hallucinations are likely to be qualitatively very different from real LSD hallucinations—less like real LSD hallucinations, say, and more like, well, dreams. But this only refutes the claim that the dream hallucinations were LSD hallucinations. And nobody was going to claim that they were LSD hallucinations anyway, since no actual LSD was involved. So this doesn't address the right question.
Stickier versions of the same problem are possible. For example, suppose I give Bill a little piece of paper and tell him it is impregnated with LSD. It is not, but because of the placebo effect, Bill believes himself to be having an LSD trip and reports hallucinations. There was no LSD involved, so the hallucinations were only imaginary. But even real hallucinations are only imaginary. Are we really justified in saying that Bill is mistaken, that he did not actually hallucinate, but only imagined that he did? That seems like a very difficult position to defend.
I seem to have wandered from the main point, which is that I had another dream last night that supports my contention that I dream in color. I was showing my friend Peter some little homunculi that had been made long ago from colored pipe cleaners, shiny paper, and sequins by my grandmother's friend Kay Seiler. Originally there had been ten of these, but in the dream I had only five. When my grandmother had died, my sister and I had split the set, taking five each. In place of the five originals I was missing, I had five copies, which were identifiable as such because they were in grayscale. Presumably my sister had grayscale copies of the originals I retained. I explained this to Peter, drawing his attention to the five full-color homunculi and the five grayscale ones.
So yes, barring philosophical arguments that I think deserve a kick in the pants, I am sure that I dream in color.
[Other articles in category /brain] permanent link
Sun, 17 Jun 2007
Square triangular numbers
A while back I made the erroneous assertion that no numbers
are both square and triangular. As I noted in a followup, this is
a rather stupid thing to say, since both 0 and 1 are obvious
counterexamples. (36 is a nontrivial counterexample.) Also, a few
years before I had actually investigated this very question and had
determined that the set of such numbers is infinite. Whoops.
I no longer remember how I solved the problem the first time around, but I was tinkering around with it today and came up with an approach that I think is instructive, or at least interesting.
We want to find non-negative integers a and b such that ½(a2 + a) = b2. Or, equivalently, we want a and b such that √(a2 + a) = b√2.
Now, √(a2 + a) is pretty nearly a + ½. So suppose we could find p and q with a + ½ = b·p/q, and p/q a bit larger than √2. a + ½ is a bit too large to be what we want on the left, but p/q is a bit larger than what we want on the right too. Perhaps the fudging on both sides would match up, and we would get √(a2 + a) = b√2 anyway.
If this magic were somehow to occur, then a and b would be the numbers we wanted.
Finding p/q that is a shade over √2 is a well-studied problem, and one of the things I have in my toolbox, because it seems to come up over and over in the solution of other problems, such as this one. It has interesting connections to several other parts of mathematics, and I have written about it here before.
The theoretical part of finding p/q close to √2 is some thing about continued fractions that I don't want to get into today. But the practical part is very simple. The following recurrence generates all the best rational approximations to √2; the farther you carry it, the better the approximation:
| p0 = 1 | q0 = 1 |
| pi+1 = pi + 2qi | qi+1 = pi + qi |
| p | q | p/q |
| 1 | 1 | 1.0 |
| 3 | 2 | 1.5 |
| 7 | 5 | 1.4 |
| 17 | 12 | 1.416666666666667 |
| 41 | 29 | 1.413793103448276 |
| 99 | 70 | 1.414285714285714 |
| 239 | 169 | 1.414201183431953 |
| 577 | 408 | 1.41421568627451 |
| 1393 | 985 | 1.414213197969543 |
| 3363 | 2378 | 1.41421362489487 |
Now, we want a + ½ = b·p/q, or equivalently (2a + 1)/2b = p/q. This means we can restrict our attention to the rows of the table that have q even. This is a good thing, because we need p/q a bit larger than √2, and those are precisely the rows with even q. The rows that have q odd have p/q a bit smaller than √2, which is not what we need. So everything is falling into place.
Let's throw away the rows with q odd, put a = (p - 1)/2 and b = q/2, and see what we get:
| p | q | a | b | ½(a2+a) = b2 |
| 3 | 2 | 1 | 1 | 1 |
| 17 | 12 | 8 | 6 | 36 |
| 99 | 70 | 49 | 35 | 1225 |
| 577 | 408 | 288 | 204 | 41616 |
| 3363 | 2378 | 1681 | 1189 | 1413721 |
I have two points to make about this. One is that I have complained in the past about mathematical pedagogy, how the convention is to come up with some magic-seeming guess ahead of time, as when pulling a rabbit from a hat, and then at the end it is revealed to be the right choice, but what really happened was that the author worked out the whole thing, then saw at the end what he would need at the beginning to make it all work, and went back and filled in the details.
That is not what happened here. My apparent luck was real luck. I really didn't know how it was going to come out. I was really just exploring, trying to see if I could get some insight into the answer without necessarily getting all the way there; I thought I might need to go back and do a more careful analysis of the fudge factors, or something. But sometimes when you go exploring you stumble on the destination by accident, and that is what happened this time.
The other point I want to make is that I've written before about how a mixture of equal parts of numerical sloppiness and algebraic tinkering, with a dash of canned theory, can produce useful results, in a sort of alchemical transmutation that turns base metals into gold, or at least silver. Here we see it happen again.
[Other articles in category /math] permanent link
Sat, 16 Jun 2007
Frances Trollope arrives in America
More than a year ago
I mentioned Frances Trollope's book Domestic Manners of the
Americans, which I have at long last checked out of the library
and begun to read. I am only at page 40 or so, but it is easy going,
and entertaining.
Trollope's book begins with her arrival from Europe in New Orleans. I was drawn in early on by the following passage, which appears on page 5:
The land is defended from the encroachments of the river by a high embankment which is called the Levée; without which the dwellings would speedily disappear, as the river is evidently higher than the banks would be without it. . . . She was looking so mighty, and so unsubdued all the time, that I could not help fancying she would some day take the matter into her own hands again, and if so, farewell to New Orleans.
The book was published in 1832.
[Other articles in category /book] permanent link
Thu, 14 Jun 2007
Harry Potter and the Goblet of Fire
I have not been too impressed with the Harry Potter
books. I read them all, one at a time, on airplanes. They are good
for this because they are fat, undemanding, and readily available in
airport bookshops for reasonable prices. In a lot of ways they are
badly constructed, but there is really no point in dwelling on their
flaws. The Potter books have been widely criticized already from all
directions, and so what? People keep buying them.
But The Goblet of Fire has been bothering me for years now, because its plot is so very stupid. I am complaining about it here in my blog because it continues to annoy me, and I hope to forget about it after I write this. The rest of this article will contain extensive spoilers, and I will assume that you either know it all already or that you don't care.
The bad guys want to kill Harry Potter, the protagonist. The Triwizard Tournament is being held at Harry's school. In the tournament, the school champions must overcome several trials, the last of which is to race through a maze and grab the enchanted goblet at the center of the maze. The bad guys' plan is this: they will enter Harry in the tournament. They will interfere subtly in the tournament, to ensure that Harry is first to lay hands on the goblet. They will enchant the goblet so that it is a "portkey", and whoever first touches it will be transported into their evil clutches.
They need an evil-doer on the spot, to interfere in the competition in Harry's favor; if he is eliminated early, or fails to touch the goblet first, all their plotting will be for naught. So they abduct and imprison Mad-eye Moody, a temporary faculty member and a famous capturer of evil-doers, and enchant one of their own to impersonate him for the entire school year.
The badness of this plan is just mind-boggling. Moody is a tough customer. If they fail to abduct him, or if he escapes his year-long captivity, their plans are in the toilet. If the substitution is detected, their plans are in the toilet. Their fake Moody will be teaching a class in "Defense Against the Dark Arts", a subject in which the real Moody has real expertise that the substitute lacks; the substitute somehow escapes detection on this front. For several months the fake Moody will be eating three meals a day with a passel of witches and wizards who are old friends with the real Moody, and among whom is Albus Dumbledore, who supposedly is not a complete idiot; the substitute somehow escapes detection on this front as well.
Even with the substitution accomplished, the bad guys' task is far from easy. Harry procrastinates everything he can and it's all they can do to arrange that he is not eliminated from the tournament. None of the other champions are either, and the villains have a tough problem to make sure that he is first through the maze.
Here is an alternative plan, which apparently did not occur to the fearsome Lord Voldemort: instead of making the Goblet of Fire into a portkey, he should enchant a common object, say a pencil. We know this is possible, since it has been explicitly established that absolutely any object can be a portkey, and the first instance of one that we see appears to be an abandoned boot. Then, since fake Moody is teaching Harry's class, sometime during the first week of the term he should ask Harry to stay behind on some pretext, and then say "Oh, Harry, would you please pass me that pencil over there?" After Harry is dead, fake Moody can disappear. A little thought will no doubt reveal similar plans that involve no substitutions or imprisonments: send Harry a booby-trapped package in the mail, or enchant his socks, or something of the sort.
In fact, they do something like this in one of the later books; they sell another character, I think Ginny Weasley, some charm that puts her under their control. This is a flub already, because they should have sold it to Harry instead—duh—and then had him kill himself. Or they could have sold him a portkey. Or an exploding candy. But I don't want to belabor the point.
Normally I have no trouble suspending my disbelief in matters like this. I can forgive a little ineptness on the part of the master schemers, because I am such an inept schemer that I usually don't notice. When evil plots seem over-elaborate and excessively risky to me, I just imagine that it seems that way because evil plots are so far outside my area of expertise, and read on. But in The Goblet of Fire I couldn't do this. My enjoyment of the book was disrupted by the extreme ineptness of the evil scheme.
One of Rowling's recurring themes is the corruption and ineptness of the ostensibly benevolent government. But perhaps this incompetence is a good thing. If the good guys had been less incompetent in the past, the bad guys might have had to rise to the occasion, and would have stomped Harry flat in no time. Lulled into complacency by years of ineffective opposition, they become so weak and soft that they are defeated by a gang of teenagers.
Okay, that's off my chest now. Thanks for your forbearance.
[Other articles in category /book] permanent link
Wed, 13 Jun 2007
How to calculate binomial coefficients, again
Yesterday's article about how to
calculate binomial coefficients was well-received. It was posted
on Reddit, and to my surprise and gratification, the comments were
reasonably intelligent. Usually when a math article of mine shows up
on Reddit, all the megacretins come out of the woodwork to say what an
idiot I am, and why don't I go back to school and learn basic logic.
A couple of people pointed out that, contrary to what I asserted, the
algorithm I described can in fact overflow even when the final result
is small enough to fit in a machine word. Consider
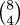 for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps.
for example. The algorithm, as I wrote
it, calculates intermediate values 8, 8, 56, 28, 168, 56, 280, 70, and
70 is the final answer. If your computer has 7-bit machine integers,
the answer (70) will fit, but the calculation will overflow along the
way at the 168 and 280 steps.
Perhaps more concretely, !!35\choose11!! is 417,225,900, which is small enough to fit in a 32-bit unsigned integer, but the algorithm I wrote wants to calculate this as !!35{34\choose10}\over11!!, and the numerator here is 4,589,484,900, which does not fit.
One Reddit user suggested that you can get around this as follows: To multiply r by a/b, first check if b divides r. If so, calculate (r/b)·a; otherwise calculate (r·a)/b. This should avoid both overflow and fractions.
Unfortunately, it does not. A simple example is !!{14\choose4} = {11\over1}{12\over2}{13\over3}{14\over4}!!. After the first three multiplications one has 286. One then wants to multiply by 14/4. 4 does not divide 286, so the suggestion calls for multiplying 286 by 14/4. But 14/4 is 3.5, a non-integer, and the goal was to use integer arithmetic throughout.
| Buy The Art of Computer Programming: Volume 2, Seminumerical Algorithms from Bookshop.org (with kickback) (without kickback) |
I haven't looked, but it is hard to imagine that Volume II of Knuth doesn't discuss this in exhaustive detail, including all the stuff I just said, plus a bunch of considerations that hadn't occurred to any of us.
A few people also pointed out that you can save time when n
> m/2 by calculating !!m\choose m-n!! instead of  . For example, instead of calculating !!100\choose98!!, calculate
. For example, instead of calculating !!100\choose98!!, calculate 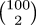 . I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.
. I didn't mention this in the original article
because it was irrelevant to the main point, and because I thought it
was obvious.
[Other articles in category /math] permanent link
Tue, 12 Jun 2007
How to calculate binomial coefficients
The binomial coefficient !!n\choose
k!! is usually defined as:
$${n\choose k} = {n!\over k!(n-k)!}$$
This is a fine definition, brief, closed-form, easy to prove theorems about. But these good qualities seduce people into using it for numerical calculations:
fact 0 = 1
fact (n+1) = (n+1) * fact n
choose n k = (fact n) `div` ((fact k)*(fact (n-k)))
(Is it considered bad form among Haskellites to use the
n+k patterns? The Haskell Report is decidedly
ambivalent about them.)
Anyway, this is a quite terrible way to calculate binomial
coefficients. Consider calculating !!100\choose 2!!, for example. The result
is only 4950, but to get there the computer has to calculate 100! and
98! and then divide these two 150-digit numbers. This requires the
use of bignums in languages that have bignums, and causes an
arithmetic overflow in languages that don't. A straightforward
implementation in C, for example, drops dead with an arithmetic
exception; using doubles instead, it claims that the value of 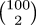 is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
is -2147483648. This is all quite sad, since the
correct answer is small enough to fit in a two-byte integer.
Even in the best case, !!2n\choose n!!, the result is only on the order of 4n, but the algorithm has to divide a numerator of about 4nn2n by a denominator of about n2n to get it.
A much better way to calculate values of 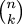 is to use the following recurrence:
is to use the following recurrence:
$${n+1\choose k+1} = {n+1\over k+1}{n\choose k}$$
This translates to code as follows:
choose n 0 = 1
choose 0 k = 0
choose (n+1) (k+1) = (choose n k) * (n+1) `div` (k+1)
This calculates !!8\choose 4!! as
!!{5\over1}{6\over2}{7\over3}{8\over4}
!!. None of the intermediate results are larger than the
final answer.An iterative version is also straightforward:
unsigned choose(unsigned n, unsigned k) {
unsigned r = 1;
unsigned d;
if (k > n) return 0;
for (d=1; d <= k; d++) {
r *= n--;
r /= d;
}
return r;
}
This is speedy, and it cannot cause an arithmetic overflow unless the
final result is too large to be represented.It's important to multiply by the numerator before dividing by the denominator, since if you do this, all the partial results are integers and you don't have to deal with fractions or floating-point numbers or anything like that. I think I may have mentioned before how much I despise floating-point numbers. They are best avoided.
I ran across this algorithm last year while I was reading the Lilavati, a treatise on arithmetic written about 850 years ago in India. The algorithm also appears in the article on "Algebra" from the first edition of the Encyclopaedia Britannica, published in 1768.
So this algorithm is simple, ancient, efficient, and convenient. And the problems with the other algorithm are obvious, or should be. Why isn't this better known?
[ Addendum 20070613: There is a followup article to this one. ]
[Other articles in category /math] permanent link
Sun, 10 Jun 2007 One of the books in the bedtime-reading rotation for my daughter Katara is A Bargain for Frances, by Russell and Lillian Hoban. (Russell Hoban is also the author of a number of acclaimed novels for adults, most notably Riddley Walker.) The plot and character relationships in A Bargain for Frances are quite complex, probably about at the limit of what a two-year-old can handle. I will try to summarize.Frances the badger is having a tea party with her friend Thelma, who has previously behaved abusively to her. Thelma's tea set is plastic, with red flowers. Frances is saving up her money for a real china tea set with blue pictures. Thelma asserts that those tea sets are no longer made, and that they are prohibitively expensive. She offers to sell Frances her own tea set, in return for Frances's savings of $2.17. Frances agrees. End of act I.
When Frances returns home with the plastic tea set, her little sister Gloria criticizes it, saying repeatedly that it is "ugly". She reports that the china kind with blue pictures is available in the local candy store for $2.07, and that Thelma knows this. Frances rushes to the candy store, where she witnesses Thelma buying a china tea set with her money. End of act II.
There is an act III, but I do not want to spoil the ending.
There is quite a lot here to engage the mind of a two-year-old: what does it mean to make a trade, for example? And Thelma is quite devious in the way she talks up the benefits of her plastic tea set ("It does not break, unless you step on it") while dissembling her own desire for a china one. Katara has not yet learned to deceive others for her own benefit, and I think this is her first literary exposure to the idea.
I mentioned at one point that Thelma had told a lie: she had said "I don't think they make that kind [of tea set] anymore" when she knew that the very tea set was available at the candy store. Katara was very interested by this observation. She asked me repeatedly, over a period of a several weeks, to explain to her what a lie was. I had some trouble, because I did not have any good examples to draw on. Katara does not do it yet, and Lorrie and I do not lie to Katara either.
One time I tried to explain lies by telling Katara about how people sometimes tell children that if they do not behave, goblins will come and take them away. Of course, this didn't work. First I had to explain what goblins were. Katara was very disturbed at the thought of goblins that might take her away. I had to reassure Katara that there were no goblins. We got completely sidetracked on a discussion of goblins. I should have foreseen this, but it was the best example I was able to come up with on the spur of the moment.
Later I thought of a better example, with no distracting goblins: suppose Katara asks for raspberries, and I know there are some in the refrigerator, but I tell her that we have none, because I want to eat them myself. I think this was just a little bit too complicated for Katara. It has four parts, and I try to keep explanations to three parts, which seems to be about the maximum that she can follow at once. (Two parts is even better.) I think Katara attached too much significance to the raspberries; for a while she seemed to think that lying had something to do with raspberries.
Oh well, at least I tried. She will catch on soon enough, I am sure.
Perhaps the most complex idea in the book is this: when Frances and Thelma agree to trade money for tea set, they agree on "no backsies". This is an important plot point. After the second or third reading, Katara asked me what "no backsies" meant.
I had to think about this carefully before I answered, because it is quite involved, and until I thought it through, I was not sure I understood it myself. You might want to think about this before reading on. Remember that it's not enough to understand it; you have to be able to explain it.
My understanding of "no backsies" was that normally, when friends trade, there is an assumption that the exchange may be unilaterally voided by either party, as long as this is done timely. You can come back the next day and say you have changed your mind, and your friend, being your friend, is expected to consent. Specifying "no backsies" establishes an advance agreement that this is not the case. If you come back the next day, your friend can protest "but we said there were no backsies on this" and refuse to undo the trade. (The trade can, of course, be voided later if both parties agree.)
So to understand this, you must first understand what it means to trade, and why. Katara took this in early on, and fairly easily. You also have to understand the idea that one or both parties might want to change their minds later; this is also something Katara can get her head around. Toddlers know all about what it means to change one's mind.
But then you have to understand that one party might want to annul the agreement and the other party might not. Tracking two people's independent and conflicting desires is probably a little too hard for Katara at this stage. She can sometimes understand another person's point of view, by identification. ("You sometimes feel like x; here this other person feels the same way.") And similarly she can immerse herself in the world-view of the protagonist of a book, and understand that the protagonist's desires might be frustrated by another character. But to immerse herself in both world-views simultaneously is beyond her.
"No backsies" goes beyond this: you have to understand the idea that an agreement might have default, unspoken conventions, and that the participants will adhere to these conventions even if they don't want to; this is not something that two-year-olds are good at doing yet. You have to understand the idea of an explicit modification to the default conditions; that part is not too hard, and everyday examples abound. But then you have to understand what the unspoken convention actually is, and how it is being modified, and the difference between a unilateral annulment of an agreement and a bilateral one. Again, I think it's the bilaterality that's hard for Katara to understand. She is still genuinely puzzled when I tell her we should leave the public restroom clean for the next person.
Really, though, the main difficulty is just that the idea is very complicated. Maybe I'm wrong about which parts are harder and which parts are easier, and perhaps Katara can understand any of the pieces separately. But at two years old she can't yet sustain a train of thought as complicated as the one required to pull together all the pieces of "no backsies". This sort of understanding is one of the essential components of being an adult, and she will get it sooner or later; probably sooner.
This is not the only part of the book that repays careful thought. At one point, during Thelma's monologue about the unavailability of china tea sets, she says:
I know another girl who saved up for that tea set. Her mother went to every store and could not find one. Then that girl lost some of her money and spent the rest on candy. She never got the tea set. A lot of girls never do get tea sets. So maybe you won't get one.One evening my wife Lorrie asked me who I thought Thelma was speaking about in that passage. I replied that I had always understood it as a pure fabrication, and that there was no "other girl".
Lorrie said that she thought that Thelma had been speaking about herself, that Thelma had saved up her money, and her mother had gone looking for a china tea set, been unable to find one, and had brought home the plastic set as a consolation prize.
The crucial clue was the detail about how the "other girl" spent the rest of her money on candy, which is just a bit too specific for a mere fabrication.
Once you try out the hypothesis that Thelma is speaking personally, a lot of other details fall into place. For example, her assertion that "A lot of girls never do get tea sets" is no longer a clever invention on her part: she is repeating something her mother told her to shut her up when she expressed her disappointment over receiving a plastic instead of a china tea set. Her sales pitch to Frances about why a plastic tea set is better than a china one can be understood as an echo of her mother's own attempts to console her.
My wife is very clever, and was an English major to boot. She is skilled at noticing such things both by native talent and by long training of that talent.
Good children's literature does reward a close reading, and like good adult literature, reveals additional depths on multiple readings. It seems to me that books for small children are more insipid than they used to be, but that could just be fuddy-duddyism, or it could be selection bias: I no longer remember the ones I loved as a child that would now seem insipid precisely because they would now seem insipid.
But the ability to produce good literature at any level is rare, so it is probably just that there only a few great writers in every generation can do it. Russell Hoban was one of the best here.
[Other articles in category /book] permanent link
Fri, 08 Jun 2007
Counting transitive relations
A relation on a set S is merely a subset of
S×S. For example, the relation < on the set
{1,2,3} can be identified as {(1,2), (1,3), (2,3)}, the set of all (a,
b) with a < b.
A relation is transitive if, whenever it has both (a, b) and (b, c), it also has (a, c).
For the last week I've been trying to find a good way to calculate the number of transitive relations on a set with three elements.
There are 13 transitive relations on a set with 2 elements. This is easy to see. There are 16 relations in all. The only way a relation can fail to be transitive is to contain both (1, 2) and (2, 1). There are clearly four such relations. Of these four, the only one that is transitive has (1, 1) and (2, 2) also. Similarly it's quite easy to see that there are only 2 relations on a 1-element set, and both are transitive.
There are 512 relations on a set with 3 elements. How many are transitive?
It would be very easy to write a computer program to check them all and count the transitive ones. That is not what I am after here. In fact, it would also be easy to enumerate the transitive relations by hand; 512 is not too many. That is not what I am after either. I am trying to find some method or technique that scales reasonably well, well enough that I could apply it for larger n.
No luck so far. Relations on 3-sets can fail to be transitive in all sorts of interesting ways. Say that a relation has the Fabc property if it contains (a,b) and (b,c) but not (a,c). Such a relation is intransitive.
Now clearly there are 64 Fabc relations for each distinct choice of a, b, and c. But some of these properties overlap. For example, {(a,b), (b,c), (c,a)} has not only the Fabc property but also the Fbca and Fcab properties.
Of the 64 relations with the Fabc property, 16 have the Fbca property also. 16 have the Faba property. None have the Facb property. There are 12 of these properties, and they overlap in a really complicated way.
After a week I gave in and looked in the literature. I have a couple of papers in my bag I haven't read yet. But it seems that there is no simple solution, which is reassuring.
One problem is that the number of relations on n elements grows very rapidly (it's 2n2) and the number of transitive relations is a good-sized fraction of these.
[Other articles in category /math] permanent link



