Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
| 1+1=2 |
| 484848 is excellent |
| Excellent numbers |
| Just put it in the damn object! |
| The envelope paradox |
| Worst mathematical notation ever |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Tue, 20 Jun 2006
484848 is excellent
Brad Murray wrote to request a proof that the number 4848...4848 is excellent:
So, are all concatenations of odd numbers of "48" excellent? I demand a proof!So okay, it wasn't a request. I have been given no choice but to comply. I hear and I obey, O mighty one!
First let's define the items we're talking about:
- a0 = 4, an+1 =
100an + 84, so that the
an are 4, 484, 48484, etc.
- Similarly, b0 = 8, bn+1 =
100bn + 48, so that the
bn are 8, 848, 84848, etc.
- Similarly, c0 = 48, cn+1 =
10000cn + 4848, so that the
cn are 48, 484848, 4848484848, etc.
- It's obvious, or even if not,
- it follows from an easy inductive proof, which
- is left as an exercise for the reader.
In order to show that cn is excellent, it then suffices to show that cn = bn2 - an2 for all n.
First we'll prove the following lemma: for all n, 4bn - 7an = 4. This follows easily by induction. For n=0, we have 4·8 - 7·4 = 32 - 28 = 4. Now suppose the lemma is proved for n=i; we want to show that it is true for n=i+1. That is, we want to calculate:
| 4bi+1 - 7ai+1 | = |
| 4(100bi+48) - 7(100ai+84) | = |
| 400bi + 192 - 700ai - 588 | = |
| 400bi + 700ai + 192 - 588 | = |
| 100(4bi - 7ai) - 396 | = |
| 100·4 - 396 | = |
| 4 |
Now the main theorem, again by induction. We want to show that:
bn2 - an2 = cn
for all n. For n=0 this is trivial, since we have 82 - 42 = 64 - 16 = 48. Now suppose we know it is true for n=i; we will show that it is true for n = i+1 as well:
| bi+12 - ai+12 | = |
| (100bi + 48)2 - (100ai + 84)2 | = |
| 10000bi2 + 9600bi + 2304 - 10000ai2 - 16800ai - 7056 | = |
| 10000(bi2 - ai2) + 2400(4bi - 7ai) + 2304 - 7056 | = |
| 10000ci + 2400(4bi - 7ai) - 4752 | = |
| 10000ci + 2400·4 - 4752 | = |
| 10000ci + 4848 | = |
| ci+1 |
I may have more to say about this later. I have a half-written article that complains about homework questions of the form "Solve problem X using technique Y," where Y is something like induction. The article was inspired by a particularly odious problem of this type:
if n + 1 balls are put inside n boxes, then at least one box will contain more than one ball. prove this principle by induction.Nobody in his right mind would prove this principle by induction. You prove it by pointing out that if the conclusion were to fail, no box would have more than one ball; since there are n boxes, each of which has no more than one ball, then there are no more than n balls, and this contradicts the hypothesis. Using induction is idiotic.
A student faced with this kind of question will conclude (correctly) that he or she is being forced to jump through a pointless hoop, and may conclude (incorrectly) that induction is useless. And students are frequently confused by pointless applications of principles. People learn better when they understand why things are happening; when students feel that they don't understand the point of what is being done, they feel that they don't understand the mechanics either.
In the real world—by which I mean what real scientists, mathematicians, and engineers do, in addition to what people in the grocery store do—I am excluding only homework assignments—we almost never get a problem of the form "solve X using technique Y". Problems we face in the real world always have the form "solve X, by hook or by crook." The closest we ever see to a prescribed technique are mere suggestions like "Well, Y might work here, so you could try that."
Questions that prescribe techniques are either lazy pedagogy or bad curriculum design. If technique Y—say, induction—is a useful technique, then it is because there is some problem X such that Y is superior to all other techniques for solving X. If all such X are outside the scope of the class, then Y is outside the scope of the class too. If, on the other hand, there is some X that is in the scope of the class, it is the instructor's job to find it and present it to the students, as an instructive example. To fail in this, and to make up a contrived and irrelevant problem in place of X, is a failure of the instructor's principal duty, which is to illustrate the subject matter by realistic and relevant examples.
For the theorem above about 484848, induction is clearly a good way to solve it; to solve the problem by direct calculation is painful.
There are other things to learn from the demonstration above. It serves as a wonderful example of what is wrong with standard mathematical style for writing up proofs. A student seeing this proof might well ask "where the heck did you get that lemma about 4b - 7a = 4? Is that something you knew from before? Did you just guess? Was it in the book somewhere?" But no, I did not guess, I did not know that before, and I did not get it from the book.
The answer is that I did the main demonstration first, starting with bi2 - ai2 and trying to get from there to ci by using algebraic manipulations and the definitions of a, b, and c. And just when everything seemed to be going along well, I got stuck. I had:
10000ci + 2400(4bi - 7ai) - 4752
This looked something like what I was trying to manufacture, which was:
10000ci + 4848
but it was not quite right. The 10000ci part was fine, but instead of 2400(4bi - 7ai) - 4752 I needed 4848.So if it was going to work, I needed to have:
2400(4bi - 7ai) - 4752 = 4848
or equivalently:
2400(4bi - 7ai) = 9600
which is equivalent to:
4bi - 7ai = 4.
So I had better have 4bi - 7ai = 4; if this turns out false, the whole thing falls apart.But a quick check of a couple of examples shows that 4bi - 7ai = 4 does work, at least for i=0 and 1, so maybe it would worth trying to prove in the general case. And indeed, the proof went through fine, and I won.
But in the presentation of the proof, everything is backwards: I pull the mystery lemma out of my ass at the beginning for no apparent reason, and then later on it happens to be what what I need at the crucial moment. Almost as if I knew beforehand what was going to happen!
There are a lot of things wrong with mathematics pedagogy, and those were two of them: artifically prescribed techniques to solve homework problems, and the ass-extraction of lemmas backwards in time.
[Other articles in category /math] permanent link
Sun, 18 Jun 2006 Whitehead and Russell's Principia Mathematica is famous for taking a thousand pages to prove that 1+1=2. Of course, it proves a lot of other stuff, too. If they had wanted to prove only that 1+1=2, it would probably have taken only half as much space.Principia Mathematica is an odd book, worth looking into from a historical point of view as well as a mathematical one. It was written around 1910, and mathematical logic was still then in its infancy, fresh from the transformation worked on it by Peano and Frege. The notation is somewhat obscure, because mathematical notation has evolved substantially since then. And many of the simple techniques that we now take for granted are absent. Like a poorly-written computer program, a lot of Principia Mathematica's bulk is repeated code, separate sections that say essentially the same things, because the authors haven't yet learned the techniques that would allow the sections to be combined into one.
For example, section ∗22, "Calculus of Classes", begins by defining the subset relation (∗22.01), and the operations of set union and set intersection (∗22.02 and .03), the complement of a set (∗22.04), and the difference of two sets (∗22.05). It then proves the commutativity and associativity of set union and set intersection (∗22.51, .52, .57, and .7), various properties like !!\alpha\cap\alpha = \alpha!! (∗22.5) and the like, working up to theorems like ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta - \alpha)!!.
Section ∗23 is "Calculus of Relations" and begins in almost exactly the same way, defining the subrelation relation (∗23.01), and the operations of relational union and intersection (∗23.02 and .03), the complement of a relation (∗23.04), and the difference of two relations (∗23.05). It later proves the commutativity and associativity of relational union and intersection (∗23.51, .52, .57, and .7), various properties like !!\alpha\dot\cap\alpha = \alpha!! (∗22.5) and the like, working up to theorems like ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot- \alpha)!!.
The section ∗24 is about the existence of sets, the null set !!\Lambda!!, the universal set !!{\rm V}!!, their properties, and so on, and then section ∗24 is duplicated in ∗25 in a series of theorems about the existence of relations, the null relation !!\dot\Lambda!!, the universal relation !!\dot {\rm V}!!, their properties, and so on.
That is how Whitehead and Russell did it in 1910. How would we do it
today? A relation between S and T is defined as a subset of
S × T and is therefore a set. Union,
intersection, difference, and the other operations are precisely the
same for relations as they are for sets, because relations are
sets. All the theorems about unions and intersections of
relations, like 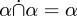 , just go away, because we
already proved them for sets and relations are sets. The null
relation is the null set. The universal relation is
the universal set.
, just go away, because we
already proved them for sets and relations are sets. The null
relation is the null set. The universal relation is
the universal set.
A huge amount of other machinery goes away in 2006, because of the unification of relations and sets. Principia Mathematica needs a special notation and a special definition for the result of restricting a relation to those pairs whose first element is a member of a particular set S, or whose second element is a member of S, or both of whose elements are members of S; in 2006 we would just use the ordinary set intersection operation and talk about R ∩ (S×B) or whatever.
Whitehead and Russell couldn't do this in 1910 because a crucial piece of machinery was missing: the ordered pair. In 1910 nobody knew how to build an ordered pair out of just logic and sets. In 2006 (or even 1956), we would define the ordered pair <a, b> as the set {{a}, {a, b}}. Then we would show as a theorem that <a, b> = <c, d> if and only if a=c and b=d, using properties of sets. Then we would define A×B as the set of all p such that p = <a, b> ∧ a ∈ A ∧ b ∈ B. Then we would define a relation on the sets A and B as a subset of A×B. Then we would get all of ∗23 and ∗25 and a lot of ∗33 and ∗35 and ∗36 for free, and probably a lot of other stuff too.
(By the way, the {{a}, {a, b}} thing was invented by Kuratowski. It is usually attributed to Norbert Wiener, but Wiener's idea, although similar, was actually more complicated.)
There are no ordered pairs in Principia Mathematica, except implicitly. There are barely even any sets. Whitehead and Russell want to base everything on logic. For Whitehead and Russell, the fundamental notion is the "propositional function", which is a function φ whose output is a truth value. For each such function, there is a corresponding set, which they denote by !!\hat x\phi(x)!!, the set of all x such that φ(x) is true. For Whitehead and Russell, a relation is implied by a propositional function of two variables, analogous to the way that a set is implied by a propositional function of one variable. In 2006, we dispense with "functions of two variables", and just talk about functions whose (single) argument is an ordered pair; a relation then becomes the set of all ordered pairs for which a function is true.
Russell is supposed to have said that the discovery of the Sheffer stroke (a single logical operator from which all the other logical operators can be built) was a tremendous advance, and would change everything. This seems strange to us now, because the discovery of the Sheffer stroke seems so simple, and it really doesn't change anything important. You just need to append a note to the beginning of chapter 1 that says that ∼p and p∨q are abbreviations for p|p and p|p.|.q|q, respectively, prove the five fundamental axioms, and leave everything else the same. But Russell might with some justice have said the same thing about the discovery that ordered pairs can be interpreted as sets, a simple discovery that truly would have transformed the Principia Mathematica into quite a different work.
Anyway, with that background in place, we can discuss the Principia Mathematica proof of 1+1=2. This occurs quite late in Principia Mathematica, in section ∗110. My abridged version only goes to ∗56, but that is far enough to get to the important precursor theorem, ∗54.43, scanned below:

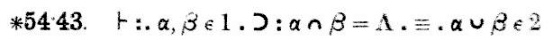
Now I should explain the notation, which has changed somewhat since 1910. First off, Principia Mathematica uses Peano's "dots" notation to disambiguate precedence, where we now use parentheses instead. The dot notation takes some getting used to, but has some distinct advantages over the parentheses. The idea is just that you indicate grouping by putting in dots, so that (1+2)×(3+4)×(5+6) is written as 1+2.×.3+4.×.5+6. The middle sub-formula is between a pair of dots. The (1+2) sub-formula is between a pair of dots also, but the dot on the left end is superfluous, and we omit it; similarly, the sub-formula (5+6) is delimited by a dot on the left and by the end of the formula on the right.
What if you need to nest parentheses? Then you use more dots. A double dot (:) is like a single dot, but stronger. For example, we write ((1+2)×3)+4 as 1+2 . × 3 : + 4, and the double dot isolates the entire 1+2 . × 3 expression into a single sub-formula to which the +4 applies.
Sometimes you need more levels of precedence, and then you use triple dots (.: and :.) and quadruple (::). This formula, as you see, has double and triple dots. Translating the dots into standard parenthesis notation, we have $$\ast54.43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. This is rather more cluttered-looking than the version with the dots, and in complicated formulas you can have trouble figuring out which parentheses match with which. With the dots, it's always easy. So I think it's a bit unfortunate that this convention has fallen out of use.
The !!\vdash!! symbol has not changed; it means that the formula to which it applies is asserted to be true. !!\supset!! is logical implication, and !!\equiv!! is logical equivalence. Λ is the empty set, which we write nowadays as ∅. ∩ ∪ and ∈ have their modern meanings: ∩ and ∪ are the set intersection and the union operators, and x∈y means that x is an element of set y.
The remaining points are semantic. α and β are sets. 1 denotes the set of all sets that have exactly one element. That is, it's the set { c : there exists a such that c = { a } }. Theorems about 1 include, for example:
- that Λ∉1 (∗52.21),
- that if α∈1 then there is some x such that α =
{x} (∗52.1), and
- that {x}∈1 (∗52.22).
So here is theorem ∗54.43 again:
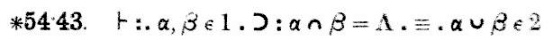
The proof, which appears in the scan above following the word "Dem." (short for "demonstration") goes like this:
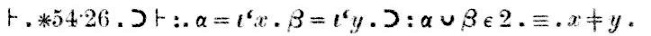



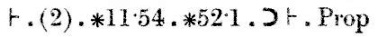
Maybe the thing to notice here is how very small the steps are. ∗54.26, on which this theorem heavily depends, is almost the same; it asserts that {x}∪{y} ∈ 2 if and only if x≠y. ∗54.26, in turn, depends on ∗54.101, which says that α has 2 elements if and only if there exist x and y, not the same, such that α = {x} ∪ {y}. ∗54.101 is just a tiny bit different from the definition of 2. Theorem ∗51.231 says that {x} and {y} are disjoint if and only if x and y are different. ∗52.1 is a basic property of 1; we saw it before.
The other theorems cited in the demonstration are very tiny technical matters. ∗11.54 says that you can take an assertion that two things exist and separate it into two assertions, each one asserting that one of the things exists. ∗11.11 is even slimmer: it says that if φ(x, y) is always true, then you can attach a universal quantifier, and assert that φ(x, y) is true for all x and y. ∗13.12 concerns the substitution of equals for equals: if x and y are the same, then x possesses a property ψ if and only if y does too.
I haven't seen the later parts of Principia Mathematica, because my copy stops after section ∗56, and the arithmetic stuff is much later. But this theorem clearly has the sense of 1+1=2 in it, and the later theorem (∗110.643) that actually asserts 1+1=2 depends strongly on this one.
Although I am not completely sure what is going to happen later on (I've wasted far too much time on this already to put in more time to get the full version from the library) I can make an educated guess. Principia Mathematica is going to define the number 17 as being the set of all 17-element sets, and similarly for every other number; the use of the symbol 2 to represent the set of all 2-element sets prefigures this. These sets-of-all-sets-of-a-certain-size will then be identified as the "cardinal numbers".
The Principia Mathematica will define the sum of cardinal numbers p and q something like this: take a representative set a from p; a has p elements. Take a representative set b from q; b has q elements. Let c = a∪b. If c is a member of some cardinal number r, and if a and b are disjoint, then the sum of p and q is r.
With this definition, you can prove the usual desirable properties of addition, such as x + 0 = x, x + y = y + x, and 1 + 1 = 2.
In particular, 1+1=2 follows directly from theorem ∗54.43; it's just what we want, because to calculate 1+1, we must find two disjoint representatives of 1, and take their union; ∗54.43 asserts that the union must be an element of 2, regardless of which representatives we choose, so that 1+1=2.
Post scriptum: Peter Norvig says that the circumflex in the
Principia Mathematica notation 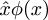 is the ultimate source of the use of the word
lambda to denote an anonymous function in the Lisp and Python
programming languages. I am sure you know that these languages get
"lambda" from the use of the Greek letter λ by Alonzo Church to
represent function abstraction in his "λ-calculus": In Lisp,
(lambda (u) B) is a function that takes an argument
u and returns the value of B; in the λ-calculus,
λu.B is a function that takes an argument
u and returns the value of B. (Recall also that
Church was the doctoral advisor of John McCarthy, the inventor of Lisp.)
Norvig says that Church
was originally planning to write the function
λu.B as û.B, but his printer
could not do circumflex accents. So he considered moving the
circumflex to the left and using a capital lambda instead:
Λu.B. The capital Λ looked too much like
logical and ∧, which was confusing, so he used lowercase lambda
λ instead.
is the ultimate source of the use of the word
lambda to denote an anonymous function in the Lisp and Python
programming languages. I am sure you know that these languages get
"lambda" from the use of the Greek letter λ by Alonzo Church to
represent function abstraction in his "λ-calculus": In Lisp,
(lambda (u) B) is a function that takes an argument
u and returns the value of B; in the λ-calculus,
λu.B is a function that takes an argument
u and returns the value of B. (Recall also that
Church was the doctoral advisor of John McCarthy, the inventor of Lisp.)
Norvig says that Church
was originally planning to write the function
λu.B as û.B, but his printer
could not do circumflex accents. So he considered moving the
circumflex to the left and using a capital lambda instead:
Λu.B. The capital Λ looked too much like
logical and ∧, which was confusing, so he used lowercase lambda
λ instead.
Post post scriptum: Everyone always says "Russell and Whitehead". Google results for "Russell and Whitehead" outnumber those for "Whitehead and Russell" by two to one, for example. Why? The cover and the title page say "Alfred North Whitehead and Bertrand Russell, F.R.S.". How and when did Whitehead lose out on top billing?
[ Addendum 20060913: I figured out how and when Whitehead lost out on top billing: 10 December 1950. ]
[ Addendum 20171107: W. Ethan Duckworth sent me a translation of this proposition into modern notation, which I discussed in a new article. ]
[ Addendum 20211028: The duplication of “calculus of classes” as “calculus of relations” was fixed the following year by Norbert Wiener. ]
[ Addendum 20230329: I discussed Wiener's invention of the ordered pair in 2021: [1] [2] ]
[ Addendum 20230328: I guessed “Principia Mathematica will define the sum of cardinal numbers p and q something like this…”. This is indeed more or less how it goes. Cardinal addition is introduced in ∗110. The 1+1=2 theorem looks like this:

[Other articles in category /math] permanent link
Sat, 17 Jun 2006
Excellent numbers
Another programmer presented the Philadelphia Perl Mongers with this
problem, apropos of something else; he had gotten the problem from a
friend of his. The problem is to find "excellent numbers". A number
n is excellent if it has an even number of digits, and if when
you chop it into a front half a and a back half b, you
have b2 - a2 = n. For
example, 48 is excellent, because 82 - 42 = 48,
and 3468 is excellent, because 682 - 342 = 4624
- 1156 = 3468.
This other programmer had written a program to do brute-force search, which wasn't very successful, because there aren't very many excellent numbers. He was presenting it to the Perl Mongers because in the course of trying to speed up the program, he had learned something interesting: using the Memoize module to memoize the squaring function makes a program slower, not faster. But that is another matter for another article.
A slightly less brutal brute-force search locates excellent numbers quite easily. Suppose the number n has 2k digits, and that it is the concatenation of a and b, each with k digits. We want b2 - a2 = n. Since n is the concatenation of a and b, it is equal to a·10k + b. So we want:
a·10k + b = b2 - a2
Or equivalently:
a·(10k + a) = b2 - b
Let's say that a number of the form b2 - b is "rectangular". So our problem is simply to find k-digit numbers a for which a·(10k + a) is rectangular.That is, instead of brute-forcing n, which has 2k digits, we need only do a brute-force search on a, which has only k digits. This is a lot faster. To find all 10-digit excellent numbers, we are now searching only 90,000 values of a instead of 9,000,000,000 values of n. This is feasible, whereas the larger search isn't.
All we need is some way to determine whether a given number q is rectangular, and that is not very hard to do. One way is simply to precompute a table of all rectangular numbers up to a certain size, and look up q in the table.
But another way is to notice that it is sufficient to be able to extract the "rectangular root" of q. That's the number b such that b2 - b = q. If we can make a good guess about what b might be, then we can calculate b2-b and see if we get back q. This is analogous to checking whether a number s is a perfect square by guessing its square root r and then checking to see if r2 = s. (Of course, it only works if you can guess right!)
But how can we guess the rectangular root of q? The computer has a built-in square root function, but no rectangular root function. But that's okay, because they are very nearly the same thing. Rectangular numbers are very nearly squares: when b is large, b2 - b is relatively very close to b2. So if we are given some number q, and we want to know if it has the form b2 - b, we can get a very good estimate of the size of b just by taking √q.
For example, is 29750 a rectangular number? √29750 = 172.48, so if 29750 is rectangular, it will be 1732 - 173 = 29756. So, no.
Is 1045506 rectangular? √1045506 = 1022.4998, so if 1045506 is rectangular, it will be 10232-1023 = 1045506—check!
The only possible problem is that our assumption that b2-b and b2 will be close may not hold when b is too small. So we might need to put a special case in our program to use a different test for rectangularity when q is too small. But it turns out that the test works fine even for q as small as 2: Is 2 rectangular? √2 = 1.4, so if 2 is rectangular, it will be 22-2—check!
So we code up an is_rectangular function:
sub is_rectangular {
my $q = shift;
my $b = 1 + int(sqrt($q)); # Guess
if ($b * $b - $b == $q) { # Check guess
return $b; # Aha!
} else {
return; # Not rectangular
}
}
This function returns false if its argument is not rectangular; and it
returns the rectangular root otherwise. We will need the rectangular
root, because that's exactly the lower half of an excellent number.Now we need a function that tells us whether we have some number a that might be the upper half of an excellent number:
my $k = shift || 3;
my $p = 10**$k;
sub is_upper_half_of_excellent_number {
my $a = shift;
return is_rectangular($a * ($p + $a));
}
$k here is the number of digits in a. We'll let it be
a command-line argument, and default to 3.We could infer k from a itself, but we'll hardwire it for two reasons. One reason is speed. The other is that we might want to accept a number like 0003514284 as being excellent, where here a has some leading zeroes; fixing k is one way to do this. We also precalculate the constant p = 10k, which we need for the calculation.
Now we just write the brute-force loop:
for my $a (0 .. $p-1) {
if(my $b = is_upper_half_of_excellent_number($a)) {
print "$a$b\n";
}
}
The program instantaneously coughs up:
01
10101
16128
34188
140400
190476
216513
300625
334668
416768
484848
530901
6401025
8701276
Most of these are correct. For example, 9012 -
5302 = 811801 - 280900 = 530901. 5132 -
2162 = 263169 - 46656 = 216513.The ones at the top of the list are correct, if you remember about the leading zeroes: 1882 - 0342 = 35344 - 1156 = 034188, and 0012 - 0002 = 1 - 0 = 000001.
The seven-digit numbers at the bottom don't work, because the program has a bug: we forgot to enforce the restriction that b must also have exactly k digits; the last two numbers in the display have four-digit b's. So we need to add another test to the main loop:
for my $a (0 .. $p-1) {
if(my $b = is_upper_half_of_excellent_number($a)) {
print "$a$b\n" if length($b) == $k;
}
}
This eliminates the wrong answers from the tail of the list. It also
skips over cases where b is too short, and needs leading
zeroes, such as a=000, b=001, but fixing that is both
easy and unimportant. The ten-digit solutions are:
0101010101
3333466668
4848484848
4989086476
I think this is interesting because it shows how a very little bit of
mathematical analysis, and some very sloppy numerical work, can turn
an intractable problem into a tractable one. We could have worked
real hard and maybe come up with some way to generate excellent
numbers with no search. But instead, we did just a little work, and
that was enough to narrow down the search enormously, to the point
where it's practical.The other thing that I think is interesting is that the other programmer was trying to solve his performance problem with optimization tricks. But when you are searching over 9,000,000,000 cases, optimization tricks don't work. At 1,000 cases per second, 9,000,000,000 cases takes about 104 days to finish. If you can optimize your program to speed it up by 50%, it will still take 52 days to finish. But cutting the 9,000,000,000 cases to 90,000 cuts the run time from 104 days to 90 seconds.
Not to say that optimizing programs never works, of course. But you have to know when optimization might work and when it can't. In this case, micro-optimization wasn't going to help; the only way to fix an algorithm that does a brute-force search of 9,000,000,000 cases is to find a better algorithm. The point of this article is to show that sometimes finding a better algorithm can be pretty easy.
[ Addendum 20060620: I wrote a followup article about how it's not a coincidence that 4848484848 is excellent. ]
[ Addendum 20160105: brian d foy has a whole website about his work on this problem. ]
[Other articles in category /math] permanent link
Fri, 16 Jun 2006
The envelope paradox
[Addendum 20151130: I have since written this up in greater and more
formal detail. If you find the details here lacking, please consult
my math.se post about
it.]
This is on my mind because someone asked about it in IRC yesterday and I was surprised at how coherently I was able to explain it on the spur of the moment. There are several versions of this paradox. My favorite version goes like this: you're going to play a game with an adversary. The adversary writes two different numbers on slips of paper and puts them in an envelope. The numbers are completely arbitrary; they could be absolutely any numbers whatsoever: zero, or π, or -1428573901823.00013, or anything else.
You pick one slip at random from the envelope and examine the number written on it. You then make a prediction about whether the other number is larger or smaller. If your prediction is correct, you win a dollar; if it is incorrect, you lose a dollar.
Clearly, you can break even in the long run simply by making your prediction at random. And it seems just just as clear that there is no strategy you can use that does better than breaking even. But this is the paradox: there is a strategy you can use that does better than breaking even. (This is what W.V.O. Quine calls a "veridical paradox": it's something that seems impossible, but is nevertheless true.)
Spoilers follow, so you might want to stop reading here for twenty-four hours and try to figure out a winning strategy yourself.
Let's call the number you get from the envelope A and the number still in the envelope B. You can see A, and you are trying to predict whether B is larger or smaller than A.
Here's your winning strategy. Before you see A, choose a random number R. If A < R, then conclude that A is "small", and predict that B is larger. If A > R, make the opposite prediction.
There are three possibilities. Either (1) A and B are both less than R, or (2) they are both greater than R, or else (3) one is less than R and one is greater.
In case 1, you predict that B > A, and you have a 50% probability of being correct. In case 2, you predict that B < A, and you have a 50% probability of being correct.
But in case 3, you win every time! If A < R < B then you see A, conclude that A is "small", and predict that B > A, which is correct; if B < R < A then you see A, conclude that A is "large", and predict that B < A, which is correct.
Since you're breaking even in cases 1 and 2, and you have a guaranteed win in case 3, you have a better-than-even chance of winning overall. There's some positive probability p (which depends on the method you use to choose R) that you have case 3, and if so, then your expected positive return on the game is p dollars per game.
The paradoxical part is that it initially seems as though you can't get any idea, just from looking at A, of whether it's larger or smaller than the unknown number B. But you can get such an idea, because you can tell from looking at A how big it is, and big numbers are more likely to be larger than B than small numbers are.
What you've done with R is to invent a definition of "large" and "small" numbers: numbers larger than R are "large" and those smaller than R are "small". It's an arbitrary definition, and it doesn't always succeed in distinguishing large from small numbers—it thinks that R+1 and 1000000R+1000000 are both "large"—but it can distinguish some large numbers from some small numbers, and it never gets confused and concludes that x is large and y is small when x is actually smaller than y. So it may be arbitrary, and extremely coarse, but it is never actually wrong.
In the cases where this very coarse method of deciding "large" from "small" fails to distinguish A from B, you get no new information, but that's okay, because you can still break even. But if you get lucky and the adversary has chosen numbers that you can distinguish, then you win.
Another way to look at the paradox is like this: suppose the adversary is required to choose his two numbers at random. Then you have a simple winning strategy: if A is positive, predict that B is smaller, and if A is negative, predict that B is larger. Even when both numbers are positive or both are negative, you win half the time; if one is positive and one is negative, you are guaranteed a win.
If the adversary knows that this is what you are doing, he can cut you back to merely breaking even, by limiting himself to always choosing positive numbers. But you can foil this strategy of his by choosing your "positive" and "negative" classes to be divided somewhere other than at 0: instead of "positive" being "> 0" and "negative" being "< 0", you make them mean "> R" and "< R". The adversary still wants to choose two numbers that are always positive, but since he doesn't know how big R is, hw doesn't know how large he has to make his own numbers to get them both to be "positive".
Still, this suggests the best strategy for the adversary: choose two very very large numbers that are close together. By doing this, he can make your expected win close to zero.
The envelope paradox is often presented in a different form: you are given two envelopes. One contains a bunch of money, say x dollars. The other contains twice as much. You open one envelope at random and examine its contents. Then you choose one envelope to keep.
A naïve analysis goes like this: I open the first envelope and see x. I can keep this envelope and collect amount x. If I switch, I have a 50% chance of ending up with 2x and a 50% chance of ending up with x/2, for an expected outcome of 5x/4. Since 5x/4 > x, I should always switch.
This is what Quine calls a "falsidical paradox": the reasoning seems good, but leads to an impossible conclusion. The strategy of always switching can't possibly be correct, because you could apply it with without even seeing what is in the envelope. You could keep switching back and forth all day, never opening either envelope, and increasing your expected winnings to infinity.
The tricky part, again, is that having seen x in the envelope, you cannot conclude that there is exactly a 50% chance of x being the larger of the two amounts. You get some information from the size of x, and if x is a large amount of money, then the probability that x is the larger of the two amounts is thereby greater than 0.5.
To do a full analysis, one has to ask the question of how the original amounts were selected. Say that the two amounts are b and 2b; let's call b the "base amount". How did the adversary select b? Let's say that the probability of the base amount being any particular amount x is P(x). It is impossible that b has an equal probability of being every number, because $$\int_{-\infty}^\infty P(x) dx$$ is required to be 1, and if P(b) is the same for every possible base amount b, then it is a constant function, and constant functions do not have the required property.
When you see x in the envelope, you know that one of two situations occurred. Either x is the base amount, and so is smaller, which occurs with probability P(x), or x/2 is the base amount, and x itself is the larger, which occurs with probability P(x/2).
Since these are the only possibilities, the a posteriori likelihood that x is the smaller number is P(x)/(P(x/2) + P(x)). This is equal to 1/2 only if P(x) = P(x/2). Although this can occur for particular values of x, it can't be true for every x. As x increases, P(x) approaches zero, so for sufficiently large x, we must have P(x/2) > P(x), so P(x/2) + P(x) > 2P(x), and P(x)/(P(x/2) + P(x)) < P(x)/2P(x) = 1/2.
[Other articles in category /math] permanent link
Thu, 15 Jun 2006
Just put it in the damn object!
The Perl Program Repair
Shop book, despite outward appearances, is coming along. A few
months ago in Pittsburgh I gave a talk about someone's module that I
didn't think was very well-written, for various reasons. Up to that
point, the book had been about a lot of small-scale stuff: repeated
code, unnecessary variables, making two passes over a data structure
when only one was necessary, C-style for loops, and such.
But unlike the previous examples, this one had been written by someone
who was actually competent. So the problems I found were
competent-programmer examples, rather than incompetent-programmer
examples. I need some more chapters of that kind of examples, or the
book will not be of much interest to competent programmers.
What kind of mistakes do competent programmers make? They make a lot of errors of object-oriented design.
This module's purpose was to emulate some Java library that lets you register an "observer" of an object. Let's say that the "observer" object is a Guard, and the object it is observing is an "Alarm". The idea is that the Alarm object registers the Guard as being an observer of the Alarm, and then whenever the Alarm calls a notify_observers method, the notify method in the Guard object is called back. Actually the Java people didn't make the names that sensible; instead of notify_observers calling the notify method in the observers, it calls the update method. Why wasn't notify_observers called update_observers, then? I dunno. It's Java. You want me to explain Java?
Okay, so for each Alarm A you need somewhere to store the list of observers of A. Where do you put that?
The author of the module put it in a global hash. I don't think it's immediately clear that this was a mistake. But I do think it was a mistake. Big problems arise; the module had a lot of bugs, mostly related to garbage collection. As a result of putting the Guard objects into this hash, they are never garbage collected. Well, not quite. The author used a weak reference in the hash, so the objects there are garbage collected.
Weak references are one of those technical solutions that fits really well into the formula "A programmer had a problem. So he used weak references. Then he had two problems." (Non-greedy regexes are another example. Some people say Perl itself is an example.) Weak references do solve a couple of very specific problems, mostly having to do with caching. For anything else, they turn out to be a bigger problem than the thing you were trying to solve. In this case, the weak references cause this delightful problem:
my $alarm = Alarm->new();
$alarm->add_observer(Guard->new);
$alarm->notify_observers("I like pie!");
Failed to send observation from 'Alarm=HASH(0x8113f74)' to '':
Can't call method "update" on an undefined value at
lib/Class/Observable.pm line 95.
See, the Guard that is observing the Alarm is immediately
garbage-collected. We could prevent the fatal error here, but that
wouldn't solve the problem, which is that that Guard should not
be garbage collected as long as the Alarm is still extant, because it
is supposed to be watching the Alarm. This was only one of several problems caused by this design, to store the observers in a global hash. Some of these could possibly be avoided if Perl were a better language, but others I think not.
My suggestion here was the following advice: Whenever you're trying to store information about an object, there is a right place to store it and a wrong place to store it. The right place: inside the object. The wrong place: anywhere else.
Rationale: What is an object? It's a place where you store all the pertinent information about some entity. So here we have some pertinent information about this entity, the alarm, namely the list of guards who are watching it. Where should we store this information? Well, we have this data structure, the Alarm object, which is supposed to store all the pertinent information about the alarm. The list of guards is part of this, so that's where it should go. Entia non sunt multiplicanda praeter necessitatem.
Now, this choice may be obvious, but it has a fair share of problems too, which is why I think the other programmer might not have made it. The add_observers method in the base class of Alarm is called upon to add the Guard to the list of observers of the Alarm. If the list of observers is stored in the Alarm object, add_observersmust make some assumptions about how the Alarm is implemented. But it turns out that once you start thinking about it, the problems turn out to have fairly simple solutions. For example, the base class needs to know what list to append the Guard to. It could assume that the list will be stored in $alarm->{Observers}, but that's iffy: it assumes that the Alarm will be made from a hash, it assumes that that hash key is not used for something else, and so on. So instead, you give Alarm a method that returns a reference to the array in which the Guard is supposed to place itself. Normally, that method is inherited from the base class itself, and returns a reference to $self->{Observers}, but the Alarm class can override that if it needs to. It can even get back the original global-variable implementation by overriding the method to return a reference to an element in a global hash.
To summarize, both designs appeared to have significant technical problems, but the problems in the design I suggested turned out to be a lot easier to solve well then the problems that arose from the design that the author chose. At least in this example, the advice that object data should be stored in the object turned out pretty well.
(Cynical advice to people wishing to become famous experts: phrase your advice so that it sounds inevitable. Anyone wishing to argue against advice like object data should be stored in the object will have an uphill battle, and risks looking like an idiot.)
Now today I was in the shower, thinking about this other piece of software I wrote recently, in which I was having, surprise, a garbage collection problem. The software is a module that is intended to provide lightweight access to flat-file databases, which is something that has been inexplicably overlooked by CPAN.
You use the module like this:
my $db = FlatFile->new(FILE => ..., FIELDS => [...], ...);
my @red = $db->lookup(color => "red");
$red[0]->set_color("blue"); # paint it blue
$red[1]->delete;
The elements of @red are Record objects, and the
Record methods like set_color and delete
need to call back to the FlatFile object that represents the
database, to inform it that records have been modified or deleted. So
each Record object needs a pointer back to the database to
which it belongs.The way I implemented this was to have a class variable in the Record class, $Record::DB, which contained the database object. But then the database object is never garbage-collected, which means it is never finalized, which means that changes to the database are not automatically written to the disk when the database object becomes inaccessible, which means that you have to call $db->flush to make sure the changes are written out, which opens the possibility that you will forget, and the module will bugger your database with a badger.
What I realized in the shower was that I had better take my own advice, that object data should be stored in the object. If the source database is a pertinent piece of information about a record, then I had better store the source database as a piece of member data in the record object, and not try this stupid thing involving a global variable.
If the advice is good, this will be a better design. I haven't done it yet, so I'm not sure. But it certainly looks like a better design.
I want to say I don't know why I used the global variable in the first place, but I do know: my original design for the record object was that it had nothing in it but the data from the record; no metadata at all. The data members were named after the fields in the database, so there was no namespace left over for metadata. That didn't work out too well, and although I resisted putting metadata into the record objects long enough to screw myself regarding where to store the owning database and some other stuff, I eventually got backed into a corner and had to redesign the object to have space for metadata. But the effects of original misdesign persisted, because I was still storing a bunch of the object's metadata in stupid global variables, until I took that shower.
That's two successes so far for my advice, which is two good signs. Now all I need is a good counterexample. Every piece of advice in this book is going to have a counterexample. That's the big problem with computer programming advice books: no counterexamples. But that's another article for another day.
[Other articles in category /prs] permanent link
Wed, 14 Jun 2006
Worst mathematical notation ever
All my blog posts lately seem to be turning into enormous meandering
rants, which isn't so bad in itself, but I never finish any of them.
So I thought I'd just cut this one short and stick to one point
instead of seventeen. But someday you're all going to have to read
the full article, which complains about how 1960s computer scientists,
math grad students, and other insecure people who hunger for
legitimacy sometimes try to get it by doing everything with as much
notation and pseudo-formal language as possible.
I was reading some lecture notes today, and I encountered what I think must be the single worst line of mathematical notation I have ever seen. Here it is:
$$\equiv_{i_0+1} = \equiv_{i_0} = \equiv$$
Isn't that just astonishing?The explanation is that the author is constructing a sequence of equivalence relations, each one ≡n derived from the previous one ≡n-1. Eventually (after i0 iterations of the procedure), the construction has nothing left to do, and the new relation is the same as the one from which it was constructed. At this point the constructed relation turns out to be a certain one ≡ with desirable properties.
[ Addendum 20220123: I've tried a couple of times to find these notes again, with no success. It's a tough thing to search for. ]
[Other articles in category /math] permanent link


