Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMAMJ |
| JA | |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 241 |
| Programming | 99 |
| Language | 93 |
| Miscellaneous | 69 |
| Book | 50 |
| Tech | 49 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 24 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Tue, 21 Feb 2017
Moore's law beats a better algorithm
Yesterday I wrote about the project I did in the early 1990s to find the best anagrams. The idea is to give pair of anagram words a score, which is the number of chunks into which you have to divide one word in order to rearrange the chunks to form the other word. This was motivated by the observation that while “cholecysto-duodeno-stomy” and “duodeno-cholecysto-stomy” are very long words that are anagrams of one another, they are not interesting because they require so few chunks that the anagram is obvious. A shorter but much more interesting example is “aspired / diapers”, where the letters get all mixed up.
I wrote:
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search.
I wrote about the brute-force search yesterday. Today I am going to discuss the clever algorithm. (The paper is Avraham Goldstein, Petr Kolman, Jie Zheng “Minimum Common String Partition Problem: Hardness and Approximations”, The Electronic Journal of Combinatorics, 12 (2005).)
The plan is to convert a pair of anagrams into a graph that expresses
the constraints on how the letters can move around when one turns into
the other. Shown below is the graph for comparing
acrididae (grasshoppers)
with cidaridae (sea
urchins):
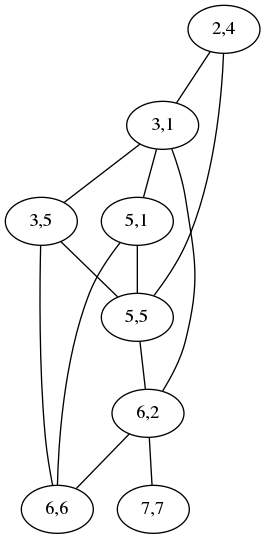
The “2,4” node at the top means that the letters ri at position
2 in acrididae match the letters ri at position 4 in cidaridae;
the “3,1” node is for the match between the first id and the first
id. The two nodes are connected by an edge to show that the two
matchings are incompatible: if you map the ri to the ri, you
cannot also map the first id to the first id; instead you have to
map the first id to the second one, represented by the node “3,5”,
which is not connected to “2,4”. A maximum independent set in this
graph is a maximum selection of compatible matchings in the words,
which corresponds to a division into the minimum number of chunks.
Usually the graph is much less complicated than this. For simple cases it is empty and the maximum independent set is trivial. This one has two maximum independent sets, one (3,1; 5,5; 6,6; 7,7) corresponding to the obvious minimum splitting:

and the other (2,4; 3,5; 5,1; 6,2) to this other equally-good splitting:
[ Addendum 20170511: It actually has three maximum independent sets. ]
In an earlier draft of yesterday's post, I wrote:
I should probably do this over again, because my listing seems to be incomplete. For example, it omits “spectrum / crumpets” which would have scored 5, because the Webster's Second list contains crumpet but not crumpets.
I was going to leave it at that, but then I did do it over again, and this time around I implemented the “good” algorithm. It was not that hard. The code is on GitHub if you would like to see it.
To solve the maximum independent set instances, I used a guided brute-force search. Maximum independent set is NP-complete, and so the best known algorithm for it runs in exponential time. But the instances in which we are interested here are small enough that this doesn't matter. The example graph above has 8 nodes, so one needs to check at most 256 possible sets to see which is the maximum independent set.
I collated together all the dictionaries I had handy. (I didn't know yet about SCOWL.) These totaled 275,954 words, which is somewhat more than Webster's Second by itself. One of the new dictionaries did contain crumpets so the result does include “spectrum / crumpets”.
The old scored anagram list that I made in the 1990s contained 23,521 pairs. The new one contains 38,333. Unfortunately most of the new stuff is of poor quality, as one would expect. Most of the new words that were missing from my dictionary the first time around are obscure. Perhaps some people would enjoy discovering that that “basiparachromatin” and “Marsipobranchiata” are anagrams, but I find it of very limited appeal.
But the new stuff is not all junk. It includes:
10 antiparticles paternalistic
10 nectarines transience
10 obscurantist subtractions11 colonialists oscillations
11 derailments streamlined
which I think are pretty good.
I wasn't sure how long the old program had taken to run back in the early nineties, but I was sure it had been at least a couple of hours. The new program processes the 275,954 inputs in about 3.5 seconds. I wished I knew how much of this was due to Moore's law and how much to the improved algorithm, but as I said, the old code was long lost.
But then just as I was finishing up the article, I found the old brute-force code that I thought I had lost! I ran it on the same input, and instead of 3.5 seconds it took just over 4 seconds. So almost all of the gain since the 1990s was from Moore's law, and hardly any was from the “improved” algorithm.
I had written in the earlier article:
In 2016 [ the brute force algorithm ] would probably still [ run ] quicker than implementing the maximum independent set algorithm.
which turned out to be completely true, since implementing the maximum independent set algorithm took me a couple of hours. (Although most of that was building out a graph library because I didn't want to look for one on CPAN.)
But hey, at least the new program is only twice as much code!
[ Addendum: The program had a minor bug: it would disregard
capitalization when deciding if two words were anagrams, but then
compute the scores with capitals and lowercase letters distinct. So
for example Chaenolobus was considered an anagram of unchoosable,
but then the Ch in Chaenolobus would not be matched to the ch in
unchoosable, resulting in a score of 11 instead of 10. I have
corrected the program and the output. Thanks to Philip Cohen for
pointing this out. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link
I found the best anagram in English
I planned to publish this last week sometime but then I wrote a line of code with three errors and that took over the blog.
A few years ago I mentioned in passing that in the 1990s I had constructed a listing of all the anagrams in Webster's Second International dictionary. (The Webster's headword list was available online.)
This was easy to do, even at the time, when the word list itself, at 2.5 megabytes, was a file of significant size. Perl and its cousins were not yet common; in those days I used Awk. But the task is not very different in any reasonable language:
# Process word list
while (my $word = <>) {
chomp $word;
my $sorted = join "", sort split //, $word; # normal form
push @{$anagrams{$sorted}}, $word;
}
for my $words (values %anagrams) {
print "@$words\n" if @$words > 1;
}
The key technique is to reduce each word to a normal form so that
two words have the same normal form if and only if they are anagrams
of one another. In this case we do this by sorting the letters into
alphabetical order, so that both megalodon and moonglade become
adeglmnoo.
Then we insert the words into a (hash | associative array | dictionary), keyed by their normal forms, and two or more words are anagrams if they fall into the same hash bucket. (There is some discussion of this technique in Higher-Order Perl pages 218–219 and elsewhere.)
(The thing you do not want to do is to compute every permutation of the letters of each word, looking for permutations that appear in the word list. That is akin to sorting a list by computing every permutation of the list and looking for the one that is sorted. I wouldn't have mentioned this, but someone on StackExchange actually asked this question.)
Anyway, I digress. This article is about how I was unhappy with the results of the simple procedure above. From the Webster's Second list, which contains about 234,000 words, it finds about 14,000 anagram sets (some with more than two words), consisting of 46,351 pairs of anagrams. The list starts with
aal ala
and ends with
zolotink zolotnik
which exemplify the problems with this simple approach: many of the 46,351 anagrams are obvious, uninteresting or even trivial. There must be good ones in the list, but how to find them?
I looked in the list to find the longest anagrams, but they were also disappointing:
cholecystoduodenostomy duodenocholecystostomy
(Webster's Second contains a large amount of scientific and medical jargon. A cholecystoduodenostomy is a surgical operation to create a channel between the gall bladder (cholecysto-) and the duodenum (duodeno-). A duodenocholecystostomy is the same thing.)
This example made clear at least one of the problems with boring anagrams: it's not that they are too short, it's that they are too simple. Cholecystoduodenostomy and duodenocholecystostomy are 22 letters long, but the anagrammatic relation between them is obvious: chop cholecystoduodenostomy into three parts:
cholecysto duodeno stomy
and rearrange the first two:
duodeno cholecysto stomy
and there you have it.
This gave me the idea to score a pair of anagrams according to how many chunks one had to be cut into in order to rearrange it to make the other one. On this plan, the “cholecystoduodenostomy / duodenocholecystostomy” pair would score 3, just barely above the minimum possible score of 2. Something even a tiny bit more interesting, say “abler / blare” would score higher, in this case 4. Even if this strategy didn't lead me directly to the most interesting anagrams, it would be a big step in the right direction, allowing me to eliminate the least interesting.
This rule would judge both “aal / ala” and “zolotink / zolotnik” as being uninteresting (scores 2 and 4 respectively), which is a good outcome. Note that some other boring-anagram problems can be seen as special cases of this one. For example, short anagrams never need to be cut into many parts: no four-letter anagrams can score higher than 4. The trivial anagramming of a word to itself always scores 1, and nontrivial anagrams always score more than this.
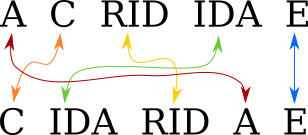
So what we need to do is: for each anagram pair, say
acrididae (grasshoppers)
and cidaridae (sea
urchins), find the smallest number of chunks into which we can chop
acrididae so that the chunks can be rearranged into cidaridae.
One could do this with a clever algorithm, if one were available. There is a clever algorithm, based on finding maximum independent sets in a certain graph. (More about this tomorrow.) I did not find this algorithm at the time; nor did I try. Instead, I used a brute-force search. Or rather, I used a very small amount of cleverness to reduce the search space, and then used brute-force search to search the reduced space.
Let's consider a example, scoring the anagram “abscise / scabies”.
You do not have to consider every possible permutation of
abscise. Rather, there are only two possible mappings from the
letters of abscise to the letters of scabies. You know that the
C must map to the C, the A must map to the A, and so
forth. The only question is whether the first S of abscise maps to
the first or to the second S of scabies. The first mapping gives
us:
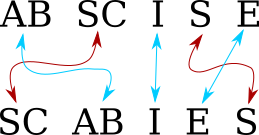
and the second gives us

because the S and the C no longer go to adjoining positions. So
the minimum number of chunks is 5, and this anagram pair gets a score
of 5.
To fully analyze cholecystoduodenostomy by this method required considering 7680
mappings. (120 ways to map the five O's × 2 ways to map the two
C's × 2 ways to map the two D's, etc.) In the 1990s this took a
while, but not prohibitively long, and it worked well enough that I
did not bother to try to find a better algorithm. In 2016 it would
probably still run quicker than implementing the maximum independent
set algorithm. Unfortunately I have lost the code that I wrote then
so I can't compare.
Assigning scores in this way produced a scored anagram list which began
2 aal ala
and ended
4 zolotink zolotnik
and somewhere in the middle was
3 cholecystoduodenostomy duodenocholecystostomy
all poor scores. But sorted by score, there were treasures at the end, and the clear winner was
I declare this the single best anagram in English. It is 15 letters
long, and the only letters that stay together are the E and the R.
“Cinematographer” is as familiar as a 15-letter word can be, and
“megachiropteran” means a giant bat. GIANT BAT! DEATH FROM
ABOVE!!!
And there is no serious competition. There was another 14-pointer, but both its words are Webster's Second jargon that nobody knows:
14 rotundifoliate titanofluoride
There are no score 13 pairs, and the score 12 pairs are all obscure. So this is the winner, and a deserving winner it is.
I think there is something in the list to make everyone happy. If you are the type of person who enjoys anagrams, the list rewards casual browsing. A few examples:
7 admirer married
7 admires sidearm8 negativism timesaving
8 peripatetic precipitate
8 scepters respects
8 shortened threnodes
8 soapstone teaspoons9 earringed grenadier
9 excitation intoxicate
9 integrals triangles
9 ivoriness revisions
9 masculine calumnies10 coprophagist topographics
10 chuprassie haruspices
10 citronella interlocal11 clitoridean directional
11 dispensable piebaldness
“Clitoridean / directional” has been one of my favorites for years. But my favorite of all, although it scores only 6, is
6 yttrious touristy
I think I might love it just because the word yttrious is so delightful. (What a debt we owe to Ytterby, Sweden!)
I also rather like
5 notaries senorita
which shows that even some of the low-scorers can be worth looking at. Clearly my chunk score is not the end of the story, because “notaries / senorita” should score better than “abets / baste” (which is boring) or “Acephali / Phacelia” (whatever those are), also 5-pointers. The length of the words should be worth something, and the familiarity of the words should be worth even more.
Here are the results:
In former times there was a restaurant in Philadelphia named “Soupmaster”. My best unassisted anagram discovery was noticing that this is an anagram of “mousetraps”.
[ Addendum 20170222: There is a followup article comparing the two algorithms I wrote for computing scores. ]
[ Addendum 20170222: An earlier version of this article mentioned the putative 11-pointer “endometritria / intermediator”. The word “endometritria” seemed pretty strange, and I did look into it before I published the article, but not carefully enough. When Philip Cohen wrote to me to question it, I investigated more carefully, and discovered that it had been an error in an early WordNet release, corrected (to “endometria”) in version 1.6. I didn't remember that I had used WordNet's word lists, but I am not surprised to discover that I did. ]
[ Addendum 20170223: More about this ]
[ Addendum 20170507: Slides from my !!Con 2017 talk are now available. ]
[ Addendum 20170511: A large amount of miscellaneous related material ]
[Other articles in category /lang] permanent link



