Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
In this section:
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Sat, 11 Nov 2017
Randomized algorithms go fishing
A little while back I thought of a perfect metaphor for explaining what a randomized algorithm is. It's so perfect I'm sure it must have thought of many times before, but it's new to me.
Suppose you have a lake, and you want to know if there are fish in the lake. You dig some worms, pick a spot, bait the hook, and wait. At the end of the day, if you have caught a fish, you have your answer: there are fish in the lake.[1]
But what if you don't catch a fish? Then you still don't know. Perhaps you used the wrong bait, or fished in the wrong spot. Perhaps you did everything right and the fish happened not to be biting that day. Or perhaps you did everything right except there are no fish in the lake.
But you can try again. Pick a different spot, try a different bait, and fish for another day. And if you catch a fish, you know the answer: the lake does contain fish. But if not, you can go fishing again tomorrow.
Suppose you go fishing every day for a month and you catch nothing. You still don't know why. But you have a pretty good idea: most likely, it is because there are no fish to catch. It could be that you have just been very unlucky, but that much bad luck is unlikely.
But perhaps you're not sure enough. You can keep fishing. If, after a year, you have not caught any fish, you can be almost certain that there were no fish in the lake at all. Because a year-long run of bad luck is extremely unlikely. But if you are still not convinced, you can keep on fishing. You will never be 100% certain, but if you keep at it long enough you can become 99.99999% certain with as many nines as you like.
That is a randomized algorithm, for finding out of there are fish in a lake! It might tell you definitively that there are, by producing a fish. Or it might fail, and then you still don't know. But as long as it keeps failing, the chance that there are any fish rapidly becomes very small, exponentially so, and can be made as small as you like.
For not-metaphorical examples, see:
The Miller-Rabin primality test: Given an odd number K, is K composite? If it is, the Miller-Rabin test will tell you so 75% of the time. If not, you can go fishing again the next day. After n trials, you are either !!100\%!! certain that K is composite, or !!100\%-\frac1{2^{2n}}!! certain that it is prime.
Frievalds’ algorithm: given three square matrices !!A, B, !! and !!C!!, is !!C!! the product !!A×B!!? Actually multiplying !!A×B!! could be slow. But if !!A×B!! is not equal to !!C!!, Frievald's algorithm will quickly tell you that it isn't—half the time. If not, you can go fishing again. After n trials, you are either !!100\%!! certain that !!C!! is not the correct product, or !!100\%-\frac1{2^n}!! certain that it is.
[1] Let us ignore mathematicians’ pettifoggery about lakes that contain exactly one fish. This is just a metaphor. If you are really concerned, you can catch-and-release.
[Other articles in category /CS] permanent link
Fri, 18 Jul 2014
On uninhabited types and inconsistent logics
Earlier this week I gave a talk about the Curry-Howard isomorphism. Talks never go quite the way you expect. The biggest sticking point was my assertion that there is no function with the type a → b. I mentioned this as a throwaway remark on slide 7, assuming that everyone would agree instantly, and then we got totally hung up on it for about twenty minutes.
Part of this was my surprise at discovering that most of the audience (members of the Philly Lambda functional programming group) was not familiar with the Haskell type system. I had assumed that most of the members of a functional programming interest group would be familiar with one of Haskell, ML, or Scala, all of which have the same basic type system. But this was not the case. (Many people are primarily interested in Scheme, for example.)
I think the main problem was that I did not make clear to the audience what Haskell means when it says that a function has type a → b. At the talk, and then later on Reddit people asked
what about a function that takes an integer and returns a string: doesn't it have type a → b?
If you know one of the HM languages, you know that of course it
doesn't; it has type Int → String, which is not the same at all. But I
wasn't prepared for this confusion and it took me a while to formulate
the answer. I think I underestimated the degree to which I have
internalized the behavior of Hindley-Milner type systems after twenty
years. Next time, I will be better prepared, and will say something
like the following:
A function which takes an integer and returns a string does not have
the type a → b; it has the type Int → String. You must pass it an
integer, and you may only use its return value in a place that makes
sense for a string. If f has this type, then 3 +
f 4 is a compile-time type error because Haskell knows that f
returns a string, and strings do not work with +.
But if f had
the type a → b, then 3 + f 4 would be legal, because context requires that
f return a number, and the type a → b says that it can return a
number, because a number is an instance of the completely general type
b. The type a → b, in contrast to Int → String, means that b
and a are completely unconstrained.
Say function f had type a → b. Then you would be able to use the
expression f x in any context that was expecting any sort of return
value; you could write any or all of:
3 + f x
head(f x)
"foo" ++ f x
True && f x
and they would all type check correctly, regardless of the type of x. In the first line, f x would return a number; in the second line f would return a list; in the third line it would return a string, and in the fourth line it would return a boolean. And in each case f could be able to do what was required regardless of the type of x, so without even looking at x. But how could you possibly write such a function f? You can't; it's impossible.
Contrast this with the identity function id, which has type a → a. This says that id always returns a value whose type is the same as
that if its argument. So you can write
3 + id x
as long as x has the right type for +, and you can write
head(id x)
as long as x has the
right type for head, and so on. But for f to have the type a → b, all those
would have to work regardless of the type of the argument to f. And
there is no way to write such an f.
Actually I wonder now if part of the problem is that we like to write a → b when what we really mean is the type ∀a.∀b.a → b. Perhaps making the quantifiers explicit would clear things up? I suppose it probably wouldn't have, at least in this case.
The issue is a bit complicated by the fact that the function
loop :: a -> b
loop x = loop x
does have the type a → b, and, in a language with exceptions, throw
has that type also; or consider Haskell
foo :: a -> b
foo x = undefined
Unfortunately, just as I thought I was getting across the explanation of why there can be no function with type a → b, someone brought up exceptions and I had to mutter and look at my shoes. (You can also take the view that these functions have type a → ⊥, but the logical principle ⊥ → b is unexceptionable.)
In fact, experienced practitioners will realize, the instant the type
a → b appears, that they have written a function that never returns.
Such an example was directly responsible for my own initial interest
in functional programming and type systems; I read a 1992 paper (“An
anecdote about ML type
inference”)
by Andrew R. Koenig in which he described writing a merge sort
function, whose type was reported (by the SML type inferencer) as [a]
-> [b], and the reason was that it had a bug that would cause it to
loop forever on any nonempty list. I came back from that conference
convinced that I must learn ML, and Higher-Order Perl was a direct
(although distant) outcome of that conviction.
Any discussion of the Curry-Howard isomorphism, using Haskell as an example, is somewhat fraught with trouble, because Haskell's type logic is utterly inconsistent. In addition to the examples above, in Haskell one can write
fix :: (a -> a) -> a
fix f = let x = fix f
in f x
and as a statement of logic, !!(a\to a)\to a!! is patently false. This might be an argument in favor of the Total Functional Programming suggested by D.A. Turner and others.
[Other articles in category /CS] permanent link
Mon, 14 Jul 2014
Types are theorems; programs are proofs
[ Summary: I gave a talk Monday night on the Curry-Howard isomorphism; my talk slides are online. ]
I sent several proposals to !!con, a conference of ten-minute talks. One of my proposals was to explain the Curry-Howard isomorphism in ten minutes, but the conference people didn't accept it. They said that they had had four or five proposals for talks about the Curry-Howard isomorphism, and didn't want to accept more than one of them.
The CHI talk they did accept turned out to be very different from the one I had wanted to give; it discussed the Coq theorem-proving system. I had wanted to talk about the basic correspondence between pair types, union types, and function types on the one hand, and reasoning about logical conjunctions, disjunctions, and implications on the other hand, and the !!con speaker didn't touch on this at all.
But mathematical logic and programming language types turn out to be the same! A type in a language like Haskell can be understood as a statement of logic, and the statement will be true if and only if there is actually a value with the corresponding type. Moreover, if you have a proof of the statement, you can convert the proof into a value of the corresponding type, or conversely if you have a value with a certain type you can convert it into a proof of the corresponding statement. The programming language features for constructing or using values with function types correspond exactly to the logical methods for proving or using statements with implications; similarly pair types correspond to logical conjunction, and union tpyes to logical disjunction, and exceptions to logical negation. I think this is incredible. I was amazed the first time I heard of it (Chuck Liang told me sometime around 1993) and I'm still amazed.
Happily Philly Lambda, a Philadelphia-area functional programming group, had recently come back to life, so I suggested that I give them a longer talk about about the Curry-Howard isomorphism, and they agreed.
I gave the talk yesterday, and the materials are online. I'm not sure how easy they will be to understand without my commentary, but it might be worth a try.
If you're interested and want to look into it in more detail, I suggest you check out Sørensen and Urzyczyn's Lectures on the Curry-Howard Isomorphism. It was published as an expensive yellow-cover book by Springer, but free copies of the draft are still available.
[Other articles in category /CS] permanent link
Mon, 03 Mar 2008
Uniquely-decodable codes revisited
[ This is a followup to an earlier article. ]
Alan Morgan wrote to ask if there was a difference between uniquely-decodable (UD) codes for strings and for streams. That is, is there a code for which every finite string is UD, but for which some infinite sequence of symbols has multiple decodings.
I pondered this a bit, and after a little guessing came up with an example: { "a", "ab", "bb" } is UD, because it is a suffix code. But the stream "abbbbbbbbbb..." can be decoded in two ways.
After I found the example, I realized that I shouldn't have needed to guess, because I already knew that you sometimes have to see the last symbol of a string before you can know how to decode it, and in such a code, if there is no such symbol, the decoding must be ambiguous. The code above is UD, but to decode "abbbbbbbbbbbbbbb" you have to count the "b"s to figure out whether the first code word is "a" or "ab".
Let's say that a code is UD+ if it has the property that no two infinite sequences of code words have the same concatenation. Can we characterize the UD+ codes? Clearly, UD+ implies UD, and the example above shows that the converse is not true. A simple argument shows that all prefix codes are UD+. So the question now is, are there UD+ codes that are not prefix codes? I don't know.
[ Addendum 20080303: Gareth McCaughan points out that { "a", "ab" } is UD+ but not prefix. ]
[Other articles in category /CS] permanent link
Wed, 27 Feb 2008
Uniquely-decodable codes
Ricardo J.B. Signes asked me a few days ago if there was a way to decide
whether a given set S of strings had the property that any two
distinct sequences of strings from S have distinct
concatenations.
For example, consider S1 = { "ab", "abba", "b" }. This set does not have the specified property, because you can take the two sequences [ "ab", "b", "ab" ] and [ "abba", "b" ], and both concatenate to "abbab". But S2 = { "a", "ab", "abb" } does have this property.
Coding theory
In coding theory, the property has the awful name "unique decodability". The idea is that you have some input symbols, and each input symbol is represented with one output symbol, which is one of the strings from S. Then suppose you receive some message like "abbab". Can you figure out what the original input was? For S2, yes: it must have been ZY. But for S1, no: it could have been either YZ or XZX.In coding theory, the strings are called "code words" and the set of strings is a "code". So the question is how to tell whether a code is uniquely-decodable. One obvious way to take a non-uniquely-decodable code and turn it into a uniquely-decodable code is to append delimiters to the code words. Consider S1 again. If we delimit the code words, it becomes { "(ab)", "(abba)", "(b)" }, and the two problem sequences are now distinguishable, since "(ab)(b)(ab)" looks nothing like "(abba)(b)". It should be clear that one doesn't need to delimit both ends; the important part is that the words are separated, so one could use { "ab-", "abba-", "b-" } instead, and the problem sequences translate to "ab-b-ab-" and "abba-b-". So every non-uniquely-decodable code corresponds to a uniquely-decodable code in at least this trivial way, and often the uniquely-decodable property is not that important in practice because you can guarantee uniquely-decodableness so easily just by sticking delimiters on the code words.
But if you don't want to transmit the extra delimiters, you can save bandwidth by making your code uniquely-decodable even without delimiters. The delimiters are a special case of a more general principle, which is that a prefix code is always uniquely-decodable. A prefix code is one where no code word is a prefix of another. Or, formally, there are no code words x and y such that x = ys for some nonempty s. Adding the delimiters to a code turns it into a prefix code. But not all prefix codes have delimiters. { "a", "ba", "bba", "bbba" } is an example, as are { "aa", "ab", "ba", "bb" } and { "a", "baa", "bab", "bb" }.
The proof of this is pretty simple: you have some concatenation of code words, say T. You can decode it as follows: Find the unique code word c such that c is a prefix of T; that is, such that T = cU. There must be such a c, because T is a concatenation of code words. And c must be unique, because if there were c' and U' with both cU = T and c'U' = T, then cU = c'U', and whichever of c or c' is shorter must be a prefix of the one that is longer, and that can't happen because this is a prefix code. So c is the first code word in T, and we can pull it off and repeat the process for U, getting a unique sequence of code words, unless U is empty, in which case we are done.
There is a straightforward correspondence between prefix codes and trees; the code words can be arranged at the leaves of a tree, and then to decode some concatenation T you can scan its symbols one at a time, walking the tree, until you get to a leaf, which tells you which code word you just saw. This is the basis of Huffman coding.
Prefix codes include, as a special case, codes where all the words are the same length. For those codes, the tree is balanced, and has all branches the same length.
But uniquely-decodable codes need not be prefix codes. Most obviously, a suffix code is uniquely-decodable and may not be a prefix code. For example, {"a", "aab", "bab", "bb" } is uniquely-decodable but is not a prefix code, because "a" is a prefix of "aab". The proof of uniquely-decodableness is obvious: this is just the last prefix code example from before, with all the code words reversed. If there were two sequences of words with the same concatenation, then the reversed sequences of reversed words would also have the same concatenation, and this would show that the code of the previous paragraph was not uniquely-decodable. But that was a prefix code, and so must be uniquely-decodable.
But codes can be uniquely-decodable without being either prefix or suffix codes. For example, { "aabb", "abb", "bb", "bbba" } is uniquely-decodable but is neither a prefix nor a suffix code. Rik wanted a method for deciding.
I told Rik about the prefix code stuff, which at least provides a sufficient condition for uniquely-decodableness, and then started poking around to see what else I could learn. Ahem, I mean, researching. I suppose that a book on elementary coding theory would have a discussion of the problem, but I didn't have one at hand, and all I could find online concerned prefix codes, which are of more practical interest because of the handy tree method for speedy decoding.
But after tinkering with it for a couple of days (and also making an utterly wrong intermediate guess that it was undecidable, based on a surface resemblance to the Post correspondence problem) I did eventually figure out an algorithm, which I wrote up and released on CPAN, my first CPAN post in about a year and a half.
An example
The idea is pretty simple, and I think best illustrated by an example, as so many things are. We will consider { "ab", "abba", "b" } again. We want to find two sequences of code words whose concatenations are the same. So say we want pX1 = qY1, where p and q are code words and X1 and Y1 are some longer strings. This can only happen if p and q are different lengths and if one is a prefix of the other, since otherwise the two strings pX1 and qY1 don't begin with the same symbols. So we consider just the cases where p is a prefix of q, which means that in this example we want to find "ab"X1 = "abba"Y1, or, equivalently, X1 = "ba"Y1.Now X1 must begin with "ba", so we need to either find a code word that begins with "ba", or we need to find a code word that is a prefix of "ba". The only choice is "b", so we have X1 = "b"X2, and so X1 = "b"X2 = "ba"Y1, or equivalently, X2 = "a"Y1.
Now X2 must begin with "a", so we need to either find a code word that begins with "a", or we need to find a code word that is a prefix of "a". This occurs for "abba" and "ab". So we now have two situations to investigate: "ab"X3 = "a"Y1, and "abba"X4 = "a"Y1. Or, equivalently, "b"X3 = Y1, and "bba"X4 = Y1.
The first of these, "b"X3 = Y1 wins immediately, because "b" is a code word: we can take X3 to be empty, and Y1 to be "b", and we have what we want:
| "ab" X1 | = | "abba" Y1 |
| "ab" "b" X2 | = | "abba" Y1 |
| "ab" "b" "ab" X3 | = | "abba" Y1 |
| "ab" "b" "ab" | = | "abba" "b" |
where the last line of the table is exactly the solution we seek.
Following the other one, "bba"X4 = Y1, fails, and in a rather interesting way. Y1 must begin with two "b" words, so put "bb"Y2 = Y1, so "bba"X4 = "bb"Y2, then "a"X4 = Y2.
But this last equation is essentially the same as the X2 = "a"Y1 situation we were investigating earlier; we are just trying to make two strings that are the same except that one has an extra "a" on the front. So this investigation tells us that if we could find two strings with "a"X = Y, we could make longer strings "abba"Y = "b" "b" "a"X. This may be interesting, but it does not help us find what we really want.
The algorithm
Having seen an example, here's the description of the algorithm. We will tabulate solutions to Xs = Y, where X and Y are sequences of code words, for various strings s. If s is empty, we win.We start the tabulation by looking for pairs of keywords c1 and c2 with c1 a prefix of c2, because then we have c1s = c2 for some s. We maintain a queue of s-values to investigate. At one point in our example, we had X1 = "ba"Y1; here s is "ba".
If s begins with a code word, then s = cs', so we can put s' on the queue. This is what happened when we went from X1 = "ba"Y1 to "b"X2 = "ba"Y1 to X2 = "a"Y1. Here s was "ba" and s' was "a".
If s is a prefix of some code word, say ss' = c, then we can also put s' on the queue. This is what happened when we went from X2 = "a"Y1 to "abba"X4 = "a"Y1 to "bba"X4 = Y1. Here s was "a" and s' was "bba".
If we encounter some queue item that we have seen before, we can discard it; this will prevent us from going in circles. If the next queue item is the empty string, we have proved that the code is not uniquely-decodable. (Alternatively, we can stop just before queueing the empty string.) If the queue is empty, we have investigated all possibilities and the code is uniquely-decodable.
Pseudocode
Here's the summary:
- Initialization:
For each pair of code words c1 and
c2 with c1s =
c2, put s in the queue.
- Main loop: Repeat the following until termination
- If the queue is empty, terminate. The code is uniquely-decodable.
- Otherwise:
- Take an item s from the queue.
- For each code word c:
- If c = s, terminate. The code is not uniquely-decodable.
- If cs' = s, and s' has not been seen before, queue s'.
- If c = ss', and s' has not been seen before, queue s'.
To this we can add a little bookkeeping so that the algorithm emits the two ambiguous sequences when the code is not uniquely-decodable. The implementation I wrote uses a hash to track which strings s have appeared in the queue already. Associated with each string s in the hash are two sequences of code words, P and Q, such that Ps = Q. When s begins with a code word, so that s = cs', the program adds s' to the hash with the two sequences [P, c] and Q. When s is a prefix of a code word, so that ss' = c, the program adds s' to the hash with the two sequences Q and [P, c]; the order of the sequences is reversed in order to maintain the Ps = Q property, which has become Qs' = Pss' = Pc in this case.
Notes
As I said, I suspect this is covered in every elementary coding theory text, but I couldn't find it online, so perhaps this writeup will help someone in the future.After solving this problem I meditated a little on my role in the programming community. The kind of job I did for Rik here is a familiar one to me. When I was in college, I was the math guy who hung out in the computer lab with the hackers. Periodically one of them would come to me with some math problem: "Crash, I am writing a ray tracer. If I have a ray and a triangle in three dimensions, how can I figure out if the ray intersects the triangle?" And then I would go off and figure out how to do that and come back with the algorithm, perhaps write some code, or perhaps provide some instruction in matrix computations or whatever was needed. In physics class, I partnered with Jim Kasprzak, a physics major, and we did all the homework together. We would read the problem, which would be some physics thing I had no idea how to solve. But Jim understood physics, and could turn the problem from physics into some mathematics thing that he had no idea how to solve. Then I would do the mathematics, and Jim would turn my solution back into physics. I wish I could make a living doing this.
Puzzle: Is { "ab", "baab", "babb", "bbb", "bbba" } uniquely-decodable? If not, find a pair of sequences that concatenate to the same string.
Research question: What's the worst-case running time of the algorithm? The queue items are all strings that are strictly shorter than the longest code word, so if this has length n, then the main loop of the algorithm runs at most (an-1) / (a-1) times, where a is the number of symbols in the alphabet. But can this worst case really occur, or is the real worst case much faster? In practice the algorithm always seems to complete very quickly.
Project to do: Reimplement in Haskell. Compare with Perl implementation. Meditate on how they can suck in such completely different ways.
[ There is a brief followup to this article. ]
[ Addendum 20170318: Marius Buzea has brought to my attention that this is exactly the Sardinas-Patterson Algorithm. The Wikipedia article claims that the worst-case running time is !!O(nk)!! where !!k!! is the number of code words and !!n!! is their total length. ]
[Other articles in category /CS] permanent link
Fri, 05 Jan 2007
Messages from the future
I read a pretty dumb article today about passwords that your future
self could use when communicating with you backwards in time, to
authenticate his identity to you. The idea was that you should make
up a password now and commit it to memory so that you can use it later
in case you need to communicate backwards in time.
This is completely unnecessary. You can wait until you have evidence of messages from the future before you do this.
Here's what you should do. If someone contacts you, claiming to be your future self, have them send you a copy of some document—the Declaration of Independence, for example, or just a letter of introduction from themselves to you, but really it doesn't need to be more than about a hundred characters long—encrypted with a one-time pad. The message, being encrypted, will appear to be complete gibberish.
Then pull a coin out of your pocket and start flipping it. Use the coin flips as the one-time pad to decrypt the message; record the pad as you obtain it from the coin.
Don't do the decryption all at once. Use several coins, in several different places, over a period of several weeks.
Don't even use coins. Say to yourself one day, on a whim, "I think I'll decrypt the next bit of the message by looking out the window and counting red cars that go by. If an odd number of red cars go by in the next minute, I'll take that as a head, and if an even number of red cars go by, I'll take that as a tail." Go to the museum and use their Geiger counter for the next few bits. Use the stock market listings for a few of the bits, and the results of the World Series for a couple.
If the message is not actually from your future self, the coin flips and other random bits you generate will not decrypt it, and you will get complete gibberish.
But if the coin flips and other random bits miraculously turn out to decrypt the message perfectly, you can be quite sure that you are dealing with a person from the future, because nobody else could possibly have predicted the random bits.
Now you need to make sure the person from the future is really you. Make up a secret password. Encrypt the one-time pad with a conventional secret-key method, using your secret password as the key. Save the encrypted pad in several safe places, so that you can get it later when you need it, and commit the password to memory. Destroy the unencrypted version of the pad. (Or just memorize the pad. It's not as hard as you think.)
Later, when the time comes to send a message into the past, go get the pad from wherever you stashed it and decrypt it with the secret key you committed to memory. This gives you a complete record of the results of the coin flips and other events that the past-you used to decrypt your message. You can then prepare your encrypted message accordingly.
[Other articles in category /CS] permanent link
Thu, 06 Jul 2006
Contravariant types
I just had a slightly frustrating discussion with some colleagues,
involving a small matter of object-oriented design. I don't want to
get into the details of the problem here, except to say that it
involved a class A and its derived class B; I was
asking for advice about the design of a "demote" method that would
take a B object and turn it into an A object.
The frustrating part was that about half of the people in the conversation were confused by my use of the word "demotion" and about whether A was inheriting from B or vice versa. I had intended for B to inherit from A. The demotion, as I said, takes a B object and gives you back an equivalent but stripped-down A object.
To me, this makes perfect sense, logically and terminologically. Demotion implies movement downward. Downward is toward the base class; that's why it's the "base" class. A is the base class here, so the demotion operation takes a B and gives you back an A.
Or, to make the issue clearer with an example, suppose that the two classes are Soldier and General. Which inherits from the other? Obviously, General inherits from Soldier, and not vice-versa. Soldiers support methods for marching, sleeping, and eating. Generals inherit all these methods, and support additional methods for ordering attacks and for convening courts martial. What does a demotion method do? It turns a General into a Soldier. It turns an object of the derived class into an object of the base class.
So how could people get this mixed up? I'm not sure, but I think one possibility is that they were thinking of subclasses and superclasses. The demotion method takes an object in the subclass and returns an object in the superclass. The terminology here is backwards. There are lots and lots of people, me included, who never use the terms "subclass" and "superclass", for precisely this reason. Even if my colleagues weren't thinking of these terms, they were probably thinking of the conventional class inheritance diagram, in which the base class, contrary to its name, is at the top of the diagram, with the derived classes hanging under it. The demotion operation, in this picture, pushes an object upwards, toward the base class.
The problem with "subclass" and "superclass" runs deeper. Mathematical terminology for sets is well-established and intuitive: A is a "subset" of B if set A is entirely contained in set B, if every element of A is an element of B. For example, the set of generals is a subset of the set of soldiers. The converse relation is that B is a superset of A: the set of soldiers is a superset of the set of generals. We expect from the names that a subset will be a smaller set than its superset, and so it is. There are fewer generals than soldiers.
Now let's consider programming language types. A type can be considered to be just a set of values. For example, the int type is the set of all integer values. The real type is the set of all real number values. Since every integer is also a real number, we might say that the int type is a subset of the real type. In fact, the word we usually use is that int is a subtype of real. But "subtype" means no more and no less than "subset".
Now let's consider the types General and Soldier of all objects of classes General and Soldier respectively. Clearly, General is a subtype of Soldier, since every General is a Soldier. This matches the OOP terminology also: General is a subclass of Soldier.
The confusing thing for data types, I think, is that there are two ways in which a type can be a "subtype" of another. A could be a smaller set than B, in which case we use the words "subtype" and "subclass", in accordance with mathematical convention. But A could also support a smaller set of operations than B; in OOP-world we would say that A is a base class and B a derived class. But then B is a subclass of A, which runs counter to the terminological implication that A is at the "base".
(It's tempting to add a long digression here about how computer scientists always draw their trees with the root at the top and the leaves at the bottom, and then talk about how many nodes are under the root of the tree. I will try to restrain myself.)
Anyway, this contravariance is what I really wanted to get at. If we adopt the rule of thumb that most values support few operations, and a few values support some additional operations, then the containment relation for functionality is contravariant to the containment relation for sets. Large sets, like Soldier, support few operations, such as eat and march; smaller sets support more operations, such as convene_court_martial.
The thing that struck me about this is that functions themselves are contravariant. Suppose A and B are types. Now consider the type A×B of pairs of values where the first component is an A and the second is a B. This pairing operation is covariant in A and B. By this I mean that if A' is a subtype of A, then A'×B is a subtype of A×B. Similarly, if B' is a subtype of B, then A×B' is a subtype of A×B.
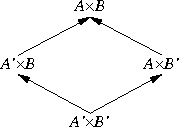
| 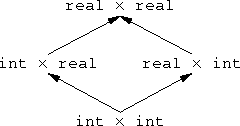 |
Similarly, +, the type sum operation, is also covariant in both of its arguments.
But function types are different. Suppose A → B is the type of functions whose arguments have type A and whose return values are type B. Then A → B' is a subtype of A → B. Here's a simple example: Let A and B be real, and let A' and B' be int. Then every int → int—that is, every function from integers to integers—is also an example of a int → real; it can be considered as a function that takes an int and returns a real. That's because it is actually returning an int, and an int is a kind of real.
But A' → B is not a subtype of A → B. Just the opposite: A → B is a subtype of A' → B.
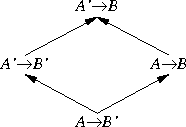
| 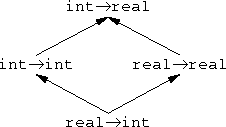 |
I remember standing on a train platform around 1992 and realizing this for the first time, that containment of function types was covariant in the second component but contravariant in the first component. I was quite surprised.
I suspect that the use of "covariant" and "contravariant" here suggests some connection with category theory, and with the notions of covariant and contravariant functors, but I don't know what the connection is.
[Other articles in category /CS] permanent link
Sun, 05 Mar 2006
My favorite NP-complete problem
At last
year's open source conference, I gave a talk about fundamental
problems of computer science. I talked about undecidable problems
and NP-complete problems, and some other stuff. It was only a
45-minute talk, but I worked hard to make it as accessible as I
could.
For the NP-completeness section, I discussed the knapsack problem. In this problem, you have a bunch of items you can take on a trip, each of which has a value and a size. Your luggage is of limited size, so the total size of the items you take on the trip must not exceed this limit. Subject to this constraint, you want to take the items whose total value is as large as possible. (Actually, in the talk, I used the decision problem version of this, rather than the optimization problem version, to avoid sticky questions from the know-it-alls in the audience.)
Knapsack is a pretty good example problem. It's simple, easy to understand, and reasonably easy to see why it might be interesting. But after I gave the talk, I thought of a much better example. I deeply regret that I didn't come up with it in time to put it in the talk. Fortunately, I now have a blog. Read on; here's the coolest NP-complete problem ever.
Each episode of Sesame Street now ends with a fifteen-minute segment called Elmo's World, featuring Elmo, a small red monster. Elmo is extremely popular, and the segments have been released on videotape and DVD. Each of these segments has a topic of interest to toddlers, such as:
| Babies | Dancing | Food |
| Bananas | Dogs | Games |
| Baths | Drawing | Hair |
| Bicycles | Ears | Hands |
| Birds | Exercise | |
| Birthdays | Families | Music |
| Books | Farms | Plants |
| Bugs | Feet | Singing |
| Cats | Firefighters | Water |

 When the segments are released
on video, they are bundled in groups of three. Usually, the three
segments will have a common theme. For example, the video Wake
Up With Elmo! (left) gathers together the three segments about
"sleep", "getting dressed", and "tooth brushing". Another video
(right) collects the segments about "food", "water", and
"exercise".
When the segments are released
on video, they are bundled in groups of three. Usually, the three
segments will have a common theme. For example, the video Wake
Up With Elmo! (left) gathers together the three segments about
"sleep", "getting dressed", and "tooth brushing". Another video
(right) collects the segments about "food", "water", and
"exercise".
Your job is to plan the video releases. Sesame Workshop gives you a list of which sets of three segments are considered to be thematically related. Your job is to select items from this list that exhaust the available segments, without using any segment more than once.
Each segment might be part of several different thematically-related groups. For example, the "dancing" segment could be released on a physical-activity-themed video, along with the "bicycle" and "exercise" segments, or it could be released on a party-themed video, along with the "birthday" and "games" segments. If you choose to release the physical activity collection, you foreclose the possibility of releasing the party collection, and you will have to find something else to do with the "birthday" and "games" segments.
This problem is NP-complete. The official computer science jargon name for it is exact cover by 3-sets, or just X3C.
 The Sesame Workshop people were not able to solve the
problem. One of the videos in the series is about flowers, bananas,
and hair.
The Sesame Workshop people were not able to solve the
problem. One of the videos in the series is about flowers, bananas,
and hair.
[ Addendum 20160515: I turned this into a talk for !!Con 2016. Talk materials are on my web site. ]
[Other articles in category /CS] permanent link
Wed, 08 Feb 2006
Generating strings of balanced parentheses
About a year and a half ago, the Perl Quiz of the Week question was to
write a program which, given an argument n, printed out all the
strings containing n balanced pairs of parentheses. For
example, if the argument was 3, the output was to contain the
lines:
()()()
(())()
(()())
()(())
((()))
in some order.Enumerating parentheses is important because the parentheses obviously correspond to all the forms that an infix expression can take, so any attempt to enumerate all possible expressions of some form can be built atop a parenthesis-enumerator. But also, there's a straightforward correspondence between parentheses and tree structures, so by enumerating parentheses you are also enumerating all possible tree structures.
There were quite a few correct solutions posted to the list, and also some wrong ones. The commonest mistake to make was to assume that any string of n+1 pairs of balanced parentheses must have the form S(), ()S, or (S), where S is a string of n pairs of balanced parentheses. But this isn't so; (())(()) doesn't have this form. The commonest strategy that worked correctly was to generate all the strings of the right length of the form (S)S, where S is a shorter balanced string. This can be done recursively as follows:
sub parens {
my ($N) = @_;
return ("") if $N == 0;
my @result;
for my $i (0 .. $N-1) {
for $a (parens($i)) {
for $b (parens($N-$i-1)) {
push @result, "($a)$b";
}
}
}
return @result;
}
print join "\n", parens(shift()), "";
Or you can organize the logic differently:
sub parens {
my $N = shift;
$pattern = @_ ? shift : "S";
if ($N == 0) {
$pattern =~ tr/S//d;
return $pattern;
}
return unless $pattern =~ /S/;
my $new_pattern_a = my $new_pattern_b = $pattern;
$new_pattern_a =~ s/S/S(S)/;
$new_pattern_b =~ s/S//;
return parens($N-1, $new_pattern_a), parens($N, $new_pattern_b);
}
print join "\n", parens(shift()), "";
A somewhat different approach was to build up the string from left to
right. Here $s tracks the string built so far, $N
counts the number of )'s that are still required, and
$unclosed counts the number of ('s that have been
added without a corresponding ). The function may append a
( to the string, increasing the number of unclosed open
parentheses, if there are fewer than $N such unclosed pairs
total, and it may append a ), decreasing both the number of
required close parentheses and the number of unmatched open
parentheses, as long as at least one open parenthesis remains
unclosed.
sub parens {
my ($N, $unclosed, $s) = @_;
$unclosed ||= 0;
$s ||= "";
return $s if $N == 0;
my @result;
push @result, parens($N, $unclosed+1, "$s(") if $unclosed < $N;
push @result, parens($N-1, $unclosed-1, "$s)") if $unclosed > 0 ;
return @result;
}
print join "\n", parens(shift()), "";
I had originally planned to do something like the first of these. But
a couple of days of intermittent tinkering revealed a completely
different and unexpected algorithm:
#!/usr/bin/perl -l
print $_ = "()" x shift();
print while s{^ ( \(+ ) ( \)+ ) \( }
{"()" x (length($2) - 1)
. "(" x (length($1) - length($2) + 2)
. ")"
}xe;
This is understandably mystifying, since in tidying it up (and getting
it to run as fast as possible) I also erased all the clues as to how I
got here to begin with. Folks on the mailing list asked how I came up
with this. What follows is a somewhat edited version of my reply. I
said at the time:
I can explain how I thought it up, although I'm not sure whether the explanation will be helpful or whether it will sound like "I just counted the legs and divided by four."By this I meant that the explanation might leave people even more mystified than the algorithm itself. I'm still not sure it won't sound like that, so I'm going to include the following one-paragraph summary that omits the details:
One of the other list members suggested an alternative representation for the strings that seemed promising, so I tried out some examples. Close examination of those examples reminded me of a technique I had used to solve some other problems, so I tried to apply it in this case with the necesary variations. It worked well enough to continue the investigation, but the alternative representation was getting in the way. So I took what I had learned from applying the technique to the alternative representation and tried to write an algorithm to do the same thing directly to the strings of parentheses. Then I optimized the result for speed and code compactness.The details follow.
I had originally planned to write a recursive solution, but before I started I thought it would be smart to investigate alternative representations. (Someday I'm going to write a long essay about this. I mentioned to Kurt Starsinic last week that the one sure sign of a program written by a novice programmer is that it will represent the data internally in the same format in which it needs to be output, typically as strings.)
One of the representations I looked at was one that had earlier been mentioned by Roger Burton West on the list. In this representation, a string of one "(" followed by n ")"'s becomes the number n, thus:
()()()() 1111
()()(()) 1102
()(())() 1021
()(()()) 1012
()((())) 1003
(())()() 0211
(())(()) 0202
(()())() 0121
(()()()) 0112
(()(())) 0103
((()))() 0031
((())()) 0022
((()())) 0013
(((()))) 0004
Now if you look at the right-hand column, and at the way the numbers,
change, it will seem awfully familiar. Or at least, it felt familiar
to me. It reminded me very strongly of a counting process. The essence of a counting process is that you find the rightmost column that has a certain property, and then you do a little transformation on it so that it gets a little less of that property and the columns to the right get reset to have more of it.
I realize that if you've never thought of it that way that is going to sound totally bizarre, so here's an example. Let's count base-10 numerals. The magic property in this case is the property of being less than 9. 0 has the largest possible amount of this property, since it is as much less than 9 as any digit can be. 8 has very little of this property, since it is just a little less than 9. 9 itself does not have any of this property, since it is not less than 9.
When you count, you find the rightmost column that is less than 9 and then you do a little transformation on it so that it has a little less of that property, so that it a little closer to 9:
387
388
389
After you have done that a few times, you get to a point where the
rightmost column's less-than-9-ness has been entirely depleted and you
can't change it any more. So you move to the next column to the left
and deplete that one instead, and you reset the rightmost column so
that it is full of less-than-9-ness again:
390
Then you continue:
391
392
...
399
and now you have to deplete the less-than-9-ness of the third column,
and reset the two to its right:
400
This may be a weird way to look at counting, but it describes all
sorts of useful processes. To count in base 2, you allow the columns
to hold 0's and 1's, and the property of interest is the property of
being a 0; you find the rightmost column that is a 0, and change it to
a 1, and change the columns to its right back to 0's.Probably the next simplest example is when the property of interest is that the n'th column contains a number less than or equal to n:
0000
0010
0100
0110
0200
0210
1000
1010
1100
1110
1200
1210
2000
2010
...
3210
This turns out to be useful if you are trying to
enumerate permutations; I wrote about it on pages 128–135 of
Higher-Order Perl, where I called it the "odometer
method". It's used again in the following section to enumerate DNA
sequences. So it's a pretty fundamental technique, and turns out to
be useful in a wide variety of settings.Another example I was already familiar with is like the base-2 counting example, but with the added restriction that you are not allowed to have two adjacent 1's:
0000000
0000001
0000010
0000100
0000101
0001000
0001001
0001010
0010000
0010001
0010010
0010100
0010101
0100000
...
We can generate these strings by repeatedly doing this:
s/00((10)*1?)$/"01" . "0" x length $1/e;
(This pattern has close relations to the Fibonacci sequence. For
example, the nth string contains a single 1 exactly
when n is a Fibonacci number. Moreover, every positive integer
has a unique representation as a sum of distinct nonconsecutive
Fibonacci numbers, the so-called "Zeckendorff representation", and
this counting thing tells you what it is. This is analogous to the
way that every positive integer has a unique representation as a sum
of distinct powers of 2, and the binary expansion tells you what it
is.)So anyway, I was already familiar with this idea, and when I saw the parenthesis numbers, it reminded me strongly of one of these counting processes. Here they are again:
1111
1102
1021
1012
1003
0211
0202
0121
0112
0103
0031
0022
0013
0004
Here the rule seems to be that you always decrement the rightmost
nonzero digit that isn't in the last column and increment the
following digit—I imagine that the digits are little heaps of
1's, and you are allowed to transfer a 1 from its
heap to the heap on its right. But there are some additional
constraints.Since a number n here represents the string ()))...), with n close parentheses, we have the constraints that the leftmost column may not exceed 1; the sum of the two leftmost columns may not exceed 2, and so on. Under these constraints, 1111 is clearly an extreme case, and no string has the 1's any farther to the left. To go from 1111 to 1102, the rightmost moveable 1, which is in the third column, moves to the right, into the fourth column, which I now imagine contains a heap of two 1's.
Now the rightmost 1 is in the second column. So I reset the columns to the right of that (getting back 1111) and then move the 1 from the second to the third column, yielding 1021. Again, I imagine that the 2 here represents a heap of two 1's. These 1's can move to the right, yielding 1012 and then 1003.
Now I'll need to move the 1 from the first to the second column, so I reset the columns to the right of that (getting back 1111 again) and move the 1 from the first to the second column, yielding 0211. Then the 1 in the third column moves, yielding 0202, and then I reset the third and fourth columns back to 0211 so that I can move a 1 from the second to the third column, yielding 0121.
My first cut at implementing this actually manipulated these digit strings directly, like this:
output while s/([1-9])(0*)([1-9])$/($1-1).($3-length($2)+1).1x length($2)/e;
As a result, it wouldn't work for n > 9. But after I
thought about it some more, I realized I didn't need to deal with the
digit strings; I could directly manipulate the parentheses in the
corresponding way. This was faster, simpler, and got rid of the
n < 10 restriction.Translated back into parentheses, the algorithm might even be simpler to understand. The property we are trying to reduce is appearances of )(, in which ( appears to the right of ). In ()()()...(), the open parentheses are as far to the right as they can be, so this represents the maximal configuration. At each step, we're going to find the rightmost moveable open parenthesis, and we're going to move it one step to the left. That is, we're going to find the rightmost )( and change it to (). If there are other parentheses to the right of the ones that moved, we'll reset them into their minimal configuration. In what follows, the )( that just changed to () is in red, and the parentheses to its right that were reset are in blue. The )( that is about to change to () in the next step is in boldface.
In the initial configuration, the rightmost )( is in positions 6-7:
()()()() 1111
We replace it with ():
()()(()) 1102
Now the rightmost )( is in positions 4 and 5. We replace it
with () and reset the following
parentheses to the minimal configuration:
()(())() 1021
The rightmost )( is on the right again, so we get:
()(()()) 1012
Now the rightmost )( is at positions 5 and 6, so the string
changes to:
()((())) 1003
Now the only )( is far to the left, at positions 2–3, so
when we change it, we need to reset the parentheses to its right:
(())()() 0211
And it continues in the same way:
(())(()) 0202
(()())() 0121
(()()()) 0112
(()(())) 0103
((()))() 0031
((())()) 0022
((()())) 0013
(((()))) 0004
After I had implemented that, I realized there was nothing stopping me
from writing all the strings backward, and doing the substitutions at
the left end of the string instead of at the right end. This is
always much cheaper in perl's regex engine because it doesn't have to
guess where to start matching in the target string. So I reversed the
whole thing. It no longer produced the parentheses in lexicographic
order (unless you read right to left) but it was substantially
faster. Another solution to the problem is "consult Knuth". Volume IV of The Art of Computer Programming will contain an entire section devoted to this problem, and includes the algorithm I described. Volume IV isn't published yet, but the relevant section is. As of this writing, it is also still available from Knuth's web site.
[Other articles in category /CS] permanent link
Fri, 28 Oct 2005 I am now reading A Digit of the Moon, which is an 1898 translation of a Sanskrit manuscript of unknown age. The story concerns a king who falls madly in love with the beautiful and wise princess Anangaraga. The custom of the princess is to marry only the one who can ask her a question she cannot answer; if a suitor fails twenty-one times, he becomes her slave for life.The king's friend propounds nineteen questions, all of which the wise and clever princess answers without difficulty. On the morning of the twentieth day, the king, after praying to the goddess Saraswarti for help, is inspired with the solution: he will ask the princess to solve his own difficulty, and to tell him what question he should ask her. "And if she tells me, then I will ask her tomorrow what she tells me to-day: and if she does not tell me, then she is mine according to the terms of the agreement, to-day: and so in either alternative, the bird is caged."
[Addendum: Despite the many notes in the text on translation details, untranslatable puns, and so forth, the author, F.W. Bain, probably wrote it himself, rather than translating it from an unknown manuscript as he claimed.]
[Other articles in category /CS] permanent link



