Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Mon, 08 Nov 2010
Semi-boneless ham
The Math Project on Wikipedia is having a discussion about whether or
not to have an article about the jargon term "semi-infinite", which I
have long considered one of my favorite jargon terms, because it
sounds so strange, but makes so much sense. A structure is
semi-infinite when it is infinite in one direction but not in the
other. For example, the set of positive integers is semi-infinite,
since it possesses a least element (1) but no greatest element.
Similarly rays in geometry are semi-infinite.
The term is informal, however, and it's not clear just what it should mean in all cases. For example, consider the set S of 1/n for every positive integer n. Is this set semi-infinite? It is bounded in both directions, since it is contained in [0, 1]. But as you move left through the set, you ancounter an infinite number of elements, so it ought to be semi-infinite in the same sense that S ∪ { 1-x : x ∈ S } is fully-infinite. Whatever sense that is.
Informal and ill-defined it may be, but the term is widely used; one can easily find mentions in the literature of semi-infinite paths, semi-infinite strips, semi-infinite intervals, semi-infinite cylinders, and even semi-infinite reservoirs and conductors.
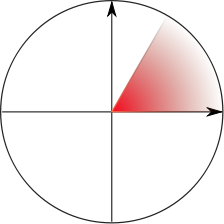
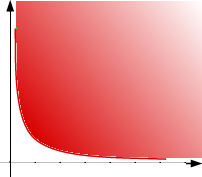 The term has spawned an
offshoot, the even stranger-sounding "quarter-infinite". This seems
to refer to a geometric object that is unbounded in the same way that
a quarter-plane is unbounded, where "in the same way" is left rather
vague. Consider the set (depicted at left) of all points of the plane
for which 0 ≤ |y/x| ≤ √3, for example; is
this set quarter-infinite, or only 1/6-infinite? Is the set of points
(depicted at right) with xy > 1 and x, y >
0 quarter-infinite? I wouldn't want to say. But the canonical
example is simple: the product of two semi-infinite intervals is a
quarter-infinite set.
The term has spawned an
offshoot, the even stranger-sounding "quarter-infinite". This seems
to refer to a geometric object that is unbounded in the same way that
a quarter-plane is unbounded, where "in the same way" is left rather
vague. Consider the set (depicted at left) of all points of the plane
for which 0 ≤ |y/x| ≤ √3, for example; is
this set quarter-infinite, or only 1/6-infinite? Is the set of points
(depicted at right) with xy > 1 and x, y >
0 quarter-infinite? I wouldn't want to say. But the canonical
example is simple: the product of two semi-infinite intervals is a
quarter-infinite set.
I was going to say that I had never seen an instance of the obvious next step, the eighth-infinite solid, but in researching this article I did run into a few. I can't say it trips off the tongue, however. And if we admit that a half of a quarter-infinite plane segment is also eighth-infinite, we could be getting ourselves into trouble.
(This all reminds me of the complaint of J.H. Conway of the increasing use of the term "biunique". Conway sarcastically asked if he should expect to see "triunique" and soforth, culminating in the idiotic "polyunique".)
Sometimes "semi" really does mean exactly one-half, as in "semimajor axis" (the longest segment from the center of an ellipse to its boundary), "semicubic parabola" (determined by an equation with a term kx3/2), or "semiperimeter" (half the perimeter of a triangle). But just as often, "semi" is one of the dazzling supply of mathematical pejoratives. ("Abnormal, irregular, improper, degenerate, inadmissible, and otherwise undesirable", says Kelley's General Topology.) A semigroup, for example, is not half of a group, but rather an algebraic structure that possesses less structure than a group. Similarly, one has semiregular polyhedra and semidirect products.
I was planning to end with a note that mathematics has so far avoided the "demisemi-" prefix. But alas! Google found this 1971 paper on Demi-semi-primal algebras and Mal'cev-type conditions.
[Other articles in category /math] permanent link


