Mark Dominus (陶敏修)
mjd@pobox.com

Archive:
| 2024: | JFMA |
| 2023: | JFMAMJ |
| JASOND | |
| 2022: | JFMAMJ |
| JASOND | |
| 2021: | JFMAMJ |
| JASOND | |
| 2020: | JFMAMJ |
| JASOND | |
| 2019: | JFMAMJ |
| JASOND | |
| 2018: | JFMAMJ |
| JASOND | |
| 2017: | JFMAMJ |
| JASOND | |
| 2016: | JFMAMJ |
| JASOND | |
| 2015: | JFMAMJ |
| JASOND | |
| 2014: | JFMAMJ |
| JASOND | |
| 2013: | JFMAMJ |
| JASOND | |
| 2012: | JFMAMJ |
| JASOND | |
| 2011: | JFMAMJ |
| JASOND | |
| 2010: | JFMAMJ |
| JASOND | |
| 2009: | JFMAMJ |
| JASOND | |
| 2008: | JFMAMJ |
| JASOND | |
| 2007: | JFMAMJ |
| JASOND | |
| 2006: | JFMAMJ |
| JASOND | |
| 2005: | OND |
Subtopics:
| Mathematics | 238 |
| Programming | 99 |
| Language | 92 |
| Miscellaneous | 67 |
| Book | 49 |
| Tech | 48 |
| Etymology | 34 |
| Haskell | 33 |
| Oops | 30 |
| Unix | 27 |
| Cosmic Call | 25 |
| Math SE | 23 |
| Physics | 21 |
| Law | 21 |
| Perl | 17 |
| Biology | 15 |
Comments disabled
Wed, 04 Jan 2012
Mental astronomical calculations
As you can see from the following graph, the daylight length starts
increasing after the winter solstice (last week) but it does so quite
slowly at first, picking up speed, and reaching a maximum rate of
increase at the vernal equinox.
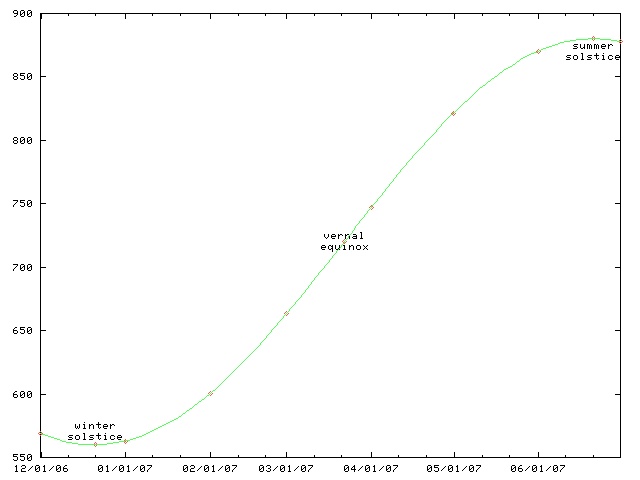
The day length is given by a sinusoid with amplitude that depends on your latitude (and also on the axial tilt of the Earth, which is a constant that we can disregard for this problem.) That is, it is a function of the form a + k sin 2πt/p, where a is the average day length (12 hours), k is the amplitude, p is the period, which is exactly one year, and t is amount of time since the vernal equinox. For Philadelphia, where I live, k is pretty close to 3 hours because the shortest day is about 3 hours shorter than average, and the longest day is about 3 hours longer than average. So we have:
day length = 12 hours + 3 hours · sin(2πt / 1 year)Now let's compute the rate of change on the equinox. The derivative of the day length function is:
rate of change = 3h · (2π / 1y) · cos(2πt / 1y)At the vernal equinox, t=0, and cos(…) = 1, so we have simply:
rate of change = 6πh / 1 year = 18.9 h / 365.25 daysThe numerator and the denominator match pretty well. If you're in a hurry, you might say "Well, 360 = 18·20, so 365.25 / 18.9 is probably about 20," and you would be right. If you're in slightly less of a hurry, you might say "Well, 361 = 192, so 365.25 / 18.9 is pretty close to 19, maybe around 19.2." Then you'd be even righter.
So the change in day length around the equinox (in Philadelphia) is around 1/20 or 1/19 of an hour per day—three minutes, in other words.
The exact answer, which I just looked up, is 2m38s. Not too bad. Most of the error came from my estimation of k as 3h. I guessed that the sun had been going down around 4:30, as indeed it had—it had been going down around 4:40, so the correct value is not 3h but only 2h40m. Had I used the correct k, my final result would have been within a couple of seconds of the right answer.
Exercise: The full moon appears about the same size as a U.S. quarter (1 inch diameter circle) held nine feet away (!) and also the same size as the sun, as demonstrated by solar eclipses. The moon is a quarter million miles away and the sun is 93 million miles away. What is the actual diameter of the sun?
[ Addendum 20120104: An earlier version of this article falsely claimed that the full moon appears the same size as a quarter held at arm's length. This was a momentary brain fart, not a calculational error. Thanks to Eric Roode for pointing out this mistake. ]
[Other articles in category /calendar] permanent link


